偶発的に起きるイベント間隔を表現する分布で指数分布を学びましたが、指数分布はよく使われますが欠点があります。
どのような欠点ですか?
指数関数はイベントが偶発的に起こる(故障率が一定)仮定で用いますが世の中には故障率が一定となる事柄は少ないです。
故障率が減少関数の場合と故障率が増加関数の場合は、それぞれ製品の初期不良、そして人の寿命を例にすると現実的ですね。
故障率が(時間とともに)減少していくものをDFR(Decreasing Failure Rate)といい、故障率が(時間とともに)増加していくものをIFR(Increasing Failure Rate)といいます。故障率が一定な分布を指数分布といいます。『現代数理統計学の基礎』を参照。
ワイブル分布は故障率についての微分方程式を解いて導かれる
故障率を指数関数で表現することでDFRやIFRを統一的に表現することができます。そのため故障率(=ハザード関数)を指数関数に当てはめて考えていきます。
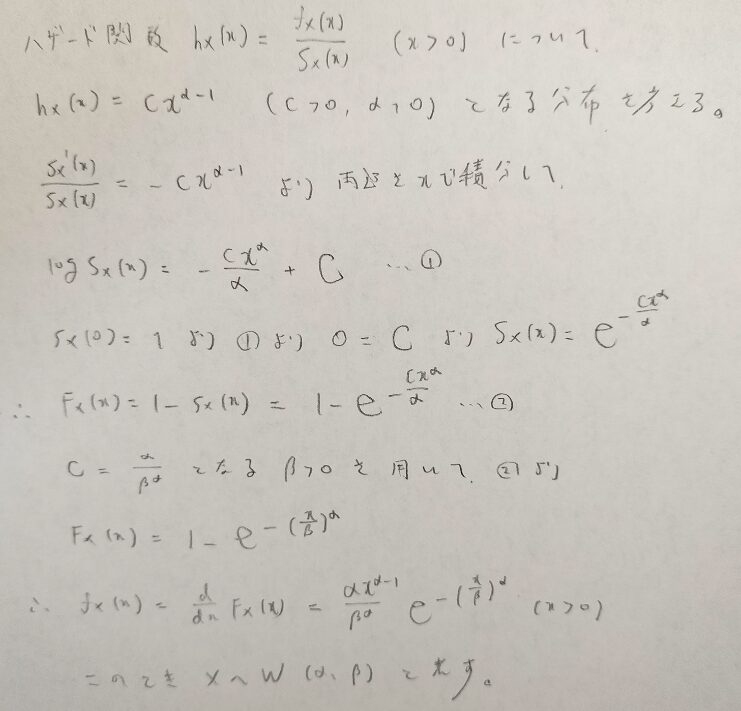
ワイブル分布の第1パラメータαをワイブル分布係数(階乗母数)、第2パラメータβをスケールパラメータ(尺度母数)といいます。
ワイブル分布の確率密度関数は本によってパラメータの取り方が異なるため多少の違いがありますのでご注意ください。今回は『リスクを知るための確率・統計入門』をベースに理論を構築しています。
αがワイブル係数というくらいなので、αにいろんな値を入れたいと思います。故障率(ハザード関数)の形が指数関数なので、αが1以上のときに故障率は単調増加なのでIFR、αが1以下のときに故障率は減少関数なのでDFRになりますね!
αが1のときは指数分布になります。指数分布のパラメータはワイブル分布の第2パラメータβについての逆数になるのでご注意ください。
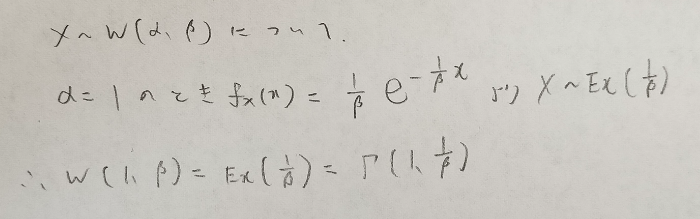
ワイブル分布の全確率と期待値と分散とk次モーメントの計算
ワイブル分布のさまざまな性質を証明する際には置換積分を行なってガンマ関数に帰着させる流れが重要になります。
ワイブル分布は確率分布なので全確率1を満たすはずです。全確率1を証明しましょう。
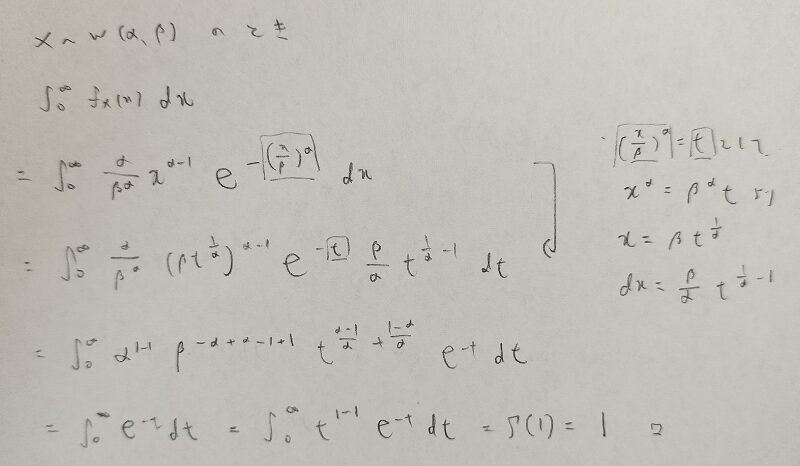
この置換積分はガンマ関数を狙った置換ですね。
その通りです。この式変形の最後の行の数式がベースとなって、期待値や分散の計算が行われます。
確かにそうですね。xなどを掛けるだけですからね。
ワイブル分布の期待値と分散を計算します。まずは期待値からです。
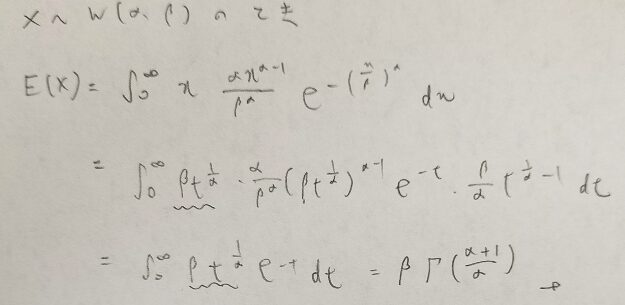
期待値の結果はガンマ関数を用いて良いのですね!
そうです!あとで紹介するレイリー分布もワイブル分布の特例なのですが、レイリー分布の期待値などもガンマ関数を用いて表現します。
次はワイブル分布の分散を計算します。
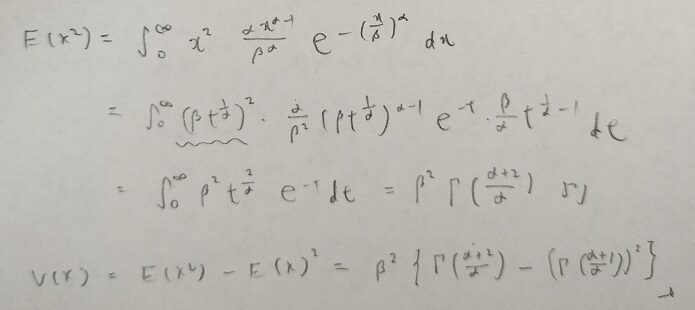
本当に分散はそのまんまの式ですね!笑
最後にワイブル分布のk次モーメントを求めます。
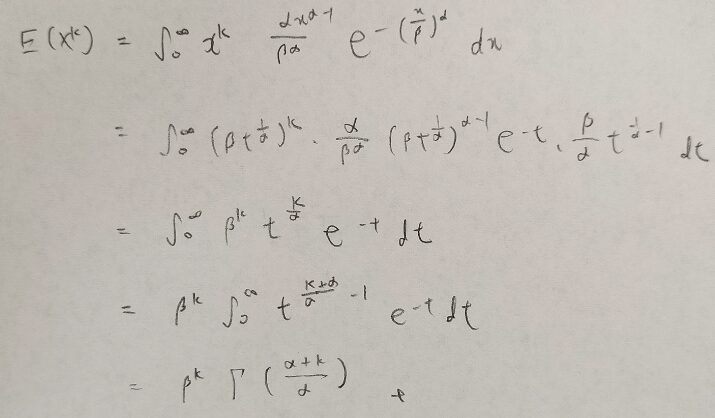
ワイブル分布についてさまざまな性質を導出しましたが、ワイブル分布は再生性を持たないのでご注意ください。
ワイブル分布の意味とレイリー分布の意味
ワイブル分布が故障率を指数関数と考えて導かれた分布だとはわかりました。ワイブル分布から派生する分布はワイブル係数αを1とした指数分布だと思いますが、他にはありますか?
αを2としたときにも有名な分布と等価な分布が得られます。その分布のスケールパラメータβを微調整するとレイリー分布という分布が得られます。
レイリー分布は電波強度などで用いる分布です。対してワイブル分布は最弱リンクモデルとも呼ばれます。鎖を引っ張るときに、最も弱い鎖を破壊してから鎖全体が破壊されるモデルを表しています。レイリー分布のレイリーはアニメ『アルドノア・ゼロ』で登場した「空が青いのはレイリー散乱だ!」のレイリーですね。
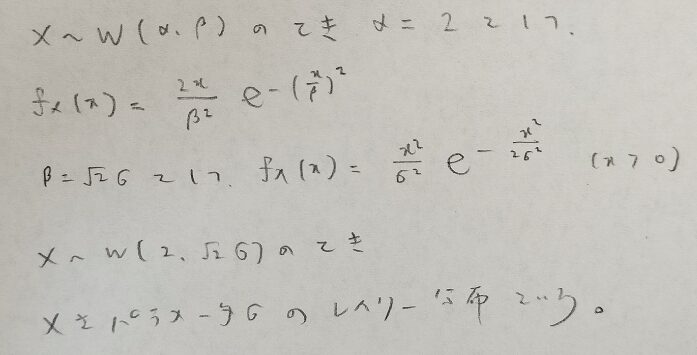
レイリー分布の期待値、分散、最頻値(モード)、中央値と正規分布との関係
2023年の統計検定1級の統計応用の理工学でレイリー分布が出題されました。こちらの解答作成という意味でもレイリー分布とワイブル分布の関係性とレイリー分布の性質についてまとめます。とくに正規分布との関係は大切でその証明にはトリッキーな証明方法が必要ですので、式変形を一緒に追っていきましょう!
レイリー分布の期待値と分散を導きます。
レイリー分布はワイブル分布の特例なので結果を導くことは簡単ですね。
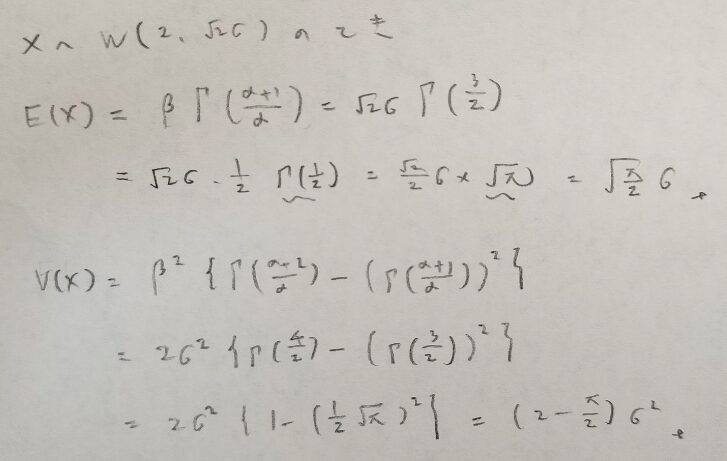
統計検定1級ではレイリー分布の他の性質の導出も出題されました。レイリー分布はどのような特徴があるか、ワイブル係数の値から推測できますか?
α=2なので故障率は単調増加(IFR)です。
そうですね。レイリー分布の値が最大になるときのx座標こそが最頻値(モード)となりますね。
モードはレイリー分布の式を微分していけば機械的に求まりますね!

最後に正規分布とレイリー分布との関係性について紹介します。
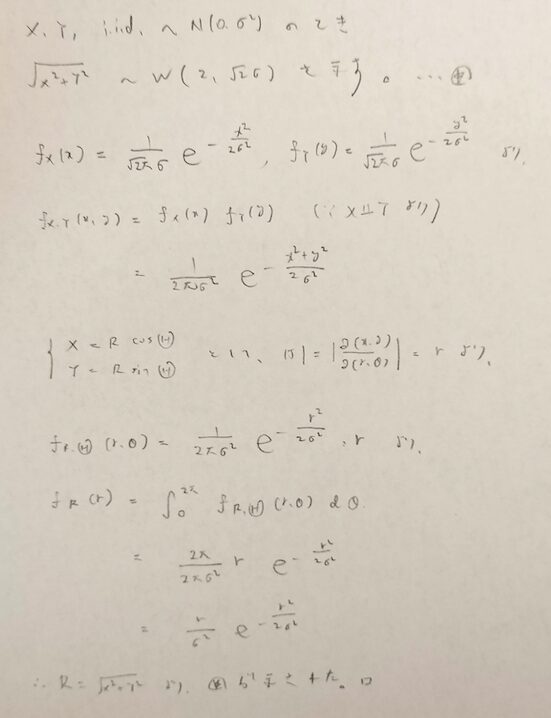
Xが正規分布に従うときにXの2乗が従う確率分布は今後よく登場するので、その分布の持つ特徴などを調べておく必要がありますね。その分布はカイ2乗分布と言いますが次回に扱います。
了解しました。レイリー分布とも関係がある正規分布はやはり確率分布の王ですね!
レイリー分布はマイナーな分布よりなため、掲載されている本が少ないです。今回は2冊の本を参考にしましたのでご紹介します。
統計検定1級受験のバイブルといわれることだけあって、必要な知識は掲載されています。ワイブル分布のIERやDFRなどもこちらに掲載されておりました。統計検定1級の過去問でも出題されています。
ワイブル分布の故障率が満たす微分方程式とその解法はこちらの本に詳しく掲載されています。本書は主要な確率分布ならばほぼ全て網羅されている素晴らしい本です。




