数学検定準1級にどうやって挑むか?について最新の傾向と合わせて対策法を教えます。
大学入試を意識して数学検定準1級の対策をするのか、
それとも数学検定準1級にギリギリ合格を目指すのかで参考書選びが変わってきます。
この記事で次のことを理解・実践できるようになります。
目次をご覧ください。
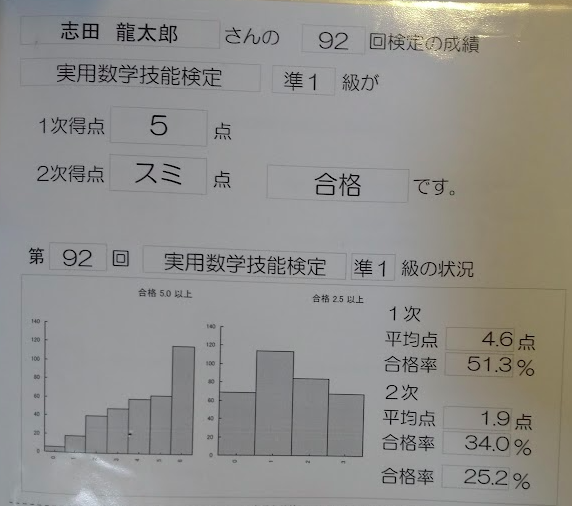
数学検定準1級の合格率と偏差値のレベル感
数学検定準1級の合格率は直近数年では15%~25%となっています。過去の合格率もあわせて考察すると合格率は20%前後で設定されています。
どのような難易度なのですか?
数学検定2級にギリギリ受かる方だと相当難しく感じる級です。
数学Ⅲの微分積分の内容が重く、文系範囲の数学内容の抜けがあると合格が難しい
大学入試の偏差値レベルだとどの辺りの難易度になりますか?
大学入試的には学校で配られる指定教材の問題集をしっかりこなせれば間違いなく受かるレベルです。
教科書の例題のみ解ける状態でギリギリ受かるかな?と言うレベル感です。
要るするに東大などの最難関大の処理量が多く大変なレベルの試験ではなく、受験数学の典型問題が解ける状態だと満点が取れるレベルの試験です。
数学検定準1級にギリギリ受かる人向けの参考書(過去問)
大学入試をあまり考えずに合格のみを考える場合はどの参考書を選べば良いですか?
数学検定2級に合格していることが前提で、2023年現在だと次の本1択です。
1次の本だと書いていますが、しっかりと読み込めばギリギリ2次で合格圏です。過去問(頻出問題)をベースにして作られているため効果は抜群なのです。
さきほど数学検定2級に合格していることが前提と書きましたが、文系範囲の内容が理解できていれば本書を購入してOKです。
本書には数検2級までの大切な内容も含まれているためです。
最短で合格することを考えると過去問の購入は不要です。この合格ナビ自体が過去問だと思って学習してください!
学習していて難所はどこでしたか?
数学Ⅲの積分のところです。ここを理解できるようになれば合格は目前です!
あとベクトルが得意になると2次でほぼ確実に合格点取れます。
大学入試を意識して数学検定準1級で高得点を目指す場合
数学検定準1級は大学入試数学では重要な問題も出てくるので、理系の数学Ⅲの予習としても最適です。
最難関大学レベルの問題は出題されないものの、1度触れておかないと初見では無理な問題が多く出題されるのが特徴です。
特に数学Ⅲ部分に顕著に見られる傾向で、たくさんの極限公式+微分公式+積分公式を覚えてないと高得点での合格は無理だと断言します!
ただし文系範囲がしっかりと解ける状態(これは数学が相当強い状態です)ならばギリギリ合格の可能性はあります。
大学入試を考えた場合はどのような参考書がおすすめですか?
僕の考えでは1対1対応の演習シリーズが最も効率よく数学の偏差値を上げられる教材です。この考えは10年前から変わりません。
本書は数学Ⅰ〜数学Ⅲまで合計6冊あります。ページ数が少ないのでやる気が起きる参考書です。青チャートの簡単すぎる計算問題がなくなった感じです。
受験数学界隈ではテンプレ化している教材なので、本書終了時には人によっては早慶の問題も問題によっては完答できるようになります。
ただし多くの大学受験生は本書を終えられずに受験本番を迎えると言うレベル感ですので概要を確認してから手に取る方が安全です。
コストパフォーマンス最適ですね!
ただし改訂が徐々にされているため、最新の三訂版を購入するようにしてくださいね!
1対1対応の演習の例題部分をマスターできたら数学検定準1級は満点取れます。
僕は中学生の頃から数学Ⅲの勉強を始めましたが、正しい参考書ルートを知っていたら、もっと早く数学検定準1級に合格できていた気がします。
だからこそ合格ナビは本当におすすめです!!