先程こんなツイートをされていましたので、どうなったのか気になっていました!笑
そうなんですよ。一様分布は連続型確率分布では最も単純なのに、離散一様分布の分散計算がダークホース的な計算量でした。
この記事では一様分布についての基本的な話題について解説していきます。
連続確率分布の確率密度関数と離散確率分布の確率関数の計算方法などの違い
今まで勉強してきた確率変数は離散型のものに限定していました。世の中には寿命の分布(指数分布といいます)など、確率変数が時間などの連続量をとるものも多くあります。この記事では連続型確率分布の最も単純な例として一様分布を考えていきます。
次のポイントは離散確率分布と連続確率分布についてのまとめです!
確率変数Xの実現値xが有限集合または加算無限集合で離散的な値をとるとき、Xを離散確率変数といい、P(X=x)を求める際は確率関数(pmf)を用います。期待値や分散の計算にはシグマ計算を用います。確率変数Xの実現値xが実数上で連続な値をとるとき、Xを連続確率変数といい、P(X=x)の値は0になるので確率関数は考えず、P(a≦x≦b)を求める際は確率密度関数(pdf)を用います。確率密度関数とは積分することによって確率となる関数のことです。期待値や分散の計算には積分計算を用います。
加算無限集合については集合論の濃度の話になります。『集合論キャンパス・ゼミ』に詳しく掲載されています。また、確率密度関数の説明は『確率統計キャンパス・ゼミ』を参考にしました。
標準一様分布の確率密度関数
連続型確率分布で最も考えやすい分布は標準一様分布です。英語名はstandard uniform distributionです。一様分布の頭文字はUとなります。
標準一様分布や一様分布と書かれたときは、連続一様分布のことを指します。
一様分布の英語名はuniform distributionですね!
それでは標準一様分布を図でイメージしてみます。全確率1に注目してください。
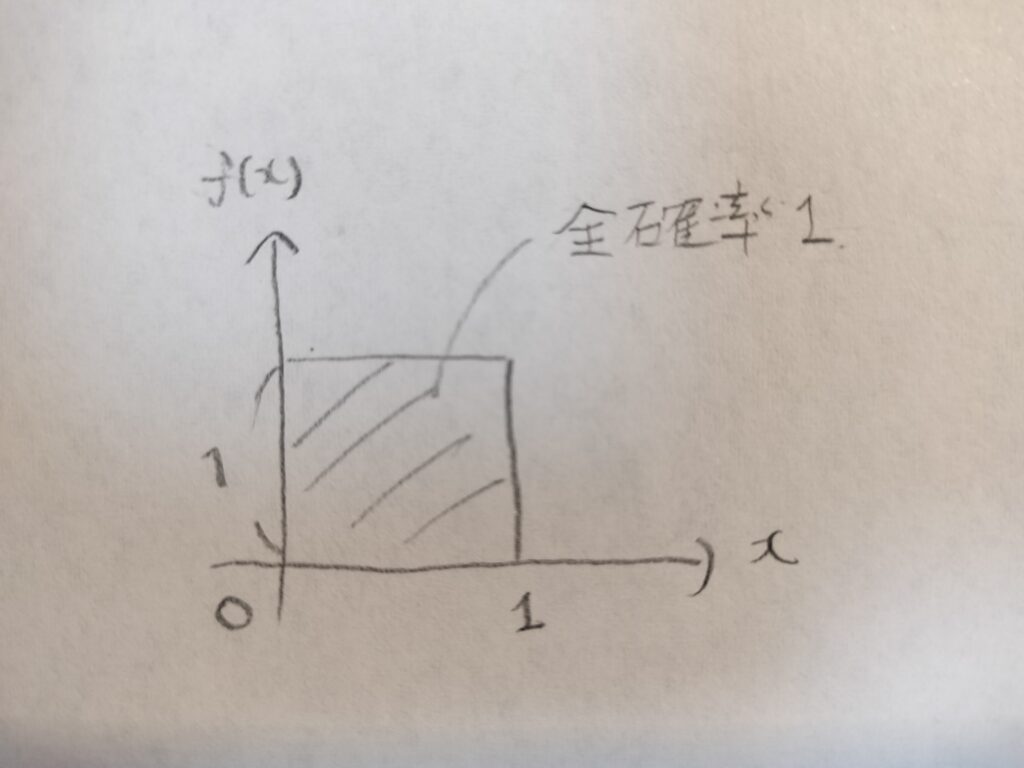
1が多いから単位分布と呼びたいところですが、単位分布は最も単純なデルタ分布の特殊なバージョンで既に命名されていましたね!
標準一様分布の一様とはどこも同じにという意味です。例えばあとで紹介する離散一様分布ではサイコロを振ったとき、どの目が出る確率も一様で1/6であるというように使います。標準とは、数ある一様分布の中でxが0~1の値を取る特殊なという意味です。
これらをまとめると、標準一様分布の確率密度関数は次のように定義できます。
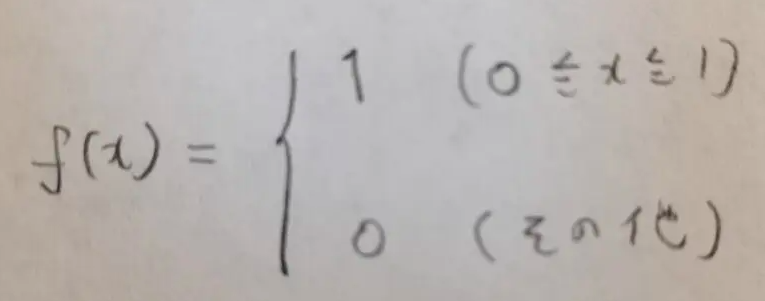
Xが標準一様分布に従うとき、X~U(0,1)と表現します。
一様分布の確率密度関数と期待値と分散の計算
次に標準一様分布から一様分布へと一般化していきましょう。
確率密度関数がどうなるのかを考えます!
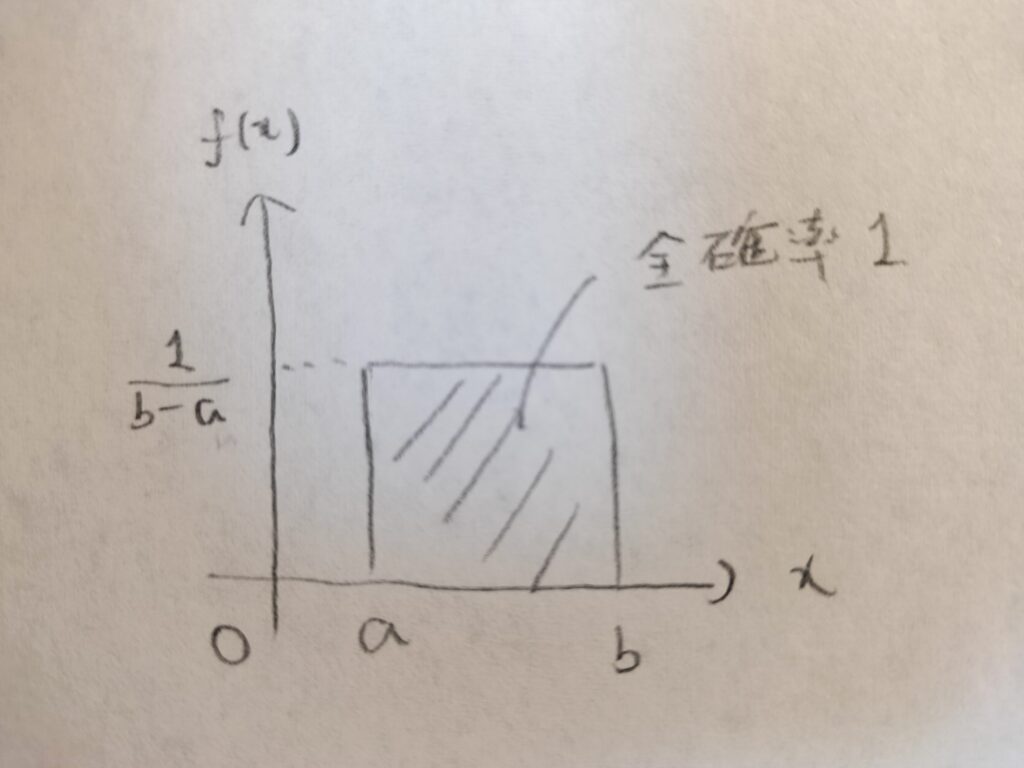
全確率1というルールから、高さ(確率密度関数の値)が判明します。このテクニックはアクチュアリー数学で頻出の一様分布同士の足し算の分布を一瞬で書くときに用います。参考書には書いておらず、過去問で先人達が編み出したテクニックとなります。
では、一様分布の確率密度関数はどうなるかわかりますか?
察しはつきました!
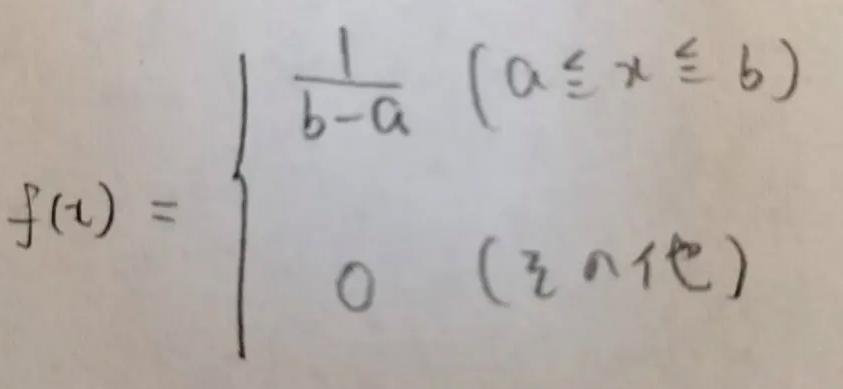
この結果でa=0,b=1とすると標準一様分布の確率密度関数になります。以後、このような考えは計算結果の妥当性として検算で利用することをおすすめします。
では一様分布の期待値を求めていきましょう。
計算結果のaとbに0と1を入れれば標準一様分布の期待値が分かりますから、一石二鳥ですね!
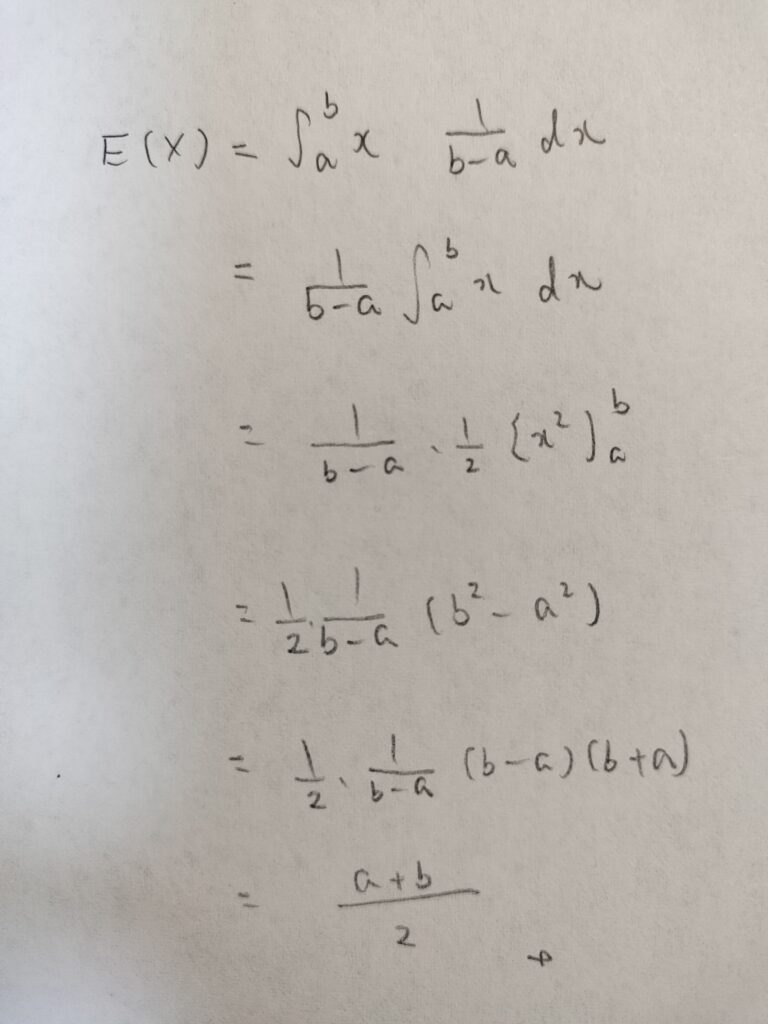
平均そのものですね。なんとなく予想ついてました!笑
因数分解を適宜おこなっていくことがポイントです。後回しにすると計算量が大変なことになります(実体験)
次に分散もやってみます!まずは連続確率分布なのでX(X-1)ではなくてXの2乗の期待値を計算することがオーソドックスな方法ですね。
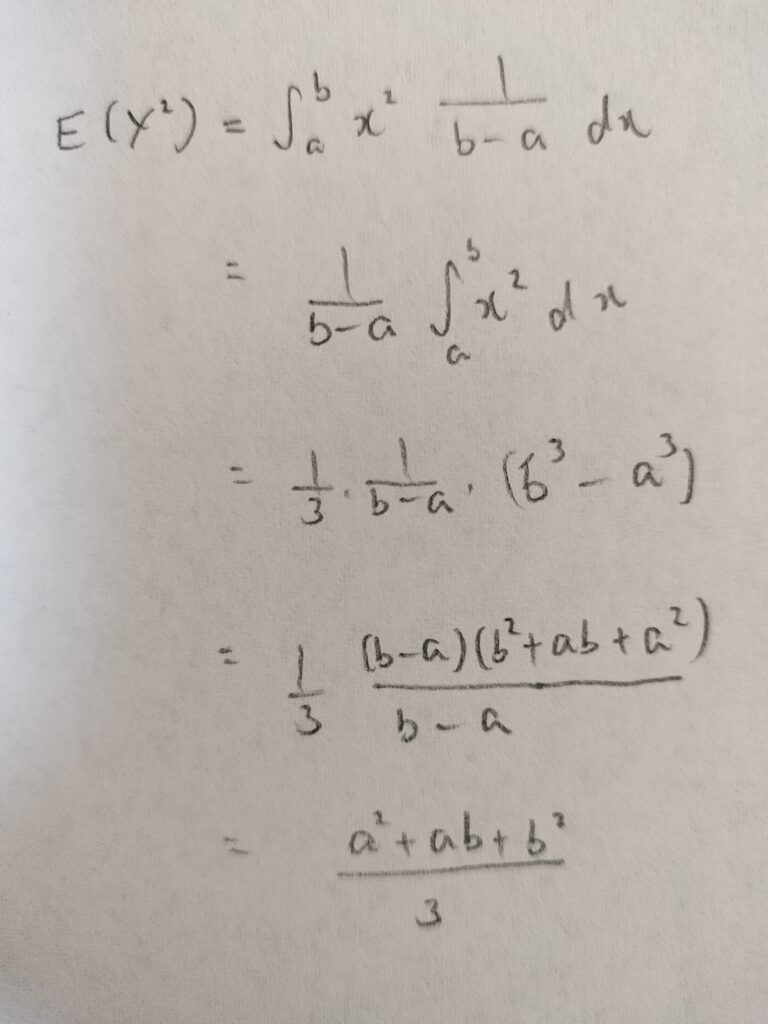
それでは分散の結果を出しましょう!
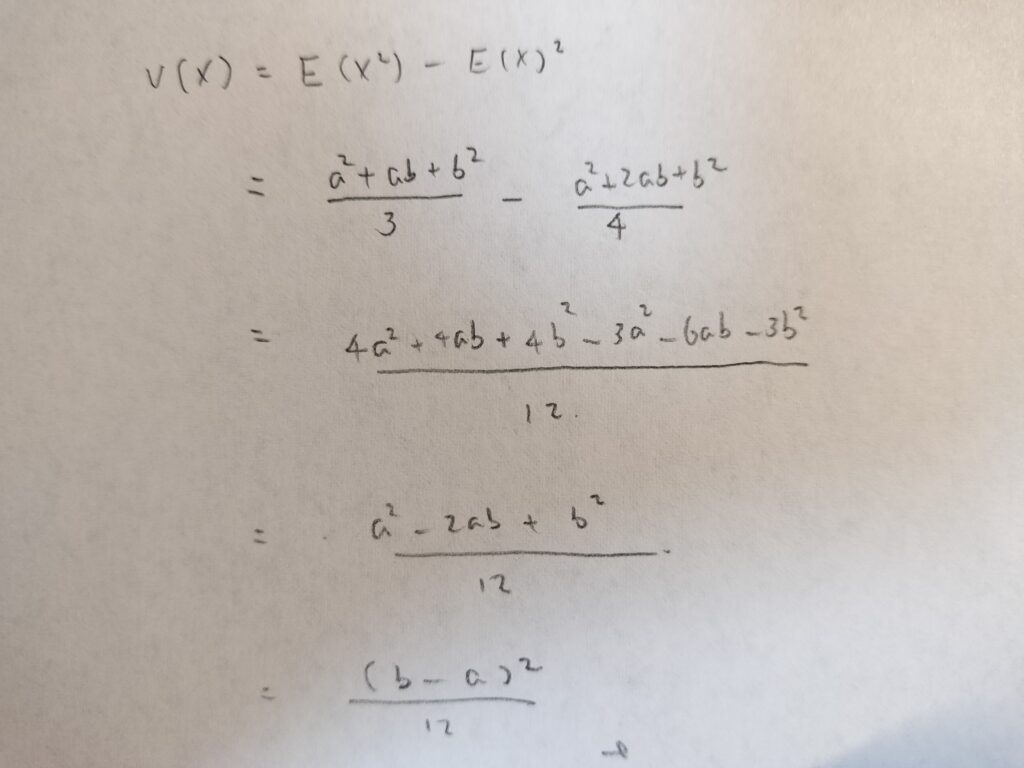
標準一様分布と一様分布の期待値と分散についてまとめました!
ありがとうございます!
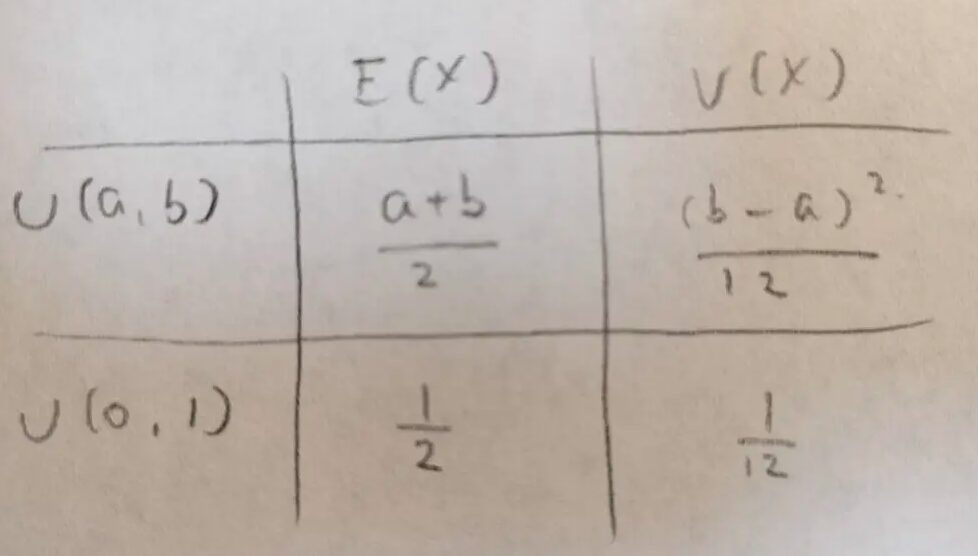
平均は予想通りでした。
分散の分母の12という数字を覚えておいてください。次の離散一様分布でも12が出てきます。
離散一様分布の期待値と分散の計算
最後に離散一様分布を扱います。
まだ離散分布あったんですか?笑。てっきり出尽くしたのかと…。
確率分布は僕たちが思っている以上にたくさんあります。『統計分布ハンドブック』は800ページ以上にわたって大量の確率分布が掲載されています。例えば2023年の統計検定1級の統計応用理工学ではレイリー分布というまったく知らない分布が登場しました。「確率分布はたくさんある」という心構えを持つことは大事です。
まずは分かりやすくするために、xが1からNまでの離散値をとる離散一様分布の期待値と分散を求めます。それからxがaからbまでの離散値をとる離散一様分布へと一般化していきます。
Xの実現値xがaからbまでの離散値をとるとき、つまりx=a,a+1,…,b-1,bのとき、X~DU{a,…,b}と表記します。例えばXの実現値xが1からNまでの離散値をとるとき、つまりx=1,2,…,N-1,Nのとき、X~DU{1,…,N}と表記します。この表記は例えば『弱点克服 大学生の確率・統計』を参考にしました。
ではX~DU{1,…,N}のとき、Xの期待値と分散を求めます。まずは期待値から
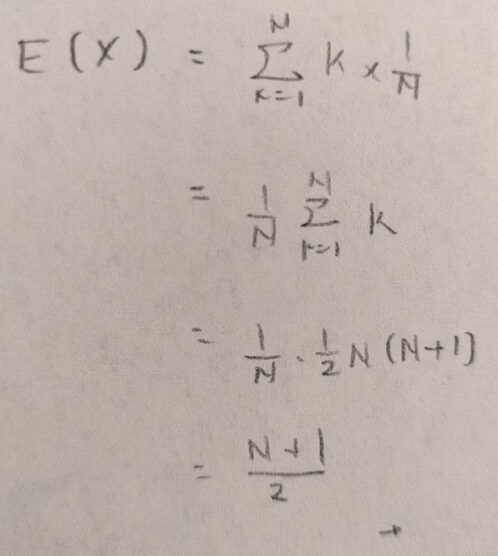
意外と簡単ですね!次は分散ですが、さっきと同じようにXの2乗の期待値を求めてから分散を計算しにいきます!
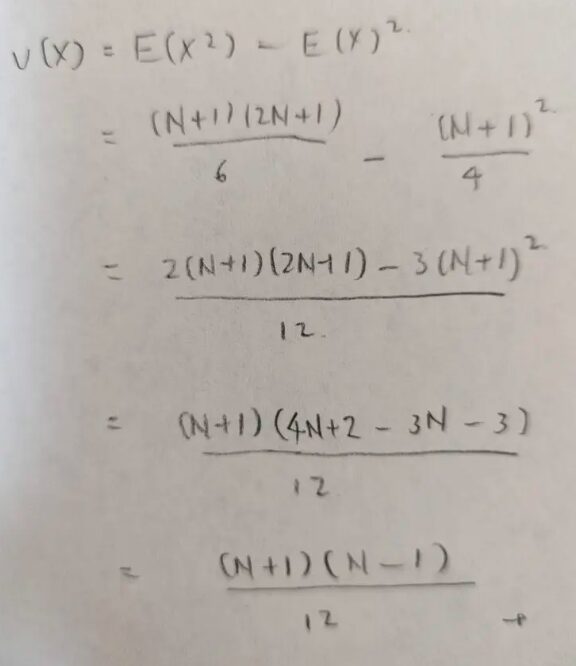
あれ?また12が出てきました!
離散量と連続量の違いはありますが、一様分布の分散は12という数が隠されているのですね。
最後にX~DU{a,…,b}のとき、Xの期待値と分散を求めます。計算が大変複雑なので、余裕がある方はご覧ください。まずは期待値から求めます。
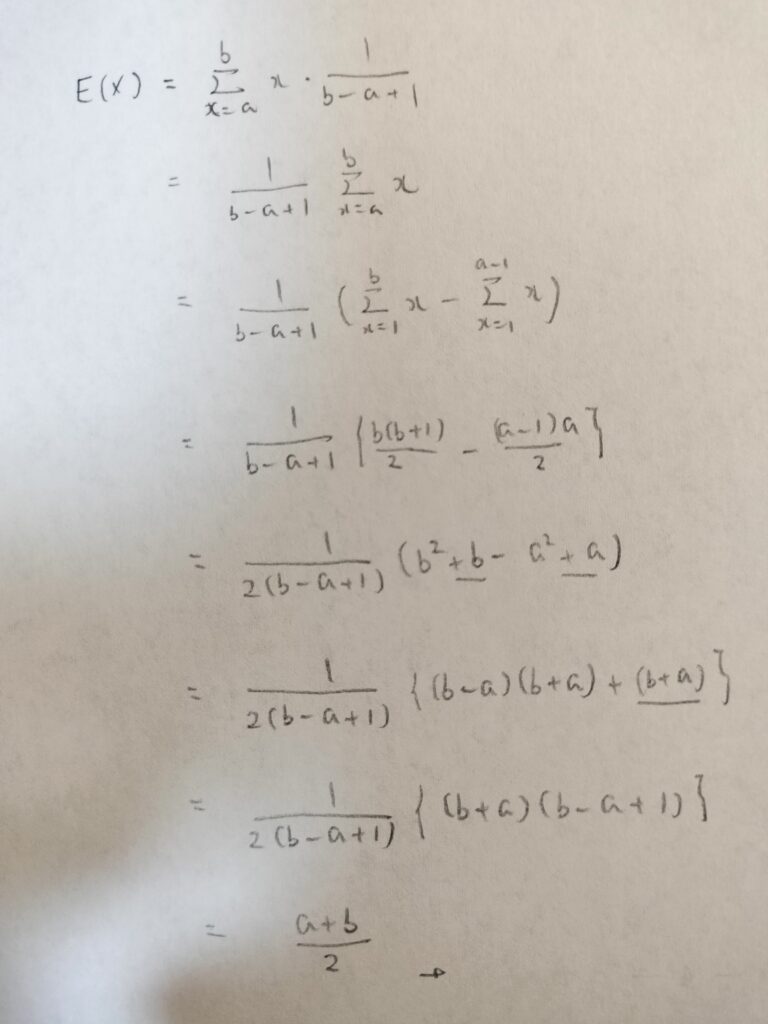
なぜ確率関数の分母がb-aではないのですか?そしてシグマの2つ目がaではなくてa-1なのはなぜですか?
まずは最初の質問から答えます。それは(連続)一様分布の考えです。今回は離散一様分布なので、植木算的な考えをすると、b-aとは間の数です。木の数はb-a+1ですね。
はい。2つ目のシグマは…
僕自身、ここで引っかかったのですが、aからbまでの和は1からbまでの和から1からaまでの和を引いて本当に求まりますか?
このようなときは1~10の和から1~5の和を引くと、本当に5~10の和が残るか(残りません)など具体例で考えてみてください。
あ!余分なものまで引かれて、残った和が1からa-1までになっちゃいました!なるほど理解できました。
次は分散です。期待値の時点でこの計算量なので、相当な計算量になりますので、よろしくお願いします。まずはXの2乗の期待値からです。
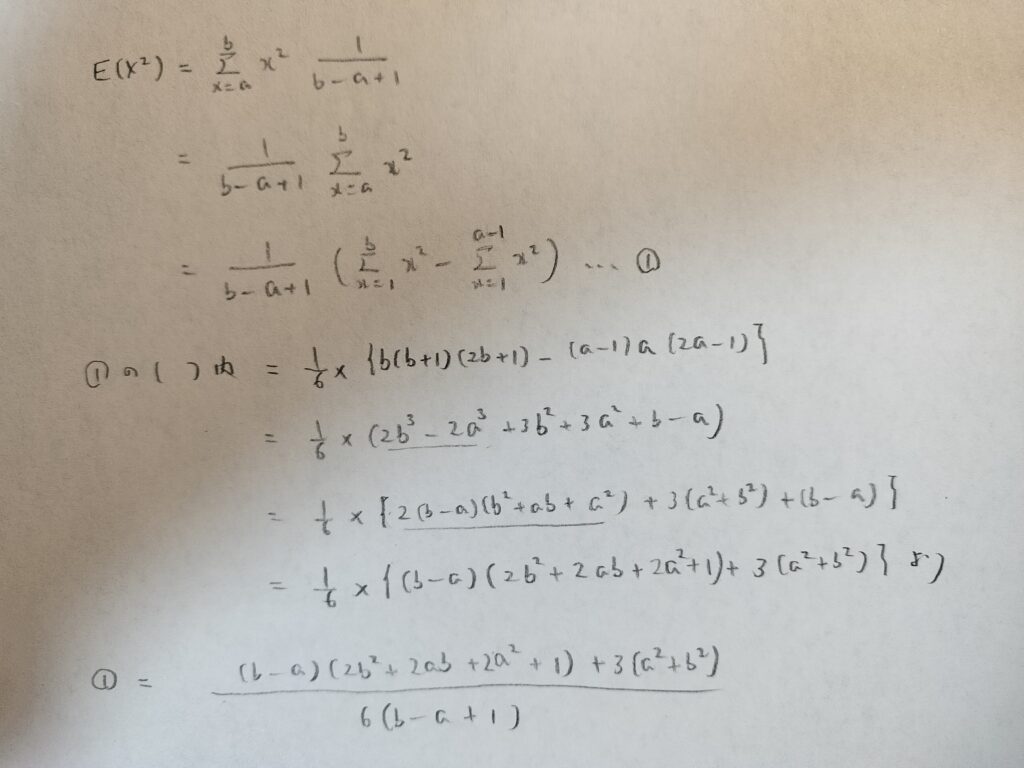
この時点で計算量やばいですね!笑
そうですね!ではいよいよ分散の計算をします。
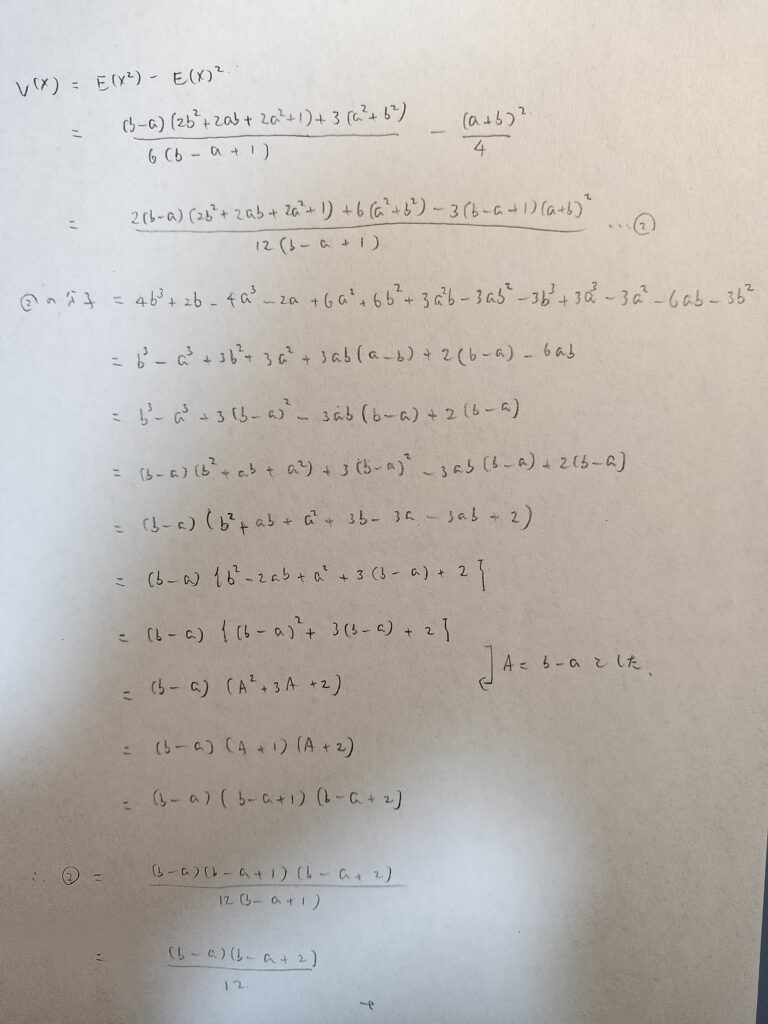
さっきの計算より計算量が多くて笑えます。
お疲れさまです。でも12が出てきて感動しませんか?
本当ですね!一様分布は離散一様分布でも(連続)一様分布でも分散は必ず12が入るのですね。
本当にこの答えが合っているのかを表にまとめて検討します。a,bにそれぞれ1,Nを入れて値は一致しているでしょうか。
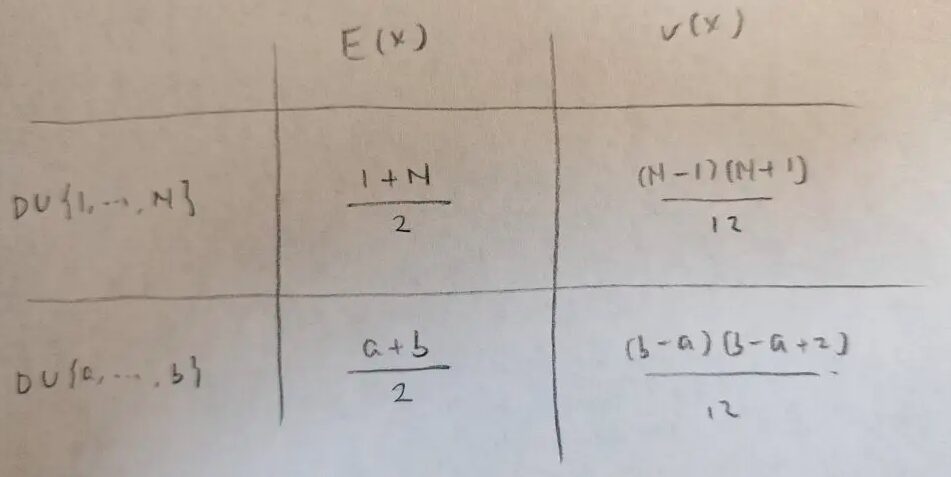
見事に一致して感動です!
ありがとうございます!最後に一様分布で離散型か連続型かで生じる差異について、こちらも表にしてみました。
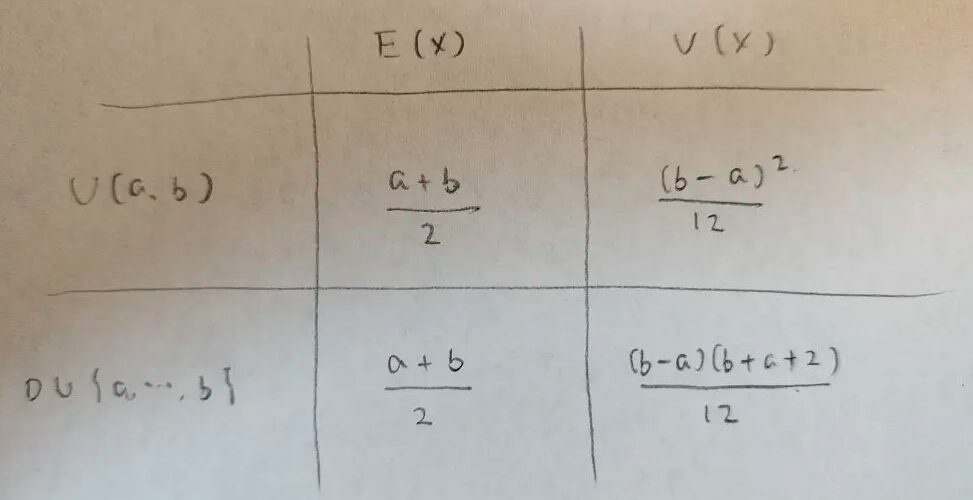
期待値は離散でも連続でも変わらないのですね。こちらは感覚的にも納得です。
分散は分子の第二因数に大きく違いが出ました。ここの差が離散か連続かの違いによるものです。
アクチュアリー数学を受験する際は、X~DU{a,…,b}のときの分散公式を覚えていないと時間切れになります。個々の場合を考えるよりも、この一般形を覚えてしまった方が計算処理は早いです。しかし統計検定1級でこれをやってしまうと(自分の経験から)採点の対象外になる可能性が濃厚です。試験によって使い分けるようにしましょう!
最後に標準一様分布、一様分布、離散一様分布の紹介の際に、参考にした資料を紹介します。
離散量の説明の際に参考にしました。本書の前半は濃度の説明になっています。濃度とは無限集合の強さを表す指標です。有限集合の濃度は要素の個数となります。では無限集合の濃度とはどのように定義をするのでしょうか。無限間には強さの階層はあるのでしょうか。本書にはその答えが分かりやすく書かれています。
確率密度関数の説明で参考にしました。とても分かりやすい本でおすすめです。まずは本書で勉強をしてから、本格的な数理統計学の本に進とスムーズです。
800ページ以上にもわたって確率分布について説明した本(というか辞書)です。
辞書系はメルカリの方も要チェックです!→『統計分布ハンドブック』





