お金持ちの人口分布はどのようになっているかご存知ですか?
正規分布になるのではないですか?
世の中の多くの事柄は正規分布に従いますが、異常値などの分布は特別な分布に従うことが知られています。これはビジネス界隈では働きアリで例えられることで有名なパレートの法則というこの世を支配すると言っても過言ではない法則が基盤となっています。参考『「超」集中法 成功するのは2割を制する人』
ある一定以上の金額を持ったお金持ちの人口分布はパレート分布という分布に従っています。
パレート分布をメインに色々な分布を教えてくれるのですね。1つ1つ関連づけて勉強していこうと思います。
標準べき関数分布は単項式を分布関数に持つ
まずは標準べき関数分布というシンプルな分布を考えます。この分布は分布関数から考えていくと存在意義を理解することができます。
中学1年生で勉強する正比例、中学3年生で勉強する二次関数、高校2年生で勉強する三次関数、などべき関数を分布関数に持つ確率分布を考えます。標準べき分布は『リスクを知るための確率・統計入門』には載っているレアな分布の1つです。
標準と名前がついているので範囲は0≦x≦1となりそうですね。
次の関数を分布関数にもつ確率変数Xに従う分布を標準べき関数分布といいます。
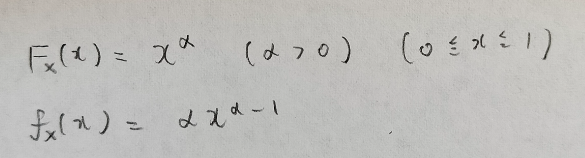
べき関数分布は標準べき関数分布を拡大したもの
標準べき関数分布があるなら、一般化されたべき関数分布もありますよね?
その通りです。こちらはxの範囲を0≦x≦βに拡大するために、標準べき関数分布をx軸方向にβ倍拡大した確率分布を考えます。
受験数学で勉強したようにxにx/βを代入すれば求まりますね。
次の関数を分布関数にもつ確率変数Xに従う分布をべき関数分布といいます。英語名のpower function distributionから便宜上PF(α,β)と表すことにします。標準べき関数分布はPF(α,1)に相当します。
べき関数分布はマイナーなためか10冊程度数理統計の本を参照したり、ネットなどで情報を調べましたがべき関数分布を表現する記号がありませんでした。そのためこの記事用にPF(α,β)という定義をさせていただきました。
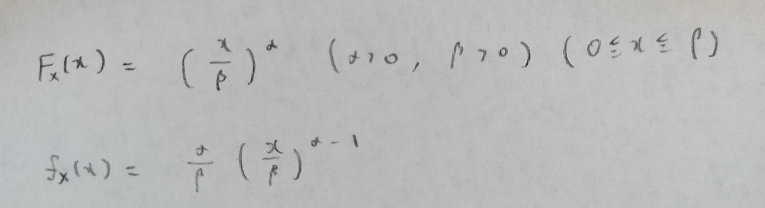
PF(1,β)はどういう分布になるでしょうか?
ちょっと待ってください。代入してみます。
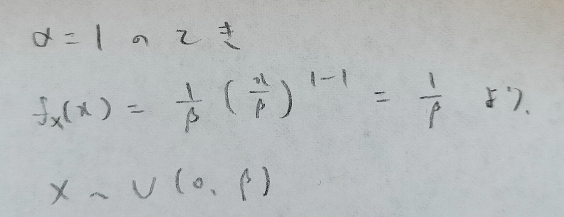
一様分布が出てきました!
正解です。実はべき関数分布はまだ先がありますので、パレート分布の話題の最中でまた戻ります。
パレート分布の分布関数を導出し期待値と分散を計算する
主役のパレート分布の登場です。こちらは導出が難しい分布ですので分かりやすく説明していきます。
ある一定以上の金額を持つ人を考えるのでしたよね。
仮定としてN(x)が上から2行目の式に従うことを仮定しています。こちらはべき関数になりますので上で説明した分布との関係性を感じます。

この方法のポイントは自然対数を自然対数を取ることにより、直線による近似が行われていることで、β以上(つまりlogβ以上)の部分では累積相対度数の考えを使うことで分布関数を算出するところにあります。
上の解説にて最後の式を確率密度関数にもつ連続確率変数Xが従う分布をパレート分布といいX~Pa(α,β)と表します。x≧βであることに注意してください。
計算うんぬんよりも、考え方が難しい分布です。
パレート分布について全確率1も証明してみます。
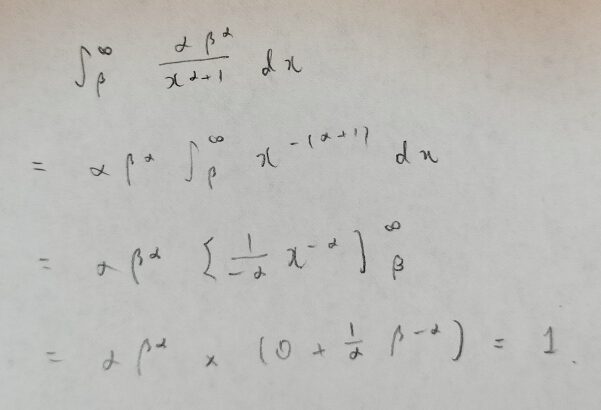
パレート分布とべき関数分布との関係
べき関数分布とパレート分布の関係を調べます。
この記事では確率変数の変数を分布関数の定義を用いて機械的に行なっています。前回の記事で紹介した置換積分を行う方法とは別の方法になります。どちらも使いこなせると素晴らしいと思います。
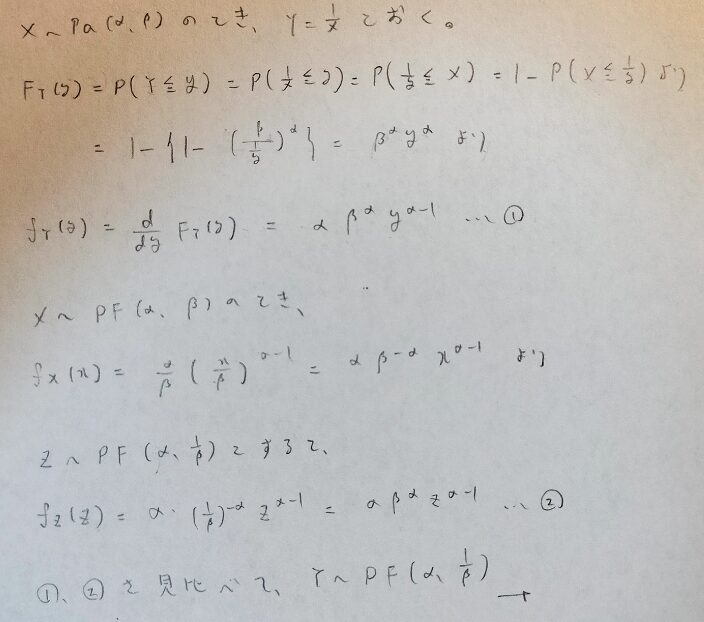
パレート分布→べき関数分布について確率変数は逆数の関係であり、PF内のパラメータはβのみが逆数となります。
数式で書かれていれば納得です。…ということは、パレート分布→べき関数分布→標準べき関数分布→一様分布の流れが完成したということですね!
その通りです。完成したのでまとめておきます。

パレート分布と指数分布との関係
指数分布がパレート分布と関連がありますので紹介します。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』に載っている公式の証明ですね!合ストには証明が載っていないので助かります!
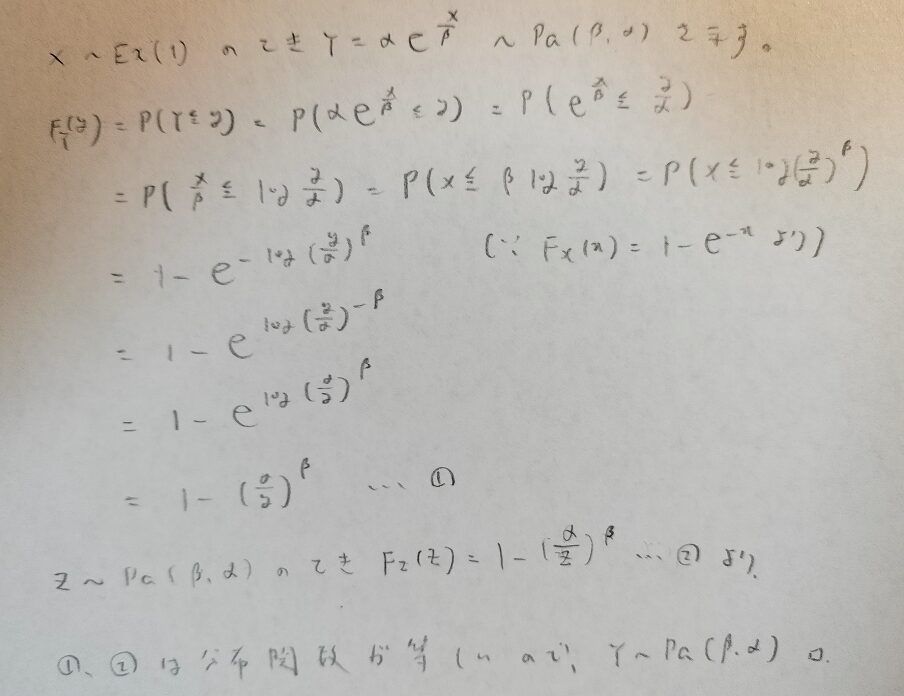
パレート分布はパラメータの順番などに注意してください。
指数分布でも似た注意がありましたね!気をつけます。
パレート分布の期待値と分散の計算
パレート分布はべき関数が元になって作られているので、期待値や分散の計算は簡単です!
まずはパレート分布の期待値を計算します。
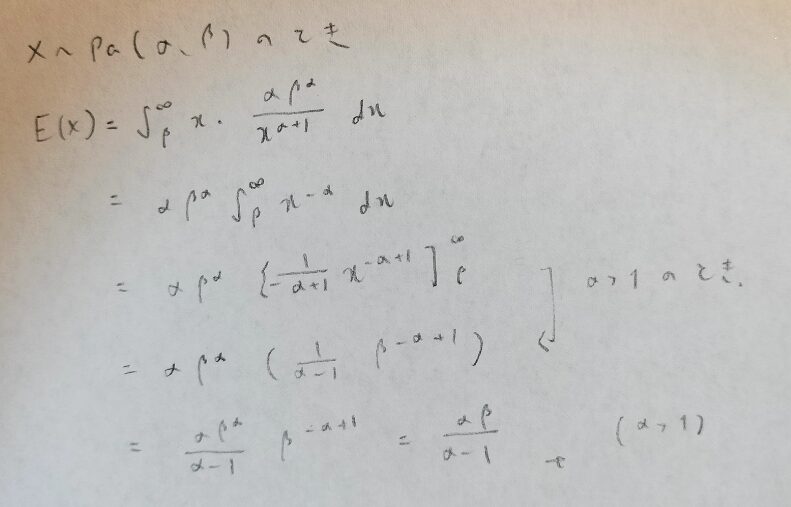
広義積分の際にαについての条件が出てきますので注意ですね!
次はパレート分布の分散ですので、まずはXの2乗の期待値を出しましょう。
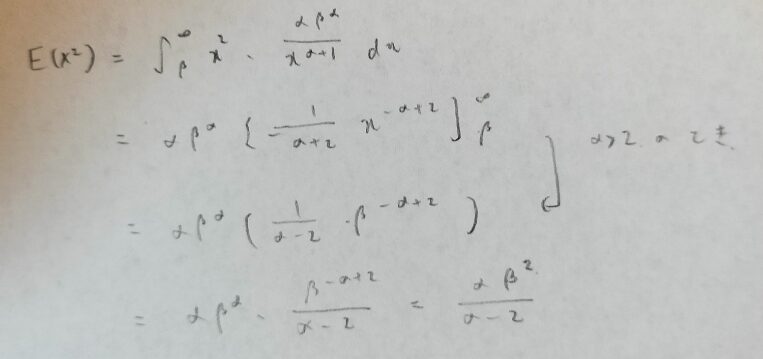
似たような結果ですね。Xのk乗の期待値も同じように計算できますね!
では最後に分散の計算をしましょう!
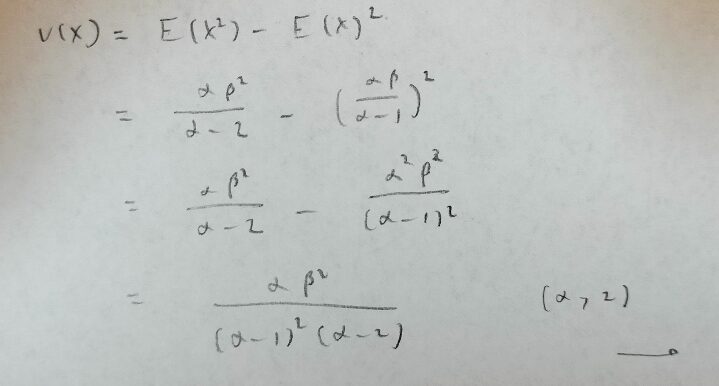
第2種パレート分布の存在意義
パレート分布にはまずは大きく2種類があって、パレート分布と第2種パレート分布です。第2種パレート分布の方がやや複雑な形です。
なぜ第2種まで行うのですか?
アクチュアリー数学などでは単項式(べき関数)が登場する分布ではパレート分布の知識が使えると時間短縮ができて有利になります。パレート分布しか知らないと、結局期待値や分散の計算を0からする羽目になります。第2種の形まで知っておくと対応できる問題の種類が増えるので反応速度が大幅にアップします。
X~Pa(α,β)とするとき、Y=X-βで定義されるYは第2種パレート分布に従うと定義して、Y=Pa2(α,β)と表記します。参考『アクチュアリー試験 合格へのストラテジー 数学 第2版』
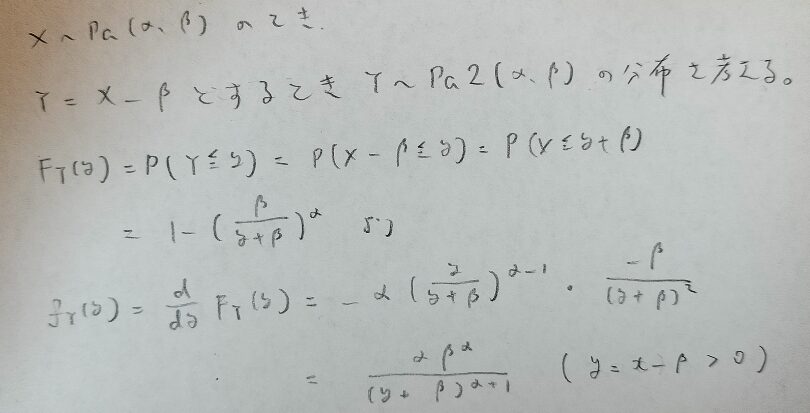
結局はパレート分布同士の平行移動ということですね。
その通りです。平行移動ということはパレート分布の期待値と分散は、第2種パレート分布になったときに、その値は変化するでしょうか?
期待値は変化するはずで、分散は変化しないはずです。それを確かめてみましょう。
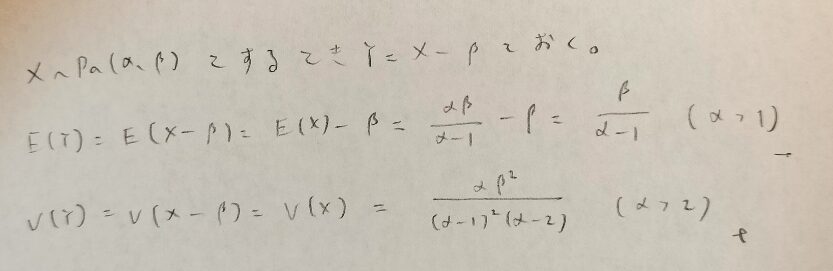
予想通りの結果になりました。パレート分布は全体的に期待値や分散の計算は簡単ですね!
第2種パレート分布と指数分布との関係
X,Yが互いに異なるパラメータの指数分布に従うときに、それらの商に従う分布は第2種パレート分布になります。パラメータには注意してください。
指数分布は色々なところに顔を出す分布ですね!笑
コーシー分布でも出てきそうな確率変数の商の分布ですね。
これは前回勉強した変数変換を用います。
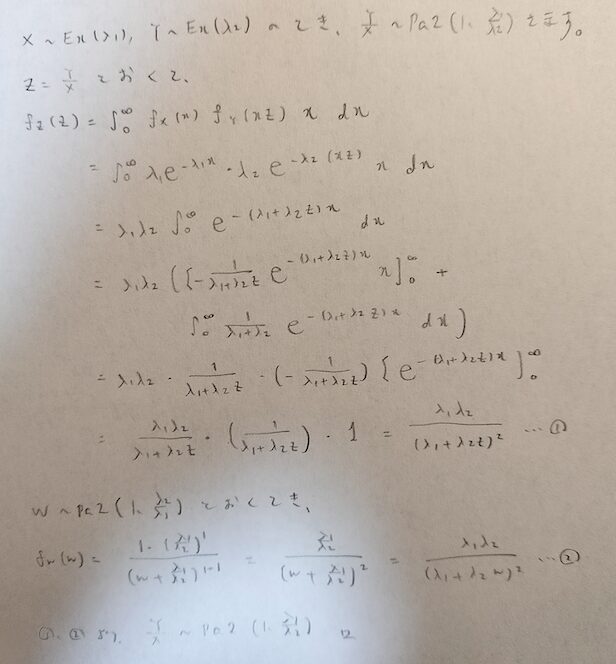
受験数学で勉強したべき関数がお金持ちに関係していて面白かったです。そして指数分布は顔が広いですね!笑
最後にパレート分布の話題を書くために参考にした本を紹介します。
パレート分布(第2種)の期待値と分散のところで使用しました。ここまで細かく公式が載っている本は本書だけです。ただし証明は自力で行う必要があります。
標準べき関数分布とべき関数分布の説明で使用しました。本書には第2種パレート分布が載っていませんがべき関数の箇所はとても分かりやすかったです。
パレートの法則について周辺知識と共に学べます。著者の野口さんは整理法の本なども有名です。




