統計検定1級の統計応用の人文科学2015年の過去問(こちら)で、スカラー量を行列微分させる問題が出ました。
その問題はその年1番の難問ですが、計算方法を知っていれば部分点を狙えた問題です。
ベクトルで微分するのはヤコビアンの計算があるので納得はいきますが、行列微分はびっくりです。
『パターン認識と機械学習』などで頻繁に登場するベクトル微分や行列微分などの特殊な微分法について、体系立ててわかりやすい順番で解説します。
納得しながら読み進めると自然と覚えてしまうと思いますのでお楽しみください。
行列を行列で微分するのは別次元の難易度です。下記の図では最も下の説明になります。
本記事ではそれ以外の微分方法に定義を与えて公式を整理していきます。
スカラー微分の定義とベクトル微分の定義と行列微分の説明

まず単なるスカラー微分は最も単純で自然な定義を与えます。
スカラーをベクトルや行列で微分するのも大して難しくはありません。
問題はベクトルをベクトル微分する内容ですがヤコビアンを求める際の一般化として自然な定義を与えます。
行列を行列で微分する定義はとても難しいので本記事では割愛します。
体系化できる内容は、線形型、2乗型、そして合成関数型です。その後は各個別での公式確認となります。
線形型(転置に注意)
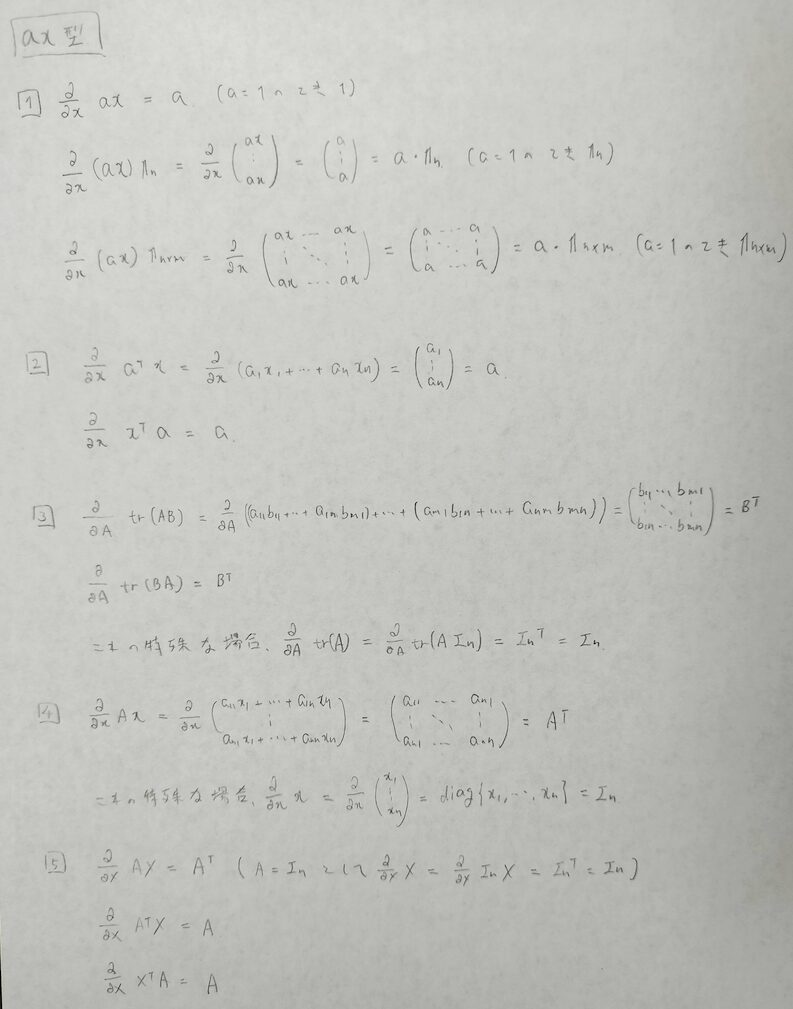
上の定義の番号に照らし合わせて適宜サイズを設定してください。
普通のaxの微分の内容がどんどん一般化されていって面白いですね。
2乗型(トレースを行列微分する内容が複雑)
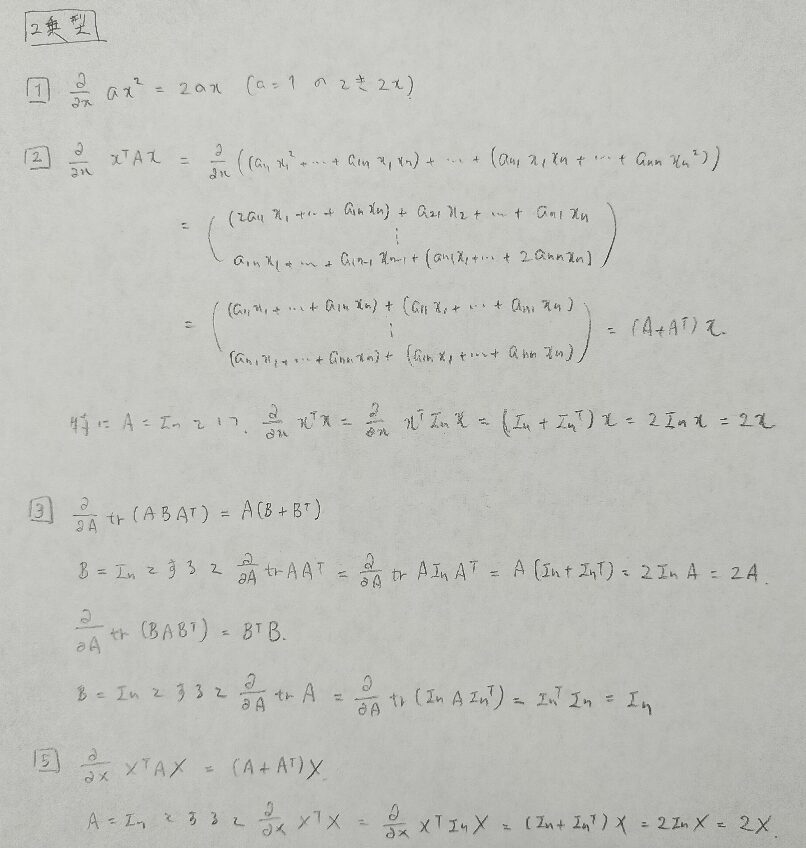
最後の行列を行列で微分するタイプの結果は今までの流れから類推可能です。
合成関数型(連鎖律)

スカラーの場合(大学受験)では外→内へ、
ベクトル微分は内→外へ。
行列微分は外→内への順。
なるほど。スカラー→ベクトル→行列とこのようなルールになっていたのですね。
まさにチェイン・ルールですね。
スカラー微分、ベクトル微分、行列微分の公式
まずはスカラーをベクトル微分する公式をまとめます。
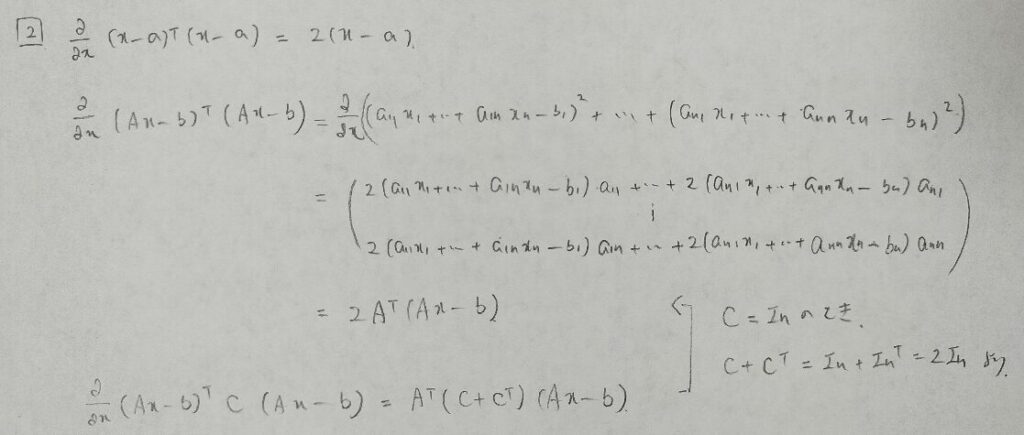
次にスカラーを行列微分する公式をまとめます。
逆行列を求める際に余因子展開を用います。
忘れてしまった方は『線形代数キャンパス・ゼミ』に詳しく説明されているのでご覧ください!
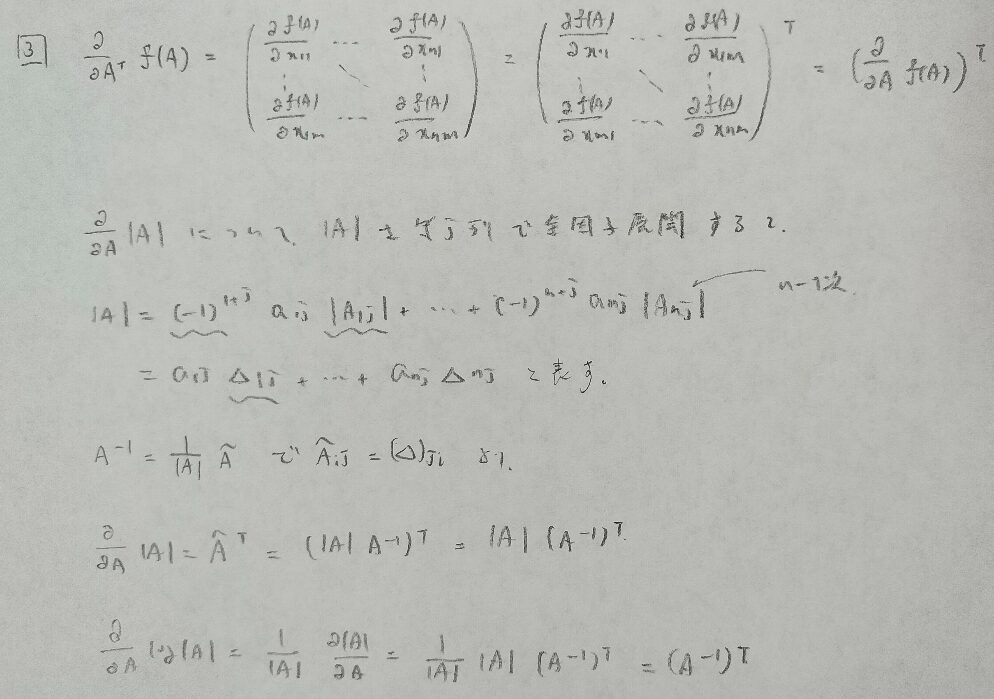
次にベクトルをベクトルで微分する公式を紹介します。
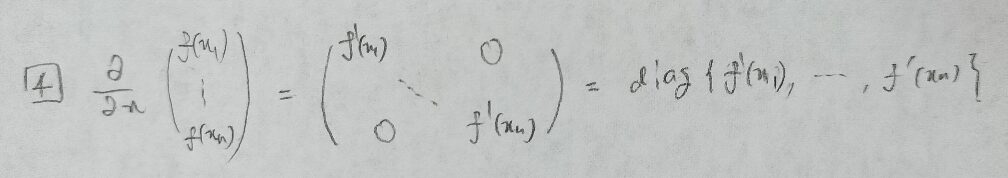
最後に逆行列の微分公式を紹介します。スカラーの場合の一般化になっていることがわかると思います。
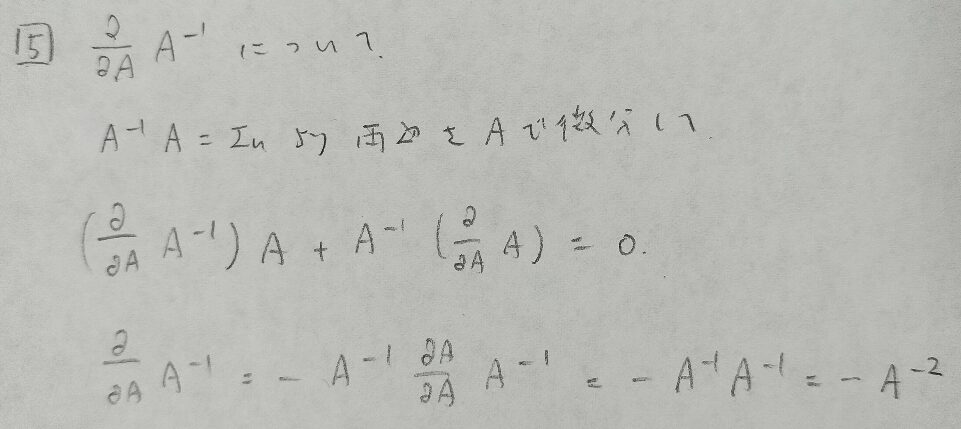
ベクトル微分や行列微分などは統計検定1級や機械学習の分野で登場します。普段は馴染みがない内容ですので、本記事にて公式を総整理できれば良いですね。





