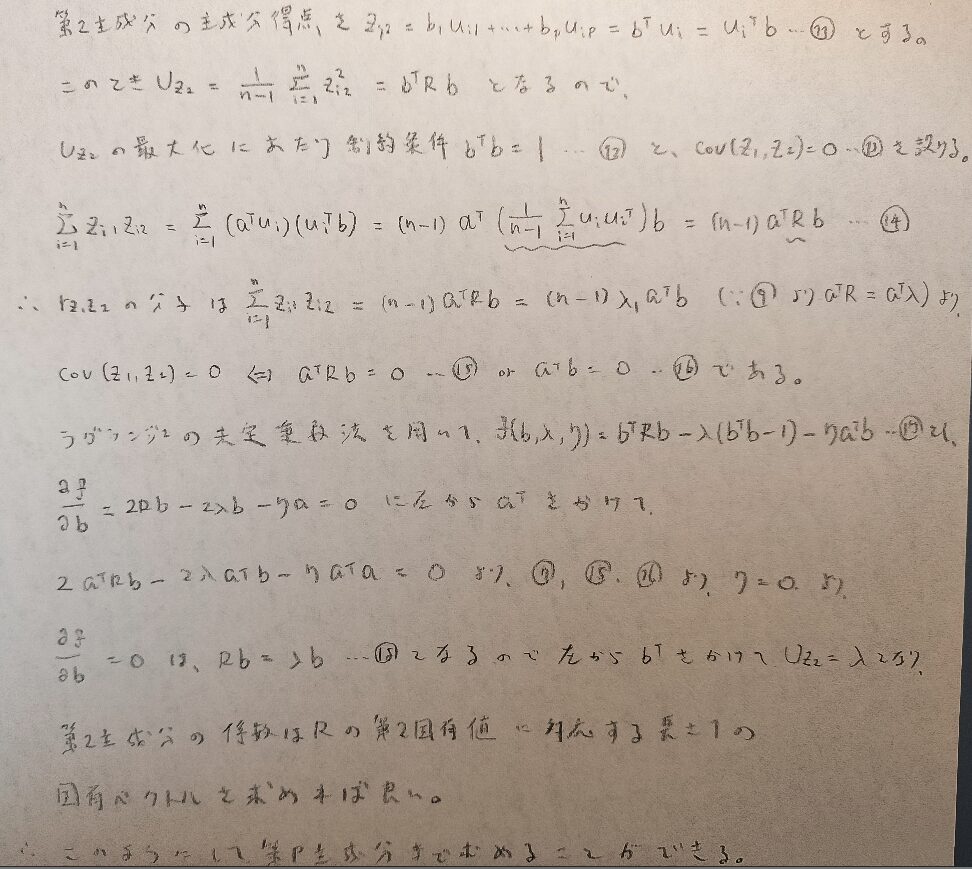数量化理論は今までで数量化1類の記事を書きました。数量化1類は重回帰分析の発展でした。
数量化2類の記事がありませんが、なぜでしょうか?
数量化2類は判別分析の発展ですが、ダミー変数の内容など数量化1類とほぼ同じなので記事にしなくても良いかなと思いました。
そして今回の数量化3類は主成分分析の発展です。前回の記事で感じた方もいらっしゃると思いますが、主成分分析では目的変数yが存在しません。そのため数量化3類でも目的変数は存在しませんのでご注意ください。
数量化3類の具体例
数量化3類の一般化は難しいので、具体例で全体的に解説します。
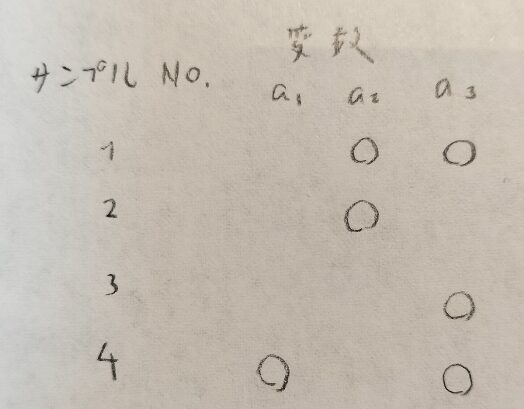
数量化3類では左側にサンプルを、右側に変数をとり、◯で表示されたものが生のデータになります。
数量化3類の目標とは一体なのでしょうか。
いくつかありますが、成分1(主成分分析でいう第1主成分)のみで表現するときは、図02のように◯が対角成分に並ぶような配列を数学的に算出するものです。

そのため数量化3類では相関係数を最大にすることをイメージした式変形を行なっていきます。
数量化3類のやり方
数量化3類の成分1の出し方
数量化3類のやり方としては、サンプルyと変数xを設定するところからスタートします。
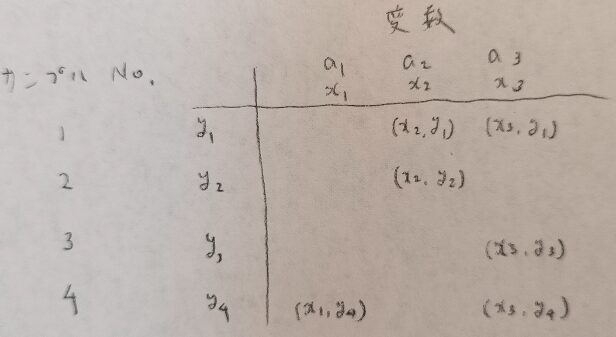
図03で設定した変数を見やすく並び替えます。

ここではxを小さい順に並び替えています。
この時にxとyの相関係数rの最大化を考えます。相関係数は定数倍しても定数を足しても変わらないため、平均が0になるような制約条件を設けます。またxやyの分散が1になるように適切な変数変換も考えていきます。
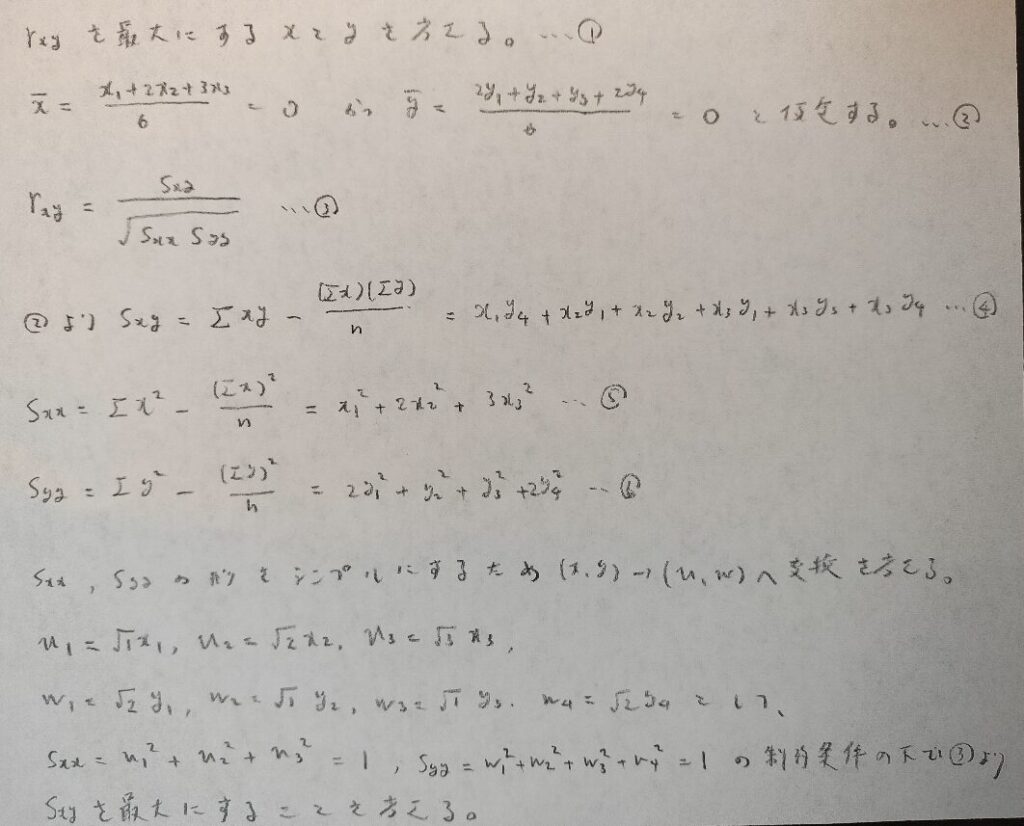
ここまで準備ができたら、主成分分析のときのようにラグランジュの未定乗数法を用いていきます。
数量化3類では第1固有値(最大固有値)は1であり、制約条件を満たさないので、第2固有値から用いることに注意しましょう。

なるほど!ここまで来れば図02が作られているのですね。具体的にはxとyそれぞれで値の大きい数字から並び替えれば◯が対角成分付近に並び出す(相関係数が1に近い)状態が完成するわけですね!
その通りです。ただ成分1だけでなく成分2まで必要な場合もあります。その場合の対処法も考えましょう!
数量化3類の成分2の出し方
主成分分析のときのように、成分1と成分2は変数v,wについて無関係という制約条件を設けます。ただし対称行列の性質から固有ベクトル同士が直交することが確認できるので、結局は成分2についても固有値問題を解けば良いことになります。
成分2は第3固有値と、第3固有ベクトルを求めればOKです。

数量化3類の寄与率と累積寄与率
数量化3類にも寄与率の概念があります。これは成分を幾つまで求めれば良いのかの指標になります。第1固有値が除外されていることにご注意ください。

数量化3類では固有値は必ず1以下になるので、成分数の判断は、累積寄与率が80%以上が目安になります。また成分数の最大数は、(変数の個数とサンプル数の小さい方)ー1個になりますのでご注意ください。
数量化3類での成分1や成分2の寄与率が主成分分析のときのようには大きくはならないときがあります。その時は成分2までを採用する習慣があります。
数量化3類と散布図を書く際の注意点
散布図については主成分分析のときと似てますか?
似ています。変数についての散布図とサンプルについての散布図を描くことになりますが注意が必要です。

ただし、主成分分析のときに扱った内容に沿うようにします。すなわち各変数の普遍分散が固有値になるように定数を掛けてから散布図を書くようにします。

これで自由度が高いように見える数量化3類の解析ができるようになりました。しかし実際はかなりの計算量なので、エクセルやpythonやrやspssなどを用いていくことになります。
この具体例は本書の内容を参考にさせていただきました。本書には詳しい散布図の具体例まで掲載されております。わかりやすく大変おすすめの多変量解析の教材です。