前回の記事で重回帰分析が終わりました。記事をアップしたのが昨日でしたが、思い返すと回帰分析の2記事(単回帰分析と重回帰分析)だけでも相当な量がありました。
今回は数量化1類ですね。名前からしてなんだか難しそうなイメージですが、実際はどうでしょう?
数量化1類は重回帰分析とほぼ変わらない内容です。重回帰分析と異なる点を意識すれば思ったよりも早い段階で活用できる段階まで到達できます。
重回帰分析があれだけの学習量だったのには理由があったのですね。
今回の数量化1類の例などのアイデアのヒントは『多変量解析法入門』から得ています。統計検定1級受験者で多変量解析の分野で名前があがる名著です。
数量化1類と重回帰分析との大きな違い
数量化1類がどのようなものかは、回帰分析との違いを知れば理解できます。
量的変数と質的変数を意識してください。質的変数は本来の数値変数ではない変数のことをいいます。たとえば「優・良・可・不可」や「所属・無所属」などです。

なるほど。数量化1類は説明変数に質的変数が入るのですね。
その通りです。そのため回帰分析のときよりもアンケート調査などで役立ちそうな感じですよね。
つまり質的変数をなんとかして量的変数に変換できれば、重回帰分析の手法が使えるわけです。
数量化1類は多重線形性に注意
質的変数のままだと回帰分析ができないので、なんとかして量的変数に変換したいです。例えば「優・良・可・不可」の場合は、それぞれを「1・2・3・4」と置き換えて良いですか?
結論はNGです。なぜならこれら4つの評価が等間隔の意味とは言えないことが大きな原因です。一般にこのような単純な数値設定には無理が出てきますので、ダミー変数を採用します。
質的変数のことをアイテムといいます。1つ1つのアイテムを構成する中身をカテゴリーといいます。今回の数量化1類はより一般的に考えて、j個のアイテムがあり、i番目のアイテムのカテゴリー数がk個とするとき、このi番目のアイテムを表すダミー変数について考えます。
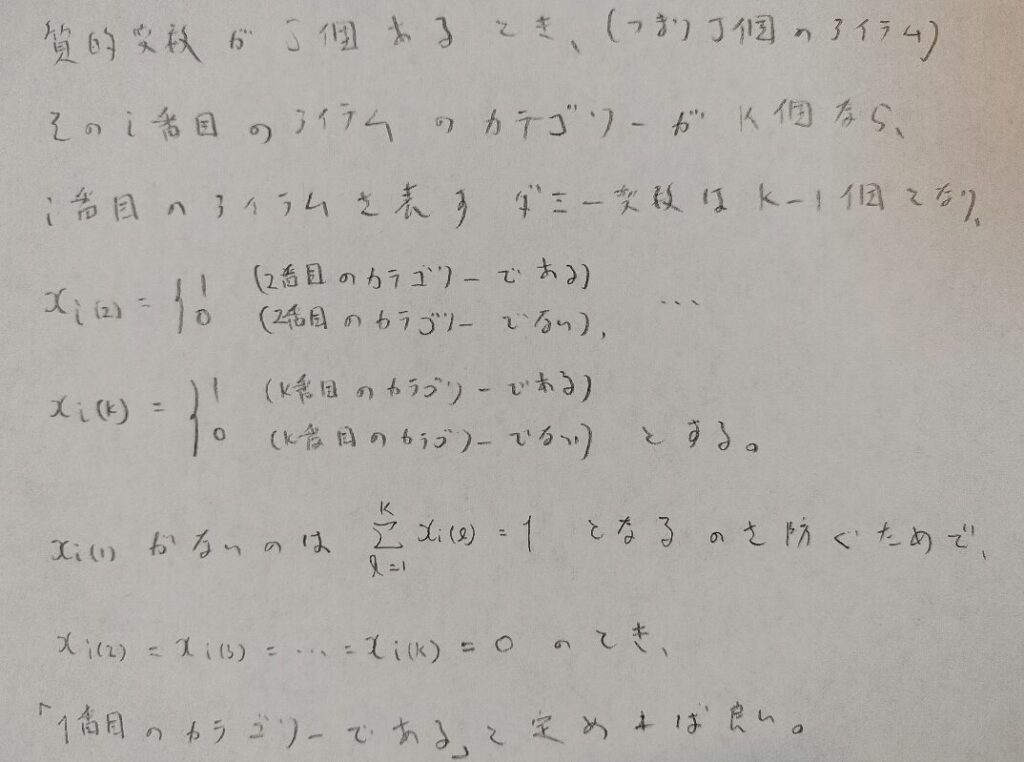
実をいうと、全体で考えたとき(後述する変数の選択を終えたあとでということ)の重回帰分析の式では、上で図02で説明したようなi番目のアイテムを表すk-1個のダミー変数だけではなく、もっと多いダミー変数を採用します。しかし後述する変数の選択を考えると、各アイテムごとで考えるダミー変数単位での重回帰分析の式において多重共線性を生じさせない工夫が必要となります。
もしも数量化1類の説明変数に量的変数が混じっている場合は、その説明変数はこれまでに考えている式に、さらに項を追加していくイメージでOKです。
数量化1類の多重共線性についての説明は『数量化理論とテキストマイニング』がとてもわかりやすいです。本書は数量化4類まで書かれており、大変詳しく学ぶことができます。
数量化1類でわかること
数量化1類の目的を知りたいです。どういった内容をゴールとして分析を行いますか?
やはり将来得られるデータの予測です。その予測を得られるまでの分析の手順を教えます。この手順はダミー変数以外はすべて回帰分析のところで学んでいる内容です。
①質的変数をダミー変数に変換して重回帰モデルを構成する
②自由度調整済寄与率を求めて回帰式の性能を評価する
③有効な説明変数を選択する
④残差とテコ比などより得られた回帰式の妥当性を検討
⑤データの予測を行う
しかし自由度の計算の部分で残差平方和の部分には要注意です。

残差平方和の自由度について混乱してしまったら、重回帰モデルを実際に書き出してみて、説明変数の個数を数えて、その個数を全体のnから引けば自動的に出てきます。−1の分は定数項を意味しています。
要するに、βが書かれている個数をnから引けばOKですね。
寄与率や、自由度調整済寄与率などの計算は重回帰分析のときと全く同じです。変数選択の方法でF値を使う流れも同じです。

ここまでで得られた重回帰式を推定して、実際に様々な条件を設定して推定した重回帰式に代入すると、条件に応じた結果(点数など)が具体的にポンと求まります。
やはり数学(統計学)は面白いですね。数量化1類をしっかりと使いこなせるようになればアンケート調査のプロになれるかも知れませんよ?笑


