QC検定2級は7割の得点率でも不合格になる恐れがある試験です。そのため確実に合格できるための勉強法を模索し紹介します。気になる内容は統計検定2級〜統計検定準1級の前半+暗記物という感じです。
QC検定2級の学習は『【新レベル表対応版】QC検定受検テキスト2級 (品質管理検定集中講座[2])』をインプットにして『新レベル表対応版】QC検定2級対応問題・解説集 (品質管理検定試験受験対策シリーズ 2) 』と過去問をアウトプットとする勉強で合格を狙います。
QC検定4級とQC検定3級を学習してわかったことですが、試験問題は策問者が関係している教材から文章が抜粋あるいは元にして出題されます。特に実践編でその傾向が顕著です。そのため試験対策としては、公式が出している本を選ぶべきだと考えての参考書選択となります。
QC的ものの見方・考え方
応急対策は「原因不明、あるいは原因は明らかだが何らかの制約で直接対策のとれない異常に対してとりあえずそれに伴う損失をこれ以上大きくしないために取られる処置、すなわち急場の現象除去の処置」です。再発防止は「問題の原因又は原因の影響を除去して、再発しないようにする処置」です。3段階の再発防止は個別対策、水平展開による類似原因の除去、仕組みの改善(根本原因の除去)です。再発防止内容は、標準類の作成と改定、教育の反省と改善、作業や仕事の方法に関する工夫と改善、目的や目標の変更です。未然防止とは「実施に伴って発生すると考えられる問題をあらかじめ計画段階で洗い出し、それに対する修正や対策を講じておくこと」です。是正処置とは発生した(顕在化)不適合に対してとる処置で原因を調査して再発防止対策を取る必要があります。予防処置はまだ発生していない(潜在的)不適合に対する処置で、未然防止のための対策が取られます。予測予防は「問題の発生を事前に予測し、それを予防する」ことです。
見える化は「問題の早期発見や解決を目的に、各種の情報を共有化するため、現状をデータで明らかにし、グラフや図解による可視化を行うこと」で「企業活動の実態を正しく見える状態を作り出し、さまざまな事象を顕在化させることで、問題設定を高度化し、問題解決を加速させること」と大きく捉えられることもあります。
見える化をアクションに結びつけるためのステップ
①現状を見えるようにする
②現状から問題を抽出する
③目標を設定し、問題に対して解決策を検討する
④目標を見えるようにする(共有できるようにする)
⑤目標と現状のギャップ(もしくは異常)を見えるようにする
⑥目標までに具体的なアクションを設定する(実現への道筋の見える化)
⑦目標に向けての行動を起こす
⑧行動の過程では目標に向けた到達状況(進捗)を見えるようにする(評価する)
潜在トラブルの顕在化とは「再発防止や未然防止を効果的に進めるために、報告されていない、表面化されていないクレーム・不良、手直しなどに目を向け、顕在化させるという行動原理」です。KYT(危険予知訓練)として実施され成果を上げることができます。
是正処置は再発防止のために行い、予防処置は未然防止のために行います。
「見える」ことにより「気づき」→「考え」→「行動する」ことが期待されます。人、設備、方法、製品ごとに「あるべき姿」と比べて異常がないかがわかるような工夫がされている。見えた結果が関係者の行動に繋がならければならない。潜在トラブル、潜在ロスの顕在化とは・・・。
品質の概念
品質管理の定義は「買手の要求に合った品質の品物又はサービスを経済的に作り出すための手段の体系」です。しかしこの規格は現在廃止されています。「市場の調査、研究・開発、製品の企画、設計、生産準備、購買・外注、製造、検査、販売及びアフターサービス並びに財務、人事、教育など企業活動の前段階にわたり、経営者を始め管理者、監督者、作業者など企業の全員の参加と協力が必要である」とも記載されます。これをTQMといい顧客指向、継続的改善、全員参加により展開されます。
品質は「対象に本来備わっている特性の集まりが、要求事項を満たす程度」とされます。ジュラン博士は「品質とは、使用目的に対する適合」としています。QCDを広義の品質といいます。QCDSを言うときもあります。品質第一とは製品の品質確保をすべての業務に最優先することです。
要求品質は「製品に対する要求事項の中で、品質に関するもの」です。要求品質を展開した表と品質特性を展開した表の二元表を狭義の品質表と言います。品質要素とは機能、性能、操作性、安全性、信頼性などです。品質特性とは品質要素をさらに具体的に表現したもの、製品の性質の違いを示す尺度を言います。技術や製造部門では品質特性が用いられ、消費者との関係では品質要素の用語が用いられます。
ねらいの品質=設計品質とはお客様の要望(要求品質)を正しくつかみ、それを実現するための能力も十分考えに入れて、このようなものを作ろうとねらった品質を言います。品質目標は現在の能力(技術)では実現できるかどうか疑問であるが、ある時期までに実現することが期待される品質水準です。できばえの品質=製造品質=適合の品質=合致の品質とはねらいの品質をどれくらい忠実に実現できたか、と言う点にかかわり品質です。品質標準とは現在一応満足でき、すでにもっている能力(技術)で実現できる品質水準です。
使用品質は品物を買手のところで実際に使ったときの良さで、品質水準は品質特性がどのようであるかの度合いで、官能特性は品質特性のうち、色、味、におい、肌ざわりなど人間の感覚によって判断されるもので、代用特性とは「要求される品質特性を直接測定することが困難なため、その代用として用いる他の品質特性」で官能特性などを工場で実現できるような品質特性に置き換えたものです。
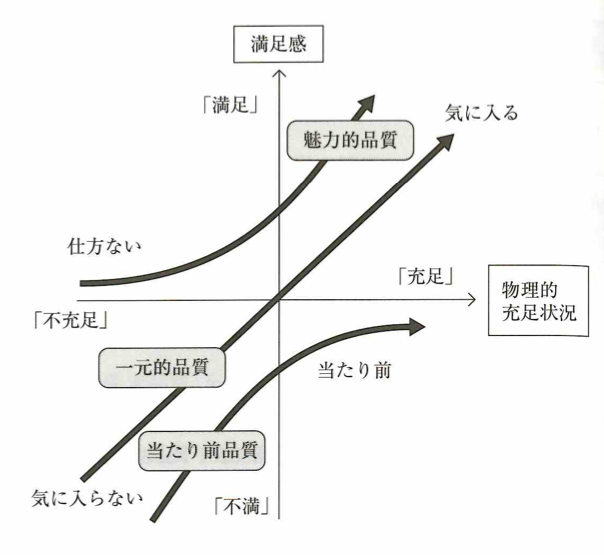
当たり前品質とは「それが充足されれば当たり前と受け取れるが、不充足であれば不満を引き起こす品質要素」です。魅力的品質とは「それが充足されれば満足を与えるが、不充足であっても仕方ないと受け取られる品質要素」です。一元的品質とは「それが充足されれば満足、不充足であれば不満を引き起こす品質要素」です。ある品質に対する評価は、時が経過するにつれ、魅力的品質→一元的品質→当たり前品歳へと変化します。無関心品質要素は「充足でも不充足でも、満足を与えず不満も引き起こさない品質要素」です。逆品質要素は「充足されているのに不満を引き起こしたり、不充足であるのに満足を与えたりする品質要素」です。
当然あると思ったのになかったのは当たり前品質、ソフトが標準装備していたことが当然だと思うのは一元的品質です。どちらかを判定するには二元表の理解+国語力が必要です。
サービスの品質は「サービス提供過程の品質」と「サービス結果の品質」で構成されます。
顧客満足(CS)は「製品またはサービスに対して、顧客が自分のもつ要望を充足していると感じる状態」です。顧客とは「個人若しくは組織向け又は個人若しくは組織から要求される製品・サービスを、受け取る又はその可能性のある個人又は組織、例 消費者、依頼人、エンドユーザ、小売業者、内部プロセスからの製品又はサービスを受け取る人、受益者、購入者 注記 顧客は組織の内部又は外部のいずれでもあり得る」です。フィリップ・コトラーの純顧客価値を提唱しており、総顧客価値を考えることにより、純顧客価値=総顧客価値ー総顧客コストで求められます。
品質とは「品物の性質」というのが一般的である。ハードウェアなどの有形なものの場合は「品質」サービスなどの無形のものの場合は単に「質」という言葉を用いる場合もある。対象とは「認識できるものまたは考えられるものすべて」要求品質とは、製品に対する要求事項の中で、品質に関するものである。ねらいの品質/質とは「顧客・社会のニーズと、それを満たすことを目指して計画した製品・サービスの品質要素・品質特性・品質水準との合致の程度」であり…。企画や設計を通して実現される製品として満たすべき高モックとその目標値を企画段階で決められ、これを受けて、設計段階ではデザイン、構造、部品などを具体的に決められる。…できばえの品質/質とは「計画した製品・サービスの品質要素・品質特性・品質水準と、それを満たすことを目指して実現した製品・サービスとの合致の程度」であり…。
充足でも不充足でも、満足を与えず不満も引き起こさない品質要素は無関心品質要素であり…。
事務部門、販売部門の品質管理、レジャー業、輸送業、通信・情報業、エネルギー供給業、構成福祉業の品質管理では、サービスの質を品質と考えることが多い。サービスの品質を評価する項目の1つに、信頼性がある。信頼性は、約束したサービスの正確な実施のことである。




