前回の『ロジスティック回帰』の自然な続きとしてプロビットモデルを考えます。
そしてアクチュアリー数学の過去問で出題された問題を用いて指数線形モデルを解説し、対数線形モデルの考え方も同時に解説します。
今回のプロビット分析の話の構成は久保川先生の『データ解析のための数理統計入門』を参考にさせていただきました。
プロビットモデルはロジスティック回帰と途中まで同じです
まずはプロビットモデルの考え方を説明します。ロジスティック回帰のときと同様にyが0か1を取るデータが複数個観測されたとします。
ポイントはyはその範囲から確率を表すと考えて差し支えないということです。
目標はこの関数を推定することです。つまりαとβの推定値を出すことになりますのでモデルを作成したのちに最尤法を用いていきます。
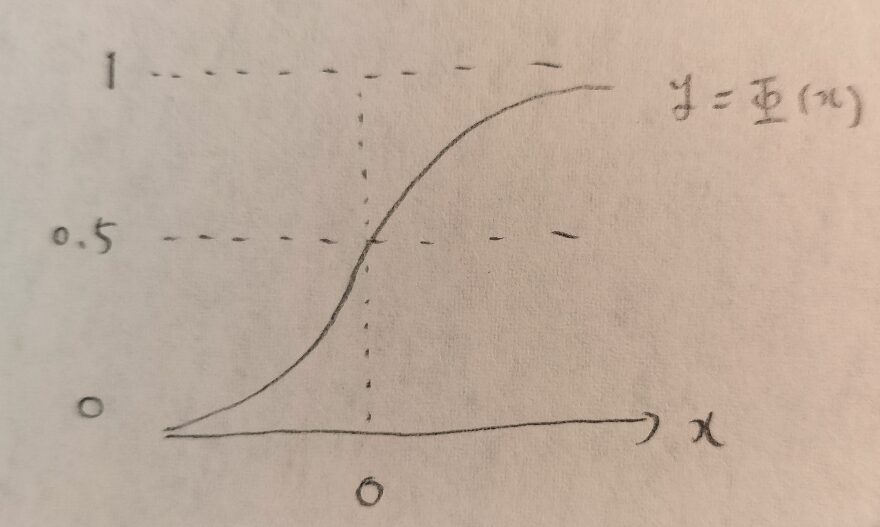
ロジスティック関数のときとほぼ似た形ですね!共通点はyが0から1までを表せるということですね!
その通りです。お気づきかと思いますが、前回のロジスティック関数も今回のΦも分布関数だったのです。
それではプロビットモデルを0から構成してみましょう。
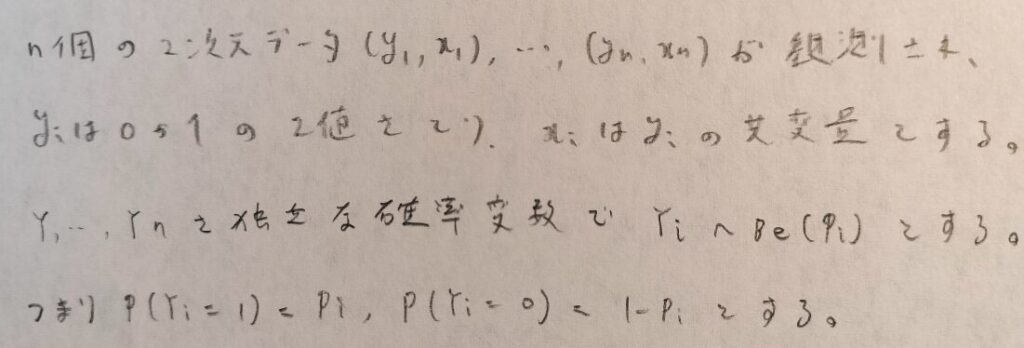
ここからロジスティック回帰との分岐が生じます。プロビットモデルでは、リンク関数としてΦを用います。
前回のロジスティック関数を用いるよりも単純な感じがします。
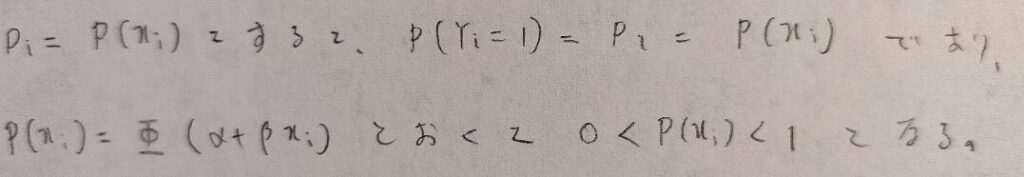
この時に考える尤度関数のことをプロビットモデルといいます。すなわち図04の第2行目をプロビットモデルといいます。
プロビットとはどういう意味ですか?
プロビットとは正規分布の分布関数の逆関数のことを指します。後ほど具体例を紹介しますが、分析の際にΦの逆関数を用いていくことになります。
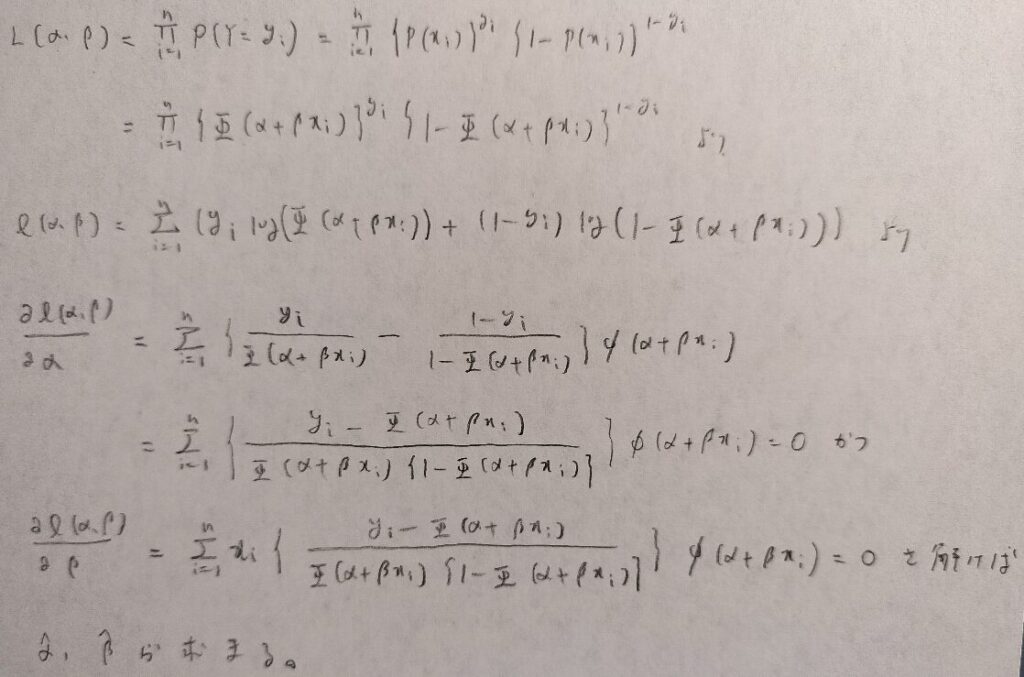
プロビットモデルの例(アクチュアリー数学2017年度)

それでは解きます。要するに元のデータyを変換したy’を求めてから単回帰分析を行うだけです。yからy’を出すときにプロビット変換を行っています。
なぜプロビット変換をすれば単回帰分析に持ち込めるかは図03の最後の行に書いていますね!
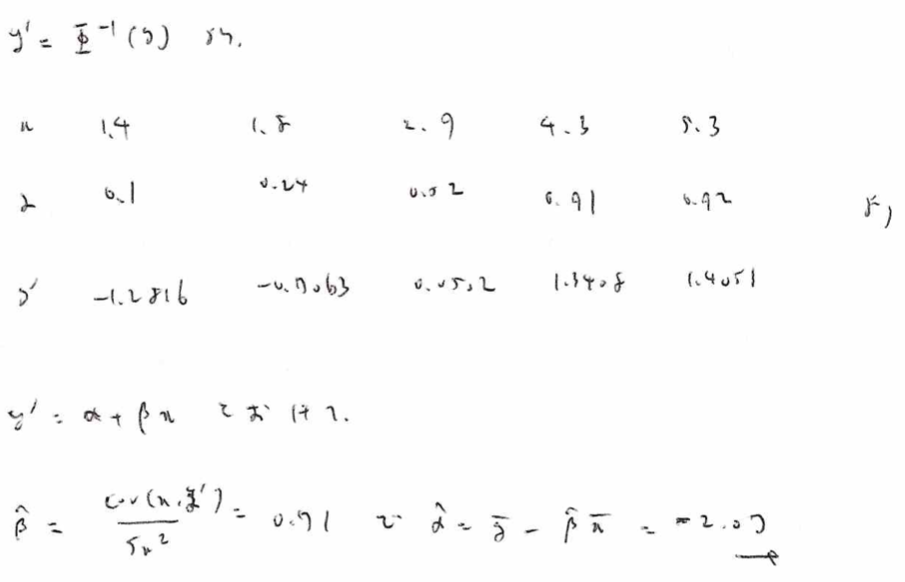
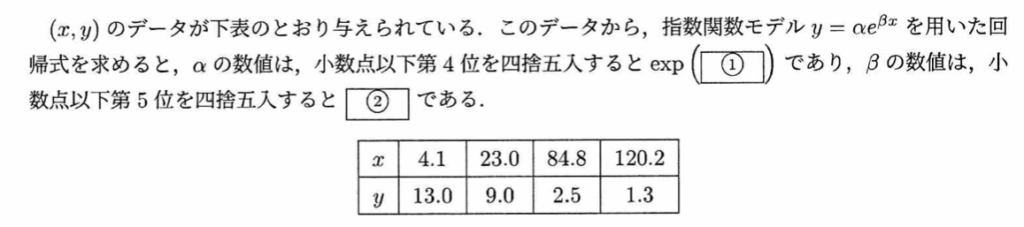
指数関数モデル(アクチュアリー数学2022年度)
指数関数モデルの問題を解く際は両辺に対数を取ることによって単回帰分析に帰着することを用います。
このように高校数学で習った関数が出てくることがあります。今回は扱いませんが重回帰分析の応用では多項式回帰や双曲線モデルなどもあります。
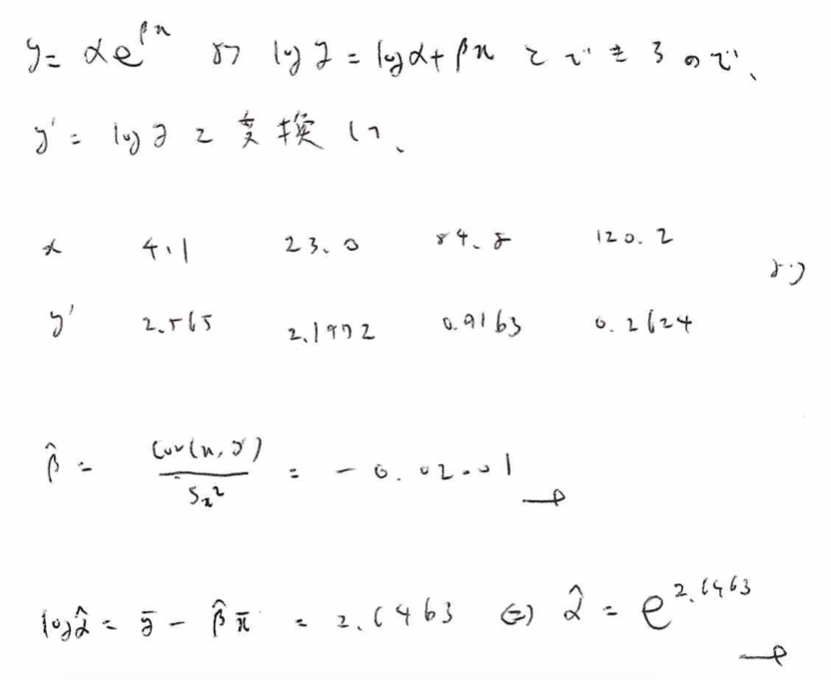
対数線形モデルの考え方
対数線形モデルはy=αx^(β)の形のモデルです。こちらも指数関数モデルと同様に両辺に対数を取ることにより単回帰分析に帰着します。
前回のロジスティック回帰から派生してプロビットモデルを考え、その他にも単回帰分析に帰着できる問題を考えました。
まだまだモデルは他にもありそうですね!次回も楽しみにしておきますね。
本記事では『データ解析のための数理統計入門』を参考にさせていただきました。
アクチュアリー数学の内容のほとんどは網羅され統計検定1級対策としても素晴らしい作りになっています。演習問題は必見です。本記事の問題の一部は『データ解析のための数理統計入門』を参考にさせていただきました。


