統計検定1級とも範囲の被る標本分布と標本調査の章を詳しく学習します。本記事は使用する書籍によってはマイナーと感じる箇所のため難易度が高いと感じると思います。
しかし掲載されている例題や問題の順番は非常に体系的ですので、本記事の問題演習を通して実力を養うことができます。
本記事ではアクチュアリー数学指定の参考書『確率統計演習 2 統計』を用いていきます。細かい問題設定は本書をご覧ください。
『確率統計演習 2 統計』で学習する他分野のリンク先をまとめています。是非ともご活用くださいね。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)
『国沢統計』第5章「標本分布論と標本調査」の例題

本章では『確率統計演習 2 統計』を用いて標本分布論を学習してから、標本調査の内容を学習します。
標本分布論
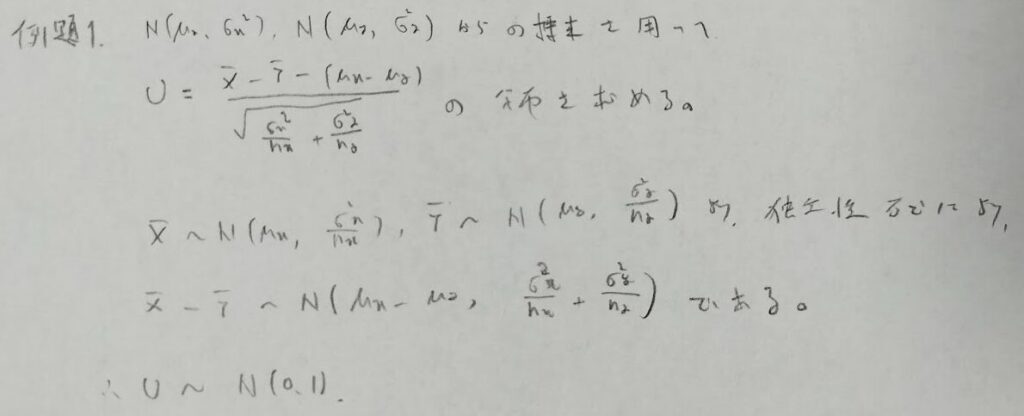
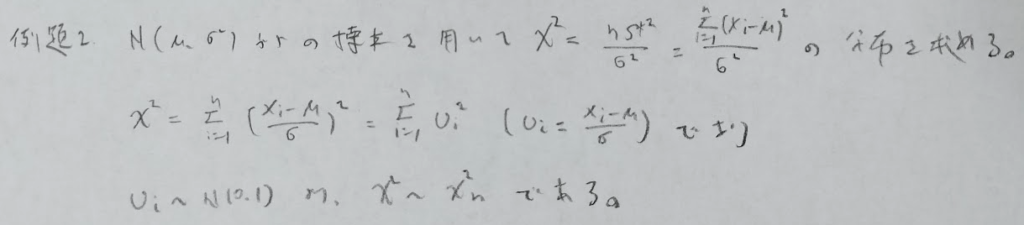
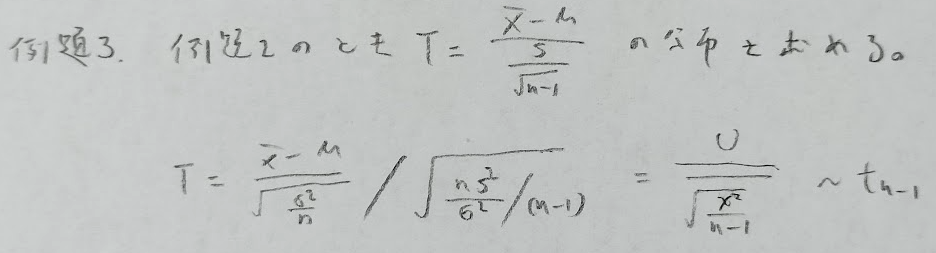
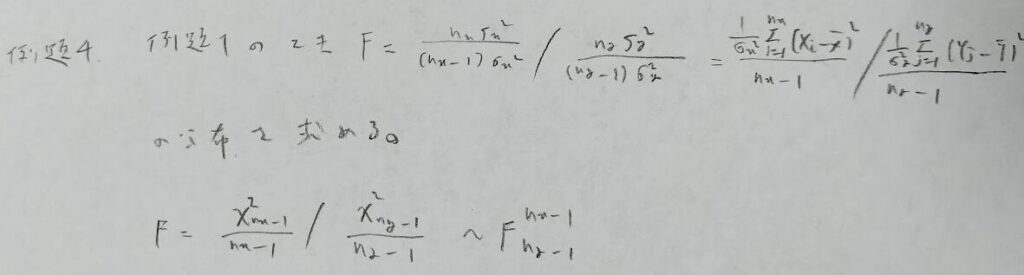
次の問題は本書『確率統計演習 2 統計』の中でも特に素晴らしい問題です。
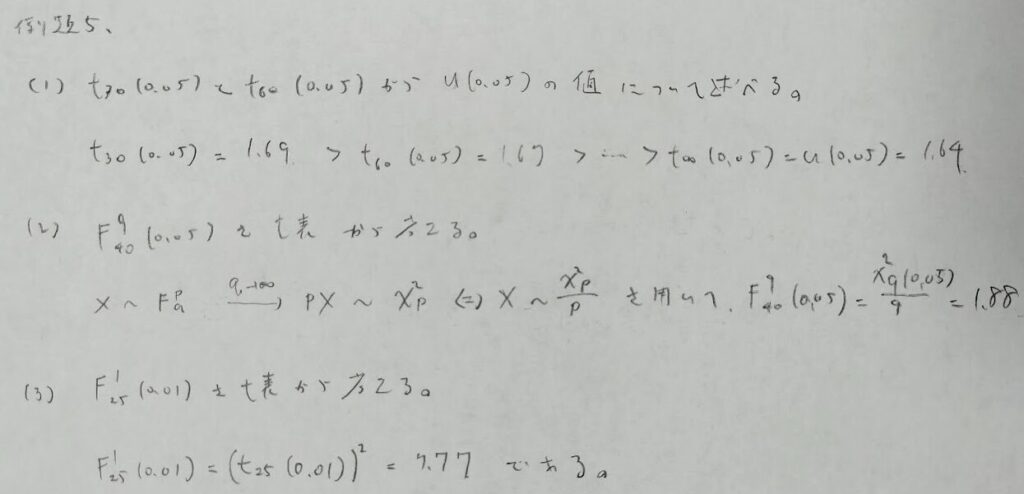
(2)は『確率統計演習 2 統計』にしか言及されていないレアな内容です。証明はスターリングの公式を用いて計算していきます。
いよいよ最難関のコクランの定理に入ります。
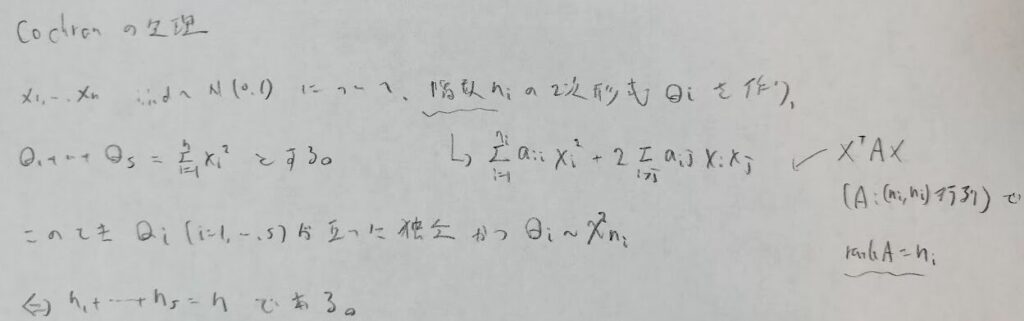
例題6は有名な性質をコクランの定理を用いて導く問題でアクチュアリー数学では未出です。しかしかなりの難問です。
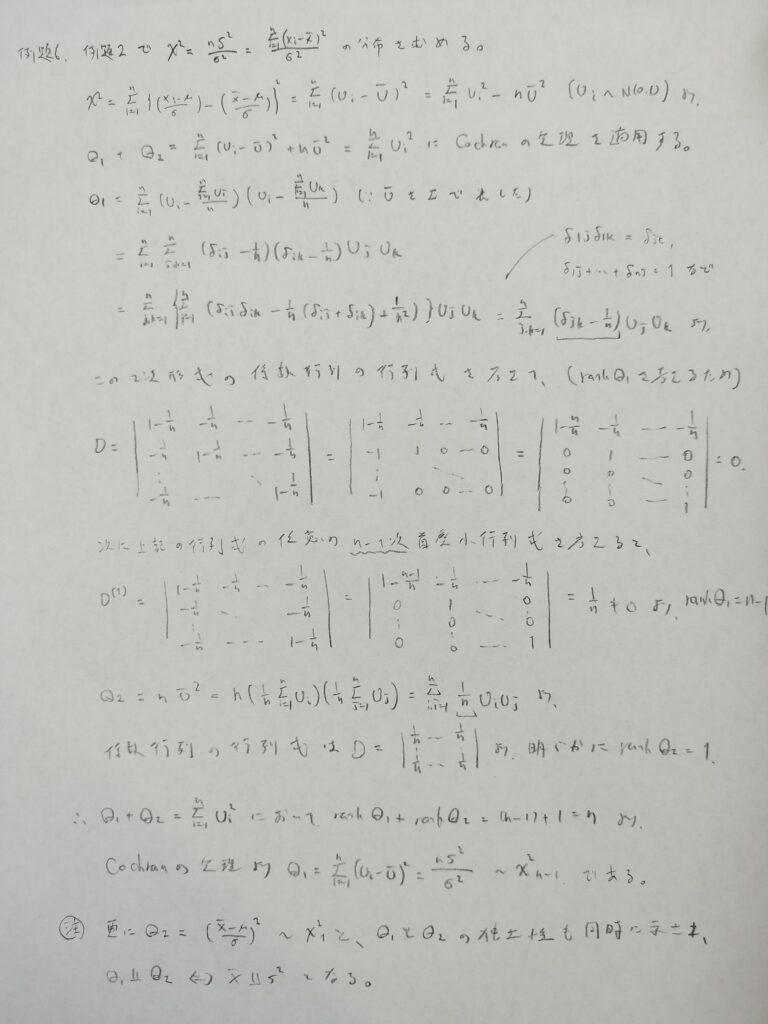
Q1については有限和でのシグマの交換は許されることなどを用いています。ランクを求めるために首座行列式の考え「行列Aの階数はAの0でない小行列式の最大次数に等しい」を用います。n次正方行列の場合は、解答のように各行から第1行を引き、さらに各列を第1列に加えています。また最後の独立性については背理法を用いることで示すことができます。
統計検定1級のバイブル『現代数理統計学の基礎』で天下り的な証明で解説されていた本問の本質がコクランの定理から派生している事実があることがわかりますね。
今回のような線型代数の知識が不安ですが、適切な本があれば教えてください。
『線形代数学』がおすすめです。これより簡単だと形式的に対角化ができるレベルくらいの本になり、これより難しいと代数学よりになるイメージがあります。
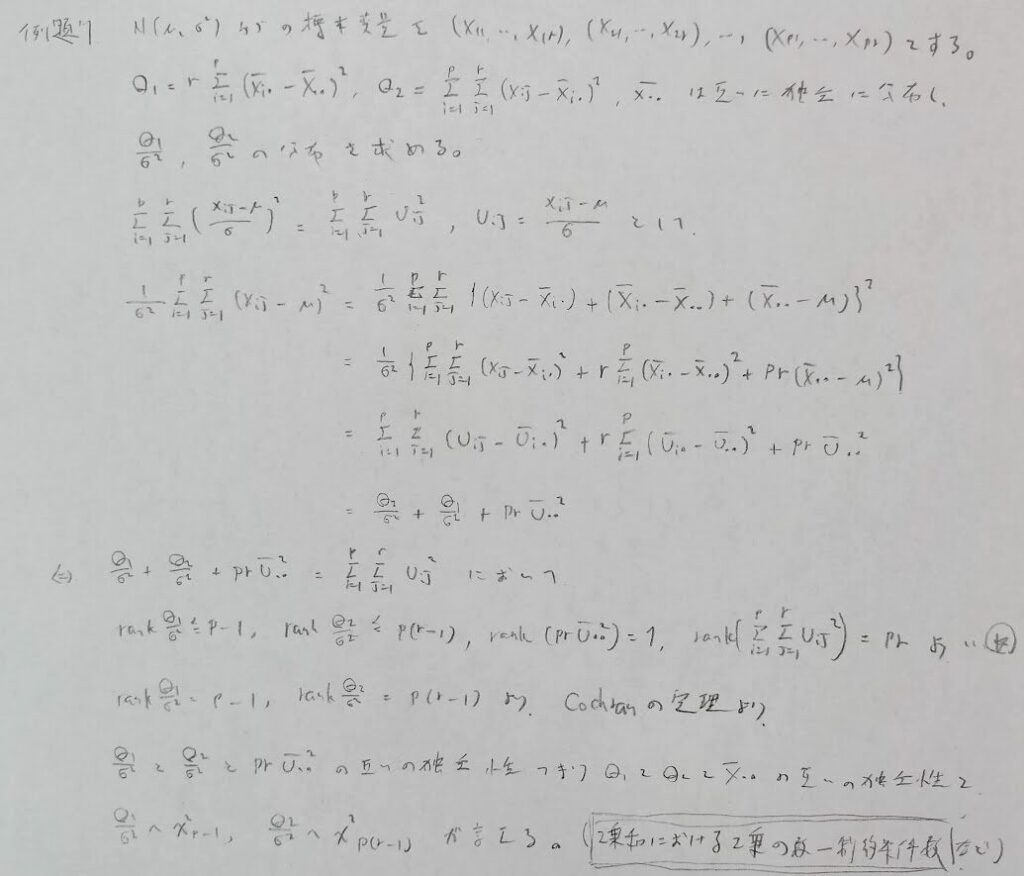
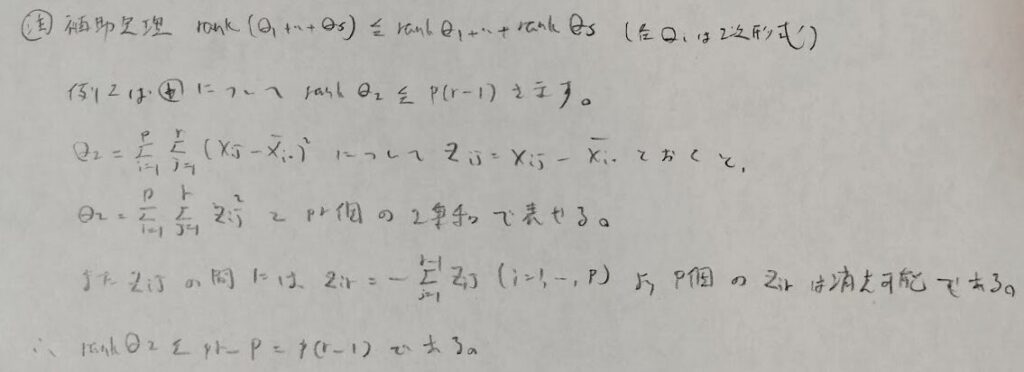
ポイントは標準正規分布の2乗を作り出す式をベースに考えることと、ランクは自由度と似たもののイメージを持つことです。
とても難しい問題ですが、減点を覚悟の上ならば一応答えまでは行きつけるようにしたい問題ですね。
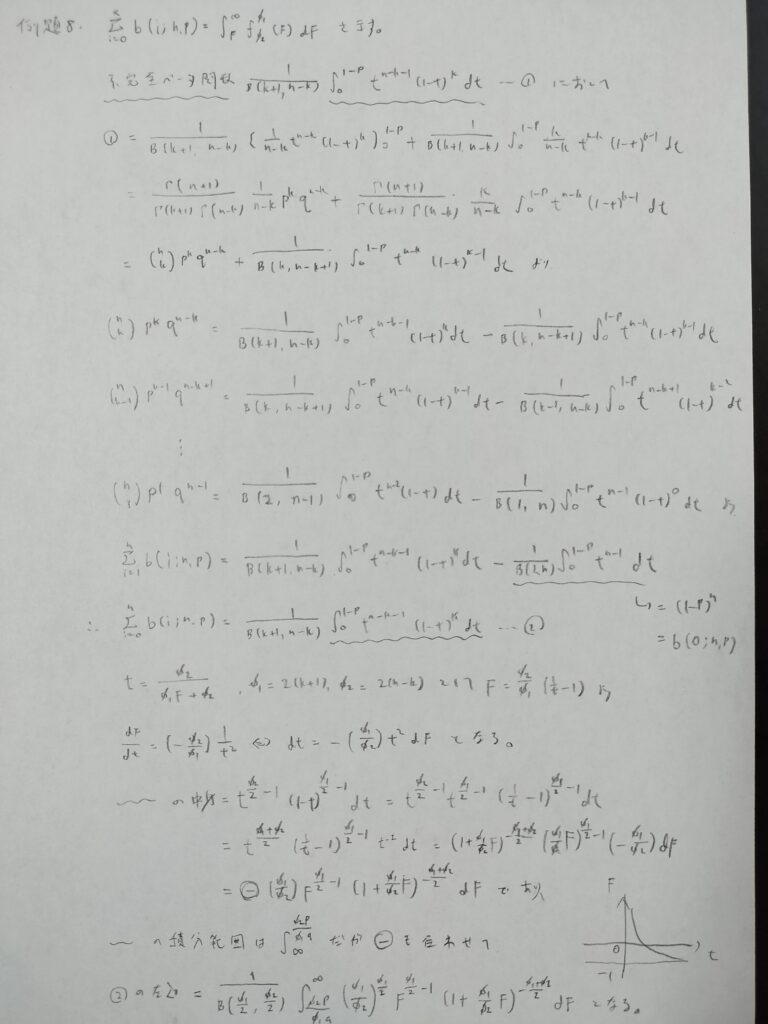
示すべき右辺の積分区間の下端のFは何か定数が入ります。『確率統計演習 2 統計』の原題を尊重してそのままの表記にしました。
①式の積分部分を不完全ベータ関数といいます。またzのz実部は0以上1以下とします。
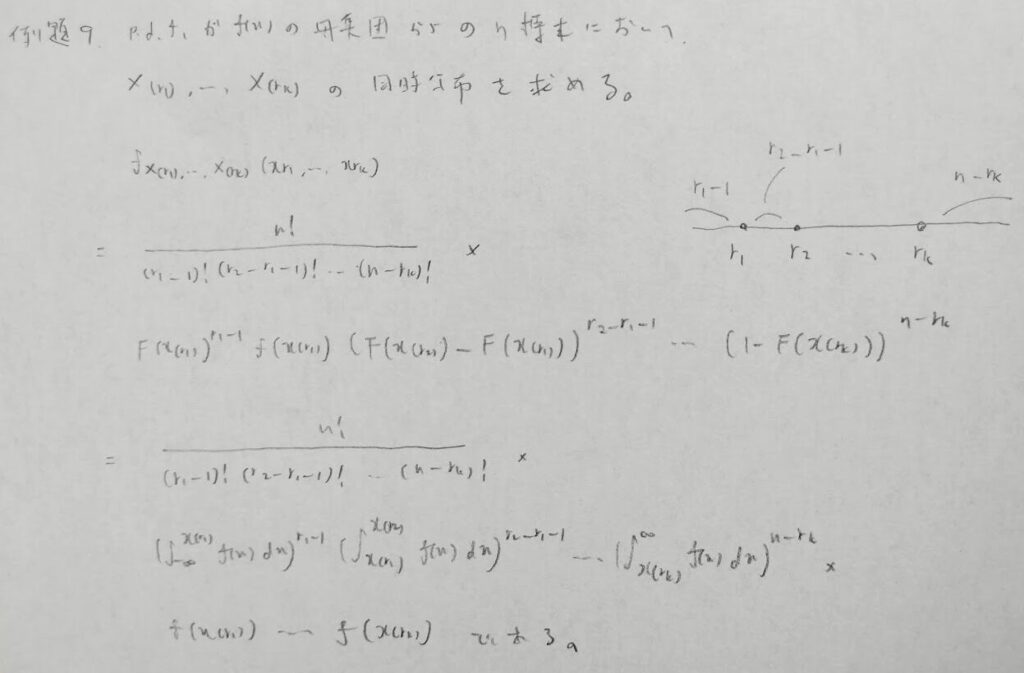
多項分布の考えを用いる方法ですね!以前に順序統計量についての解説記事のこちらの記事に詳しく解説されていましたね。
そうですね。基本的に事象・各事象に対応する確率・各事象が生じる回数の3つに注目すればこれ系の問題は解くことができます。またこれらの厳密な考えは『現代数理統計学の基礎』での学習が分かりやすかったです。
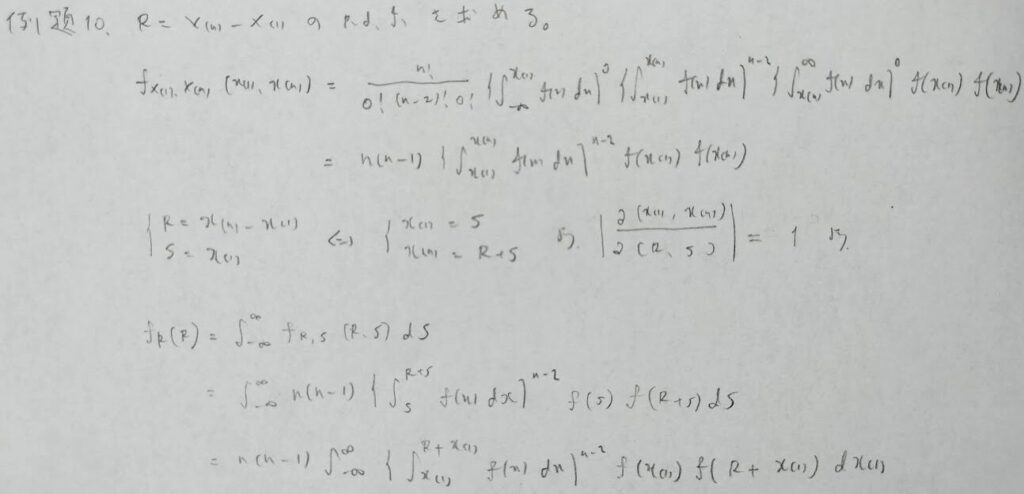
標本範囲の分布では、最小値のとりうる範囲の考察が大事になります。公式として暗記するかは迷うところです。
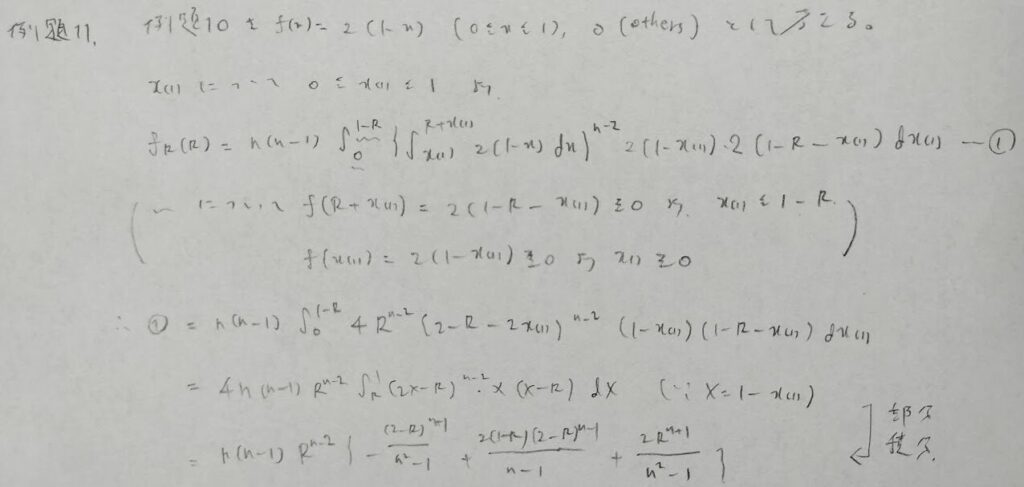
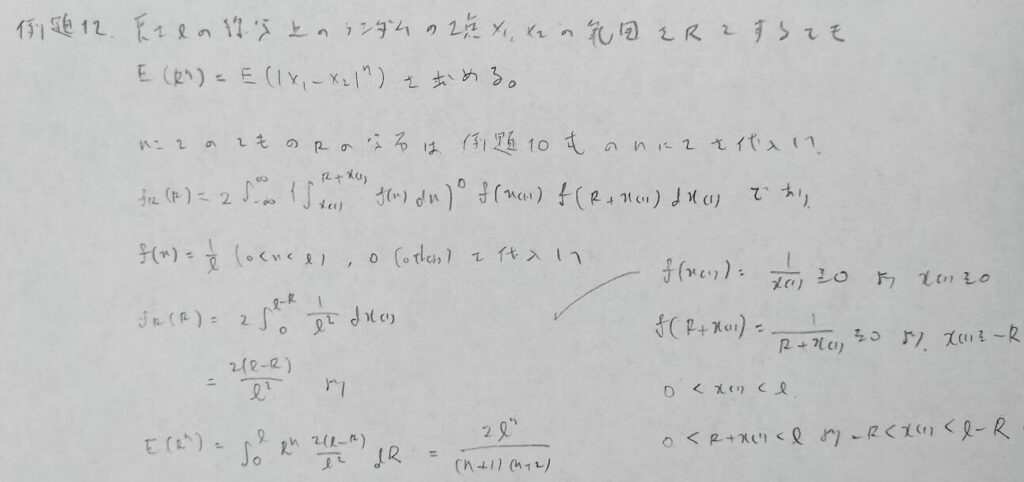

標本を用いていろいろな性質が導かれていくのは面白いですね。信頼係数との融合問題は『確率統計演習 2 統計』にのみ掲載されており、アクチュアリー数学でも出題歴があります。
u+v=1でなく1以下というのが特徴です。これによりuの積分区間が求まります。
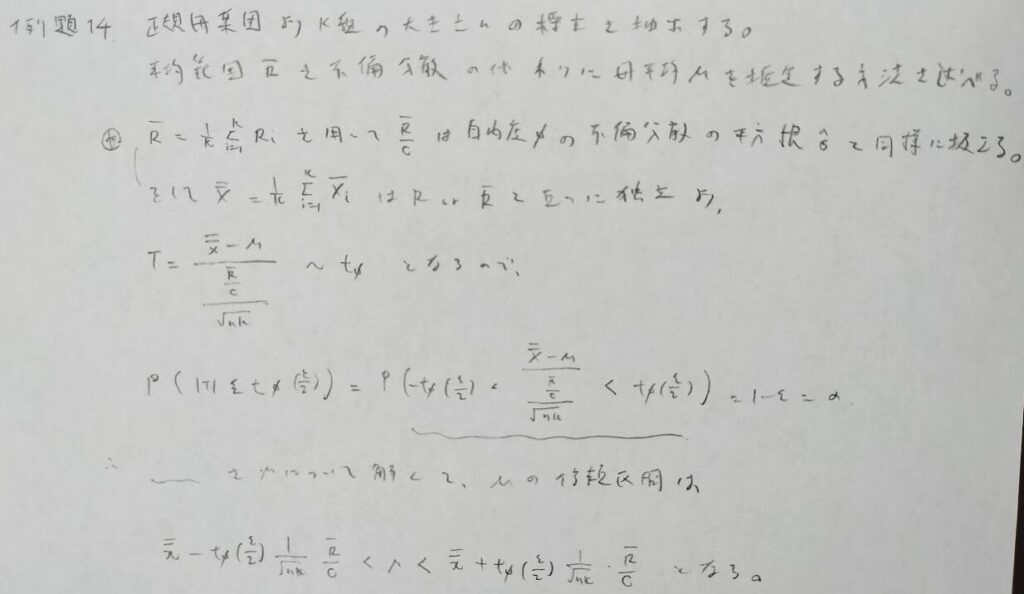
例題14は全体の標本数がnkであることに注意しましょう。解答中の☆の式は知識として持っていないと解けない問題です。この知識も『確率統計演習 2 統計』にのみ掲載されています。とてもカバー率が高い本ですね。
cと自由度φを求めるためには事前に「平均範囲の分布へのカイ二乗近似」に関する表が与えられるはずです。
普遍分散の平方根への近似であることにより、t分布が関係していることはすぐにわかりますね!
標本調査
本節の内容は抽出法になります。まずは任意抽出法、層別抽出法、2段抽出法についての公式を覚えておきましょう。アクチュアリー数学では0から公式を導いていては時間制限でタイムアップになってしまうからです。統計検定1級ですとここの内容は難問率が高い分野になります。
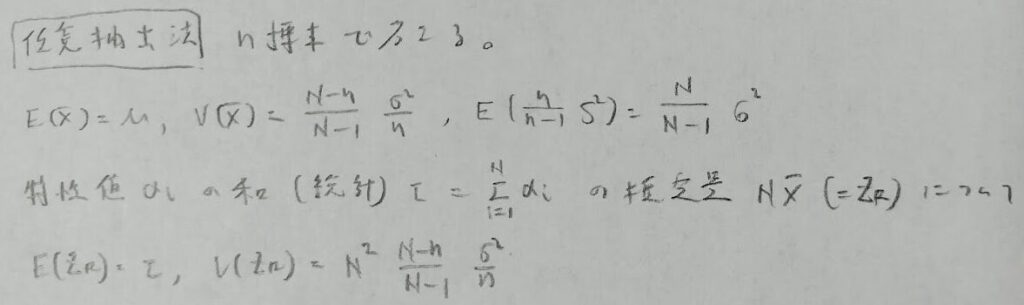
Rはランダムサンプリングの頭文字です。

ポイントは各層は任意抽出法になっているので、層別抽出法は任意抽出法のそのままの応用となっているということです。また、層別抽出法はさらに細かい種類に分かれます。

pは比例の英語表記proportionalの頭文字です。
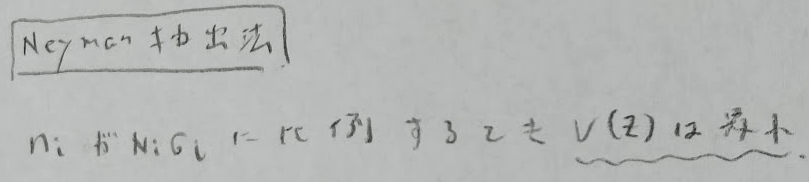

最後に2段抽出法を紹介します。最後なだけあってこれがもっとも理解しにくいです。

標本の値はxで、実際の値はαで使い分けています。
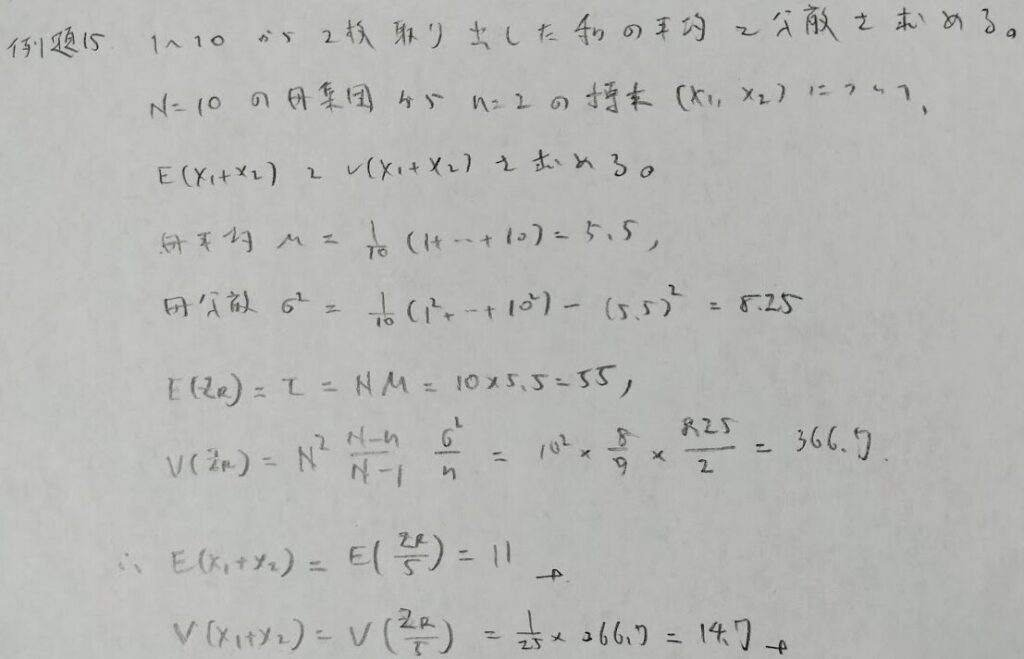
『確率統計演習 2 統計』では上記の解き方をしていますが、どうもτを持ち出す方法が分かりにくい(本番で思いつきにくい)ので別解も載せておきます。
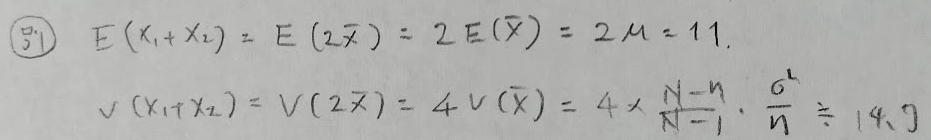
絶対こっちの方が応用効きやすいと思います!笑
確かにそうですが、どちらの方法でも母平均と母分散は求めないといけません。

任意抽出法の公式は全て覚えましょう!アクチュアリー数学でも頻出の公式となります。
アクチュアリー数学で覚えるべき公式が結構あると気づきました。公式を覚えやすい参考書はありますか?
『アクチュアリー試験合格へのストラテジー』が体系的に載っているので覚えやすくおすすめです!
『国沢統計』第5章「標本分布論と標本調査」の問題

本章では『確率統計演習 2 統計』を用いてコクランの定理を用いる問題から学習します。コクランの定理自体が類書に載っていない場合が多く、最初から難易度MAX付近ですが頑張りましょう!
Cochranの定理とその応用
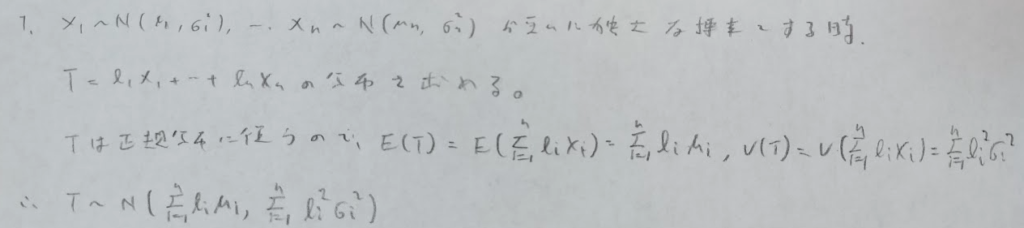
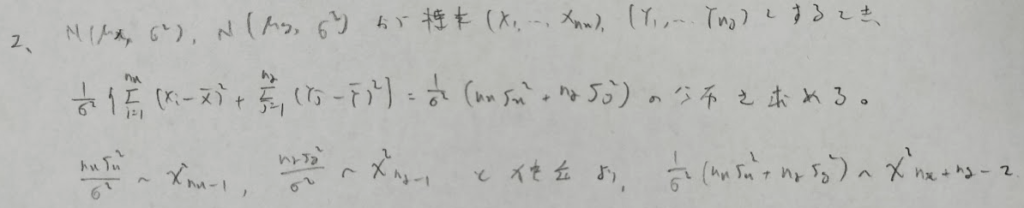
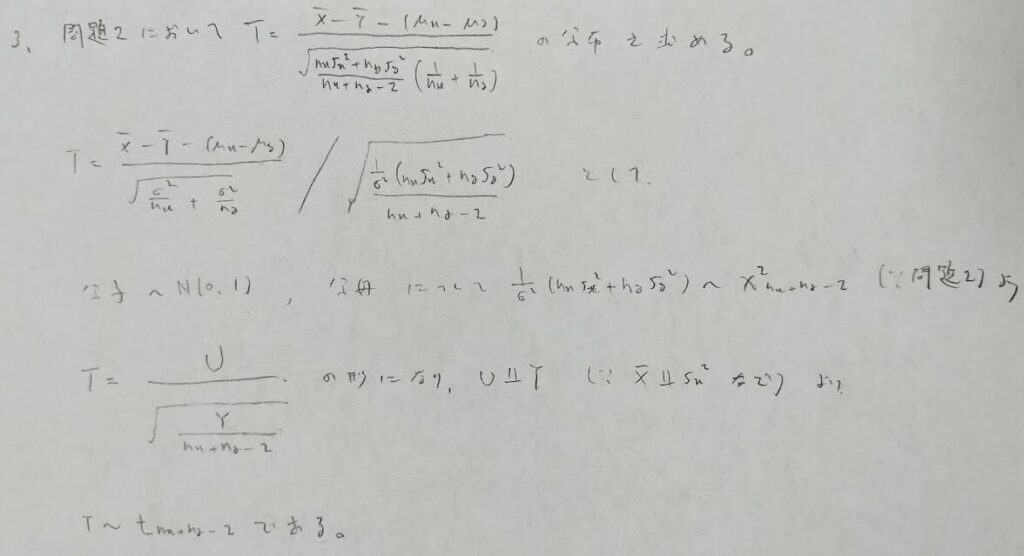
問題4はかなりの難問です。

第5行目の方針は、Xの標本平均も、標本分散も、すべてn個のUの標本から作られているという考え方です。
解答中の定数cの値を求めたいです。
了解です。下記に計算しておきましょう。ポイントはガンマ関数の利用です。またn次元超球の体積の簡易的な求め方も紹介しておきますね。

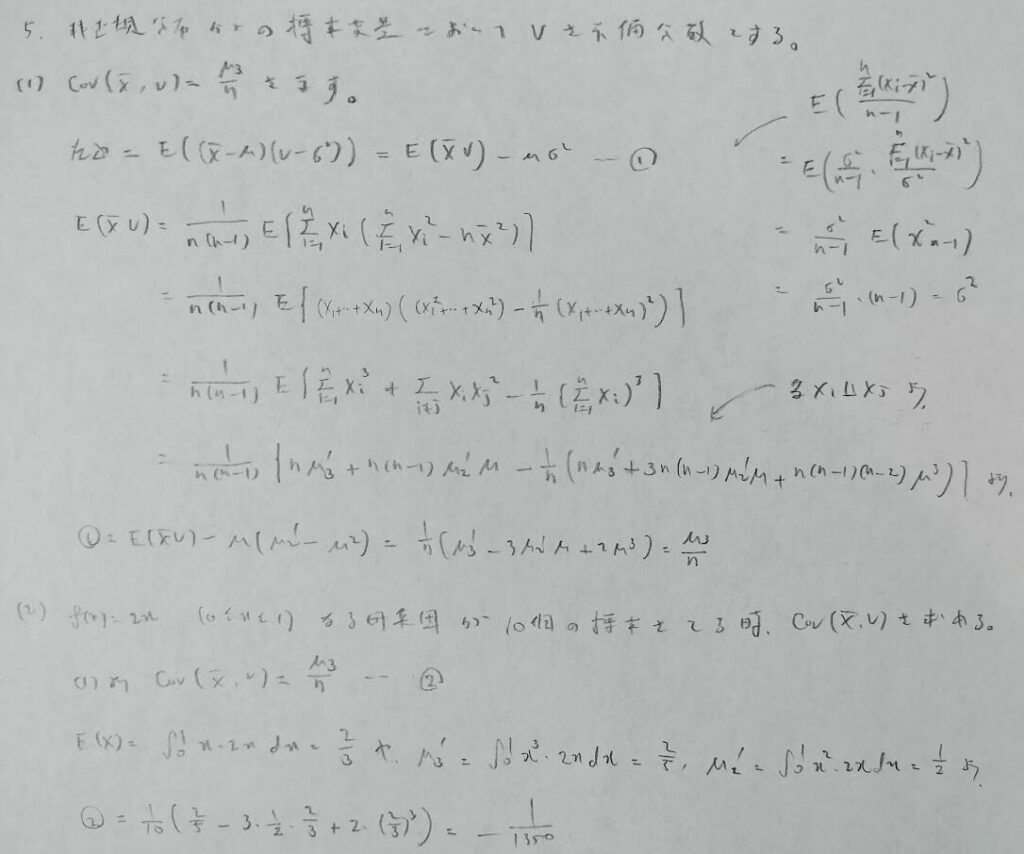
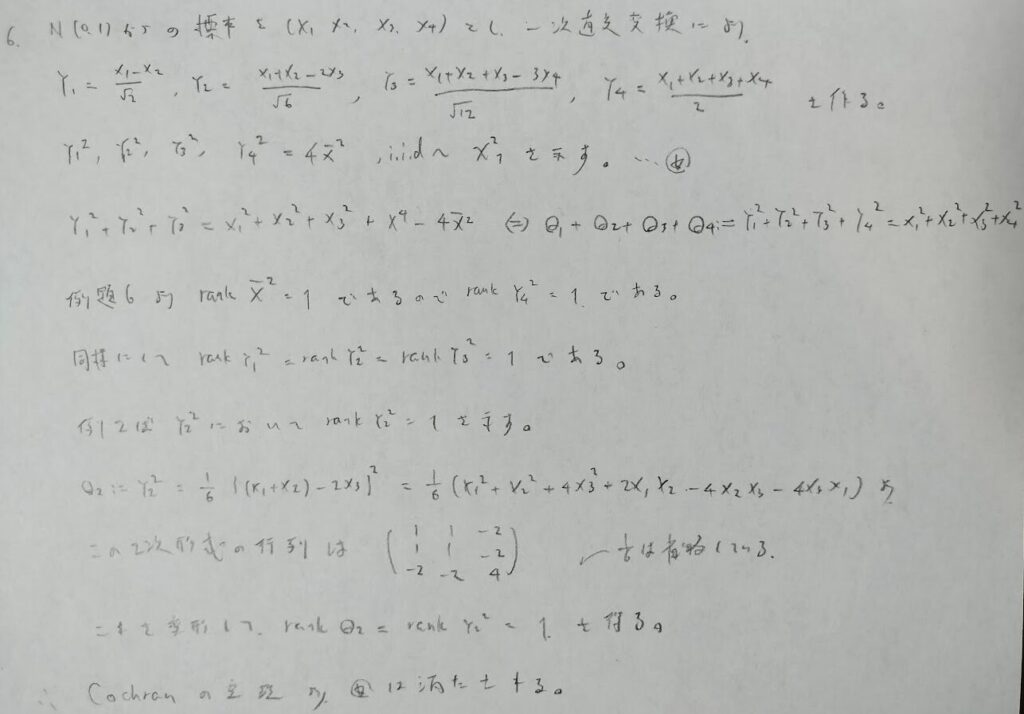
次の問題7は『確率統計演習 2 統計』の中での最難関の問題です。
問題7は最後の方が処理できず解答不能となっています。そのため途中までの答案を掲載します。答えの形がどのような感じになるのかも推測できず、最難問扱いとしています。
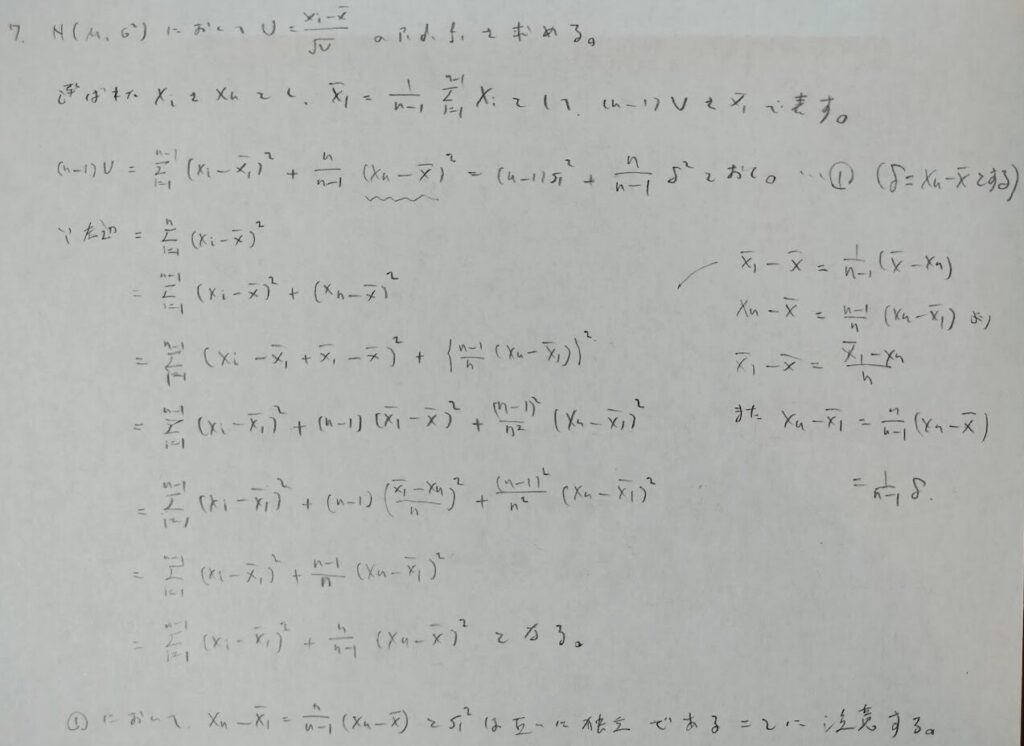
ここから処理可能な方はコメントからご教授いただけますと幸いです。
いろいろな分布をした母集団からの標本変量の性質の問題
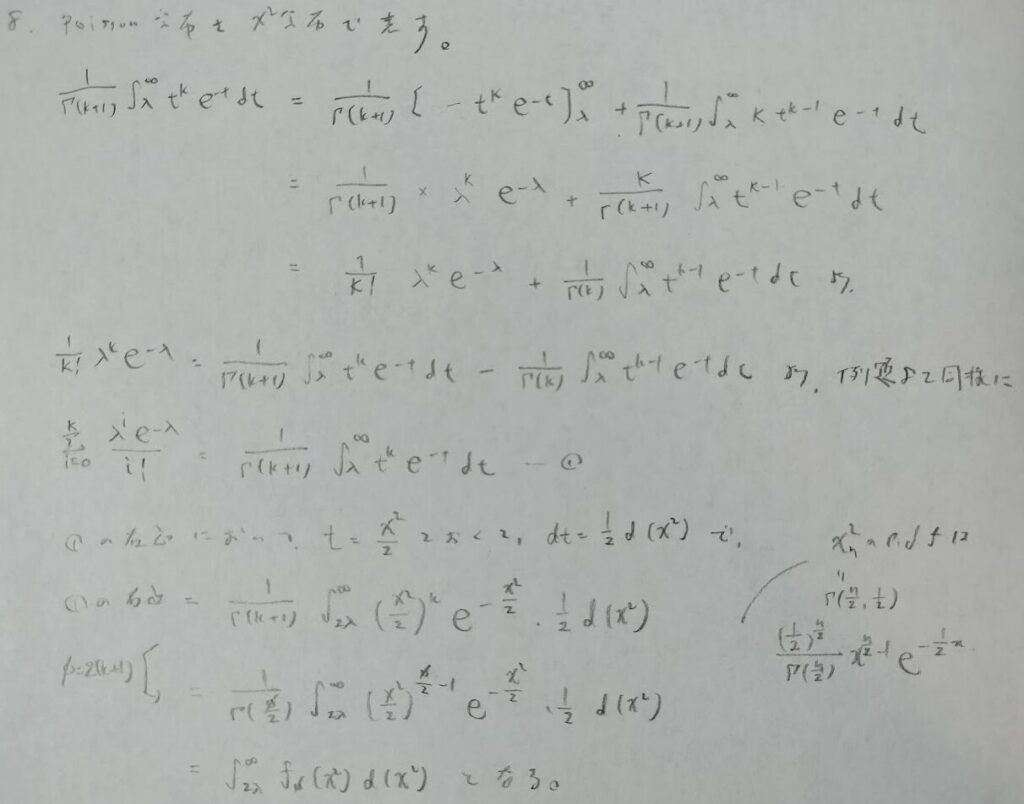
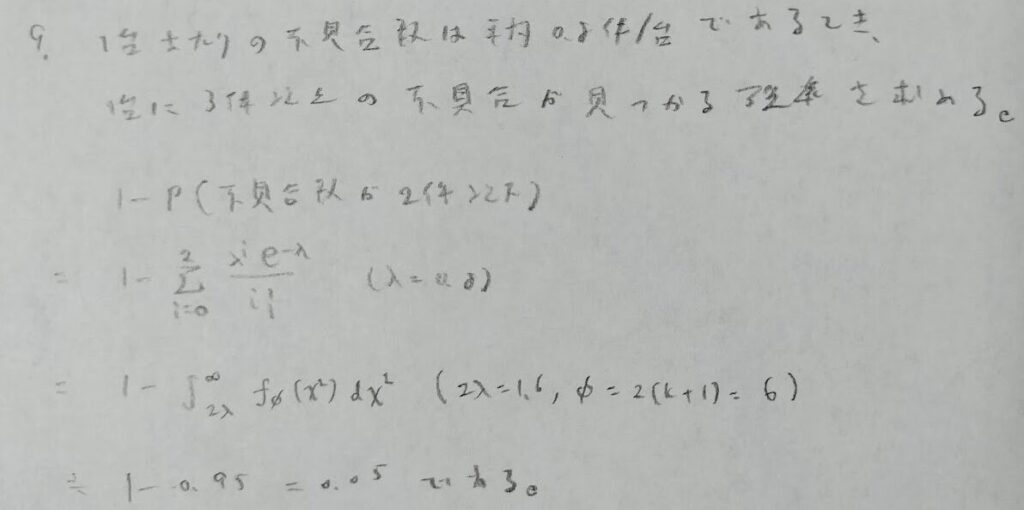
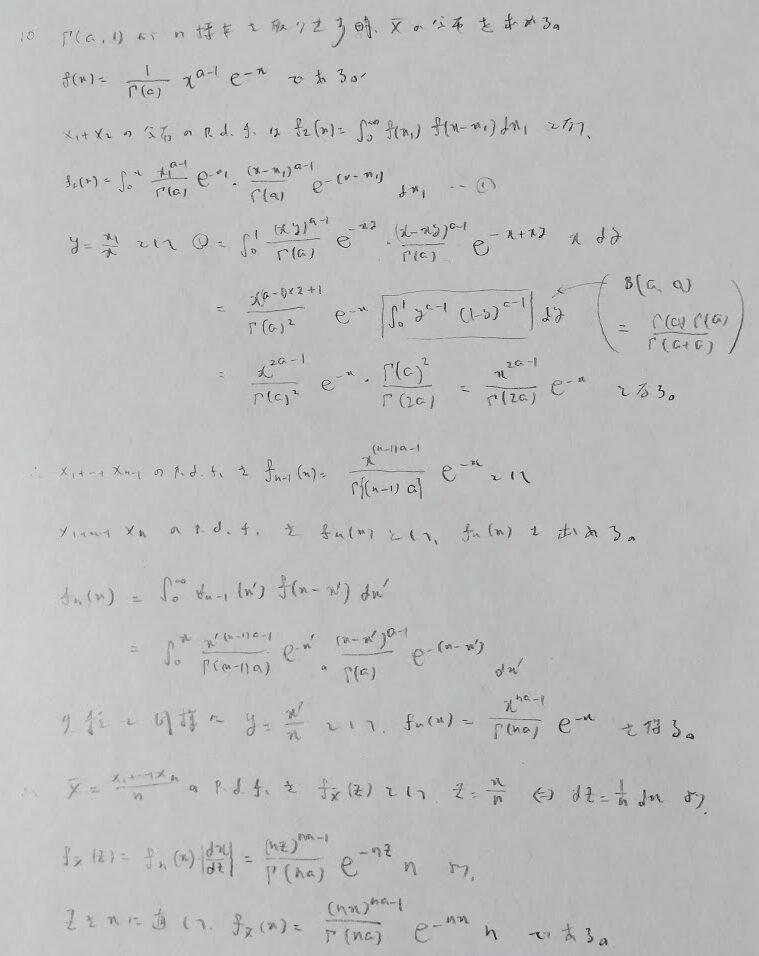
本問のポイントは意外とできない特殊な置換法です。ベータ関数に帰着させるための置換を行っています。ベータ分布に関する記事はこちらです。
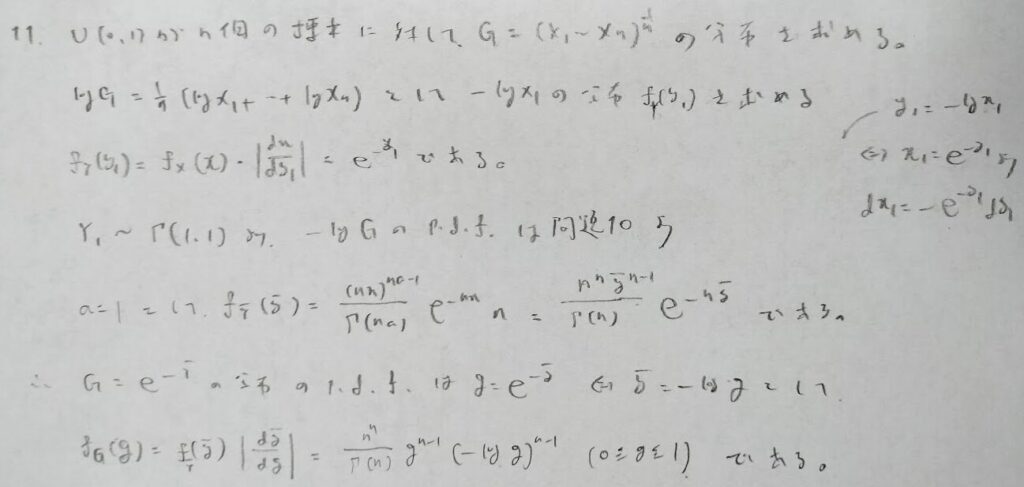
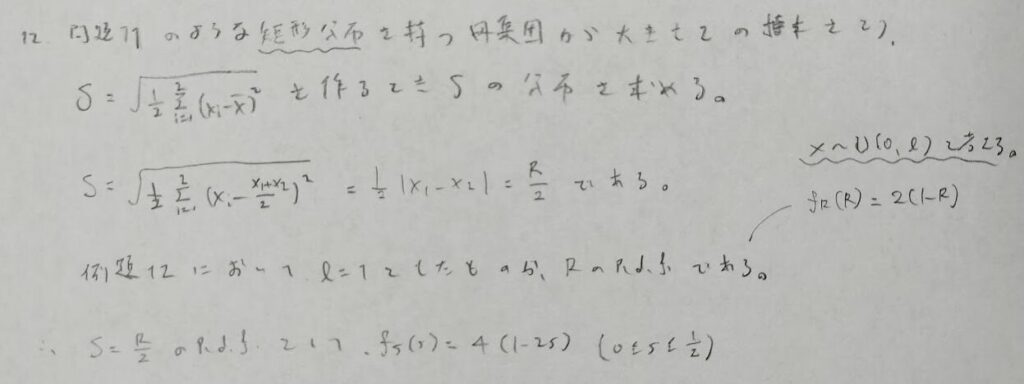
矩形分布とは一様分布の別名です。
順序統計量の分布の問題
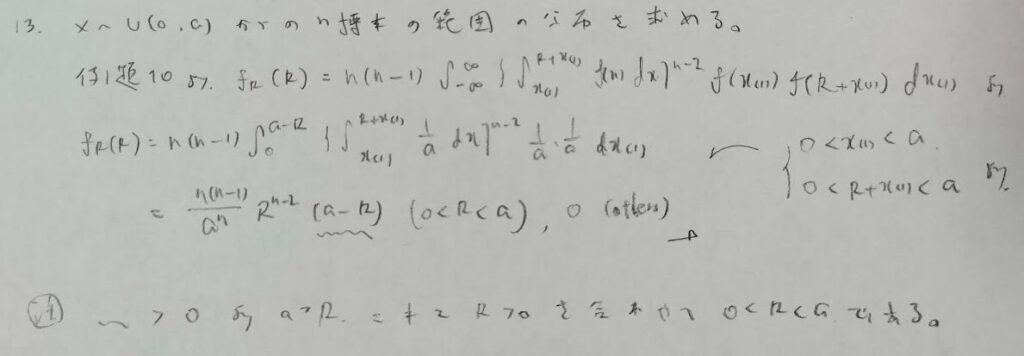
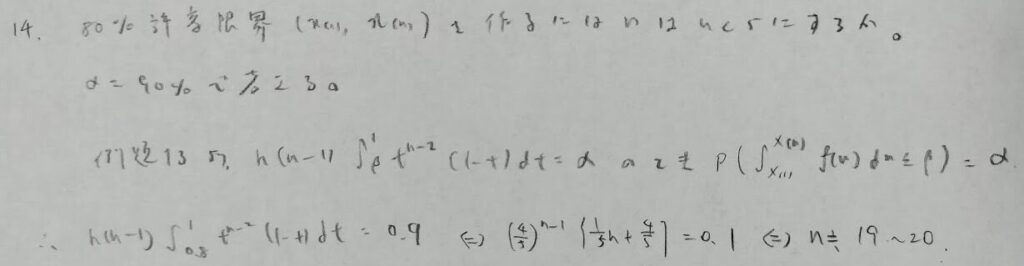
例題13の解き方がわからないと完答できない問題です。


今回は2つの母分散が既知という扱いなのでt検定が登場することはありませんでした。
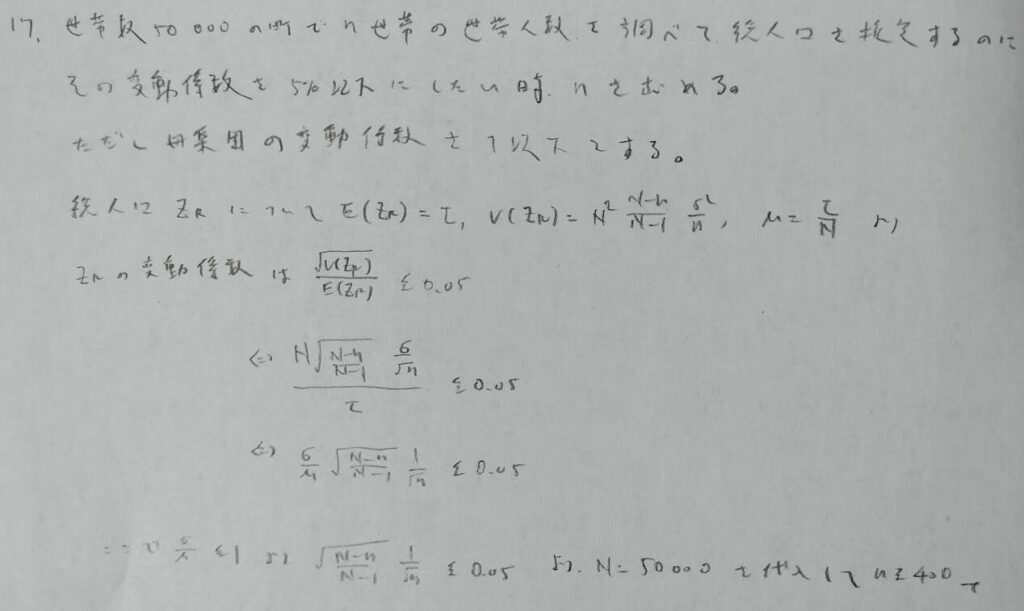
統計検定でも出題されている変動係数ですが、それと比べると難易度の高さが雲泥の差で難しいです。アクチュアリー数学では頻出のパターンなので定石として解けるようにしたい問題です。


比例抽出法と任意抽出法の推定値の公式は異なるように見えますが、任意抽出法の公式を覚えてしまえば、近似を用いて導出可能です。

2段抽出法は公式が1つなのでスパッと覚えてしまいましょう!
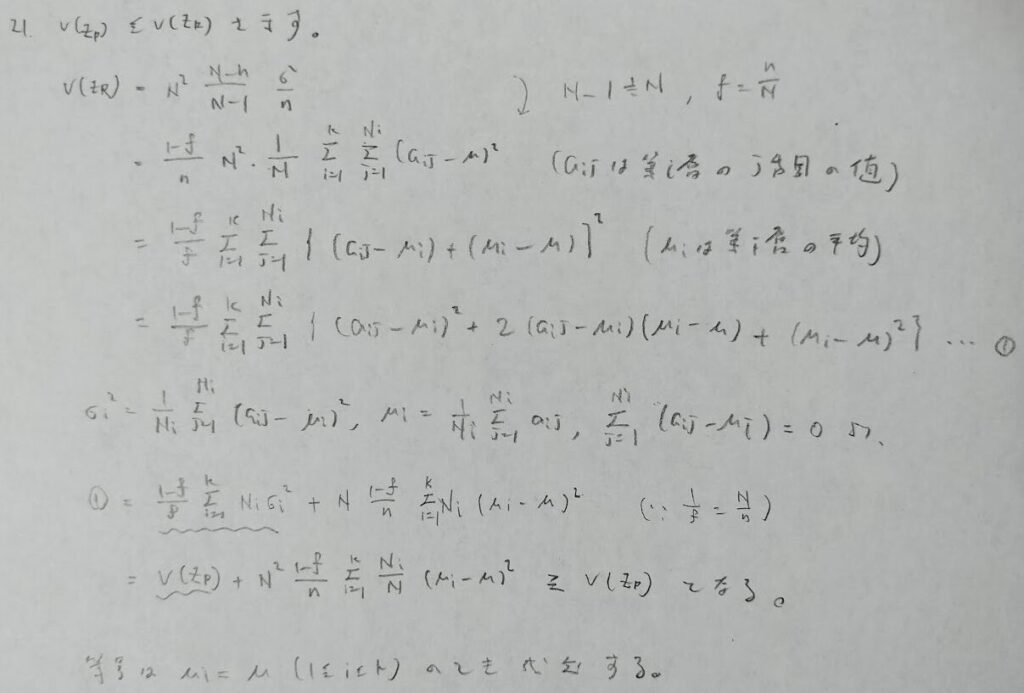
比例抽出法は任意抽出法よりも精度が高いです。
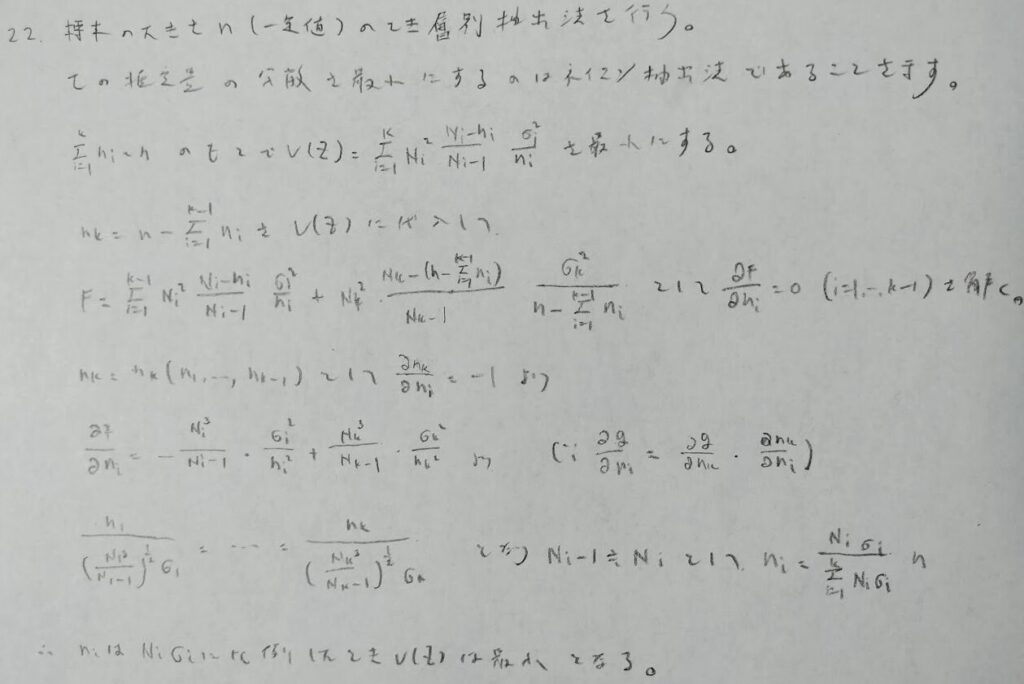
標本数が一定のときはネイマン抽出法が良い抽出法になります。
やっと第5章が終わりました!とても重たい章でしたね。
そうですね。推定や検定と違ってあまり目立たない部分なので対策が手薄になってしまう危険がある章でしたね。1回では未消化部分が多いと思いますので何度も本記事で復習していきましょう!
『確率統計演習 2 統計』で学習する他分野のリンク先をまとめています。是非ともご活用ください。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)





