アクチュアリー数学の統計分野の指定教材『確率統計演習 2 統計』のメイン級の部分である統計的検定の問題を解説します。関連事項のリンクページはこちらになります。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)
第4章はかなりのボリュームです。アクチュアリー数学の統計分野において推定と検定の2大分野のうちの1つですので当然ですが、それでもかなりの分量です。
『確率統計演習 2 統計』ではサラッと書いてある箇所には詳しい計算などの解説も入れていますので、少しずつご覧くださいね。
特に指定がない限り、母集団分布は正規母集団とします。
『国沢統計』第4章「統計的検定」の例題

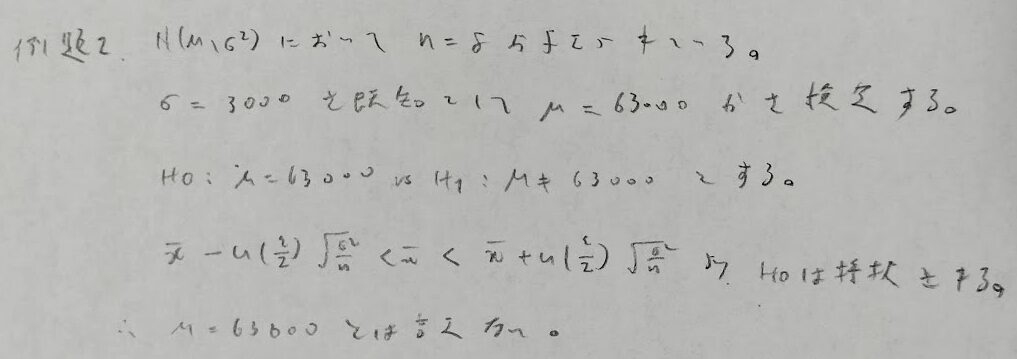
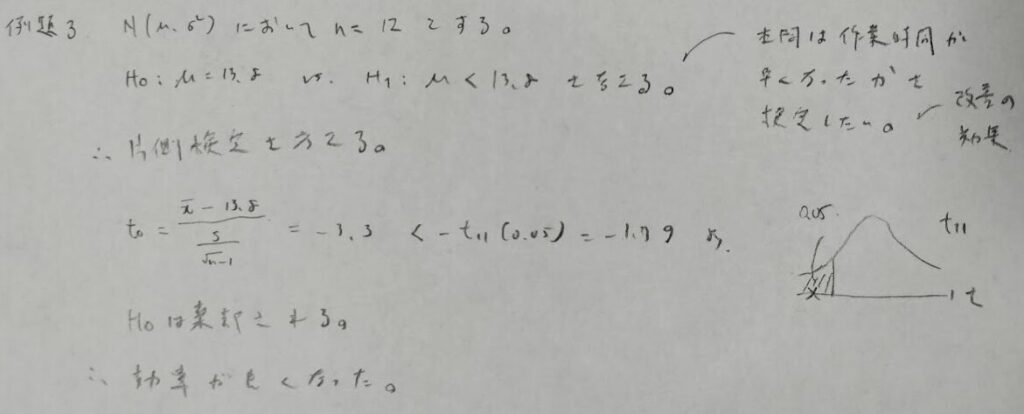
時間が改善されたということは作業時間が早くなったということです。本問の片側検定は左側検定になります。

アクチュアリー数学の頻出問題ですが難問です。本問は抜取検査の問題を検定の応用問題として解いたものです。第一種過誤と第二種過誤から考えればシンプルな考えで答えまで到達できます。本問はサンプル数と棄却域を求めることが本質です。帰無仮説と対立仮説を等号を用いて設定することがポイントです。次の例題5でその意味がわかります。
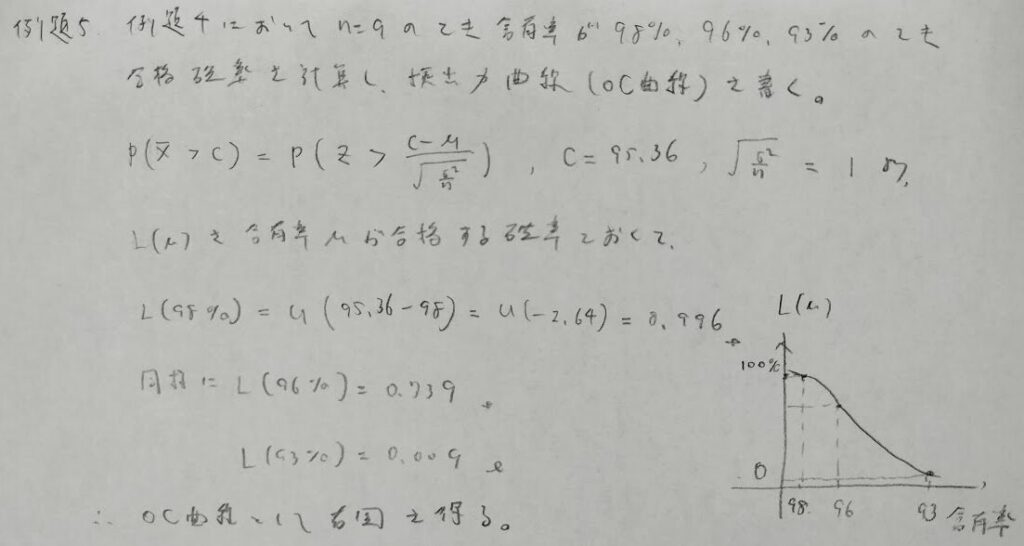
検出力曲線のことを抜取検査ではOC曲線といいます。
先ほどの例題4はさまざまな解法がありますが、上述の解き方をすると、なぜ検出力曲線を考えるのか?の意味が明確になりますね。
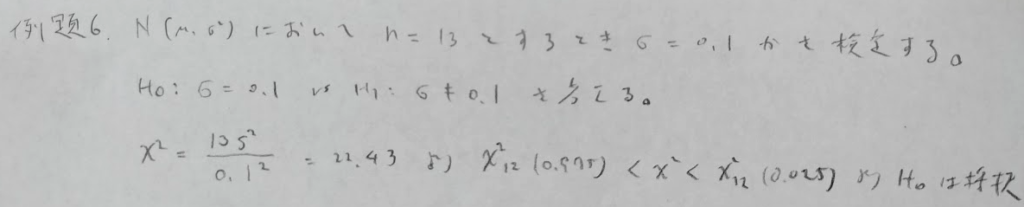
特に指定がない限り、母集団分布は正規母集団とします。

『確率統計演習 2 統計』の原題ではサラッとしか問題が書いていなかったので、どのような仮定を用いるのかが不明確でしたので、僕なりに解答を作ってみました。サンプルで与えられた表は過去のデータに対しても適用して良いとの旨を問題文から感じ取りました。特に(3)の全体のバラツキに関する問題が何を答えるべきか判断に苦しみました。
アクチュアリー数学で出題される場合は、しっかりとした文章が書かれていると思うので皆さんもご心配なさらないようお願いします。

母平均の差の検定では、等分散検定の結果で2つの母集団の分散が等しいと判断された場合はt検定を用います。等分散検定の結果で2つの母集団の分散が等しくないと判断された場合はウェルチの検定を用いることになります。ウェルチの検定は例題10で扱います。
本問では不純物が多いと品質が悪いと考えていますので、問題文をよく読んで、片側検定の場合は対立仮説がどうなるか?をしっかりと把握しましょう。
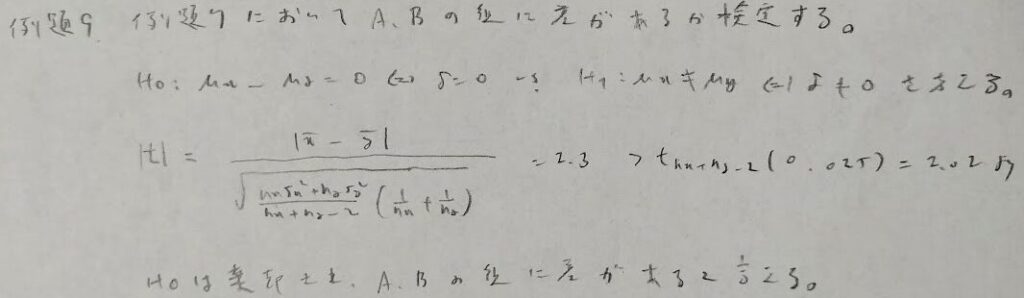
例題7でF検定は実施済です。
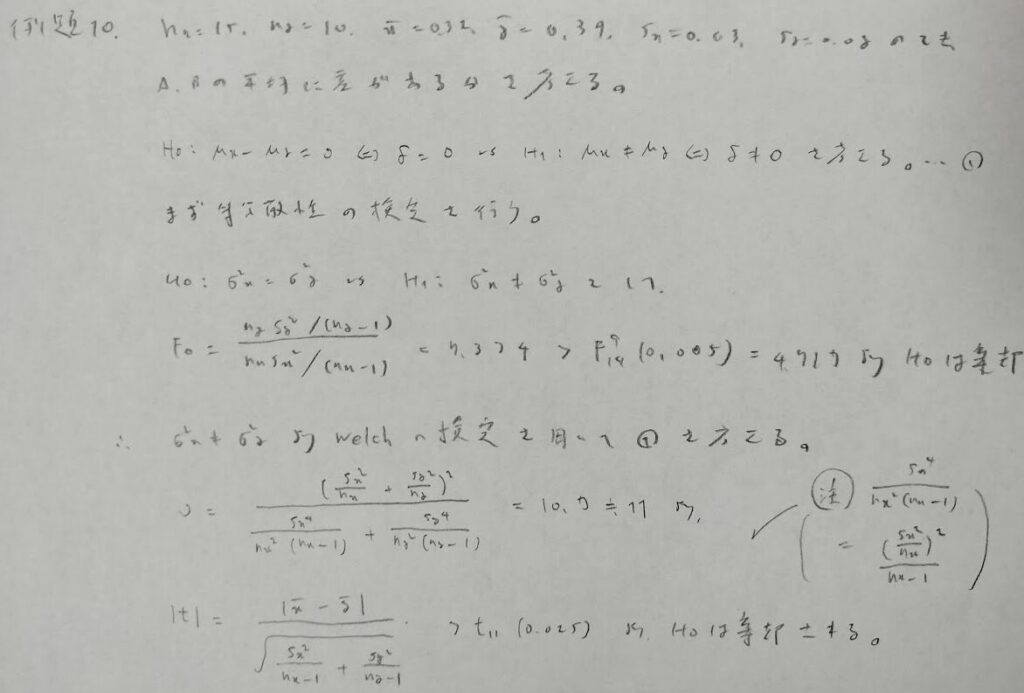
覚えにくい検定ですがポイントは次のとおりです。
①覚えるところはt分布の自由度を求める式
②注を参考に自由度νの式は4次式が絡むと覚えましょう。
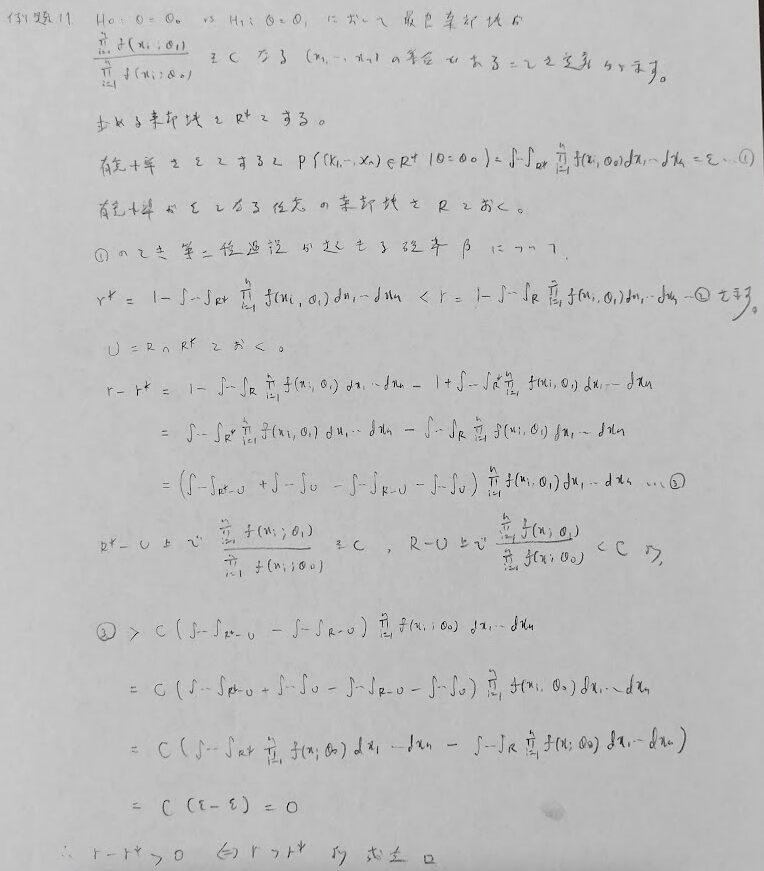
本問の棄却域は一様最強力検定としてネイマンピアソンの基本定理から導かれるものです。この問題の意図はその棄却域が最良(最強力)であることを定義から示すことにあります。一様最強力の場合は対立仮説が複合仮説になります。
良い検定とは?の意味が問われる問題です。第一種過誤を決めた後に第二種過誤をなるべく小さくするような検定の棄却域を最良棄却域といいます。本問はそのままの問題としてアクチュアリー数学に出題されています。最難問クラスの問題です。解答上のテクニカルなポイントは共通部分Uを設定することです。


対立仮説が両側の検定場合は一様最強力検定は一般に存在しません。
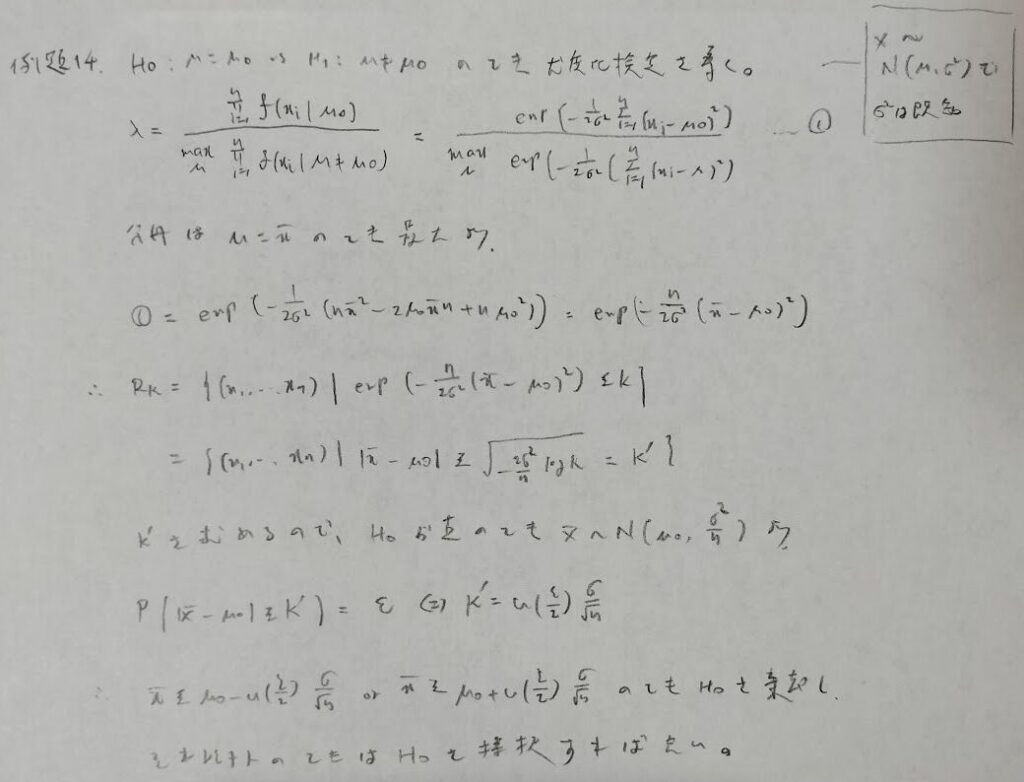
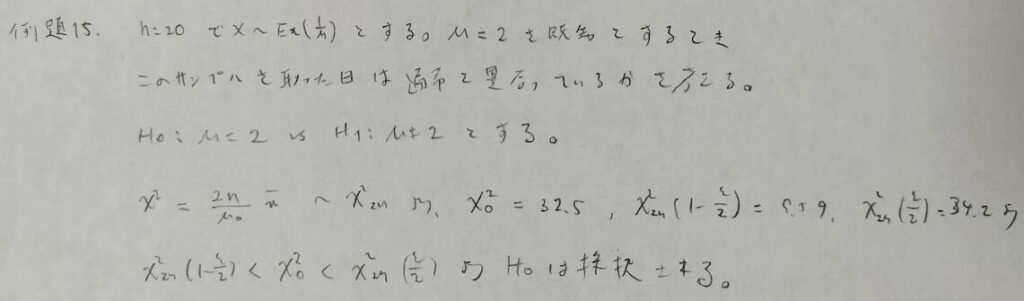
しかし片側検定の場合はε/2がεとなることにより(当日が通常より多いという対立仮説を考える場合)帰無仮説は棄却されます。
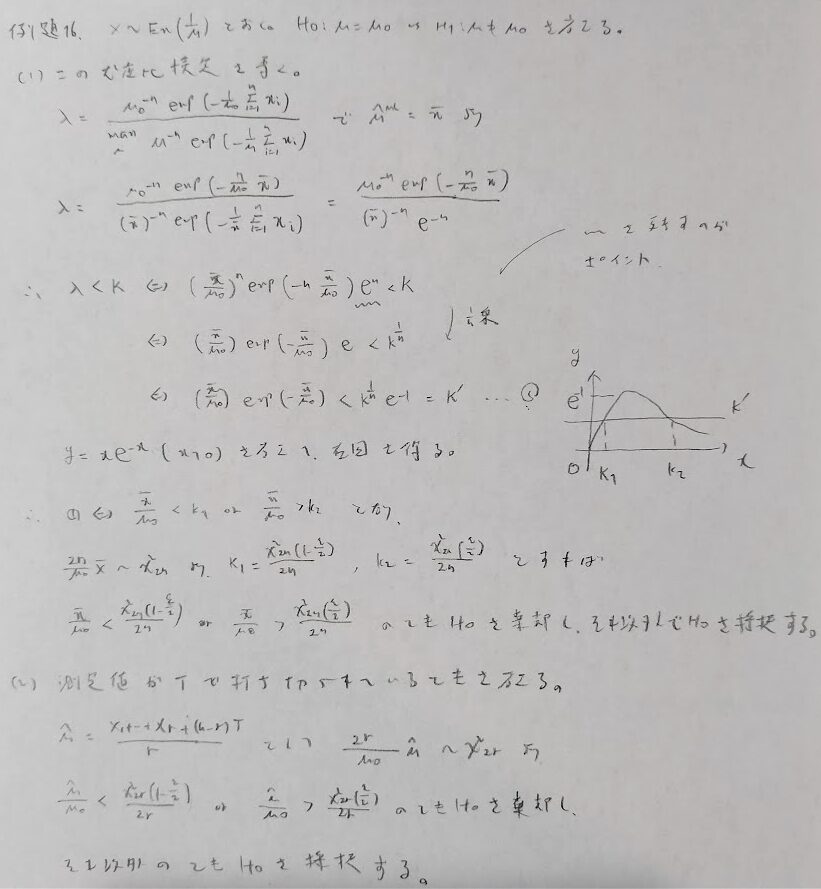
統計検定1級にも出そうなボリュームです。途中でkについてn乗根を取っているのは、尤度比が正であるからです。

『確率統計演習 2 統計』の原題では「〜以上で可決」となっていますが、厳密には「〜より多い場合は」だと思います。そのため上のような解答にしました。

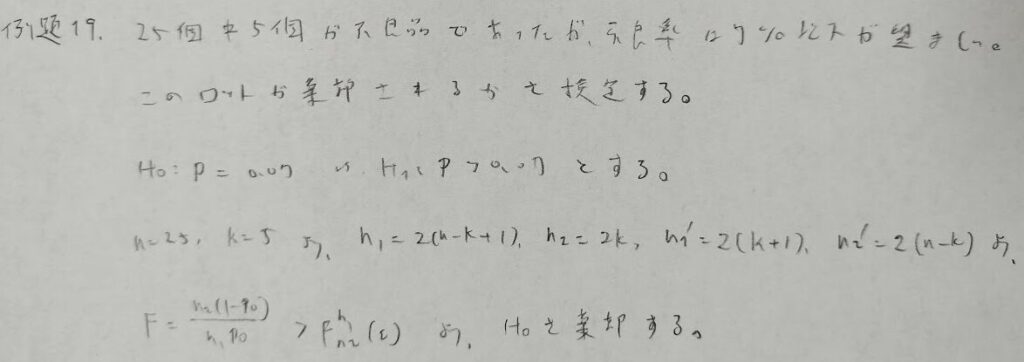
帰無仮説は厳密には不等号を用いますが、計算の都合上、等号で考えています。
棄却域の確認が難しいですが、アクチュアリー数学本番では暗記して行った方が身のためです。

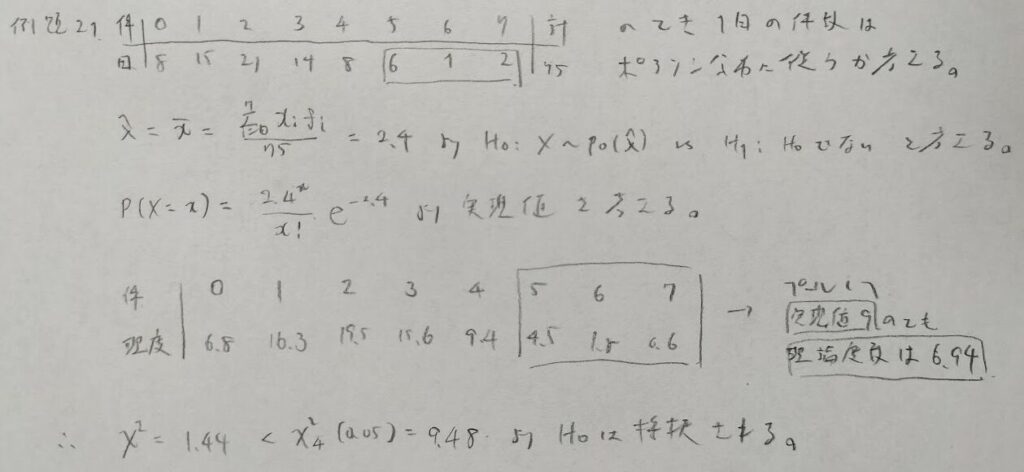
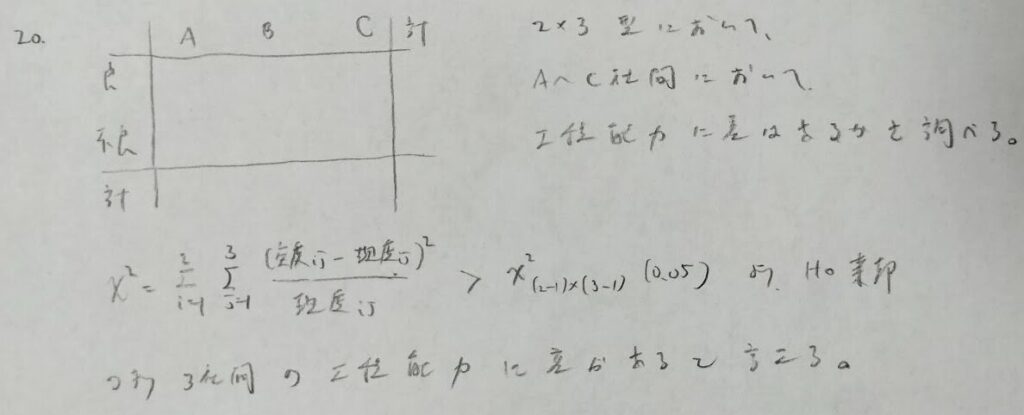
理論度数が5未満のセルはプールします。λの推定も含めると自由度は4になります。
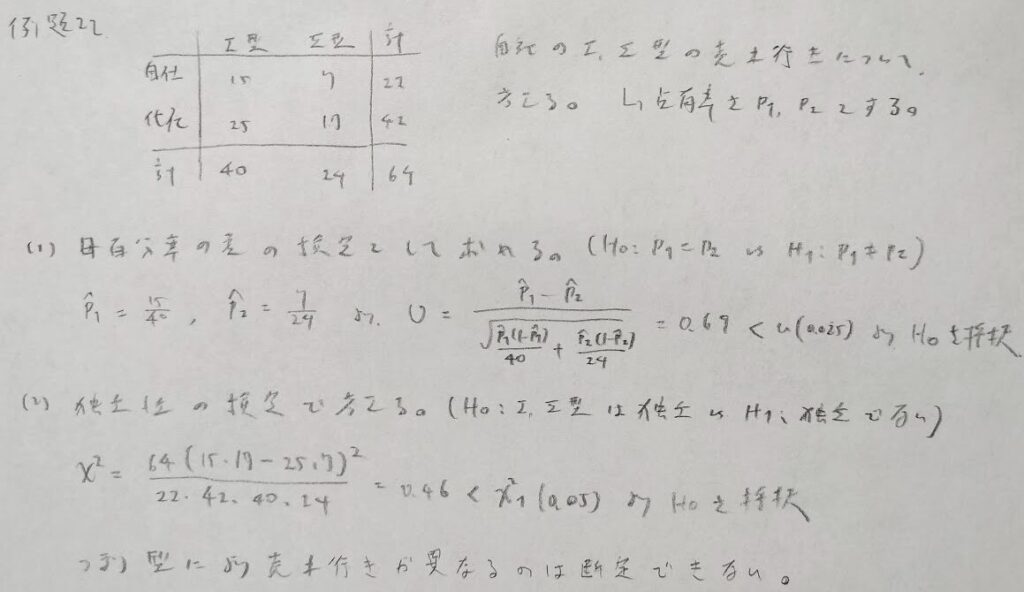
2×2の独立性の検定は、母百分率の差の検定と同じことを行なっています。
1つでも理論度数が5未満ならイェーツの補正を行います。

全てのセルの理論度数は5以上である必要があります。
いよいよ終盤です。ポアソン分布に関する検定の応用に入ります。

ソーンダイク曲線(Thorndike曲線)はポアソン分布の母平均の検定において便利です。λ=npは二項分布とポアソン分布の関係から来ています。

ソーンダイク曲線のcはポアソン分布の累積分布関数の最後に足すまでの場所を特定するものなので、実現回数kと比べることにより検定が可能となります。

二項分布のポアソン近似についてはヒントが与えられるはずです。詳しくはこちらの記事に書いています。
『国沢統計』第4章「統計的検定」の問題
演習問題の解説になります。こちらは例題の類似問題などがメインのため詳しい数値設定などは『確率統計演習 2 統計』をご覧ください。
平均値の差δに関する検定の問題
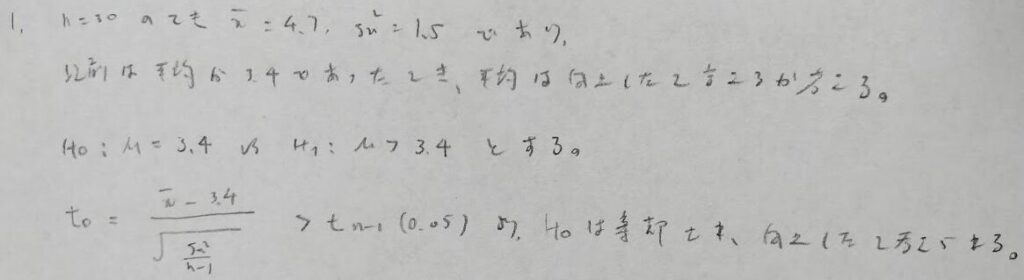
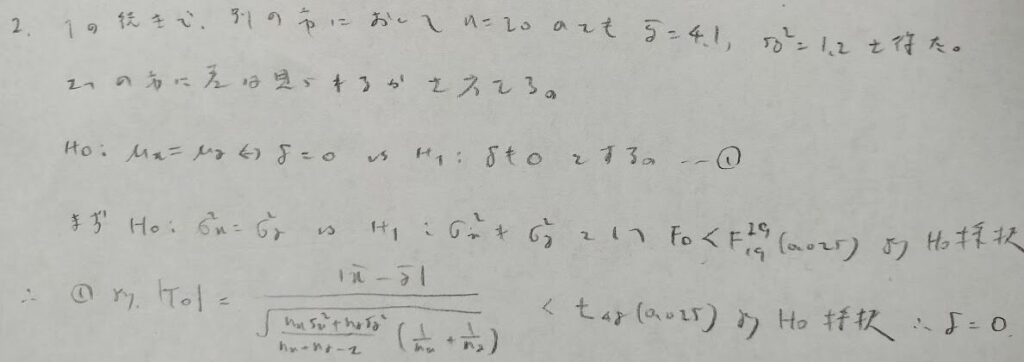
プールした分散を用いたいので等分散検定(F検定)を用いるべきです。検定のし忘れに注意しましょう!
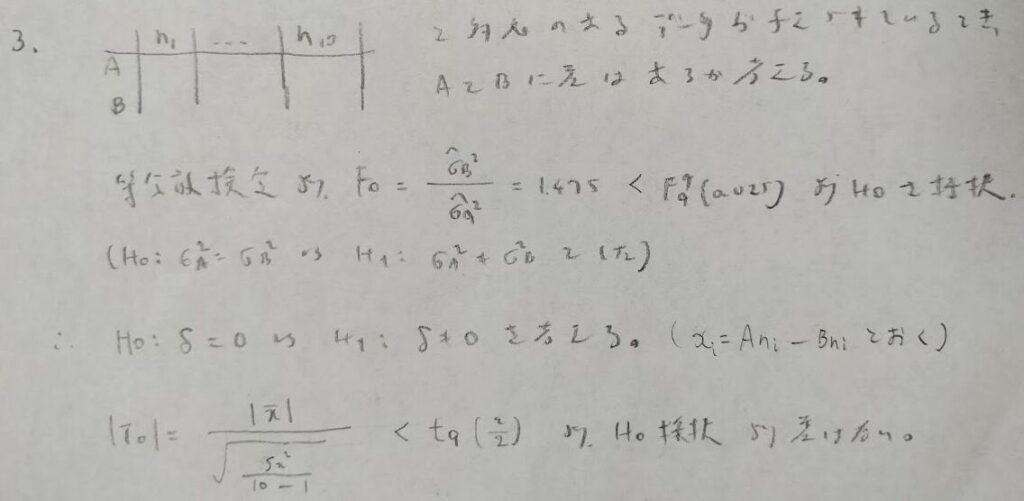
対応がある場合と対応がない場合の検定の方法は異なりますので注意しましょう!具体的にはt分布の自由度が変化します。


サンプル数が多ければ検出力が高まりますので、細かい不等式は後回しでOKです。今回はnが52と切り上げでわかったので52以上がnの条件になります。
本問はアクチュアリー数学で頻出の問題です。第一種過誤を考える際に棄却域の設定をCという文字を通して設定しています。今回は片側をはじめから考えることにより計算量を減らしています。それを行なって良い根拠は標準正規分布の対象性です。棄却域の設定に応じて第二種過誤の式が変わってきますのでご注意ください。
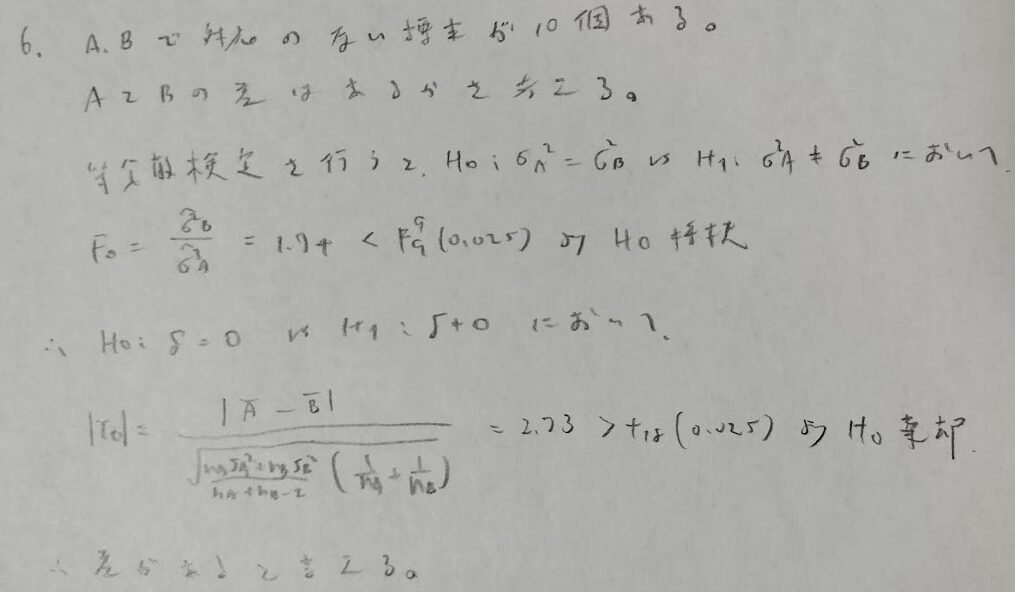
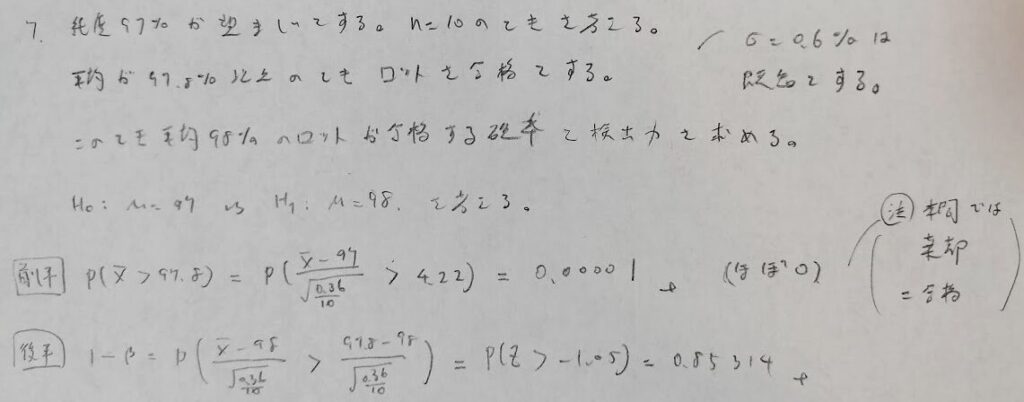
本問では棄却=合格の意味です。単に言葉の良し悪しだけで棄却の意味とを結びつけないようにしましょう。その意味で本問は引っかけ問題です。
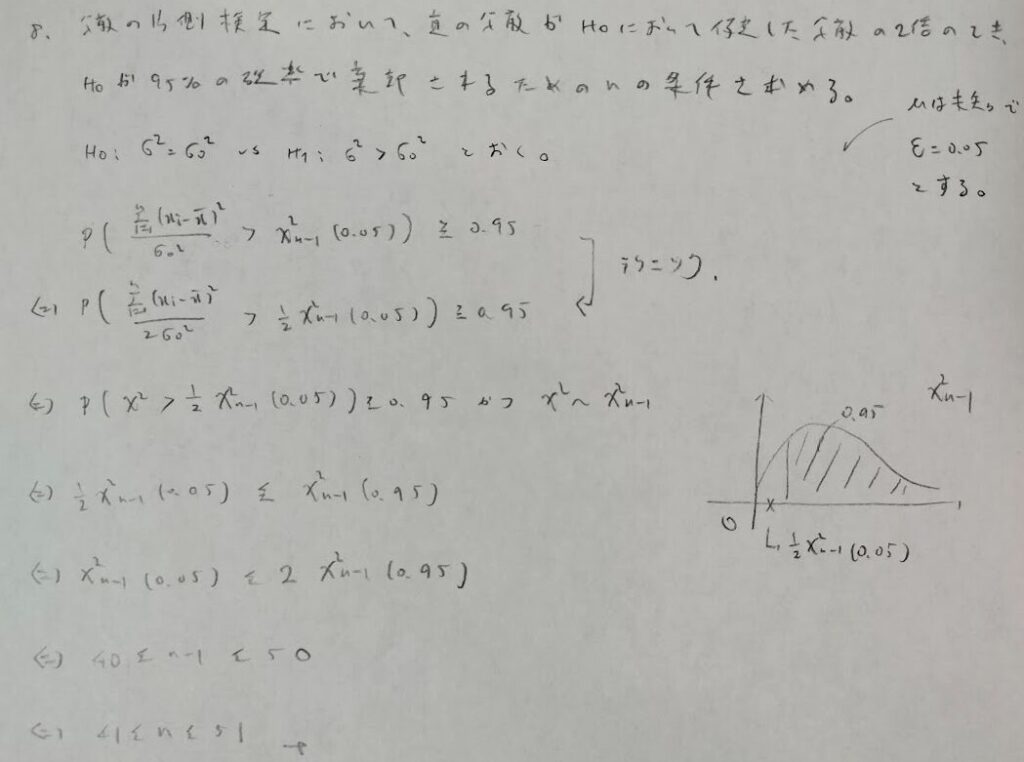
本問はアクチュアリー数学で頻出ですが検定問題において混乱を招く問題でベスト3に入ります。式変形のテクニック後の不等式は検出力の式になっています。第一式は有意水準が0.05であることを用いるために必要です。
寿命分布の平均値μに関する検定の問題
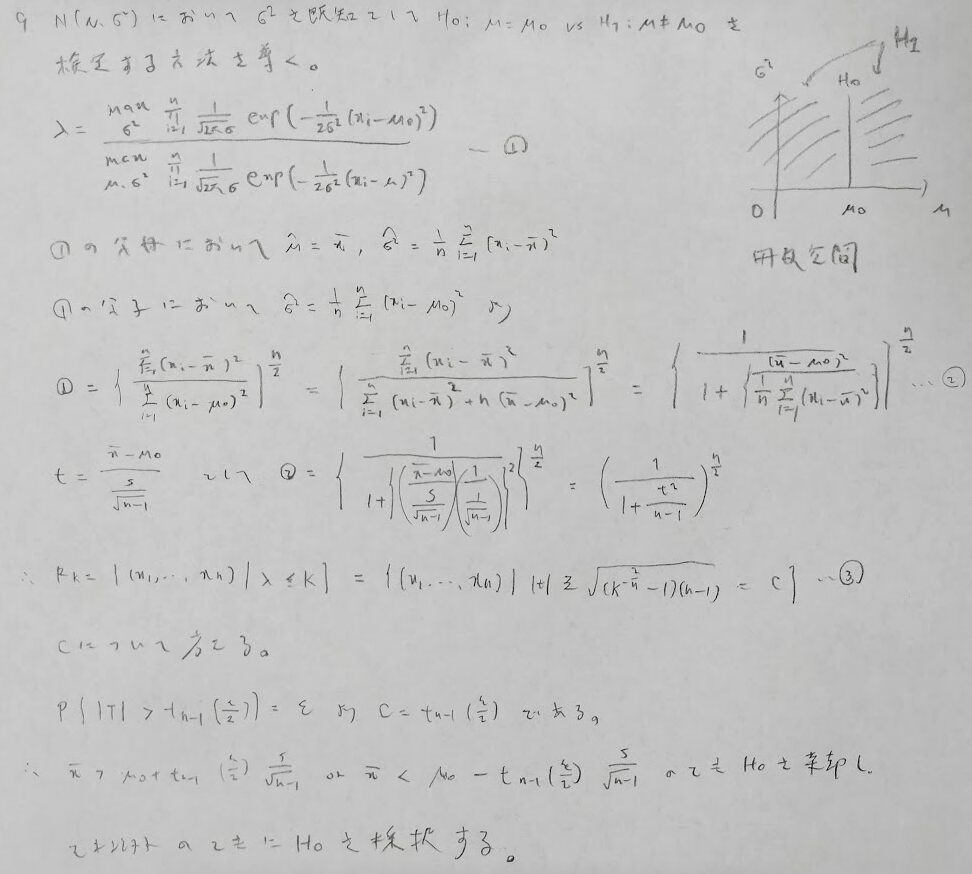
t検定統計量を途中で持ち込むのがコツです。それによりt分布との関連性が見えやすくなります。

2つの確率変数が絡み合う結果になるので、最尤法を考える際は同時分布を考えることになります。
アクチュアリー数学では誘導形式で出題されましたが、0からの記述となると1日がかりで頑張って計算しまくって結果に行き着くレベルの計算量になります。特に答案の下から4行目のtの置き換えは結果から逆算しないとほぼ確実に思いつかないレベルの難易度です。
尤度比検定の中では群を抜いていの難問ですね。
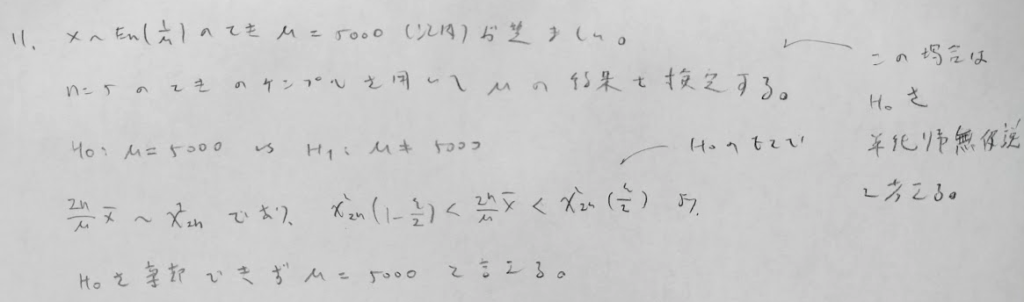
本問は原題が紛らわしい設定でした。帰無仮説が単純帰無仮説だと読み取れれば良いのですが、問題文の読み取りが難しいです。詳しくは『確率統計演習 2 統計』をご参照ください。
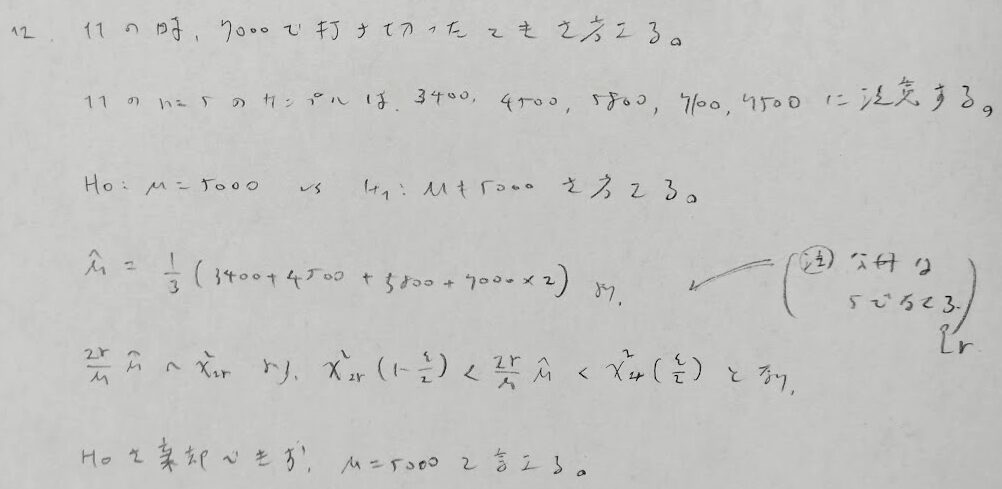
打ち切りの場合の母平均の推定値の計算では分母に注意しましょう。分母は実際に測定をしたサンプル数です。打ち切りの場合は推定値が厳し目に出てくるように設定します。詳しくは最尤法で計算すれば結果が得られますが、アクチュアリー数学本番では導いている時間はないので、公式を覚えてしまいましょう。検定統計量が従うカイ二乗分布の自由度も2r(rは分母の値)になるので注意しましょう。
百分率pに関する検定

何を問われているか?に注意しましょう。欠勤率なので帰無仮説は出勤率ではなく欠勤率5%の方を用います。
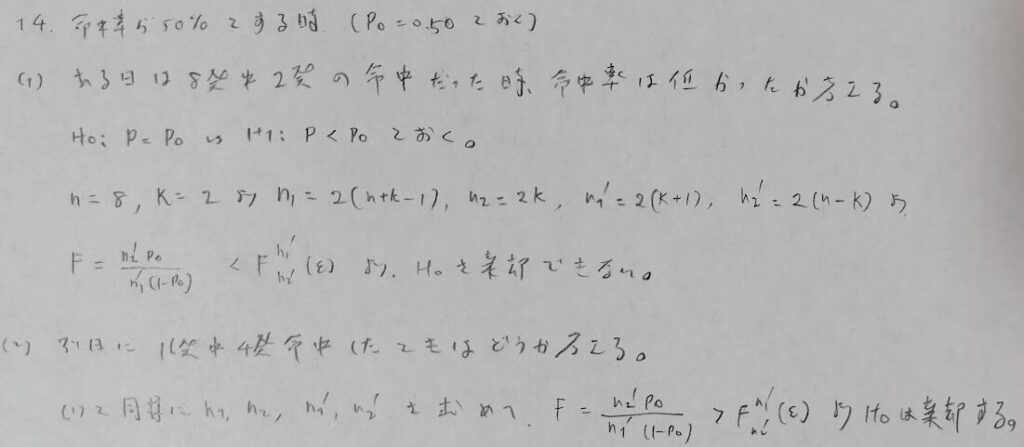
命中した数が5未満なら精密法で検定します。
命中した数はそう多くはないイメージなので精密法と相性いいですね。
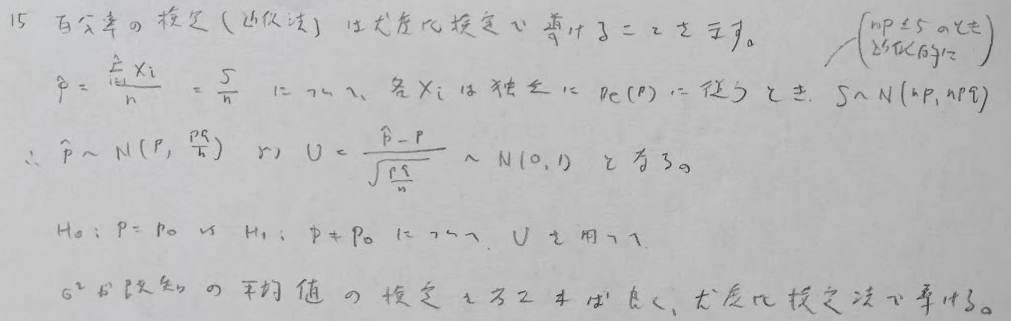
本問は尤度比検定を導くもので、これは既存の検定の形を導くテクニックをとっています。

本問は最強力検定を導くものです。
分子のSについての棄却域を定めれば自動的にpの推定値の信頼区間が得られます。実現回数Sの回数によって検定を行なっています。
分割表による独立性の検定の問題
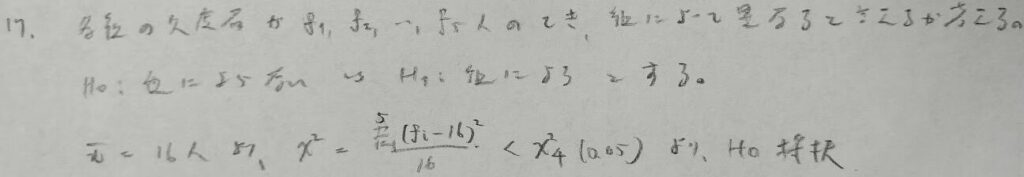
このような問題は実生活でも特に使えそうなタイプですね!
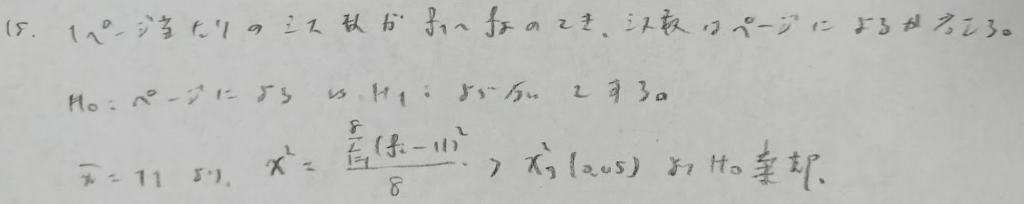
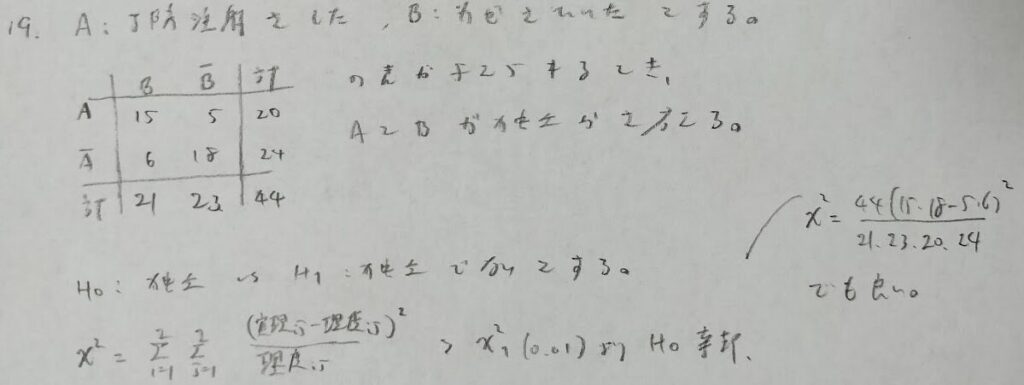
Poisson分布の平均値に関する検定およびThorndike曲線を用いた検定

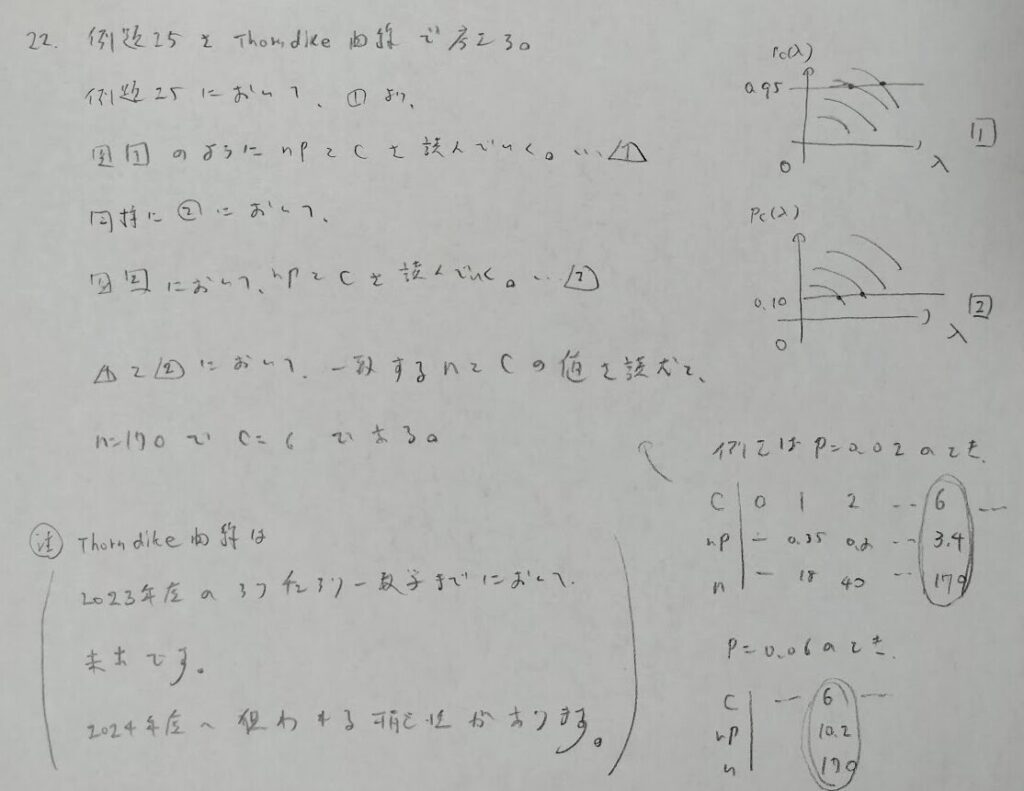
『確率統計演習 2 統計』の第4章は以上となります。
例題が重たいと感じました。やはり尤度比検定周辺が計算量が多く、精密法が絡むところは深い理解が要求されていると感じました。
次の章(こちらです)では統計検定1級でも出題される分布間の相関についての内容になり、見方によってはマニアックな章になり計算量も増えます。しかし途中式もしっかりと書いていくので一緒に頑張りましょう!
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)