統計検定1級でも出題される区間推定に関する問題をアクチュアリー数学指定教材『確率統計演習 2 統計』を題材として解きまくります。アクチュアリー数学の方が精密法などを中心により細かい学習が要求され、特に例題の最後の方は難問ラッシュになっております。ここら辺のレベルは統計検定1級の合格水準を超えておりますので難易度の上昇にご注意ください。
第2章の点推定の内容を未学習の方は下記からご覧ください。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)
本記事における信頼係数は特に指定がない限り95%とします。
本記事ではアクチュアリー数学の試験対策のため、理論的な側面より実践的な計算方法の確認をメインで行います。理論部分は統計検定1級対策書『現代数理統計学の基礎』で効率的に学ぶことができます。過去に特集記事を書いておりますので、こちらをご覧下さい。
『国沢統計』第3章「区間推定法」の例題
具体的な問題内容は『確率統計演習 2 統計』の本文をご参照ください。よろしくお願いします。


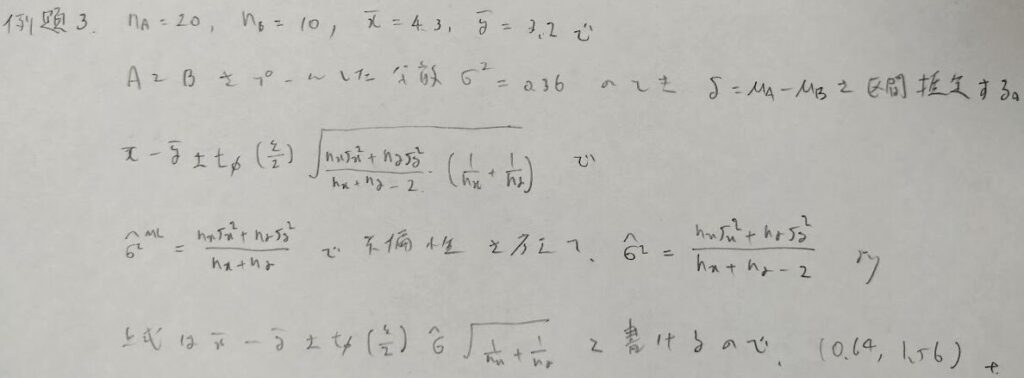
やや変化球な出題だと思います。上から3行目の式を覚えておければスムーズに答えまで辿り着くことができます!
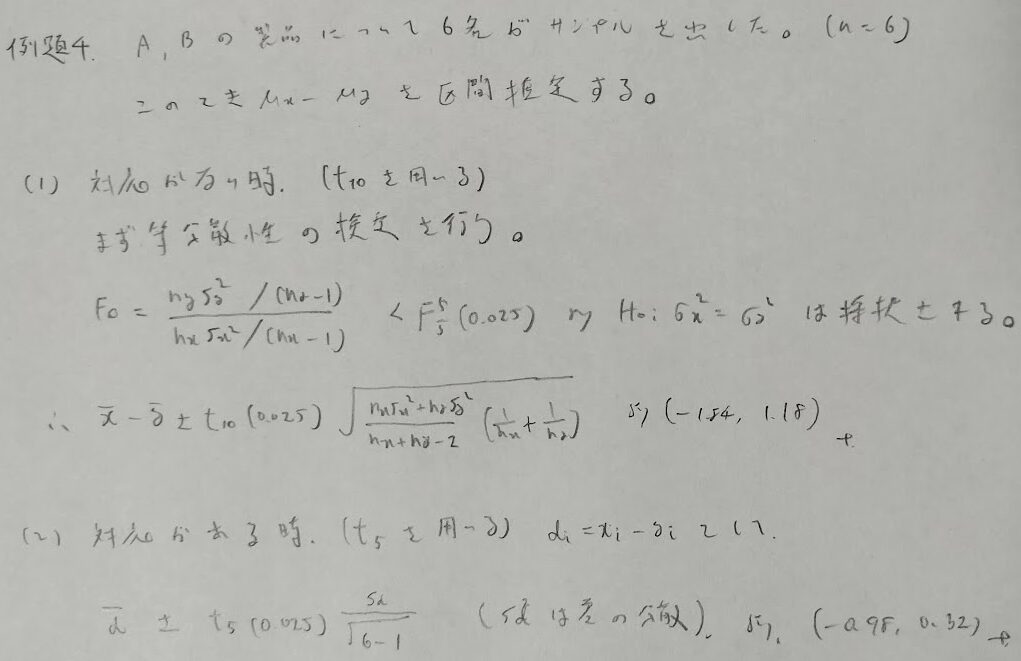
分散未知の場合の2つの母集団の母平均の差の区間推定は、対応がある場合と対応がない場合の2パターンが考えられますので問題文を読んでどちらが問われているか?を考えましょう。実はこの内容は統計検定2級『統計検定2級対応 統計学基礎』の内容です。対策記事はこちらになります。
アクチュアリー数学の統計分野の指定教科書は統計検定2級の対策書としてもよく名前の上がる東大出版の『統計学入門 (基礎統計学Ⅰ) 』です。東大の名前があるので身構えてしまいそうですが、丁寧にわかりやすく書かれた良書です。
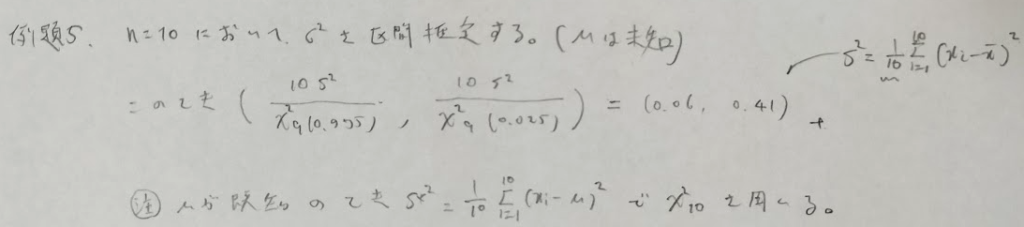
母平均が未知でも既知でもsなどの計算の分母はサンプル数になります。違うのはカイ2乗分布の自由度だけです。
二項母集団の母百分率pの区間推定について、実現回数が5以上の時は近似法で5未満の時は精密法を用います。
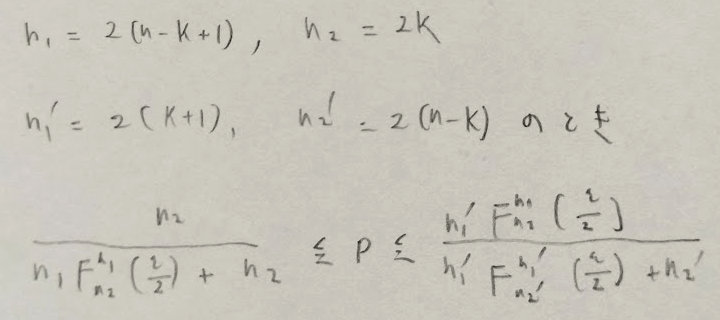
二項母集団の精密法の公式はアクチュアリー数学の中で最も覚えにくい公式ですよね笑


アクチュアリー数学で頻出です。アクチュアリー数学で最も実践的な公式や例題が掲載されている『アクチュアリー試験 合格へのストラテジー 数学 第2版』にも類題が代表的な問題として掲載されています。

統計的検定でなく区間推定の考えで具体的な改善の数字を出しています。なかなかレアな問題でアクチュアリー数学で未出です。また統計検定準1級では2つの母集団間に相関がある場合も考えているのでルート内がやや複雑な形になります。具体的問題は『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』に掲載されています。解説記事はこちらです。

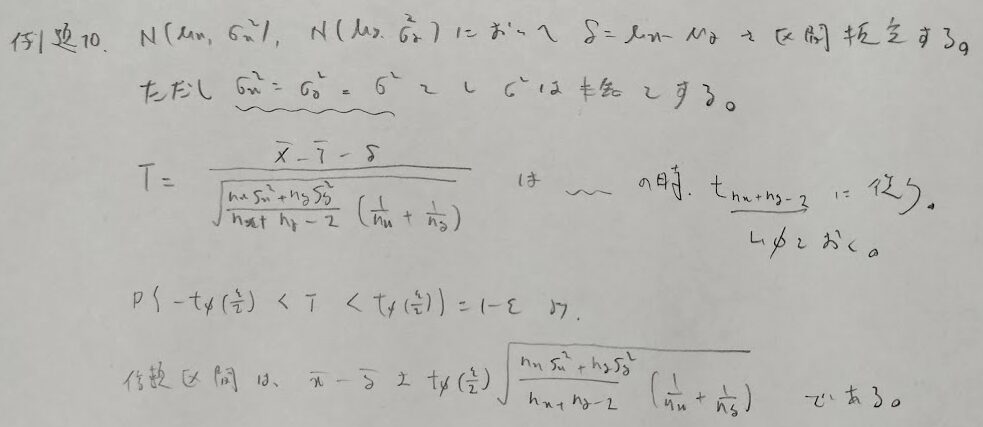

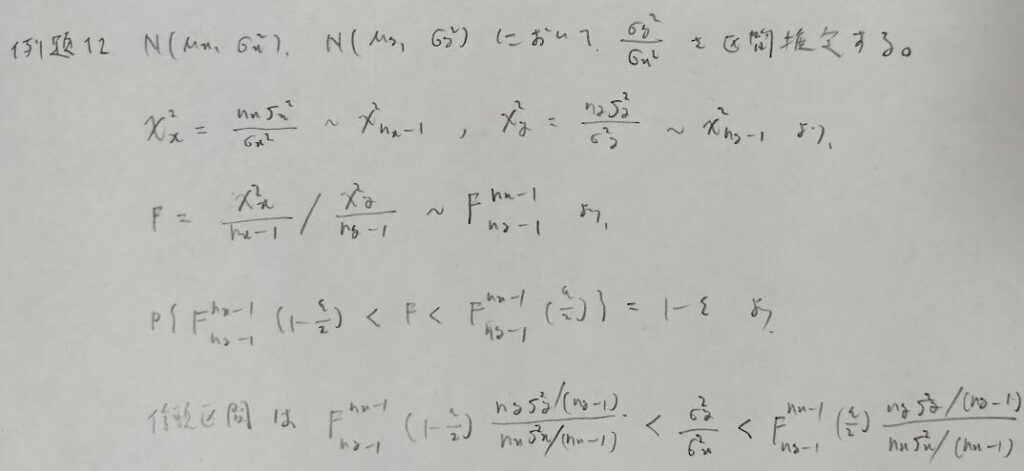
例題12の結果は覚えにくいので、事あるごとに導けるようにした方が良いと考えます。

(特に最後のあたりが)かなりややこしいです。後で似たような区間推定(精密法など)が登場しますが、ここまでややこしくはありません。とにかく二項母集団の精密法は誘導で出されない限り、結果を覚えてしまった方が良いです。
精密法の考え方では第2行目の式を立式できるか?が大切です。またF分布と二項分布の関係は複数回の部分積分を繰り返してΣ計算とリンクさせます。h1(p)とh2(p)の見つけ方は、pについて解いて不等式の向きに注意すればOKです。最後のpの推定値をpに置き換える理由は、通常の信頼区間の構成法ではpが登場するものの、このパターンではpは登場せずにpの推定値が残ってしまうためです。しかしワルド法の考えから一概にもこのように考えてはNGだとは言い切れません。
仕方なく対処しているような感じですね。詳しい理由は不明ですが複数の分布を経由していることが原因と思われます。
この現象は後程考えるポアソン母集団におけるパラメータλを精密法にて区間推定する場合にも出てくることになります。
アクチュアリー数学の試験は合格ラインが6割です。このような問題で細かい部分が出題された場合(例えば2023年度)ここに時間を割くよりも、大問1などの小問集合で計算さえ合えば得点が獲得できる問題に時間を割くべきです。『アクチュアリー試験 合格へのストラテジー 数学 第2版』にも具体的な作戦が掲載されています。
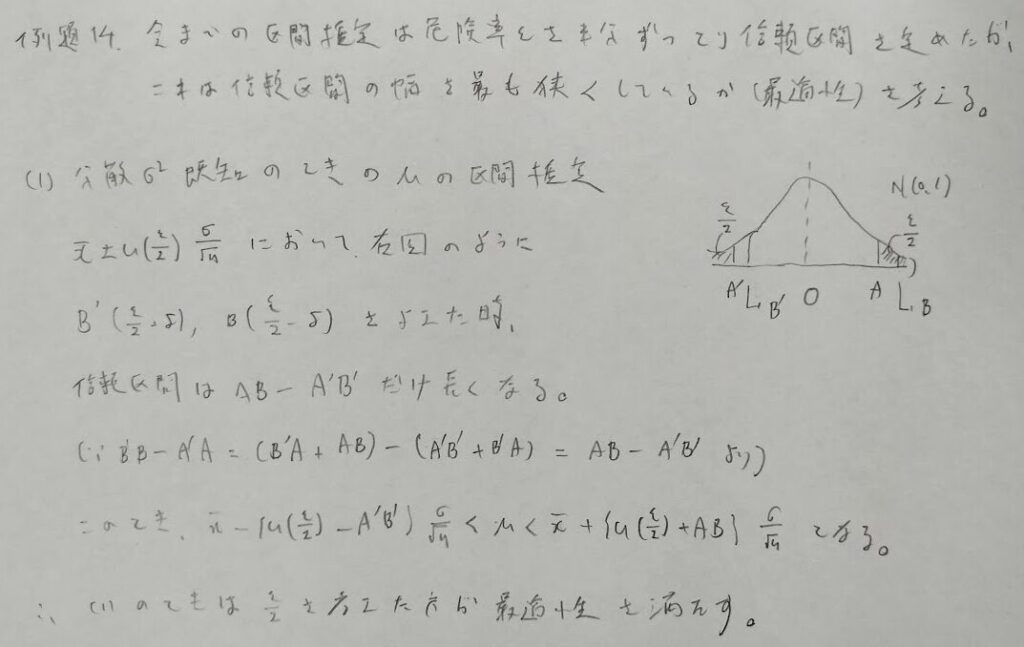
左右対称の場合は最適性を持ちます。
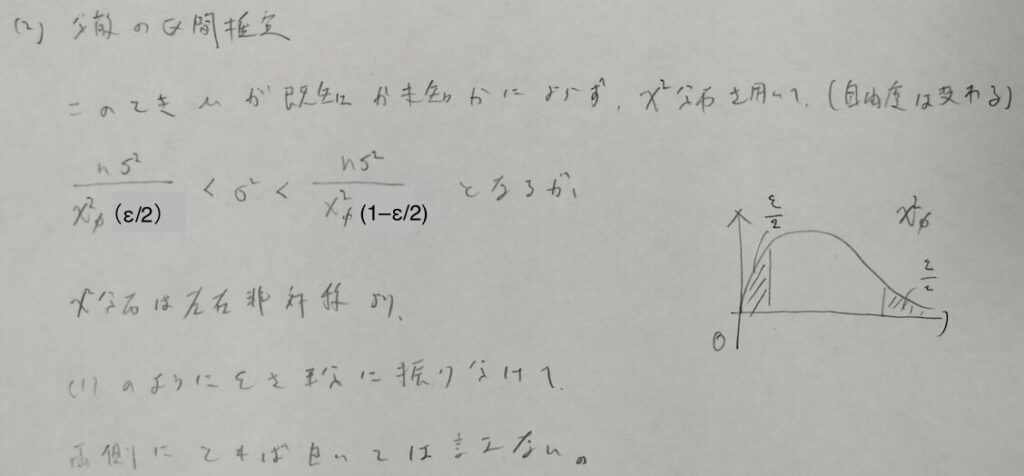
左右非対称の場合は最適性を持ちません。
分子のsは母平均が既知の場合と未知の場合で計算方法が異なりますが代表的な文字としてSを用いています。
ここまでは二項母集団の精密法が群を抜いて難しかったのですが、次からは紛らわしい区間推定法が続々と登場します。
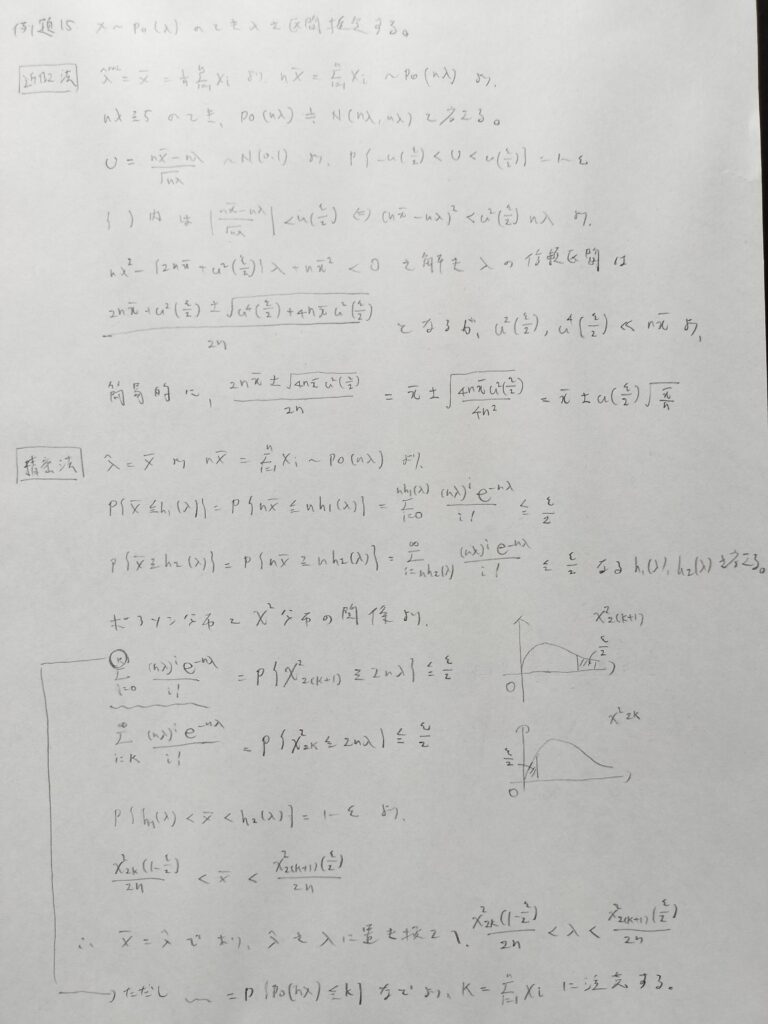
近似法の部分もやや難しいですね。近似の近似という感じですね。
この近似法の結果は推定値の期待値と分散を用いて、正規母集団のときと同様の関係式が成り立っていますので、覚えることだけはスムーズにいけそうですよね。ただし精密法の結果はちゃんと覚えないとアクチュアリー数学では時間切れになります。

こちらは正規近似を用いる近似法的な手法ではなく、カイ2乗分布に帰着させる方法で信頼区間を構成しますのでご注意ください。
指数分布のパラメータ推定では打ち切りなどの設定が多々ありますが、大枠は変わらず、手作業が課されるのはμの推定値の計算方法がだけです。
(2)の最後の自由度2nのカイ2乗分布に従うことの厳密な証明は積率母関数を用いる方法ですが、計算量が多すぎて本番で出題された場合は誘導形式か、情報が既知として与えられると思われます。さすがに全部計算させるとそれだけで30分くらい経過してしまいますので笑

とにかく理解がしにくいという意味で難問です。実際、アクチュアリー数学でも未出です。2022年に似た問題が違う解き方で解く方針で出題されました。
例題17はとにかく範囲の確率密度関数の立式が壁になります。順序統計量の内容から一般化されますが、アクチュアリー試験では覚えていないと時間切れになります。またデータの最小値の範囲をしっかり考えないと間違えますのでご注意ください。そして片側信頼区間を作成するのは確率密度関数の非対称性からきています。ここから答えは(R<)a<???という形になると判断できます。下から5行目の式はaの信頼上限???に対応する式です。とてもややこしい問題です。

かなり変わった問題です。経験分布関数から分布関数を区間推定する問題です。本問の(2)は点推定の考えを用います。誤差の部分は問題で出題された場合は確実に表が与えられますのでご安心ください。
『国沢統計』第3章「区間推定法」の問題
具体的な問題文の数値設定はアクチュアリー指定教材『確率統計演習 2 統計』をご参照ください。
平均値μに関する区間推定の問題

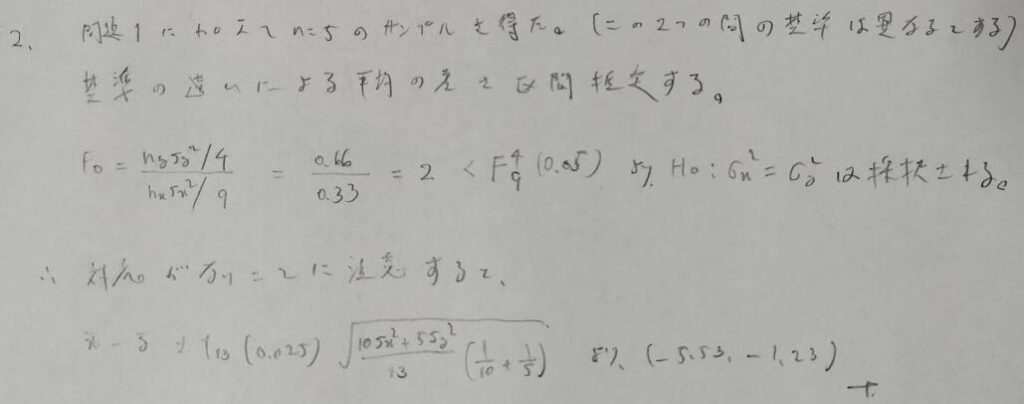
分散 σ2に関する区間推定の問題
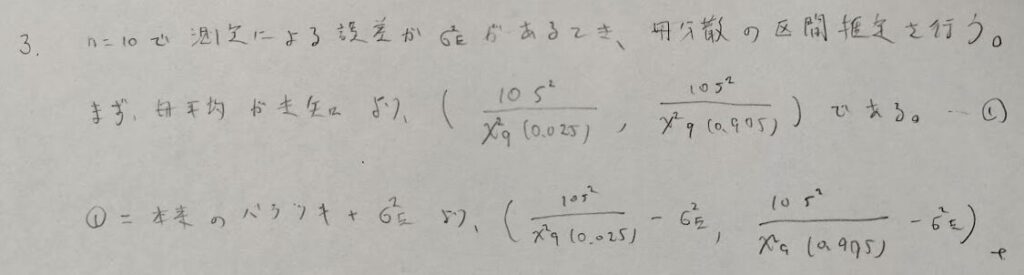
統計検定には見られないが、アクチュアリー数学特有のパターンです。測定誤差を最後に引き算しましょう!

百分率pに関する区間推定の問題
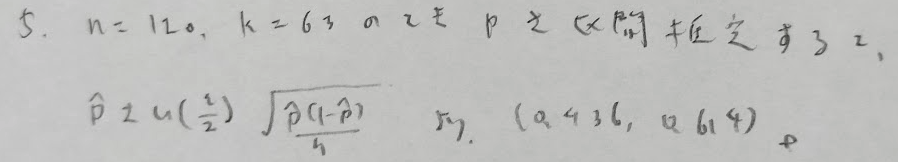
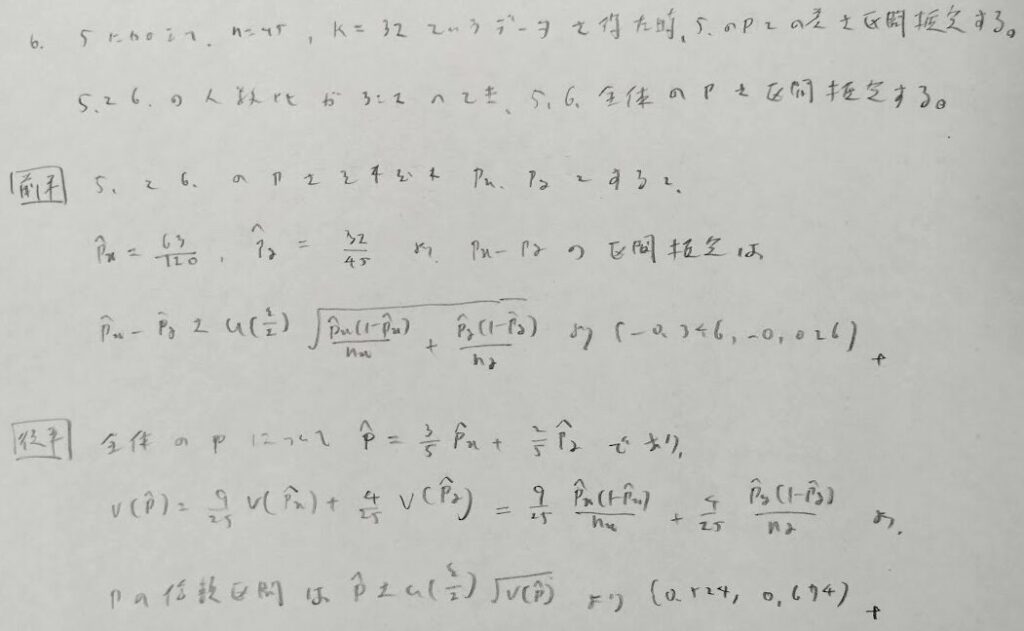
後半がメインです。まずはpの推定値を立式してから考えるとうまくいきます。

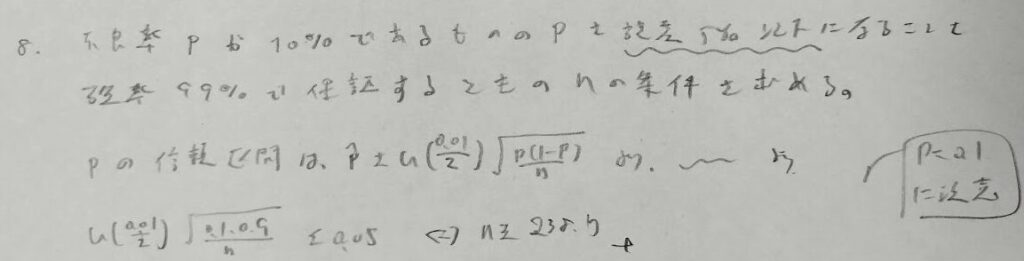
例題7ではpの推定値が与えらえれていましたが本問ではpそのものが与えらえれています。その際はpの値をそのまま用いていきます。
信頼区間の作り方の問題
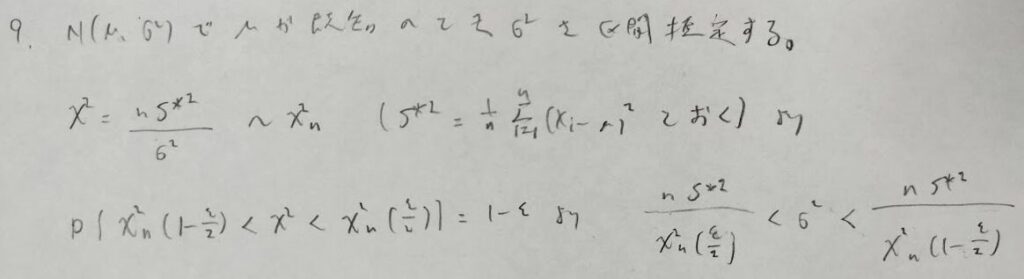
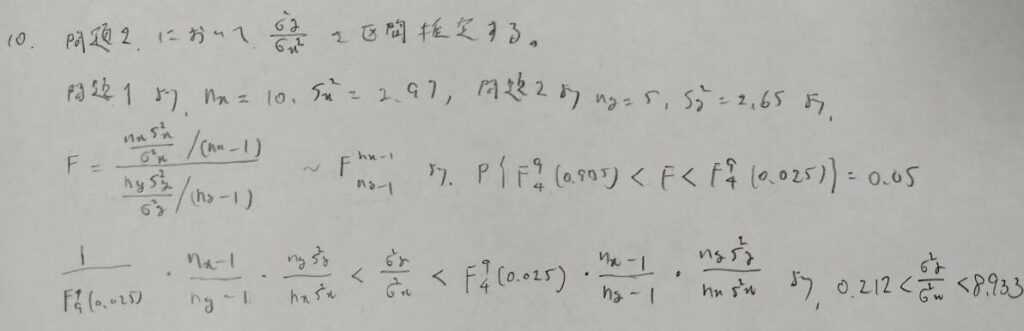
公式として覚えようとすると頭がゴチャゴチャになるので、導けるようにしましょう。ポイントは求めたい母分散の逆数を意識して統計量を作ることです。結局最後は計算結果の後に所望の信頼区間が自動的に算出されます。
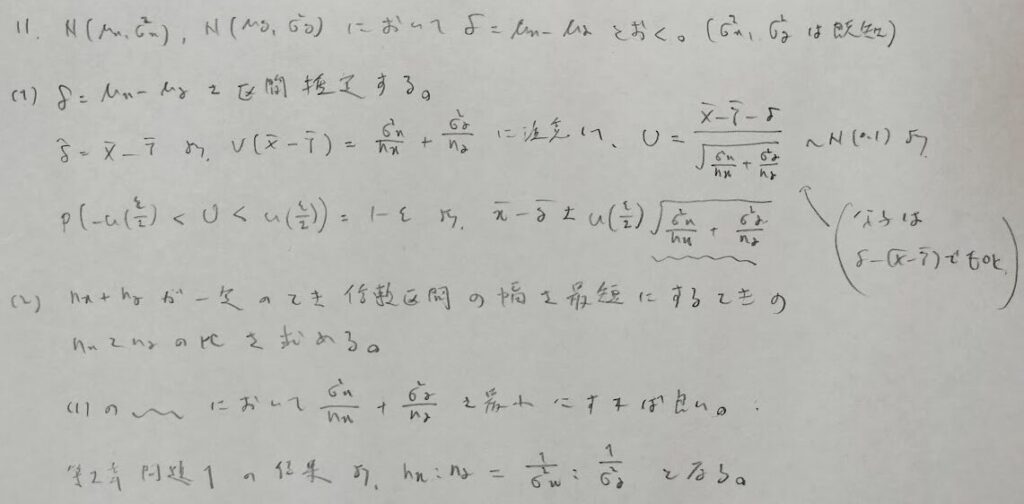
アクチュアリー数学本番では微分している時間も勿体無いので、このパターンが出てきたら逆比!と覚えてしまいましょう!

先ほどの問題もそうですが、解答の書き初めに出ている推定量は最尤推定量です。最尤推定量から出発すればうまい統計量を作成しやすくなると『リスクを知るための確率・統計入門』に詳しく書かれています。
指数分布およびPoisson分布の母平均に関する区間推定、その他の区間推定の問題

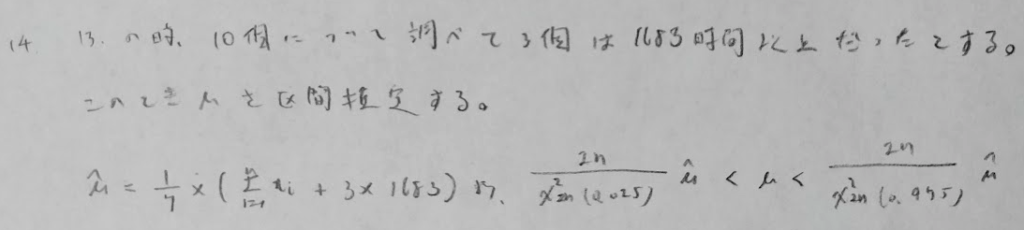
指数分布のパラメータの区間推定で登場するカイ2乗分布の自由度は2n(分子の2nは変換で登場した数値)で固定ですが、
ポアソン分布のパラメータの区間推定でのカイ2乗分布の自由度は2(k)と2(k+1)がそれぞれ左右に生じます。
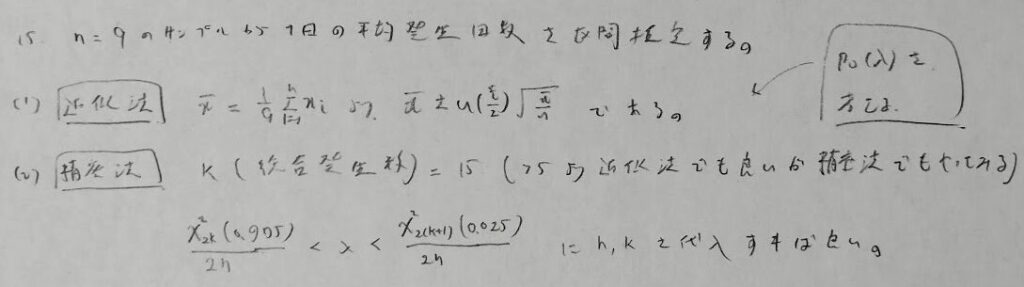
左辺はより小さく、右辺はより大きくの精神で考えれば、0.975や0.025がどっちだっけ?がなくなります。

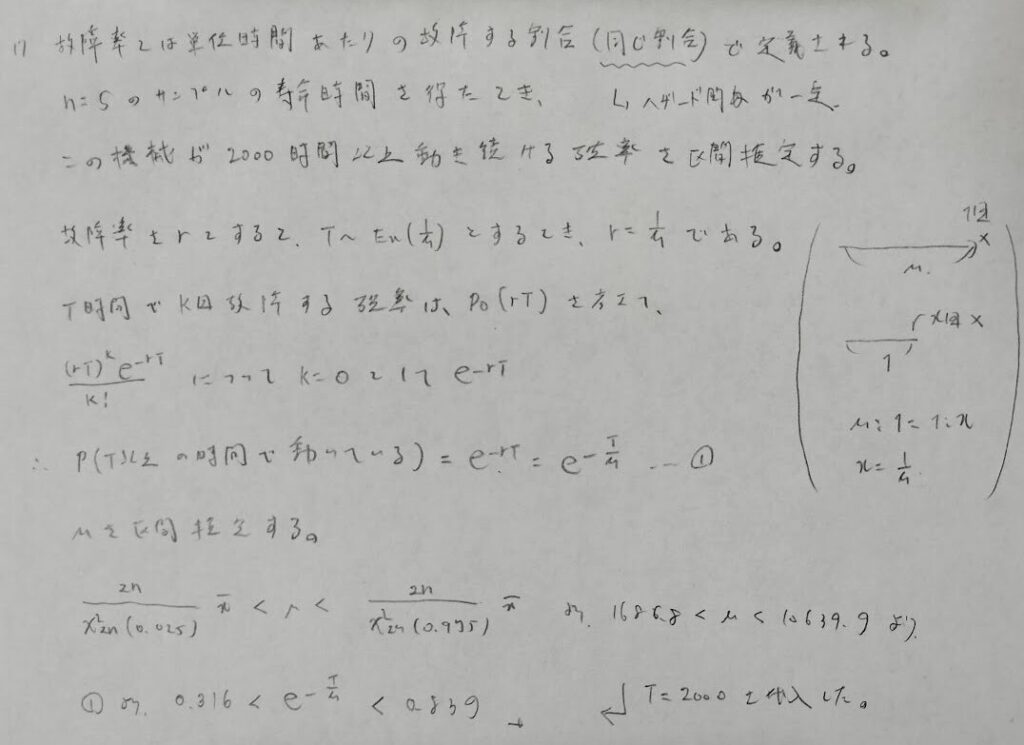
かなり実践的な内容です。アクチュアリー数学にも今後出てきそうな設定の問題です。
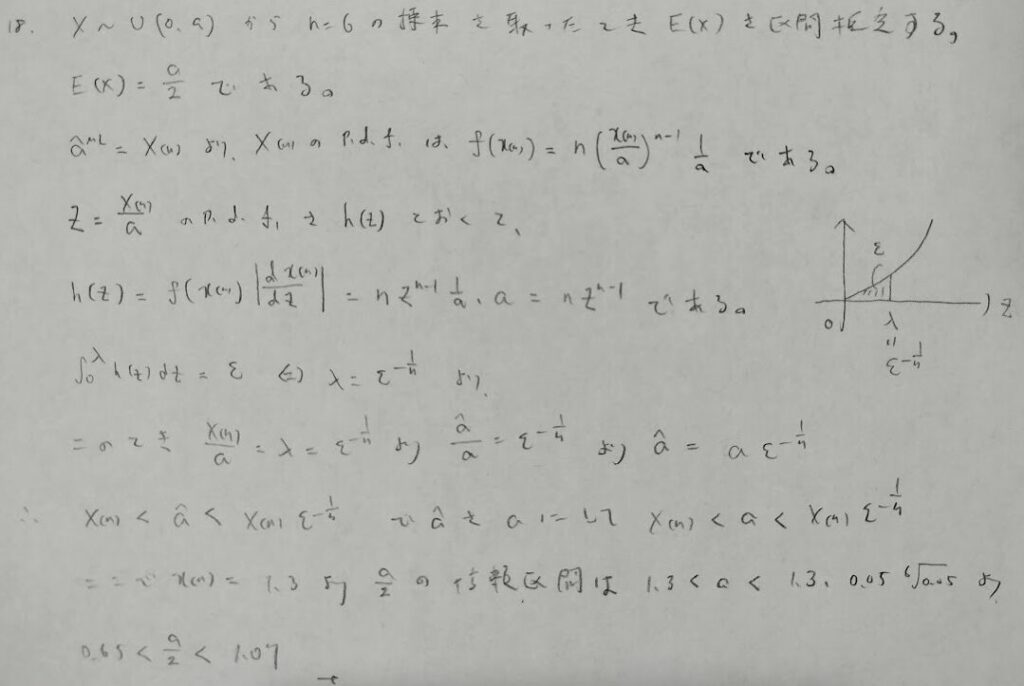
難問です。aの区間推定がメインです。最尤法より求めた最大統計量の確率密度関数を考えます。これは左右非対称となるので片側信頼区間を構成します。すなわち信頼上限を求めることになります。ここで欲しいのはaと最大統計量の間の関係になるので、これらの従う変数Zの確率密度関数を求めていきます。最後の仕上げは例題17と同じように考えます。例題17より本問の方が難易度が高いです。
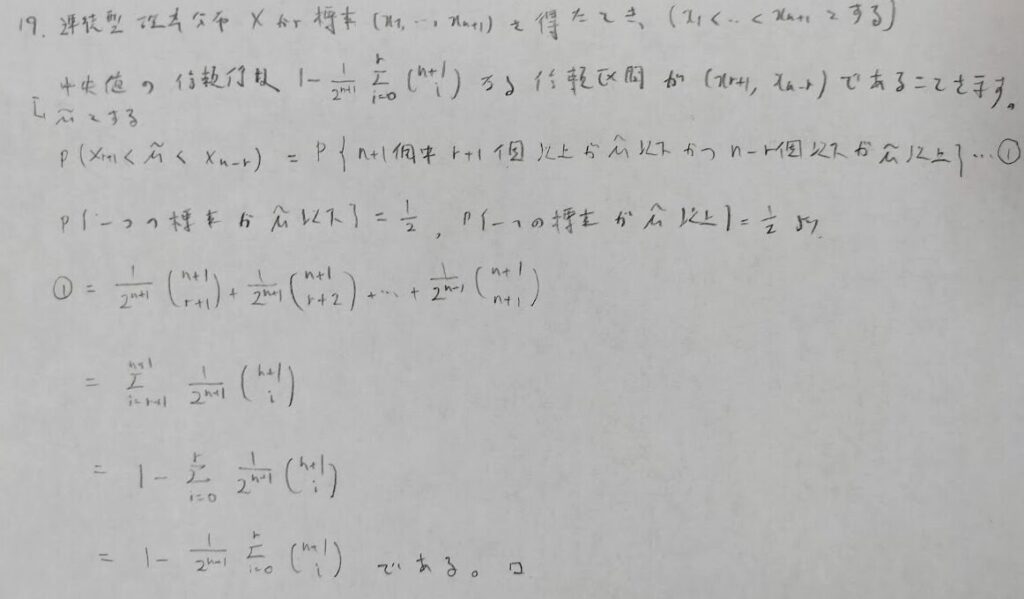
二項分布が絡んできます。アクチュアリー数学では未出です。
以上で第3章の区間推定法の問題は全て終了です。
一様分布が絡む区間推定がとても難しかったです。
次回は第4章の『統計的検定』になります。続きはこちらからご覧ください。また問題の詳しい設定などは『確率統計演習 2 統計』を手元に学習くだされば幸いです。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)







