アクチュアリー数学で統計分野での公式教材として指定される問題集は『確率統計演習 2 統計』になります。本書はアクチュアリー数学試験で最も出る教材です。大問が同じ問題で出題されることが何度も何度もあります。また未出問題もあることが特徴です。
アクチュアリー数学では第1章の出題頻度が低いため、第2章から第8章までの例題と問題を解説していきます。本記事は第2章の記事になります。
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)
アクチュアリー数学の確率分野で公式が指定する問題集『国沢確率』の解説記事はこちらから各章へ飛べます。
『国沢統計』第2章「統計的推定」の例題
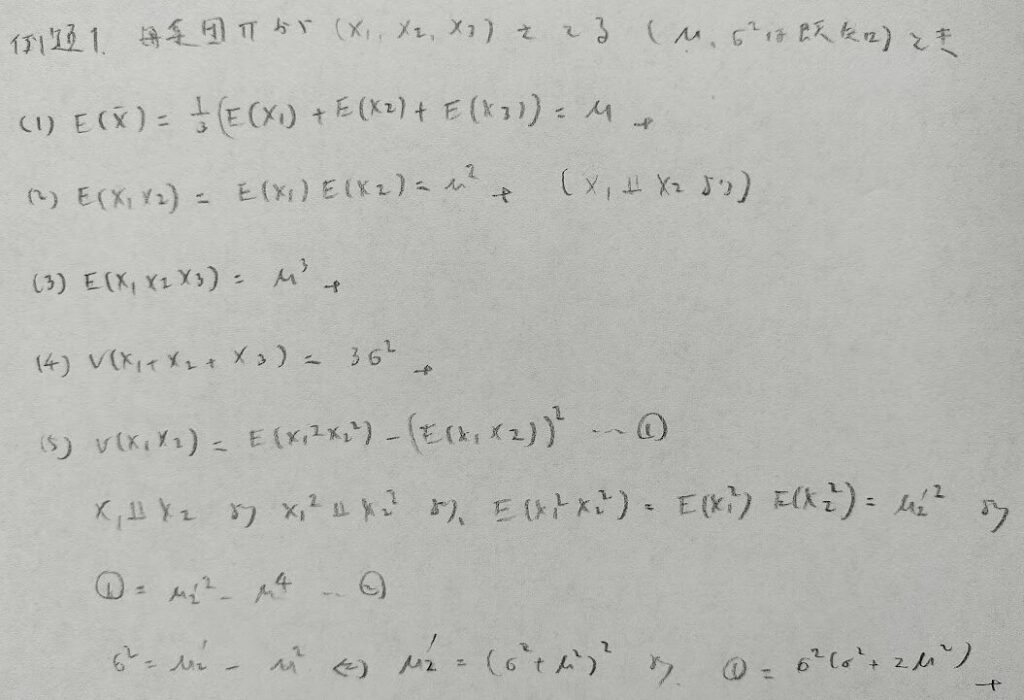
母集団からの標本はすべて独立と考えることが大切です。また以下の問題では何も述べられていない場合は母平均μ、母分散の正の平方根をσとし、標本サイズはnとします。
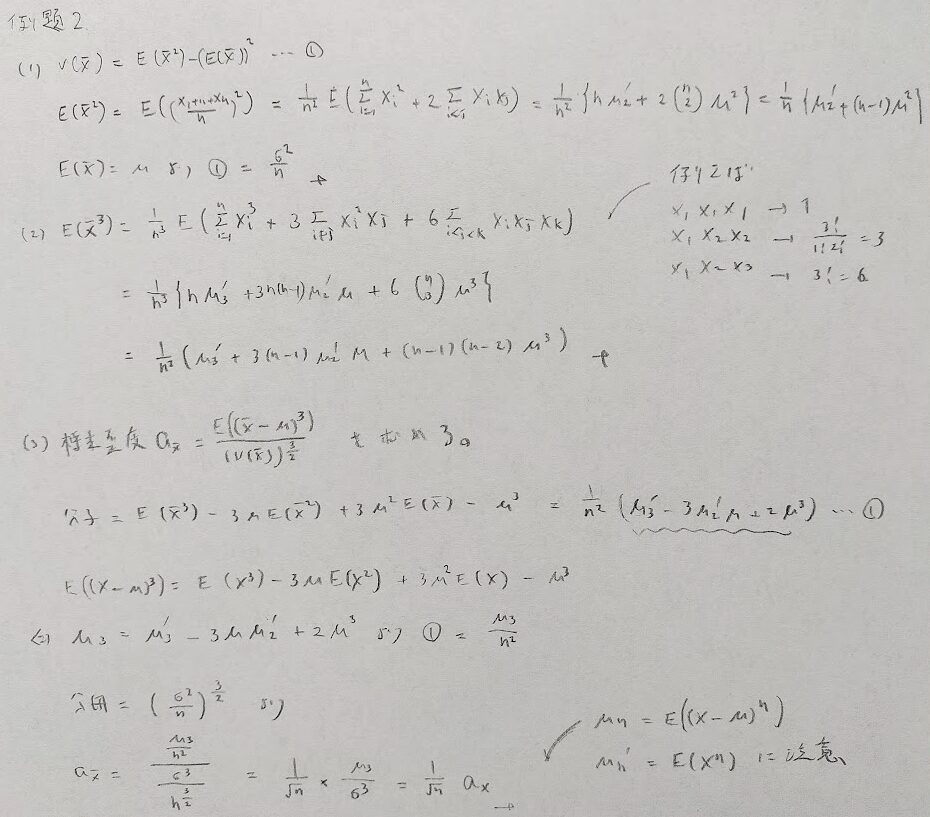
標本歪度はXの標本平均に関する標本歪度を求めていますのでご注意ください。
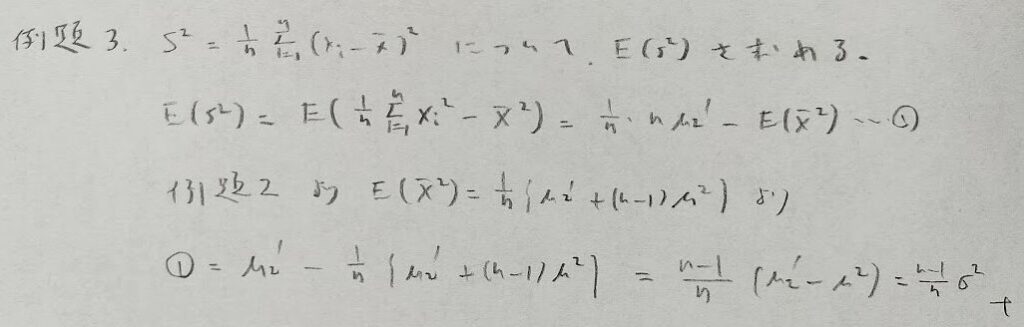
θの推定量の効率は、θの有効推定量を、θの推定量の分散で割った値と定義され、Eff(θの推定量)と定義されます。また、θの望ましい推定量とは、不偏性+有効性+十分性+一致性を満たす推定量として定義します。
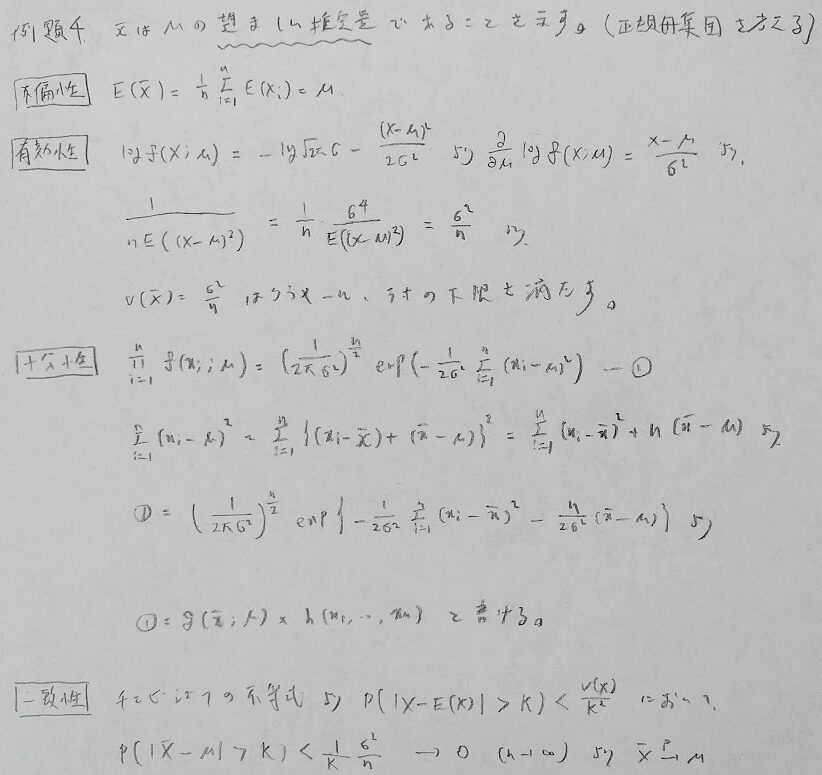
本記事では「十分性」としていますが、一般的な十分性との混合を避けるために、記述試験の際は「充足性」の方が良いと感じます。

十分性のRは実数ではなく領域のRという意味です。特定の領域において、十分推定量で条件下した確率が真のパラメータに依存することを示せばOKです。
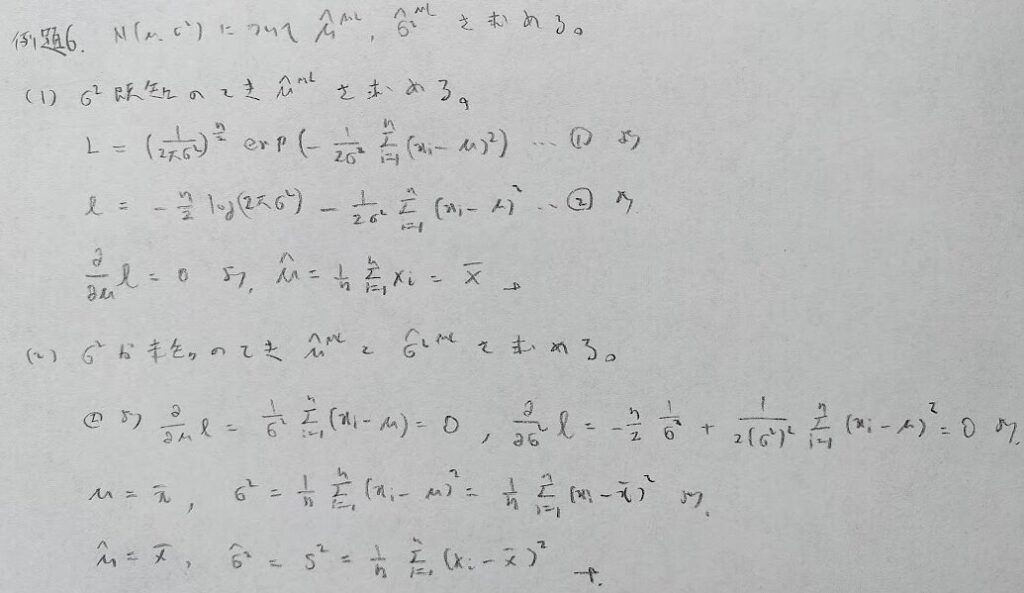
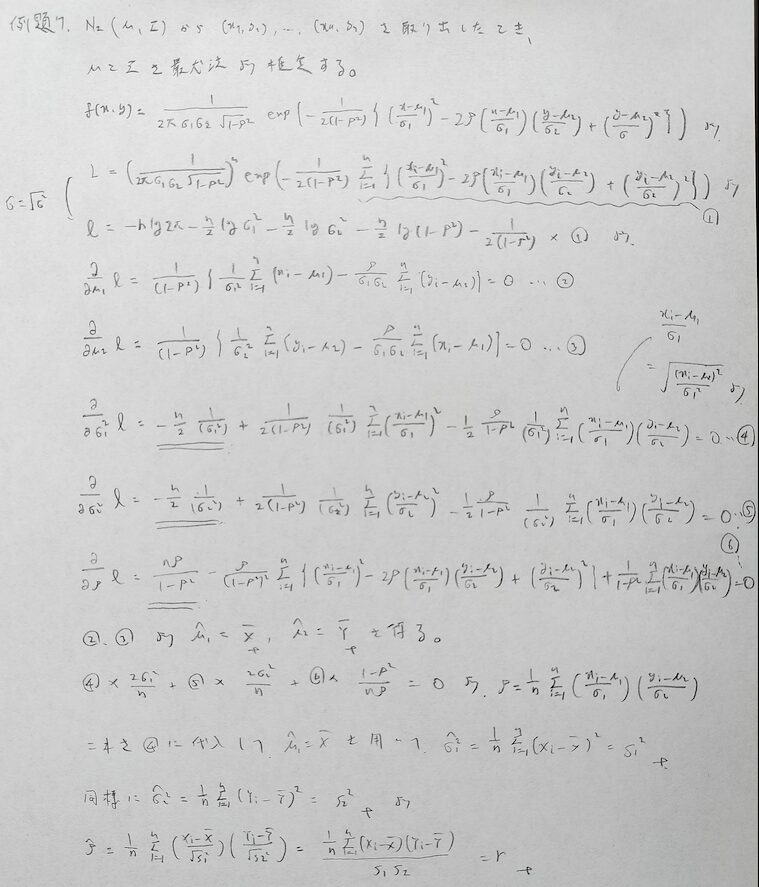
2変量正規分布の最尤推定の問題はこの分野にて計算量のレベルが最難関です。初見では本番で間に合いませんので解き方の流れを一緒に確認しましょう。

指数分布は表現の仕方に注意します。また線形変換ではないので、不偏性は保たれないだろうと思って問題を解くと良いです。一致性からのテイラー展開は王道です。
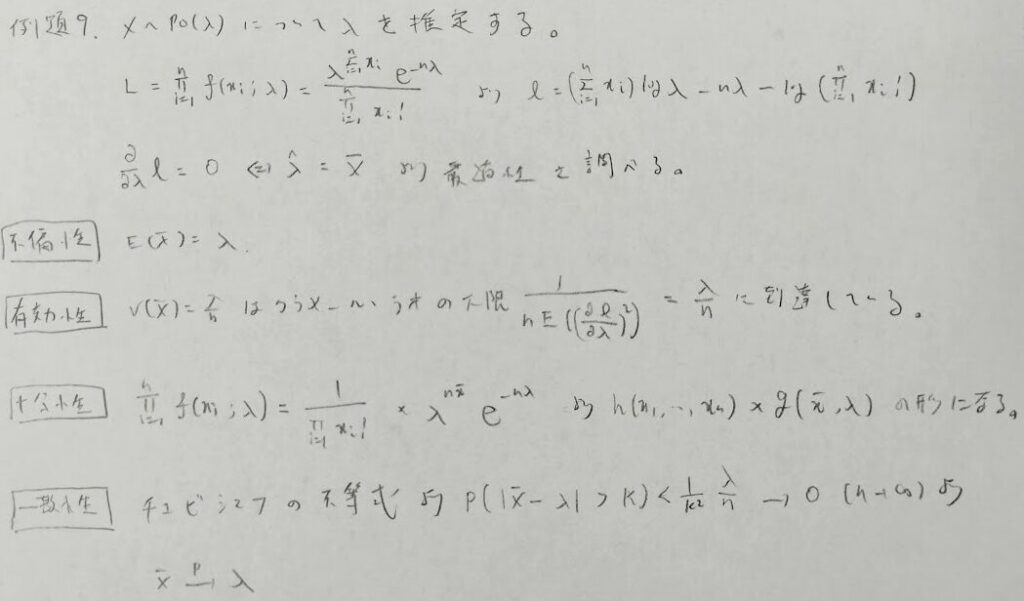
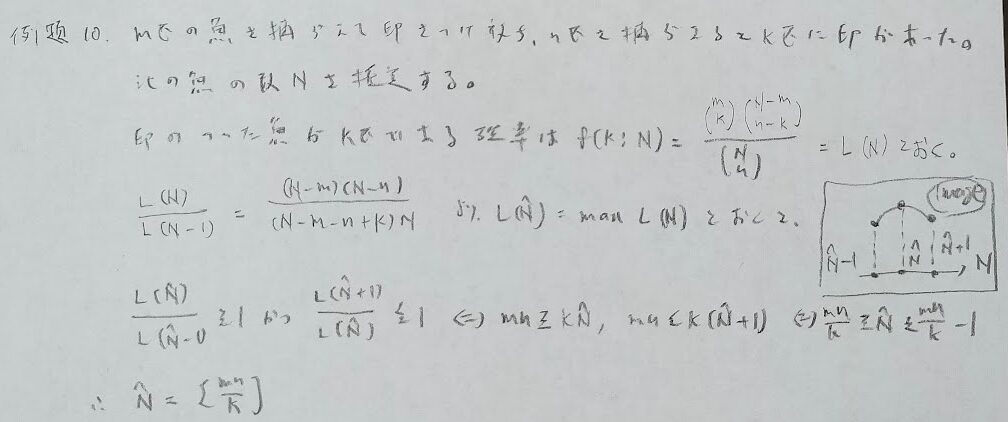
ガウス記号を用いる部分の根拠がわかりやすい解き方ですので、このまま把握してしまいましょう!ガウス記号内が整数になる場合の最尤推定量は2つあります。
発展事項として推定量同士の関係をまとめます。
①正則条件のもとで有効推定量が存在し、それは十分推定量です。
→有効推定量は十分推定量
②有効推定量は十分推定量の関数で表せます。
→有効推定量は十分推定量の関数
③最尤推定量は不偏性を持っていませんが手を加えて不偏にすることができます。
→最尤推定量は不偏推定量とは限らない
④有効推定量が存在するとき、最尤推定量に等しく一意です。
→有効推定量は最尤推定量
⑤十分推定量が存在するとき、最尤推定量は十分推定量の関数で表せます。
→最尤推定量は十分推定量の関数
十分推定量(複数存在)が基本的な構成量のイメージですね。また有効推定量は厳しい推定量だということもイメージできました。
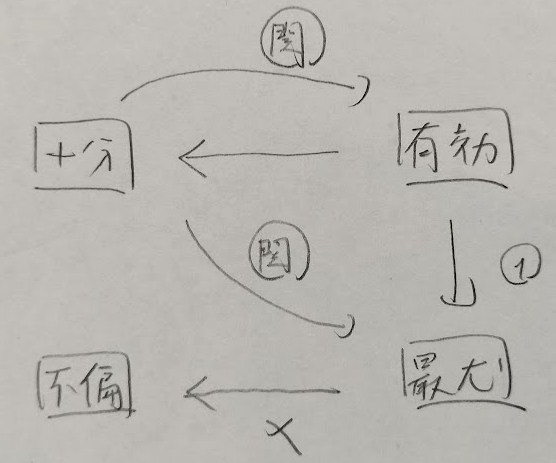
モーメント推定量は別枠ですね笑
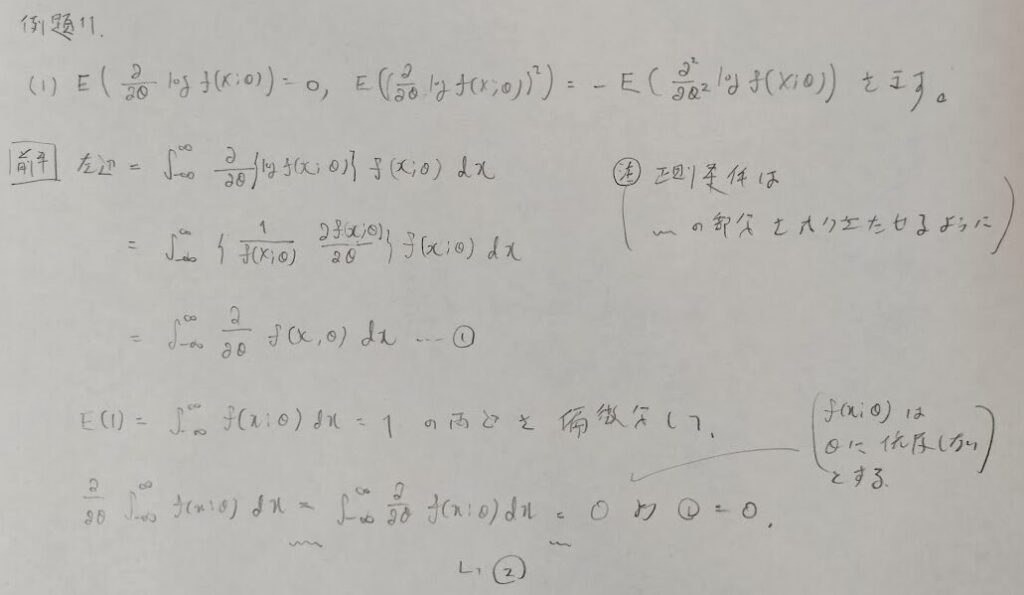
正則条件はそれがないと証明が進まなくて困る部分で適用していくものです。
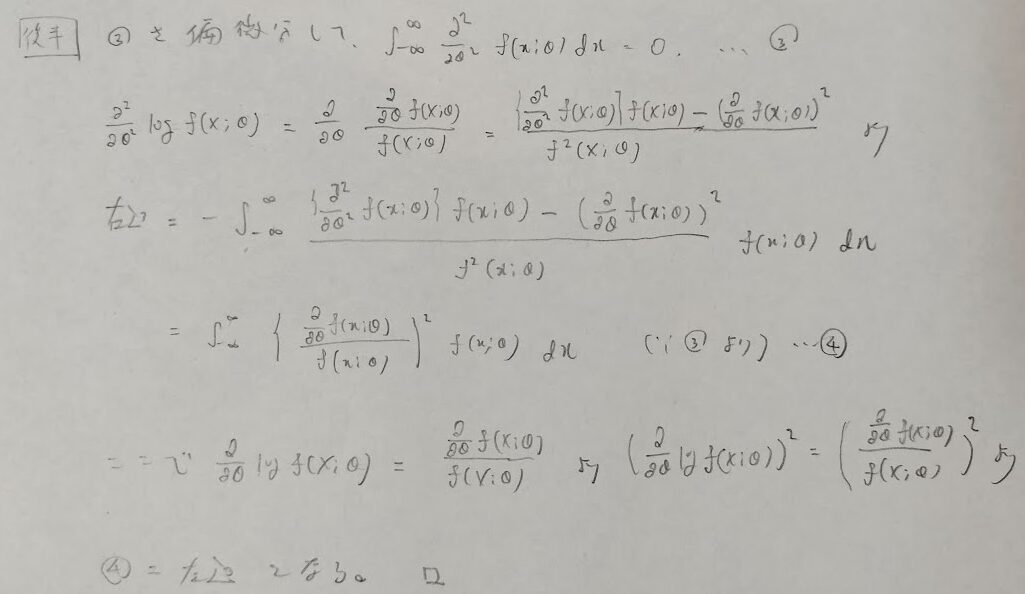
『確率統計演習 2 統計』にはフィッシャー情報量の言葉は出てきませんが、本問はフィッシャー情報量の効率的な求め方を導く問題です。

ポイントはθでの偏微分から期待値の形に持っていくことです。logを出すところが技巧的です。最後にシュワルツの不等式を用います。

クラメール・ラオの不等式の等号成立条件を考えれば自ずと導かれる結果となります。
『国沢統計』第2章「統計的推定」の問題
推定法と標本平均および標本分散の性質の問題
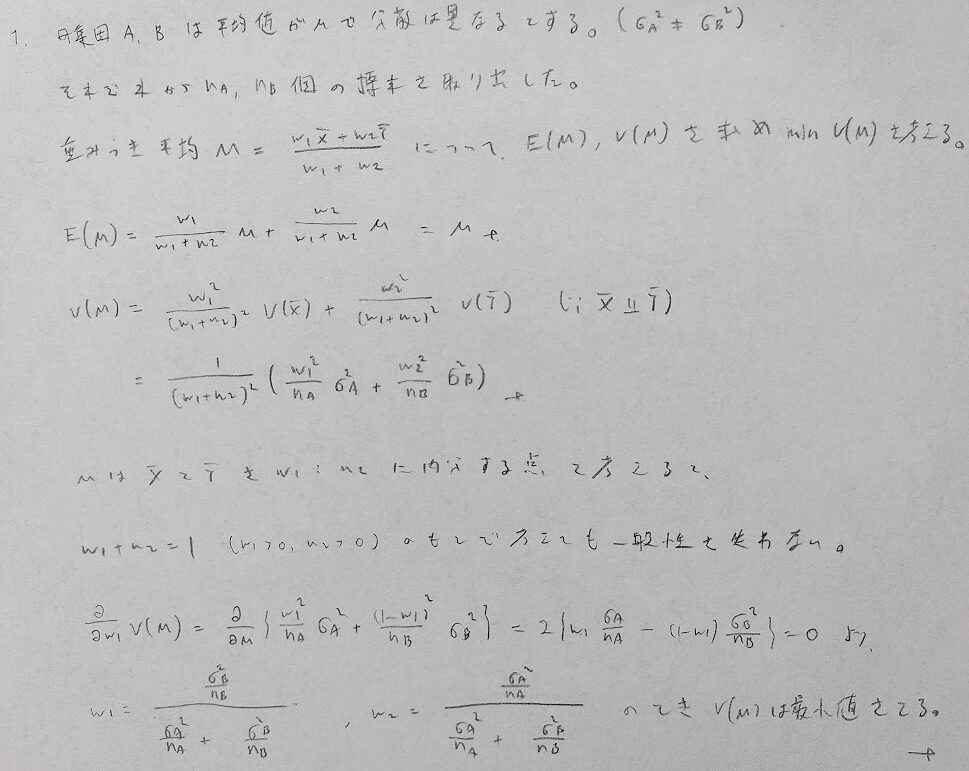
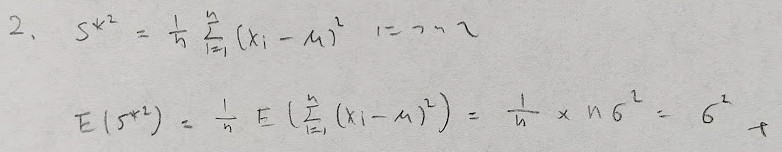

標本平均に関する標本尖度の問題は計算量が膨大になるので、一工夫必要でしたね。
推定量の求め方の問題
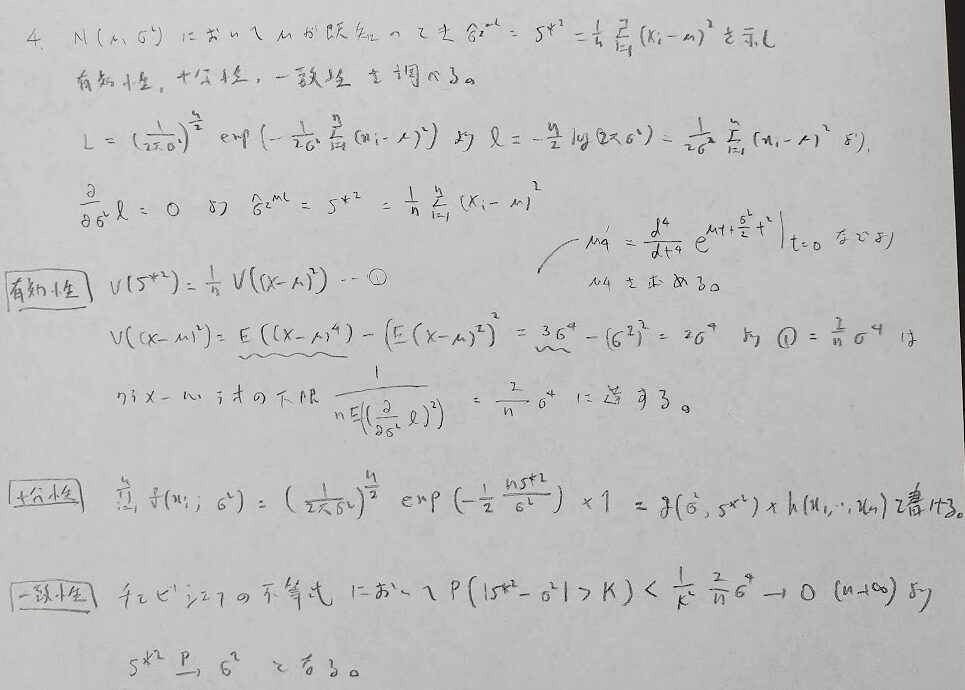
標準正規分布でないときはモーメント母関数からの微分で求めた方が良さそうです。次の問題もこの結果を用いています。
正規分布の4次モーメントはアクチュアリー数学では暗記してしまった方が良いかも知れません。
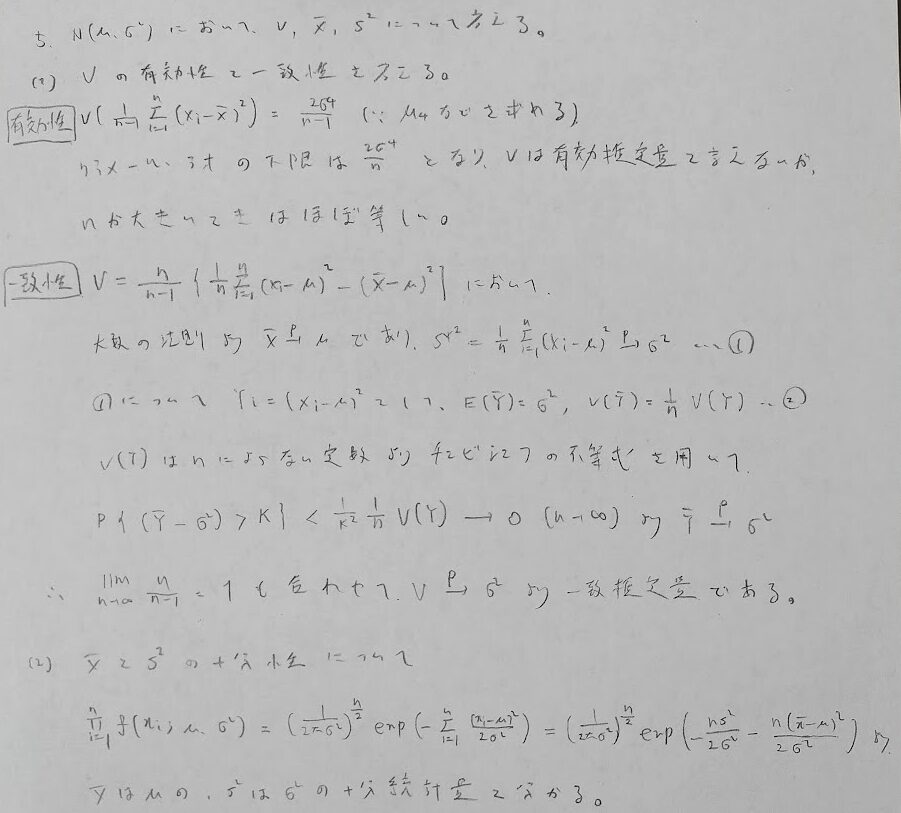
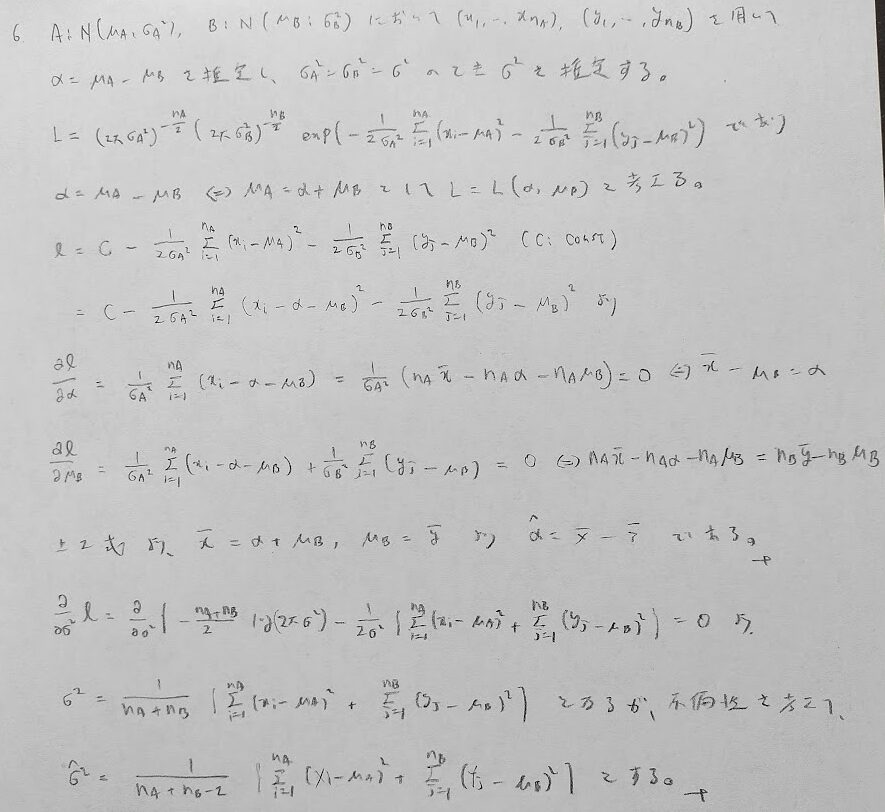
本問での注意は変数を増やしていることです。2変数関数として偏微分しているので、偏微分の仕方に注意しましょう!
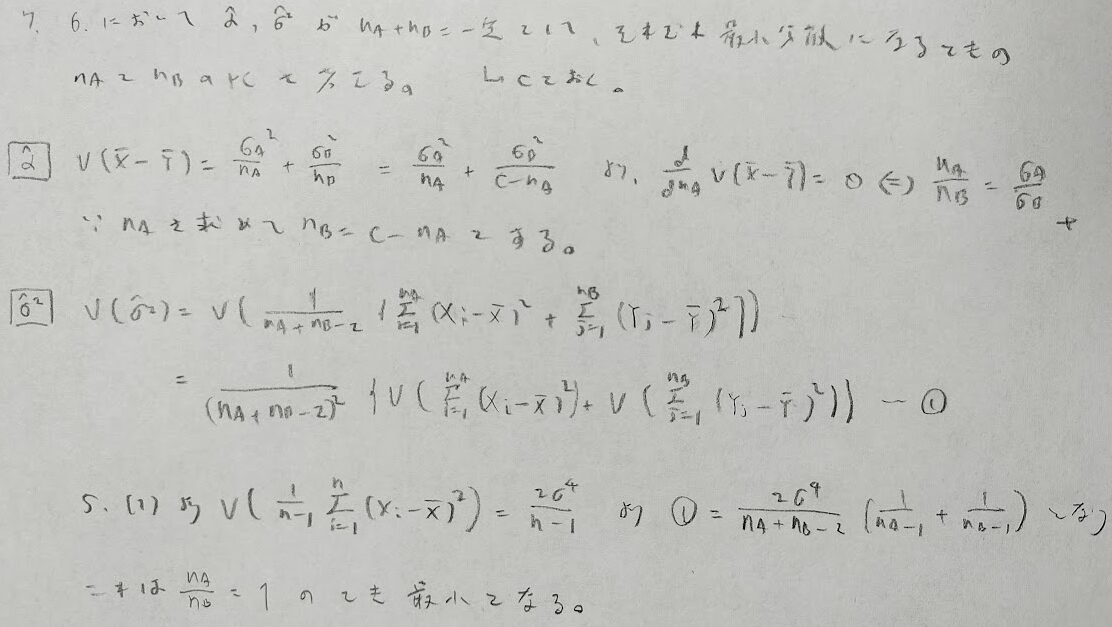
正規分布の平均値周りの4次モーメントを覚えていないと時間内に解き終わらない問題です。
問題8は難問です。いろいろな要素が絡み合っています。

最後の波線の式は2つの関数に分けて考えると自明な結果となります。
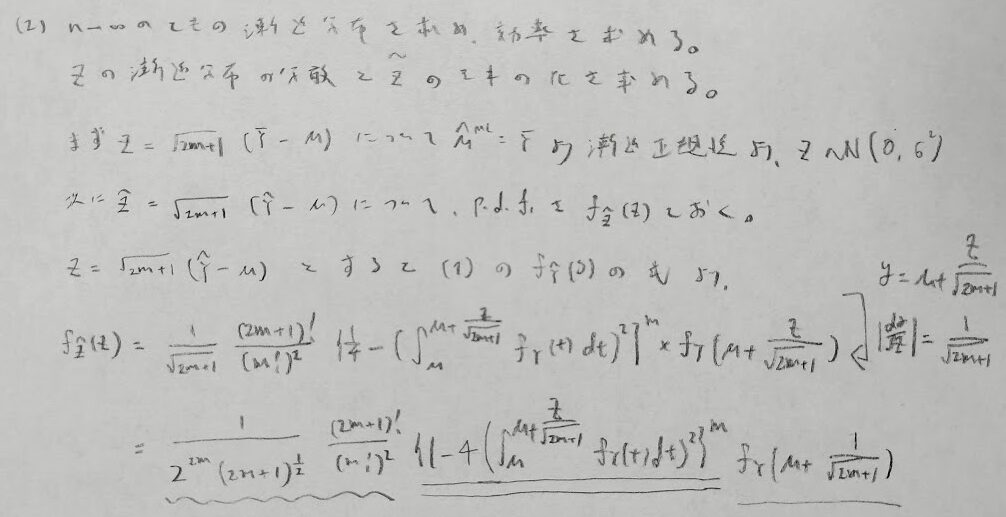
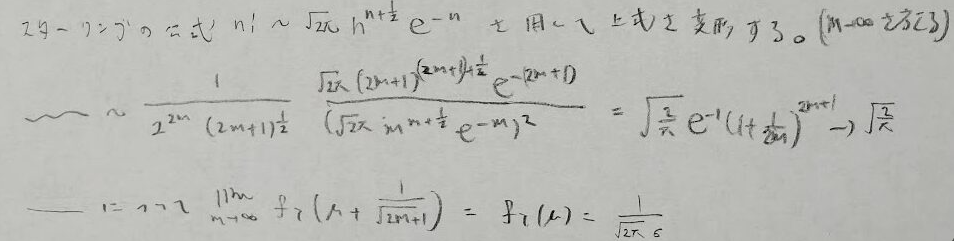
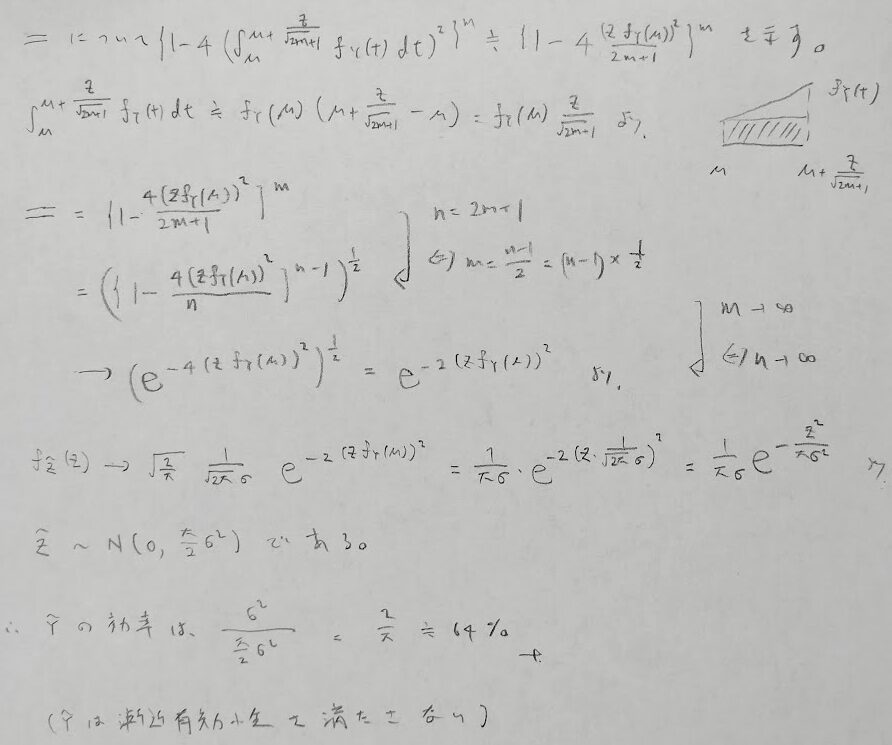
かなり難しい問題です。ノーヒントですが、アクチュアリー数学2018年の大問3には標準一様分布と順序統計量とベータ分布の関係を用いて変数変換を行うことを誘導しています。
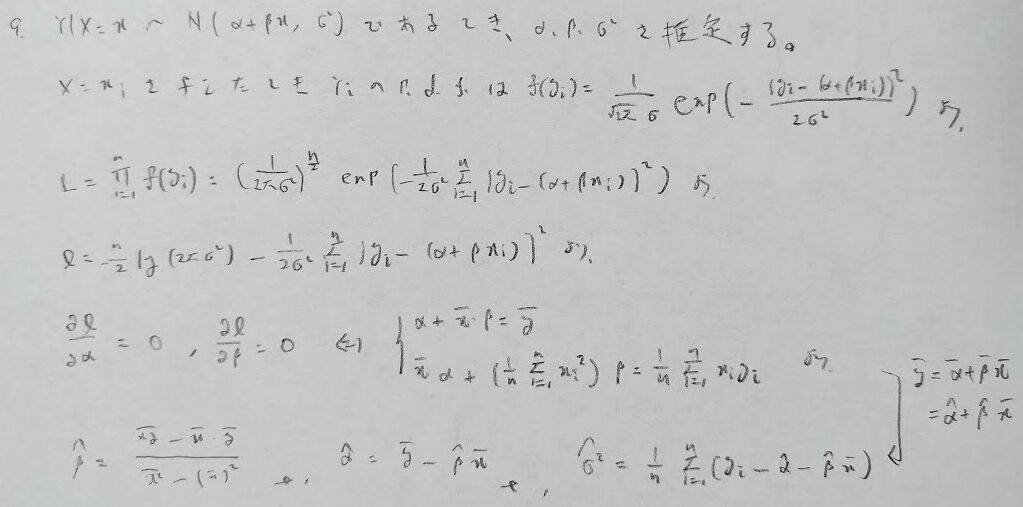
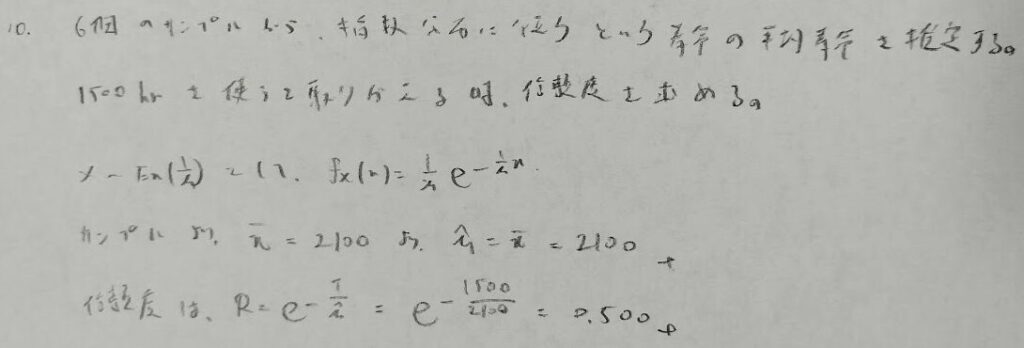
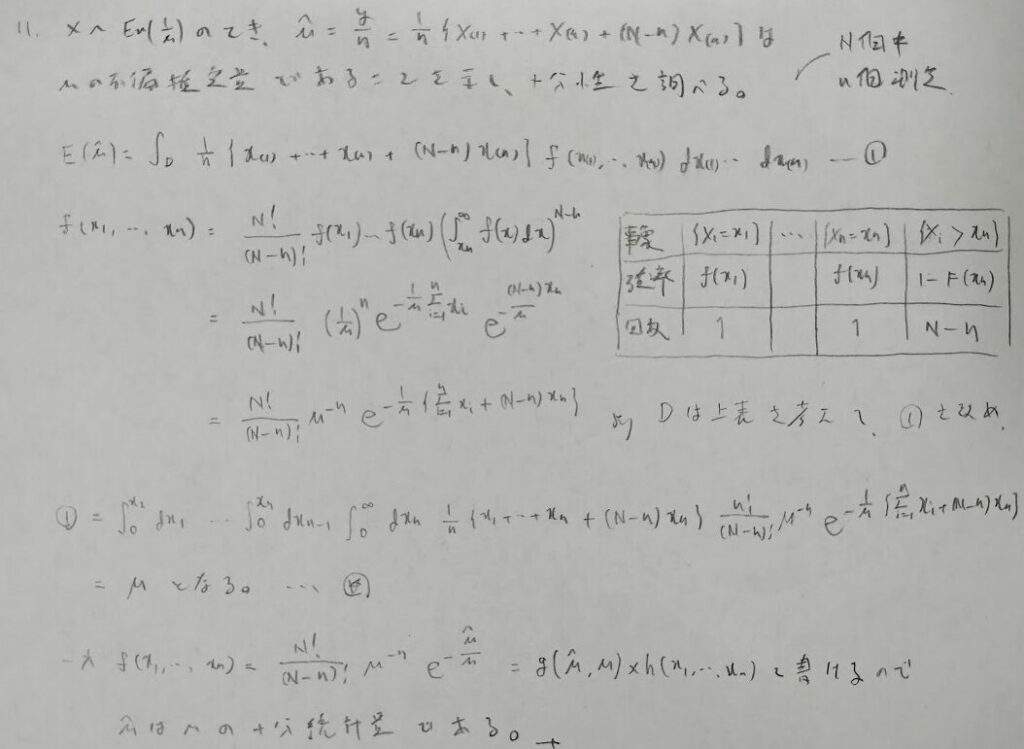
☆の部分はかなり煩雑ですが、アクチュアリー数学ではμとなる(不偏性が満たされる)ことを抑えておけば十分だと思います。
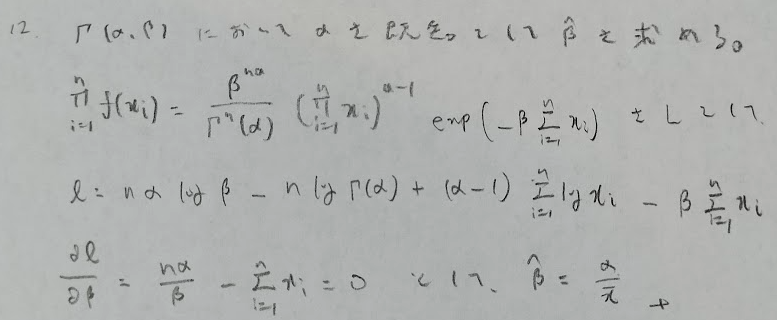
αを形状パラメータ、βを尺度パラメータといいます。今回はαが既知なので最尤法を用います。2つとも未知の場合はモーメント法を用います。

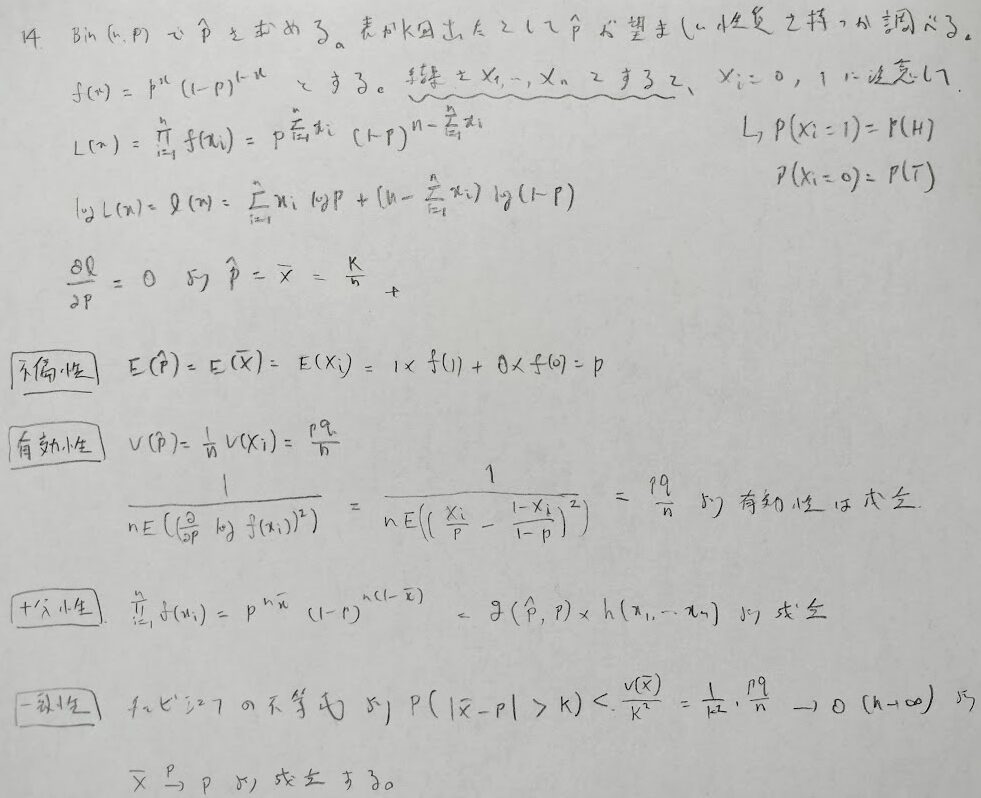
サンプルの出る順番は固定して考えます(同時分布を求めています)ので二項係数は不要です。
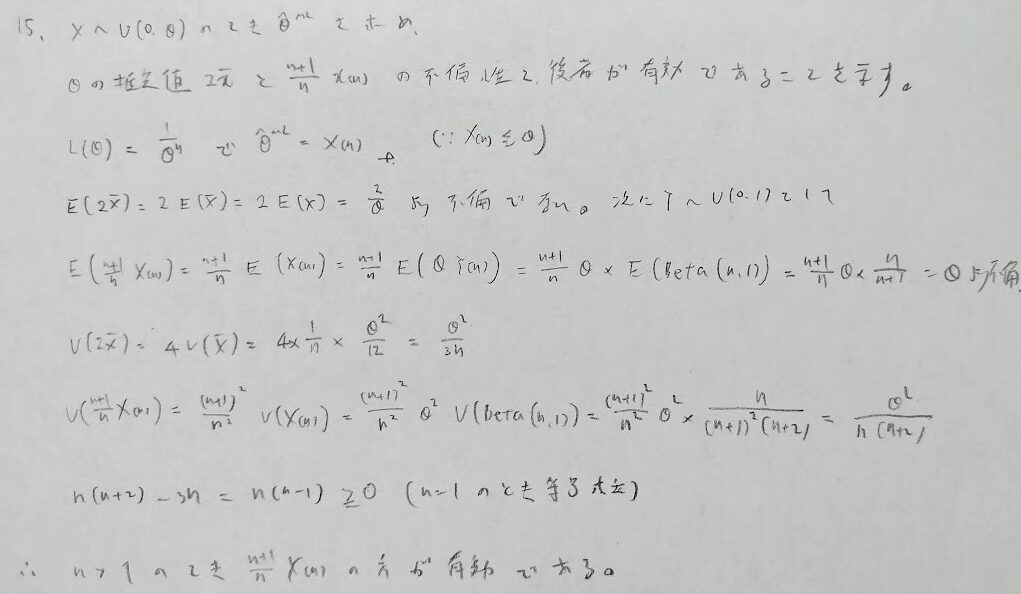
一様分布の(左端が0の場合の)右端の有効性の高い推定法です。主に来客人数の推定で用いることができます。サンプル数が与えられているときに活用できます。具体例は問題18で再喝します。
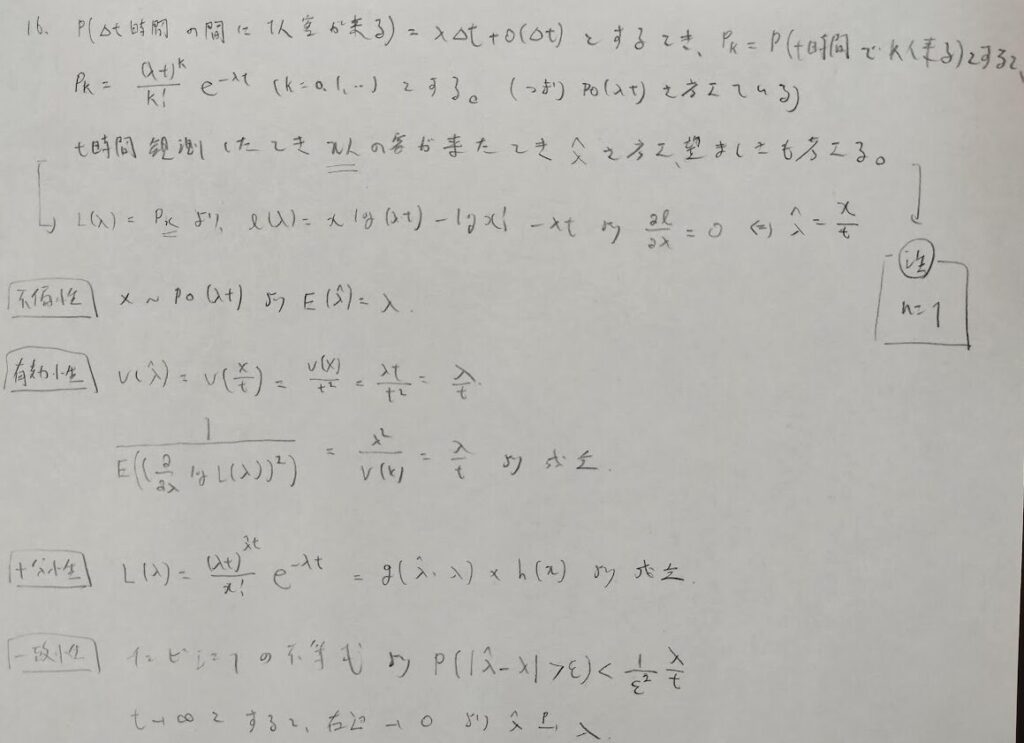
サンプル数が1なのでご注意ください。また最後のチェビシェフの不等式ではtを長くすれば推定量は真の推定量に近づくと考えてtを無限としました。


一様分布の右端の推定で、サンプル数が与えられているときの推定法は『確率統計演習 2 統計』にしか書かれていません。アクチュアリー数学でも出題されていますので、求め方は覚えておいた方が良いです。
次回の内容はこちらになります。頑張りましょう!
第2章:統計的推定
第3章:区間推定法
第4章:統計的検定
第5章:標本分布と標本調査
第6章:分散分析(統計検定1級のため学習)
第7章:相関係数と回帰分析
第8章:管理図、簡易解析法(管理図のみ学習)