アクチュアリー数学の確率分野の指定教材『確率統計演習 1 確率』は統計検定1級にも通用する有用な参考書です。
今回はアクチュアリー数学の試験範囲である第6章に登場する問題の解説を行います。
以前の章の問題で出てきた設定をそのまま用いる問題も多くなることから、各章のリンクを載せておきますね。
『国沢確率』第6章「大数の法則と中心極限定理」の例題
今回の例題は全部で4問しかありませんが第1問から難問です。
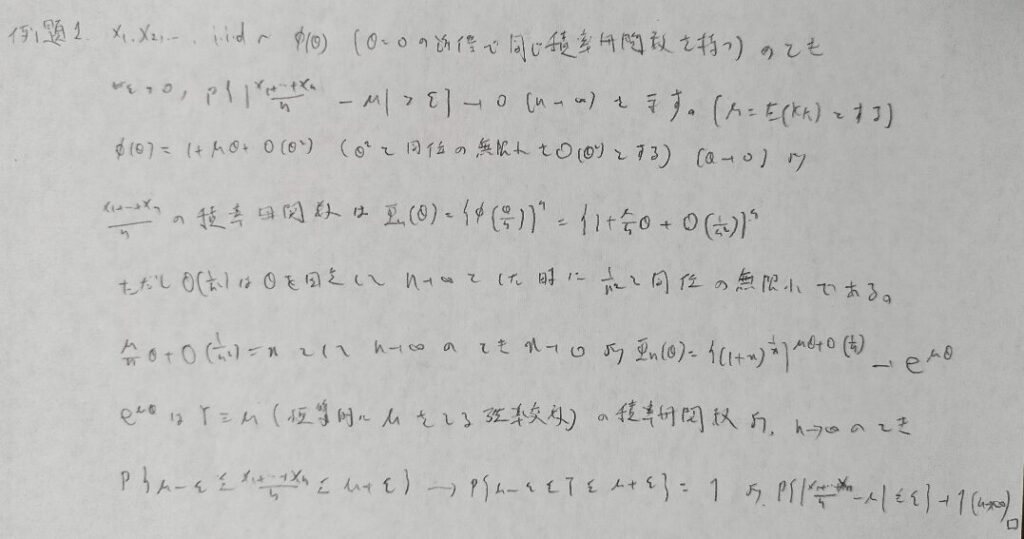
eのマクローリン展開の中にランダウの記号を入れるのがコツです。
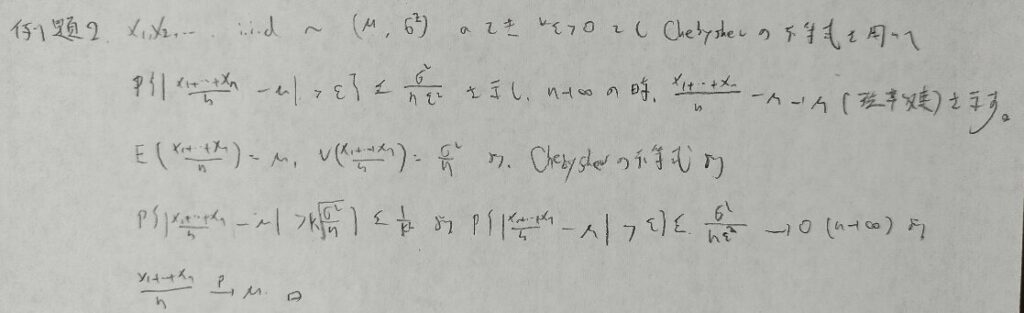
確率収束とチェビシェフの不等式は相性が良いです。

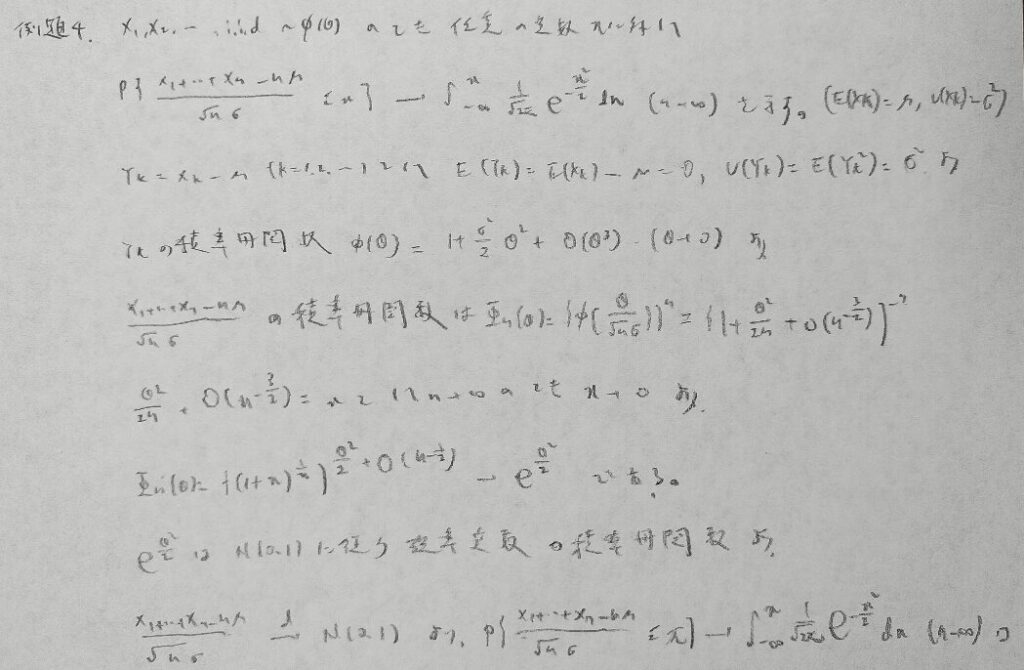
以上で例題を終了します。積率母関数の形でまずは置いてしまうのが鉄則ですね。
『国沢確率』第6章「大数の法則と中心極限定理」の問題
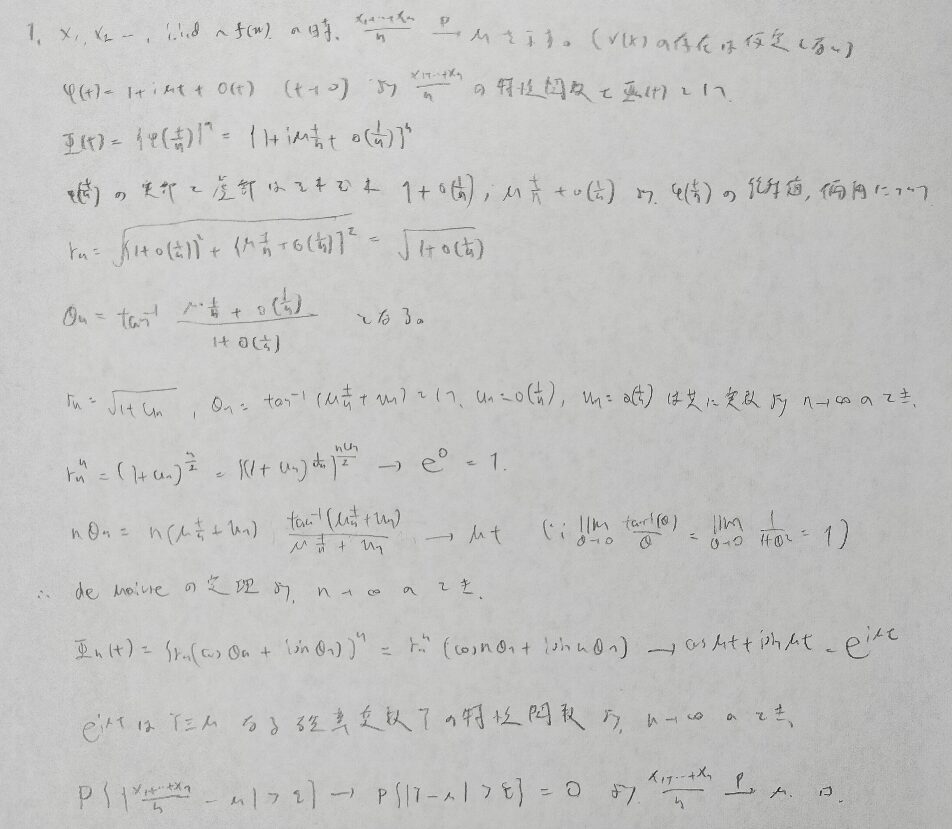
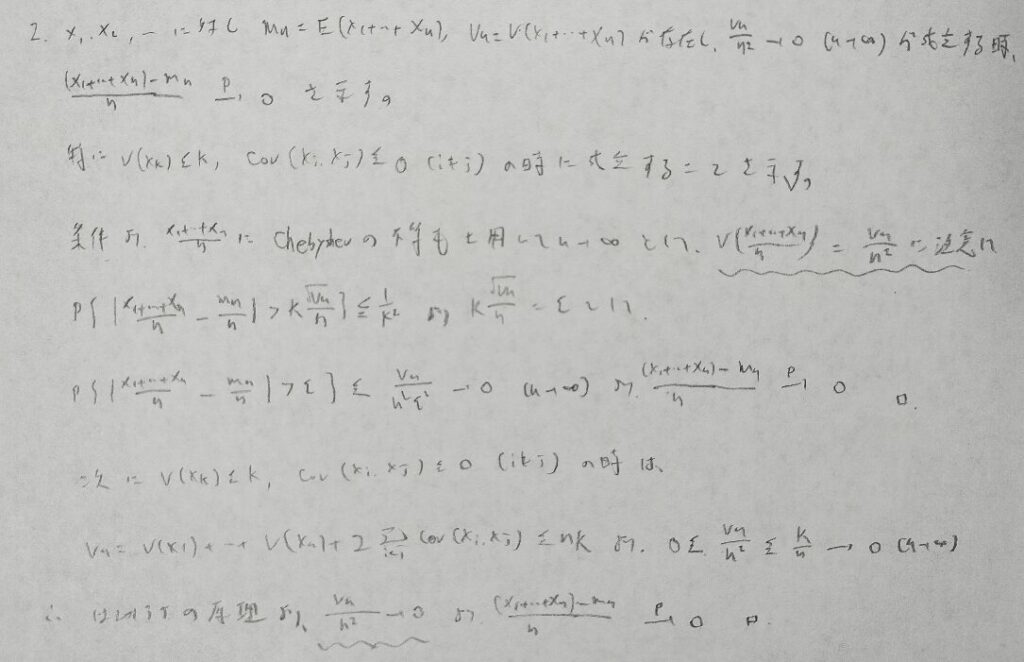

大事な問題ですが証明はテクニカルに見えますが事象で考えてから確率を考えていく王道の証明法となっています。
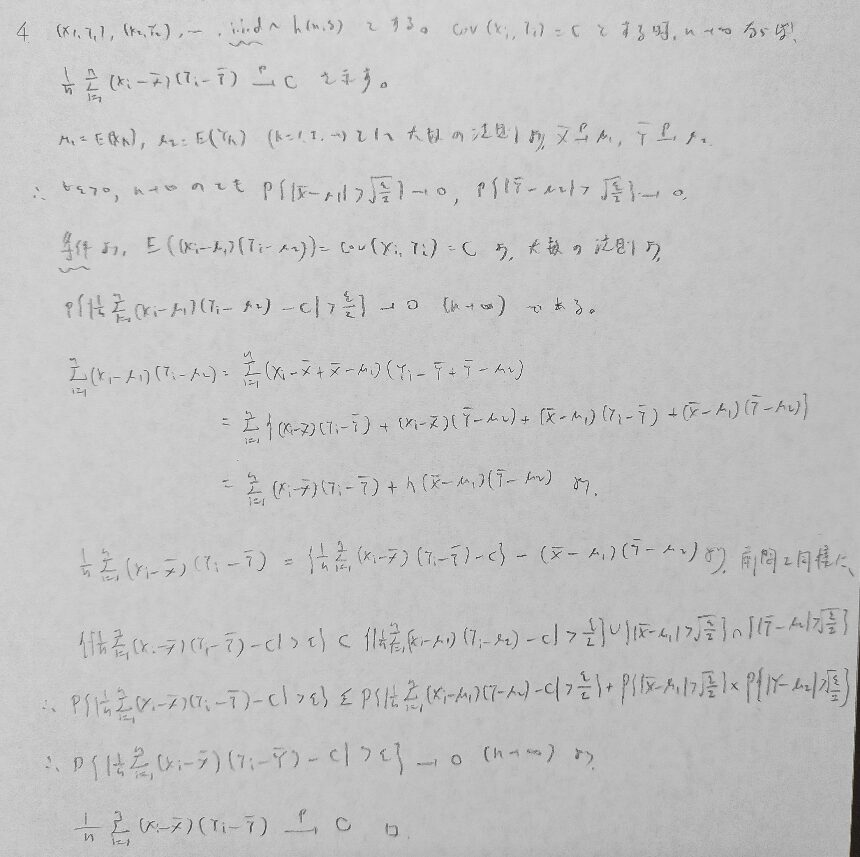
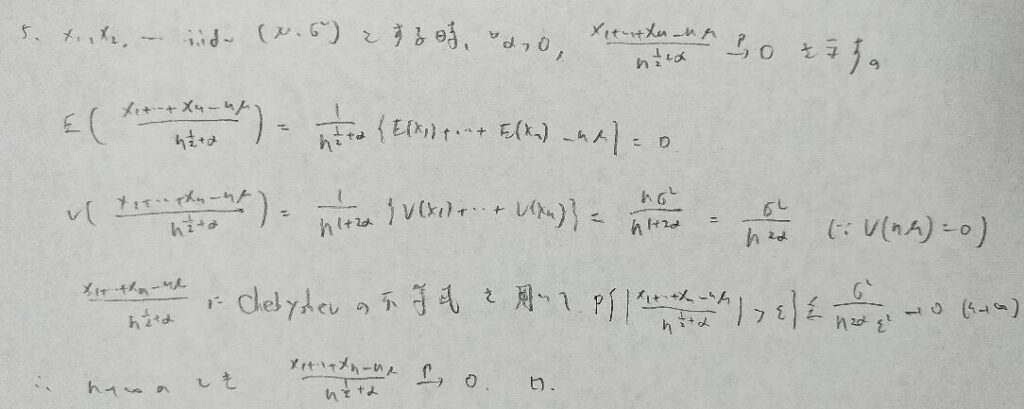
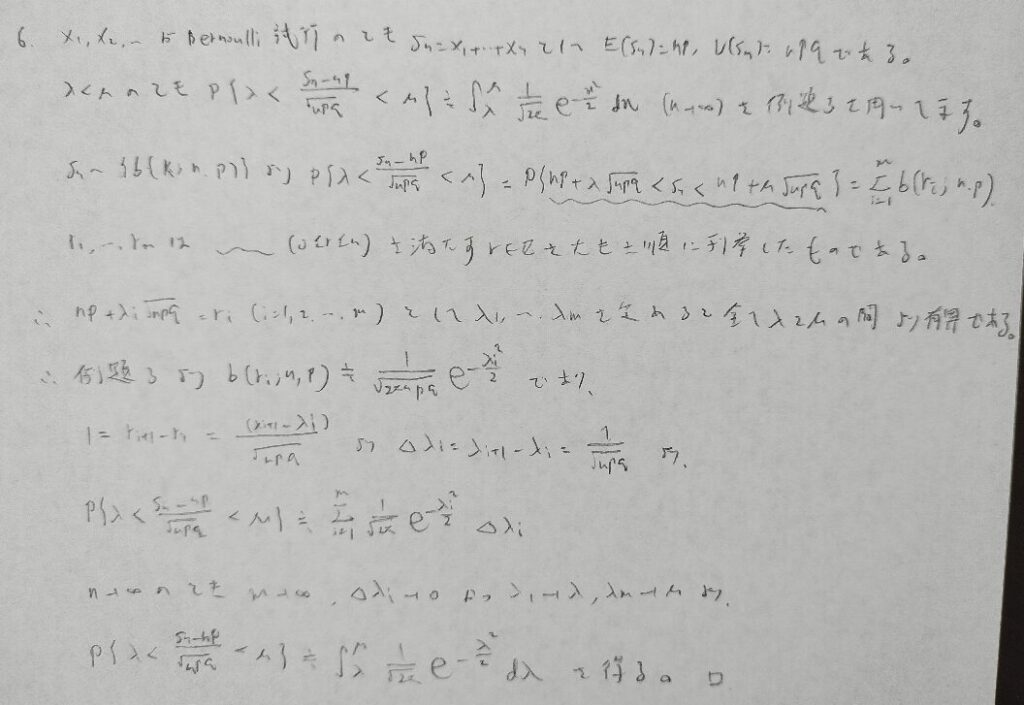
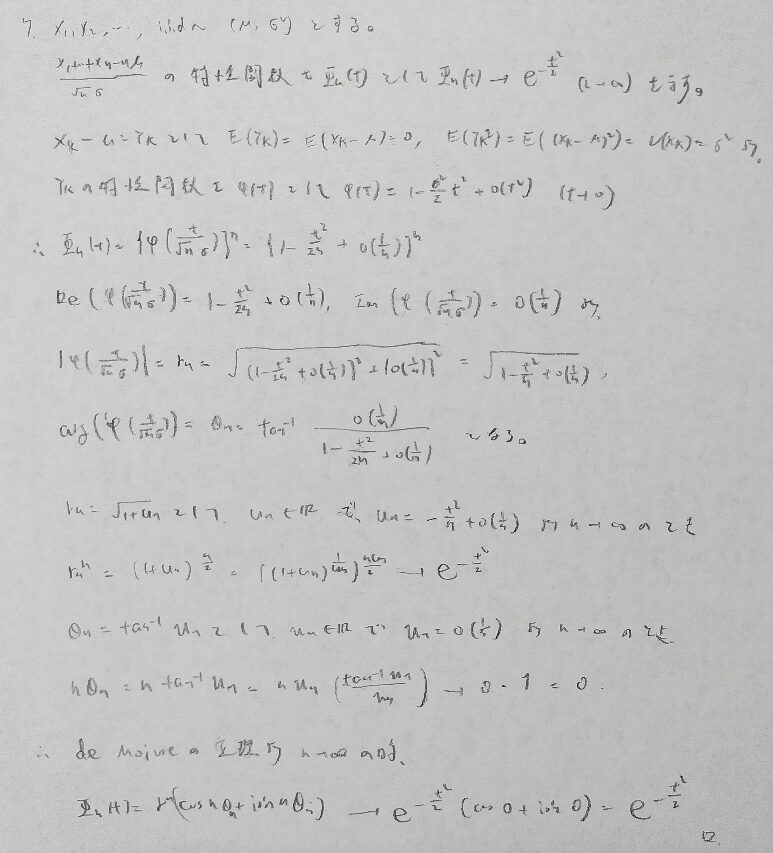
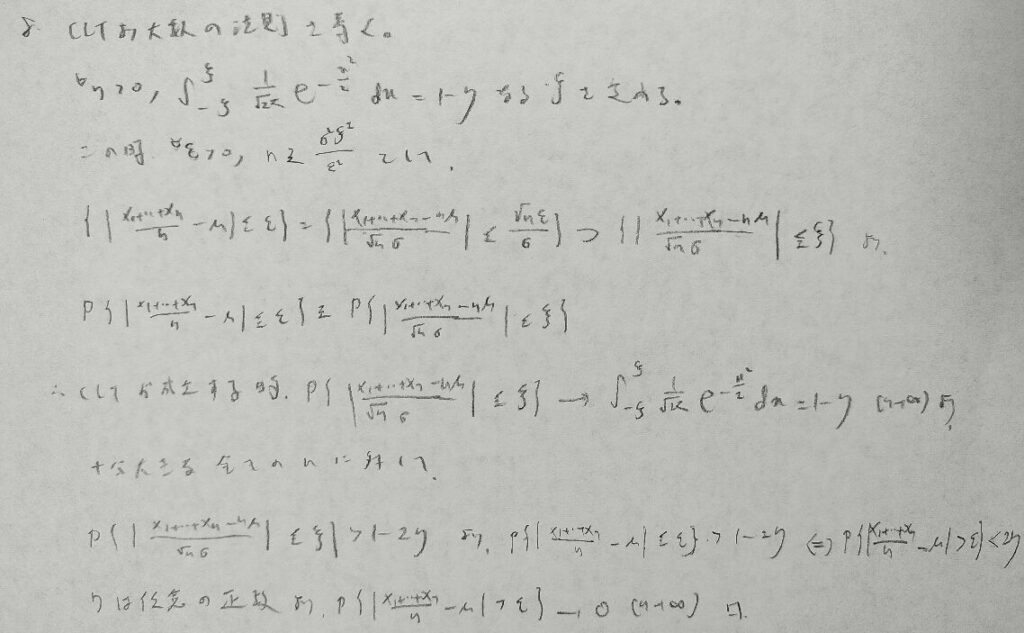
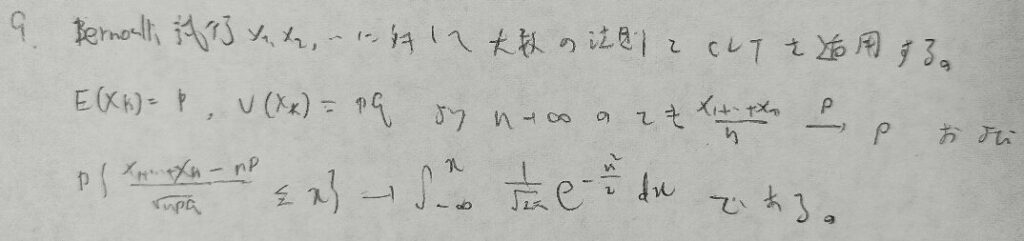
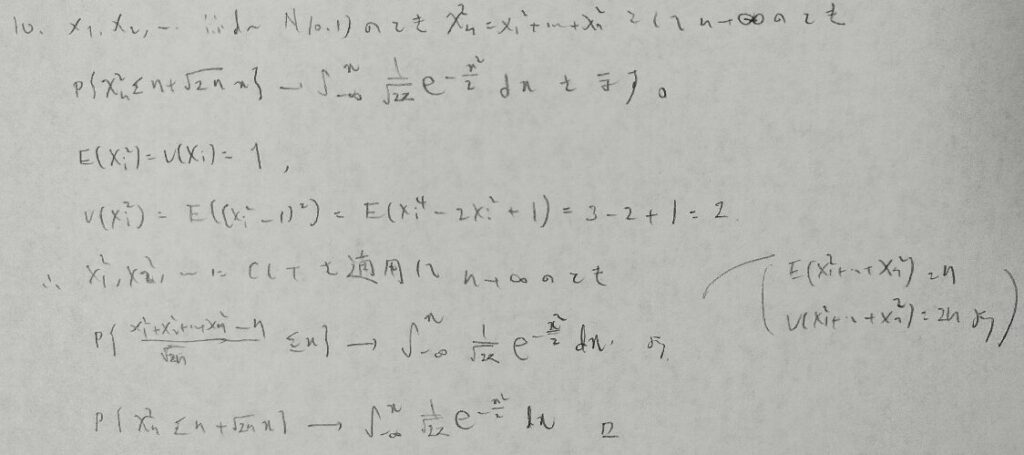
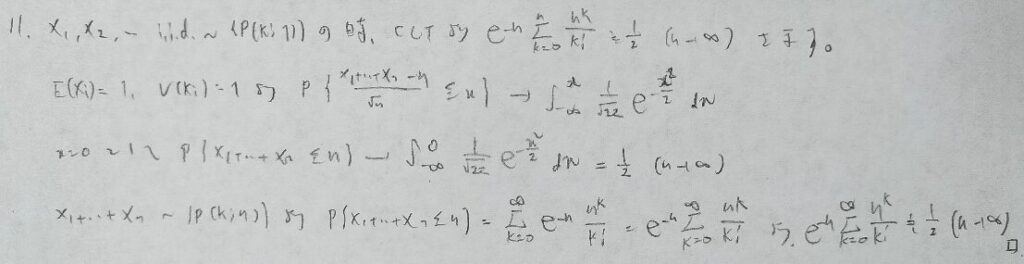
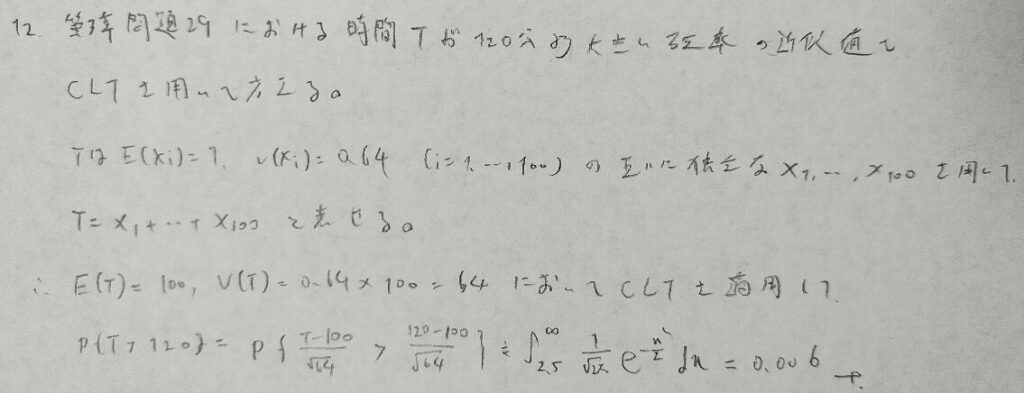
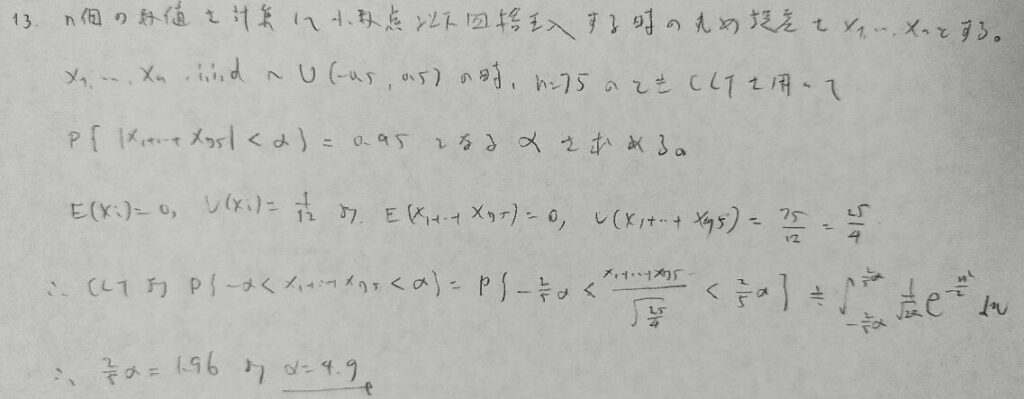
アクチュアリー数学で出題されています。

この問題から最後の問題までマルコフ連鎖の難問が続きます。
『確率統計演習 1 確率』に登場する各章の問題のラスト付近はほぼ全てマルコフ連鎖に関する問題でしたね。

極限分布の定義は覚えておいた方が良いですね。
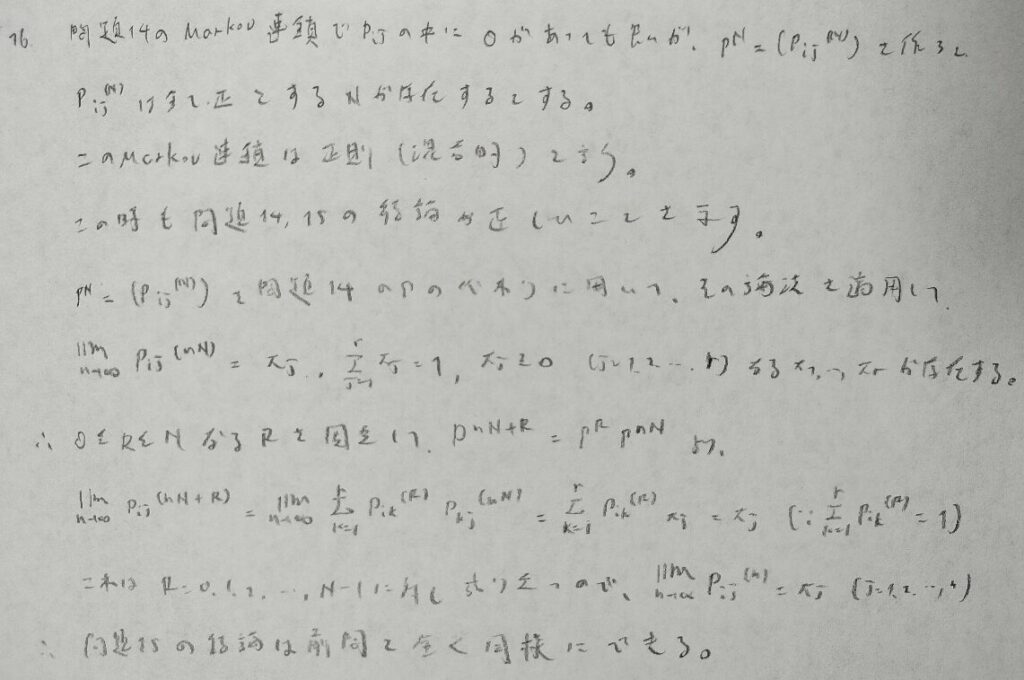
正則という言葉が登場しましたね!
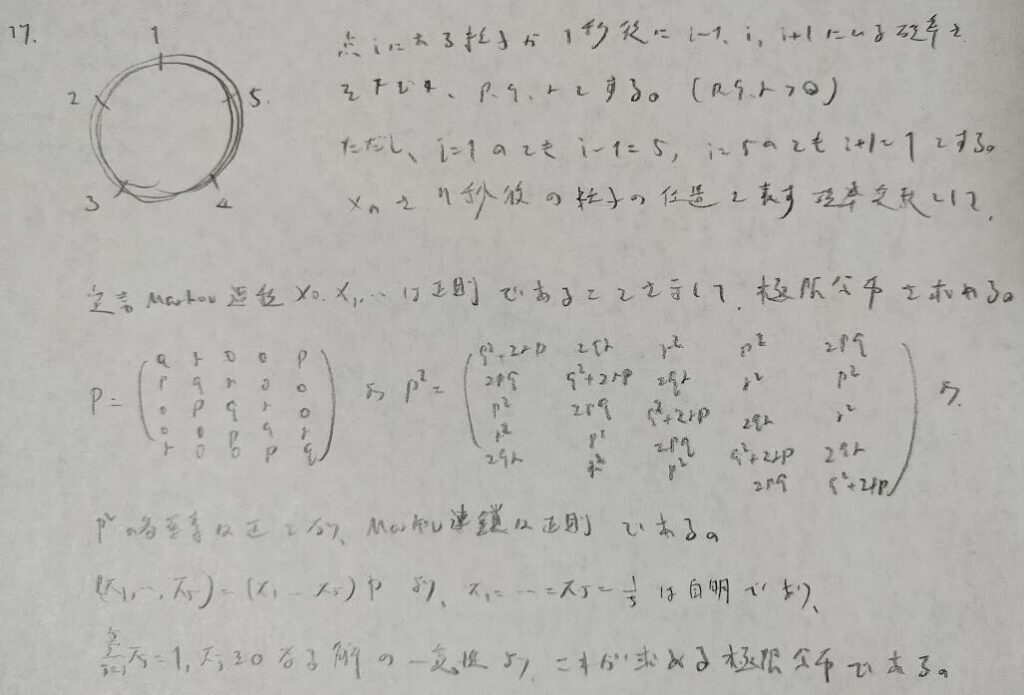
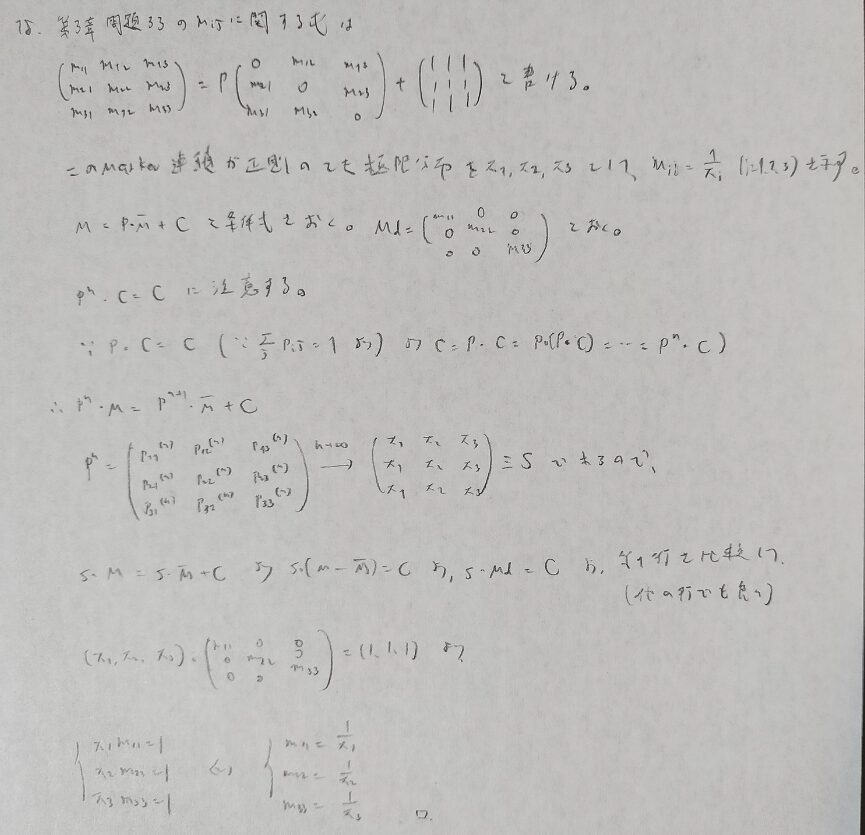
『確率統計演習 1 確率』の第6章の例題と問題は以上となります。
『確率統計演習 1 確率』もついに全部解き終わりましたね!
やはり本書の特徴としてマルコフ連鎖を少しずつ深めていく形式が採られていることが挙げられると感じます。アクチュアリー数学ではマルコフ連鎖は本書に登場した問題の中では本番で未出の問題も多々ありますので、演習する価値は十分にあります。ただし本番をよりも難しい難問が目立つので、ご自身で吟味してみてください。
最後に復習用として『確率統計演習 1 確率』の第1章〜第6章までの記事をまとめておきますのでご活用ください!
第1章:事象と確率
第2章:確率変数と分布
第3章:平均値、分散
第4章:変数変換と和の分布
第5章:積率と積率母関数
第6章:大数の法則と中心極限定理


