アクチュアリー数学や統計検定1級の統計数理対策でとても有用な『確率統計演習 1 確率』の積率母関数(モーメント母関数)についての解説になります。
この章は今までに学習してきた章の内容が頻繁に登場します。特に演習問題で以前登場した問題の設定がそのまま使われますので、各章の復習をおすすめします!
演習問題について第3章の期待値の章の問題と同程度(約50問)のボリュームとなります。途中で複素関数の知識が要求されますので難易度は本書の中でも随一となっております。函数論のおすすめ参考書は『複素関数キャンパス・ゼミ』が初見でもわかりやすいので強く推奨しています。
目次[非表示]
『国沢確率』第5章「積率と積率母関数」の例題
積率母関数はアクチュアリー数学や統計検定1級で頻出事項となっています。『確率統計演習 1 確率』のバラエティに富んだ問題数は類書で随一となっております。
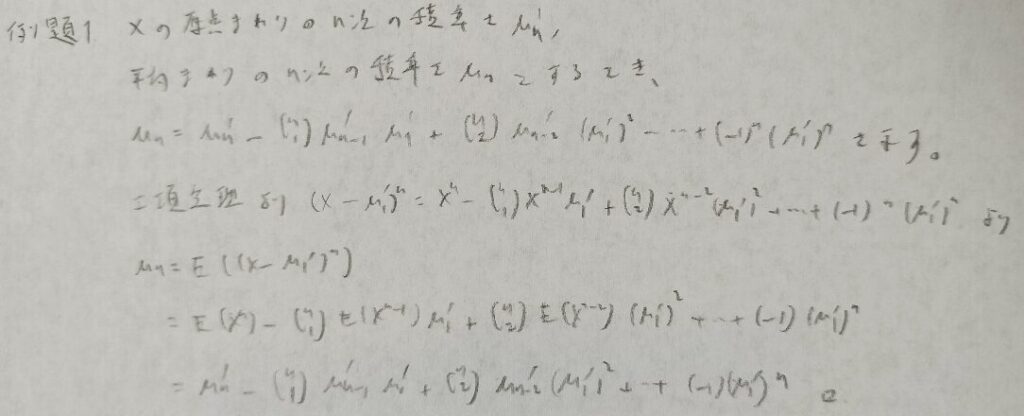
原点まわりの積率と平均まわりの積率の間の関係式を求める問題です。大事そうな問題なのに『確率統計演習 1 確率』にしか載っていない問題です。
E記号の中で定数は外に出せるということを使う問題です。

積率と確率密度関数の関係の問題です。理論上大切な問題です。
この問題は統計検定1級よりも難しい問題ですね。全体的に本書の問題の難易度は高いです。



収束する数列は有界であるという定理を使っています。
こういう大学教養レベルの微分積分の学習はどうすれば良いですか?
解析概論に手を出すのはレベルが高いので松坂先生の『解析入門』をおすすめしています。3冊セットなのでページ数は多いですが具体例が多くとても素晴らしい本です。
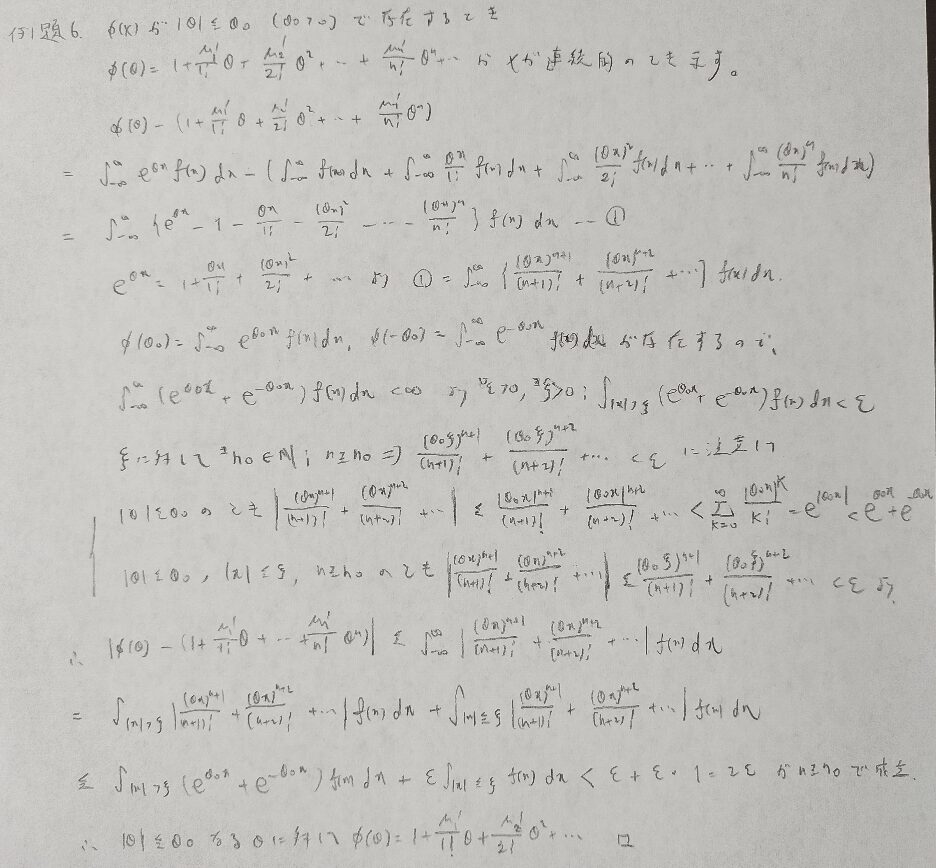
本章が難しいと思われる理由の1つにイプシロンデルタ論法が登場する問題が多いことが挙げられます。後半の演習問題は特に多いのでイプシロンデルタ論法を用いる問題はリストアップしておきます。
難問ですが①積分を2つに分ける②存在するξに対して…という手順を意識して答案を見てみましょう。

2021年のアクチュアリー数学の大問に出題されました。厄介なのはこの証明の後に普通に問題が続くところです。
アクチュアリー数学は大変難しい試験ですね。『確率統計演習 1 確率』に出てくる問題をしっかり把握しておきたい気持ちになりました!


積率を求めるためにマクローリン展開をしてみましょう!

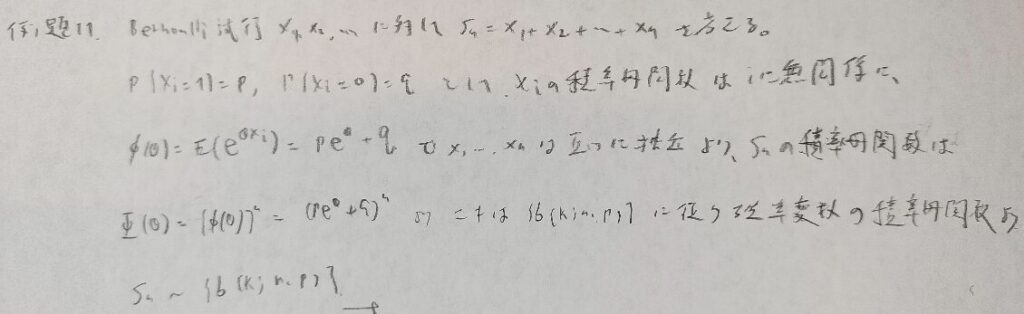


無意識のうちに使っていそうな定理の証明問題です。後半部分の証明方法がテクニカルです。
自明としたいところをしっかりと書いていますね!
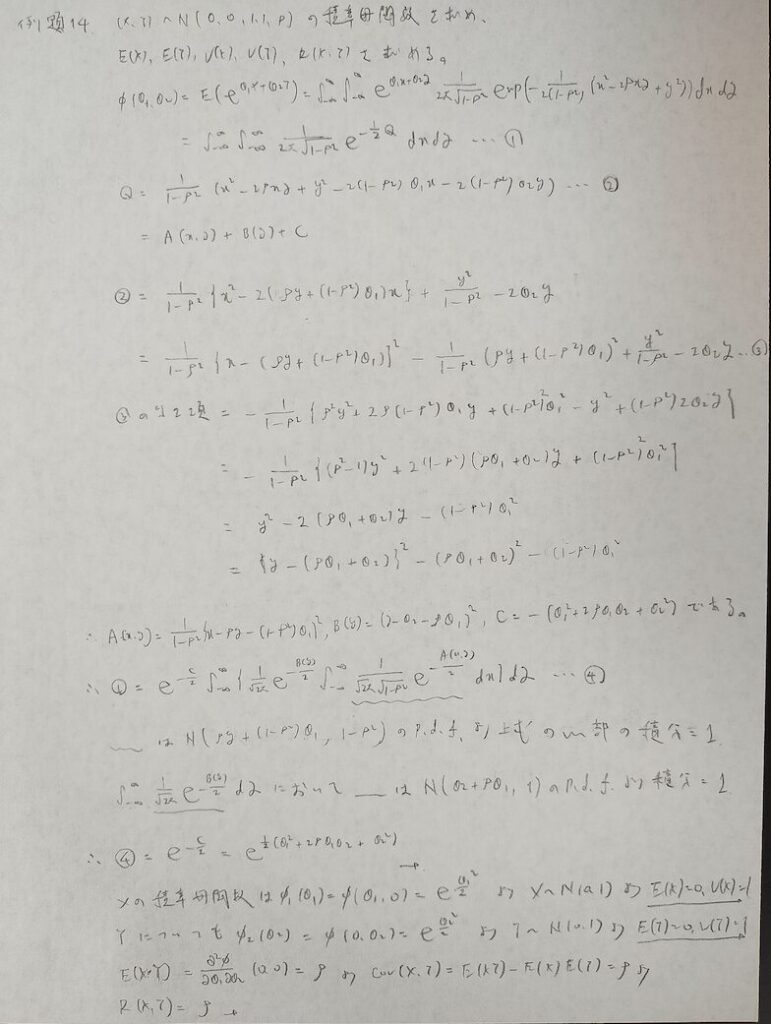
アクチュアリー数学に出題されています。誘導形式とは言え初見では時間内に解ききれません。
演習問題にも類題がありますが、特にどのような変数変換をしたか?を重点的に意識した学習をしましょう!
『国沢確率』第5章「積率と積率母関数」の問題
本章の演習問題がボリューミーなので区分けをしました。
積率→1~5
積率母関数→6~14
具体的な確率分布→15~19
再生性→20~25
確率母関数→26~32
キュムラント母関数→33~34
積率母関数(多変量)→35~46
マルコフ連鎖→47~50
イプシロンデルタ論法を用いる問題は9~11,32になっています。また特に確率母関数に関する問題が多めです。難問も多いのでしっかりと学習したいですね!
積率の問題

大切な定理の証明問題です。『確率統計演習 1 確率』は問題集という形をとっていますが実質は手を動かして学ぶタイプの確率前半の参考書だと感じます。

第2式の二項展開がテクニカルです。統計検定1級には未出の問題です。
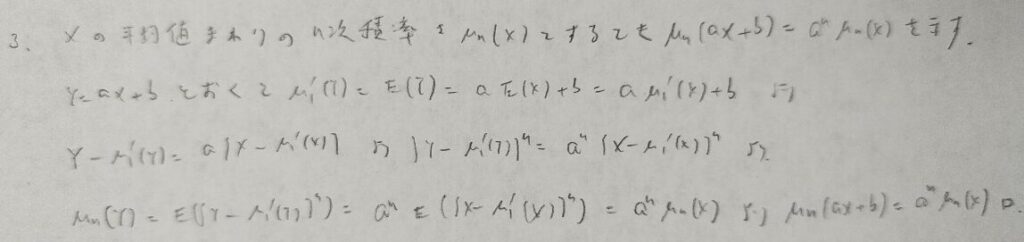

分散と歪度と尖度の不変性に関する問題です。分散については既知とします。

数理統計の分野でヴァンデルモンドの行列式が出てくるのには驚きました!
大学院入試で頻出のテーマですからね。線形代数に習熟していないと解けない問題でした。
線形代数に関して問題演習をこなしたい場合は『明解演習 線形代数』がおすすめです。これより難しい演習本だと本格的な大学院の入試問題となってしまいます。
積率母関数の問題


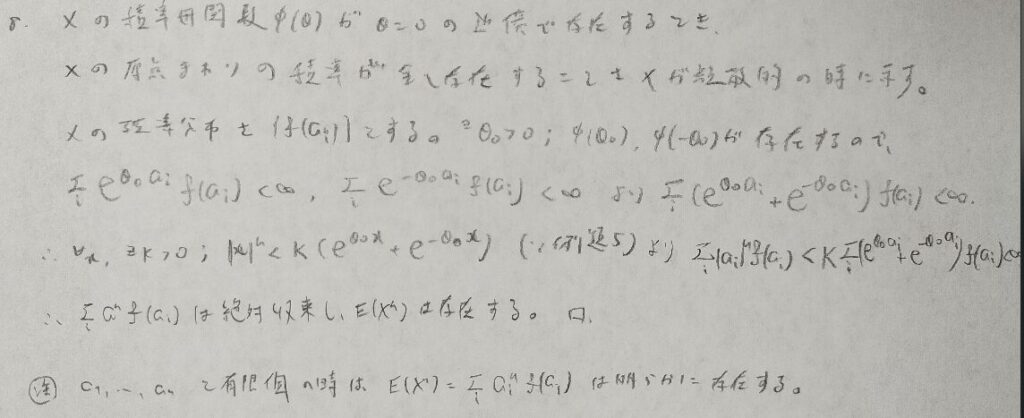


ここら辺でよく登場する不等式の定理について証明をしておきます。ジョルダンの不等式の系とでも言っておきましょう。
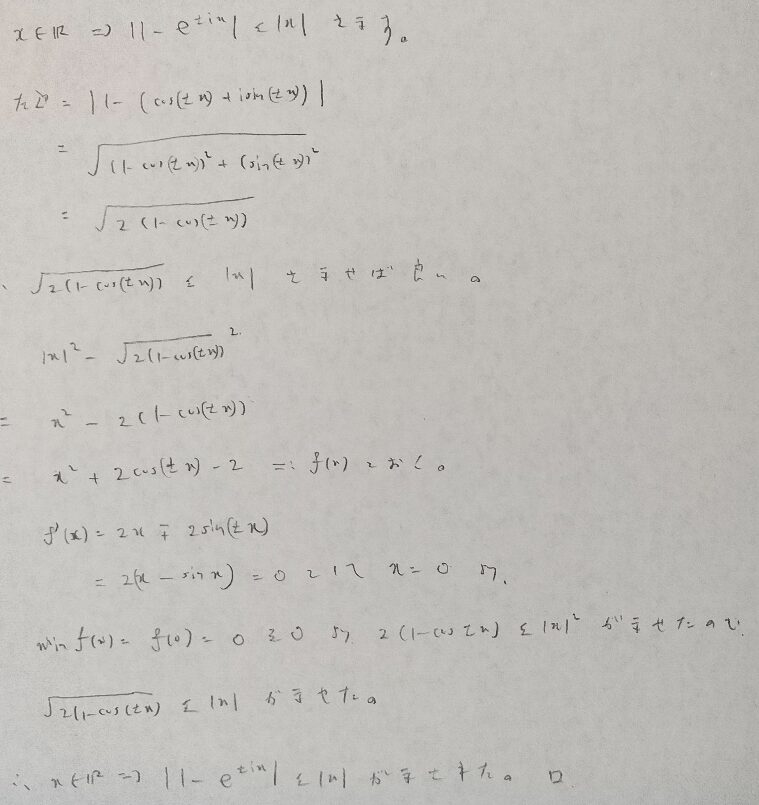


このテクニックは今後も使う問題が多いので詳しく書きました。

まさかの平均値の定理を持ち出す難問です。
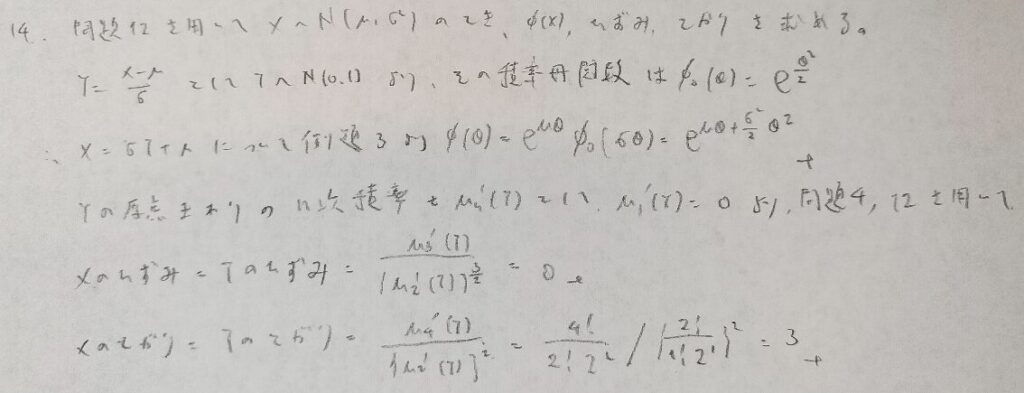
具体的な確率分布の問題
先ほどと比べると簡単な問題が続きます!

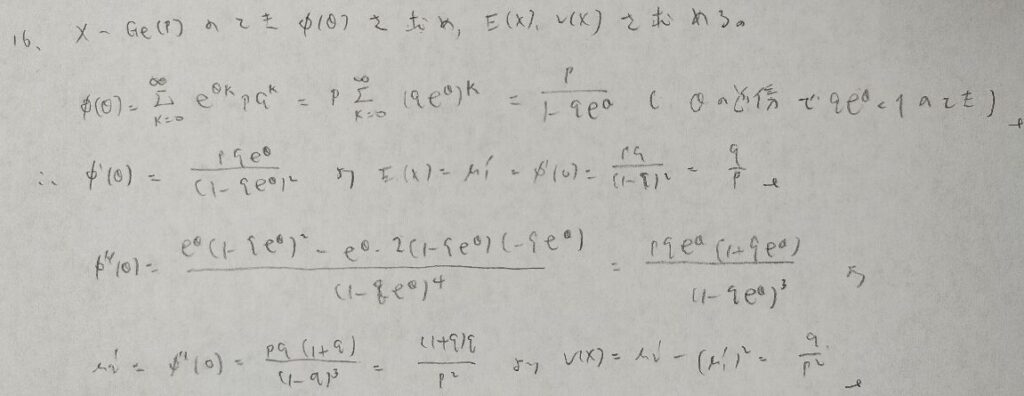

さりげなく級数展開していますね!

一様分布だからといって導出が簡単な訳ではありません。

再生性の問題



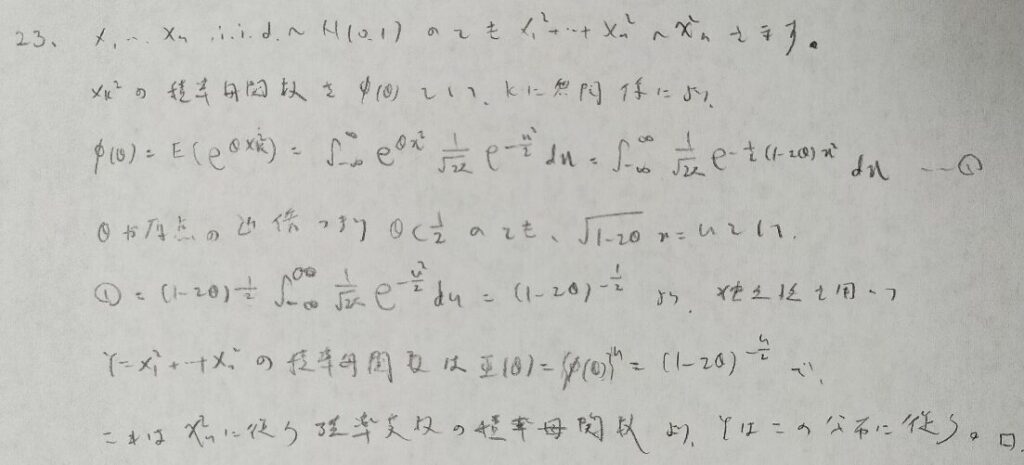
有名定理がここで証明されました。


確率母関数の問題
『確率統計演習 1 確率』の積率母関数の章に価値を見出すポイントの1つに確率母関数の問題の多さにあると思います。とにかく類書にない良問揃いです!

初っ端から難問です。形式的には簡単なのですがきちんと示すにはアーベルの定理を用います。
こちらも先ほどご紹介した松坂先生の『解析入門』に多くの類題が載っており勉強になります。

このQ(s)の設定はアクチュアリー数学での出題があります。受験者はしっかりと流れを身につけたいですね。

難問です。先ほどのQ(s)記号を用いて分散を表します。

本問もアクチュアリー数学に出題されています。
こんな問題初見で解ける人いるのかな?!と思われるような超難関試験ですね。

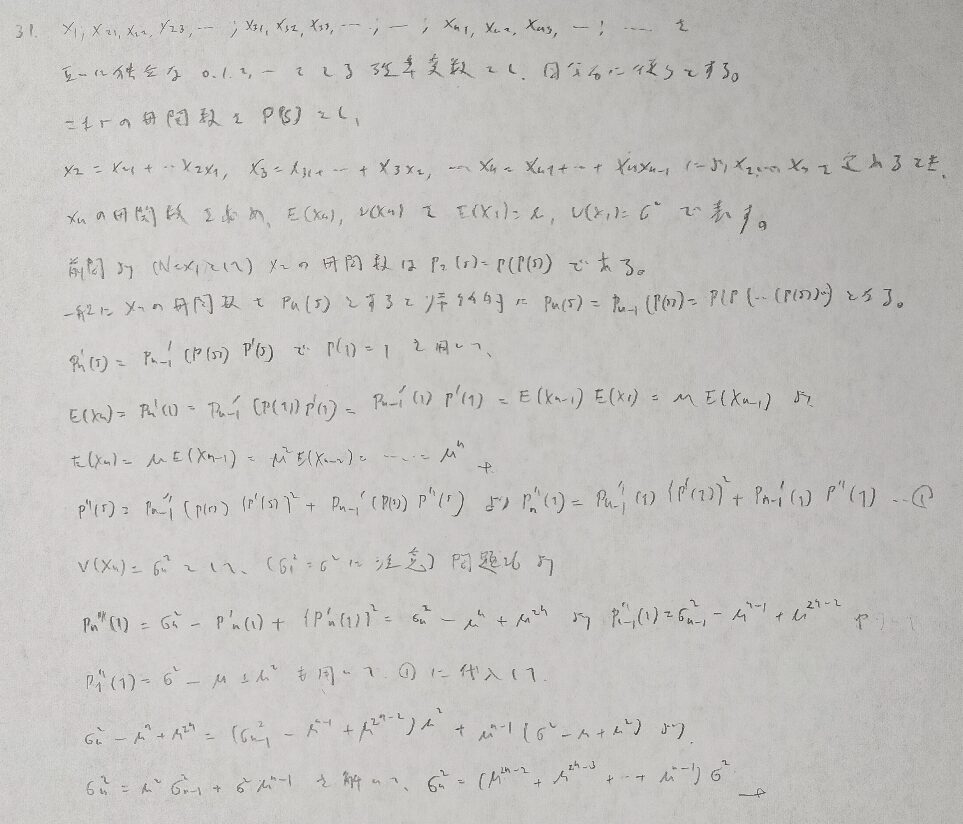
問題30が解けないと絶対に解けない問題です。アクチュアリー数学では未出です。

やはりラストはイプシロンデルタ論法でしたね。
キュムラント母関数の問題
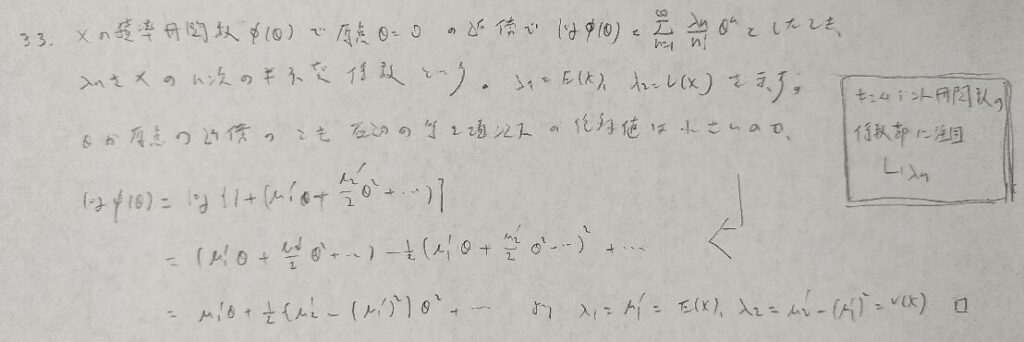
キュムラントのことを半不変係数とも言います。

積率母関数ではなくキュムラント母関数を用いる理由の1つとして取り上げられる問題ですね。
積率母関数(多変量)の問題

アクチュアリー数学に出題されています。
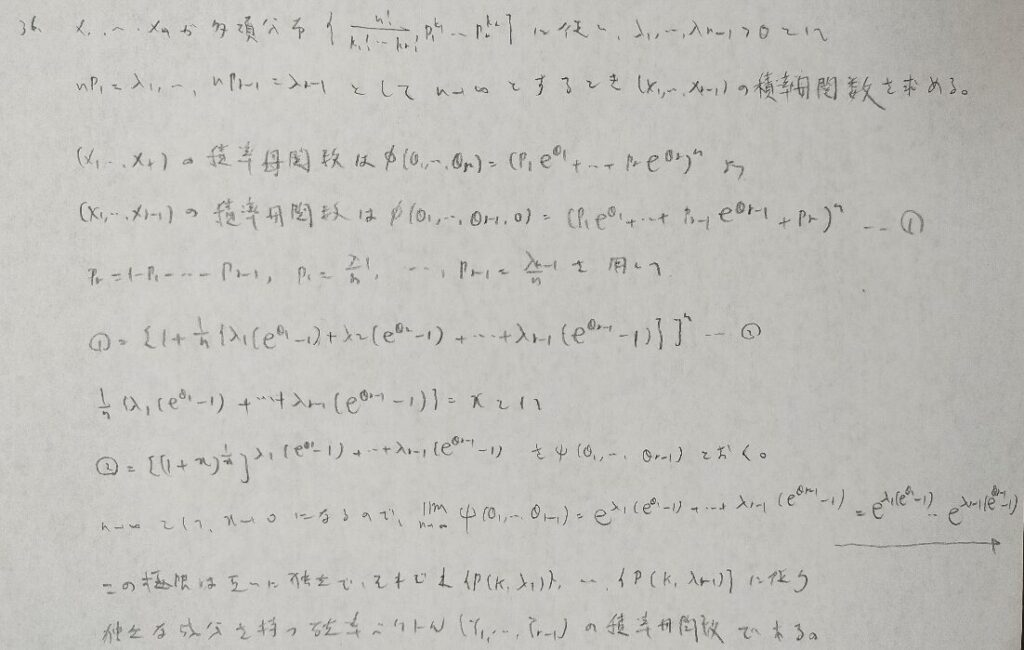
アクチュアリー数学で出題されていますが統計検定1級では未出です。

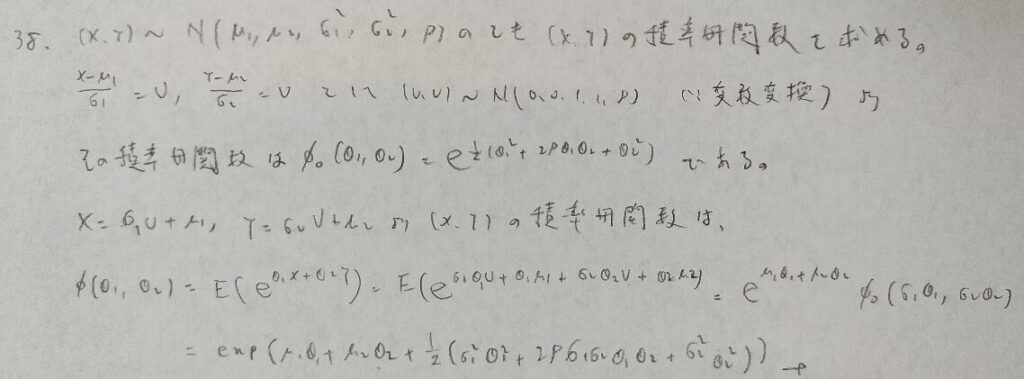
導き方と結果それぞれ大切です。
結果には納得がいきます。


標準化に似た雰囲気の問題ですね。


アクチュアリー数学に出題されていますが統計検定1級には未出です。

ついに登場してしまいましたね。偏微分方程式。
偏微分方程式は解析学の1つのゴールですのでとても難解です。大学院入試の問題を解くためのレベルに達することが目標ならば『偏微分方程式キャンパス・ゼミ』が簡潔に要点が絞られていておすすめです。


難問ですがどの参考書にも載っている定理を積率母関数を経由して証明する問題です。
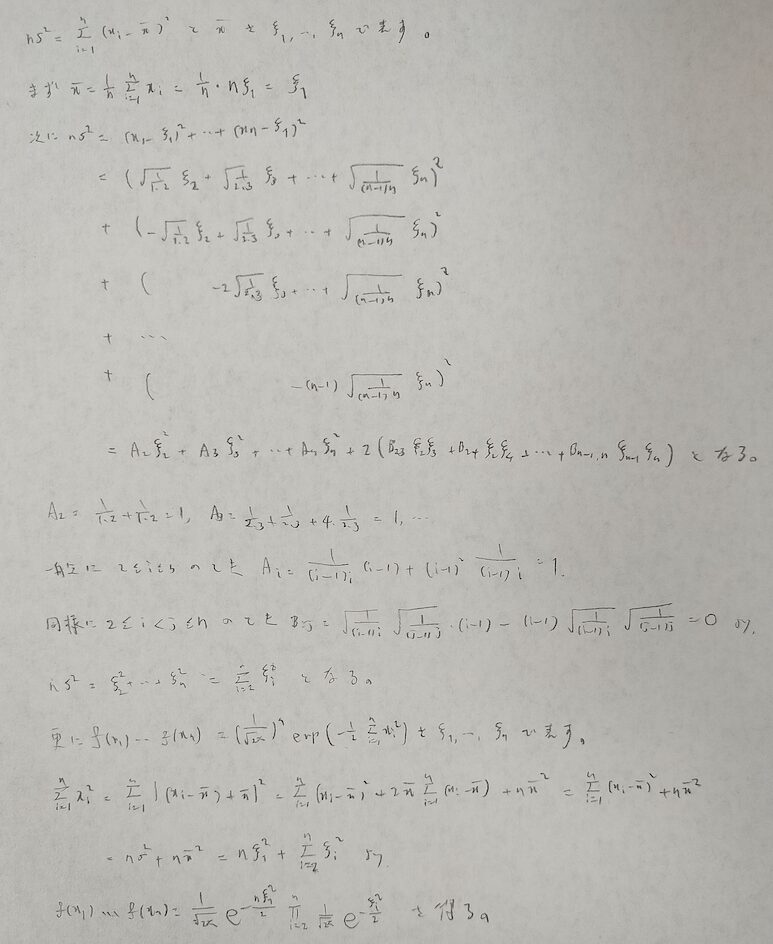


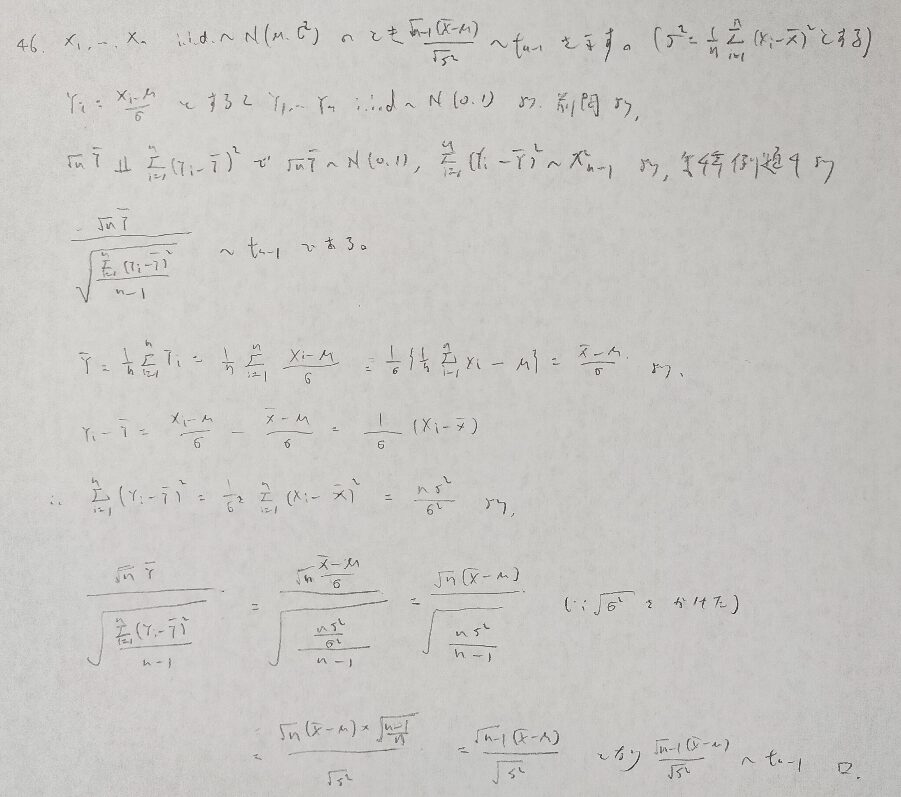
積率母関数の流れのみからt分布を導出しました。王道は統計検定1級のバイブル『現代数理統計学の基礎』がわかりやすく導出されています。本書の問題解説の記事はこちらです。
マルコフ連鎖の問題
難問揃いです。アクチュアリー数学の難易度を凌駕していると考えます。初見では飛ばしても差し支えないでしょう。

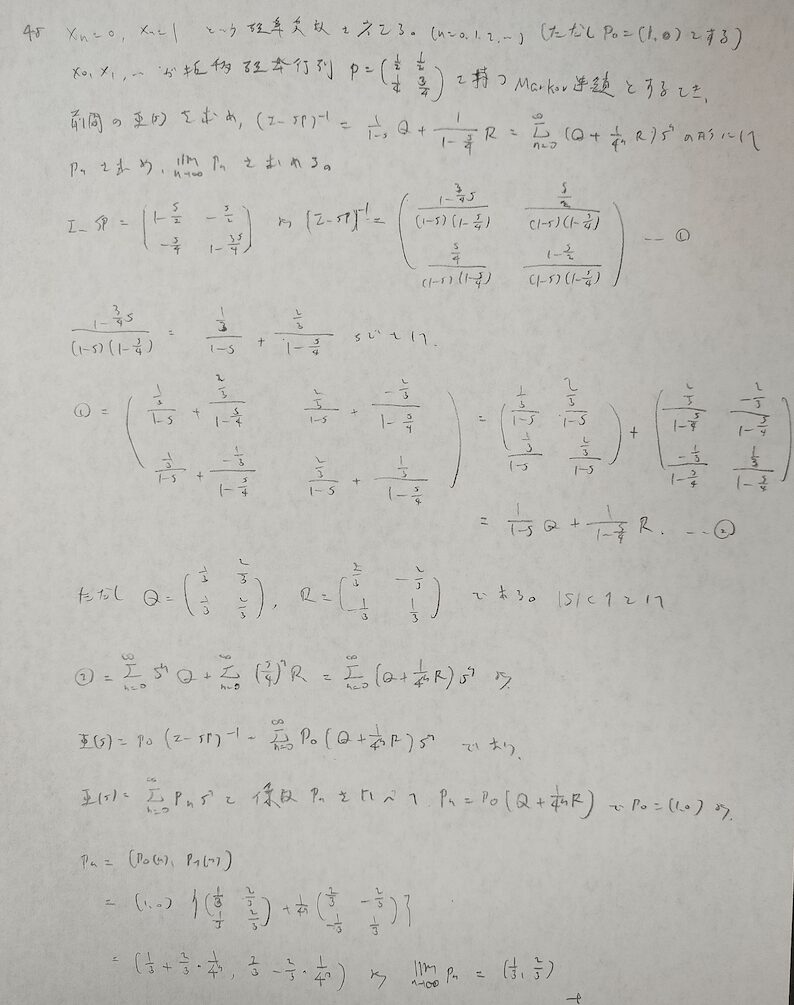
マルコフ連鎖と級数は相性が良いです。


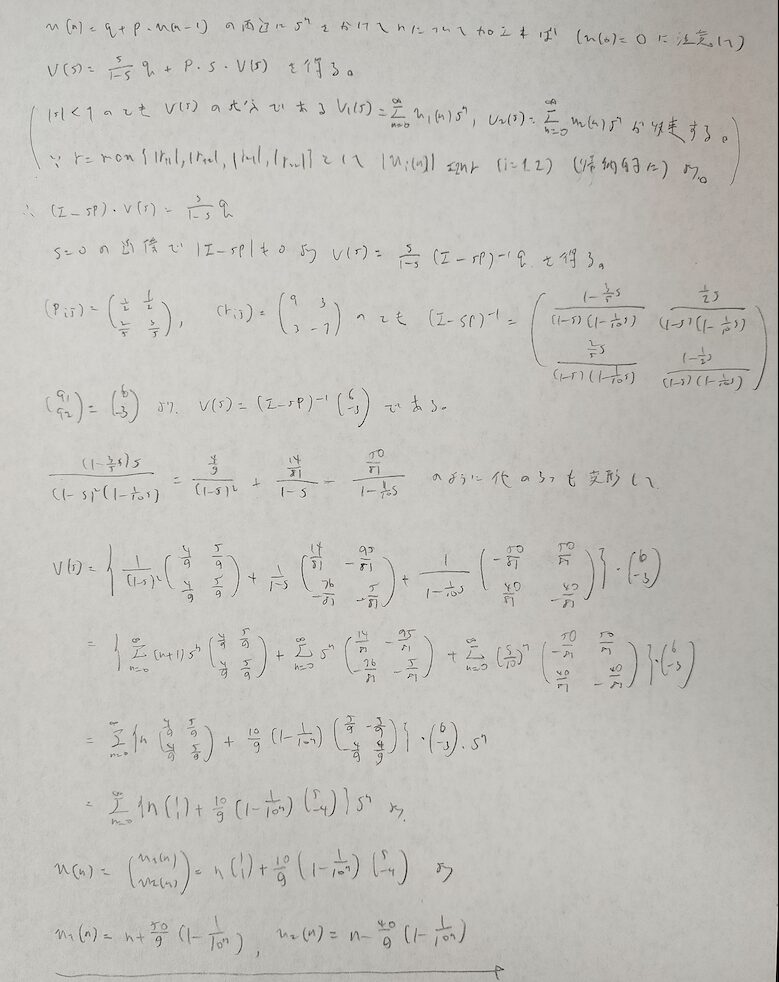
本問より難しい問題が過去に1度だけアクチュアリー数学で出題されています。80年代の問題ですがおそらくその問題がアクチュアリー数学での最難問です。
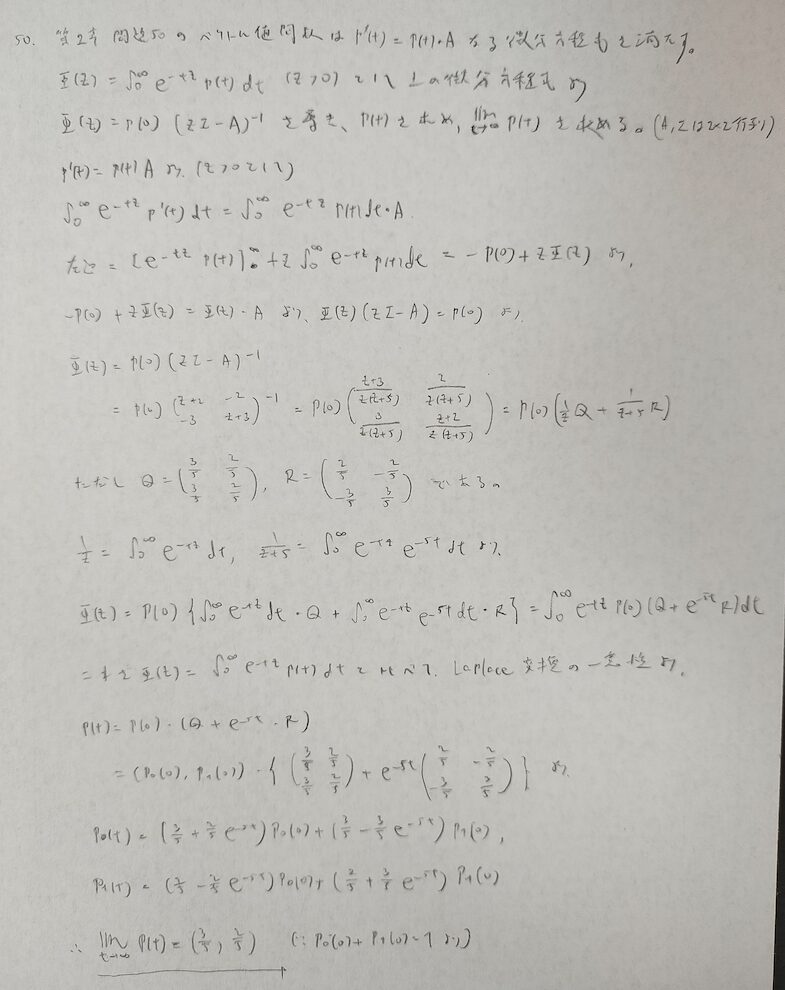
最後の方、難し過ぎません?笑
『確率統計演習 1 確率』の問題は全体的に難しいのですが、本章が難しいと感じる要因の1つに他分野の数学との融合問題が目立つことにあると思います。
『確率統計演習 1 確率』はアクチュアリー数学の指定教材です。しかし実際は本書に掲載されている問題で試験では未出の問題が多くあります。今年のアクチュアリー数学に合格したい方は本書をしっかりと学習することが王道の勉強法になって来ているのかも知れません。なぜなら近年のアクチュアリー数学は難化傾向にあるからです。
いよいよ次回(こちらです)で最後です。一緒に頑張りましょう!!









