アクチュアリー数学の指定問題集である『確率統計演習 1 確率』の期待値と分散に関する章の解説を行います。主に期待値の問題が中心となります。
終盤の問題では前章を参考にする問題が多くなります。下記に国沢確率のブログの記事のリンク一覧を掲載します。
第1章:事象と確率
第2章:確率変数と分布
第3章:平均値、分散
第4章:変数変換と和の分布
第5章:積率と積率母関数
第6章:大数の法則と中心極限定理
終盤のマルコフ連鎖との融合問題がとても難しいです。過去にアクチュアリー試験で類題が出題されていますが、その問題が歴代最難関の問題です。
『国沢確率』第3章「平均値、分散」の例題
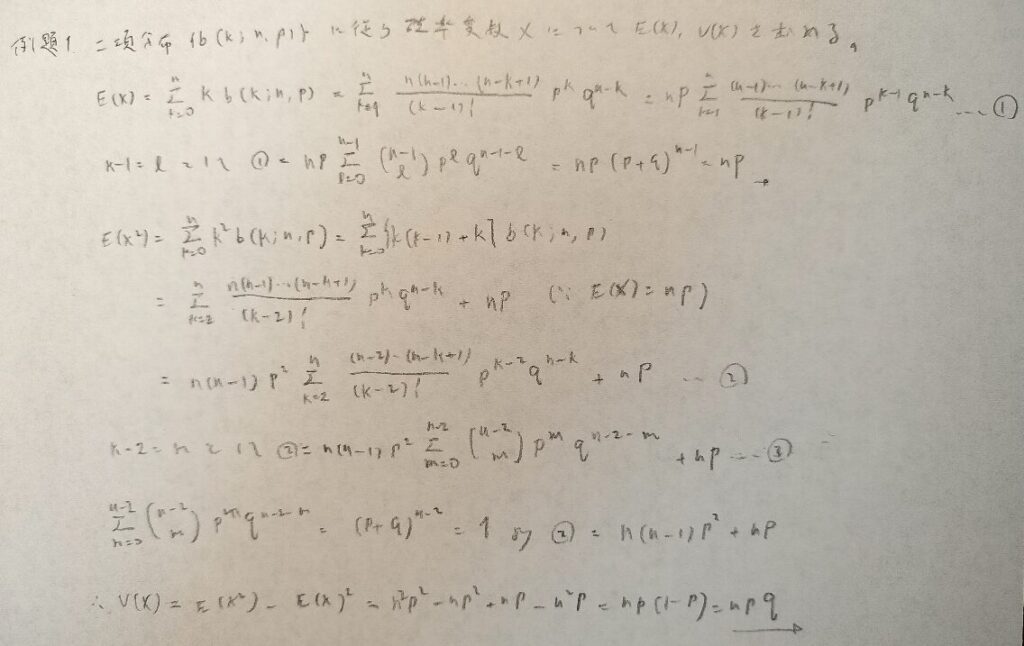
期待値の導出の仕方は①k=0の場合は必要か?を考えて1スタートにする②定数を括り出して文字の置き換えをして③確率和1より期待値を算出します。
分散は階乗表示を意識すると離散確率変数の場合はスムーズに導出することができますね。
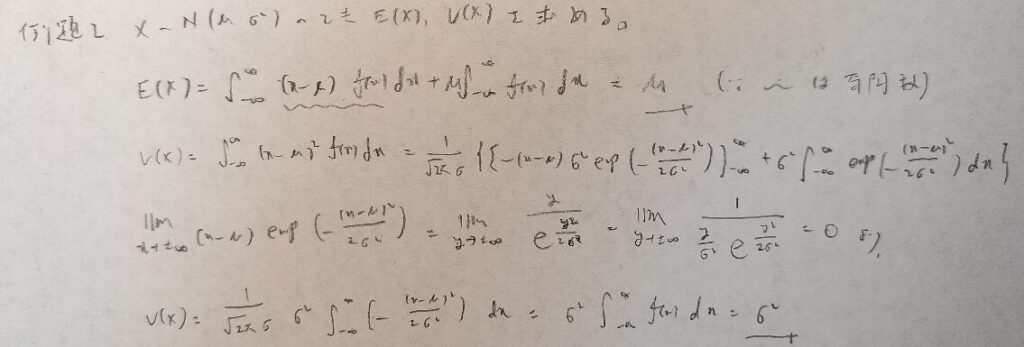
正規分布の場合の期待値の導出はテクニカルで、2行目の波線のような式変形を行います。
全確率1を用いるためですね!
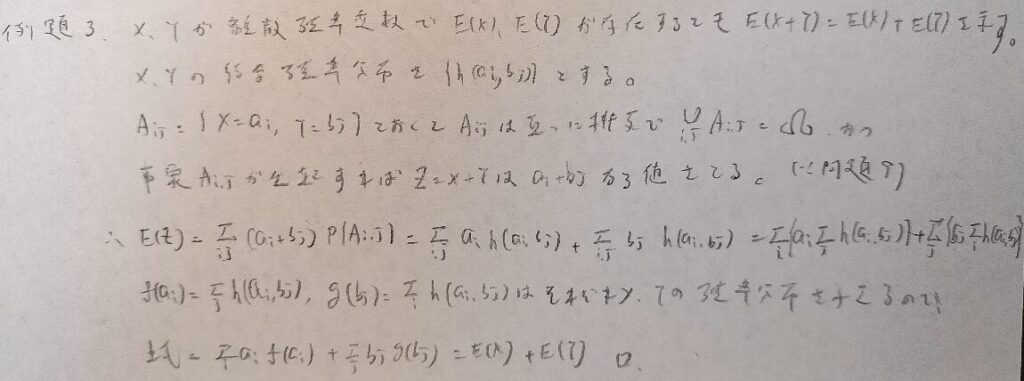

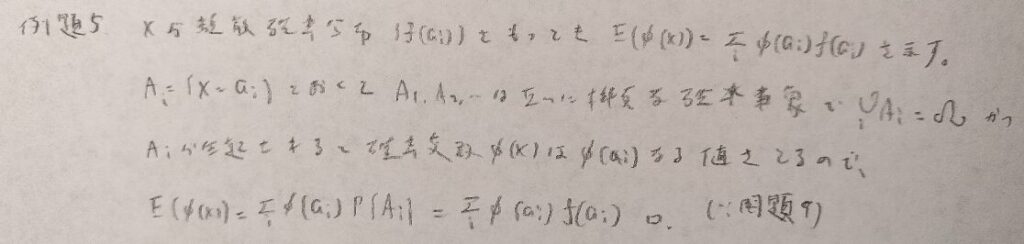
この問題から問題9が影を潜めてきます。
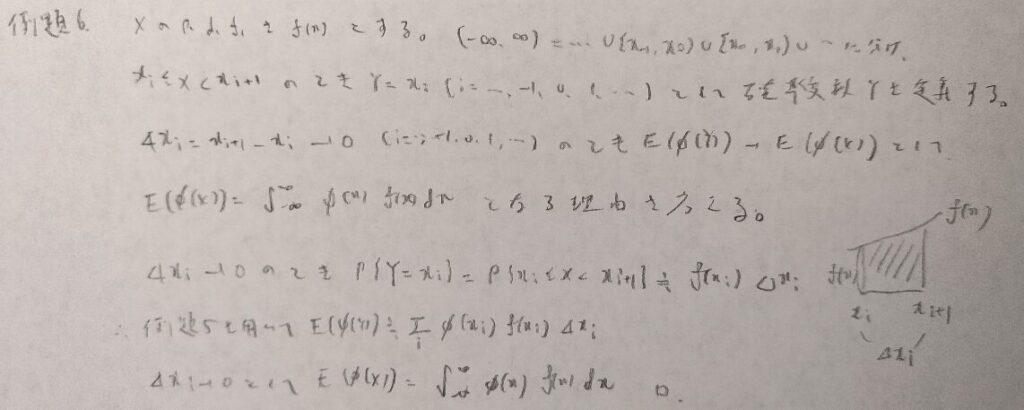
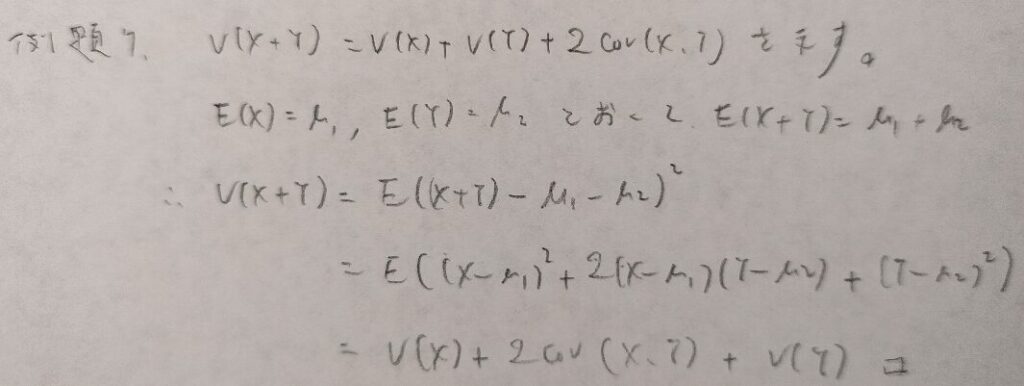
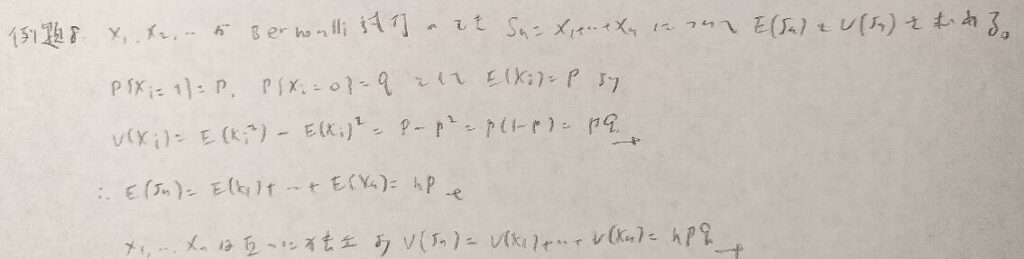

この証明はとてもエレガントです。後の問題で似たような方式を用いる証明問題があります。汎用性が高い証明のようです。
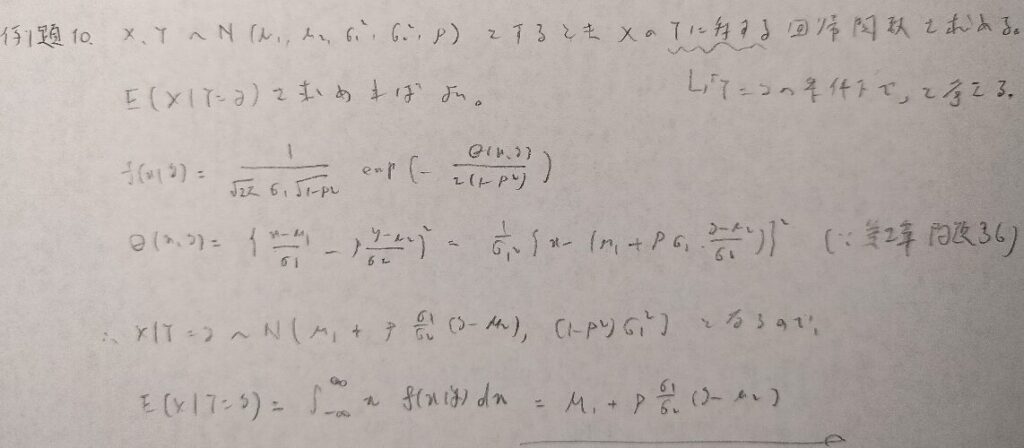
回帰関数という言葉は本問が初出です。定義をしっかりとおさえましょう!
『国沢確率』第3章「平均値、分散」の問題
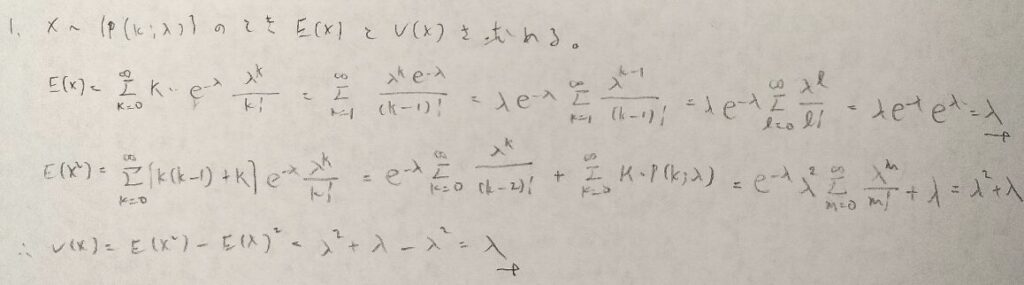
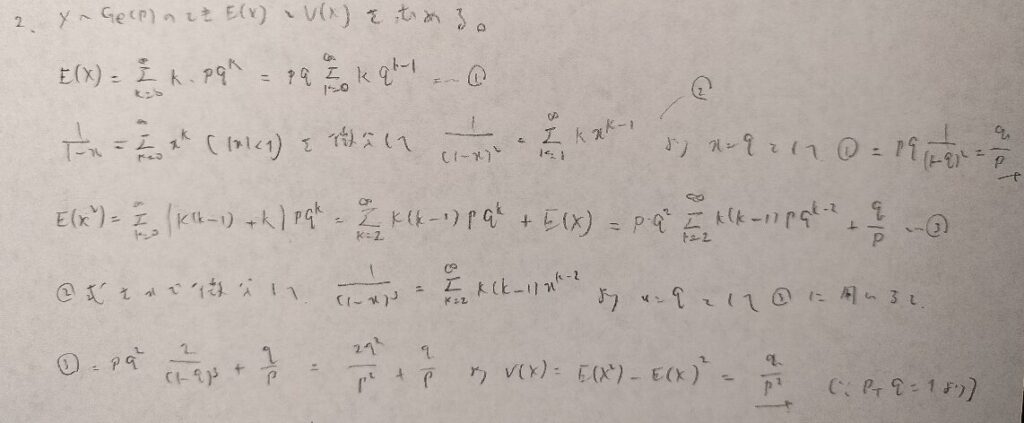
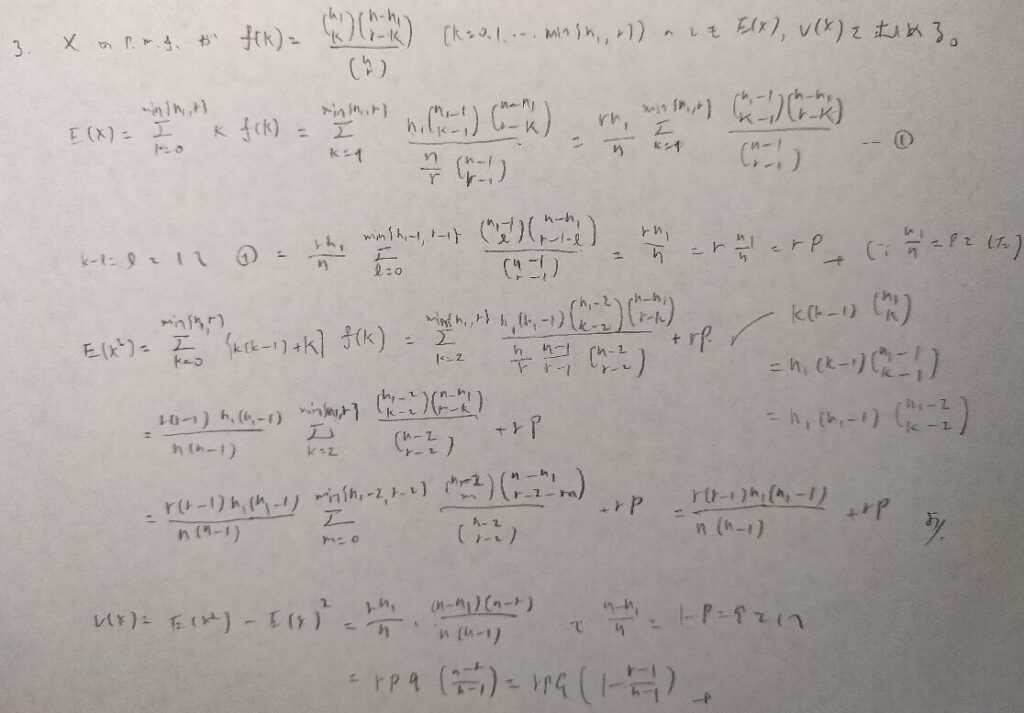
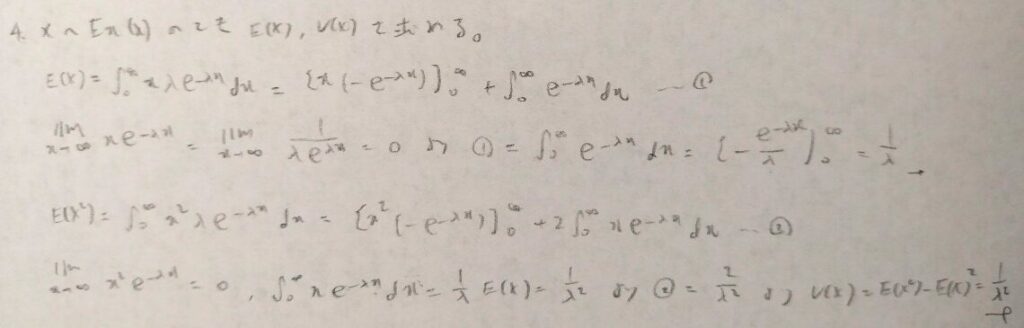
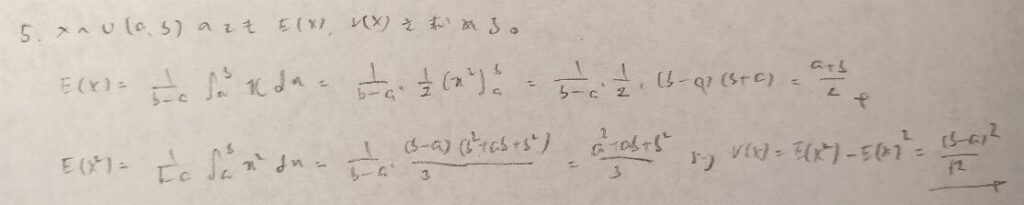
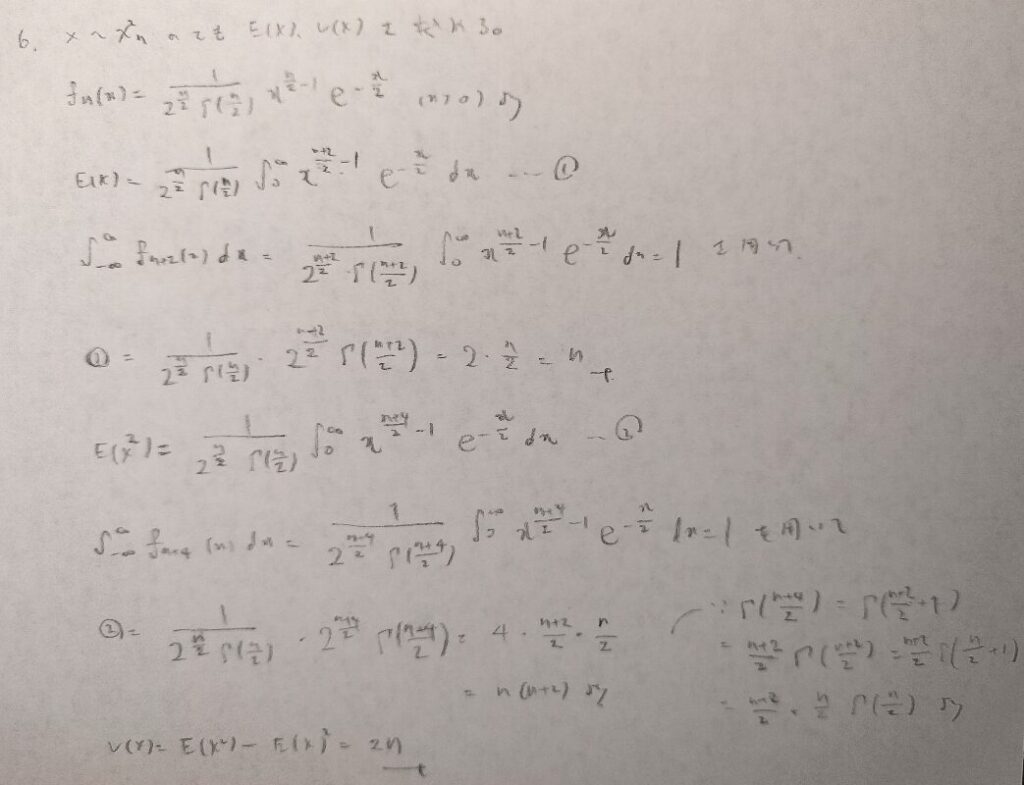
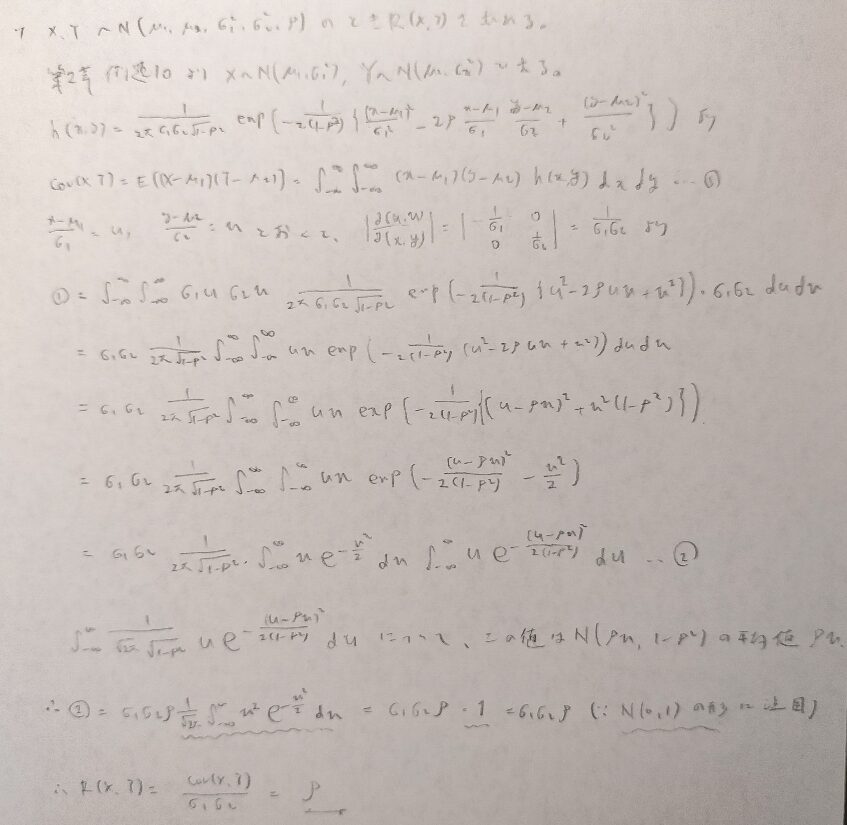
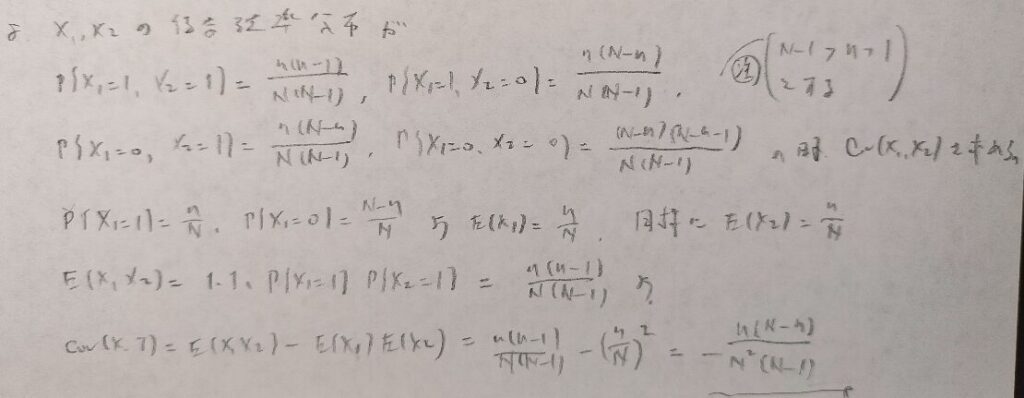
アクチュアリー数学の中での頻出問題です!

本章の中での中核となる定理です。類書ではあまり見かけないですが大事な問題です。
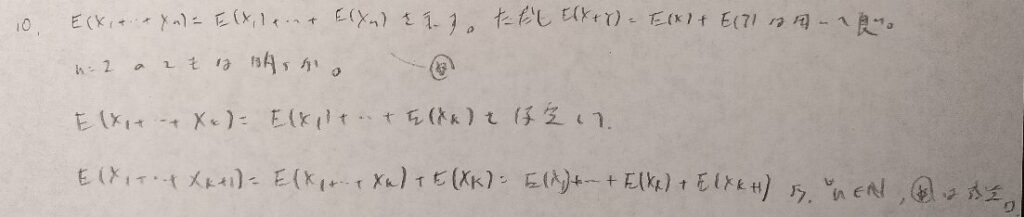
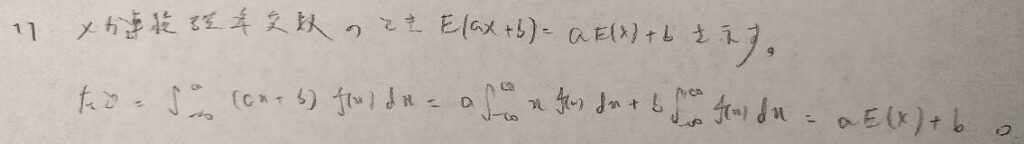
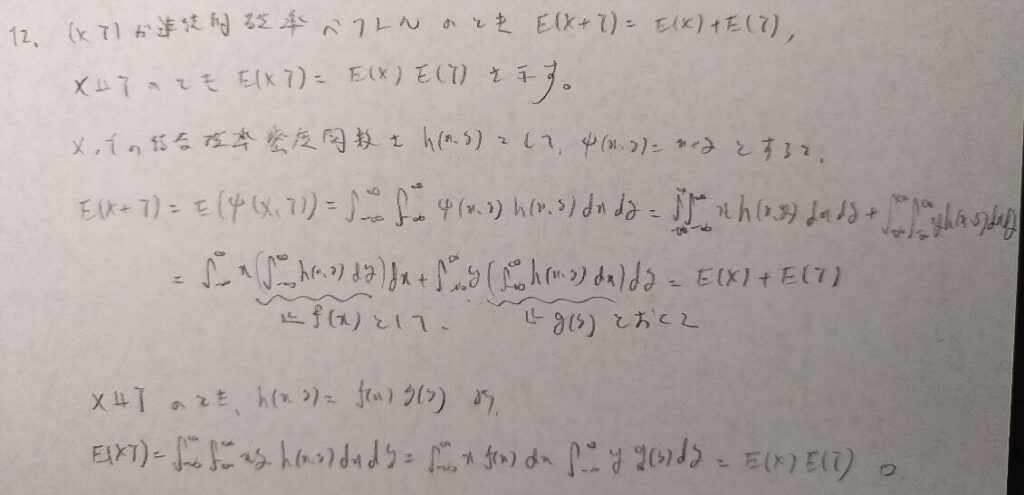
和の期待値の証明が初見ではやや気づきにくい方法で行っています。重積分を行う意味をしっかりと把握しましょう!
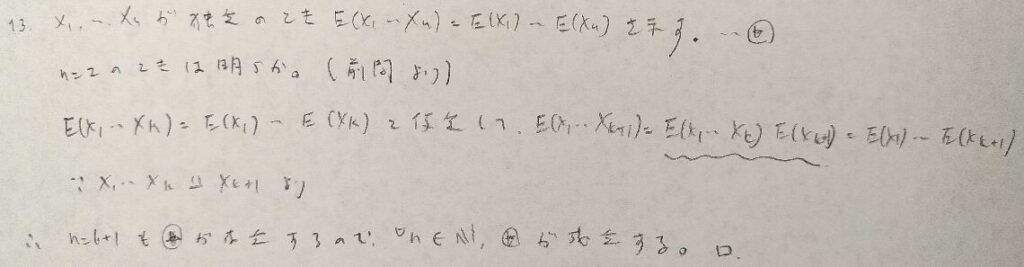
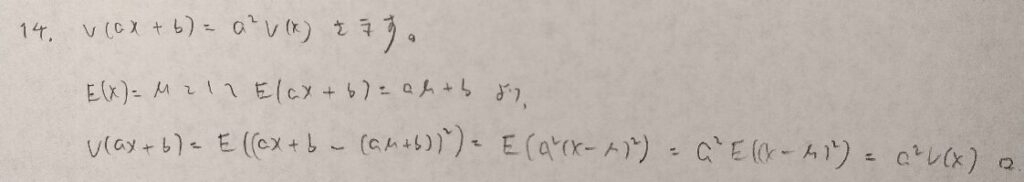
初めに期待値を設定しておくと証明が楽です!
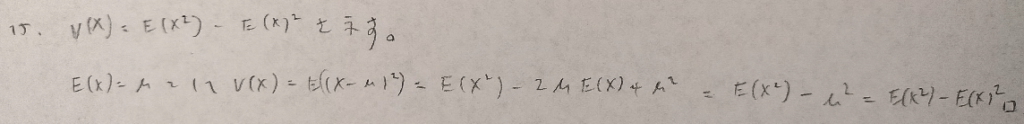
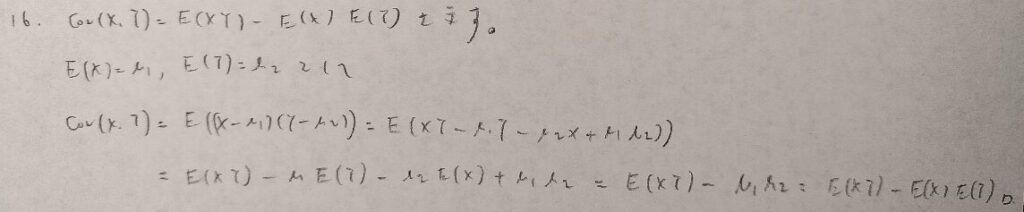
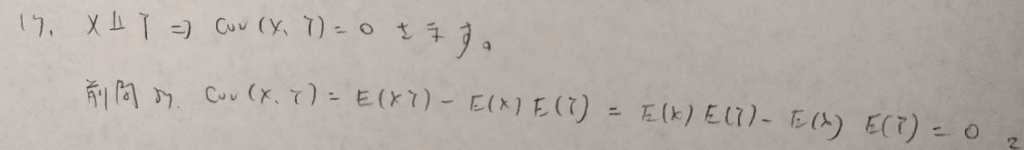
逆は一般に不成立です。正規分布の場合は同値です。
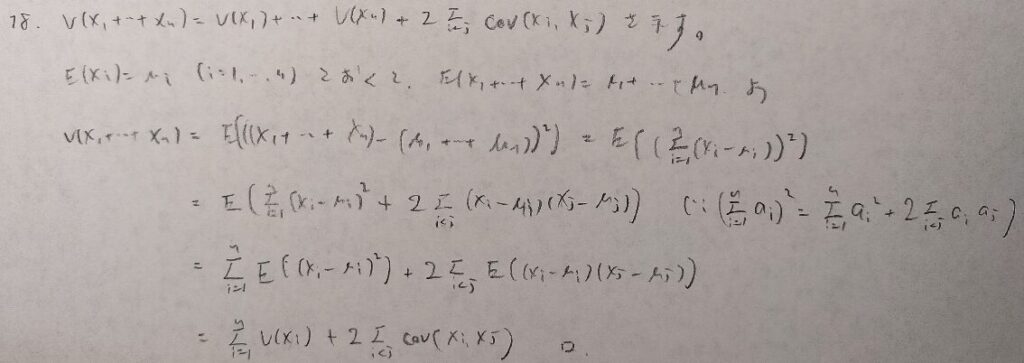
アクチュアリー数学受験者ならば自明と思えるような公式です。本番では即座に本公式を用いて計算していくことになります。
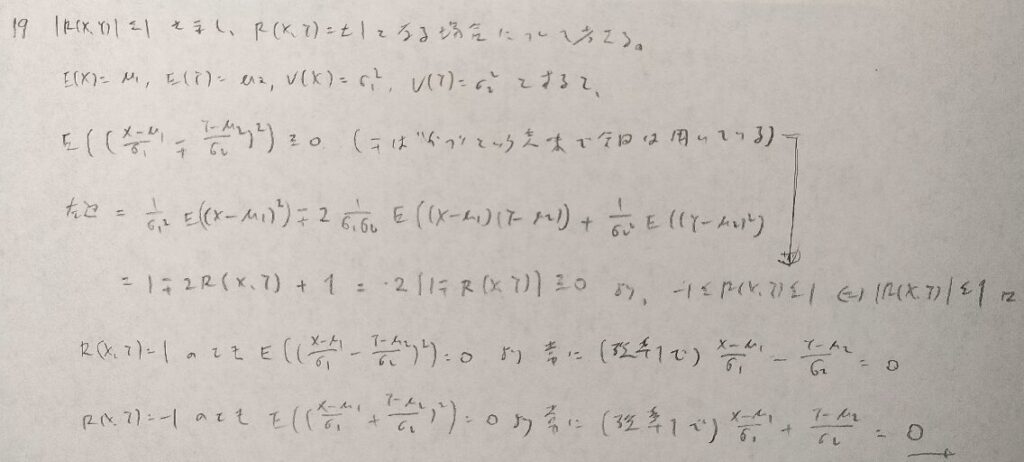
とても綺麗な証明ですね!
僕が知る中ではこの証明が最もエレガントで即答に近い内容です。
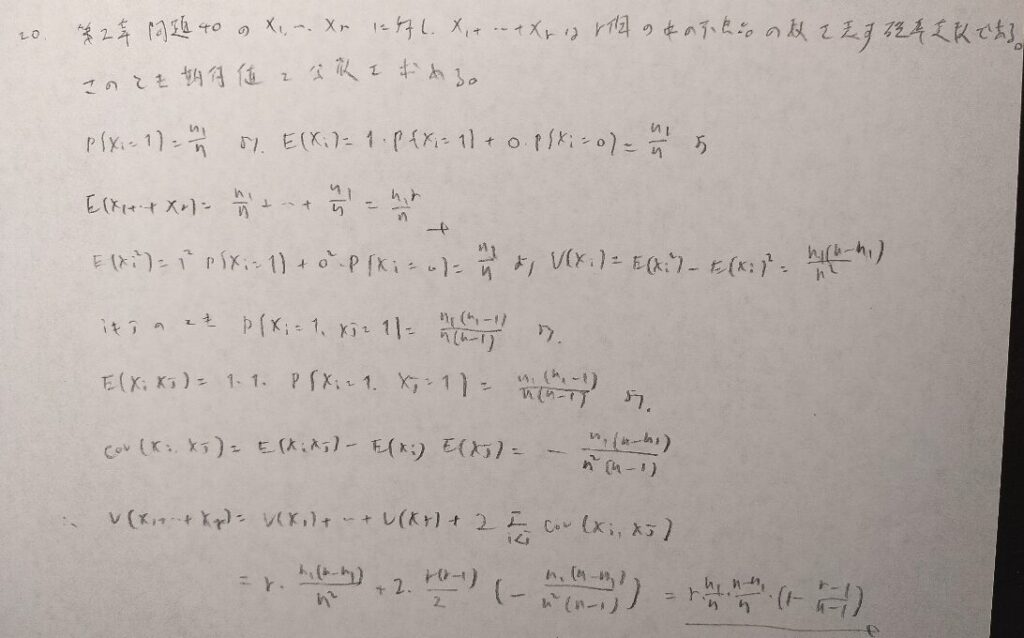
問題文に沿って確率変数を設定すれば後は流れ作業です。
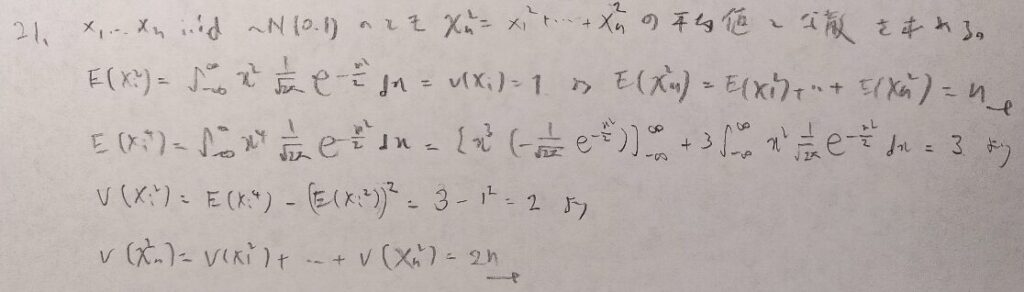
この解答で注目するのは第3行を構成する部分です。とても美しい流れだとは思いませんか?
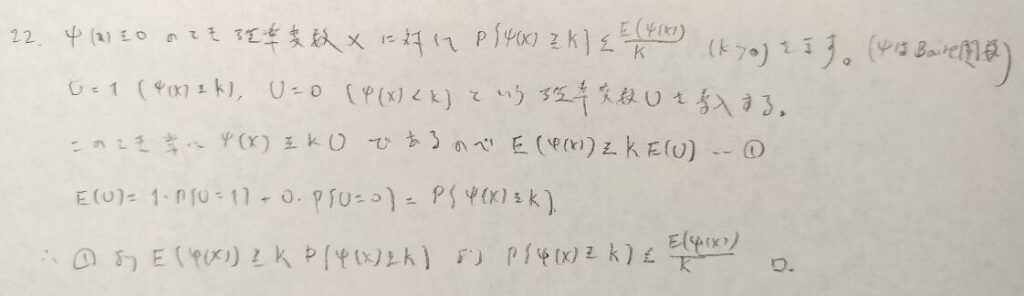
先ほどのチェビシェフの不等式で考えた証明法を用いるのですね!
このタイプの証明は本書『確率統計演習 1 確率』でのみ載っています。本当に素晴らしい書籍だと思います。

難問です。そして本問はアクチュアリー数学で未出のため大問対策で要チェックです。
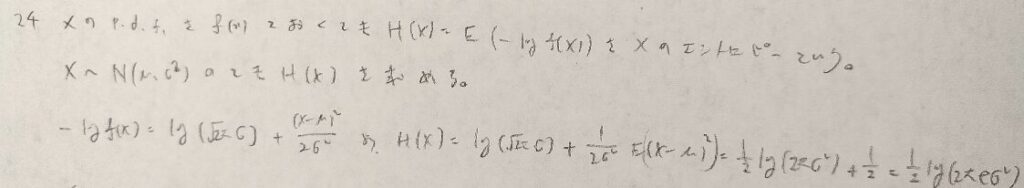
物理の問題ではなく数学の問題でのエントロピーの登場です。アクチュアリー数学では昔に出題されて以降、出題されていません。
小問集合で狙われそうですね。
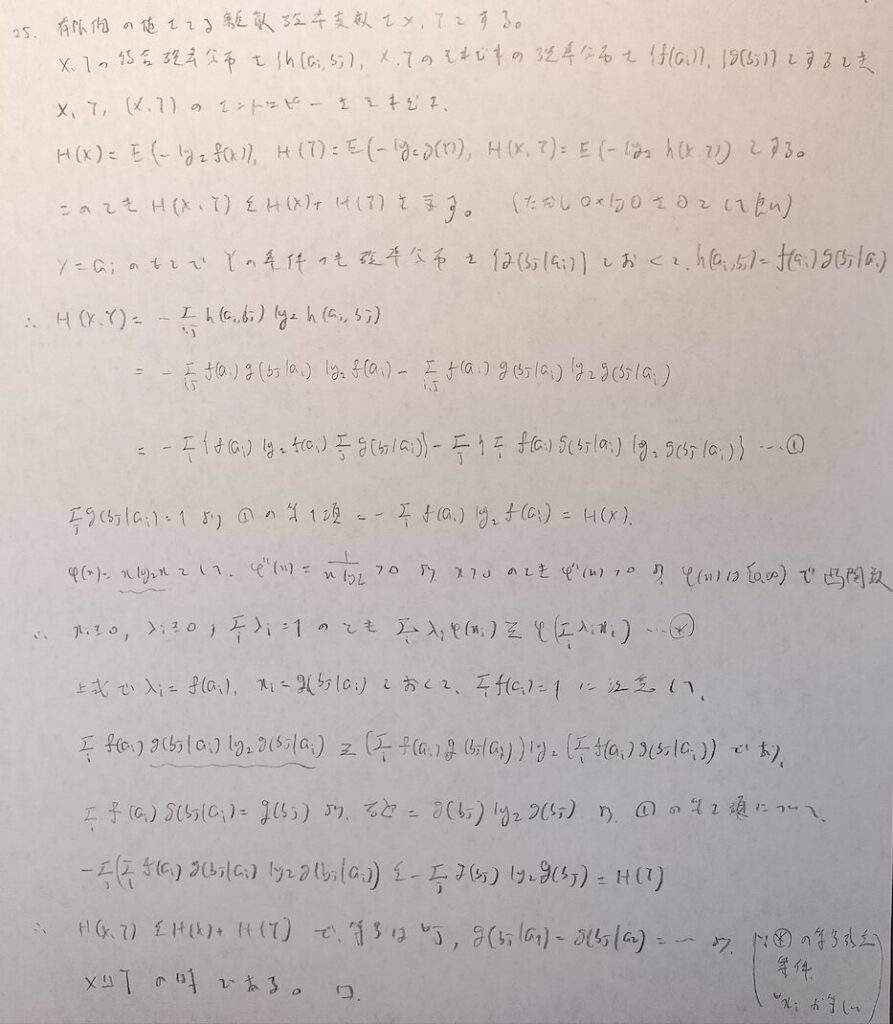
多次元の場合の問題ですが難問です。対数の底である2は変数の量に相当していると考えられます。
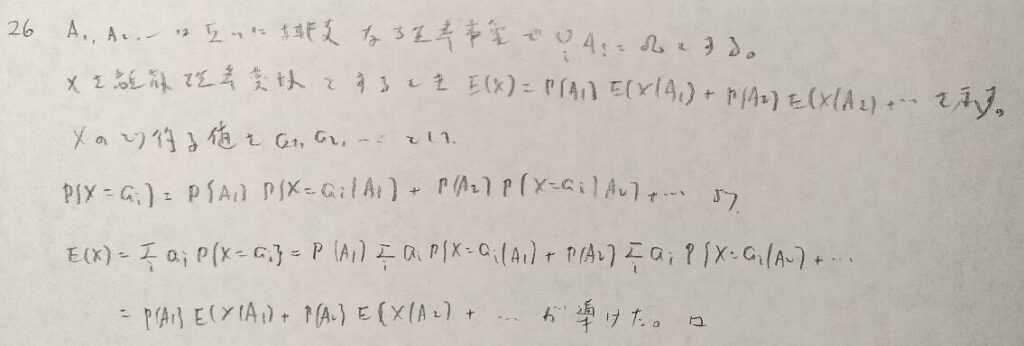


マルコフ連鎖とは異なる概念です。
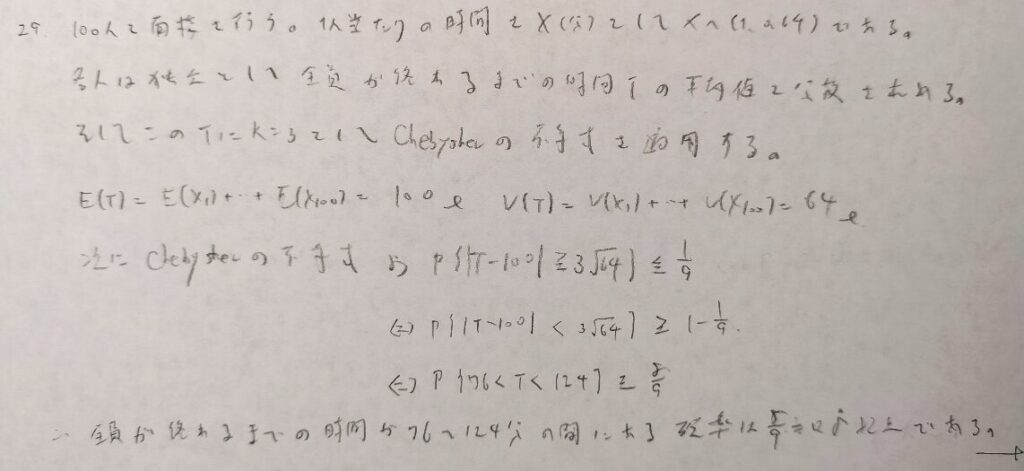
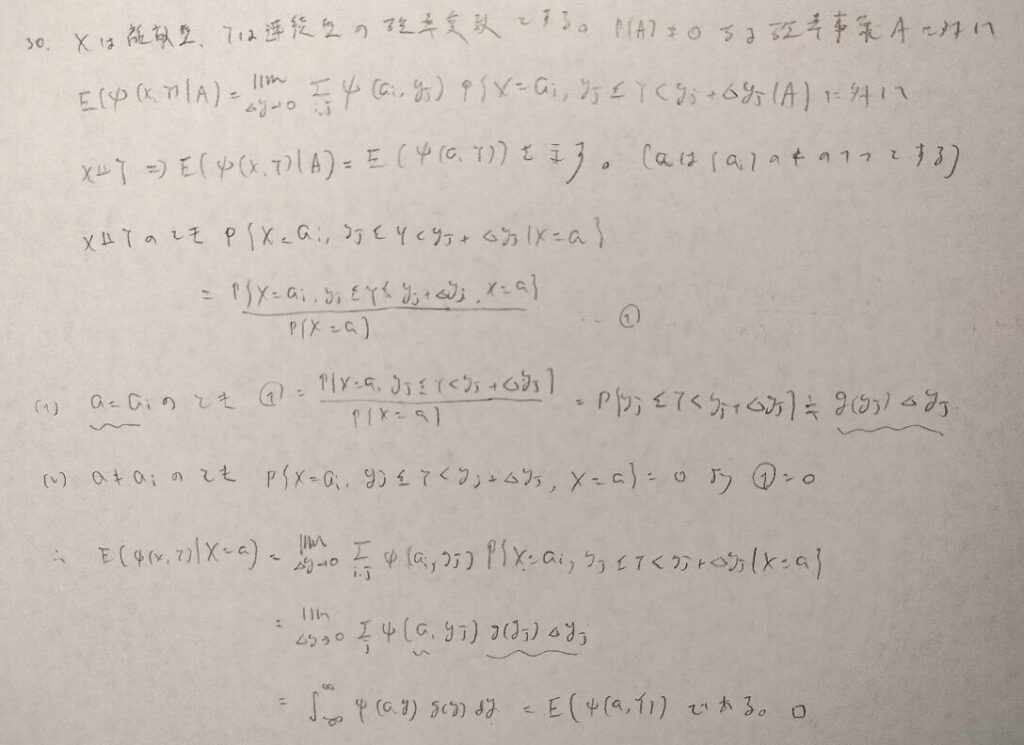
難問です。1行1行しっかりと式を追っていきましょう。
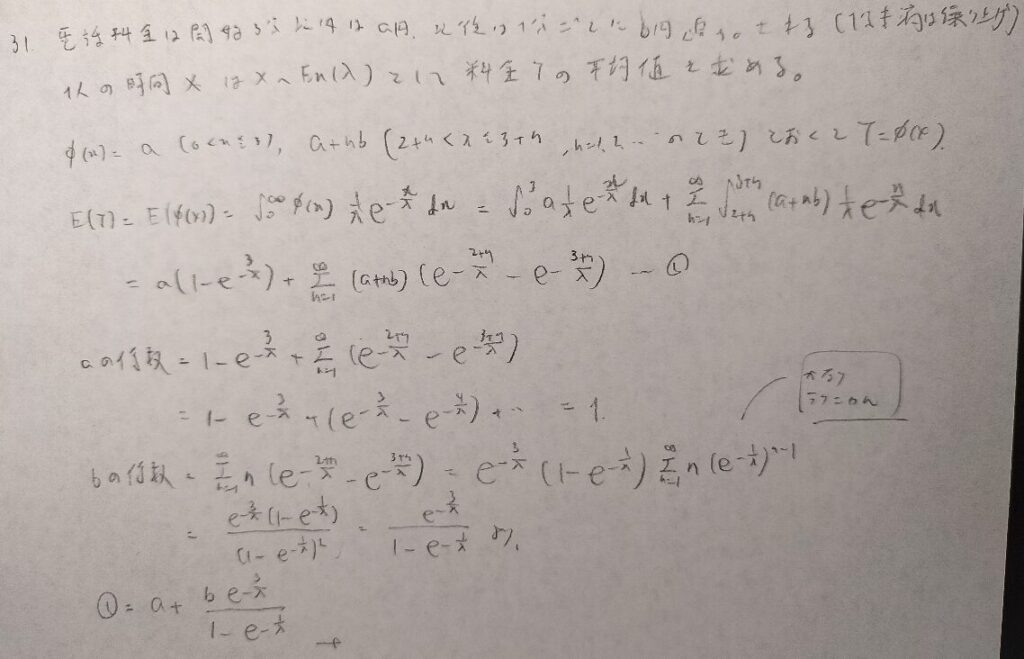
アクチュアリー数学の過去問でよく見る問題ですね。
『確率統計演習 1 確率』では下から3行目の式変形が技巧的に書かれています。確かにこのように変形できれば級数の和はすぐに出せますね。
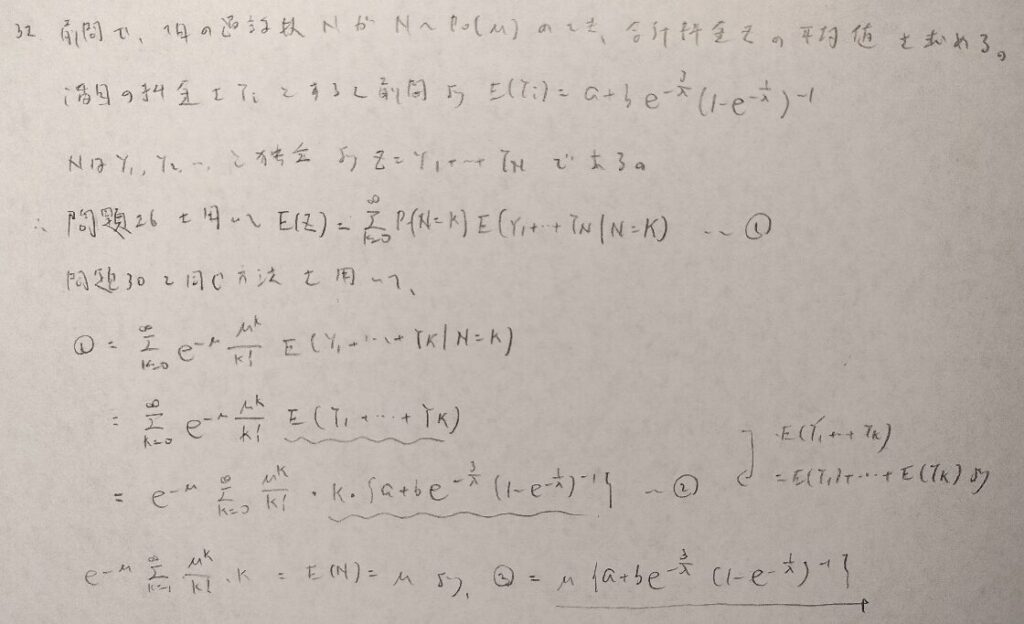
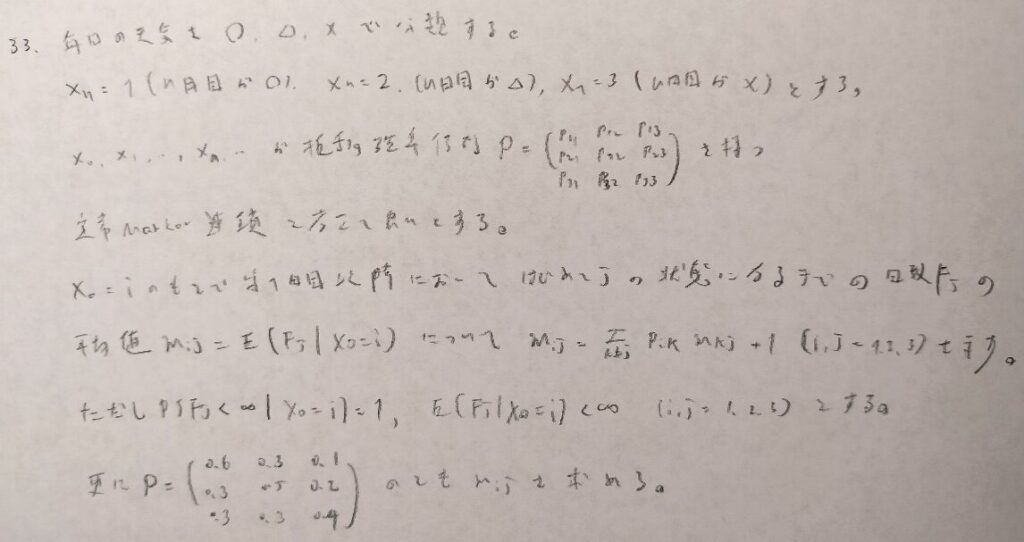

難問です。本章ラスト付近はどれも難しい問題になります。
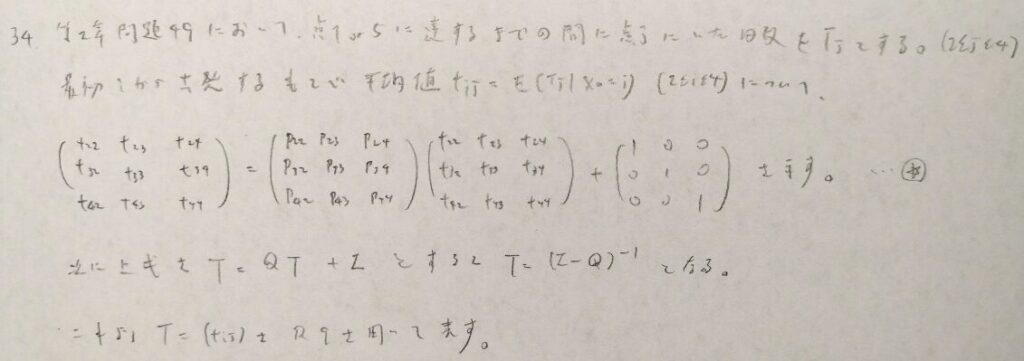

おそらく本問が本章の最難問です。とても難しい問題です。
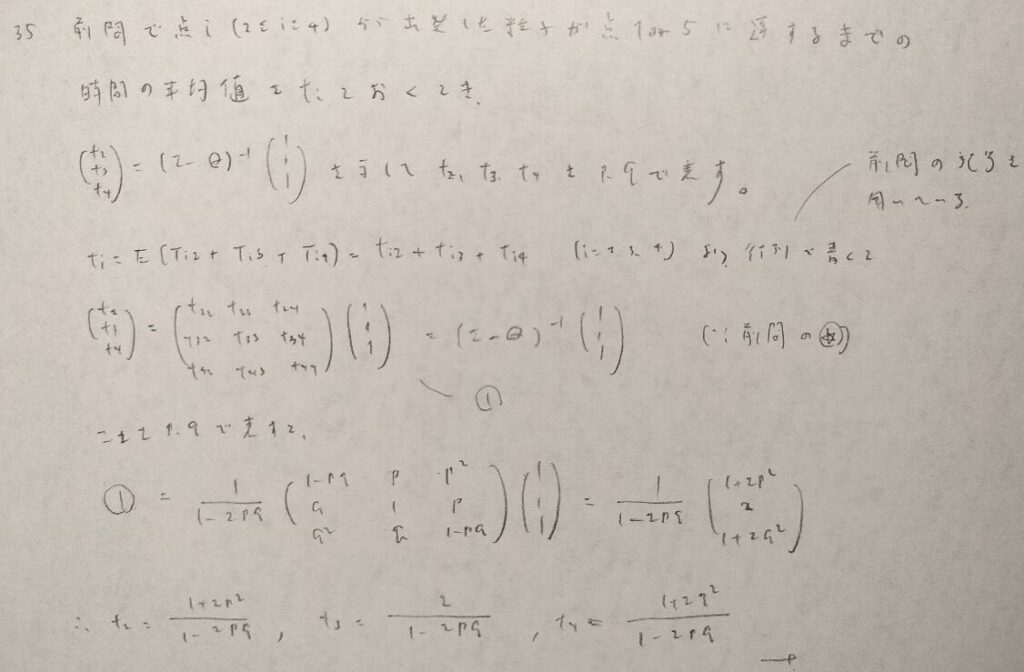
移動する時間を単位時間1と捉えています。
以上で第3章を終わります。
最後の怒涛の難問ラッシュが大変でした。しかし第2章の方が全体的に難問が多かった気がします。
皆さんは第2章と第3章(本章)のどちらが難しかったと思いましたか?次回も『確率統計演習 1 確率』を片手に第4章の変数変換を頑張りましょう!


