アクチュアリー数学の指定問題集である『確率統計演習 1 確率』を解いていく第2弾です。第1弾では事象と確率を勉強しました。
第1章:事象と確率
第2章:確率変数と分布
第3章:平均値、分散
第4章:変数変換と和の分布
第5章:積率と積率母関数
第6章:大数の法則と中心極限定理
この第2章はとても問題が多かったですね。
確率分布に関する問題はほぼ網羅している感じでしたね。そして確率微分方程式が本格的に出題されていて驚きました。
アクチュアリー数学では昭和の中期に確率微分方程式が出ていましたが、ここ最近は息を潜めています。最近は新傾向が続いているため復活する可能性があります。
この第2章の記事の問題のレベルは極めて高いため、下記の本の確率変数部分の問題が一通り解けることが『確率統計演習 1 確率』の第2章挑戦の一応の目安となります。
もしくは岩沢先生のリスク本『リスクを知るための確率・統計入門』の該当部分でもOKです!
第2章の問題の終盤はマルコフ連鎖から確率微分方程式の流れですが、その他にも体系的に問題がまとめられており、この質でこの分量の問題に触れることができるのは『確率統計演習 1 確率』以外にはありません。対策書として名前が上がることのある『明解演習 数理統計 (明解演習シリーズ 3) 』は統計分野も勉強できる利点がありますが、ほとんどが基本的な内容のため、本記事で用いる『確率統計演習 1 確率』の問題の方が難易度が高いです。
それでは早速、例題から順に見ていきましょう!
『国沢確率』第2章「確率変数と分布」の例題

Xが確率変数であることを示すには「Xが属する任意の区間が確率事象となる」ことを示せばよいです。ある事象Xが確率事象とはn回中に事象Xがr回が起こった時に、その比が一定値pに近づくときpを確率、Xを確率事象と言います。確率および確率事象はコルモゴロフ(kolmogorov)の公理を満たします。
この公理が後の問題でも使われるので覚えておきましょう。
コルモゴロフの公理1:加算個の確率事象の和集合や積集合や補集合、空集合や全事象も確率事象である。
コルモゴロフの公理2:確率は0以上1以下の値をとる。
コルモゴロフの公理3:各確率事象が直和で表されているとき、同様に確からしい時は確率が等しいと考えて良い。
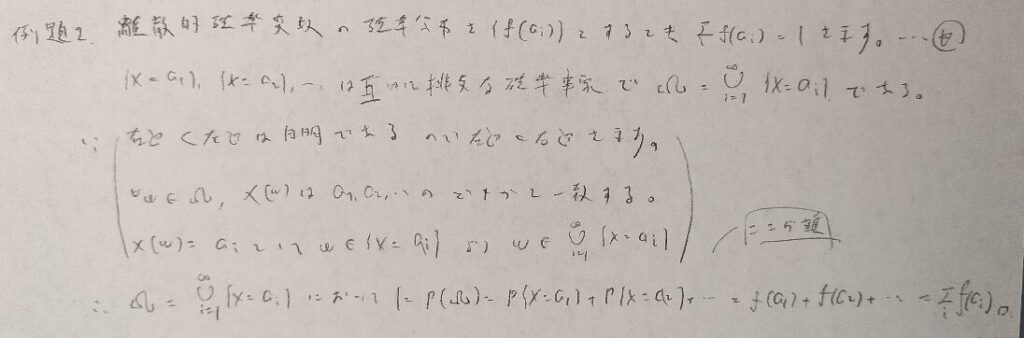
互いに排反な確率事象であることの確認を忘れずに行いましょう!
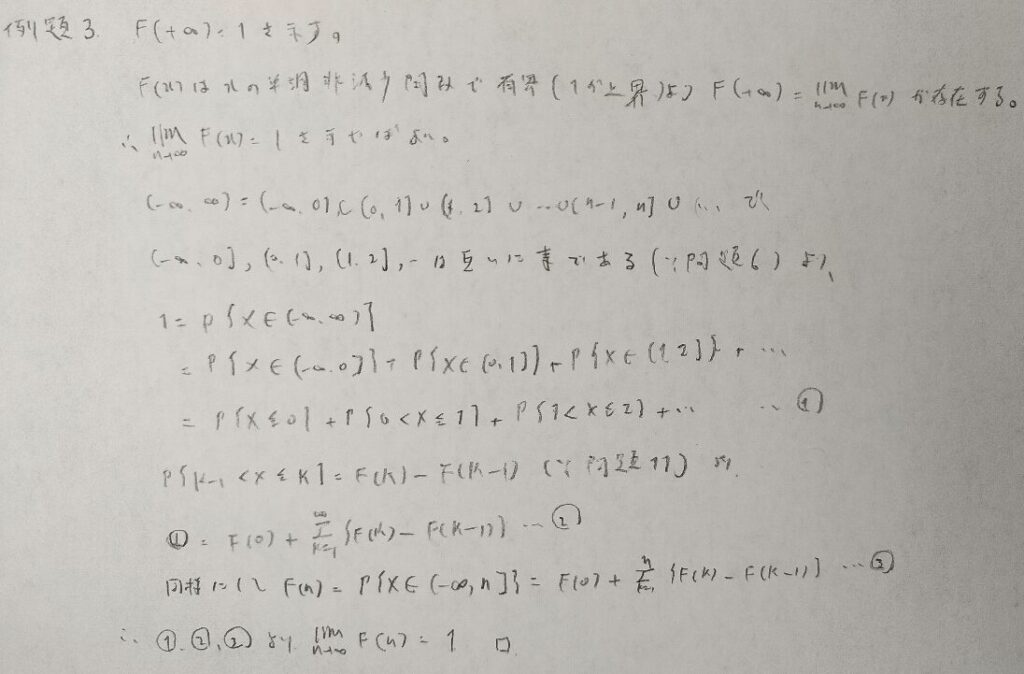
なんだか序盤から難しいですね。
『確率統計演習 1 確率』は微分積分(大学前半程度)の理解できていることが前提で進められています。その点が他書にはあまり見られない特徴です。この問題では有界単調数列は収束するという定理を用いています。
解析学の本はたくさんありますよね。少なくともここ10年でその数は増えていますよね。本当に入門向きの本では、この問題を解くための定理は学べないので、かといって『解析入門 Ⅰ(基礎数学2)』などは難しすぎて理解すらできません。ちょうど良い本はありますか?笑
松坂先生の『解析入門(上) ・解析入門(中)・解析入門(下)』の解析の3冊はとてもおすすめです。微分積分というよりは解析学全般を網羅しています。3冊ということもあって具体例が多く挫折しないで読み進めることができます。
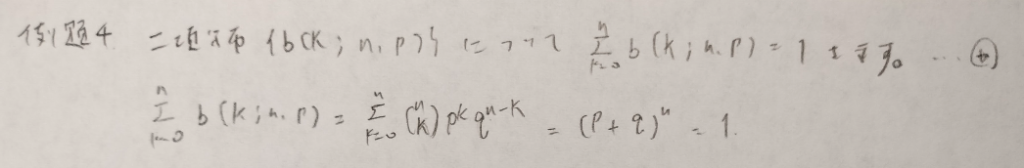
分布のときは{ }表記で、式として表記する際は{ }を省きます。
この表記法は便利ですね!
『確率統計演習 1 確率』では他にポアソン分布もこのような表記法が採用されています。
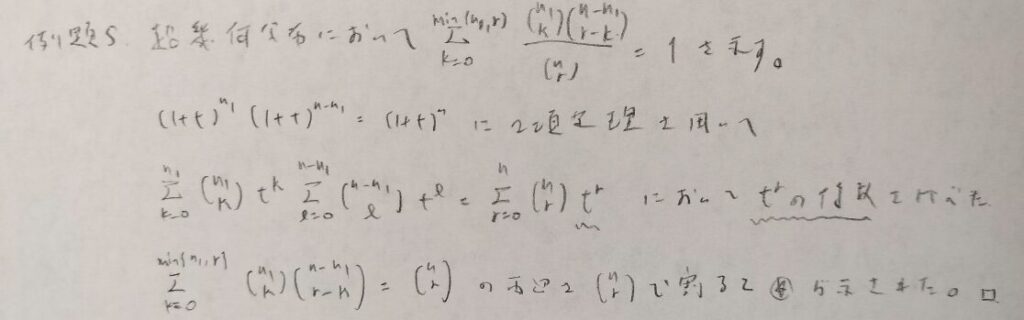
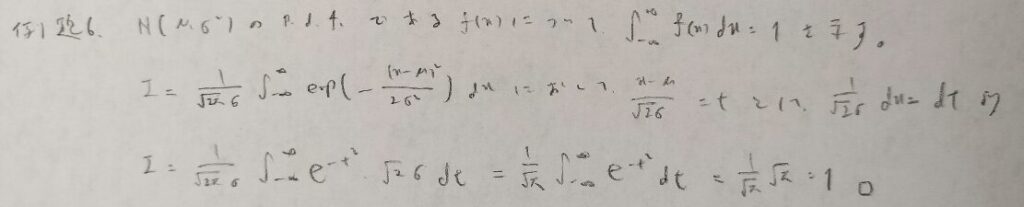
置換積分の方法を覚えておきましょう!今回はガウス積分に帰着させます。
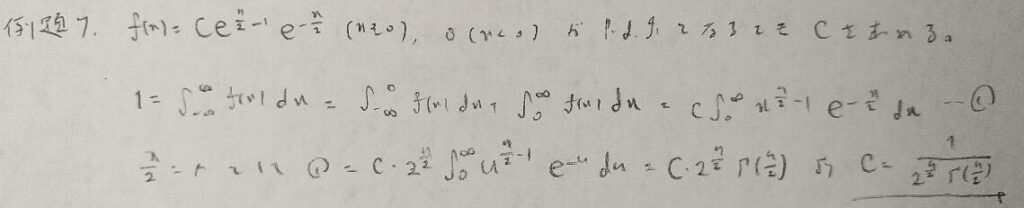
ガンマ関数に帰着させたいから…と考えればどのように置換するかが見えてきますね!
2023年の統計検定1級や2023年のアクチュアリー数学でも似たような問題がありましたね。
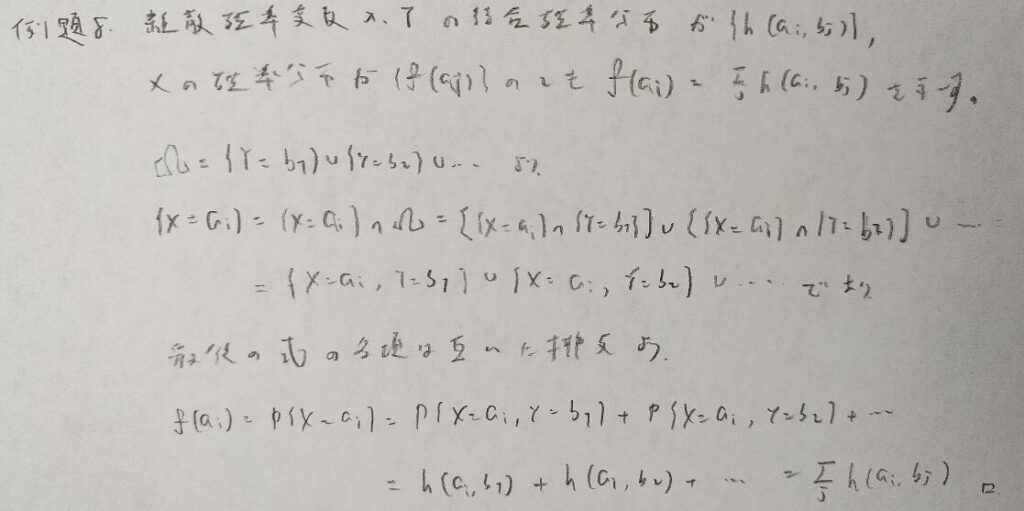
下から5行目の式が本質部分です。
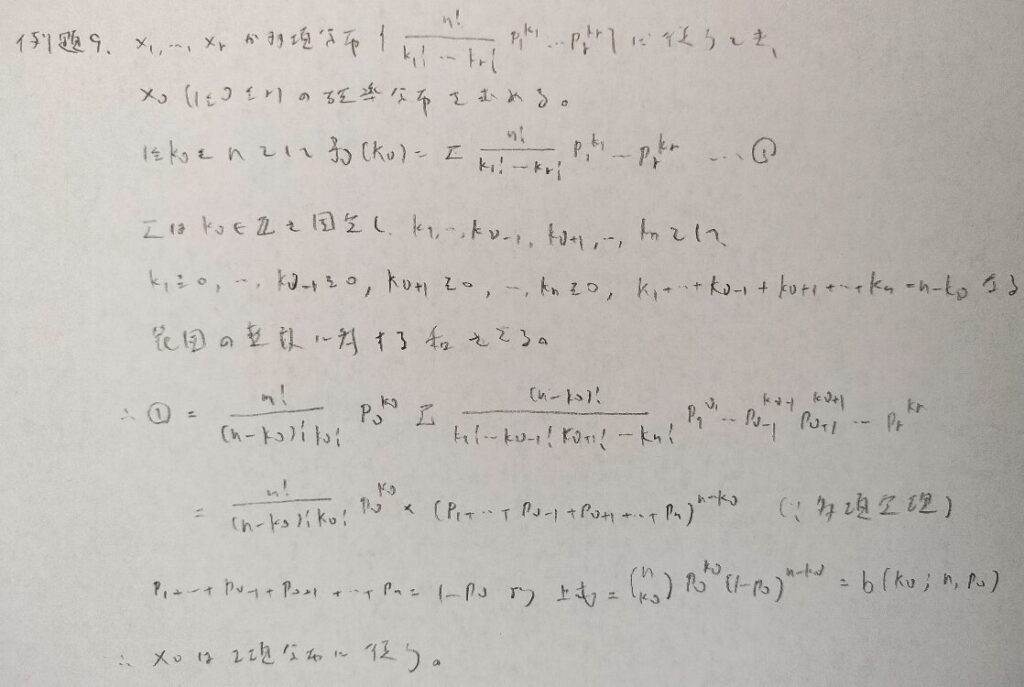
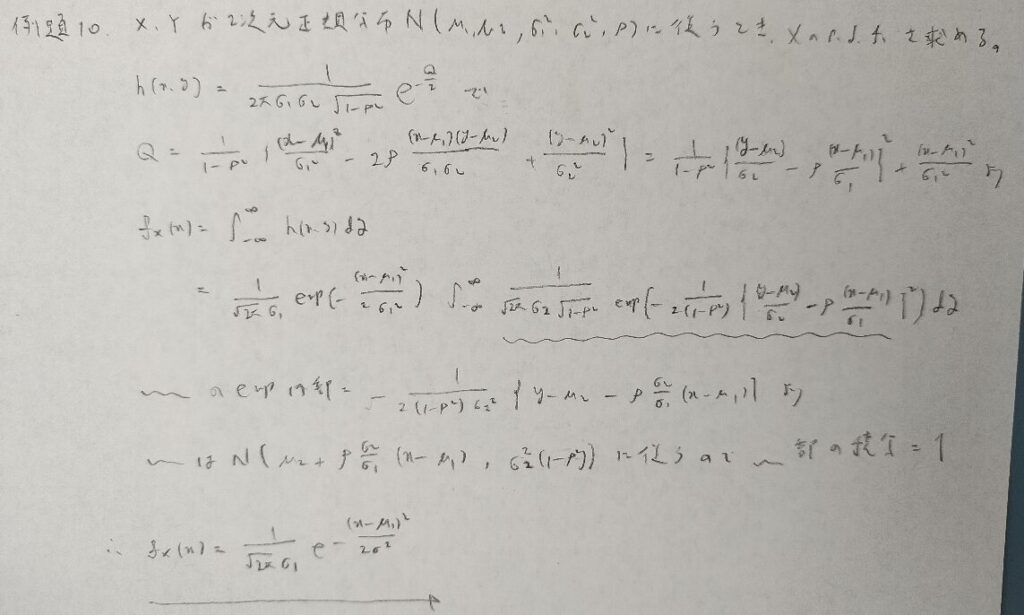
平方完成部分が他書よりも上手くて素晴らしいと思いました。暗記の価値が高いです。
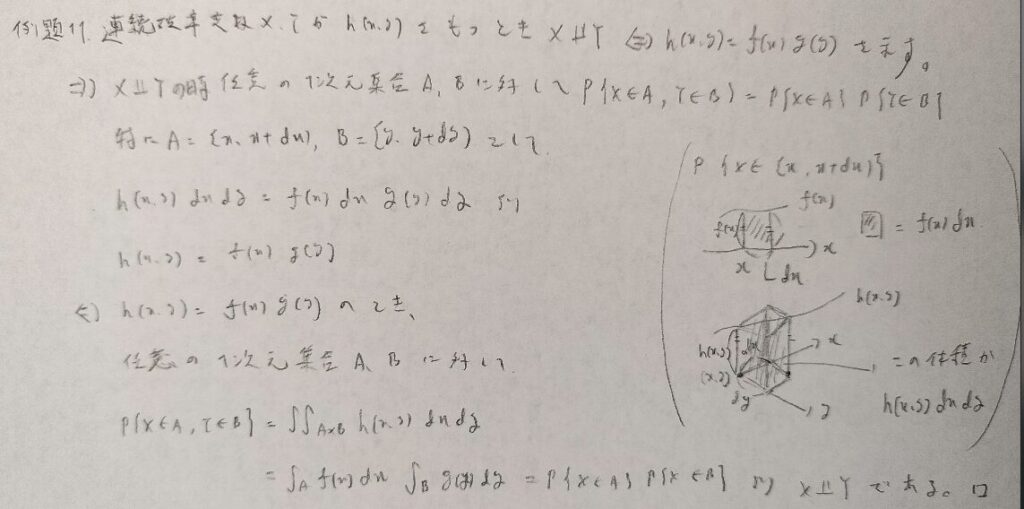
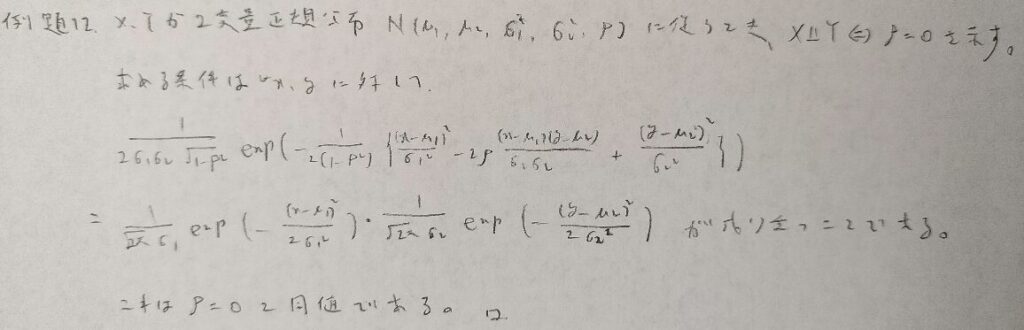
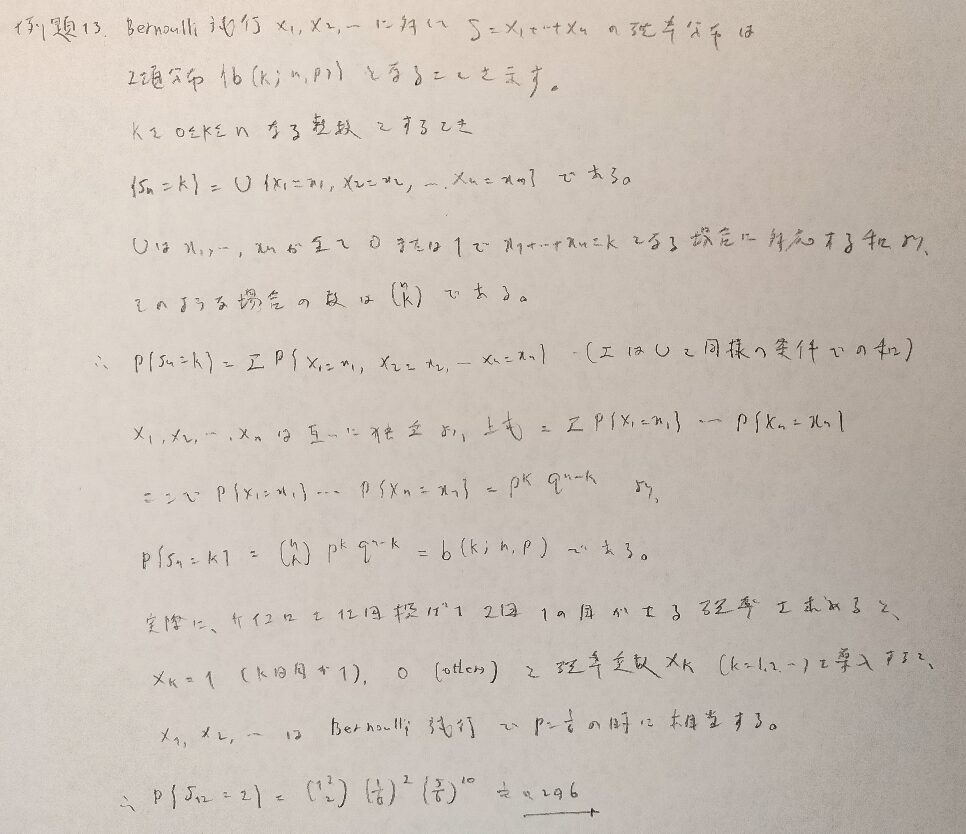
やっと例題が終わりましたね。
次の問題は全部で53問もあります。1日で頑張ろうとせずに何日かかけて理解できるように頑張りましょう!
全ての問題を分析するとパターンが見えてきました。そこで第2章では問題をパターンごとに分けて解説していきます。
問題1〜5:確率変数の問題
問題6〜14:和集合に関する問題
問題15〜25:正規化定数の問題
問題26〜44:有名性質に関する問題
問題45〜53:マルコフ連鎖と確率微分方程式
『国沢確率』第2章「確率変数と分布」の確率変数の問題
前半の問題から難易度が高い問題が並んでいます。わからない場合は『明解演習 数理統計 (明解演習シリーズ 3)』や『リスクを知るための確率・統計入門』を片手に学習していきましょう!

高校数学で学習する当たり前のことをきちんと証明しています。

この結果は後の問題で複数回登場します。とても大事な問題です。


普通に難しいと思います。1つ1つ式変形を追わないと置いていかれそうです。
コルモゴロフの公理が背後に潜んでいますので要注意です!
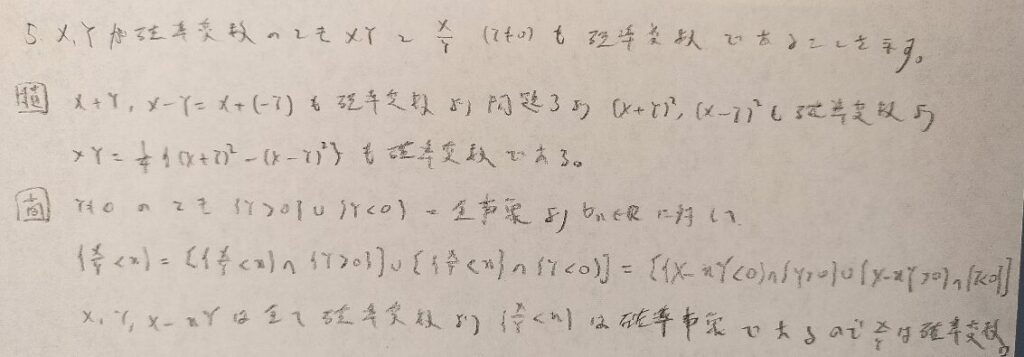
確率変数の問題は全部で5問ありました。かなりのボリュームでしたね。
『国沢確率』第2章「確率変数と分布」の和集合に関する問題



先ほどから似たような証明のパターンが続いていますね!
『確率統計演習 1 確率』は問題集ながら、体系立てて問題を掲載してくれているので、学習効果が高いと感じます。

普段から当たり前のように用いている内容の証明です。
ここまでが和集合に関する問題でしたね!
次の問題からは分布関数に関する問題になります。
『国沢確率』第2章「確率変数と分布」の分布関数の問題
分布関数関連の証明問題では開区間か閉区間かに注意していきましょう。
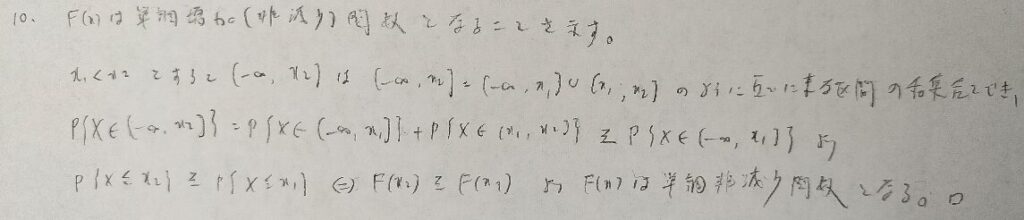
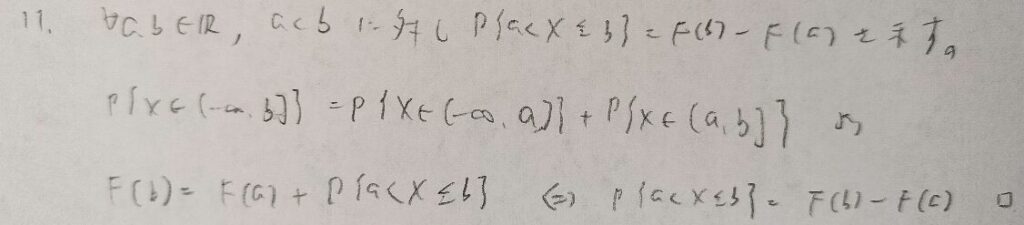
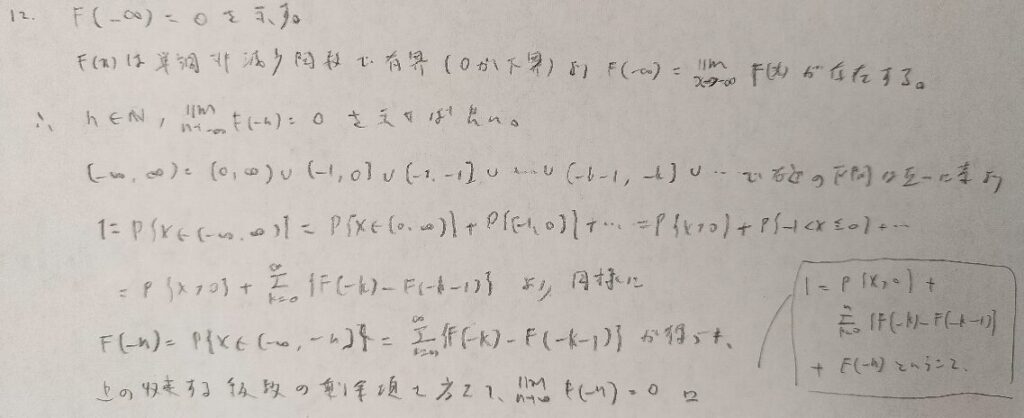
ここから数題は級数の収束と剰余項が0に収束することを用いる問題を扱います。初見ではまず解けない難問になります。
僕はこの問題が解けなくて数時間答案と格闘していました笑
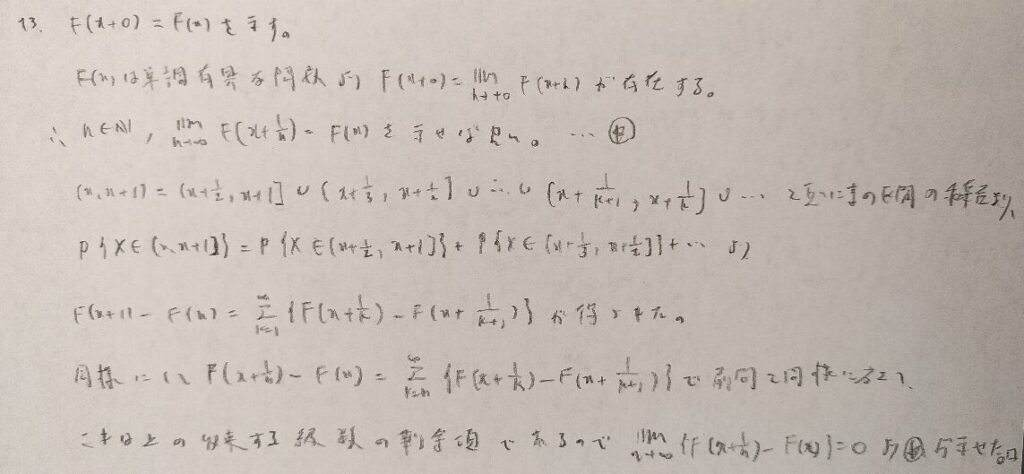
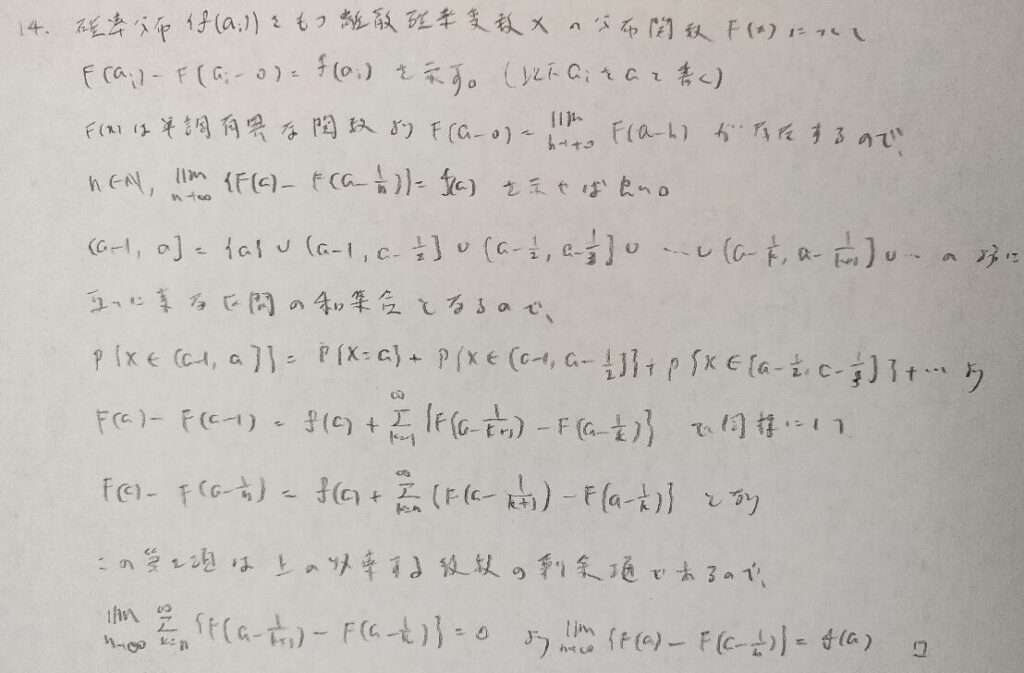
何問か問題を通してお気づきかと思いますが、剰余項を持ち出す証明は1点のみを吟味させるイメージの問題で用いる感じです。
『国沢確率』第2章「確率変数と分布」の正規化定数の問題
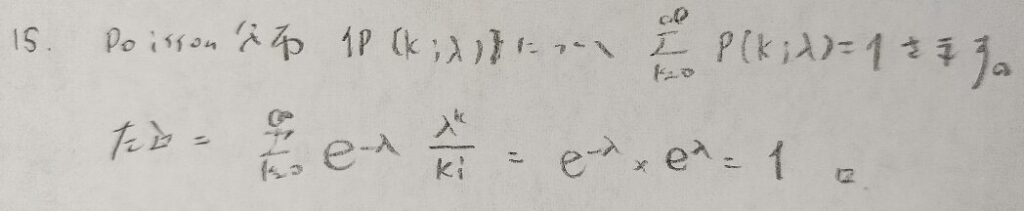
一気に難易度が下がりましたね!笑
ここからは問題の解くスピードが上がるのではないでしょうか。先ほどの例と同様に『確率統計演習 1 確率』では二項分布やポアソン分布は途中式に挿入できる形を提唱しています。
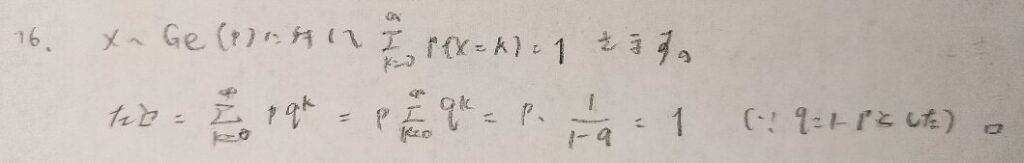
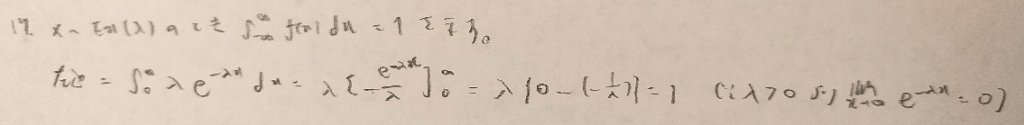
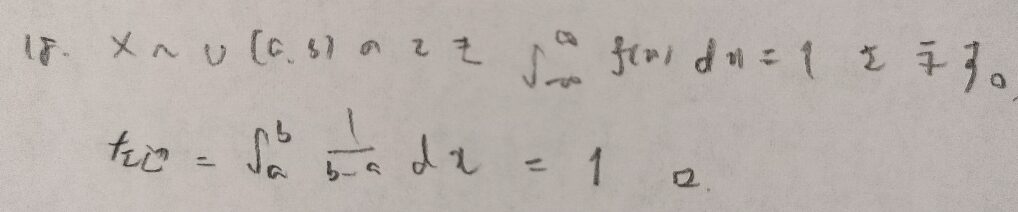
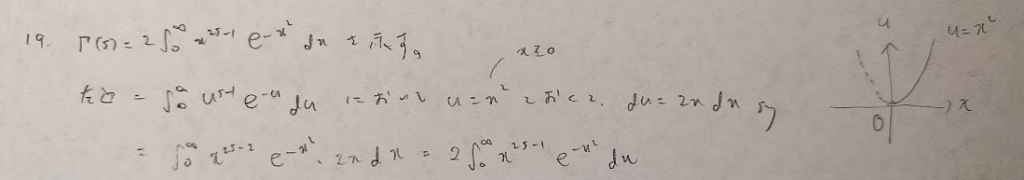
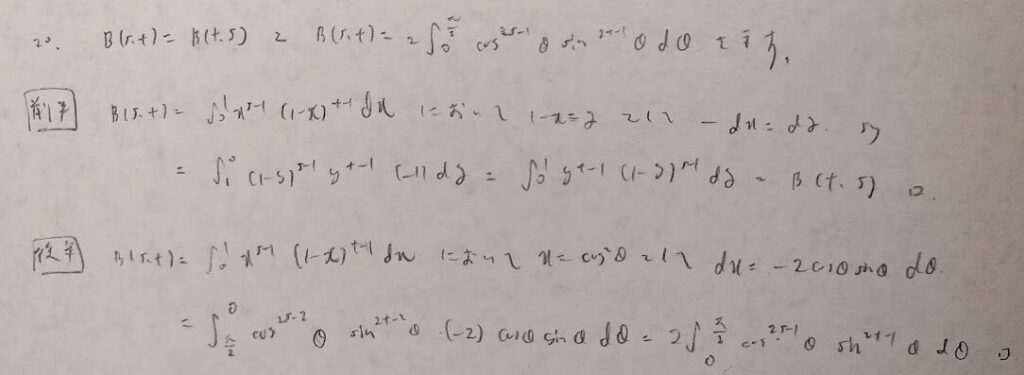
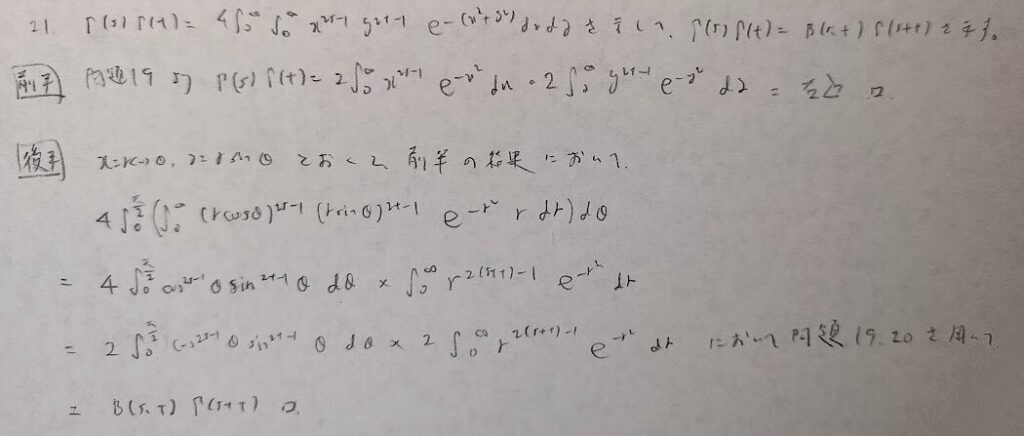
ここまでがガンマ関数とベータ関数の性質の証明ですね!
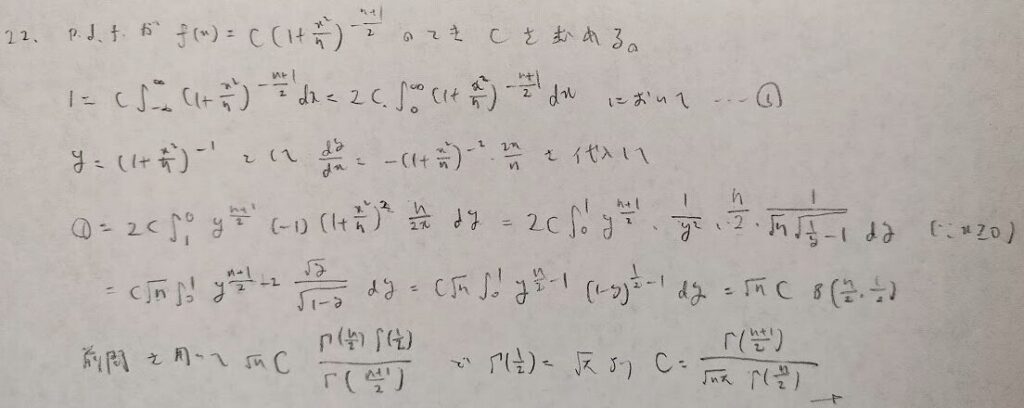
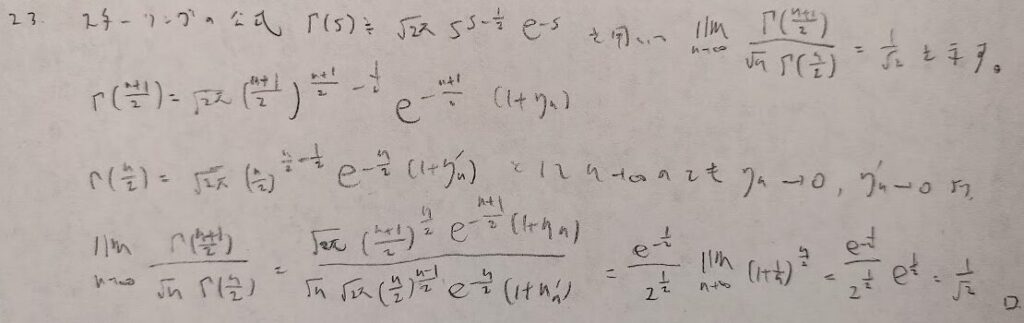
スターリングの公式はCLTを用いて鮮やかに証明できます。こちらの記事で証明をしています。使用している本は『基本確率 (経済の情報と数理 2)』です。
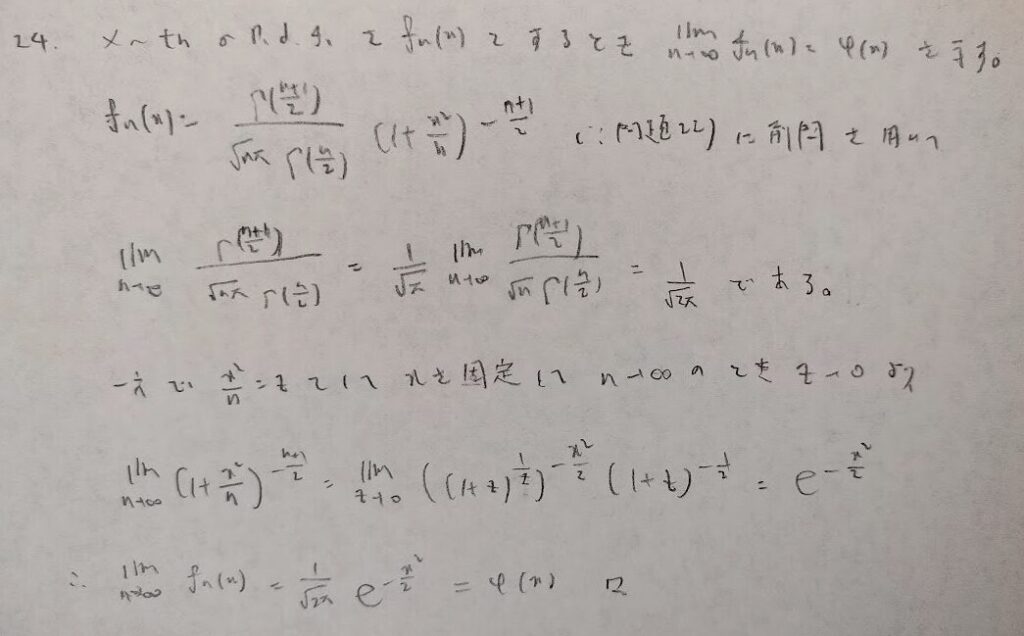
この問題の背景にはt分布で自由度を∞にすると標準正規分布に近づくということです。
『現代数理統計学の基礎(共立講座 数学の魅力 11)』にサラッとサラッと載っていたことを思い出しました笑
この本は統計検定1級で最も大事な本なのでとても有名な本ですよね。こちらの記事で『現代数理統計学の基礎(共立講座 数学の魅力 11)』の例題と演習問題をすべて解説しています。
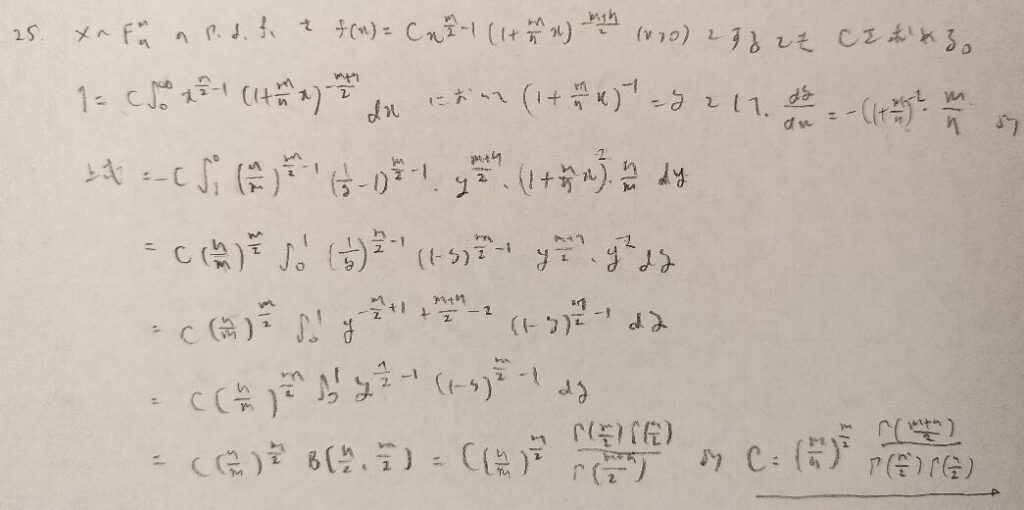
主要な確率分布の中で最も気付きにくい置換積分がこの問題です。yをおくときに−1乗を忘れないようにしましょう!
必ずご自身で1度やってみましょう!初見だとこの問題だけで10分以上かかってしまうと思います。
ここまでが正規化定数の問題でしたね!
『国沢確率』第2章「確率変数と分布」の確率分布の有名性質に関する問題

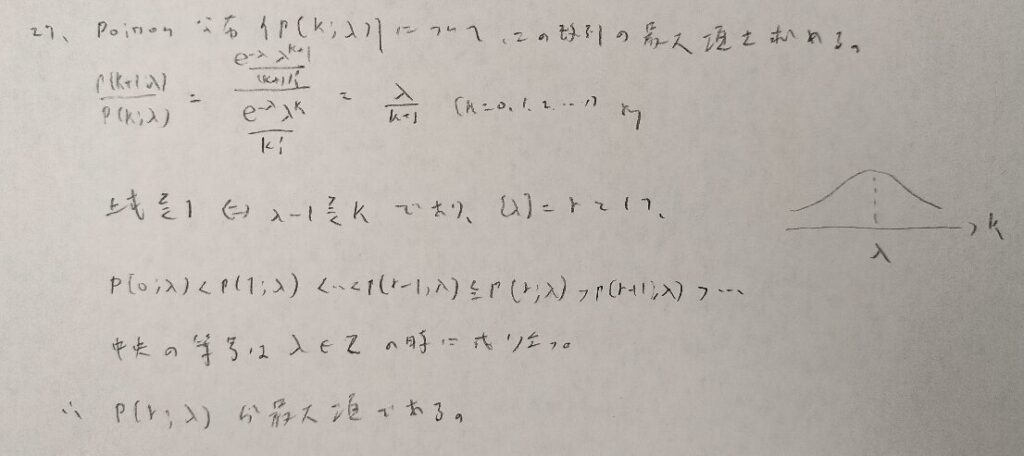
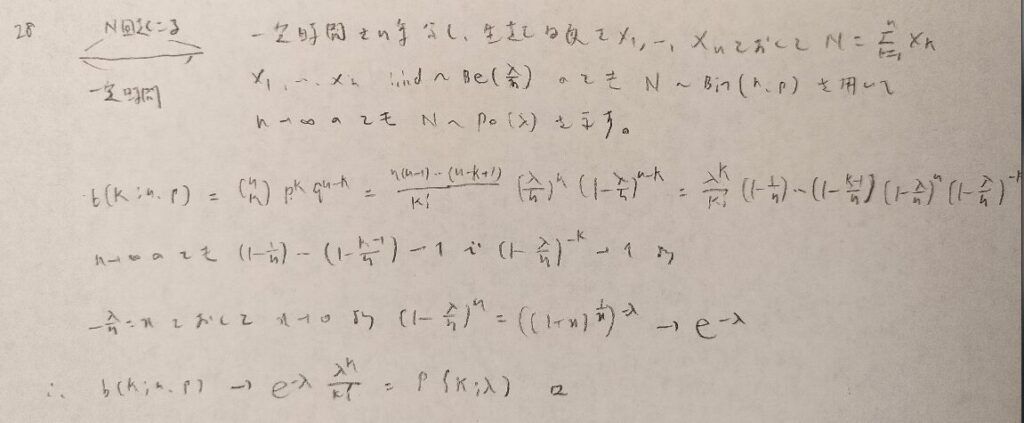
この問題は二項分布をポアソン近似する際に用いる内容です。
試行回数を大量に行うときに用いる近似法でしたよね。
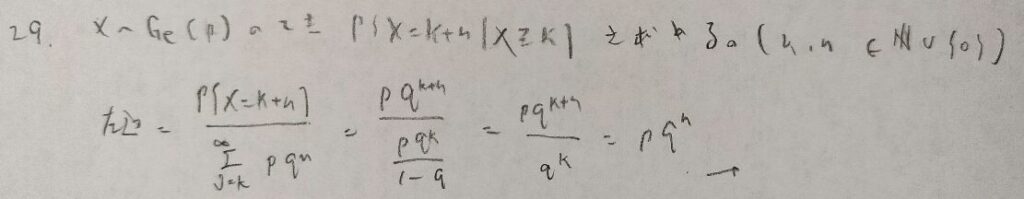
無記憶性を用いれば数式を使わなくても答えを出すことができます。
無記憶性を持つ分布は離散型だと幾何分布(ファーストサクセス分布)で連続型だと指数分布に限ることをこちらで証明しています。
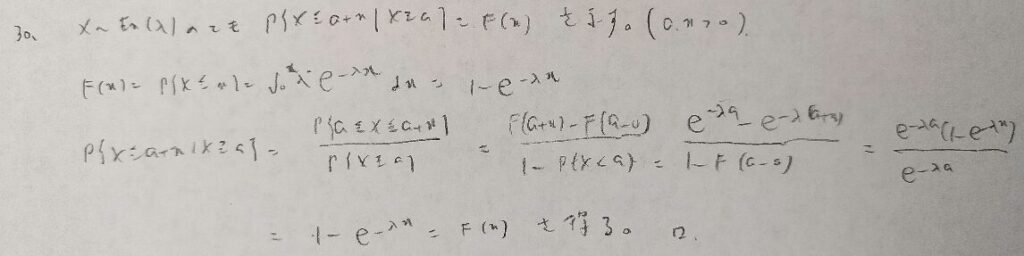
この2問は無記憶性に関する問題ですね。
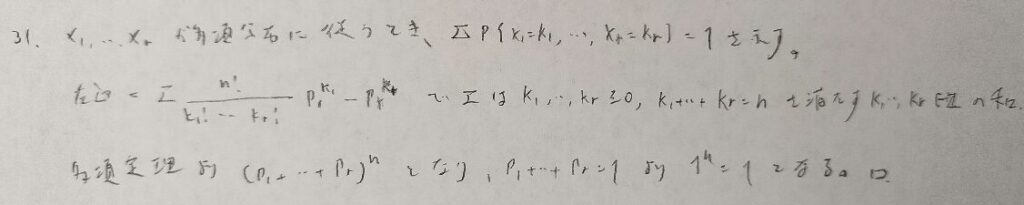
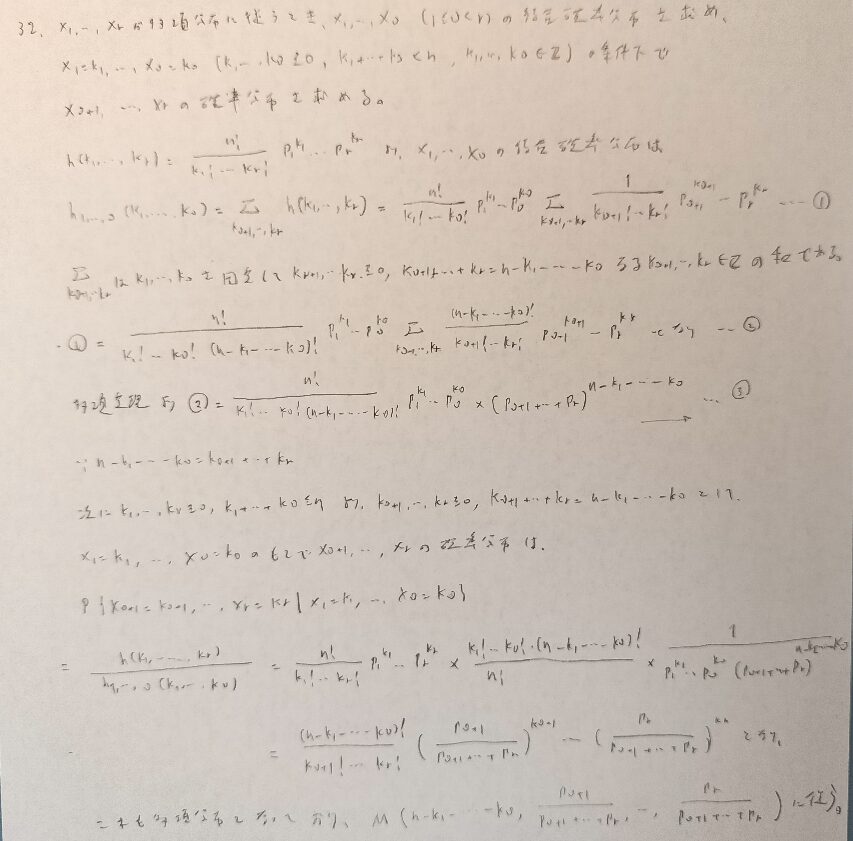
難問です。しかし数式を使わないと、自然な流れで答えの分布を推測することはできます。アクチュアリー数学は答えのみですので、なぜこのような答えになるか?を考えて暗記しておくと良いと思います。本問は5行目が本質です。
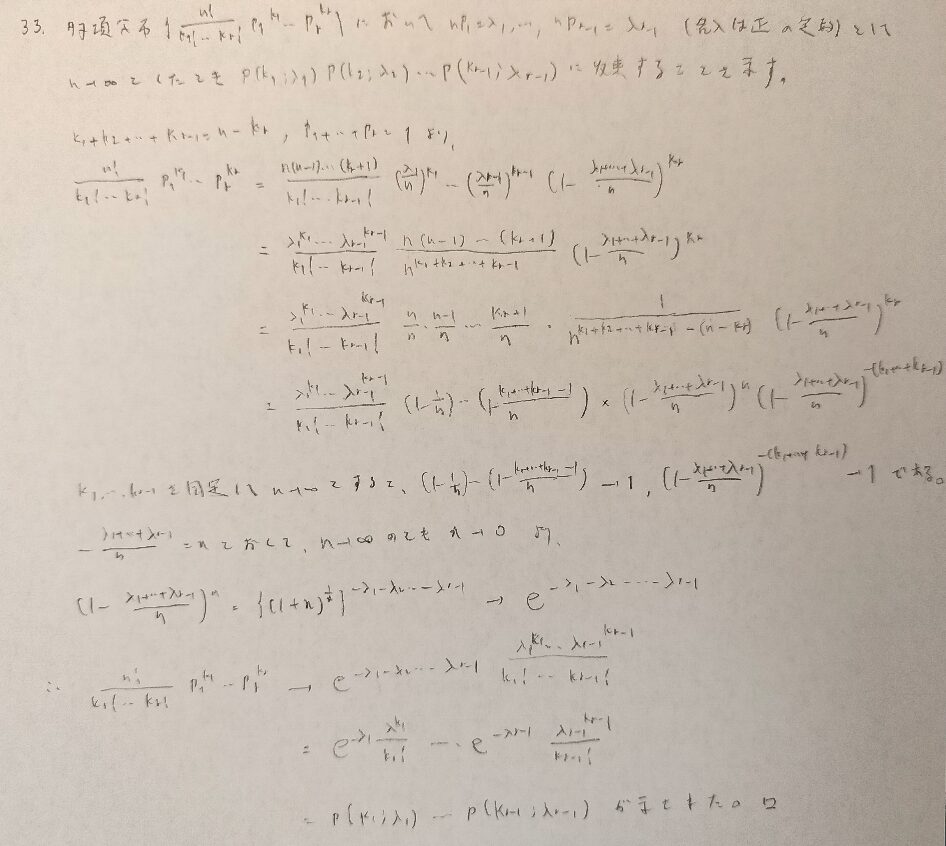
この問題は二項分布のポアソン近似の多項分布バージョンですか?!
その通りです!あまり知られていない公式ですので、統計検定1級にも誘導付きで出題されるかも知れません。アクチュアリー数学では当然できるようにしておかないといけません。
多項分布シリーズはこれで終了ですね!
『国沢確率』第2章「確率変数と分布」の結合確率分布の問題
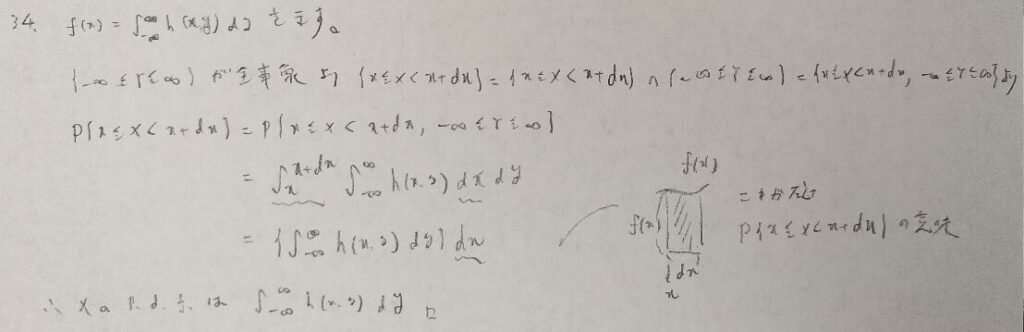
この問題も当たり前のことを証明しています。右に書いている図が本質的です。
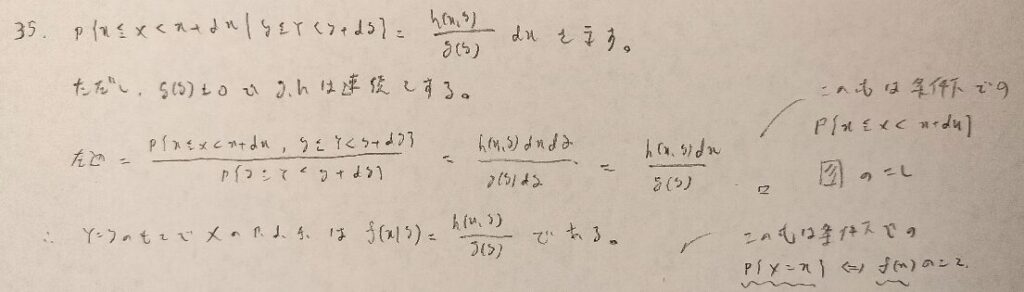
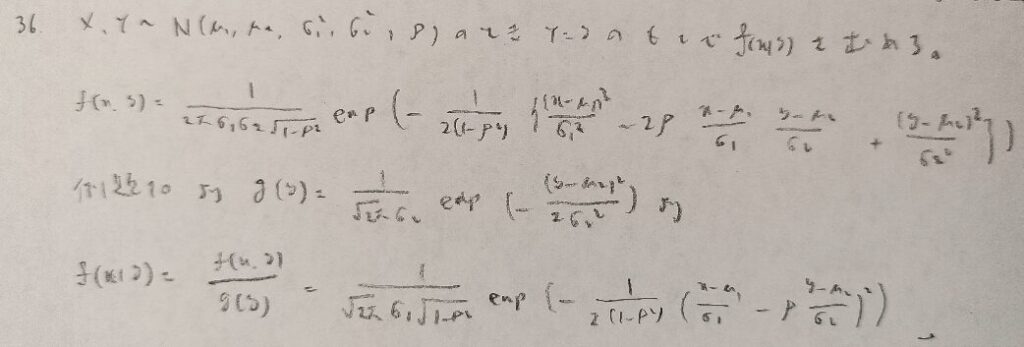
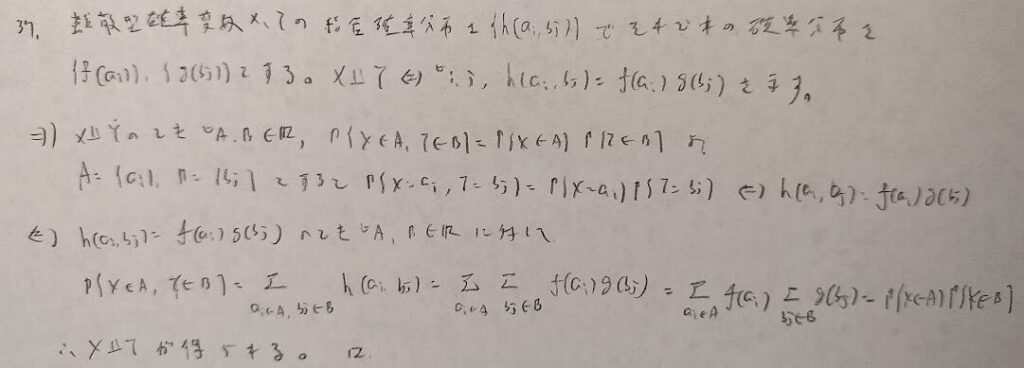
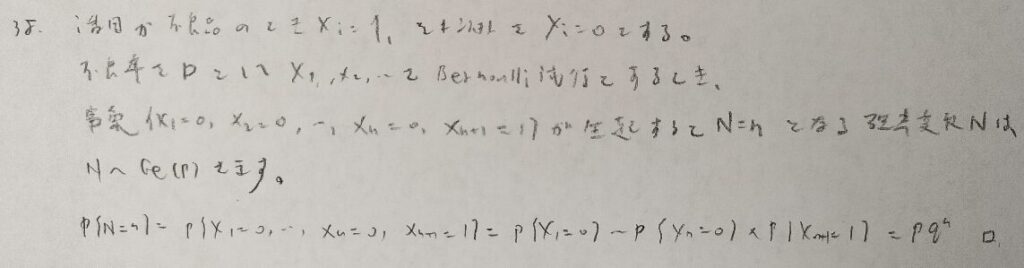
幾何分布をベルヌーイ試行を用いて求める問題です。

超幾何分布と順列は深い関係があります。
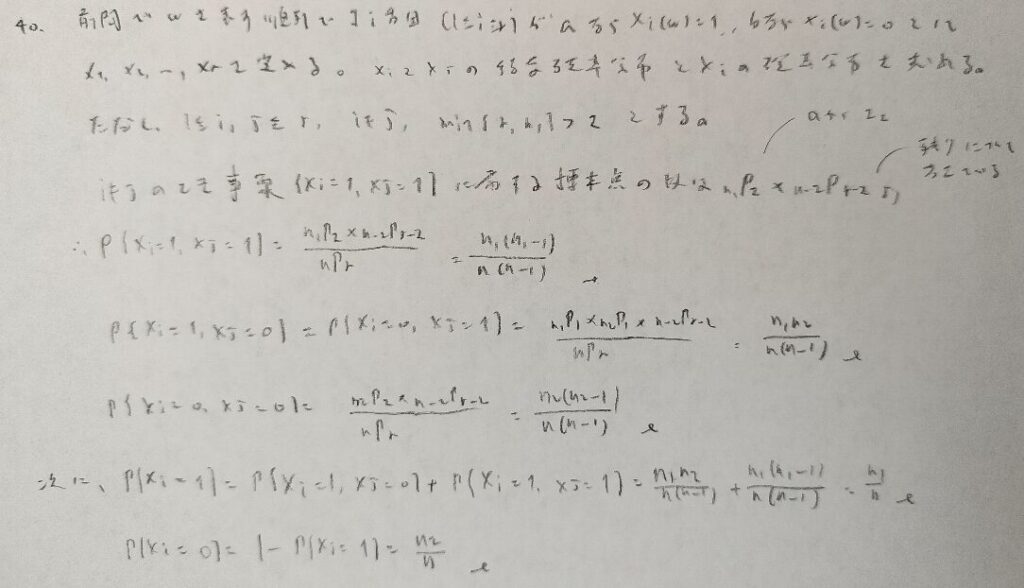
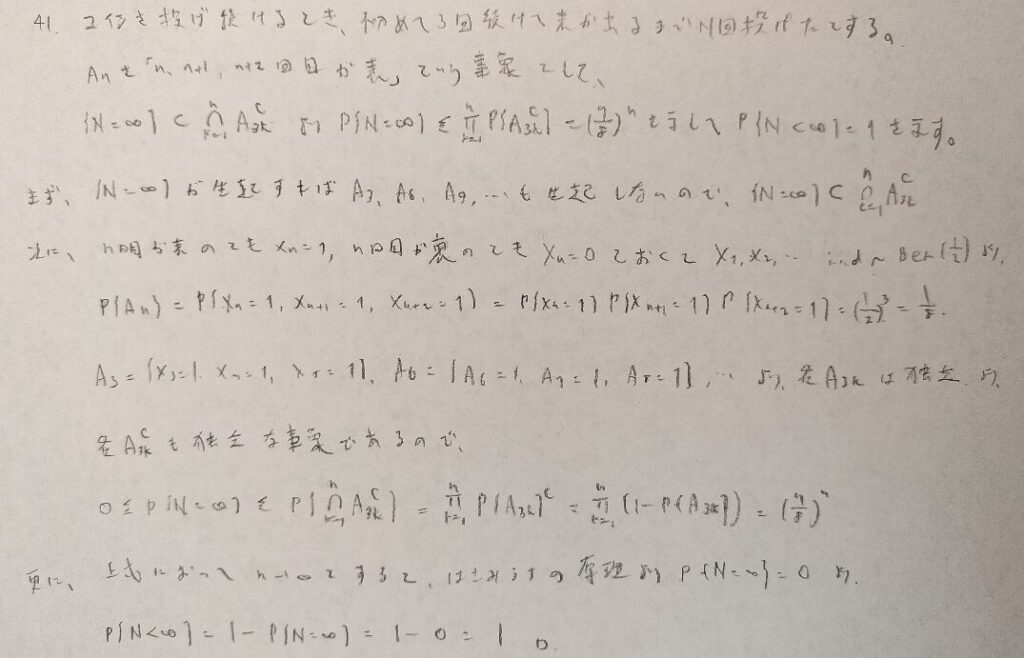
今後、集合の包含関係を用いて確率の不等式評価を用いる問題が増えてきます。
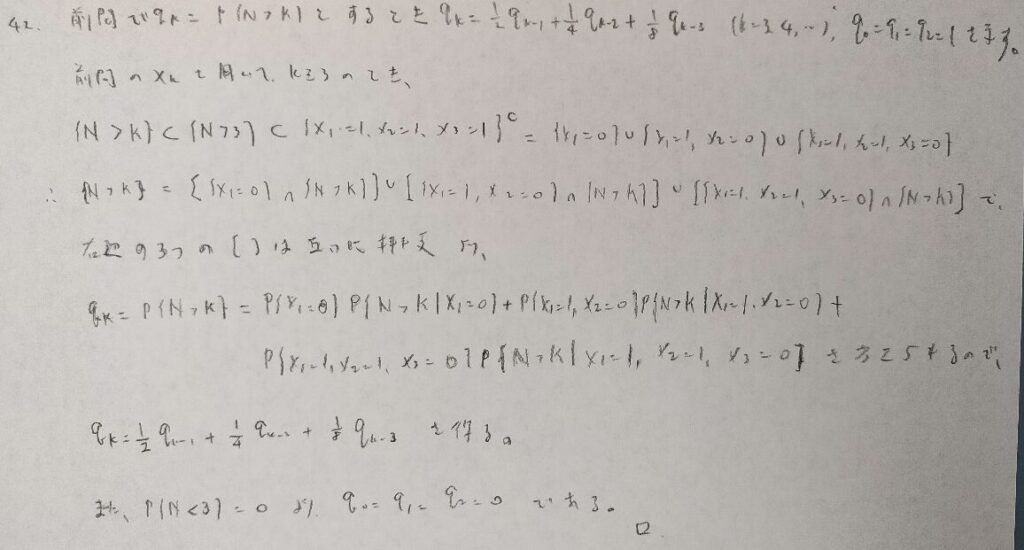
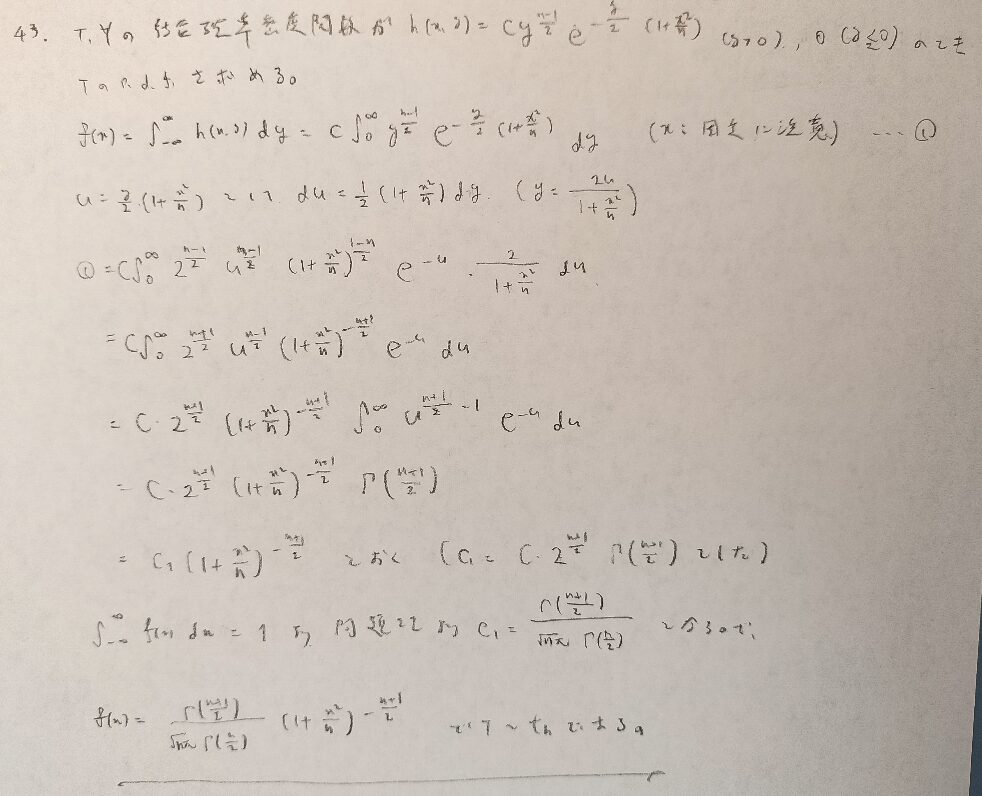
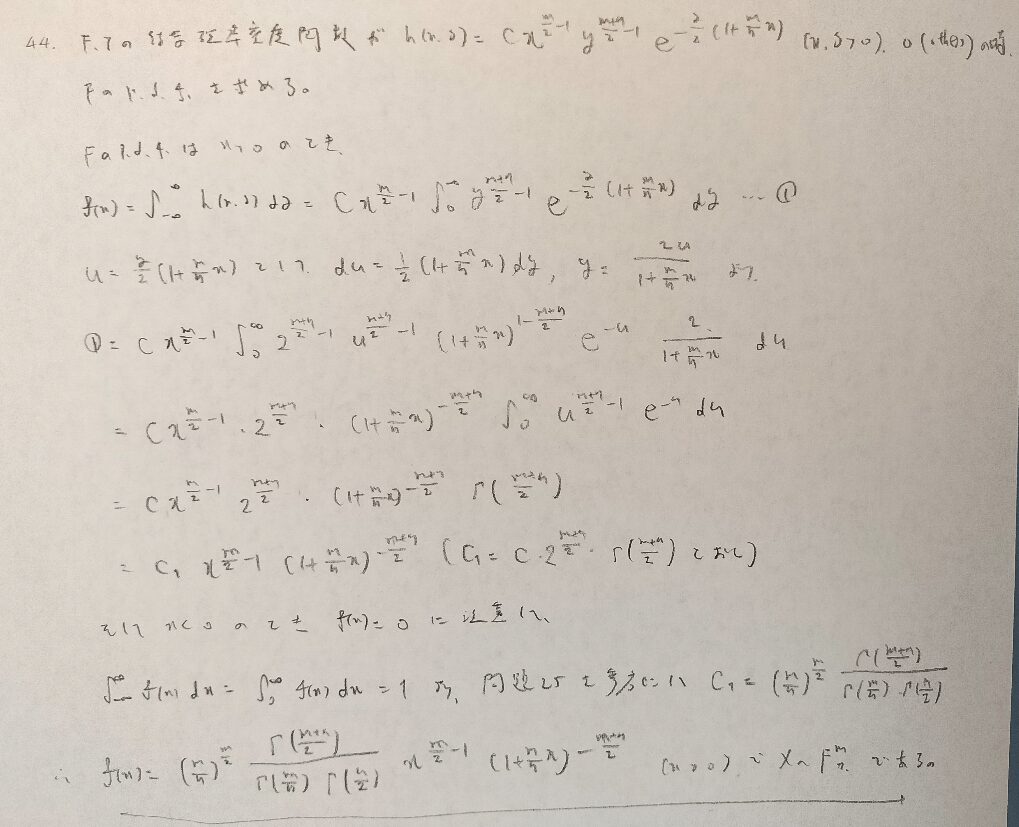

結論は自明ですが、この問題をきちんと数式を用いて導出させる参考書は『確率統計演習 1 確率』のみです。本問は球座標変換(球面変換)を用いています。
『国沢確率』第2章「確率変数と分布」のマルコフ連鎖と確率微分方程式の問題
いよいよ終盤です。マルコフ連鎖からの確率微分方程式の流れをお楽しみください。
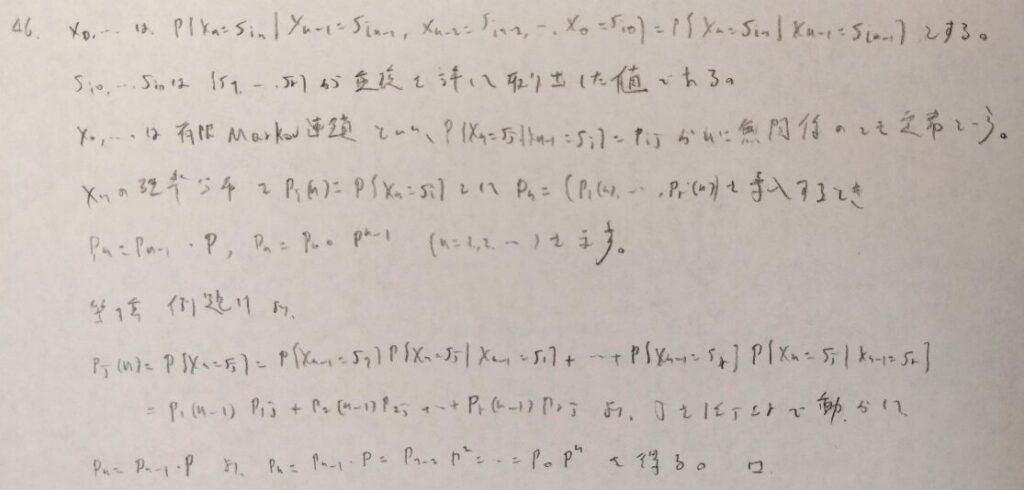
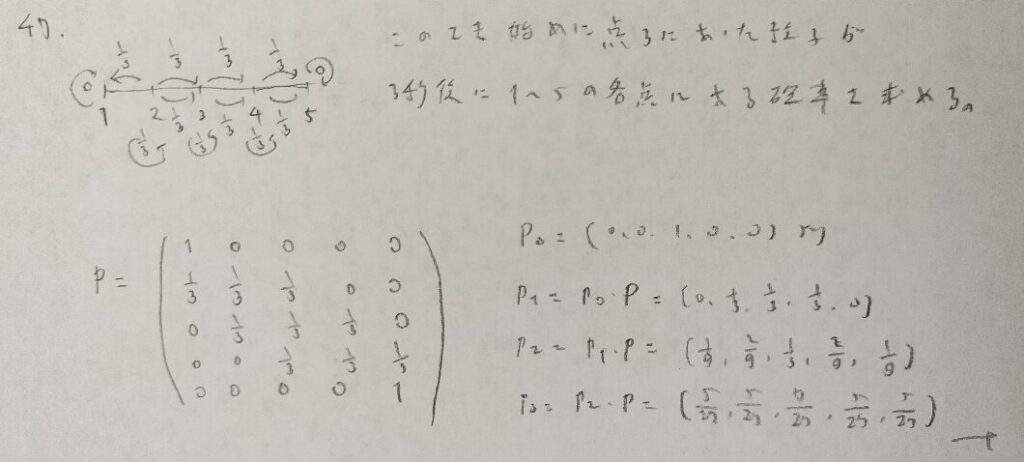
本問のような設定を吸収マルコフ連鎖といいます。
本問の問題の難易度は統計検定準1級程度です。準1の合格対策はこちらにて丁寧に解説しています。
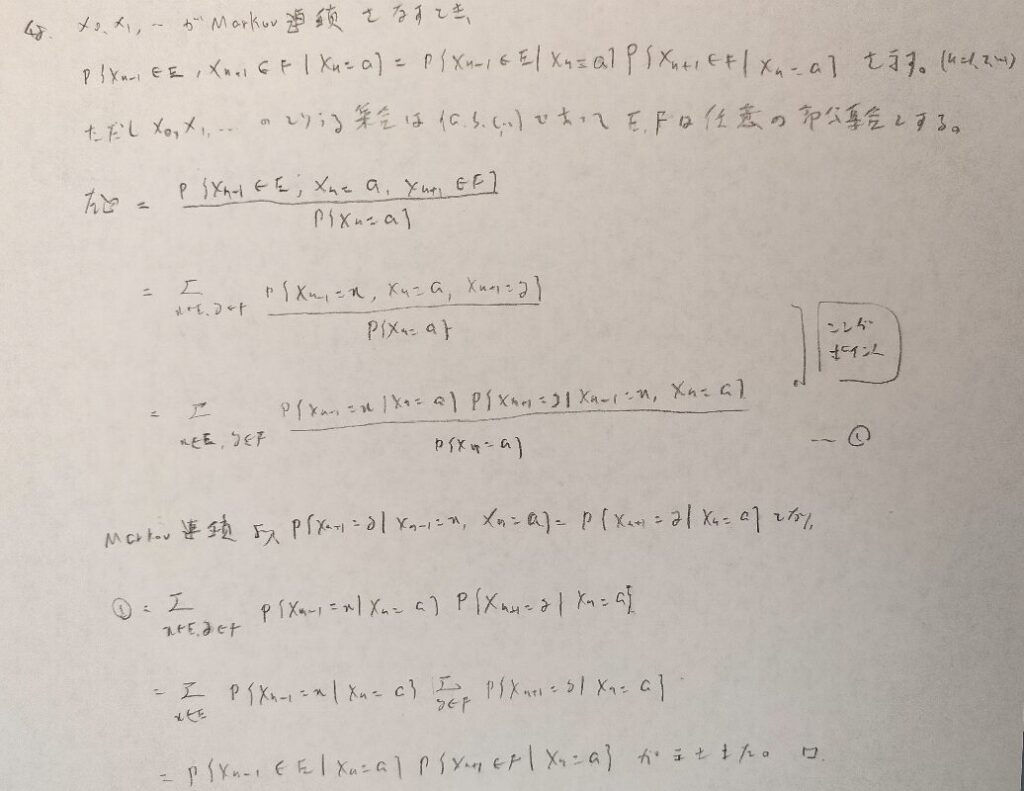

とても難しい問題です。何度も繰り返しながら解答を再現できるように頑張りましょう!アクチュアリー数学では未出問題です。

確率微分方程式を解く流れは、まず確率漸化式を立てる要領で立式をする→次に微分の定義式に合わせるために式変形をする→hで割る際にランダウのo記号の内部の次数が1減ることに注意してhを0に近づける。

本問などでは常微分方程式の基本的な知識が求められます。具体的には1階線形常微分方程式が解けることが求められます。しかし表面的に解ければ良いので数学検定1級(合格法はこちら)の微分方程式の内容を超えないイメージです。
常微分方程式のおすすめの本はありますか?
僕はこちらの本『常微分方程式キャンパス・ゼミ』を強くお勧めします!とても体系立てて書かれているので本当に早い理解が得られる素晴らしい本です。

前問もそうですが、このタイプの問題では帰納的に一般解を求めていくことになります。

やっと終わりました。もう疲れて倒れそうです。
お疲れ様でした。この第2章を解くのに1週間(実際は6日)かかりました。とてもヘビーな章でした。
でもその分だけ大きな学びがある章でしたね。疲れたけど楽しかったです!
次回は期待値の章です。『確率統計演習 1 確率』を片手に一緒に頑張っていきましょう!!









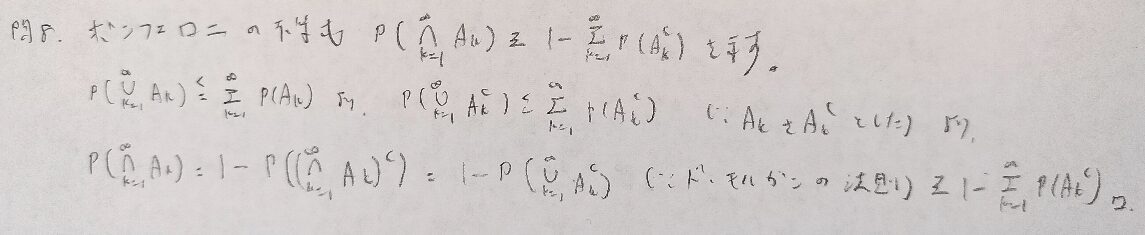
-scaled.jpg)

