多変量解析の1つの山場である主成分分析について解説します。
判別分析よりも数段難しい印象です。なぜこんなに難しく感じるのでしょうか?
線型代数の知識を知っている状態で解説している書籍が多い理由と、次元を削減していく内容なので行列処理で理解していかないと理解が難しくなる理由があるためです。
今回の主成分分析は線型代数の固有値の知識をかなり用います。線型代数の知識について不安な方は、数学検定1級の記事をご覧になってください。具体的な学習法が書かれています。
この記事では主成分分析をp変数と一般化した状態で行列表示で解説していき、解説がしづらい部分は個別に解説を行う手順で説明していきます。
主成分分析はアンケートなどをなるべく少ない変数で説明しようという分析になります。とても応用範囲が広くて面白い分析になります。この記事では模試の結果をどのように分析するか?という例を用いて解説します。
主成分分析とは
主成分分析とは一体何を目的に行うのでしょうか。この説明を明確にするために行列表現を用いてわかりやすく解説します。
主成分分析の解釈の例
p変数(ここでは数学、英語、社会、理科の4変数)のデータのサンプルがn個(例えば10人のデータならnが10となります)あったとき、4よりも少ない変数で各受験者の結果を分析する手法を考える問題が主成分分析で解決します。
4変数を総合的学力と文系理系の2つの変数に落とせば良いのではないのでしょうか?
このことを数学を用いてしっかりと説明できる手法が主成分分析です。さっそく理論を追っていきましょう。
主成分分析では不偏分散を考える
主成分分析の概要を行列表現を用いて解説します。ここで注意して欲しいのは式変形の都合上、不偏分散を用いていくことです。なお、後述する相関係数関連の話では標本分散を使おうが不偏分散を使おうが値に変化はないので、そこはご安心ください。

次に主成分分析の理解の要となる相関係数行列Rが登場します。
相関係数行列Rは今まで勉強してきた回帰分析や判別分析で登場しなかった内容で難易度が一段と増します。
主成分分析と相関係数行列の関係
固有値問題に持ち込むために、図02の前半ではよく使う結果を式変形を用いて証明しておきます。後半は相関係数行列が登場する場面です。
この記事での不偏分散の記号には2乗が書かれておりません。この表現は『多変量解析法入門』を参考にしました。
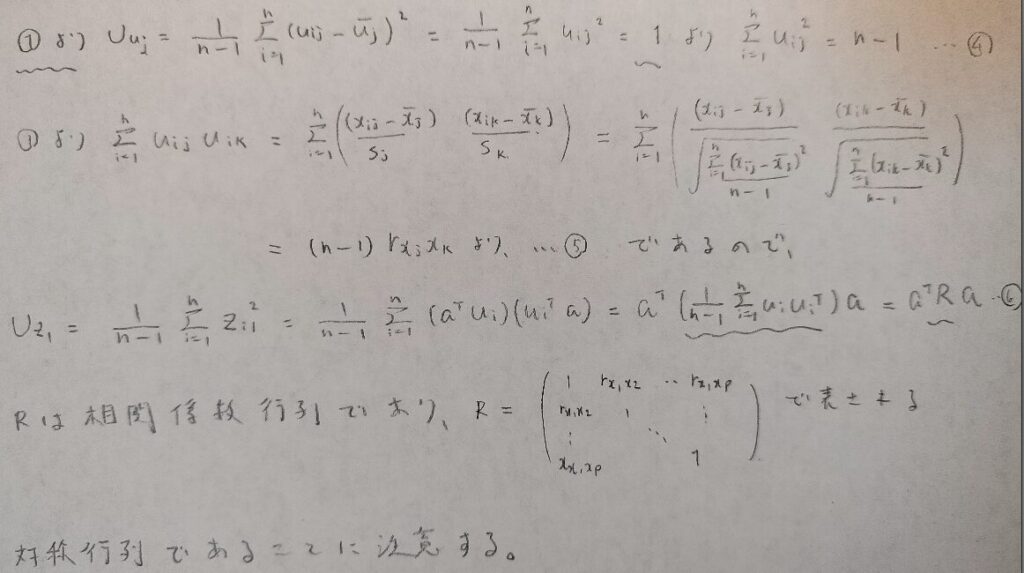
第1主成分Z1の不偏分散は相関行列を対称行列に持つ2次形式で表現されるのですね!これは驚きです。
二次形式が出てきたということは固有値問題が絡んでくることは予想できますね。
主成分分析と固有値問題
ここではラグランジュの未定乗数法を用いて固有値問題へと帰着させていきます。
ラグランジュの未定乗数法については『微分積分キャンパス・ゼミ』にわかりやすく解説されています。
この本は数学検定1級対策でも有名なシリーズで初チャレンジャーの方におすすめです!

このような感じで第1主成分の不偏分散の最大値は最大固有値(第1固有値)となり、第1主成分の係数は第1固有値に対応する固有ベクトルになります。
同様な流れで第2主成分についても議論ができます。ただし第1主成分の状況と被らないようにするために制約条件が増えますので、次の図04にてご確認ください。
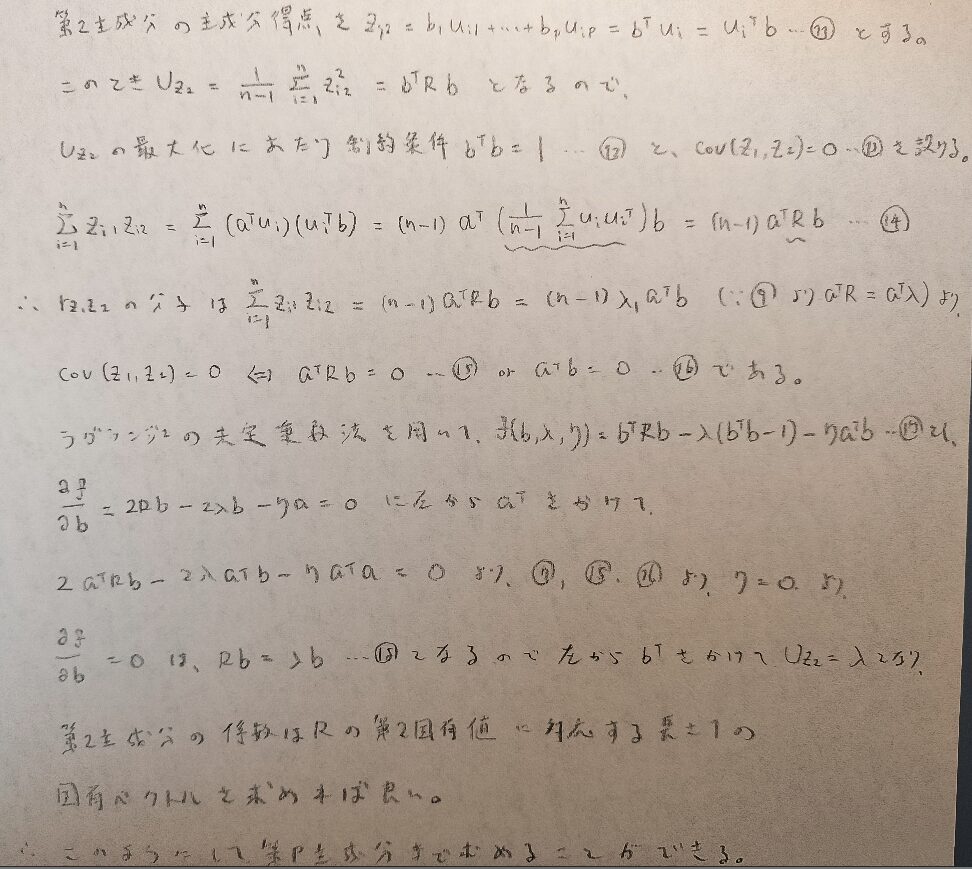
主成分分析(エクセルでも用いる)の解釈
主成分分析が行なっていることを説明します。ポイントは相関係数行列Rの近似になります。ここではまず線型代数の基本的な内容から復習します。

正定値などの概念は線型代数の入門書には載っておりません。すなわち数学検定1級の内容から見ると出題されれば難問の部類になります。つまり、大学院入試レベルということである一定以上の難易度の線型代数の書籍を参考に勉強する必要があります。具体的には『線形代数学』がおすすめです。
次にこの固有値の和の概念を主成分分析の内容に落とし込みます。すなわち寄与率の出番です。

このように主成分分析とはスペクトル分解に基づいた相関係数行列Rの近似のことなのです。これが行列表現を用いた結論になります。
主成分分析(pythonでも用いる)の寄与率について
ここからは個々の内容に焦点を当てて解説していきます。
寄与率の具体的な定義が欲しいです!
了解しました。寄与率とは各成分が全体に与えている影響力を表す指標です。

確かにこのように定義すれば納得です。
主成分の定め方は①固有値が1以上で②累積寄与率が80%を超えるという目安で設定します。
例えば記事冒頭の模試の例ではデータサンプルが与えられて主成分を求めて上の注意に従った結果、第2主成分までで良いという結果になったとします。
主成分分析(rでも用いる)の因子負荷量について
主成分分析の解釈を行うために最後に必要なものは因子負荷量です。これは各主成分と各変数の相関係数で定義されます。そして因子負荷量を求めるための公式(図08の3行目)が存在します。
図08ではこの証明を具体例を通して行なっています。用いる数式は記事前半で出てきた数式④⑤⑥辺りです。

因子負荷量には固有値と固有ベクトルの両方の情報が必要になってくるわけですね。固有値問題ってとても大事なのだと実感しました!
その通りです。では最後に主成分分析の分析の仕方をまとめます。因子負荷量と主成分得点(序盤の図01参照)の違いに注意しながら下記の内容をお読みください。
①因子負荷量や固有ベクトルから、主成分の意味を考える
→模試の例だと第1主成分が全体成績で第2主成分が文系理系の区分け
②因子負荷量を散布図にプロット(この例では第1主成分と第2主成分の2次元の散布図)し、変数の分類を行う
→模試の例だと英語、数学、理科、社会(の4変数)がどの位置(第1主成分と第2主成分の2次元の散布図内)に属するか?の判断
③各主成分の式に各サンプルのデータの値を標準化して代入し、主成分得点(模試の例では具体的な数値のこと)を求め、主成分得点の散布図(今回も第1主成分と第2主成分の2次元)を描き、サンプルの特徴付けや分類を行う。
→模試の例だと10人がどの位置(第1主成分と第2主成分の2次元の散布図内)に属するか?の判断
これらにより10人の模試の成績を4次元から2次元へと落とした客観的な解釈ができ、納得ができる解釈が行えます。今回の例では4教科という4次元量の分析が、総合的学力と文理の成績という第1主成分と第2主成分の2次元量を用いて、散布図に10名をプロットすることにより、誰が最も賢いのか?などが視覚的に表現できます。
たとえ何次元であっても低い次元に落とし込んで内容を説明できるという強力な手法が主成分分析の正体だったのですね。ここまでくると数学はとても実用的な学問の一面があると感じます。
主成分分析を初めて知った時は感動モノですよね。ただその分、内容は高度です。この記事を何回か見直して、行列表現を中心とした手法を一緒に理解していきましょう!




