区間推定はこれまで2つ学習しました。まずは正規分布の母平均と母分散の区間推定、次に指数分布の母平均の区間推定です。このうち正規分布の方は初歩的な内容で、指数分布の方は統計量の従う確率分布のところでカイ2乗分布が登場して難易度が上がりました。
指数分布の区間推定では打ち切りの関係で3パターンに分けましたよね。最尤推定量がわかれば信頼区間がわかるところが感動しました。
今回のポアソン分布の区間推定では、別の観点から2パターンに分けて考えます。
目次[非表示]
ポアソン分布の母平均の最尤推定量
ポアソン分布の母平均の区間推定を行うために、まずは母平均の点推定(多くの場合は最尤法)により最尤推定量を求めておきます。
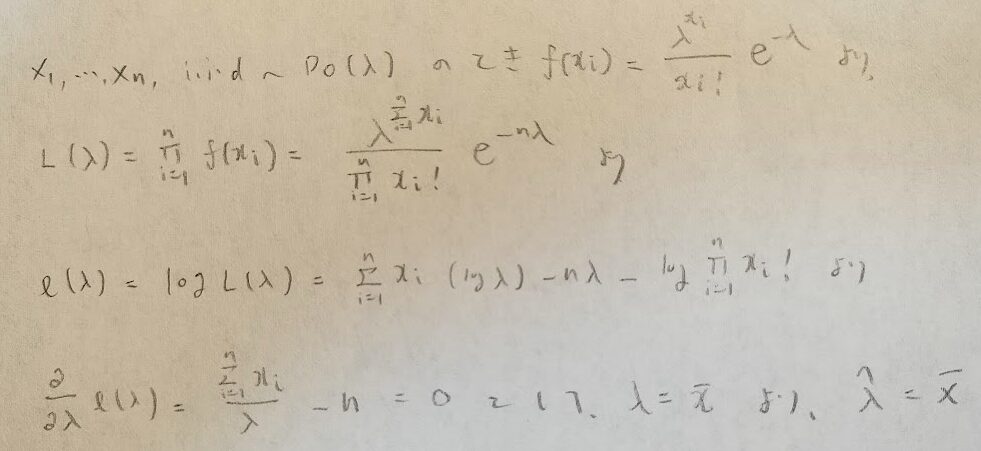
ポアソン分布の母平均の区間推定(精密法)
まずはnが少ない場合(多い場合は簡単なので後述します)の方法(精密法)から学びます。少ないとはどういうことか?については近似法のところで解説します。
概要
まずは全体的な精密法の内容から説明します。精密法の説明の前半部分のカイ2乗分布との関連性がある(1)と(2)の関係式を求めるところがポアソン分布の母平均の区間推定を行う際のポイントとなる部分です。
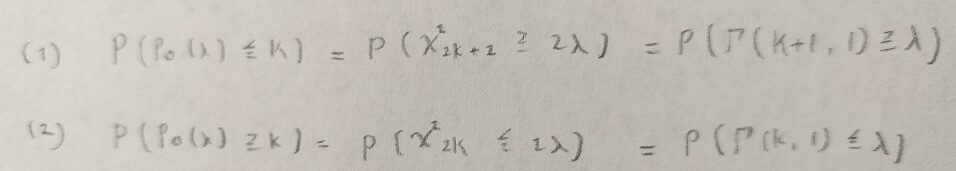
カイ2乗分布との関連性がある(1)と(2)の関係式を求めるところは区間推定の概要を説明したあとで3種類の方法を紹介します。
今回も信頼係数を1-εとしています。
それではポアソン分布の母平均の区間推定の概要をご覧ください。
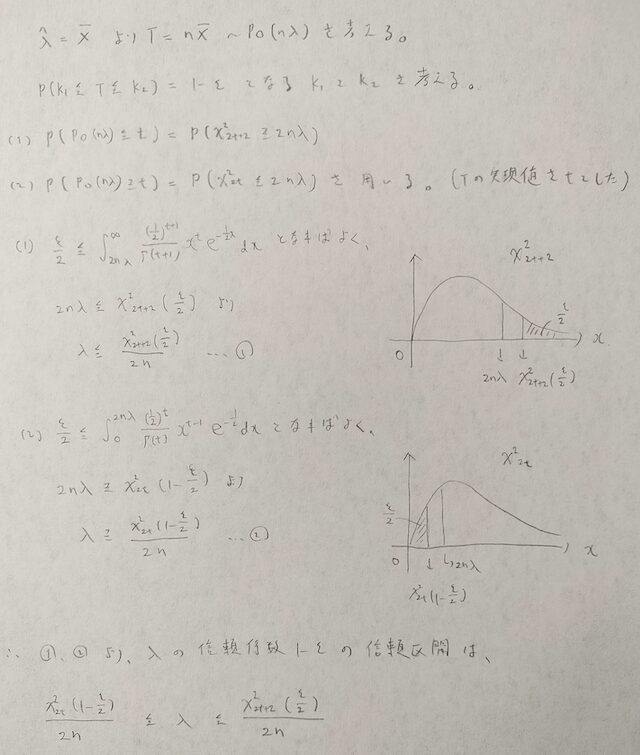
それではポアソン分布とカイ2乗分布の関係を3種類の方法で説明していきます。ご自身に合った方法が見つかれば良いですね!
ポアソン分布とカイ2乗分布の関係(ポアソン分布と指数分布の意味から求める方法)
『リスクを知るための確率・統計入門』を参考に最もスマートにポアソン分布とカイ2乗分布の関係を求める方法を紹介します。本書は他書では飛ばされがちな部分を言語化して説明してくれている部分が目立ち、内容の本質的な部分の理解にとても役立ちます。
ポアソン分布と指数分布の関係を利用します。両者の関係があやふやな方はこちらの記事から復習をお願いします!
示すべき等式(1)と(2)でそれぞれの4つ目の等式の形に注目してください。このように変形して1を作っておくことがポイントです。
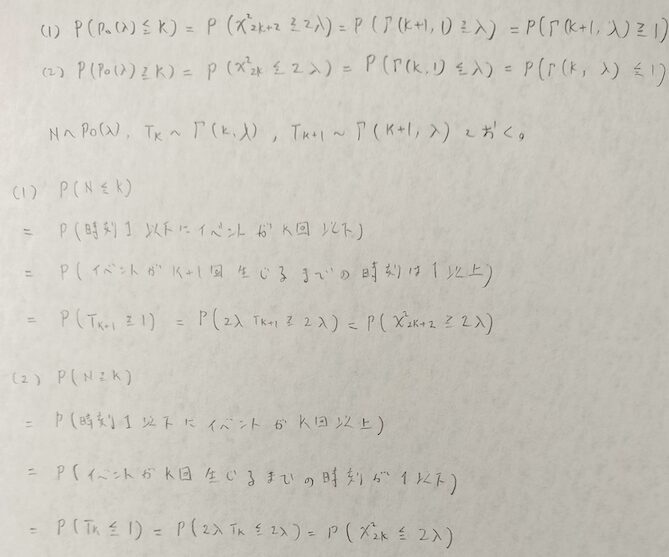
ポアソン分布とカイ2乗分布の関係(ガンマ分布の分布関数を用いる方法)
この方法では示すべき式をゴリ押しで計算していく方法です。
ガンマ分布の分布関数を知っていないとできない証明法です。ガンマ分布についてはこちらの記事をご覧ください。
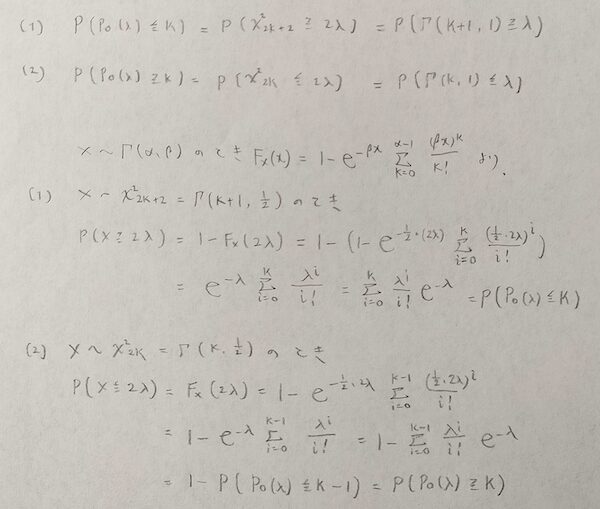
確かにこの方法では計算をしていくだけなので、そんなに頭を使うことはないですね。
ポアソン分布とカイ2乗分布の関係(置換積分を用いる方法)
3つ目の方法はもっとも有名な方法であり、アクチュアリー数学でも過去に3回出題されている内容になります。
『明解演習 数理統計』にも似たような方法が例題として紹介されていました!この本はアクチュアリー数学での統計部分に対応しています。学習の初期の段階での使用がおすすめです。また明解演習は指定教材の『確率統計演習 2 統計』が難しい方や、理解するためのサブ本としてもおすすめです。
3種類の証明内容の中でもっとも難しい内容です。(1)と(2)の証明はほとんどやっている内容は同じなので(1)を理解できればOKです。
波線部分を積分しているという理解がポイントです。
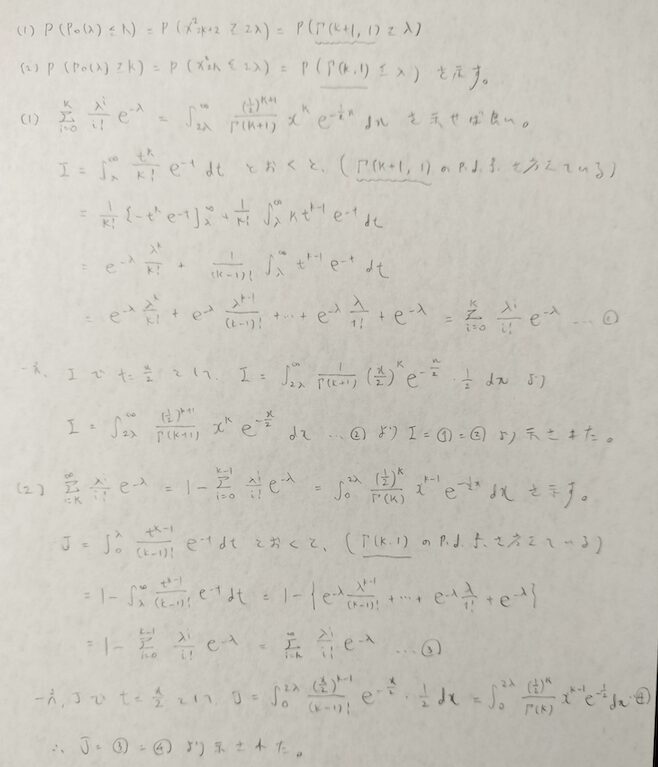
ポアソン分布の母平均の区間推定(近似法)
次にnが大きい場合に用いる近似法を用いてポアソン分布の母平均の区間推定をします。こちらの方が精密法よりも簡単です!
近似とは何に近似するのですか?
中心極限定理を覚えていますか?nが大きいときは期待値と分散が存在する同一母集団から抽出した確率分布を足し合わせたら正規分布に近似できるという内容です。つまり正規分布に近似できることを利用した方法を近似法といいます。
図07の波線部分についてこの記事の最後に考察を入れます。まずは図07をざっと追ってください。
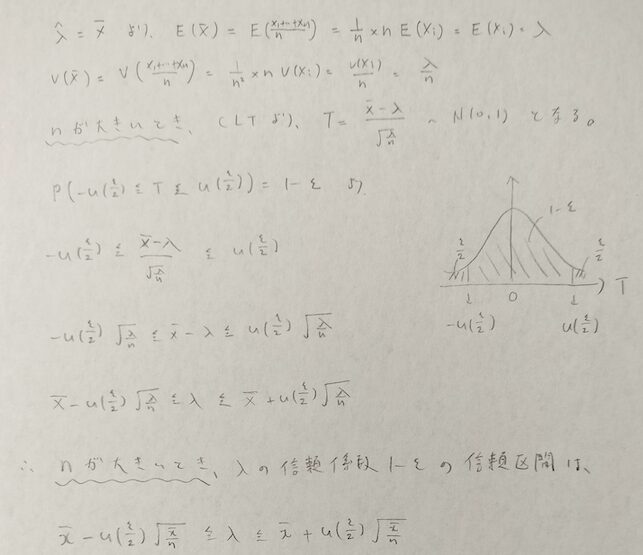
nが大きいとか小さいなどはどのような基準によるものですか?
色々な書籍を調べましたが、境目の数字についての詳しい言及はありませんでした。アクチュアリー数学試験を例にとっても、近似法を使用すべき場面で精密法で行えとの指示のある問題もあります。あくまで一例として次の図08の境目である5に注目してください。
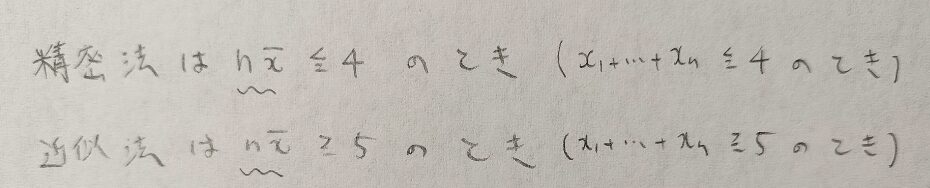
実現値の合計が4以下ならば精密法で、5以上なら近似法を用います。なぜ実現値の合計の意味合いについては次の記事である二項分布のパラメータpの区間推定のところも合わせてご覧いただくと理解が深まると思います。
ポアソン分布は事故などのポツポツと起こり得るものを対象とした分布でしたね。ポアソン分布の実現値の合計はイベントの合計(事故の合計)と考えれば、事故の数が5件以上と聞くと、事故の数が多いと考えるのは自然な気もしてきました。
ポアソン分布の精密法と近似法を使い分けるのは、(一般的に考える)標本nの数を参考にするよりも、イベント合計数を用いて自然な判断をしていきます。





