二項分布から派生する分布にポアソン分布があります。
負の二項分布だけではないのですか?
二項分布では成功回数がメインとして考えており、負の二項分布では失敗回数がメインでした。
では成功確率pを一定に保ったまま試行回数nを無限に大きくして見たとき、二項分布はどのような分布になるでしょうか。そしてその分布はどのような場面で用いるのでしょうか。
今回はマクローリン展開の知識が必要になります。やさしめの解析学の参考書『微分積分キャンパス・ゼミ』などでサラッと見てから勉強されることをおすすめします!
ポアソン分布の導出
まずは自然対数を底に持つ指数関数のマクローリン展開から始めます。
マクローリン展開って何ですか?
数学Ⅲで習った一次近似の拡張です。つまりある条件下で関数はxの多項式で表現できる定理があります。
例えば下図のようにマクローリン展開を行い、式変形をして右辺を1に調整します。
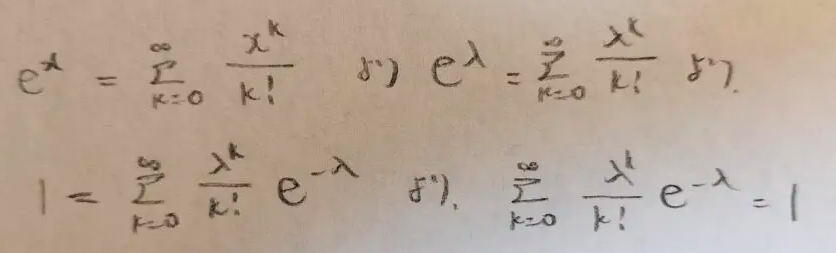
一番上の式のxに1を代入すると数学Ⅲで習った自然対数の底eの近似値が出てきますね。
e=2.71828…となりますね。
最後の式の右辺が1なので、左辺のシグマ内の式が確率変数と考えられます。この確率関数に従う確率変数Xはどのような意味を持つのでしょうか。
λ(定数)という文字を導入したので用いていきましょう。二項分布における成功確率pを一定と考えます。ただし試行回数nを無限に大きくすることを考えるので、そのうちの成功回数λは滅多に起こらないくらい小さい値になるはずです。
これらの設定を意識しながら、二項分布の極限を考えてみましょう。これをポアソンの少数法則といいます。
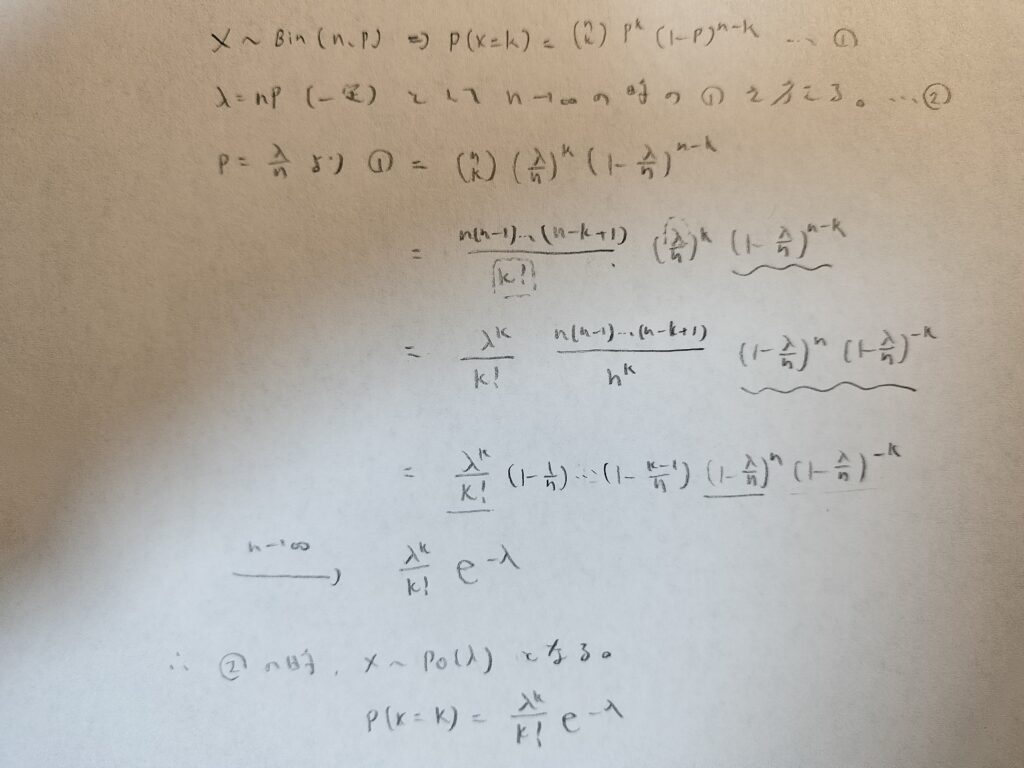
最後にマクローリン展開の知識を用いました。
うまく式変形を追っていけば一人でもサッと書けるような証明だと思いました。
ポアソン分布とは試行回数がとても大きい中で滅多に起こらない試行を考えるときに用いる分布です。ポアソン分布の具体例は年間の交通事故の件数など、滅多に起こってはいけない状況を考える際に用います。
ポアソン分布の期待値と分散を計算を通して導出します
ポアソン分布の期待値と分散を導出するためには次の3つの方法のいずれかを選びます。
①確率母関数などの母関数を求めてから微分する方法で『現代数理統計学』がこちらを採用しています。
②確率和1の式を変形して求める方法→本記事ではこちらを扱います。
③定義に従ってシグマ計算をする方法
母関数についての初歩は『確率統計キャンパス・ゼミ』がとても詳しく書かれていて分かり易かったです!
では②の方法でかなりテクニカルに証明を行います。出典は『データ解析のための数理統計入門』になります。
証明の流れは確率和1の式を変形する
→両辺をλで微分して期待値の定義式に合わせるために両辺に定数を掛ける。
→次にX(X-1)の期待値を同じ方法で導出して分散の公式を用いて分散を求める。
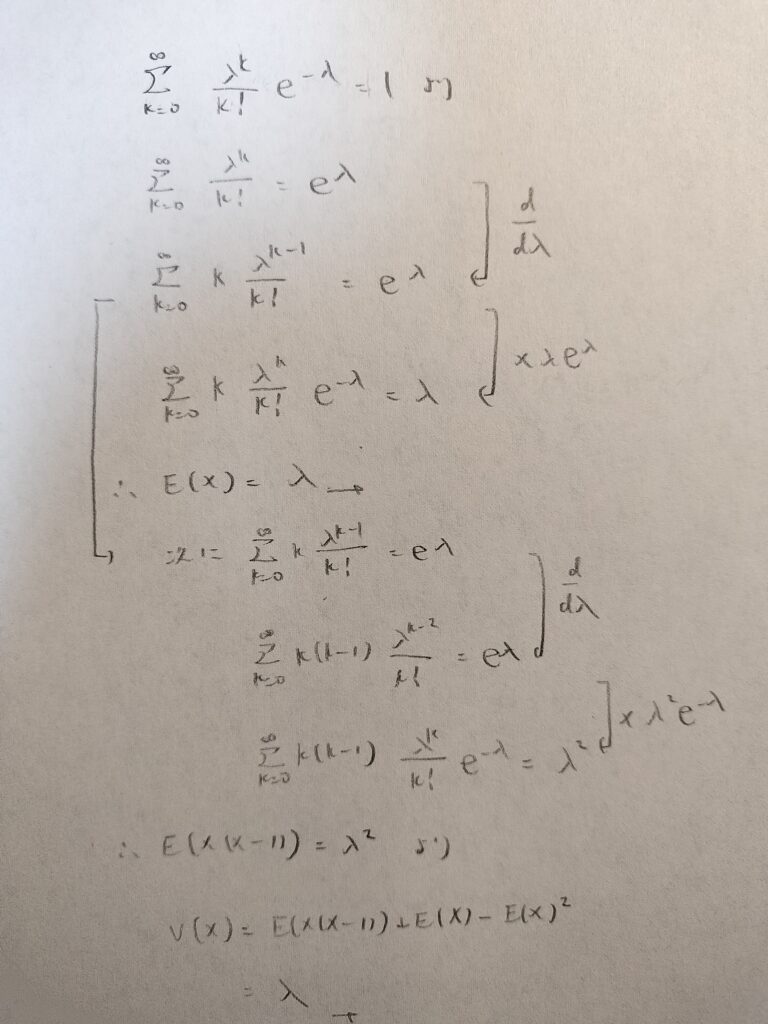
すごくシンプルで美しい証明だと思います!
そうですよね。『データ解析のための数理統計入門』の著者の久保川先生のわかりやすさが伝わってきますよね。
ポアソン分布は世の中で結構使われてそうですね!
ポアソン分布はイベントが起きる回数が従う確率分布です。回数は離散量なので離散型の確率分布になります。
対してイベントの時間が従う確率分布は指数分布を考えます。時間は連続量なので連続型の確率分布になります。
ポアソン分布と指数分布は表裏一体の関係です。今後の記事にて指数分布を紹介します。
ポアソン分布は二項分布とも指数分布とも関係がある友達が多い分布だったのですね!
最後に本記事にて参考にした参考書を紹介します。
ポアソン分布関連の話題では、マクローリン展開についてとても分かりやすく書かれています。関数を多項式で表すという衝撃を味わった本として思い入れがある本です。数学検定1級の微分積分の範囲に対応しています。
ポアソン分布では期待値と分散を鮮やかに求める手法を提供しています。他の本では見られない証明なども多く必見です。統計検定1級の新しいバイブルになると確信しています。
昔からある有名な本です。ポアソン分布関連の証明はオーソドックスなもので書かれています。統計検定1級のレベルを上回る内容で、難しい内容が多い本格派の教科書です。
数学検定1級の2次のレベルにも対応する数理統計学の入門書です。僕がこれを購入したのは中学生の頃でしたが、1から分かりやすく書かれているので理解はし易かったです。ポアソン分布関連では積率母関数関連の話題も書かれておりました。数のある本の中でも「母関数って便利ですよね!」を体感できる名著です。






