統計検定1級で偏相関係数を間接的に出させる問題が出ています。この偏相関係数を解説している書籍は少なく、お手上げ状態の方もいらっしゃると思います。
私も困っていました。公式も覚えにくいし、どうやってあの式が出てきたのかも分からないので、その問題は飛ばしてしまいました。
ここでは相関係数の内容を発展させた偏相関係数の話題や、さらにその内容に関連するパス解析という多変量解析の手法を解説します。永田先生の『多変量解析法入門』はとてもおすすめですので紹介しておきますね!
重回帰分析における標準偏回帰係数の重要性
パス解析でメインとなるのは回帰係数の標準化という考えです。順に説明していきます。
重回帰分析では各変数の偏回帰係数の大小を比べることには意味はありません。
それはなぜでしょうか?
それは各変数では単位が異なりますし、単位が変換されればそれに伴って偏回帰係数も変化するからです。
具体的にどのように偏回帰係数が変化するかを具体例を通して見ていきましょう。
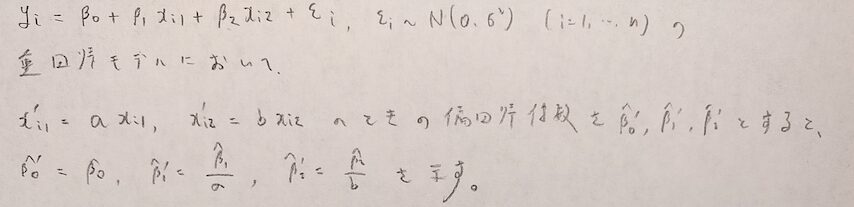
それではこの事実を証明します。
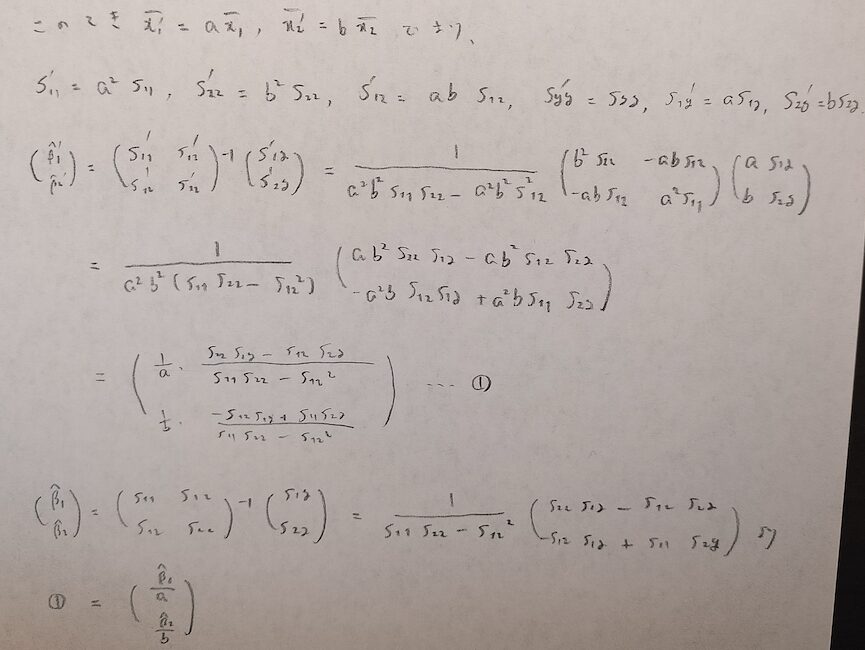
重回帰分析では各変数を標準化してから得た偏回帰係数(標準偏回帰係数)について大小を比べることに意味があります。
この標準偏回帰係数と偏回帰係数の間の関係を調べましょう。

それでは図03の①式から予測式を立てて先に進みます。
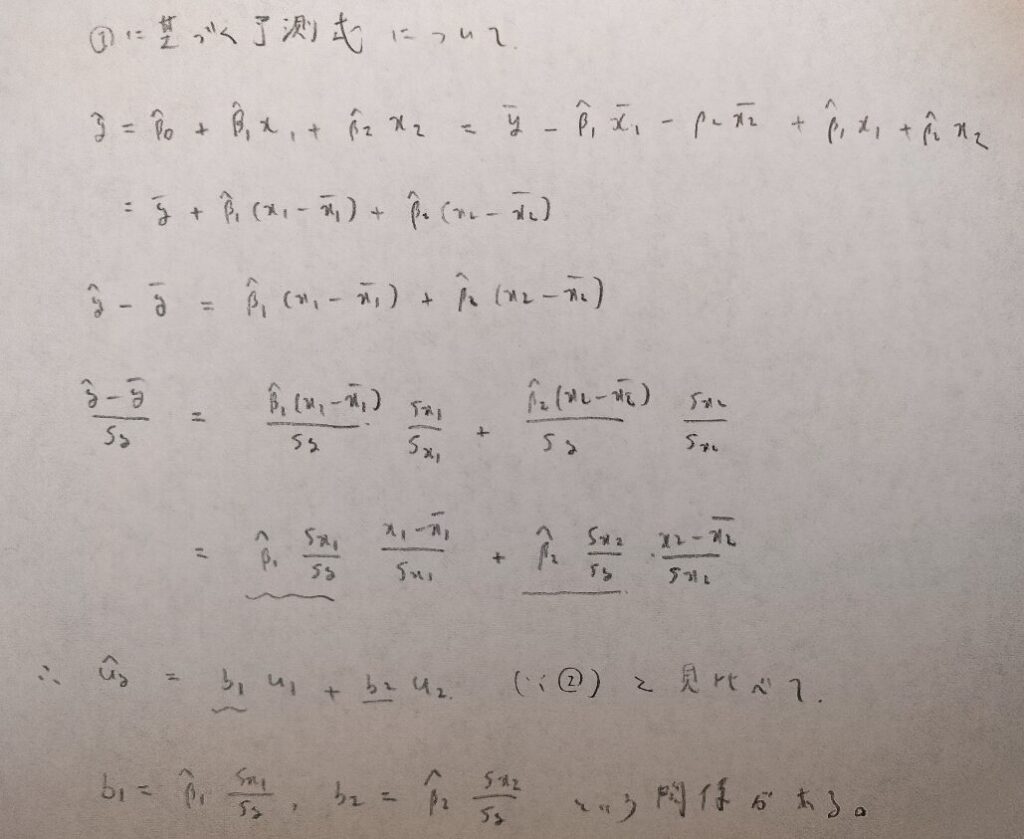
標準偏回帰係数では定数項が0になることが大事ですので覚えておきましょう。
(標本)偏相関係数の意味と導出法
まずは偏相関係数についてのツイートを紹介します。偏相関係数とは一体どういう問題から生じたのか?そしてどうやって偏相関係数の式を導くかを書いています。
基本的に標本偏相関係数と偏相関係数の証明は本質的に同じです。ここでは偏相関係数の証明として解説します。

それでは偏相関係数の式を計算で示してみましょう。ここでは残差の意味が大事です。残差とはzの影響を取り除いたxやyの変動部分を表すため、各残差の相関係数を考えれば良いという流れになっています。

それでは実際に相関係数を求めていきます。計算量が多くなりますので順に説明します。
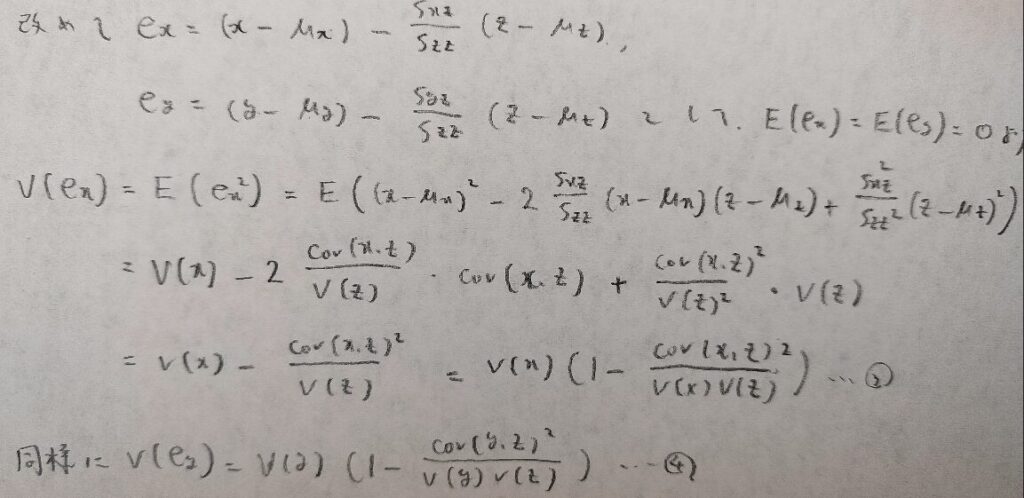
図07は相関係数の分母に相当する部分でしたので、次に相関係数の分子に当たる部分を計算します。
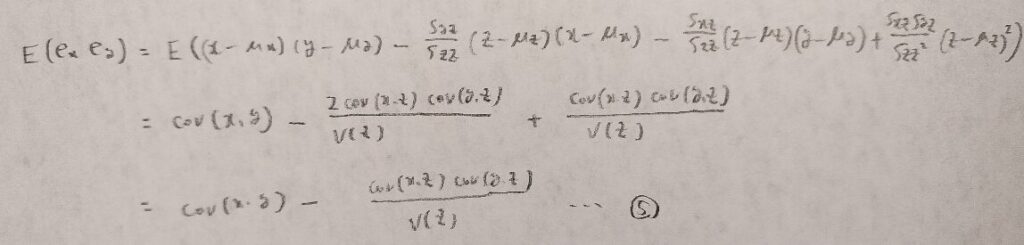
準備が整ったので、偏相関係数の値を一気に出していきます。
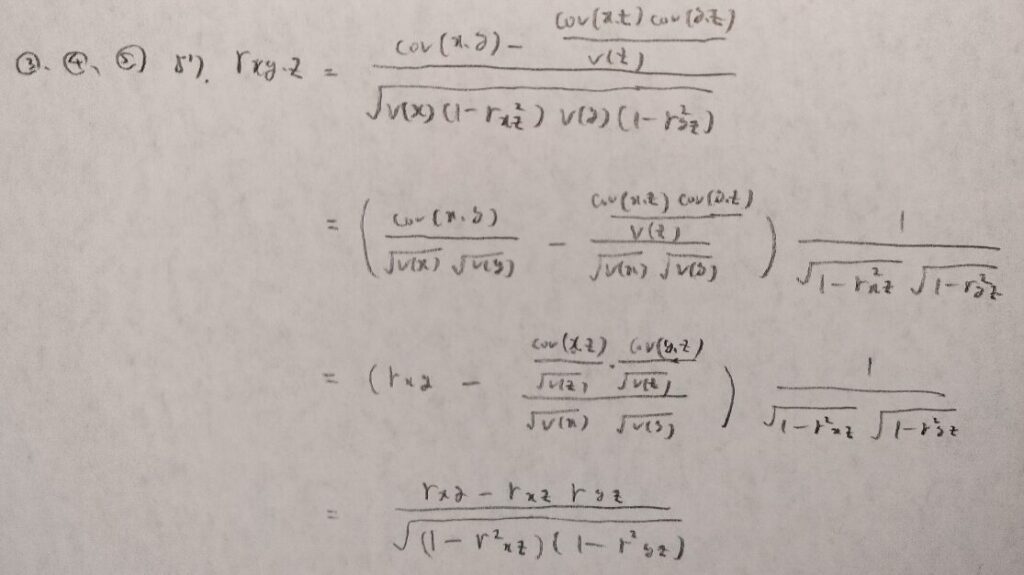
1つ1つ確認しながら計算すれば何とかできそうですね!
パス解析は変数間の関係を道のように示したパスダイヤグラムを用います
いよいよパス解析を紹介します。例を簡単にするため4つなどではなく3つの変数で考えます。
図10は3つの変数間の関係を表したパスダイヤグラムといいます。αはパス係数と呼ばれるもので、重回帰分析における偏回帰係数と同じ意味です。
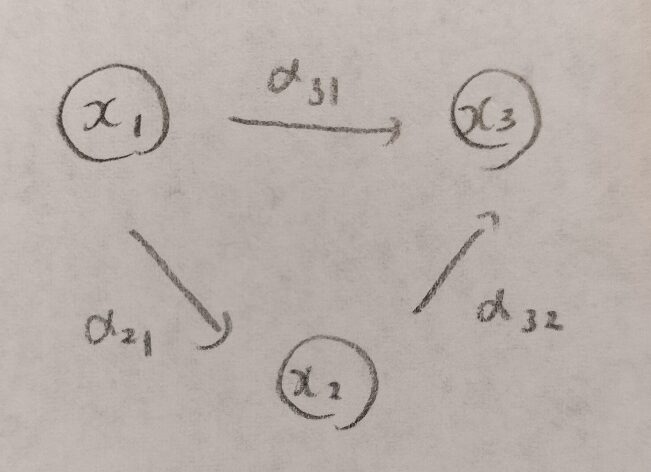
パス解析は変数間をパス係数を設けることによって自由に設定できることから、重回帰分析の発展版と考えることもできます。
パス係数の番号の順番はベクトルの始点と終点と同じ考え方ですね。右の数字から左の数字へと進んでいくという感じですね!
その通りです。それでは各変数間の母相関係数を考えていきます。
図11の①式や②式を線形構造方程式と呼びます。
各変数が標準化されていることにご注意ください。その理由は重回帰分析における定数項をなくすためです。
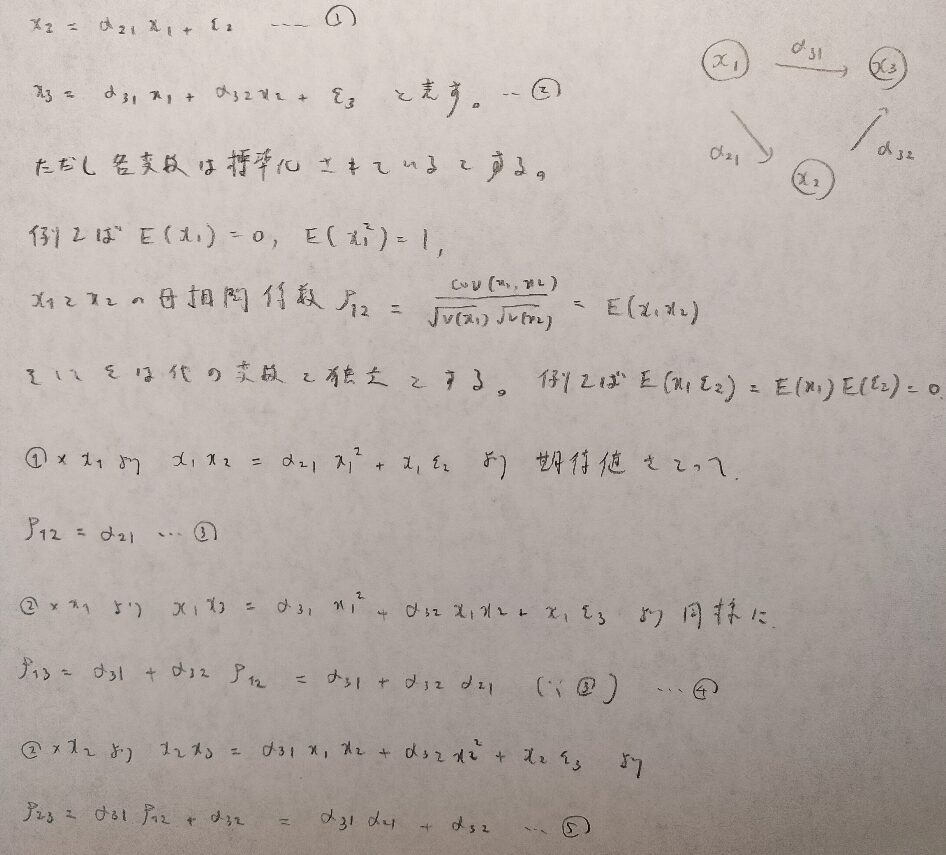
変数が4つでも5つでも、相関係数はとあるものの足し算で表現されていることに気づきましたか?ヒントはパス係数の意味についてです。
図11の③式では1から2へと直接進むパス(道)のことを言っていますね。④では第2項が1→2→3と間接的に2を通っていますが1から3へと進んでいますね。
そんな感じです。変数間の関係を道(パス)で表現しているからパス解析と呼ばれているのですね。
それでは相関係数は直接進む道と間接的に進道の和で表されるのでしょうか?

実はもう1つ擬似相関と呼ばれるものが足されます。
あれ?これって偏相関係数で出てきた考えですね。
その通りです。パス解析を行うと相関係数はそう単純にものではないとお分かりいただけたと思います。

相関係数=直接効果+間接効果+擬似相関
なるほど。擬似相関に対して、効果同士の和を総合効果と呼ぶのですね。今日も面白かったです!ありがとうございました。


