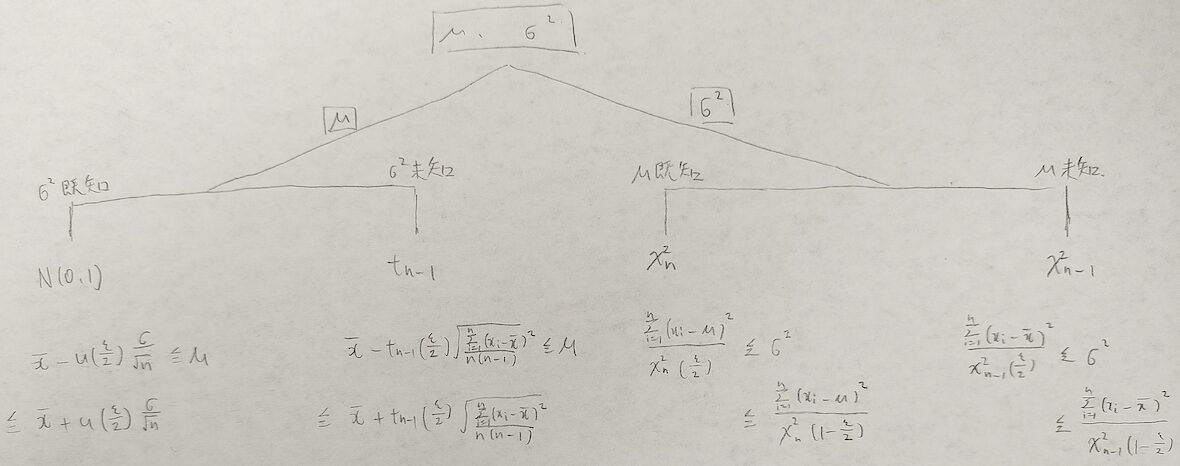
今回は2つの母集団について扱います。3つ以上の母集団については分散分析の話になり難易度が上がるため、また後日に取り上げていこうと思います。
今回はどのようなことを調べていくのですか?
2つの母集団の母平均の差の区間推定を行います。そのときの区間推定の手法は複数あり、どのような時にどの手法を用いるか?に関して場合分けが生じます。
母分散が等分散か?に関する判断で検定という考えが出てきますので、本記事から検定の話題も取り入れていきます。
信頼係数は一貫して1-εとします。これは検定での応用を考えたときに便利な表現だからです。
母平均の差の区間推定(母分散が既知の場合)
区間推定を行うための手順を復習しておきます。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
まずは母平均の差の区間推定では最も単純な場合を考えます。それは母分散が既知の場合です。
それはなぜですか?
中心極限定理をすぐに使える形だからです。今回は母平均の差の区間推定を行いたいので、図01の序盤のように母平均の差の最尤推定量を求めることを考えます。母分散が既知でも未知でも、母平均の最尤推定量は標本平均になるイメージを持つと、最終結果は予想しやすいです。
この最尤推定量の出し方については次の章にて解説します。それでは図01をご覧ください。

母平均の差の区間推定(母分散が未知だが等分散の場合)
母平均の差の最尤推定量と母分散の不偏推定量
今度は母分散が未知の場合を扱います。区間推定のためにまずは母平均の差についての推定量(これは最尤推定量とは限らない)を求めていくことになります。
この時って前に似た話題を勉強しましたね。正規分布を例にとって4つに場合分けして内容を整理した覚えがあります。
今回は母分散が未知なので、母分散の推定値は不偏分散になると予想ができます。
それでは図02をご覧ください。
母平均の差は定数となるので、その値をδとおいています。そのため尤度関数はδと母集団Yの母平均を変数にとっています。この方法は『確率統計演習 2 統計』を参考にしました。
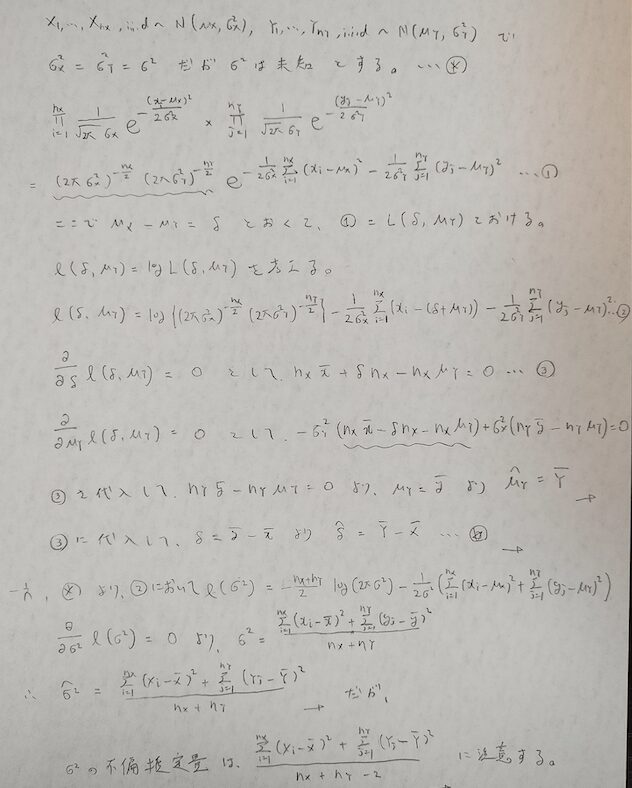
結局予想していた通りになっていますね。
先ほどの母分散が既知の場合の母平均の差の最尤推定量については、図02の流れで母分散をそのまま代入すれば、今回と同じ結果が得られます。
母分散の推定量を不偏分散にする理由は実際の区間推定の流れを説明する際に、また解説します。
この不偏分散の分母に-2とついていますが、本当にこの結果が不偏推定量なのか不安なので証明をお願いします。
了解しました。下準備としてカイ2乗分布に従う統計量の復習をお願いします!
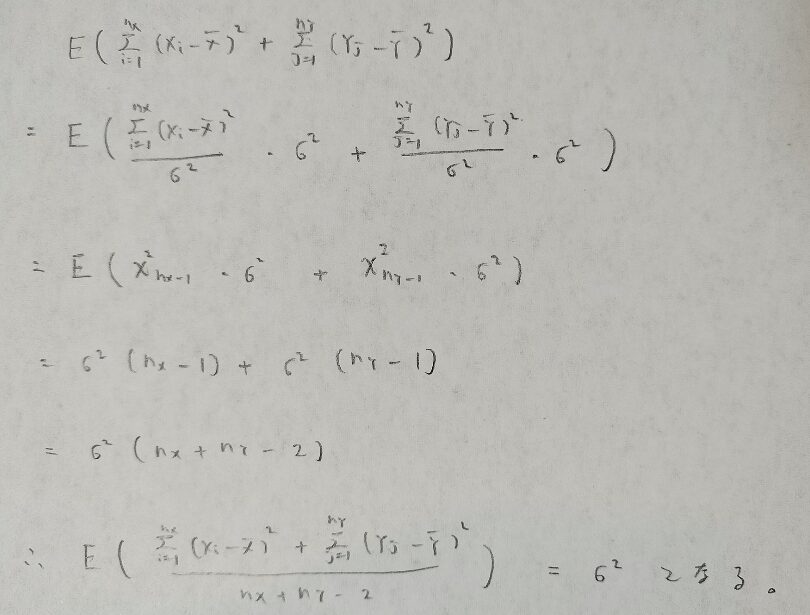
母平均の差の区間推定(母分散が未知だが等分散の場合)の解説
それでは準備が済んだので、いよいよ区間推定に移ります。
t分布に従う統計量を作り出す(スチューデント化)を行います。とても技巧的ですので、t分布についての記事をお読みでない方は、まずはこちらをお読みください。

私にはかなり複雑に感じましたが、それでもうまくいったのは、母分散が等分散だからですよね?
その通りです。もしも母分散が等分散と言えないときは、かなりお手上げ状態になります。ここで2つの問題点が生じます。
1.母分散が等分散かどうかの判定はどのように行うのか?
2.母分散が未知で、しかも等分散ではないときに、母平均の区間推定はどのように行なうのか?
『確率統計演習 2 統計』には数多くの推定や検定が収録されています。これらの種類はとても多いですが、本書に収録されているのはアクチュアリー数学での範囲内での推定や検定に限られます。それでも実用には十分な量となっています。
母分散の比の区間推定とF検定(等分散の検定)
母分散の比の区間推定
今までの記事では区間推定をメインにしていたため、検定の話は控えていました。しかし今回はどうしてもF検定が必要になるので、初めての検定としてF検定を紹介します。
F検定に進む前に、まずは母分散の比の区間推定を行います。
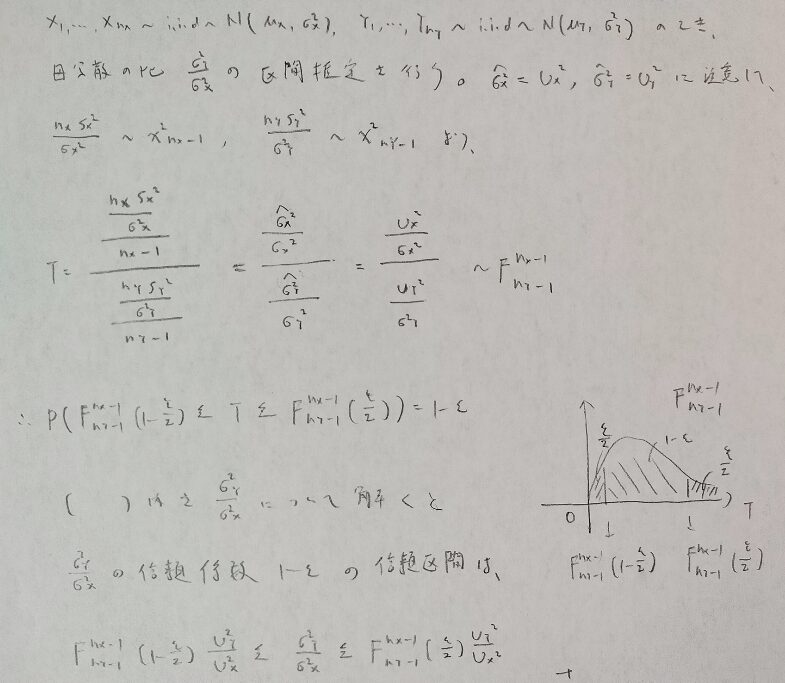
理論面ではこれで問題ないですが、F分布表には一般に下側ε点が載っていません。このことが次に登場するF検定(ここでは等分散検定)で大事な意味を持ちます。(『確率統計演習 2 統計』を参考)
エクセルでも使われるF検定(等分散の検定)
ここでは検定の流れを説明します。
「ありそうもないことが起こった時は仮説を疑う」これが検定の基本的な考え方です。(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
後から疑うと思われる仮説を帰無仮説といい、それに反する仮説を対立仮説と言います。ありそうもないことがどれくらいの確率か?を判断するときの確率を有意水準といいます。有意水準は通常εで表現します。「ありそうもないことが起こった時」の確率がε以下のときに、帰無仮説を疑い取り消します。そのことを帰無仮説を棄却するといいます。反対に「ありそうもないことが起こった時」の確率がεを上回ったときは、帰無仮説を受容すると表現します。
帰無仮説を棄却する(棄却域を求めていく)ことは、具体的にどのような基準で行われていくのでしょうか。図06をご覧ください。一緒に考えていきましょう。図06の上から3行目に登場する統計量を、検定統計量といいます。今回はF統計量といいます。F統計量の値がどの値に収まるか?で帰無仮説を棄却するかの判断を行います。
母分散の推定量として不偏分散を用いているのはF分布の定義に当てはめていくためですね。
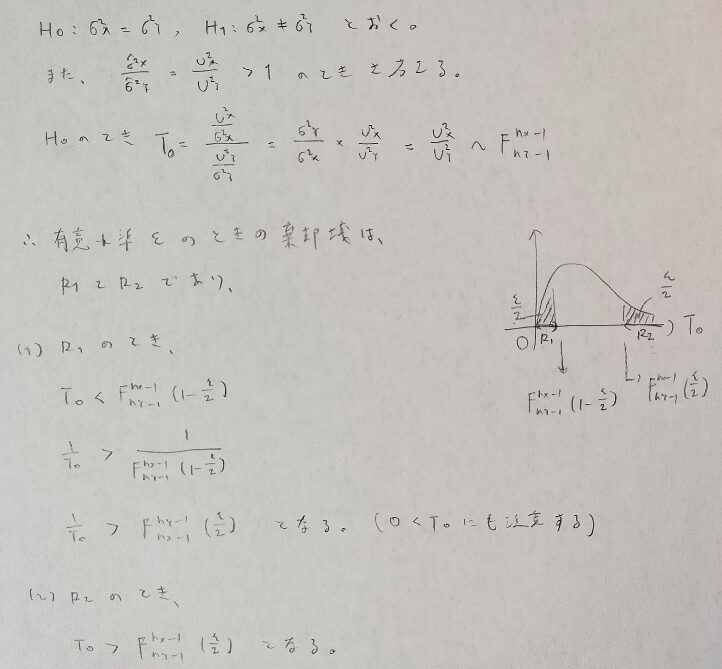
左側の棄却域で、このように変形する理由はF分布表に下側ε点がないことが多いからなのですね。
その通りです。そのためF検定を行う際は、F統計量の値において分子と分母の値がどちらが大きいか?を意識していくことになります。統一のために分子の方を大きいとします。理論面ではなく、実用性を考えた結果なのです。
母平均の差の区間推定(母分散が未知で等分散でない場合)
いよいよウェルチの検定(区間推定のことをウェルチの方法といいます)関連の話になります。非常に難しいですが、一緒に頑張りましょう。
母分散が未知で、しかも等分散でない状況のときに、母平均の差の区間推定をどのようにするか?を勉強します。この内容は多くの参考書には非掲載です。そのためアクチュアリー数学の過去問『2017年度の大問3』を参考に区間推定の流れを構築しました。

まずは母平均の差の推定量を考えます。今回も母分散が未知なので不偏推定量を取ります。計算方法は図02をご参照ください。
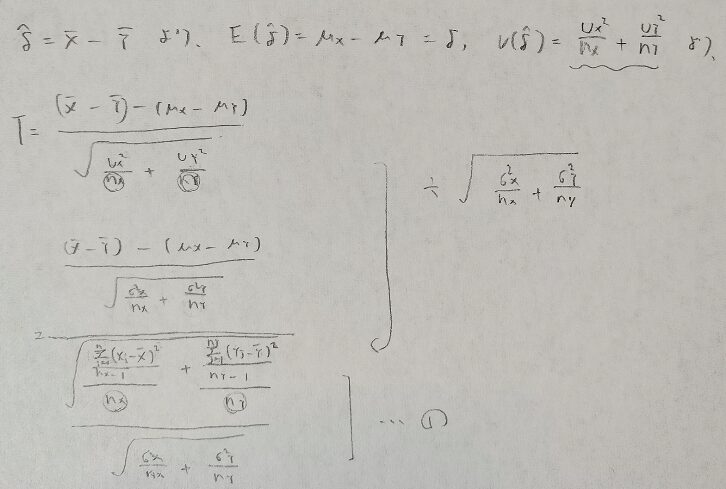
今回も統計量Tが従う分布を考えたいので、スチューデント化を試みます。
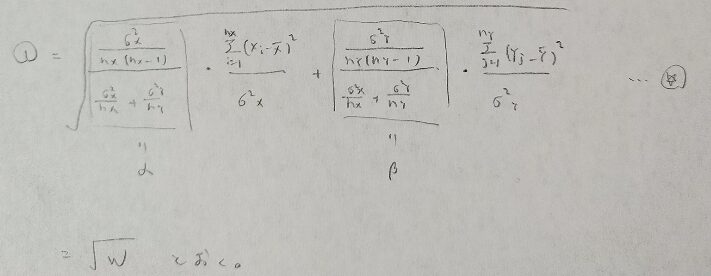
このように統計量Wを設定しておきます。
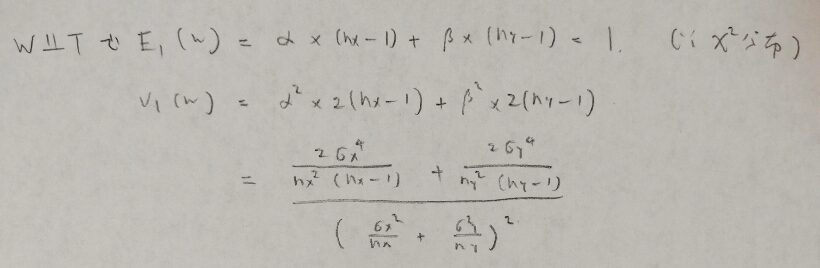
図09の☆の形からカイ2乗分布が出てくるとわかるので、素直に式変形をしていきます。しかしこのままではt分布の自由度が出てきませんので、次のように工夫していきます。
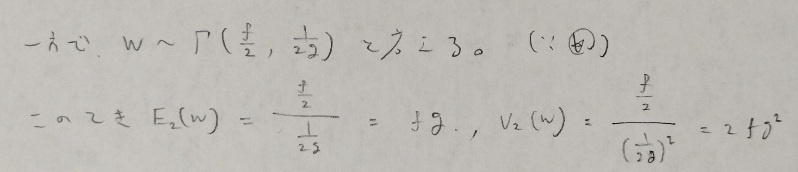
このWの従う分布の形からカイ2乗分布が作れれば、統計量Tが従うt分布の自由度が判明することになります。
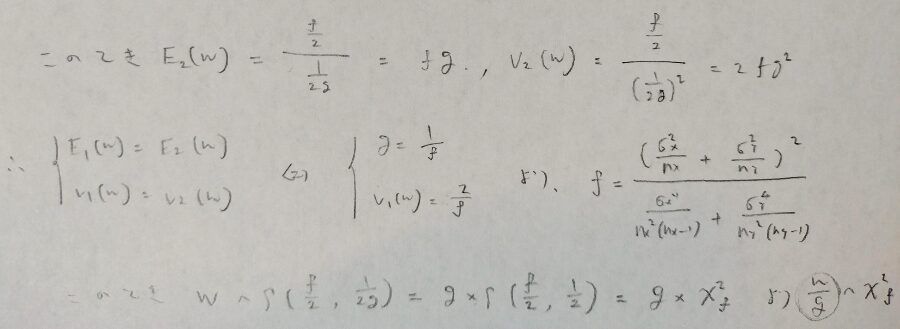
ここまで来ればもうすぐおしまいです!
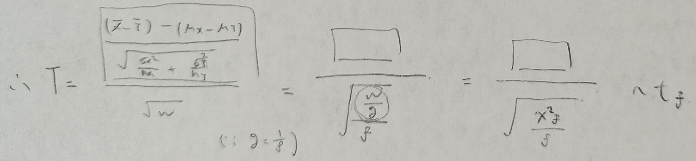
t分布の自由度fはどのように計算するのですか?図12の結果だと母分散がわからないので、詰んでしまう気がします。
大丈夫です。対応する推定量(不偏分散)を代入すればOKです。

では結論を書きます。アクチュアリー数学ではこちらを公式として使用すると使いやすいのでおすすめです。
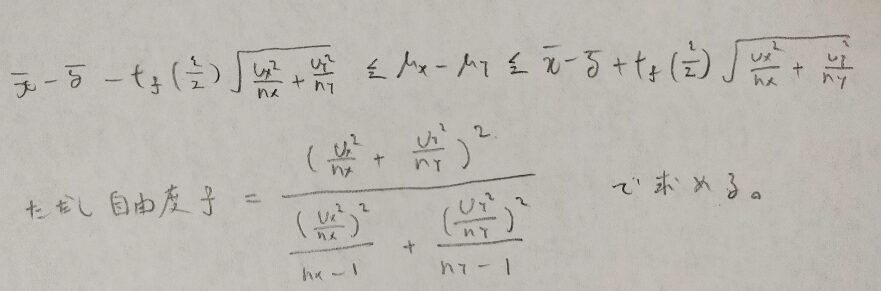
ウェルチの方法を検定に応用するとウェルチの検定になるのですね!
その通りです!とても難しい流れでしたが、何度も繰り返し学習して力をつけていきましょう。