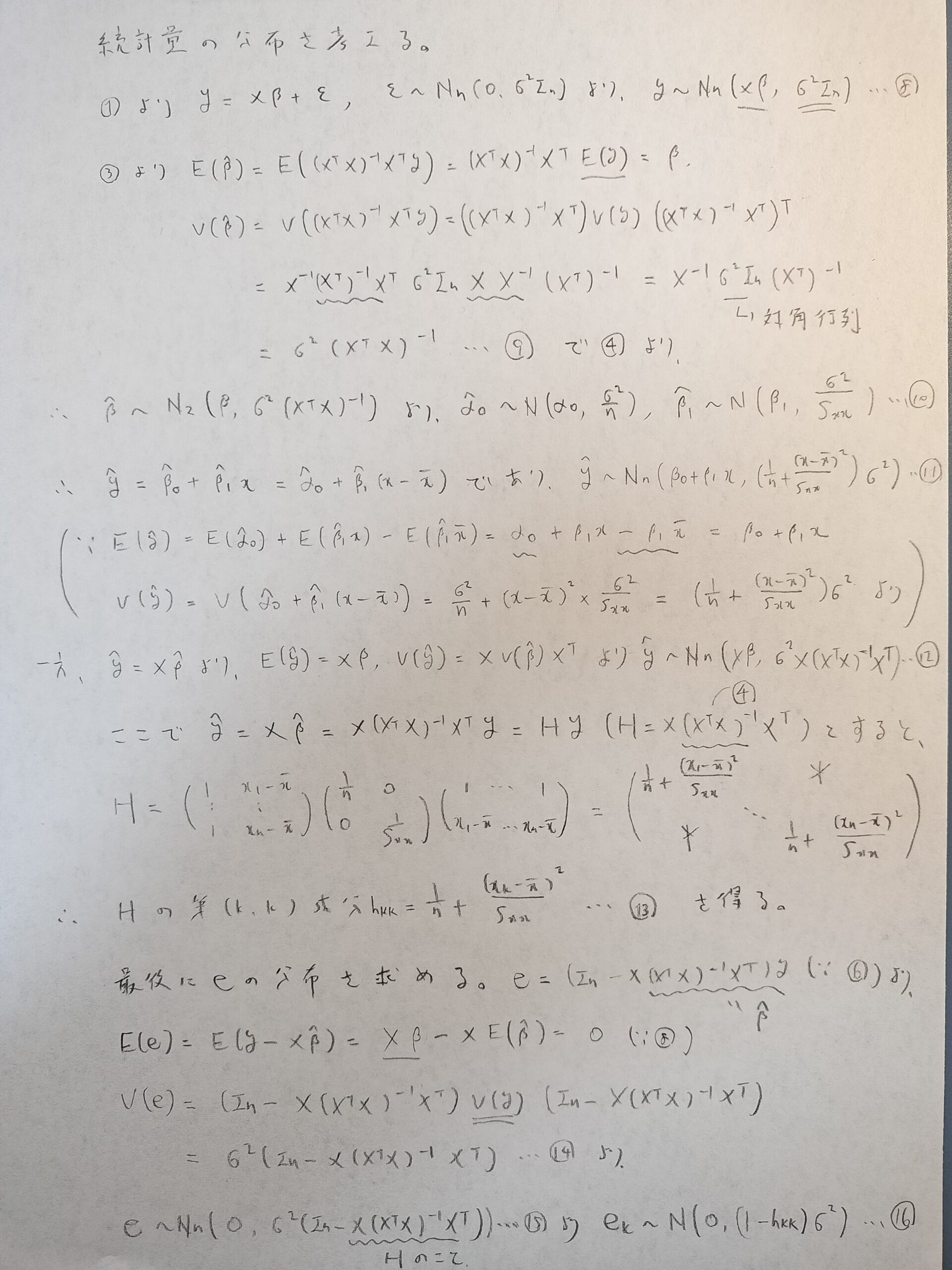前回の記事で単回帰分析を詳しく解説しましたので、今回は重回帰分析になります。とても難しいのですが、多変量解析の中では2番目に登場する内容です。単回帰分析よりも精密な分析が可能です。
重回帰分析は便利そうなのは伝わりました。では、どのように難しいのですか?
重回帰分析は重回帰モデルを行列表示して進めていくと、ほとんどが単回帰分析のときと変わらないとお気づきになると思います。しかし、テコ比などの具体的な計算となると、単回帰分析とは計算量が大きく異なり難易度が増します。
本記事では重回帰分析の内容をほぼすべて消化すべき、重回帰モデルの行列表示してからさまざまな内容を行列表示(『多変量解析法入門』参考)していきます。その後に、行列表示では説明しきれない部分を解説していきます。
重回帰分析の内容のほとんどは単回帰分析と被っています。単回帰分析を未習の方は前回の記事を一読されることをおすすめします。
重回帰分析(英語は multiple regression analysis)の行列表現
まずは行列表示を行いますので、正規分布ではなく、多変量正規分布が登場することにお気をつけください。それ以外の部分は単回帰分析のときとほとんど変わりません。
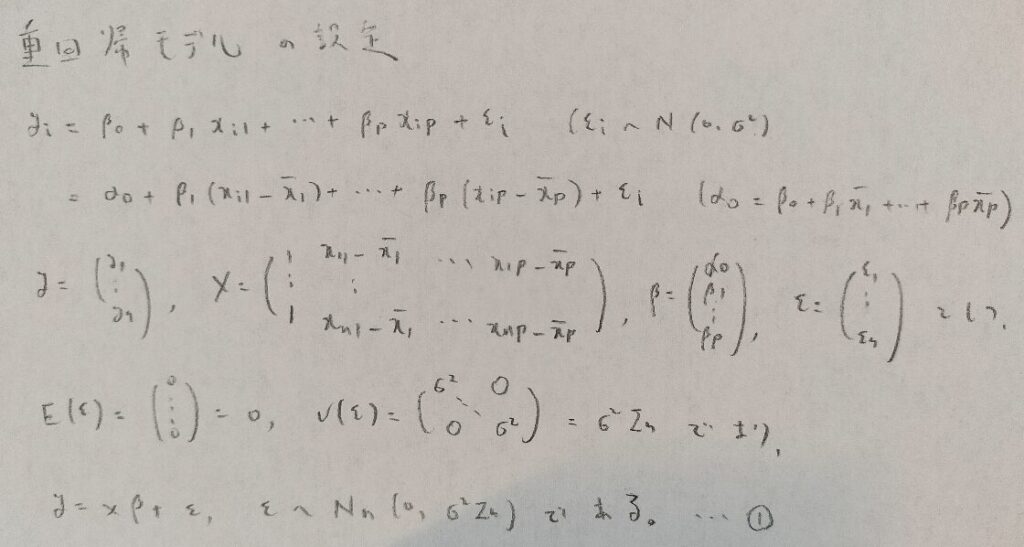
次に最小2乗法を用いていきます。この推定結果は記事の後半で再登場します。
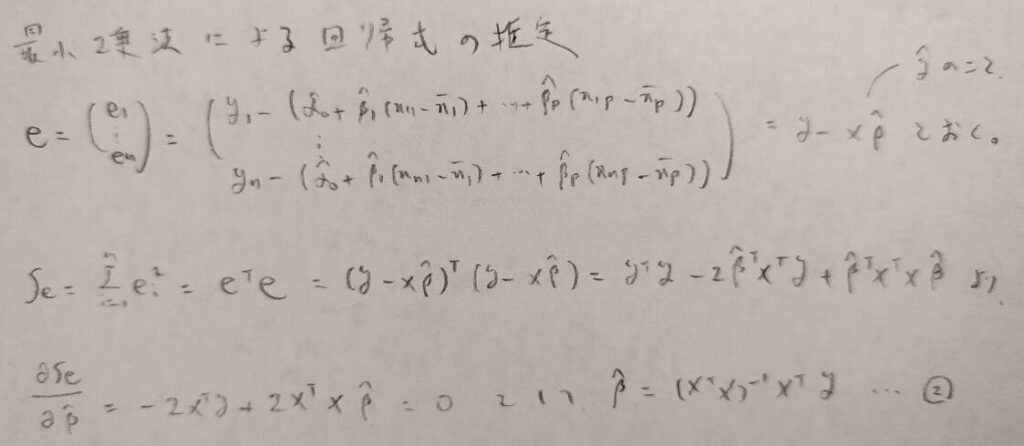
次に単回帰分析のときと同様に、各統計量の分布を求めていきます。ここで登場するテコ比関連の内容が最も難しいです。

重回帰分析(エクセルでも用いる)の偏回帰係数の推定値と多重線形性
それではここからは行列を全面的に出した解説では限界を感じたため、素直に式変形を行いながら、重回帰分析の内容を深掘りしていきます。
まずは多重共線性の内容まで一気に学びます。「変数を増やしはしたが、増やさなくても良かった」つまりある変数が他の変数によって表される場合に、多重共線性を持つといいます。
重回帰分析では、どの変数を用いていくか?が大事になっていきそうですね。
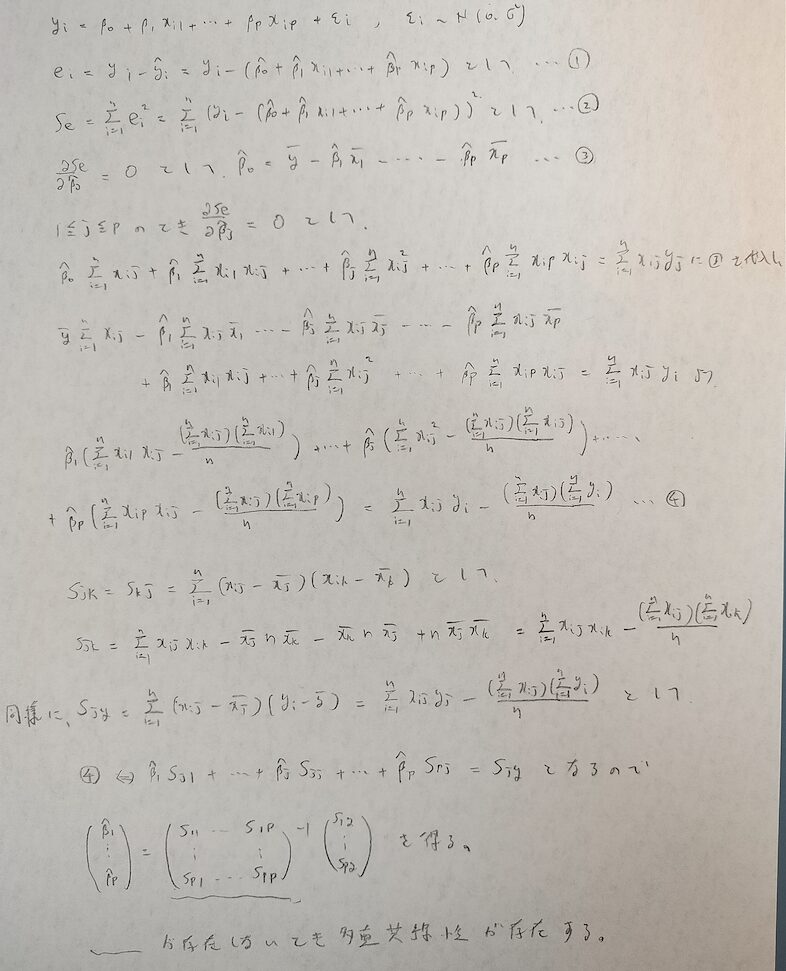
最後の方に登場するS記号を大事にしてください。Syyは全平方和のことですが、それ以外は図04で定義した意味を持ちます。
重回帰分析の残差平方和と平方和の分解の書き方
次に図04の最後の式で定まる各βの推定量を用いて、残差平方和を出してみます。その際に全平方和が登場することにご注目ください。
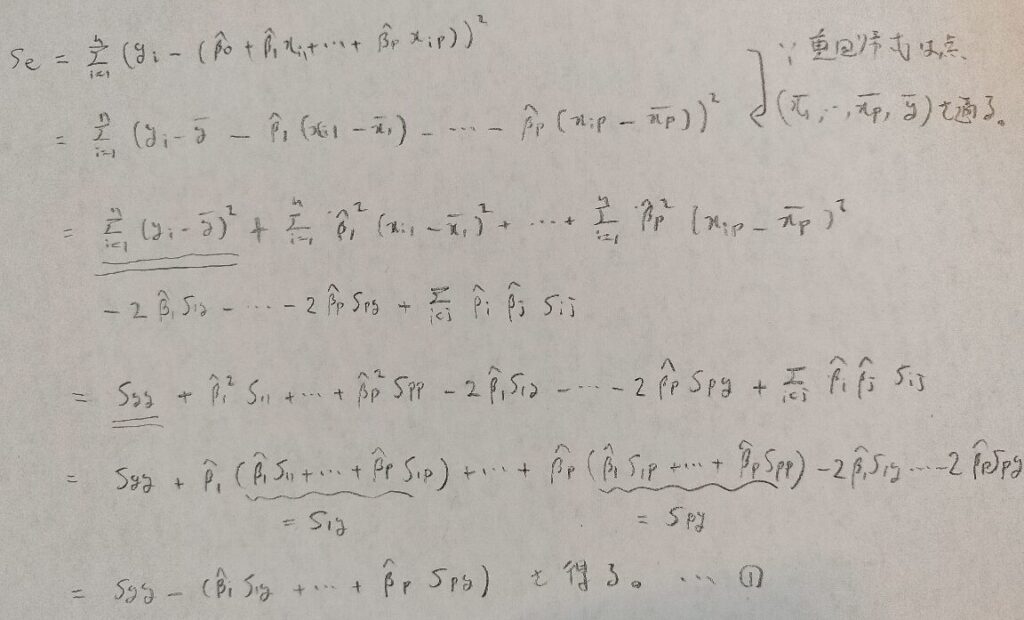
次に残差平方和の値と自由度を用いて母分散の推定値を出します。ここも単回帰分析のときと同じ内容です。
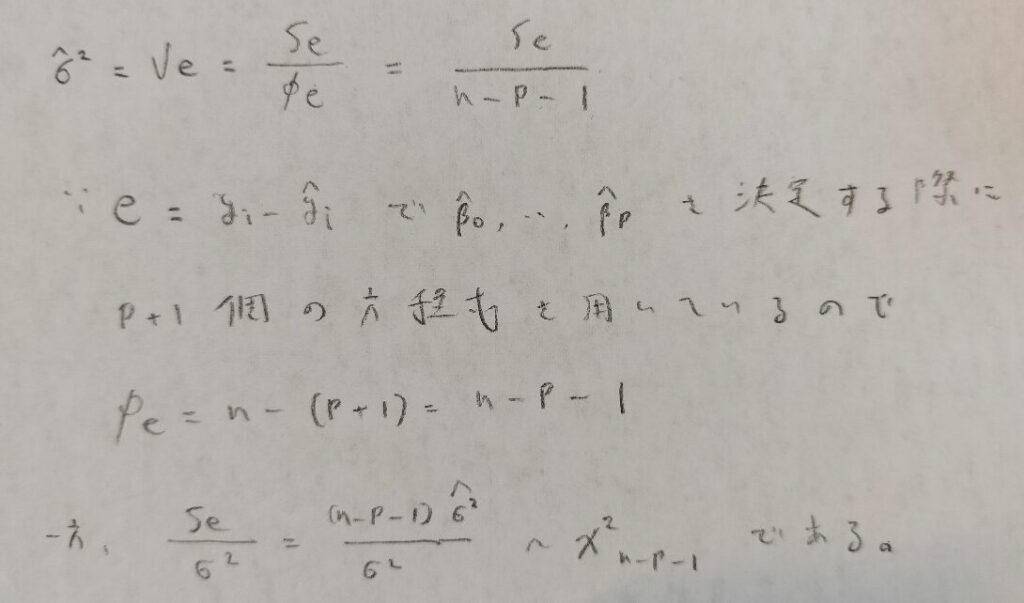
次に平方和の分解にいきます。
単回帰分析とほぼ同じですが、残差平方和の自由度が異なります。そのため回帰変動の自由度も異なってきます。
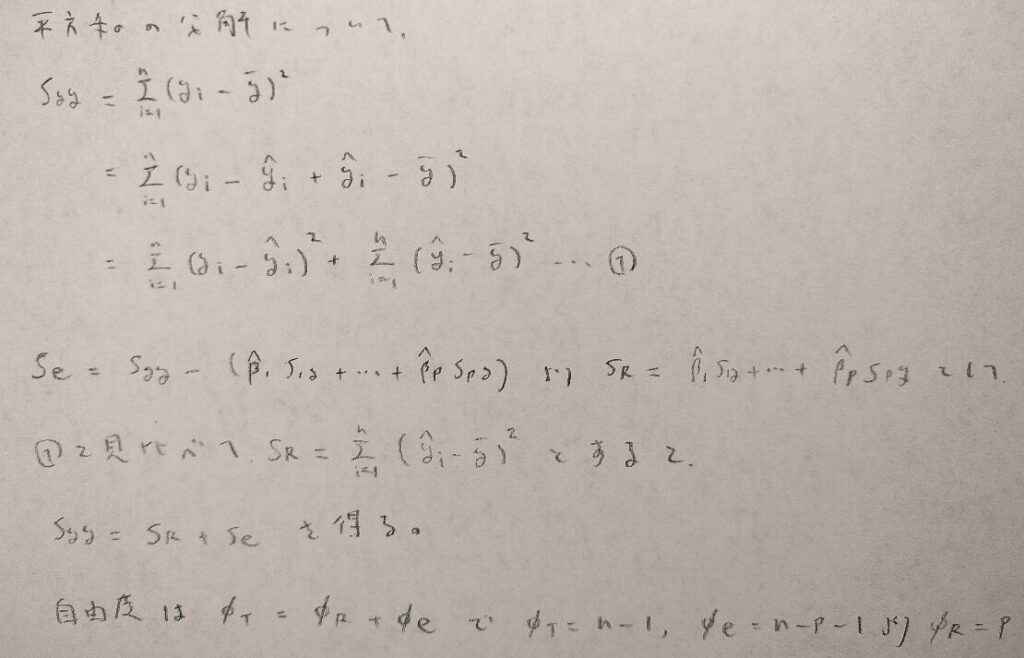
私には①が自明に思えないこともあって、証明をお願いします!
了解しました。証明とは別に、①の内容は分散分析(内容はかなり高度になります)の際に頻繁に登場してくる平方和の分解式になります。余談ですが分散分析では4重シグマなども登場してきます。
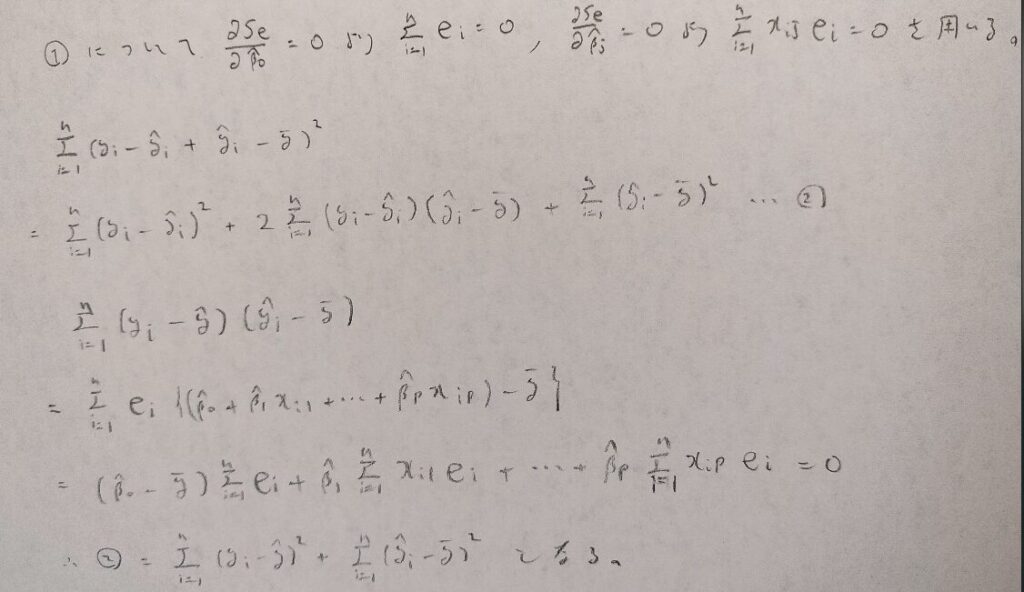
重回帰分析の寄与率(決定係数)と重相関係数との関係の結果
単回帰分析では相関係数の2乗が決定係数(寄与率)という綺麗な公式がありましたが、重回帰分析では一体どうなるのでしょうか。順に見ていきます。
Rの分母の式の2個目のΣのyハット・バーってなんだか記号の限界を感じます笑

Rの表現が異なるだけで、自由度調整済寄与率の式まで単回帰分析のときと同じ流れです。
ここでも①式を証明しておきます。

重回帰分析の変数の選択(変数増減法)
単回帰分析にはなかった考えが、ようやく登場します。どの変数を用いるべきか?という考えです。
AICなどもありますが、ここでは統計検定1級にも出題された変数増減法を学びます。ここではF分布の内容が大事になってきます。
F値が大きいほど、違いが顕著に出てくる!という粗い理解でも大丈夫です。
例えばF値に出てくるM1というのはモデル1という意味です。

とにかく回帰変動を大きくしていきたいので、F分布の知識を用いて根拠を持って出していこう!という内容です。
変数選択を行い、質の良い重回帰分析ができるようになります。
重回帰分析のハット行列から導かれるテコ比(t値やp値も再登場)
ここではテコ比の計算を頑張って出していきたいと思います。
テコ比はxのみで決まる量なので、単回帰分析のときには扱いやすかった覚えがあります。
図12をご覧ください。単回帰分析と同じように、まずは残差分析で用いる標準化残差や残差のt値について触れています。これらの値の大きさを調べることにより、サンプルの異常性がわかります。例えば3以上なら注意で、2.5以上なら留意とします。
残差のt値のところでテコ比が現れるので、テコ比を深く調べていきましょう。
ハット行列Hは2次形式ではありませんので、ご注意ください。また、図12の4業目から5行目はブロック行列の考えを用いて逆行列を求めています。
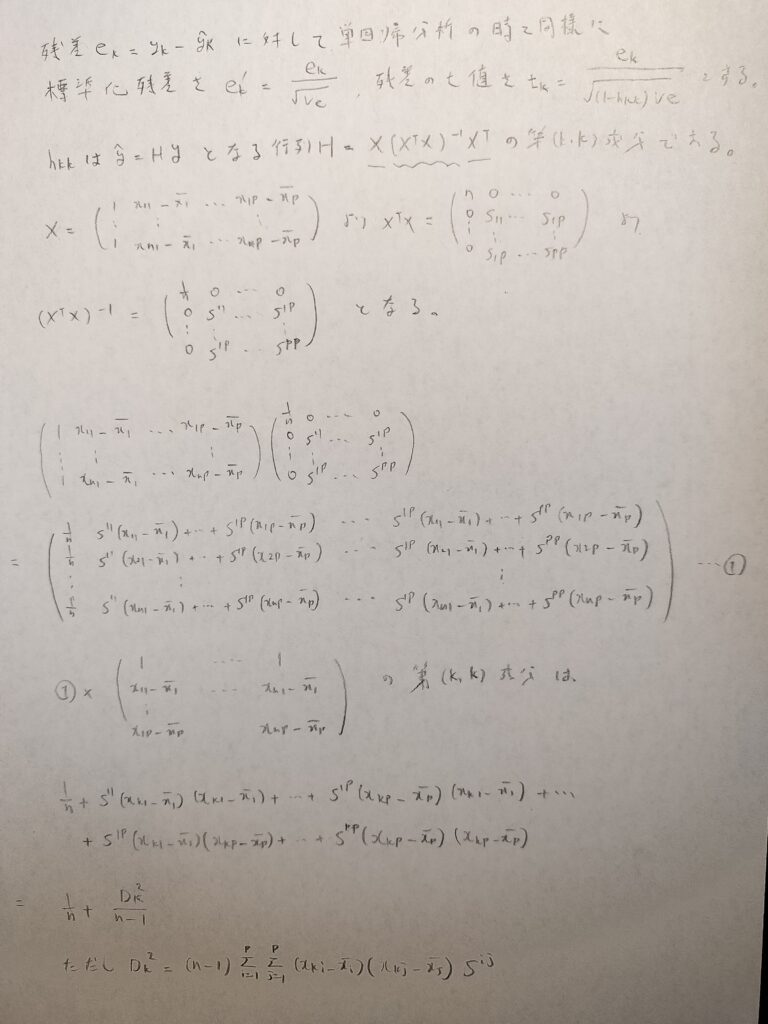
テコ比については単回帰分析と同様に、2.5×(説明変数の数+1)/nの値よりも小さくなることが望ましいです。要するに2.5×(テコ比の平均)より小さくなる方が良いとのことです。ちなみにテコ比の範囲は1/n以上1以下で単回帰分析のときと同じです。
重回帰分析のテコ比はマハラノビスの距離の2乗が関わってきます。この距離は判別分析で大事になる量です。
さらにこのマハラノビス距離が登場するもう1つの話題にも触れておきましょう。記事前半で学んだ内容がまたここで再登場します。
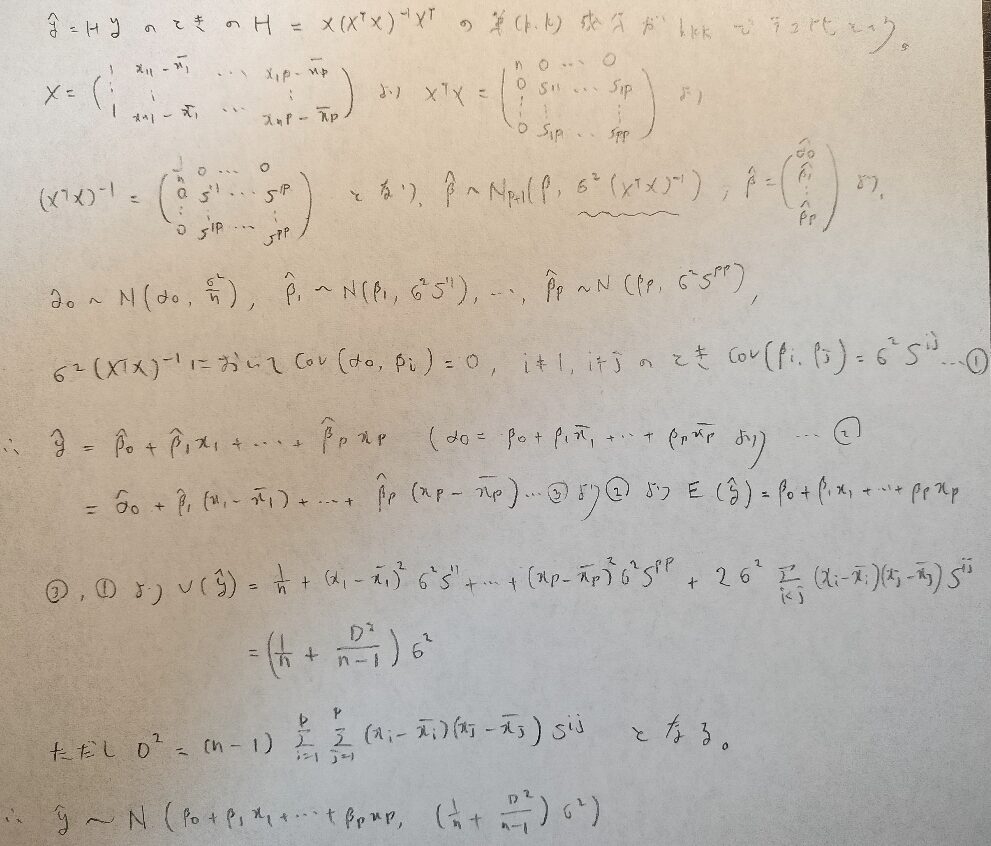
重回帰分析が単回帰分析と違って、行列表示ができても具体的な計算が難しく感じるのは、その背後にマハラノビス距離が見え隠れしていたのが原因なのかも知れませんね。
重回帰分析の母回帰の区間推定と予測区間
いよいよ最後ですね!
ここでは未来を予測できるかも?!の予測区間について学びます。
ここからの信頼係数は1-εとします。
まずは母回帰の区間推定です。
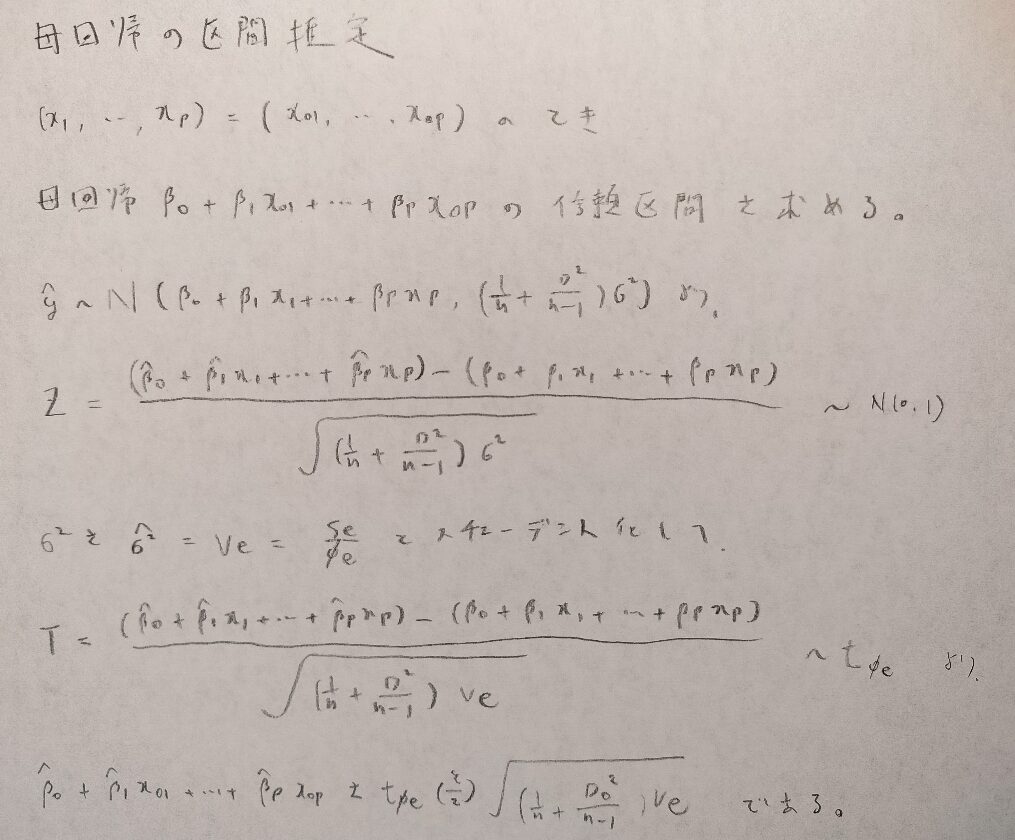
次に区間予測です。ここが回帰分析の最終地点と言っても良いです。
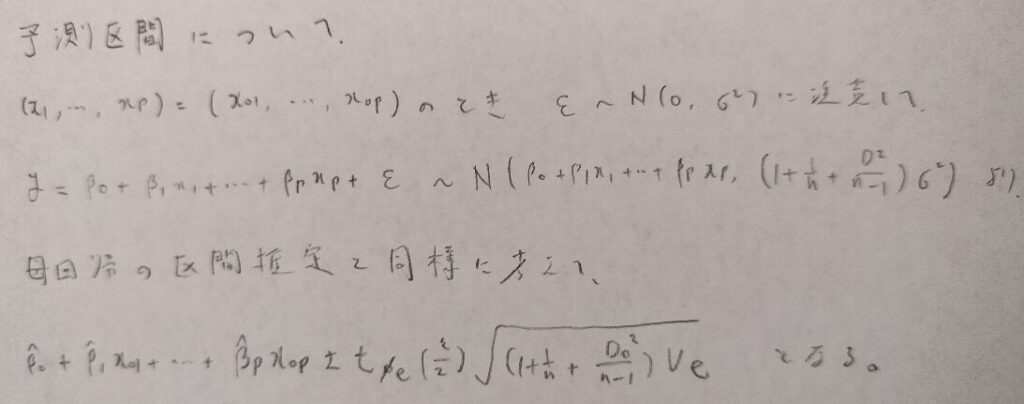
区間予測では誤差項がある分だけばらつきが大きくなります。
これで前回の単回帰分析とあわせて回帰分析はすべておしまいです。お疲れさまでした。
『多変量解析法入門』は名著です!統計検定1級で多変量解析が登場する分野での受験をお考えの方に、全力でおすすめします!