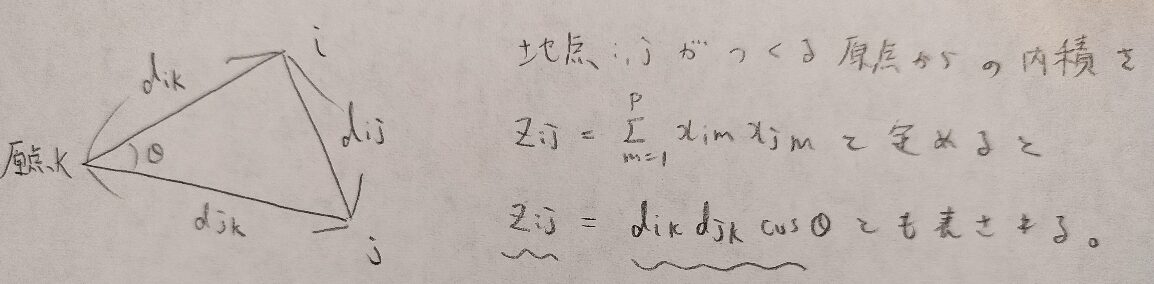多変量解析の中でも特に抽象度が高い内容を勉強します。
多次元尺度構成法という名前からして難易度が高そうです!
統計検定1級の公式参考書『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』の中でも統計応用(人文科学)の中でのみ登場する難し目の手法になります。
本来ならば多変量解析は統計検定1級の統計応用などの共通部分で出てくる感じなのですが、この多次元尺度構成法は共通分野から外れていることからもレベルが一段と上がっているという認識になります。
僕は統計応用(理工学)を考えているのでなおさら、難しいなと感じている内容になります。
ただしこの多次元尺度構成法は振り返ってみれば「どうしてこんなマジックのような手法が数学的に行えるのだろうか」となる面白い手法です。大変難易度が高い手法ですが、その面白さが伝わるように多次元尺度構成法の面白さを紹介したいと思います。
多次元尺度構成法は大きく分けて2種類あります。非計量MDSと計量MDSです。
非計量MDSから紹介していきます。
多次元尺度構成法(非計量MDS)の解析法
先ほどから思っていましたが、MDSとは何ですか?
MDSとはMulti Dimensional Scalingつまり多次元尺度構成法の英語です。
非計量MDSとは非計量、つまり仮定で具体的な距離(または距離のようなもの例えば親近性)が与えられていないものと考えてください。このような尺度を順序尺度といいます。
図01では10個のサンプルがどれくらい類似点があるか?という親近性(ただし今回は非計量MDSなので1〜10(一般にはnでもOKです)までのアバウトな値として用います)を下三角行列の形で考えます。

なるほど。そこから10個のサンプルの座標をなるべく正確に特定しようという手法ですね。
ただし親近性は数学では用いづらいので、距離に変換していきます。親近性が高い(数字が10に近い)ほど2つの対象物は近い距離にあると考えるので、図02のような変換は納得がいく変換になります。
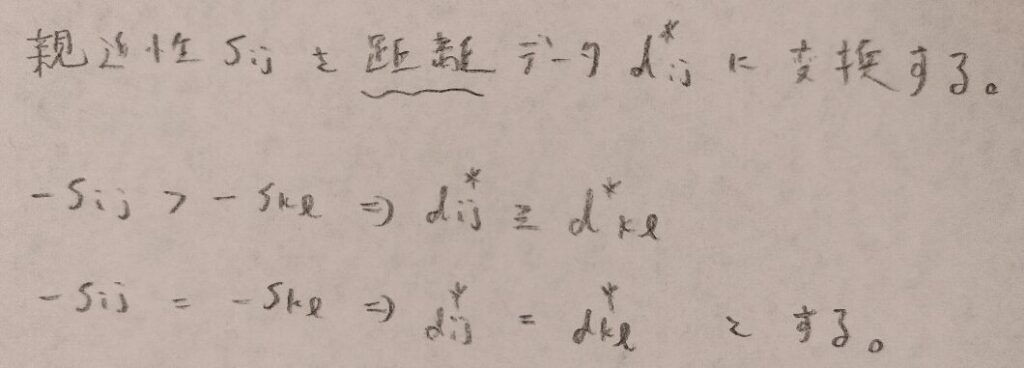
ここで用いる距離とは高校数学などで用いる距離とは限りません。たとえば実際の座標間の距離計算ではユークリッド距離を一般化したミンコフスキー距離を用います。
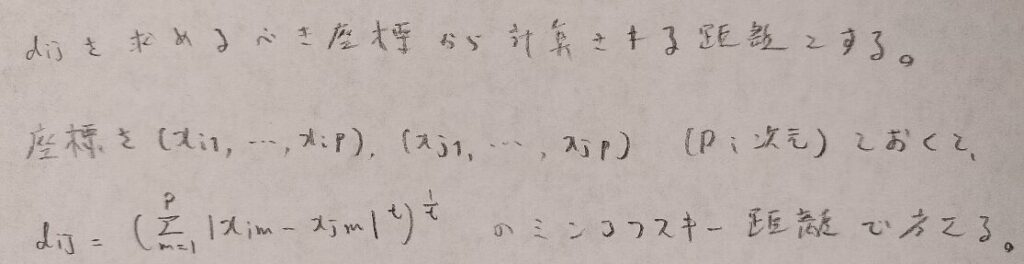
この座標が何次元か。そして距離をどのようなミンコフスキー定数tを用いて計測するか?などが未判明なので、計算自体は手計算ではほぼ無理でpython,エクセル,rなどの計算ソフトを利用していくことになります。
さらに座標の特定に用いる決定的な要因はストレスと呼ばれる図04で定義される量を最小にする座標となります。
非計量MDSでは次元Pとミンコフスキー定数tを定めてから、ストレスを最小にする座標を計算していきます。実務ではクラスカルの最急降下法が用いられます。
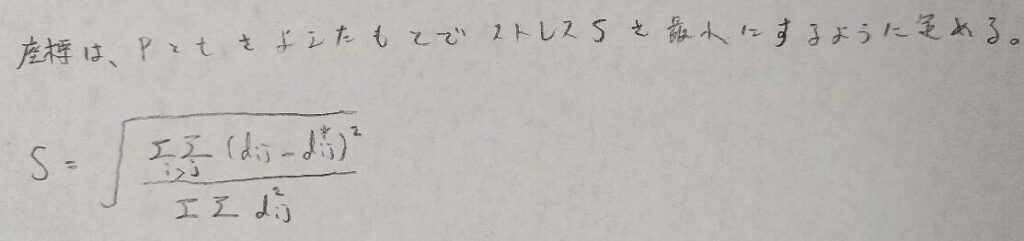
クラスカルによってストレス数値と適合の意味について言及がありますので紹介します。
ストレスSの数値と適合度の解釈(クラスカルの方法)
Sが0.200→良くない
Sが0.100→悪くはない適合
Sが0.050→良い適合
Sが0.025→非常に良い適合
Sが0.000→完全な適合
大変な量の計算を経て、10個のサンプルの座標が判明することになります。P次元ならばP個の座標軸がありますが、この座標軸が表す意味を知るために座標軸の回転を行います。座標軸の表す意味の判断としては中心から遠いサンプルを見ると判断がつきやすくなります。
また縦軸に座標間の距離で横軸に親近性をプロットした散布図を書き、階段上の線(ミンコフスキー距離での数値)にデータが乗る感じならば現在の解(座標)で距離をうまく再現できていることを表していることから、再現性の確認ができます。これをシェパードダイヤグラムといいます。
アンケートのような10段階の親近性のみで、10個のサンプルの座標が次元も含めて判明してしまい、そららの関係性が一目瞭然で判明するという驚愕の手法でしたね。ただし仮定の段階で判明しているのが10段階での類似性の評価のみなので、解析手法が複雑になるのは否めませんね。
多次元尺度構成法(計量MDS)の考え方
計量MDSの方法として有名なトガーソンの方法を解説します。
例えば数カ所間の距離のみが仮定で与えられているとします。このときの数カ所の場所をピンポイントで特定しようというものが計量MDSの考えです。
これまたマジックのような手法ですね笑

ここでは高校数学でお馴染みの内積という考えが大活躍します。
内積の2種類の計算が計量MDSの解析に大きな役割を与えます。距離のデータから座標のデータへ近づけるための大きな役割です。
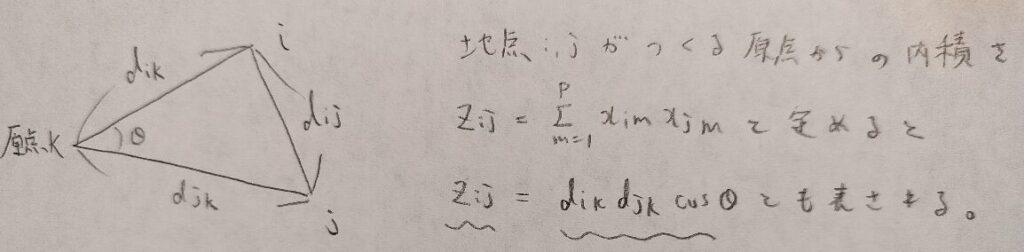
次に高校数学で学んだ余弦定理が活躍します。
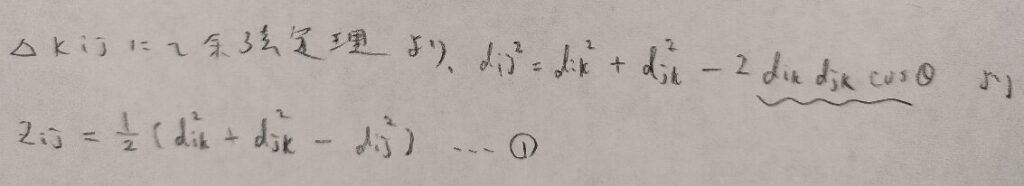
この①の式が記事後半のキーポイントになります。①式は複雑そうに見えますが、やっていることは内積を距離で表現しているだけです。
ここまでできればあとは、仮定から得られる距離の関係を座標の情報に変換するために行列表現に移行するだけになります。
今回は地点kが原点なのでn次元で考えなくてnー1次元で考えて良いということですので、このことに注意して図08をご覧ください。
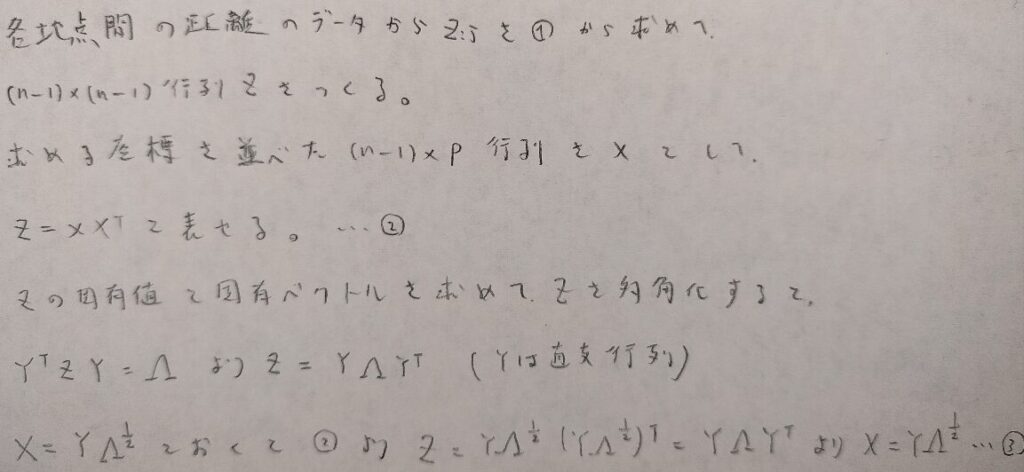
ただし結局は固有値計算で大量の計算を強いられるので、この計量MDSも数式処理ソフトを用いていくことになります。
計量MDSで誤差がある場合の対処法
最後に計量MDSにおいて、家庭に誤差が含まれてしまう場合は、原点をどこに設定するかで結果の座標が大きく異なってしまいます。そのため誤差がある場合はn個の地点の重心を原点に設定します。
図09にて重心を原点に設定した場合に、仮定で与えられる各距離から内積を算出する計算式を導いています。
統計検定1級に出てきそうな問題ですね。
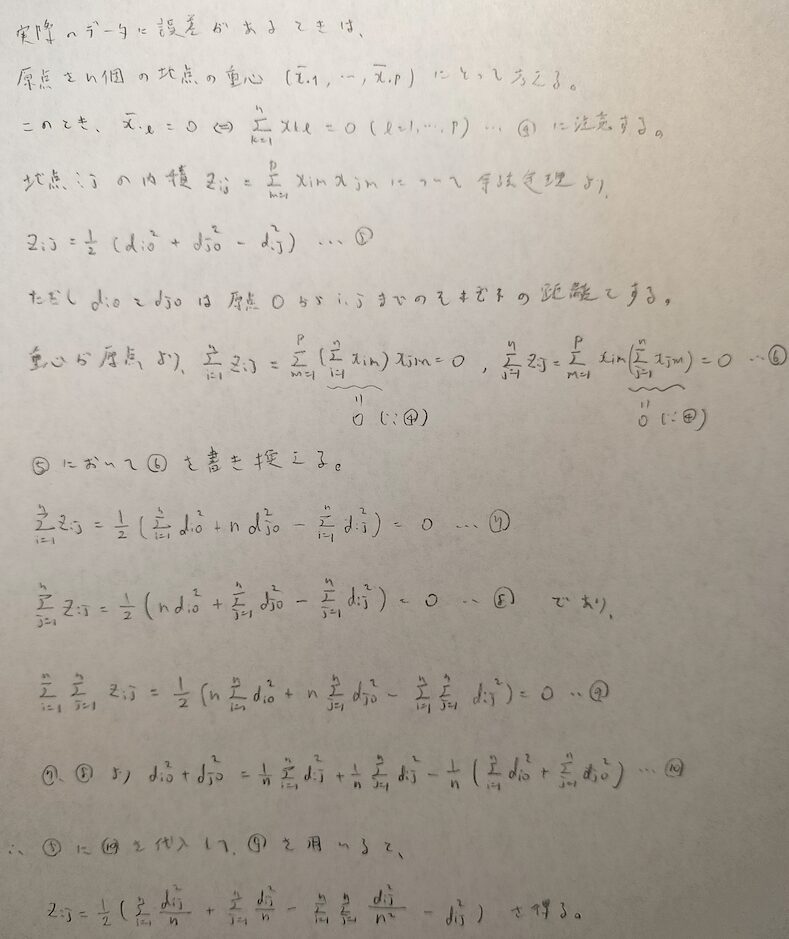
統計検定1級にこれが出てきたら確実に難問扱いになります。小問が欲しいところですね笑
多次元尺度構成法は手計算では無謀な解析手法ですが、最終的に求めたいのは非計量MDSでも計量MDSでも座標なのだという認識を持つことが大切なのですね。