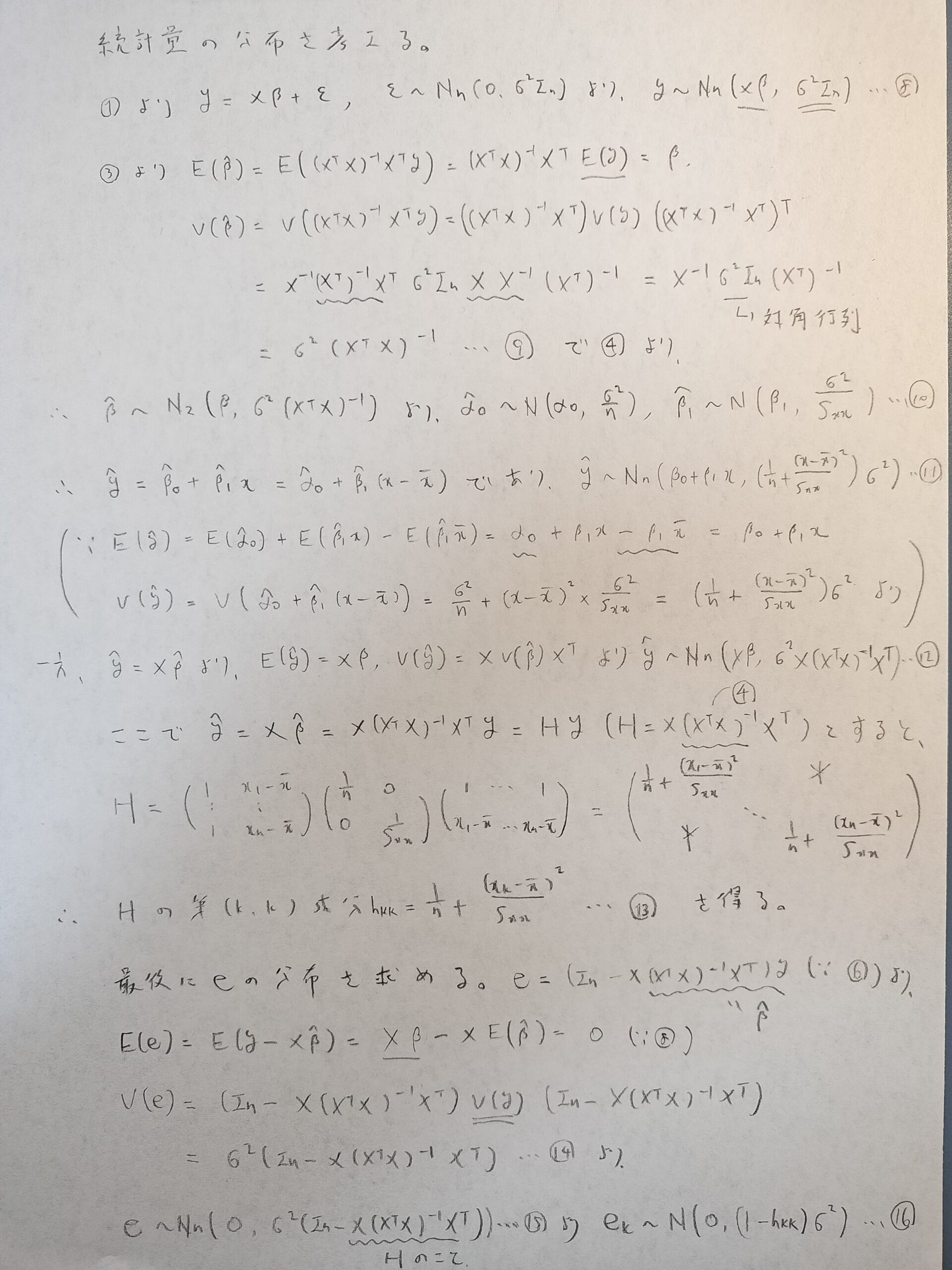統計検定1級でもアクチュアリー数学(二項回帰という名称で出題)でも出題範囲となっているロジスティック回帰について解説します。
ロジスティック回帰は単回帰分析の応用です。下記の記事にて内容をご確認ください。
本記事はアクチュアリー数学よりも難易度が高い統計検定1級を見据えた内容で構成します。
参考書籍として久保川先生の『データ解析のための数理統計入門』を使用します。本書は統計検定1級のバイブルとして有名な『現代数理統計学の基礎』の続編に当たる書籍です。
この書籍は前半部のみ演習問題があり、後半部は演習問題がありません。ロジスティック回帰の章は後半部に相当するので、演習部分のある『データ解析のための数理統計入門』を参考にしました。
ロジスティック分布とジグモイド関数(pythonでも用いる)と各性質の証明
ロジスティック回帰を理解するために、ロジスティック分布を学習します。ロジスティック分布は連続型確率変数の1種です。この章では名著『現代数理統計学の基礎』の章末問題を用いてロジスティック分布の一般形の期待値と分散を導出する流れを学びます。まずはロジスティック分布の持つ各性質を調べていきましょう。
ロジスティック分布が確率密度関数であることの証明
ロジスティック分布の持ついくつかの性質を調べます。
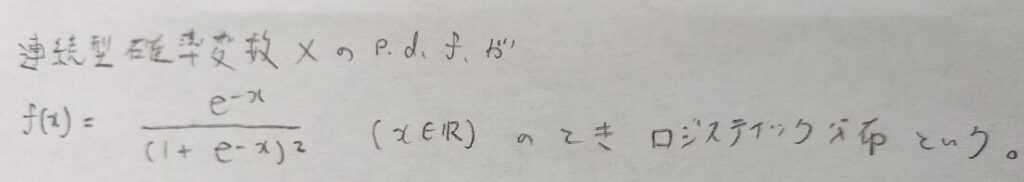
この関数が確率密度関数としての性質を満たしているか?を調べます。
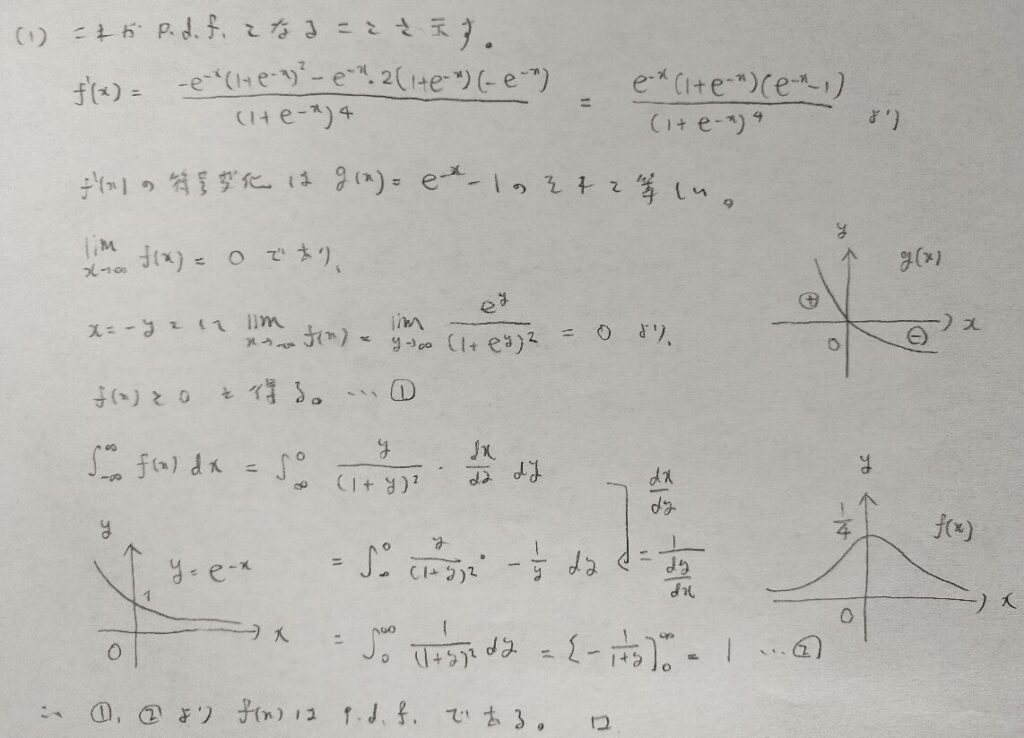
ジグモイド関数をロジスティック分布の分布関数として計算!微分の関係も大切
次にロジスティック分布のy軸についての対称性とジグモイド関数の導出に関する問題を考えます。
ジグモイド関数とはロジスティック分布の分布関数のことです。
ロジスティック分布とロジスティック関数は異なるものなのでご注意ください。
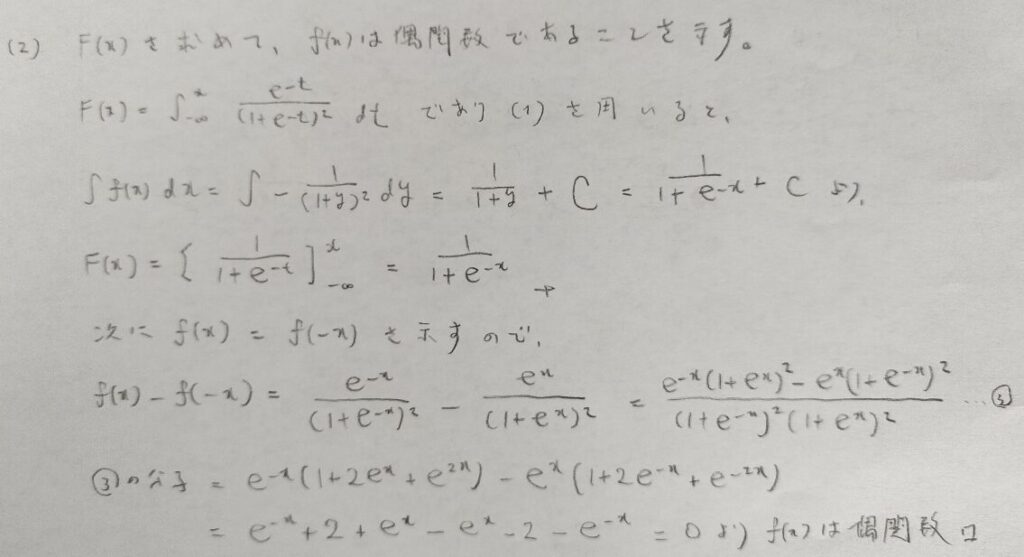
ジグモイド関数は学力向上などで使われるS字カーブの別名とも言われています。
ロジスティック分布と標準一様分布
ここではロジスティック分布の変数変換の問題で一様分布が絡む問題を考えます。結論でロジスティック分布に似た結論が出てくることにご注目ください。
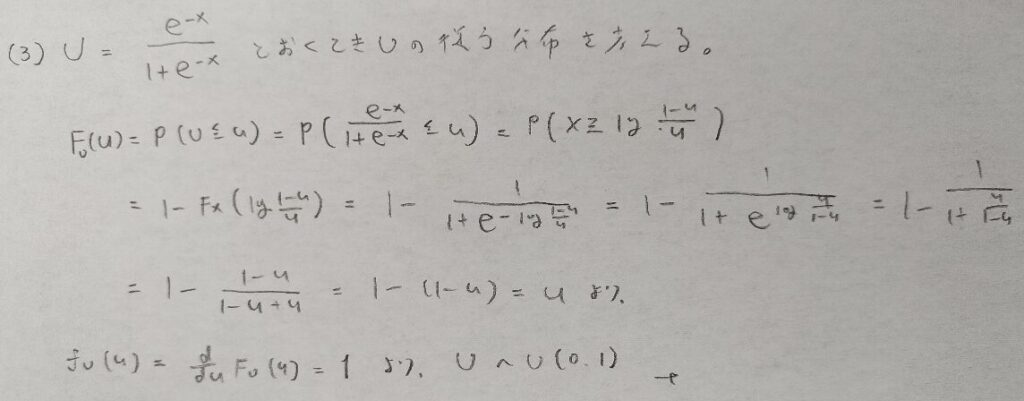
この問題は素直な問題ですね。久保川先生の模範解答と異なる方法で解いていますね。
僕は技巧的な方法は思いつかなかったので、分布関数を経由する方法で解きました。
ロジスティック分布とハザード関数
次にロジスティック分布の変数変換ならびにハザード関数を求めてみます。ハザード関数の問題での結論ではジグモイド関数が出てくることにご注目ください。
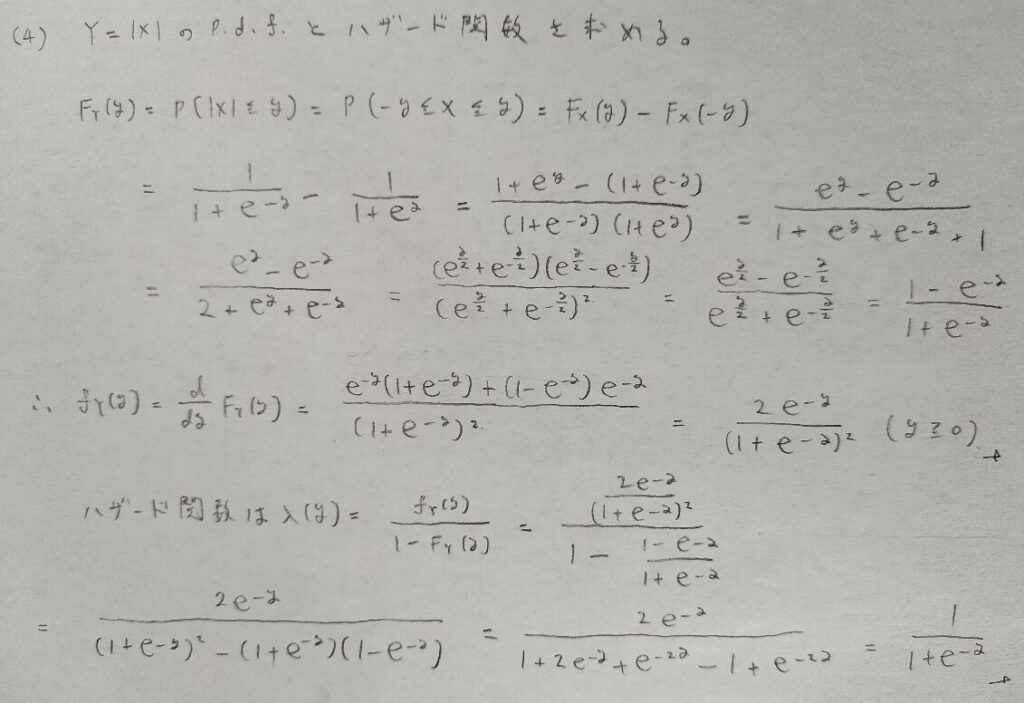
とても不思議な結論でしたね。
ロジスティック分布の一般化
最後の小問はロジスティック分布を一般化させる問題です。
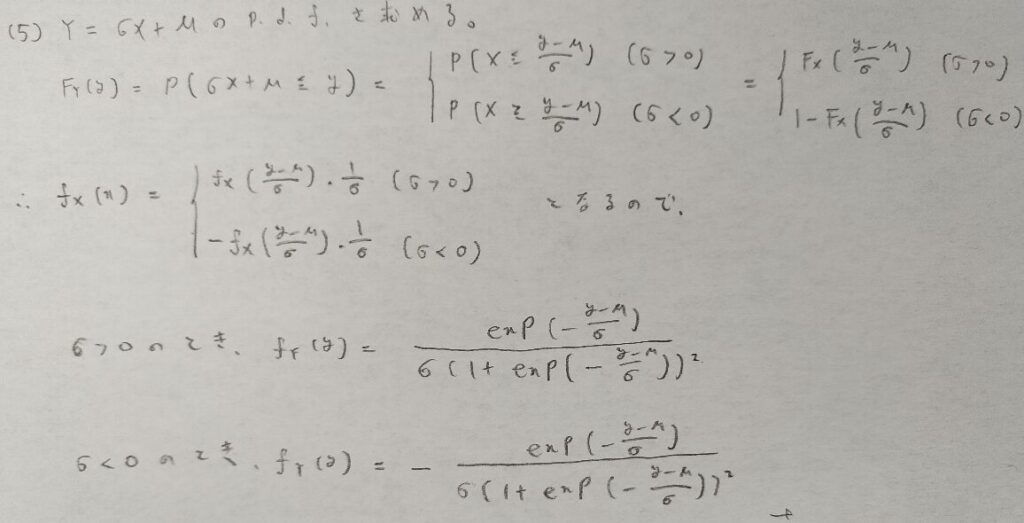
『現代数理統計学の基礎』の原題には注釈がありませんが、ロジスティック分布においてσは正であることにご注意ください。
σが正であることは、正規分布などでもお馴染みのルールですね。
図06のσ>0の時の答えがロジスティック分布の一般式になります。次の章の図07に詳細を載せます。
ロジスティック分布の積率母関数から期待値や分散を導出
この章ではロジスティック分布の期待値と分散を導出します。積率母関数を経由する流れで計算していきます。まずはロジスティック分布を復習として紹介します。
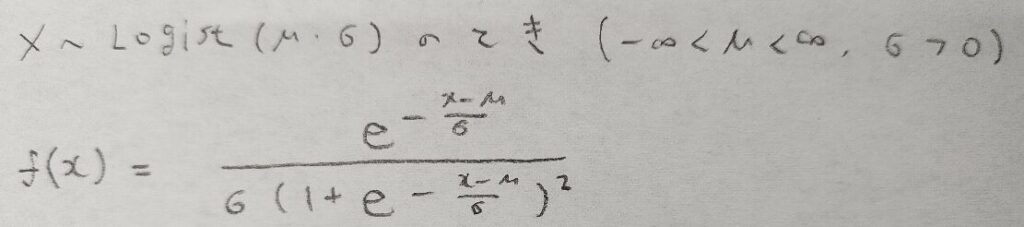
ロジスティック分布の積率母関数
ここでは特殊な置換積分を行います。逆にいうとこの置換積分を知らないと処理不能になります。
機械学習の分野ではお馴染みの文字の置き換えです。
最後はベータ関数に帰着させて終了ですね!
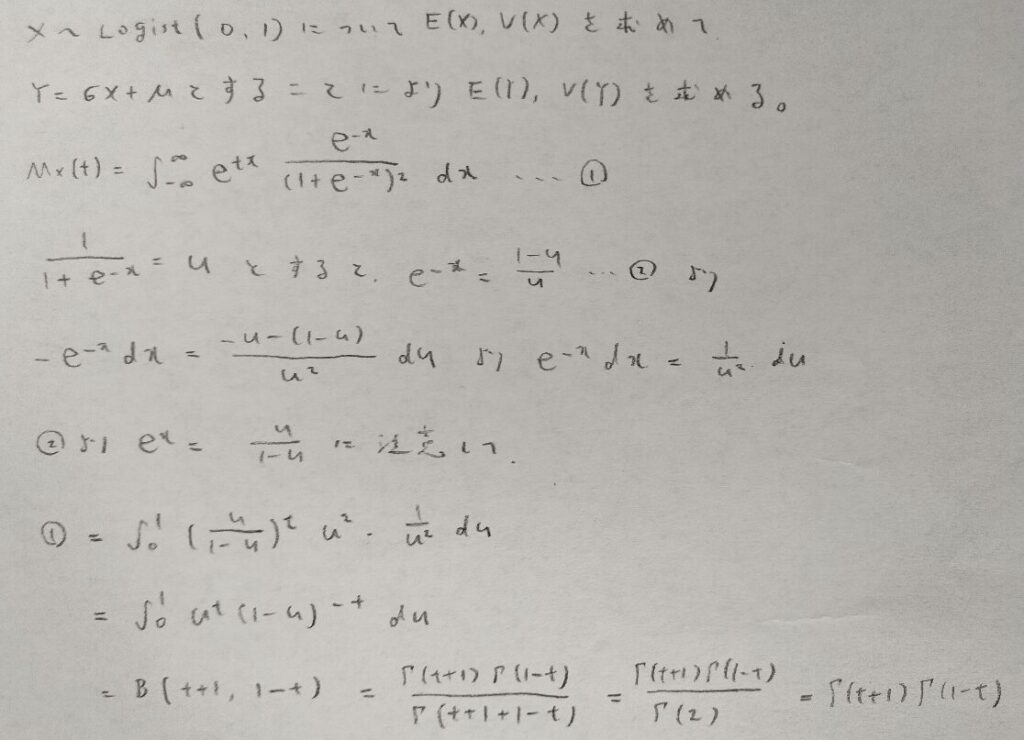
ベータ関数についての記事はこちらで復習できますのでご確認ください。
ロジスティック分布の期待値
積率母関数が求まりましたので次の手順で期待値を求めます。
①Xの期待値を求める。
②変数変換を用いてYの期待値を求める。
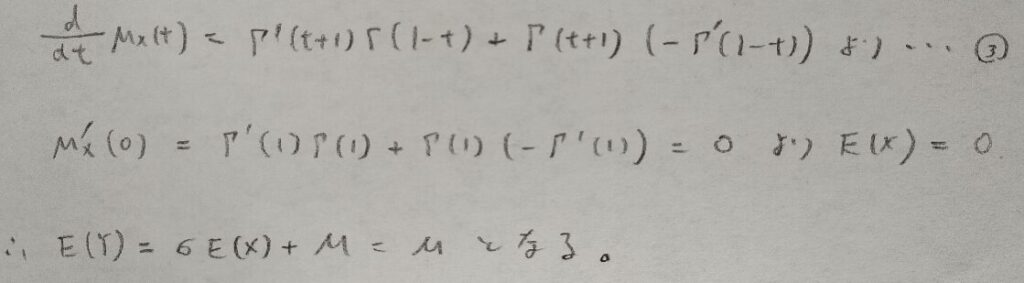
Xの期待値が0なのは図02の解答の図からも察することはできますね!ですのでこの結果は覚えやすいです!
ロジスティック分布の分散
このtweetにあるように、ロジスティック分布で難しいのは分散の導出です。できるだけ丁寧に説明していきます。

オイラー定数γが絡んでいるようですね。
その通りです。ディガンマ関数の周辺はとても難易度が高いです。オイラー定数γに関する参考図書『オイラーの定数ガンマ ―γで旅する数学の世界』を紹介します。
ロジスティック分布の分散でまさかのζ(2)が出てくるなんてとても面白いですよね!
この章の最後にロジスティック分布の期待値と分散の結果をまとめます。
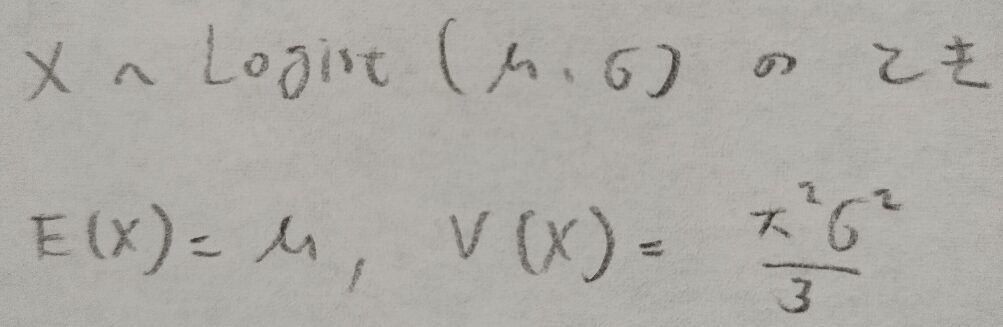
ロジスティック関数から考えるロジスティック回帰(ロジットモデルとオッズ比の関係)
ここからロジスティック回帰に入ります。まずはなぜロジスティック回帰が必要なのかを考えます。
ジグモイド関数の正体
図12のようなyの値が0か1から成るデータでは単回帰分析よりもS字カーブのようなジグモイド関数が登場する回帰分析を行った方がよりデータにフィットする結果が得られそうです。
この時のジグモイド関数をロジスティック関数といいます。
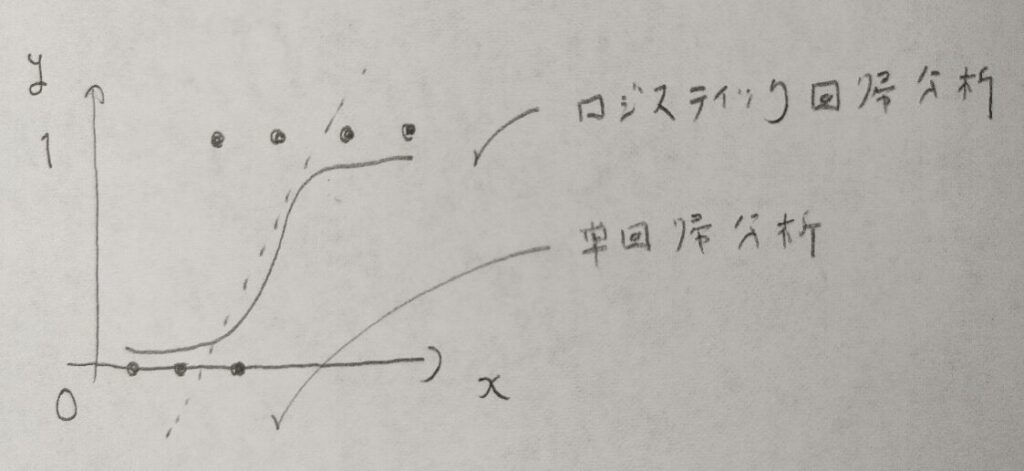
このわかりやすい図は『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考にさせていただきました。
ロジスティック回帰(rでも用いる)の導出
それではロジスティック関数を導きます。yが取る値が2値しかないのでベルヌーイ分布を登場させます。このようなデータを2値データといいます。

なるほど。yが2値の0か1なので、ちょうど確率と捉えれば良いのですね!
その通りです。この発想が図14の第1行になっています。先を見ていきましょう。
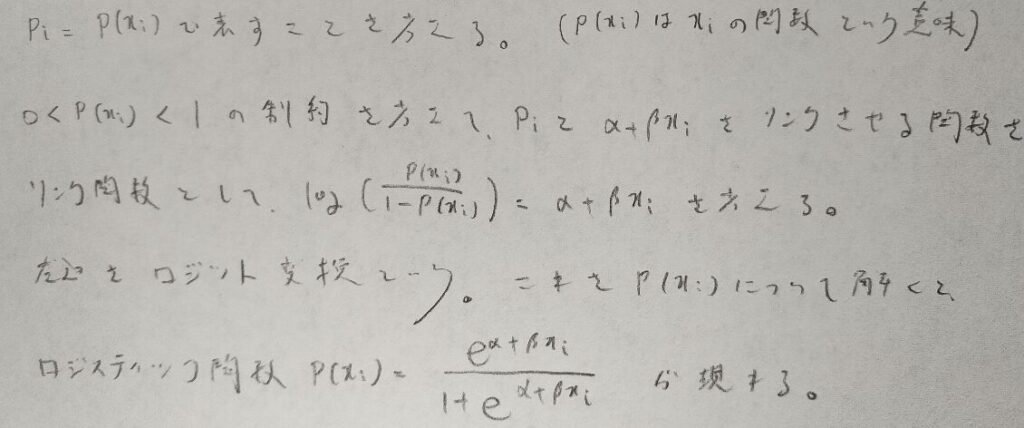
図14の第3行の対数の中の式において分子をpと捉えて対数の中身をオッズといいます。またオッズに対数をとったものを対数オッズ=ロジット(関数)といいます。この場合はpのロジット関数になります。すなわちロジスティック回帰分析とは、対数オッズをxの1次式で表すモデルを用いた回帰分析です。
確かに図14の最後の結果を見ると、pは0から1を動こうことが確認できますね。
そしてこのロジスティック関数の振る舞いはβの符号によって異なります。

ロジスティック回帰モデル(pytyonでも用いる)のパラメータの推定
それではロジスティック回帰モデルのパラメータを推定します。
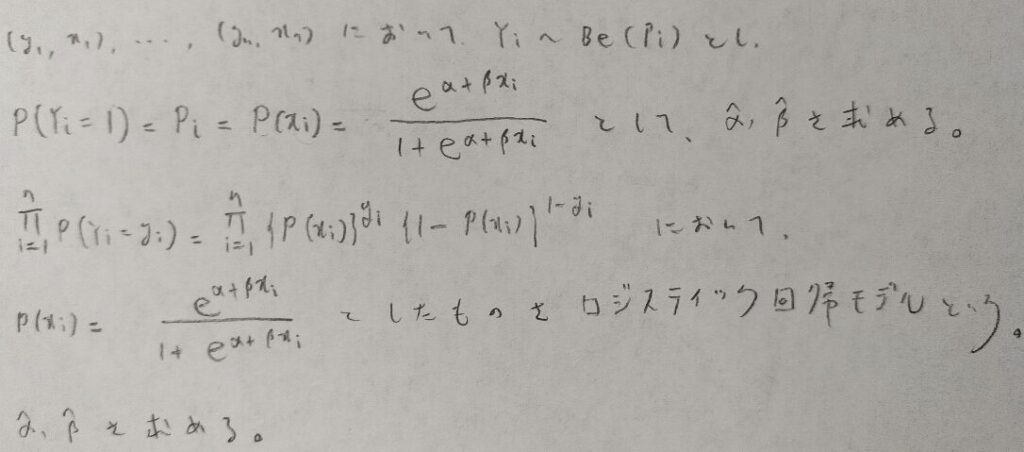
ここでは最尤法を用います。
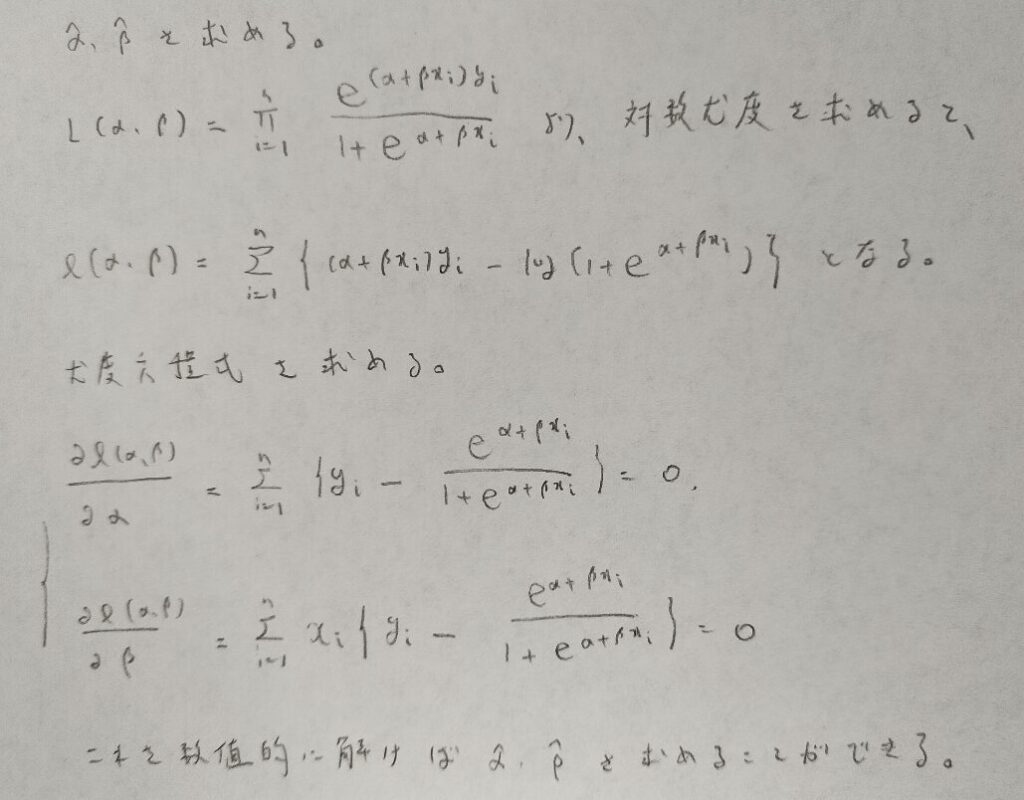
ロジスティック回帰の検定とp値の求め方
ロジスティック関数が推定できたら、それが意味をなすか?の検定を行います。
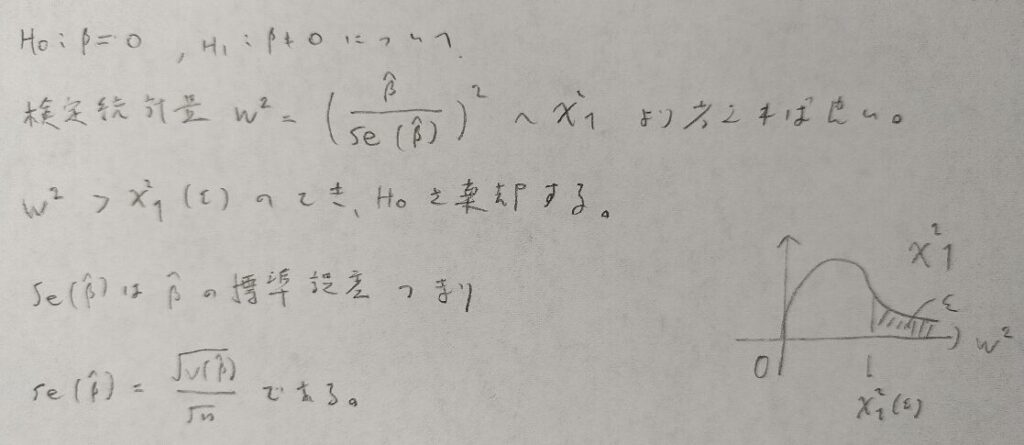
検定統計量の分母は標準誤差です。この解釈は母集団分布からβ^の標本を取り出す標本平均を考えるイメージです。すると検定統計量の分子はβ^から0を引いたものになる解釈になります。
2項ロジスティック回帰(エクセルでも用いる)も最尤法で出せます
ここからロジスティック回帰の応用に入ります。まずは2項ロジスティック回帰です。
この名前は先ほどベルヌーイ分布を用いて考えたことの対比で二項分布を用いることによることに由来しています。
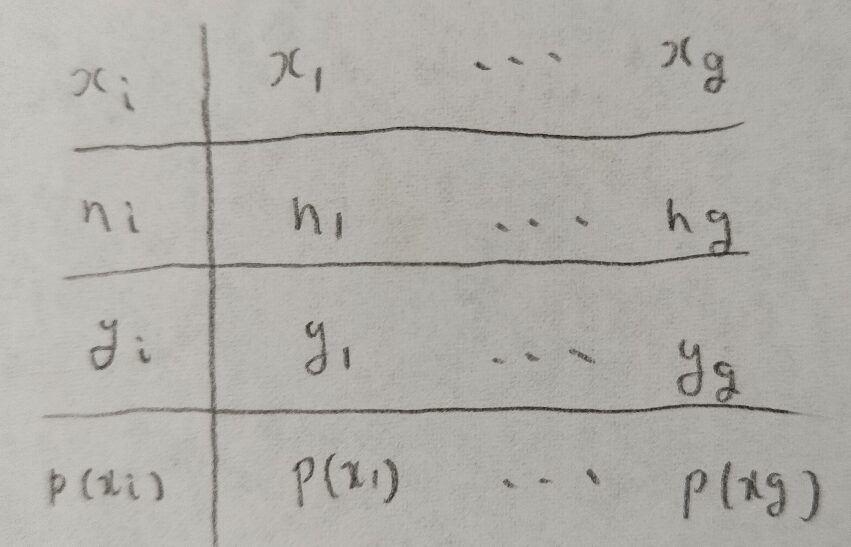
この表においてロジスティック回帰を行います。
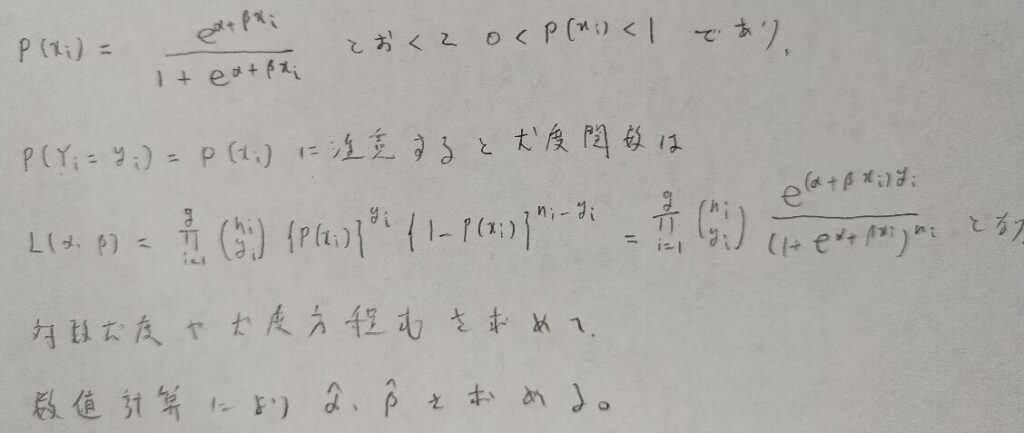
要するに尤度関数の立式の際に用いていたベルヌーイ分布を二項分布に変えた応用なのですね!
その通りです。どの方面への応用かを考えればOKです。
複数の共変量を持つロジスティック回帰をわかりやすく計算します
ロジスティック回帰の次の応用は複数の共変量を持つロジスティック回帰を考えます。
どのような方向への応用なのかを考えながら図21をご覧ください。
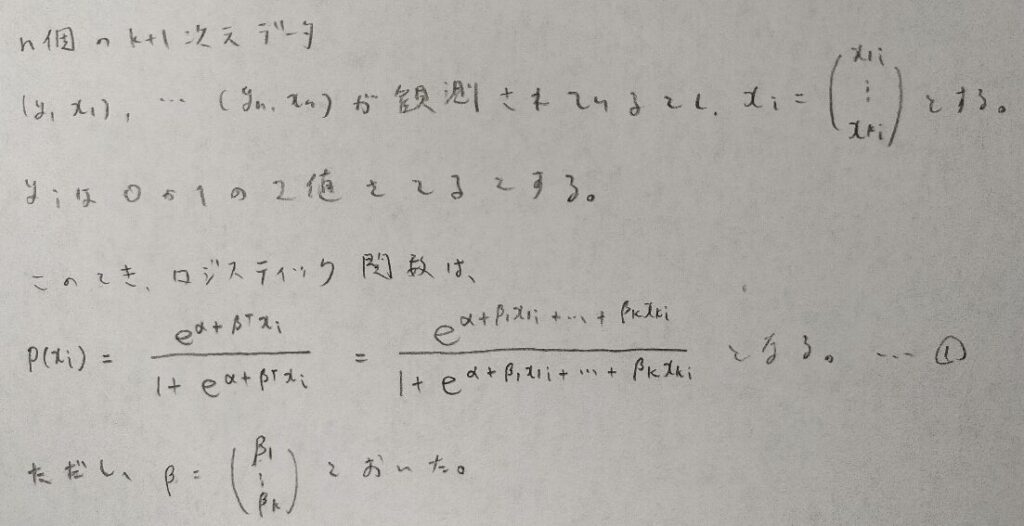
なるほど。変量xが多次元になっただけですね!
その通りです。このように応用されても、ロジスティック関数の基本的な形は変わりません。
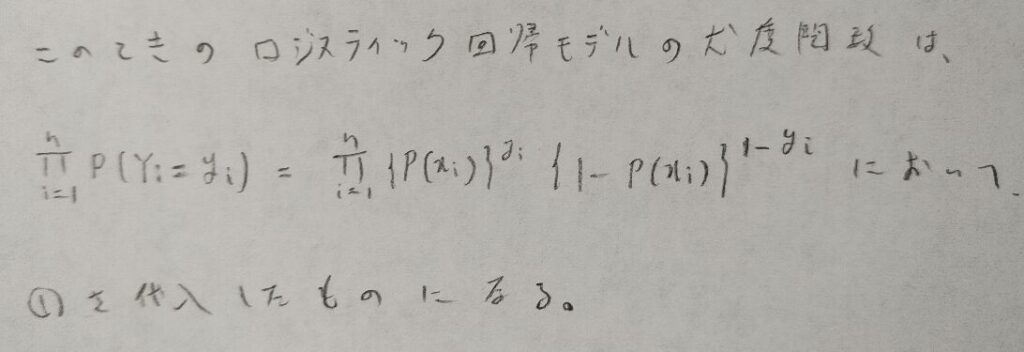
ロジスティック回帰については以上です。
ロジスティック回帰は0か1の白黒思考が元ネタのような回帰でしたね。今回も楽しかったです。ありがとうございました!