パレート分布を覚えていますか?
パレート分布は超お金持ちの分布のイメージでした。
『統計学大百科事典 仕事で使う公式・定理・ルール113』によるとパレート分布は低所得者層の分布を表すには精度が悪いというデメリットがあります。
対数正規分布はこれらのデメリットを解消できる分布です。
対数正規分布がどのようにして導かれるのか紹介をお願いします!
本記事ではX~N(μ,σの2乗)、Z~N(0,1)、Y~LN(μ,σの2乗)とします。標準正規分布に従う確率変数Zを持ち出すのはφ(z)やΦ(z)を用いることができるためです。
対数正規分布の確率密度関数を正規分布の確率密度関数から導きます
正規分布と対数正規分布は自然対数を底とする指数関数で結ばれています。
対数正規分布の定義と確率密度関数の導出は以下の計算で行われます。
対数正規分布を表す記号LNは英語名log-normal distributionに由来しています。
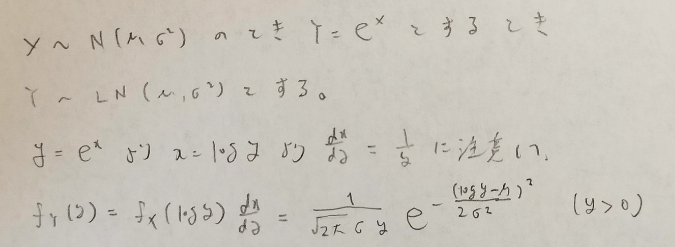
正規分布はXの実現値の取りうる範囲は実数全範囲で、対数正規分布はYの実現値を取りうる範囲は正の実数なんですね。
対数関数の定義域は正の数であることを思い出せば納得のいく結果ですね。
対数正規分布のyの範囲は正の実数全体です。期待値計算などで実数全体としないように注意しましょう。
対数正規分布の分布関数を標準正規分布の分布関数で表現する
対数正規分布と正規分布の関係は指数関数で結ばれているので、対数正規分布の分布関数は正規分布の分布関数で表せそうです。
標準正規分布の分布関数を利用して対数正規分布の分布関数を表現してみましょう。こちらの考えは『リスクを知るための確率・統計入門』を参考にしました。
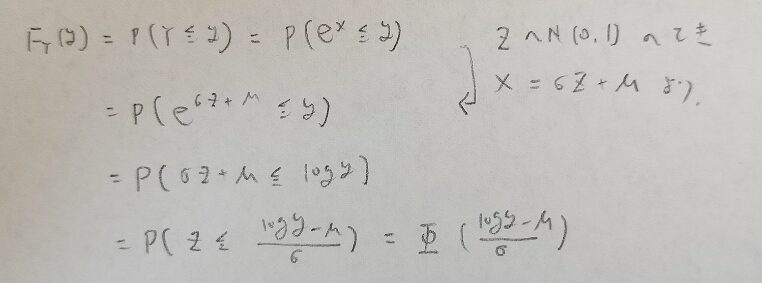
一応、確認なのですが…
なんでしょう?
正規分布の時と同じように対数正規分布の第1パラメータと第2パラメータはそれぞれ期待値と分散を表しているのですよね?
対数正規分布については、そうではありません!
対数正規分布の第1パラメータと第2パラメータはそれぞれ期待値と分散を表すわけではないことに注意してください!ただ単に対数正規分布は第1パラメータと第2パラメータの文字を用いて表現しますよという気持ちの表現です。
対数正規分布の期待値と分散を対数正規分布の原点周りのt次モーメントと正規分布の積率母関数との関係を用いて計算する
正規分布と対数正規分布の関係性を理解していると、対数正規分布のさまざまな特性値をうまく導くことができます。
正規分布の積率母関数そのものが対数正規分布の(原点周りの)t次モーメントになっています。下の数式変形でご確認ください。
ということは期待値や分散などは自動的に求まってしまうのですね!
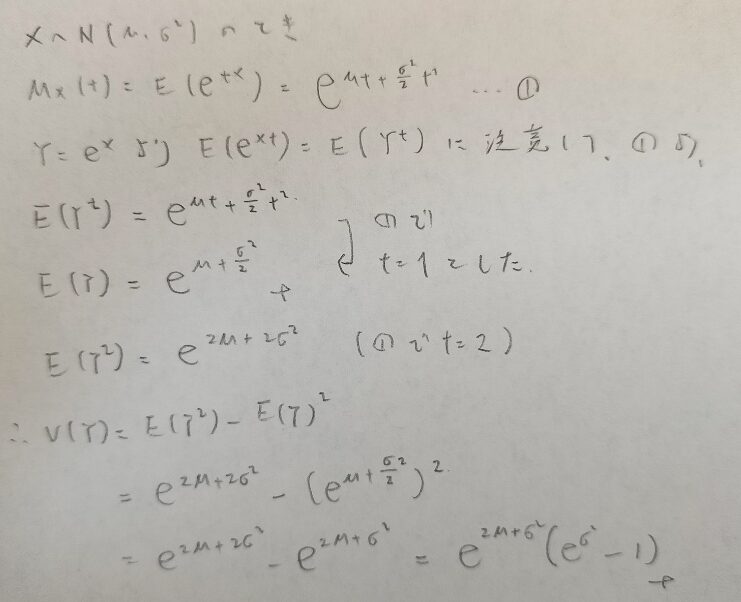
対数正規分布の中央値
最後に対数正規分布の中央値について『データ解析のための数理統計入門』を参考にして解説します。
この問題はアクチュアリー数学では未出です。頭を使う問題なのでそろそろ出題されても良い頃合いです。
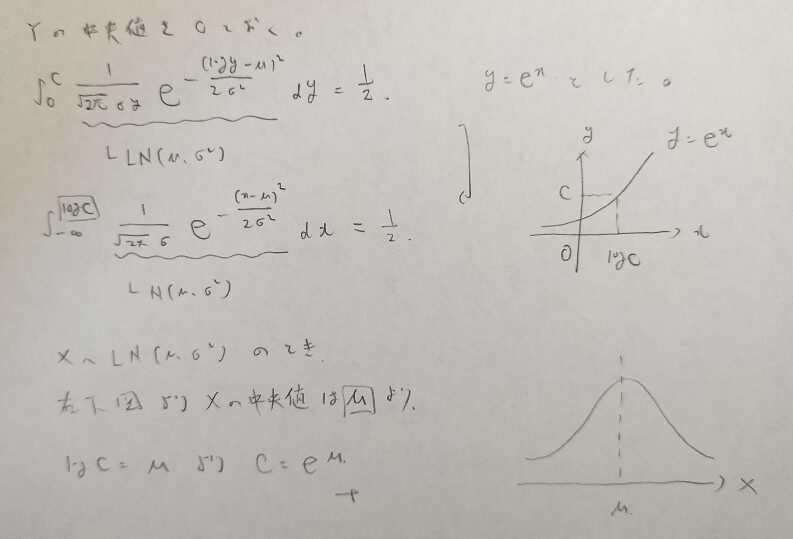
正規分布の期待値がμならば、対数正規分布の期待値がeのμ乗なのは、正規分布と対数正規分布との関係性を考えれば納得できる結果です。
対数正規分布と正規分布の間の関係性の重要性がとても大事な回でしたね。
正規分布を学習する際には対数正規分布も合わせて理解しておくと良いです。
対数正規分布を標準正規分布の分布関数Φ(・)で表現する提案はこちらの本からヒントを得ました。
対数正規分布の中央値を求める問題で参考にしました。本書の出版は2023年の秋と新しいので、初見問題が多く、統計検定1級の受験者にとっては大事な本になります。
パレート分布の欠点について参考にしました。対数正規分布はファイナンス分野で活躍する分布であることがわかります。本書は統計検定1級のカリキュラムに対応しています。





