統計検定2級に合格できましたので、さっそく統計検定準1級の勉強を開始します。
具体的には統計検定準1級の公式参考書『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』を学習した後に、
統計検定準1級の過去問を解いて仕上げていきます。
このワークブックがかなり大事になるということですね!
統計検定2級では公式参考書が合格には必ずしも必須ではないというお話をしました。
統計検定準1級では公式参考書の理解度がそのまま合格率になるようです。
ワークブックの解説記事では大きく4つに分けます。
第1部:確率と確率分布
第2部:統計的推測
第3部:多変量解析法
第4部:種々の応用
このような4分割を行う理由は、統計検定準1級のスコアレポートがこの4分野に分けられるからです。
統計検定準1級ではこの4分野を中心に問題が作られていると推察できます。
本記事は第1部:確率と確率分布を掘り下げていきます。
具体的には章の問題の解説→各章の見逃すポイントを学習していきます。
問題文は『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』をご参照ください。
よろしくお願いします!
統計検定準1級ワークブック解説:第1章『事象と確率』
例1−1
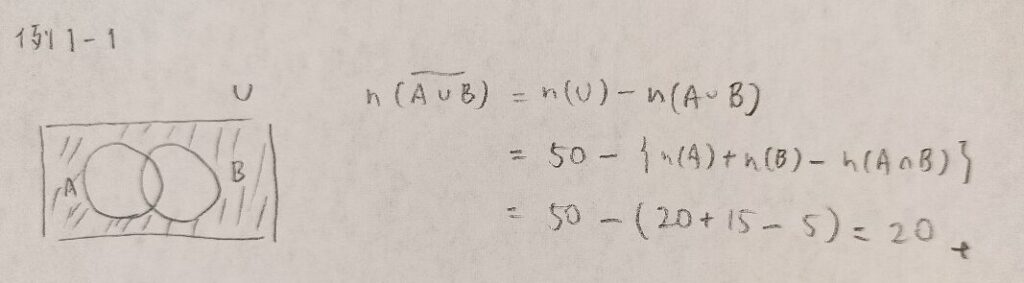
問1.1
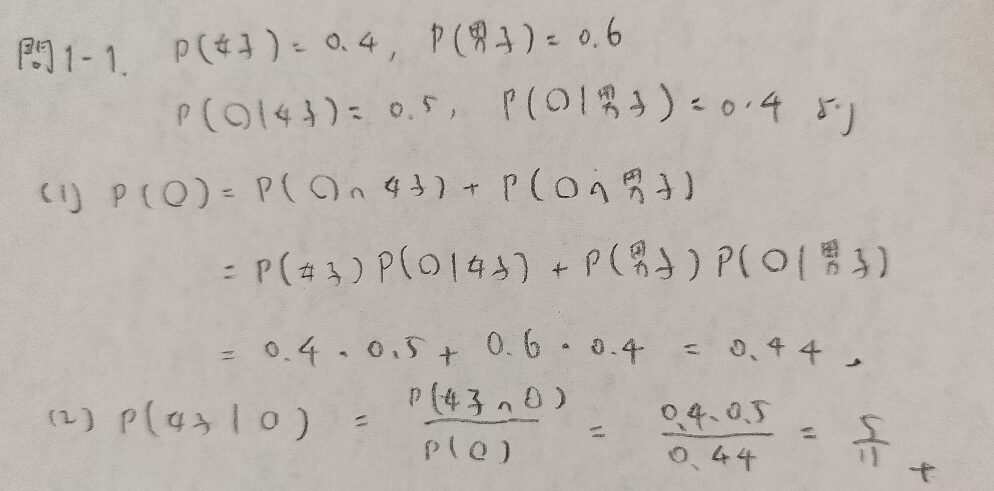
問1.2
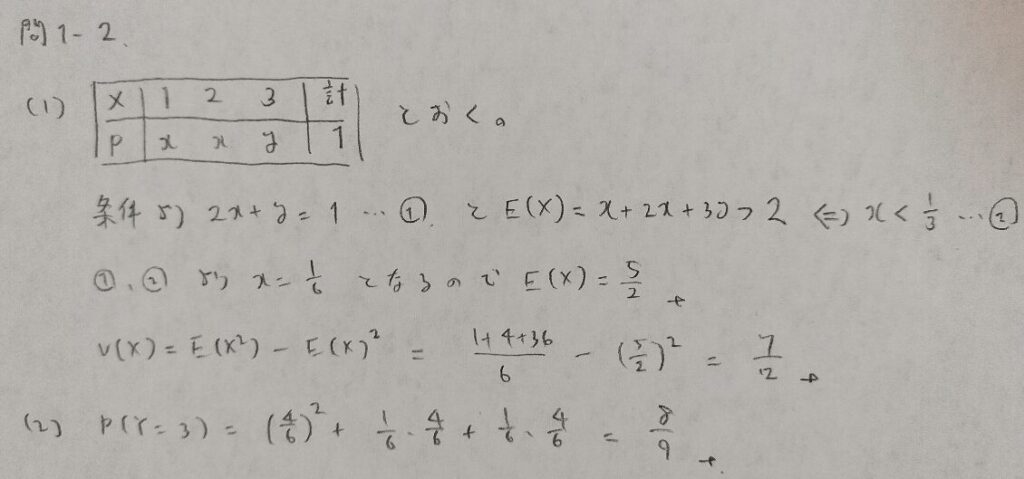
問1.3
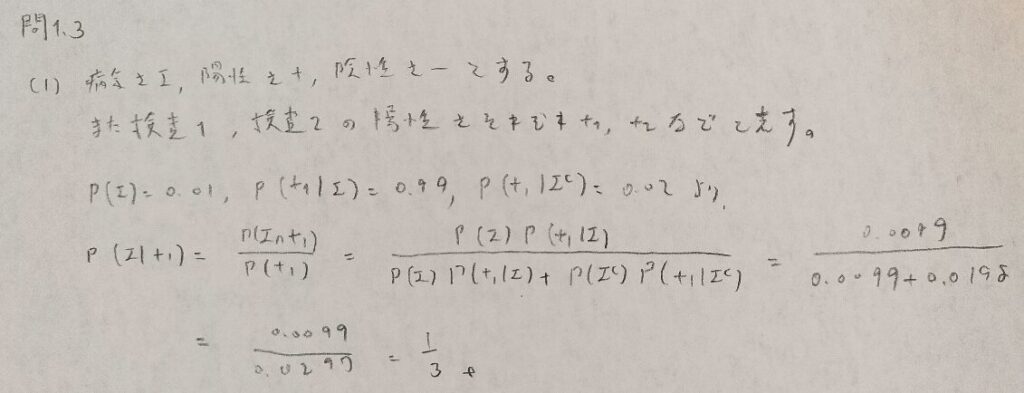

第1章メモ

統計検定準1級ワークブック解説:第2章『確率分布と母関数』
例2−1
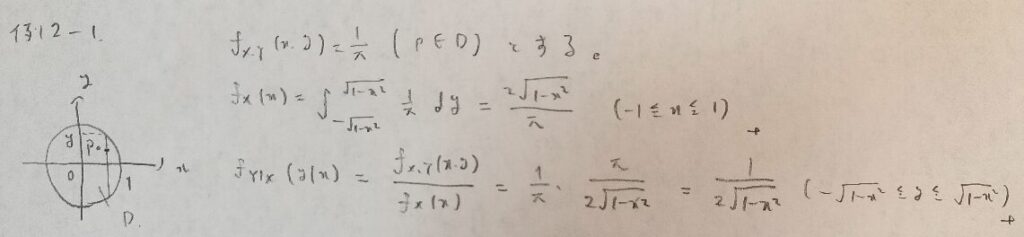
例2−2
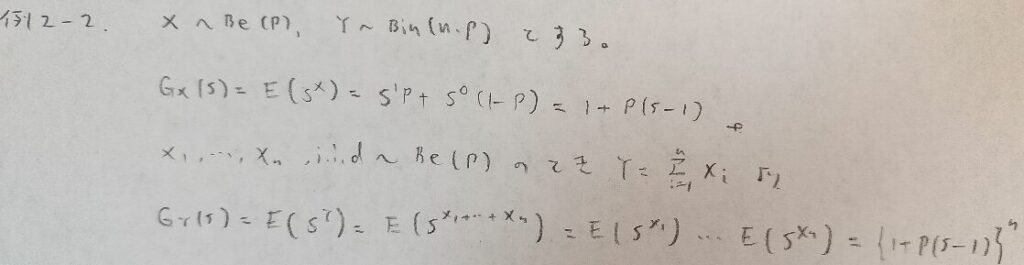
問2.1
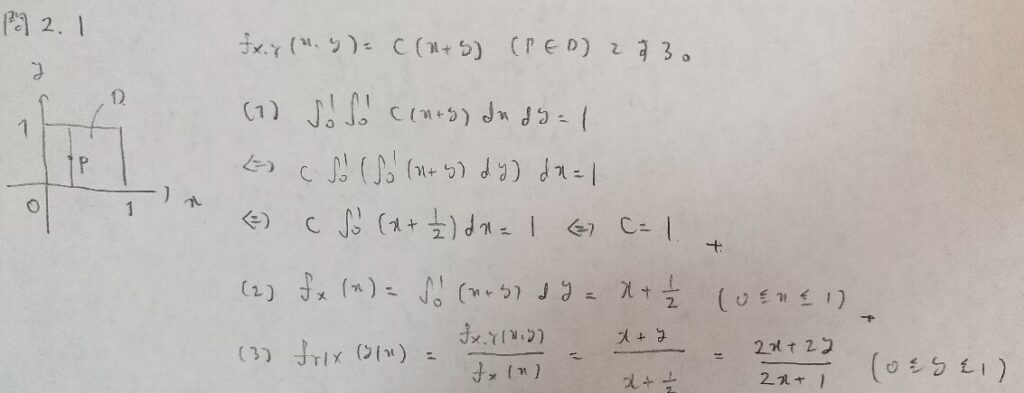
問2.2
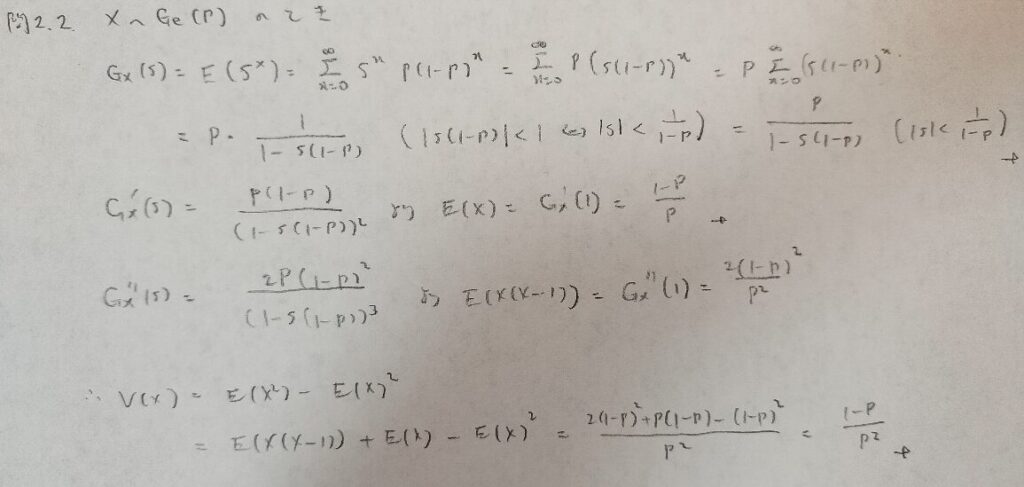
問2.3
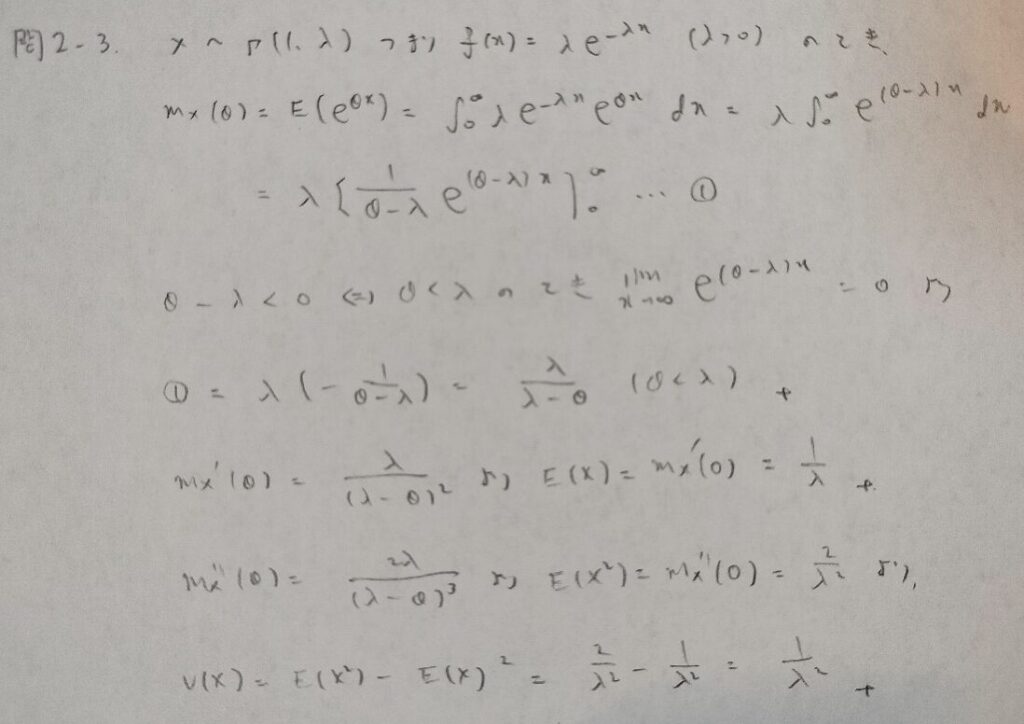
第2章メモ
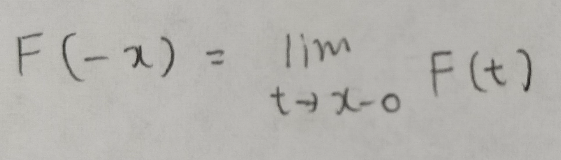

統計検定準1級ワークブック解説:第3章『分布の特性値』
例3−1
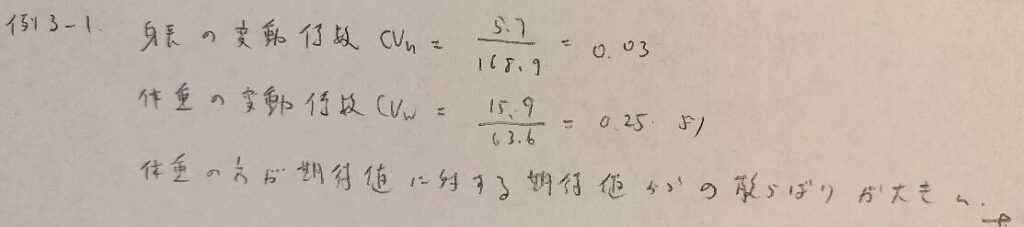
例3−2
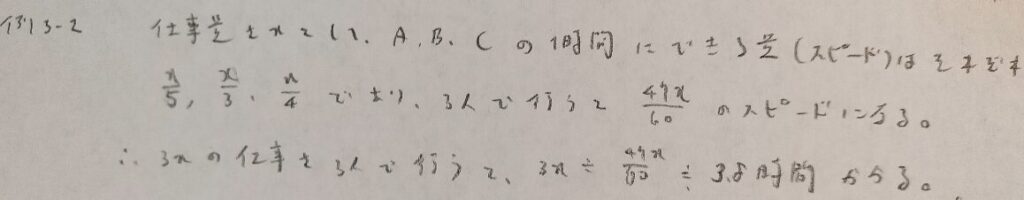
問3.1
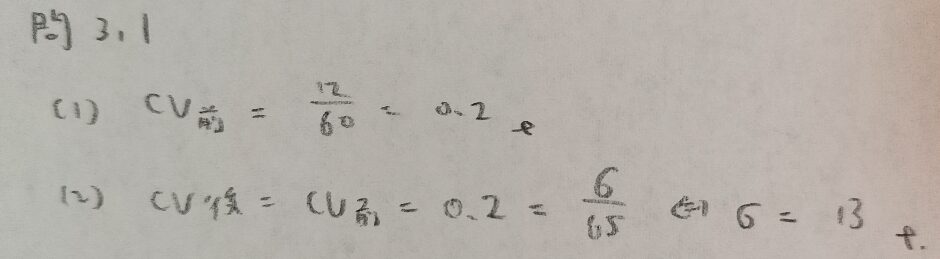
問3.2
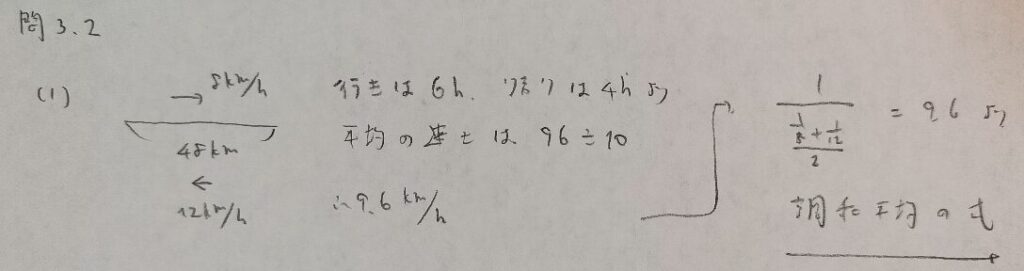
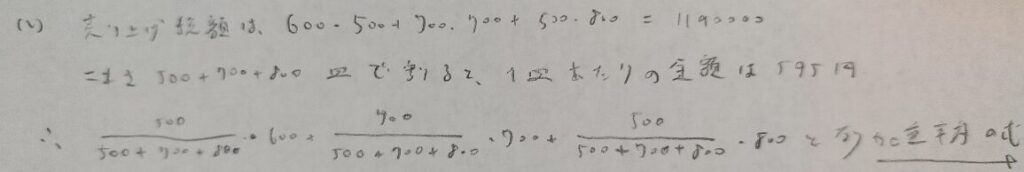
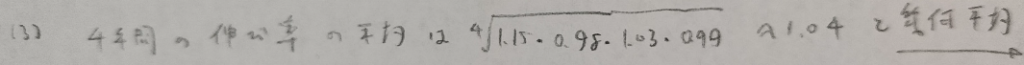
問3.3

第3章メモ

統計検定準1級ワークブック解説:第4章『変数変換』
例4−1
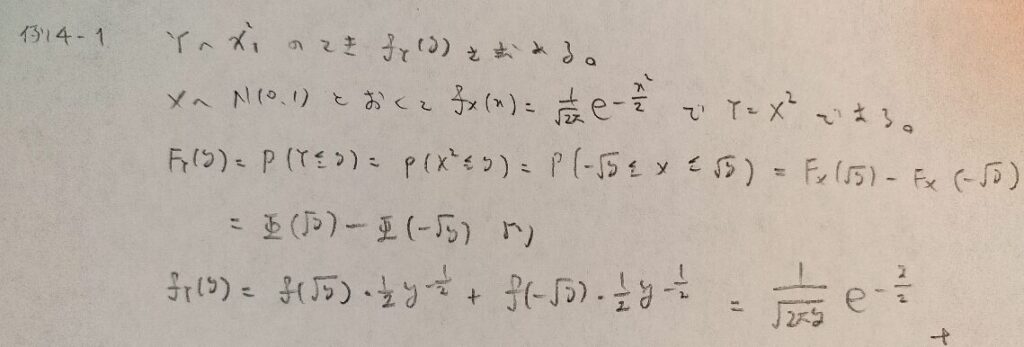
問4.1
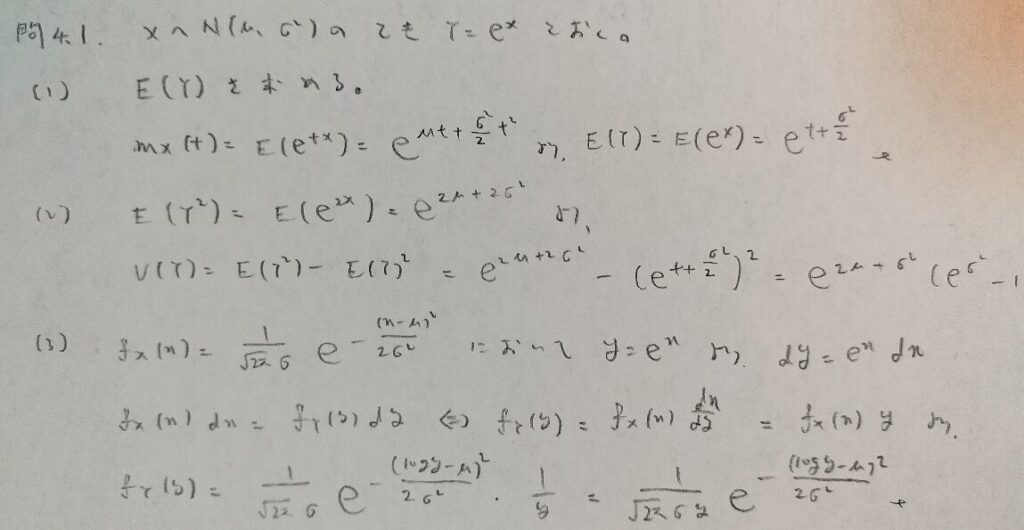
問4.2
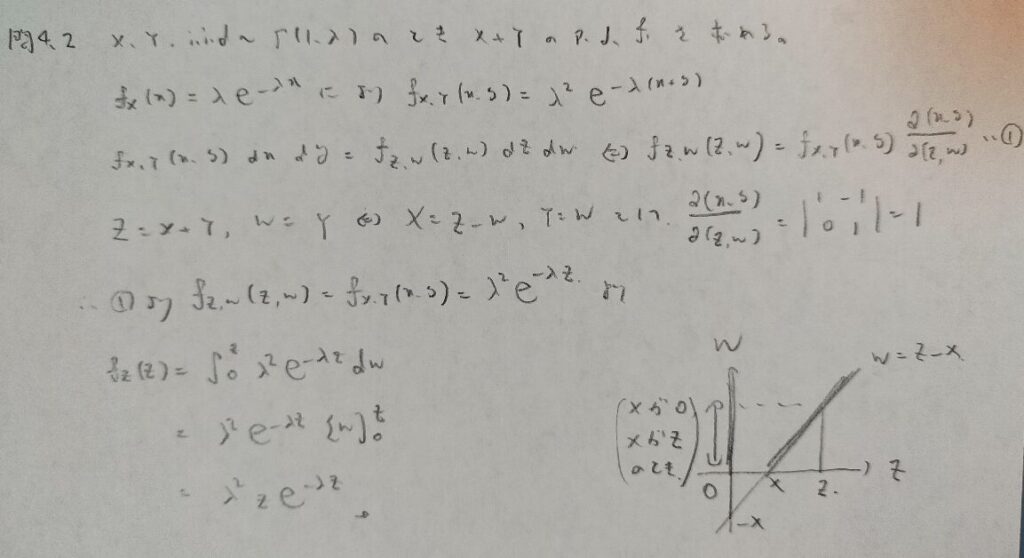
第4章メモ

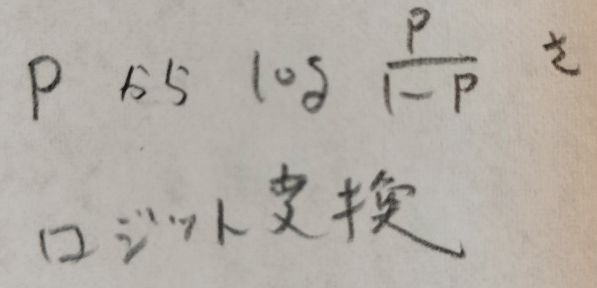
様々な誤差が積み重なったデータは正規分布に従い、様々な積が積み重なったデータは対数を取ると正規分布に従う。
その他はベキ乗変換やBOXーCOX変換がある。
統計検定準1級ワークブック解説:第5章『離散型分布』
例5−1

問5.1
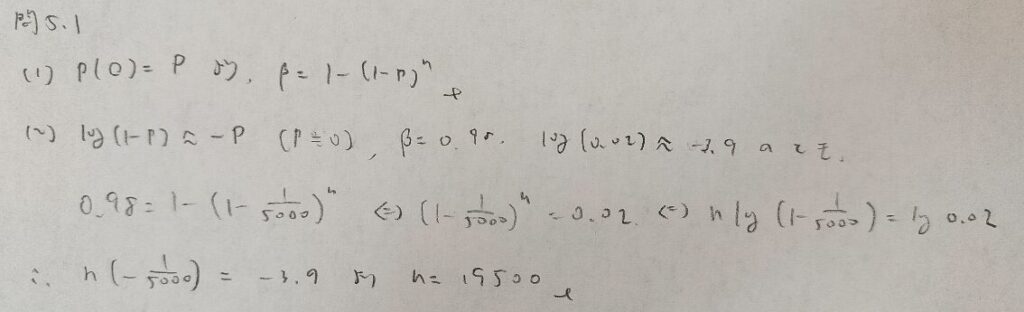
問5.2
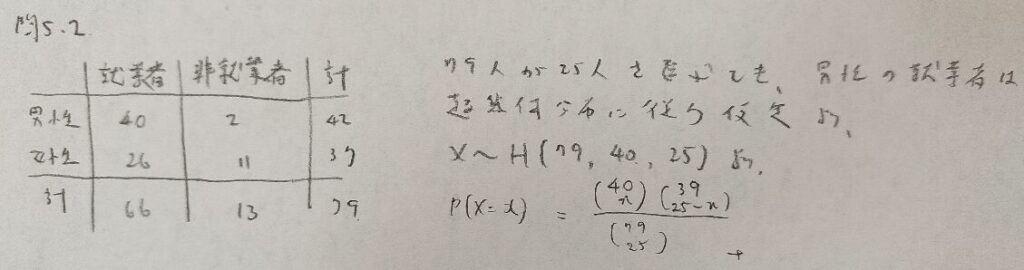
問5.3
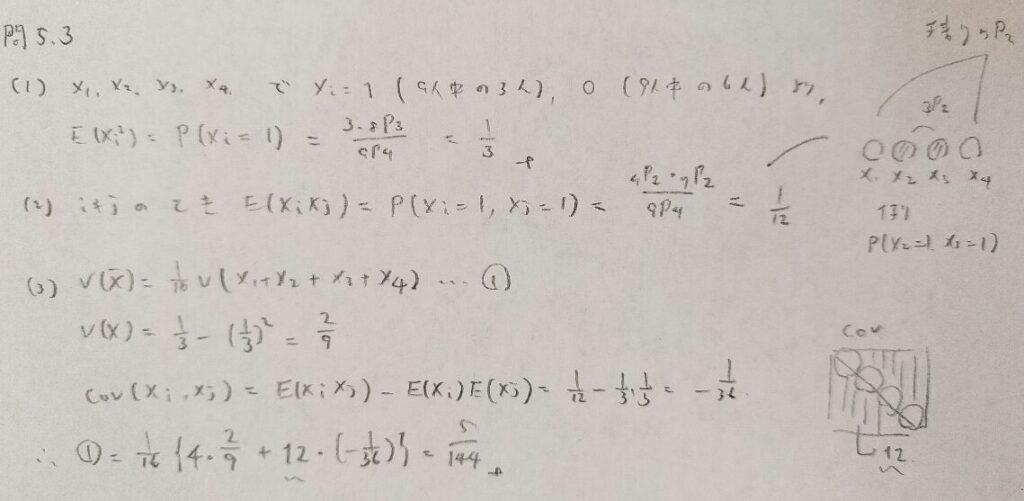
問5.4
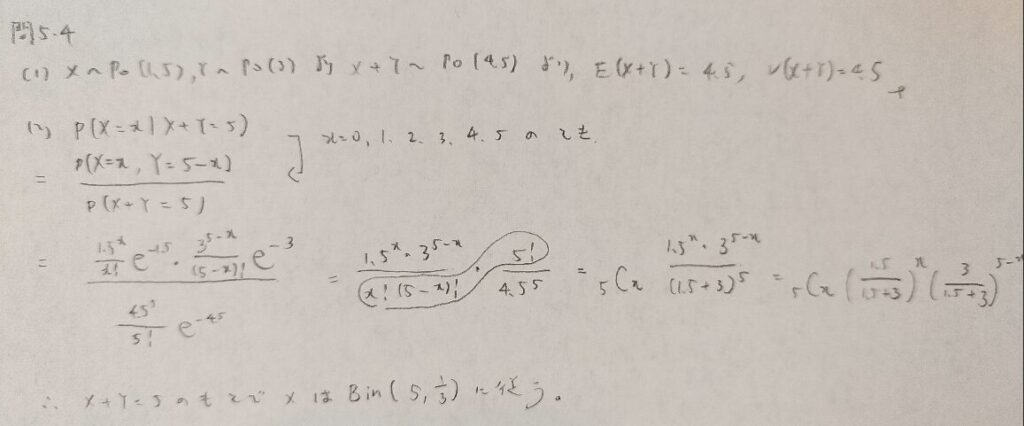
問5.5
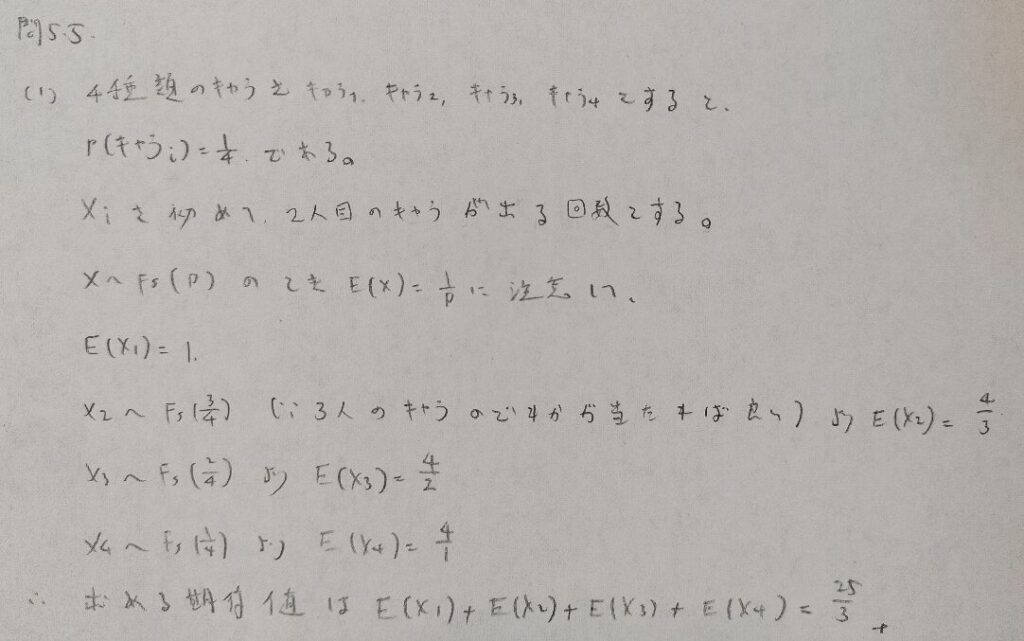

第5章メモ
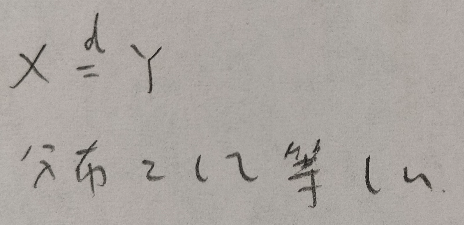
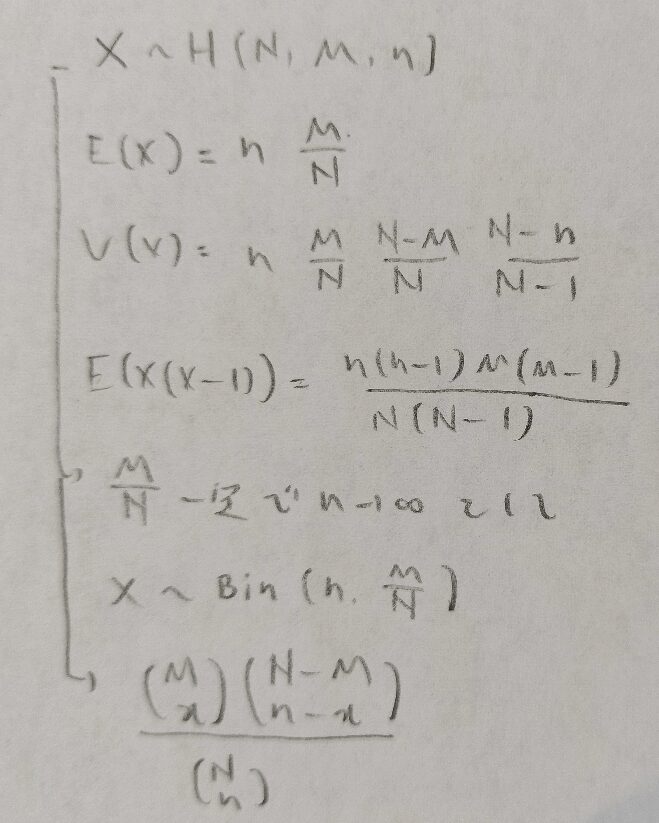
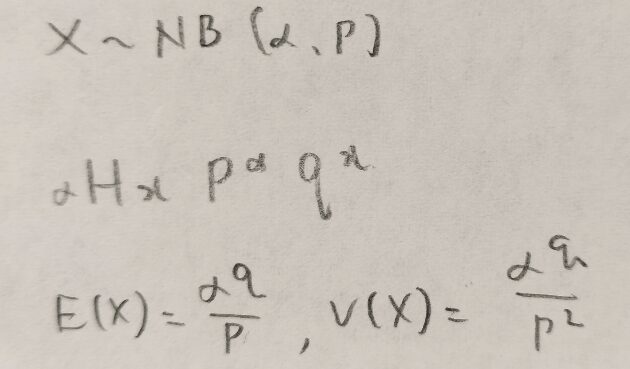
統計検定準1級ワークブック解説:第6章『連続型分布と標本分布』
問6.1
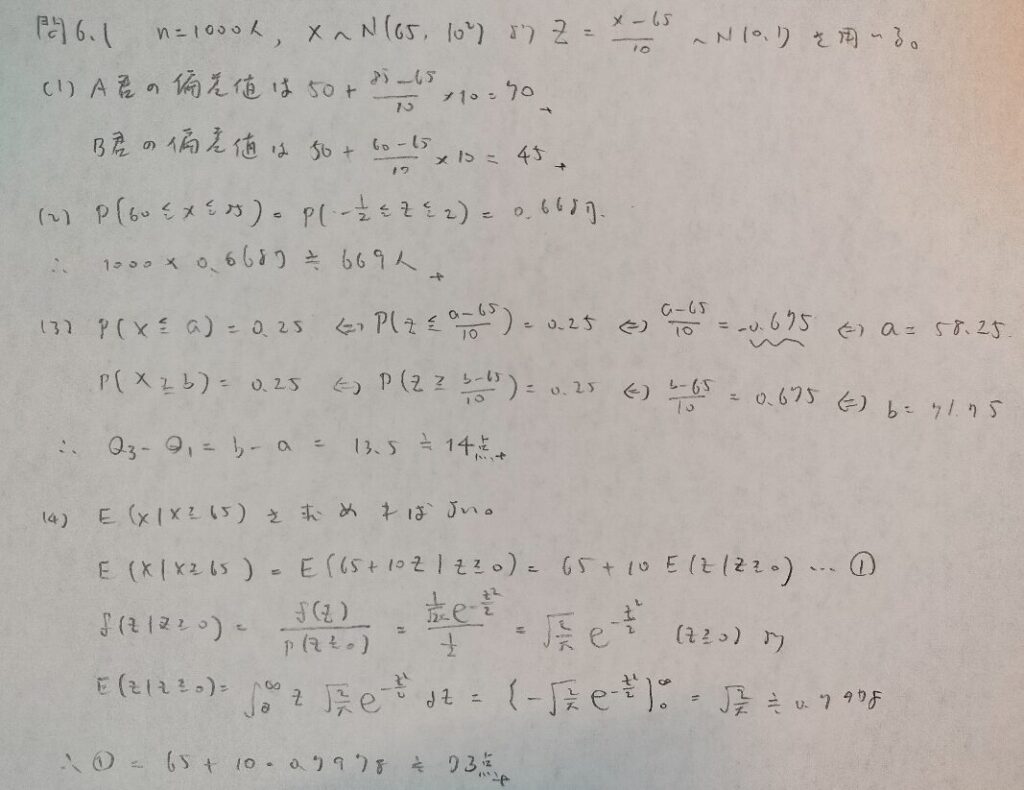
問6.2
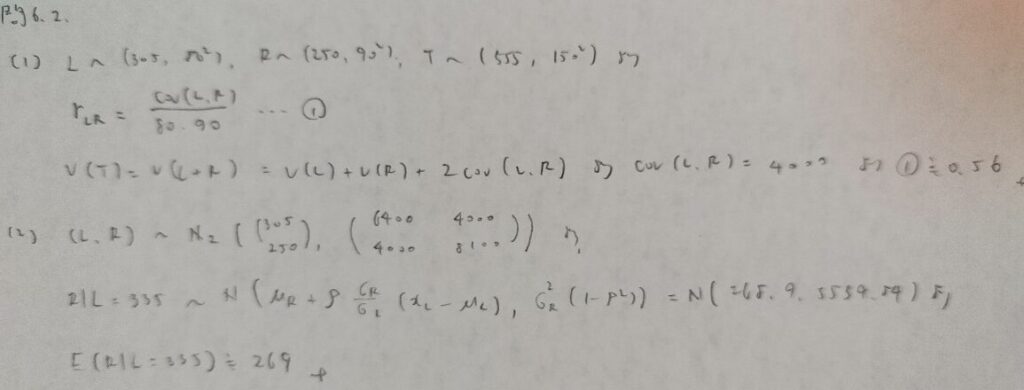
問6.3
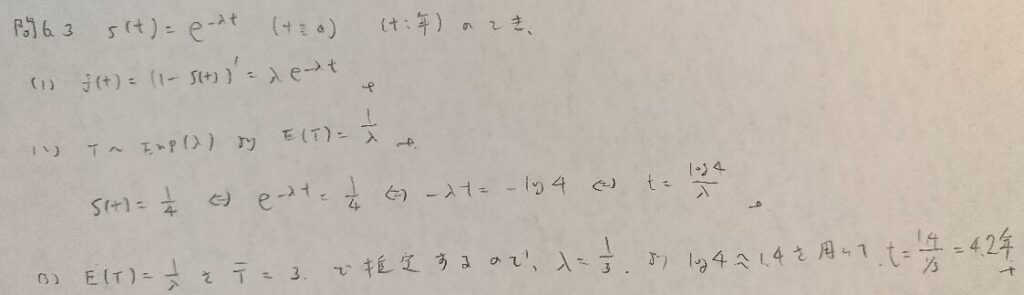
問6.4
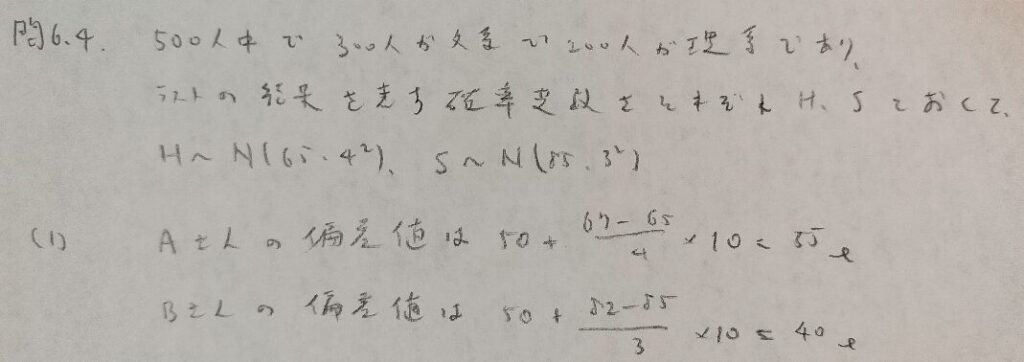
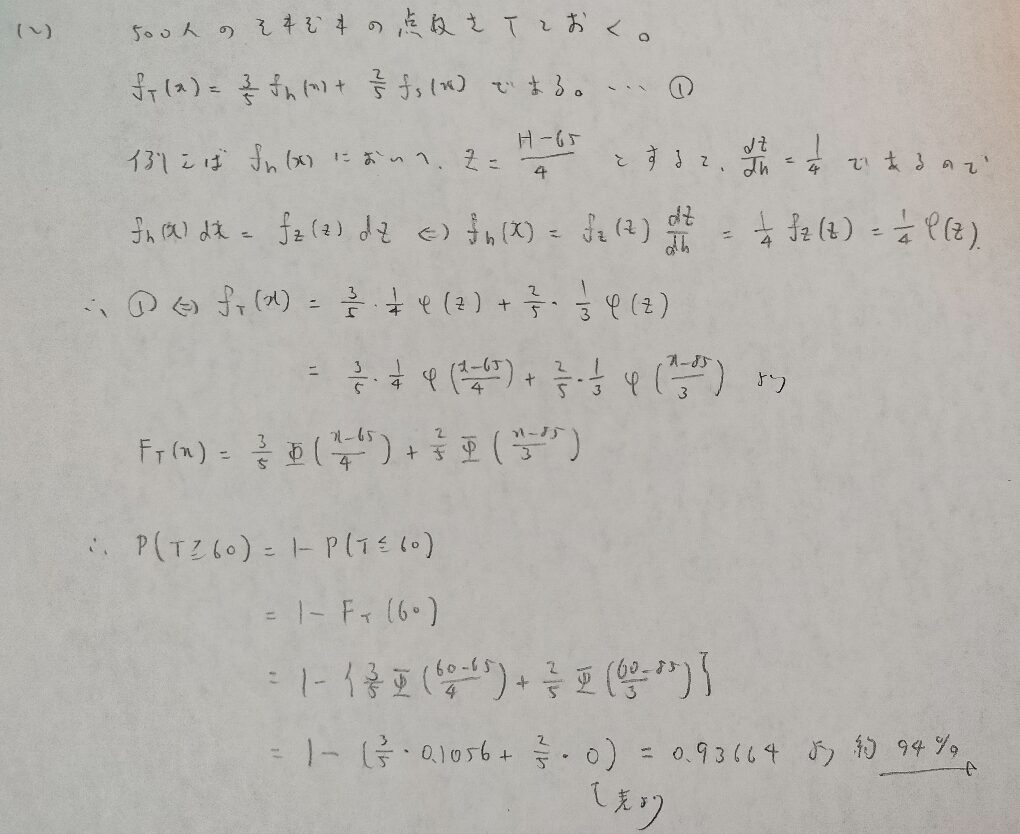
第6章メモ
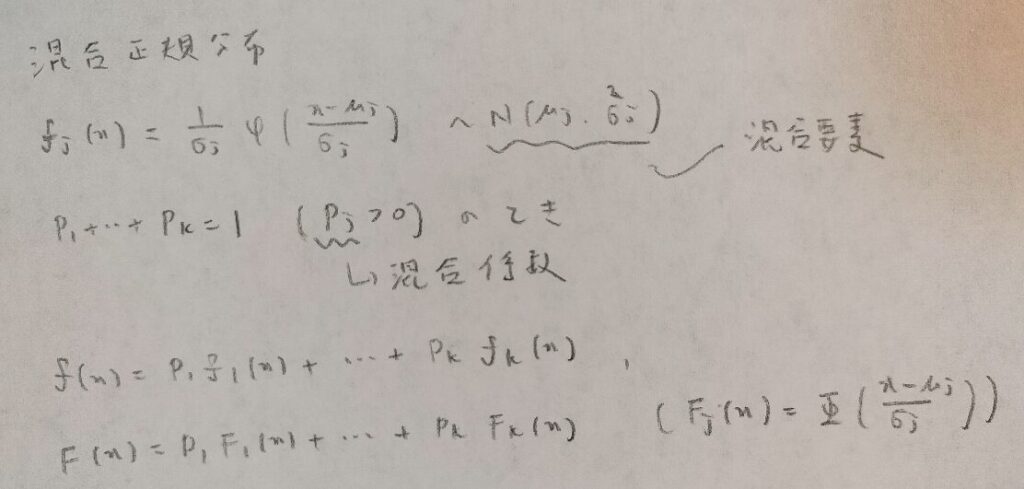
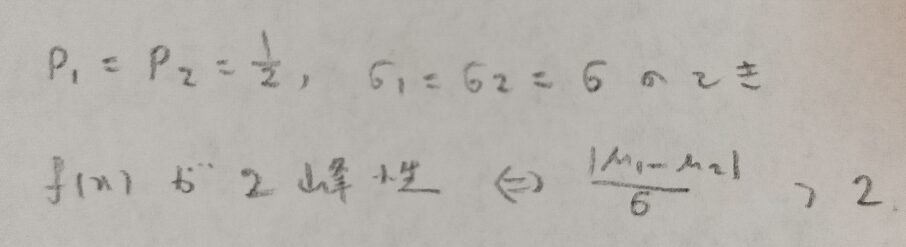
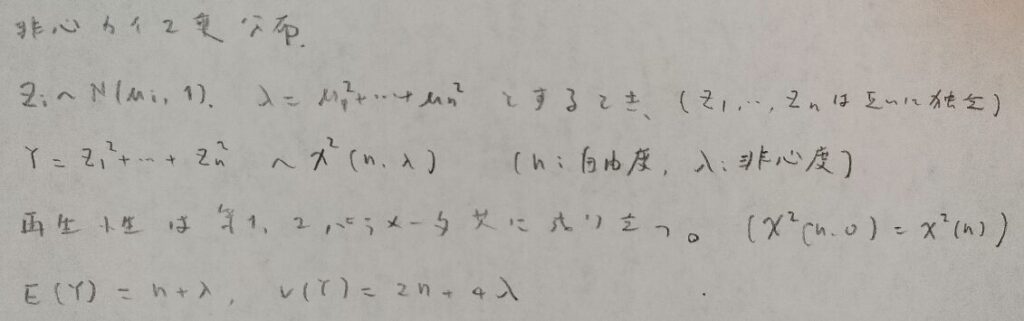
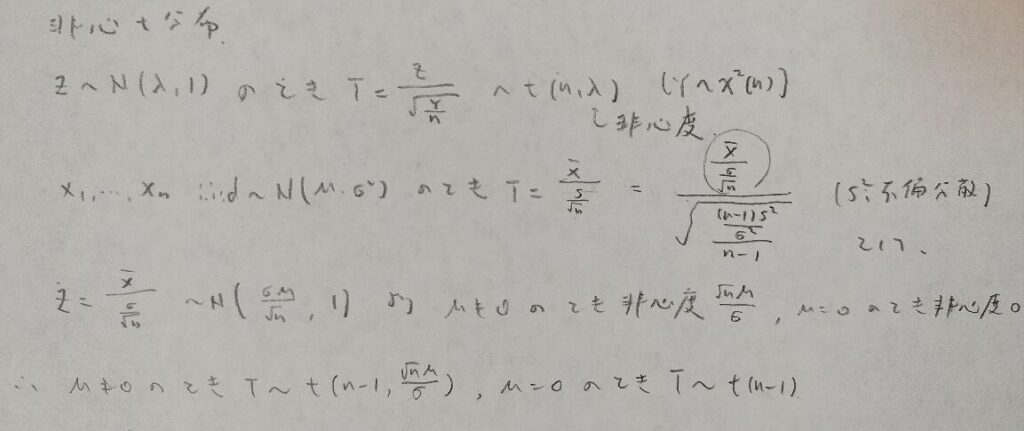
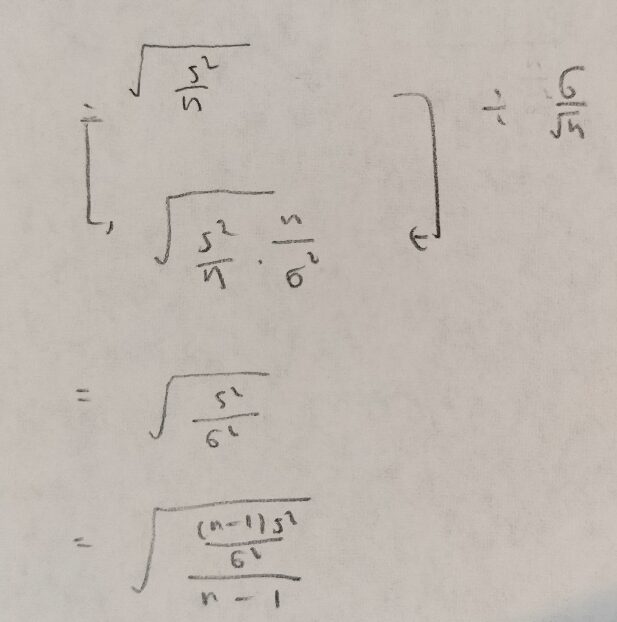
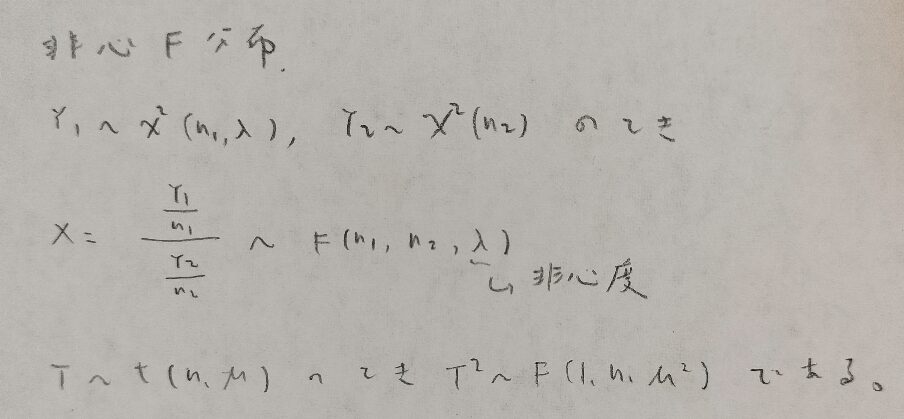
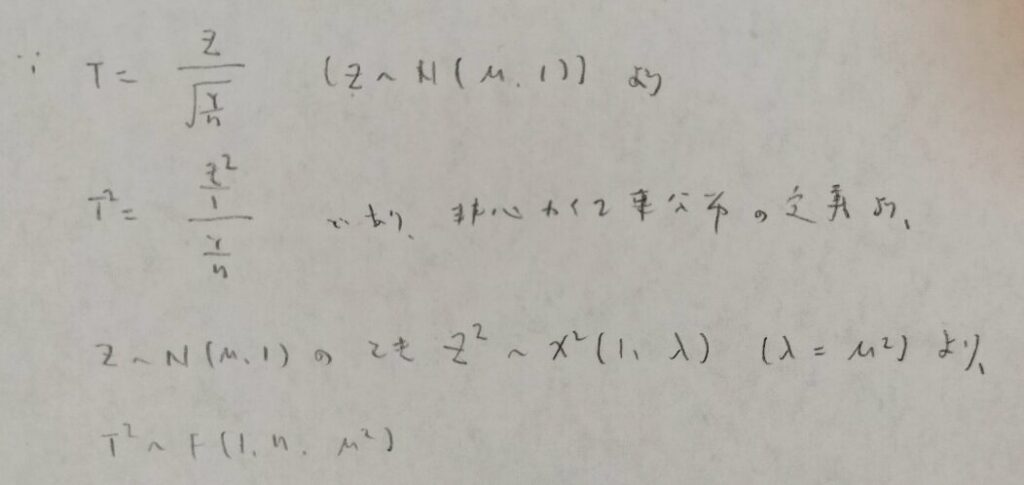
統計検定準1級ワークブック解説:第7章『極限定理、漸近理論』
例7−1

例7−2
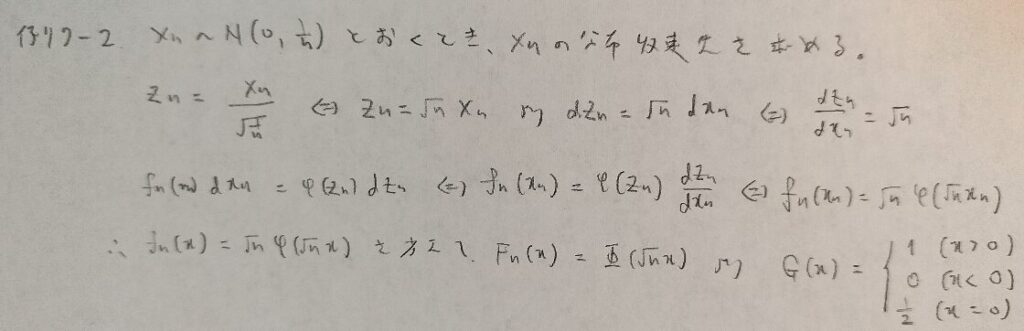
例7−3
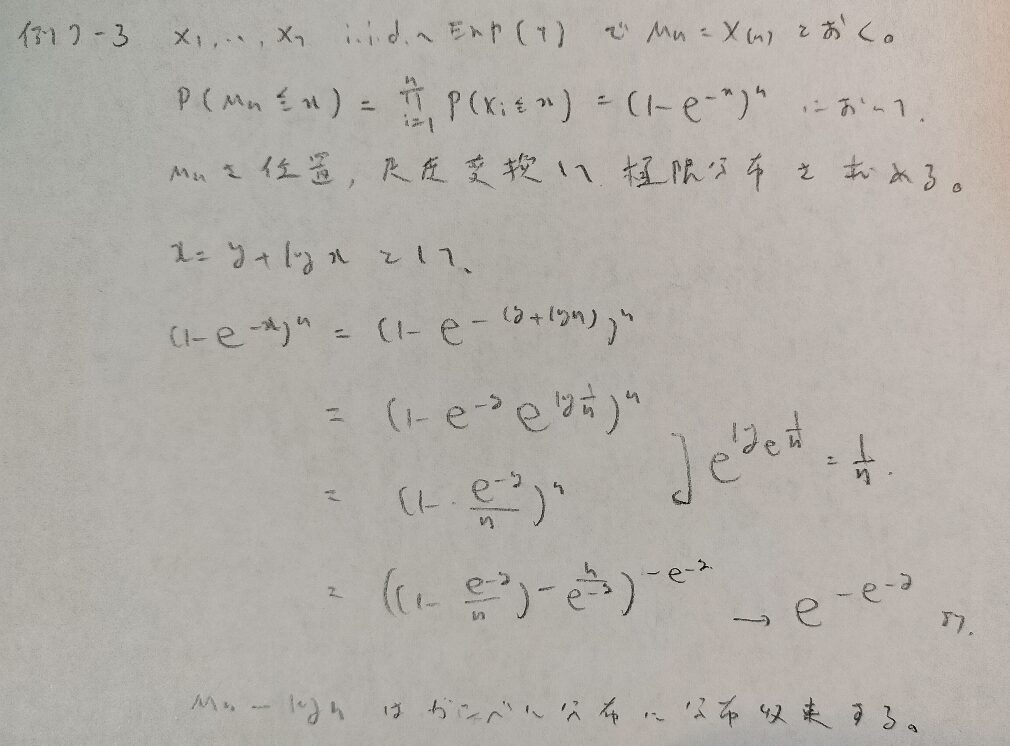
例7−4
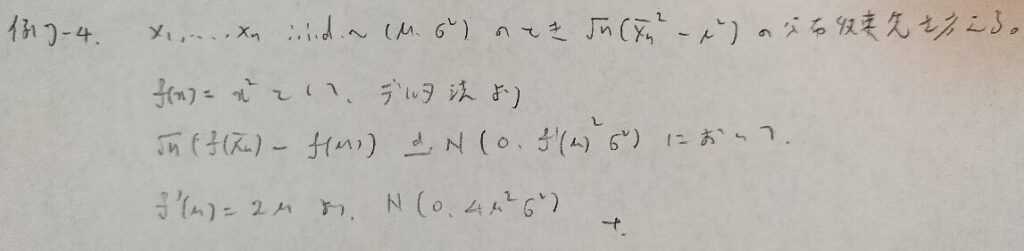
例7−5
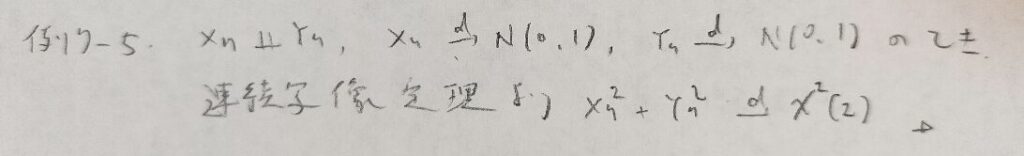
問7.1
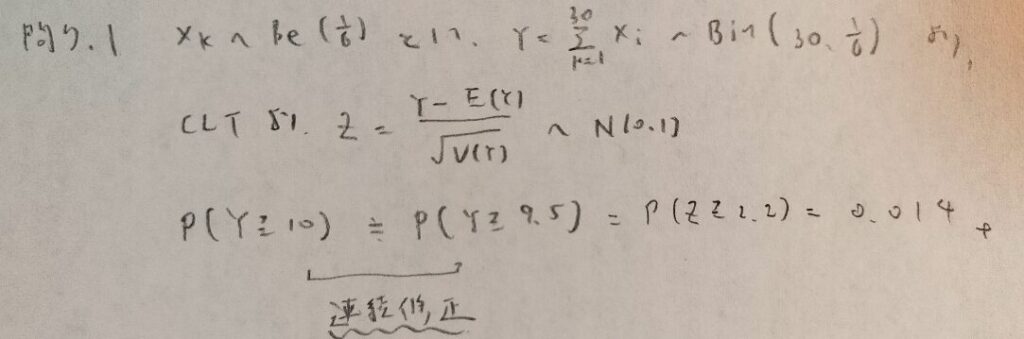
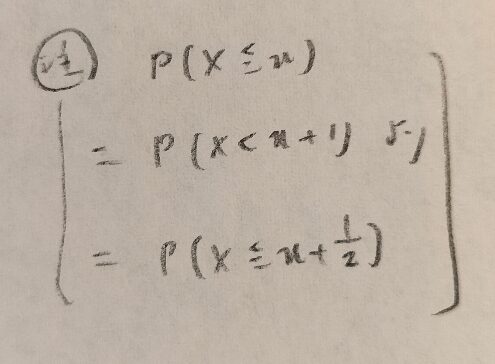
問7.2
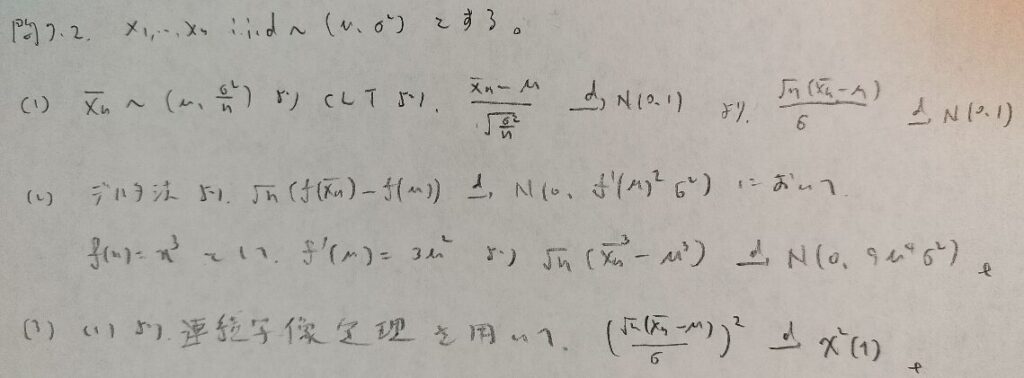
第7章メモ
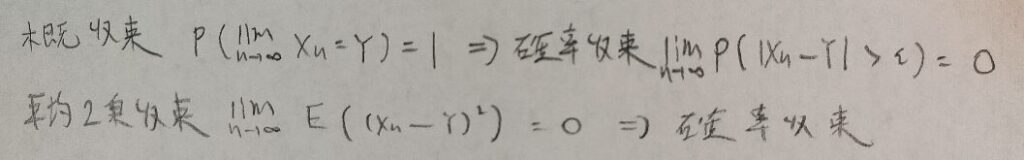
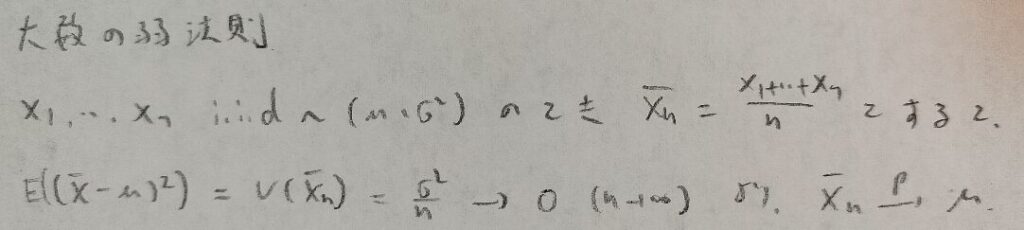
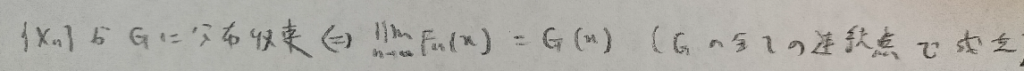
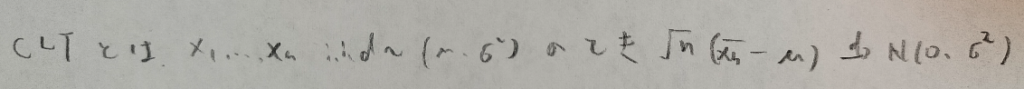
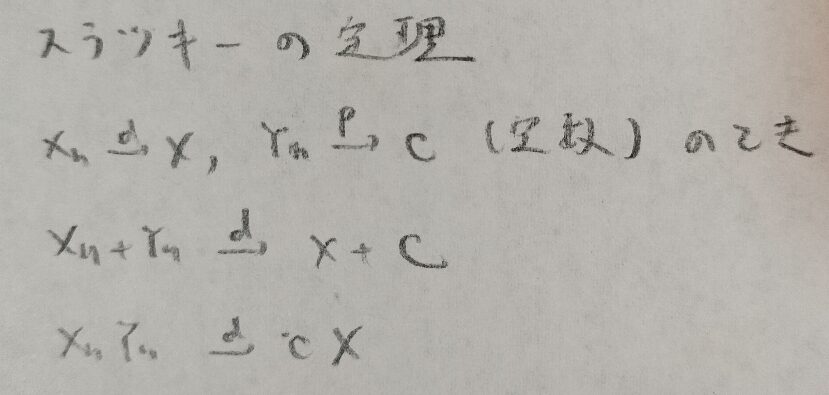
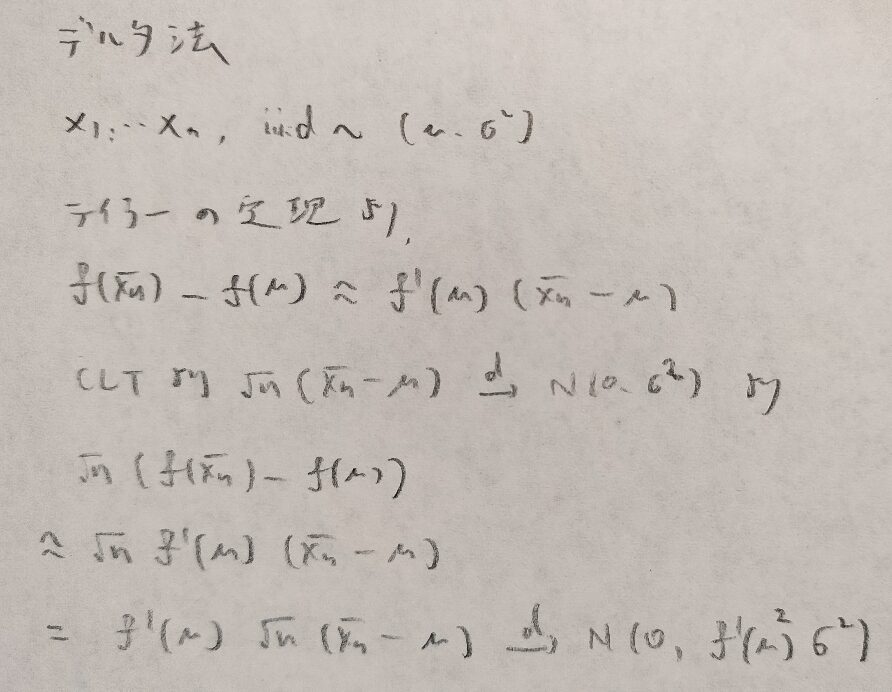

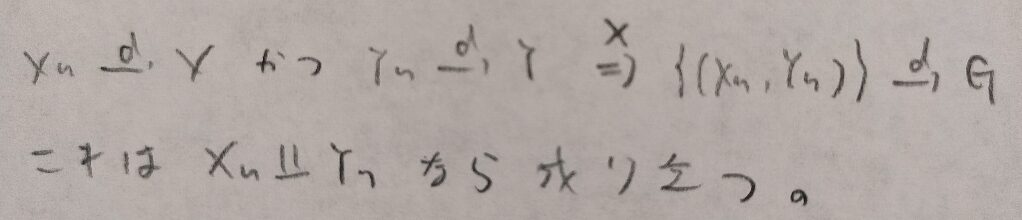
以上になります。『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』は後半から一気に難しくなるので、しっかりと頑張っていきましょう!


