統計検定1級の統計数理に合格するための完全対策の記事になります。過去問の効果よりも『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』の方が学習効率の高かった統計検定準1級と比べて、統計検定1級は過去問の過学習が起きづらい試験でもあります。そのため過去問攻略は合格における必須事項となります。それと同時に統計検定1級の統計数理は実は満点を取るのが、統計応用よりも難しいことは良く知られています。どの程度の難問が出題されているのかも、本記事で学習していただくと体感できます。
統計検定1級の合格者から最も良いとされている参考書が統計検定1級攻略のバイブルである『現代数理統計学の基礎』です。本記事も本書を参考にして問いている問題が多数あります。1級受験者は是非とも所持しておきたいアイテムとなります。
この記事は、統計検定1級の統計数理にしっかりと合格するために作られています。統計数理は毎年大問が5題出題されますが、本番で「どれを解こうかな?」と迷っている時間がかなり命取りになります。また毎年難問と呼ばれる問題が1〜2問ある確率が高く、またそれらの問題は再度出題されることは稀です。つまり、難問を除く≒確実に得点したい大問3題に集中して解説していきたいと思います。
実際、難問と呼ばれる問題は公式参考書である『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』に由来することが多いです。そのため難問対策(頻出問題以外の過去問対策)は下記の書籍で学習するのが効率が良いと考えます。
『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』は特に統計応用のための参考書という感覚ですので、あらかじめ入手しておくことは理に適っていますね。
その通りです。頻出問題や典型問題は『現代数理統計学の基礎』で、応用問題や難問は『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』を片手に実力を養っていくのが最も良い戦略だと確信しています。
統計検定1級の過去問の解説記事を大きく3つに分類して既に掲載しておりますので、過去問集(リンクは下述)と併せてご参照ください。
統計検定1級の統計数理の過去問解説→このページ
統計検定1級の統計応用の共通問題の過去問解説→こちら
統計検定1級の統計応用の人文科学の過去問解説→こちら
統計検定1級で最も難易度が高い小問があるのが、実はこの統計数理の難問なのです。「そもそも解法が思いつかない」か「計算量が膨大でその小問だけで試験時間を全部使ってしまう」レベルの最難問も見受けられます。よって合格のためには、そういった難問を避けて、確実に取れる問題を減点されることなく解き切ることが最重要となります。
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定1級 公式問題集[2016〜2018年]
日本統計学会公式認定 統計検定1級 公式問題集[2019~2022年]
各年度によって傾向が見られるようです。合格率も参考にしながら一緒に学習を頑張っていきましょう!
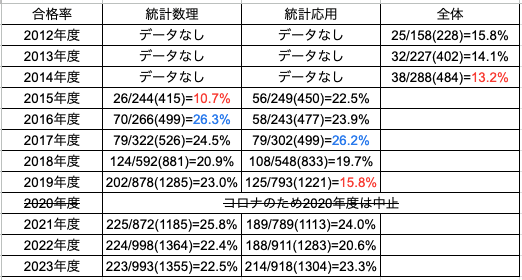
統計検定1級「統計数理」の過去問:2012年
2012年の合否を分ける問題は順序統計量の確率密度関数の導出(おそらく簡易版で良い)とデルタ法の理解です。難問として最強力検定や3変量正規分布が出題されました。特に問5は極めて難易度が高いので、合格のためには問1〜問3までを取りこぼさないことです。全体合格率は15.8%
2012年問1:順序統計量

2012年問2:カイ2乗分布とベータ分布の関係
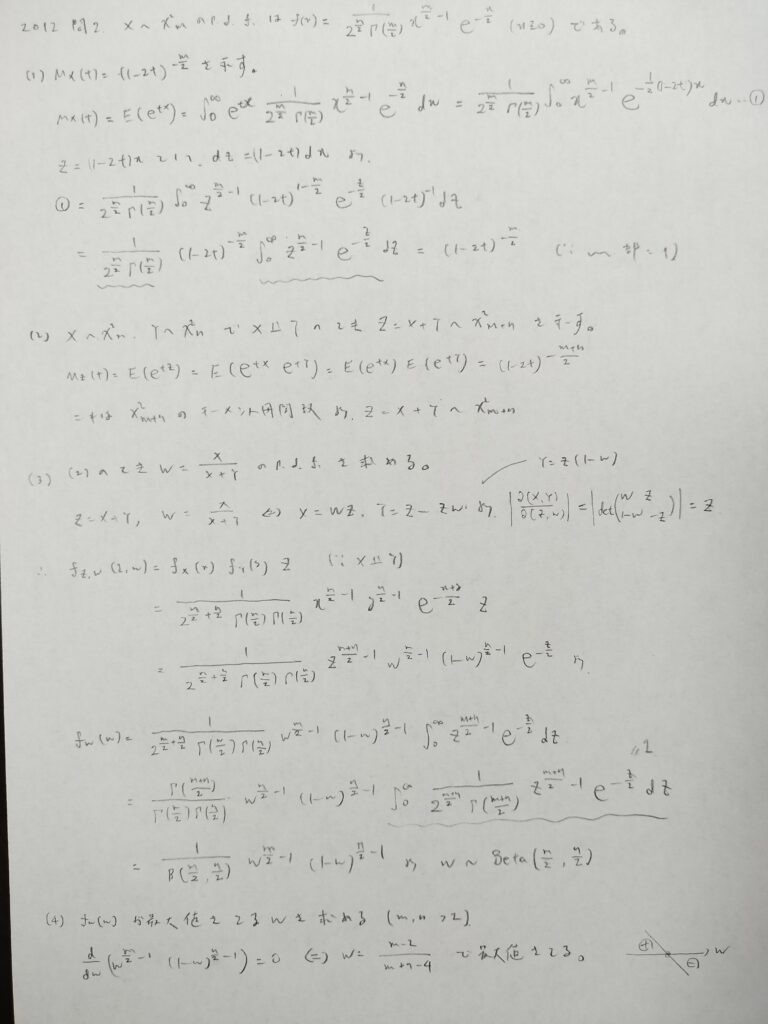
結構な盲点であるカイ2乗分布とベータ分布との関係の問題で統計検定1級の統計数理のバイブルである『現代数理統計学の基礎』でも登場しています。また最後の問題は符号変化に関係する部分がwの1次関数となるので最大値を取ることが確定します。
2012年問3:指数分布とデルタ法

模範解答では漸近分散を一気に求めていますが、「デルタ法を用いよ」とあるのでデルタ法の応用として漸近分散を導きました。
統計検定1級「統計数理」の過去問:2013年
各大問の最後の問題は難しい問題が多いので、3題のうち最終問題以外をしっかりと取ることが合否を分けるセットです。問1はサービス問題のため除外します。2023年の秋現在での傾向を考えると、問1〜3を選択するのが良いでしょう。この中では問2が難しいです。問5は計算量が多いので選択肢から除外し、問4はノンパラメトリック検定ですが、頻度が少ないので『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』での学習をおすすめします。全体合格率は14.1%
2013年問1:一様分布

原題の図から優弧や劣弧という表現をしましたが、実際は円周上に2点を取るということです。
アクチュアリー数学の小問のような問題です。XとYが従う一様分布にどのくらい早く気づけるか?で合否が分かれそうです。
2013年問2:条件付き分布
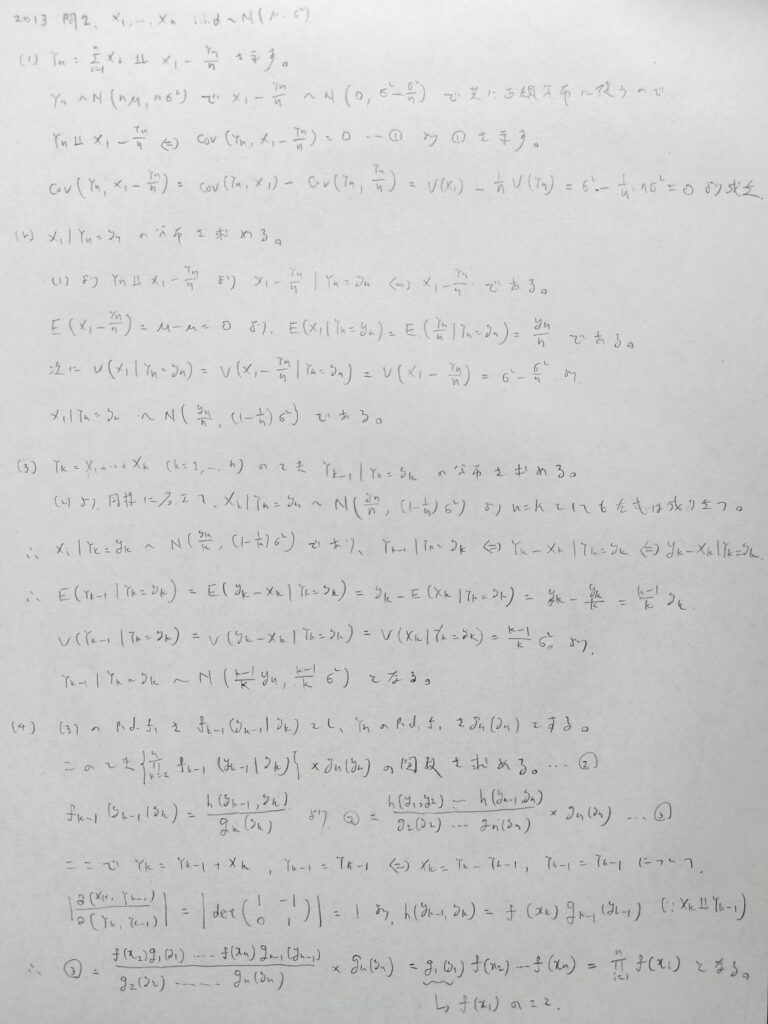
統計検定1級の黎明期の問題ではかなりの傑作問題です。統計検定1級の問題はかなり作り込まれているなという印象です。他の本を探しても類題が登場していない素晴らしい問題です。
最後の2題は分かればすぐですが、その前の問題も含めてセンスが問われる問題で、これぞ合否を分けるという感じですね。
2013年問3:二項分布と被覆確率
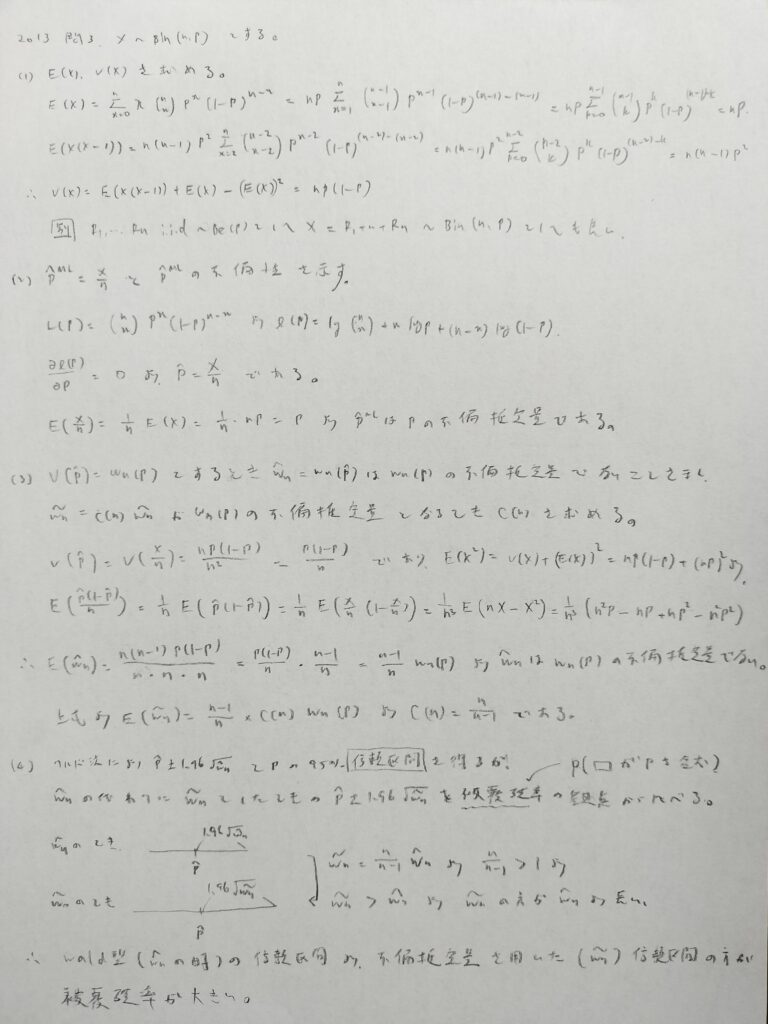
統計量が離散型の場合はワルド型の信頼区間と不偏推定量を用いた信頼区間は一致しないことがある。実際、ワルド型の方の被覆確率は信頼係数に届かないことが多い。また不偏推定量を用いた信頼区間も信頼係数に届かないことがあるが、ワルド型よりはましであることを背景に持つ出題と思われる。
本番で(4)の信頼区間の長さに注目することに気付ければ確実に合格できるでしょう。
実際は(3)の計算に耐えられたか?が合否を分けそうですね。
統計検定1級「統計数理」の過去問:2014年
統計検定1級の統計数理は2014年度と2015年度が難化しています。今年度の中のセットでは問1が最も易しいので選択すべきです。残りは問5の適合度検定は計算量が多いので除外し、問4も行列計算が大量のため非現実的です。そのため消去法で問2と問3を選択せざるを得なくなります。問3は基本的なことをしっかり記述すれば良いので合否を分けたのは問2のガンマ分布だと思われます。全体合格率は13.2%
2014年問1:一様分布と条件付き期待値

条件付き期待値が出てくる意味をしっかりと理解しましょう!『現代数理統計学の基礎』がとてもわかりやすくおすすめです。
(1)が正解できるか?が全てです。基本的な問題なのですがかなりの盲点だと思われます。
2014年問2:ガンマ分布
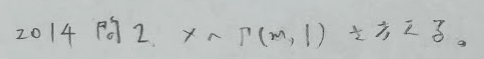
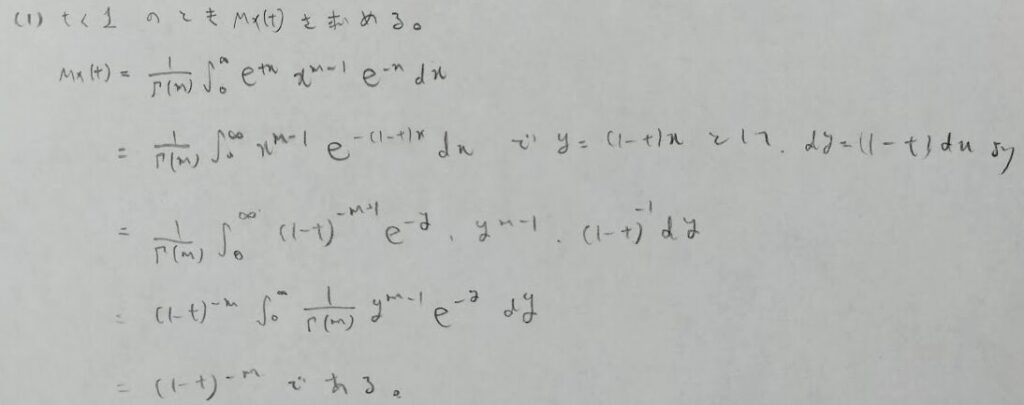
t<1は置換積分の箇所での1-t>0を解いた結果から来ています。そのため置換積分後の積分区間に変化はありません。(上端と下端が逆転しません)
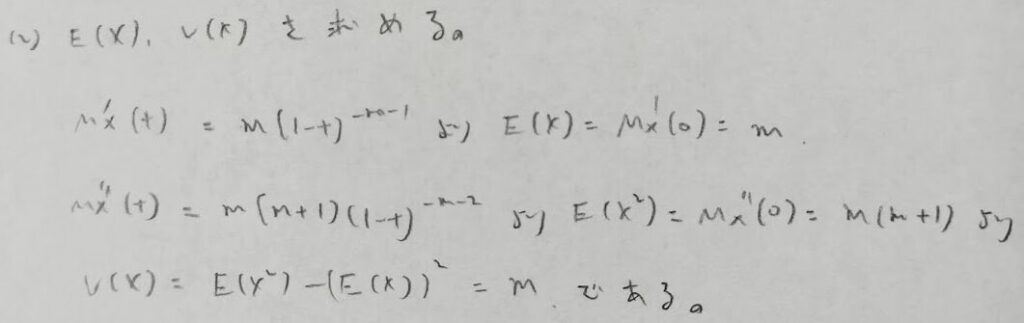

おそらくこの問題が解けたか?がボーダーラインだと思われます。

この解法は統計検定1級のバイブル『現代数理統計学の基礎』に丁寧に解説されています。知っていれば即答できる問題でした。
順序統計量関連の話題を一気におさらいしたい方はこちらをご覧ください。ベータ分布や多項分布の話題からスムーズに順序統計量が理解できるように解説しています。
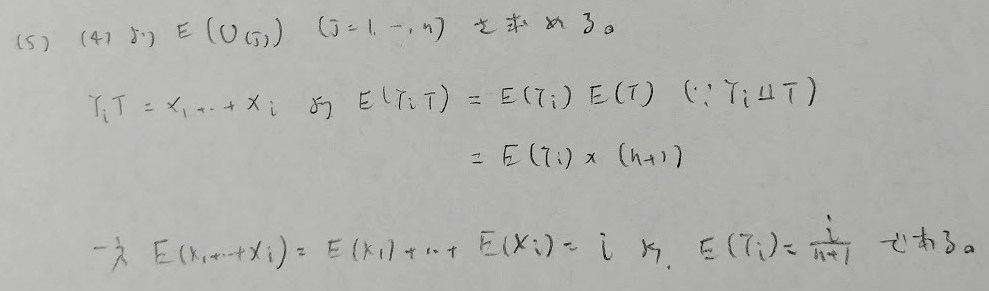
この問題も結果はわかるのだけど、解き方が気づかないと解けない問題でしたね。
統計検定1級の統計数理は2014年と2015年の問題の難易度は別格です。
2014年問3:信頼区間

最後の問題では正規分布では独立と無相関が同値だという内容を用いることに気付けなければ解けないので、気づけるか?という点でかなりの難しさです。
前問と比べると計算量は一部を除いて少ないので、最後の問題以外でしっかりと正解したい問題ですね!
統計検定1級「統計数理」の過去問:2015年

統計検定1級の統計数理で文句なしでの最難関のセットです。難易度が異常です。どの問題を選択しても合格ラインの6割を突破するのは厳しいでしょう。また小問が多すぎです。特に問5は小問が6つもあり1つ1つが重たいです。問4は適合度検定にちなんだ問題で計算量が多く、トリッキーな考えをする問題も多々あります。どの3問を選ぶかは消去法で問1〜問3になります。このセットの中では問2で1完できないと不合格でしょう。この時点で2015年度の統計検定1級の統計数理の合格ハードルが跳ね上がります。問3で半分くらい粘って、残り時間で慎重に計算しながら問1で取りこぼさない作戦しか合格への道はないと思います。合格率は10.7%
2015年問1:正規分布と推定量

2015年度の統計検定1級の統計数理の中では2番目に易しい問題であることに驚きを隠せません。高次モーメントの計算が遅いとその時点で不合格になります。また最後の問題では平均二乗誤差の分解も問われており、そこをクリアしても最後の最小値の計算が待ち構えていて、計算量が本当に半端ないです。
平均二乗誤差は統計検定準1級(合格体験記はこちら)の内容ですので『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』での学習がおすすめです。
2015年度の統計検定1級の統計数理の最難関さが伝わってきます。難易度がやばいですね。ただしこの問1の中に大事なエッセンスがギュッと詰まっています。試験問題としては難しいですが、学習用教材としては最高の教材です!
『現代数理統計学の基礎』の演習問題が解けないと太刀打ちできません。未読の方は演習問題だけでも解いておいた方が良いです。
2015年問2:p値と検出力と一様最強力検定
2015年度の統計検定1級の統計数理では最も簡単なセットなので、ここで1完できないと不合格になります。
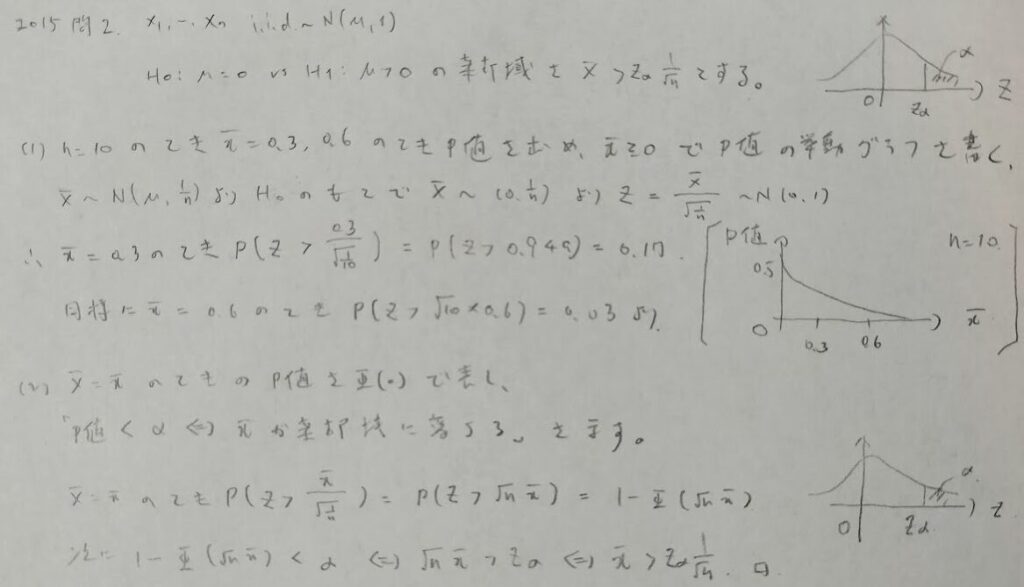
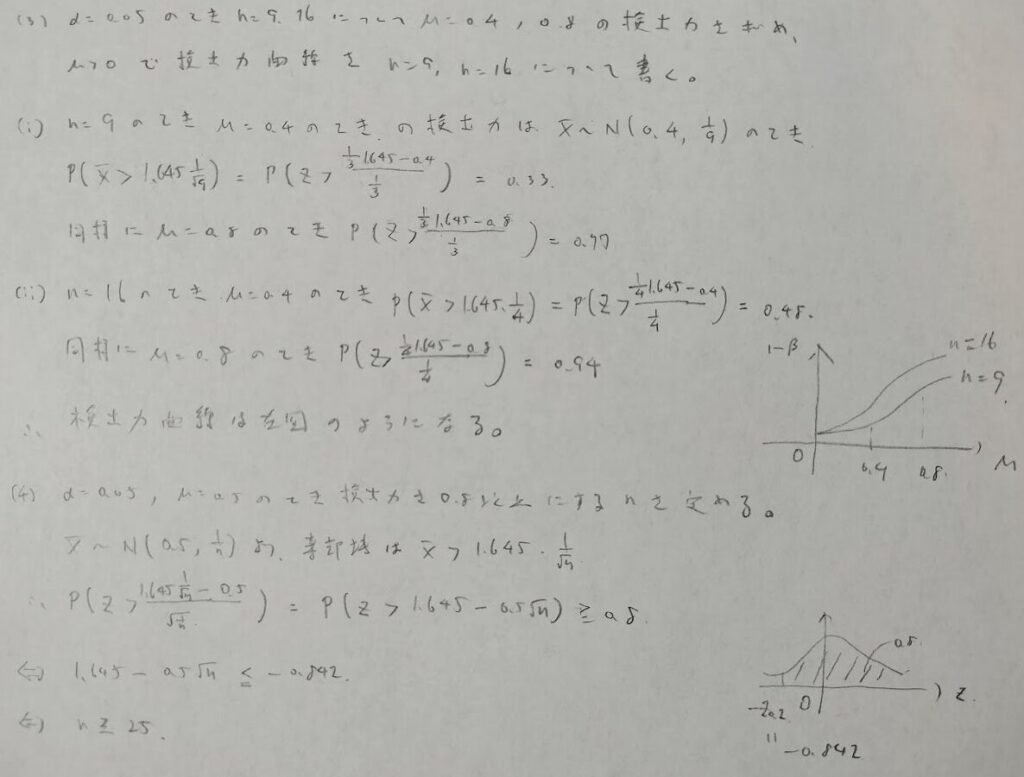
少し変形すれば検出力曲線は分布関数のグラフを変換したものだとわかるので、滑らかな曲線となります。
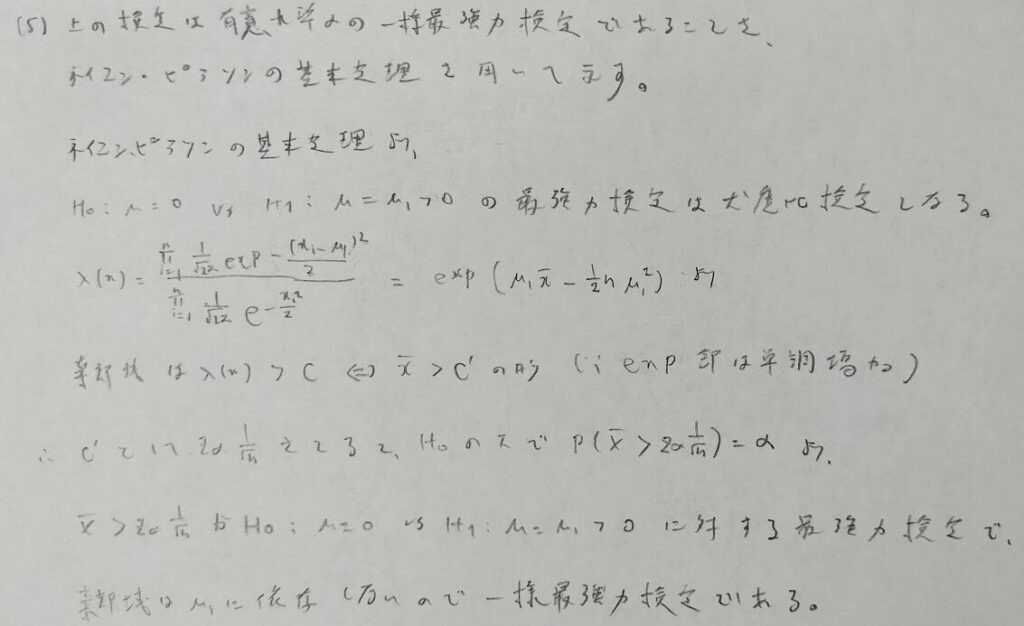
2015年問3:重回帰分析
かなり重たい問題ですが、それでも部分点は狙いやすい大問です。(2)までを確実に取ってあとは諦めることが合格への戦略としては正しいと考えます。(1)の正答までの距離が長いのが難易度の高さを引き立てています。
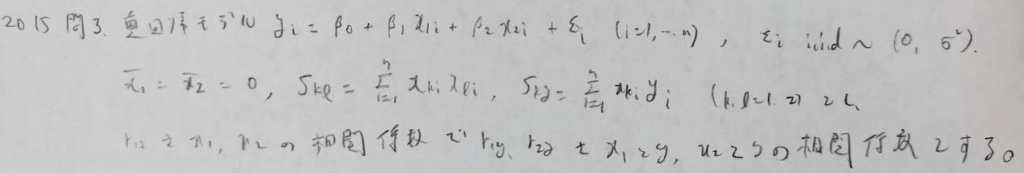
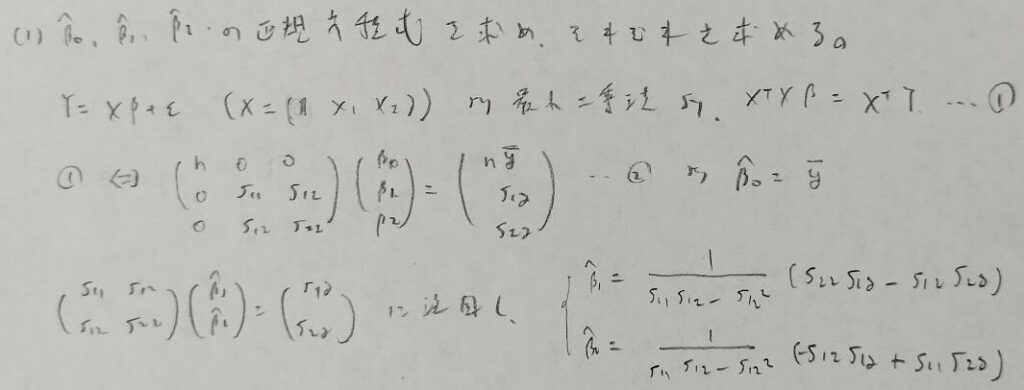
統計検定1級の制限時間の中では特に断りがない限りは正規方程式は暗記していって差し支えないと思います。そうでないとこの問題だけで大変な時間を浪してしまいます。
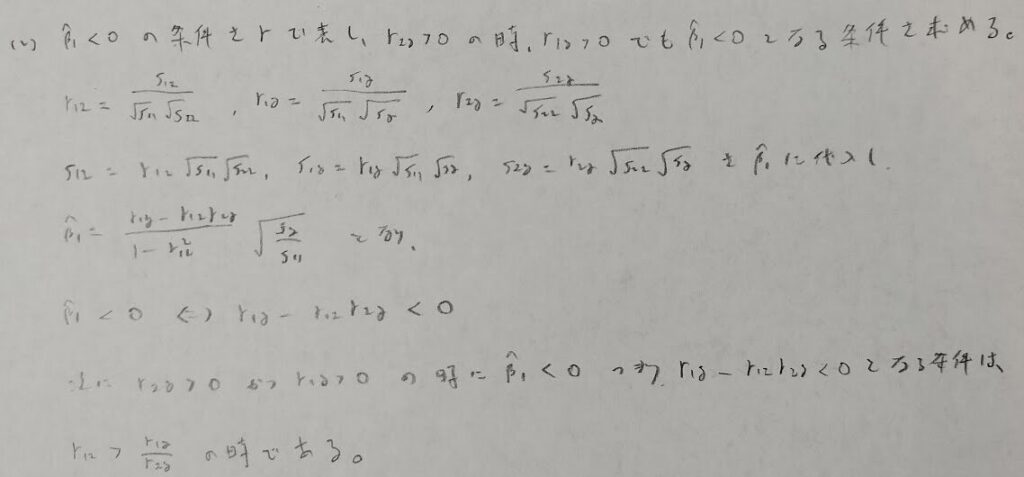
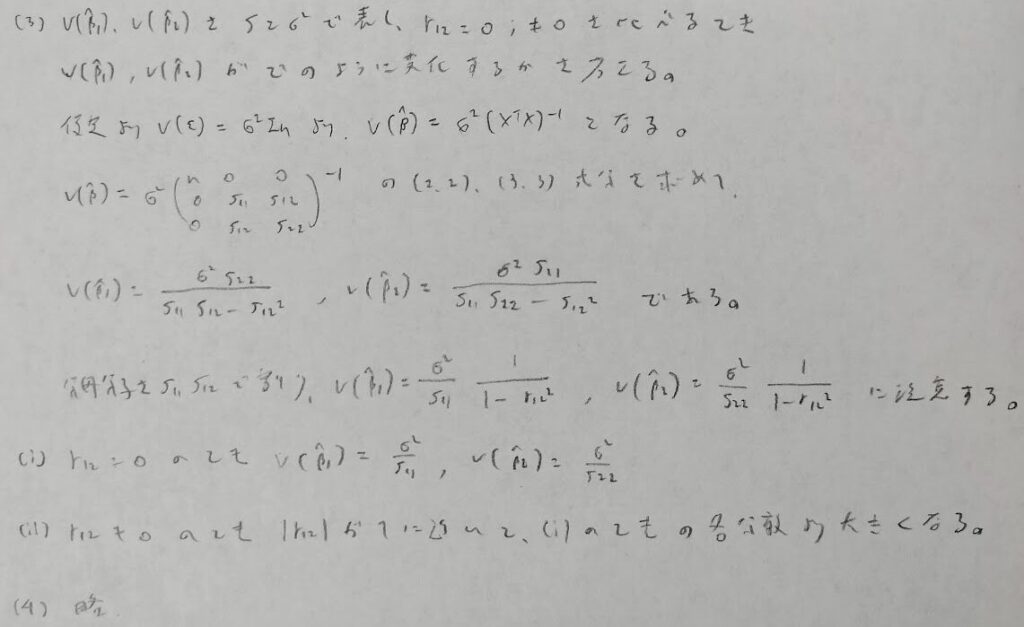
最小二乗推定量の分散共分散行列は、誤差分散の分散共分散行列が単位行列の母分散倍の時に、有名な公式が成立します。またこの公式も覚えておかないと時間内に解き切るのは無理です。
あれ?最後の問題はなぜ略なのですか?
思い切って略にした理由は、(3)までで十分な重量級の計算をこなしており、さらに(4)ではそれをはるかに上回る計算量の問題で、統計検定1級の過去問では2023年の秋現在で類題の出題はないため、学習効果が落ちると判断したためです。というより(3)まで本番で解けたら絶対受かるのでご安心ください。それだけ統計検定1級の2015年度の統計数理は最難関のセットなのです。
統計検定1級「統計数理」の過去問:2016年
2015年度の最難関のセットと変わって大幅な易化が起こりました。問5は明らかな難問なので除外し、問1〜4までどれを解くかで迷います。問3の最後は有名不等式を知っているか?の問題なので今回は除外。問4のモンテカルロ法は新傾向なので以後出題される可能性があり、選択して解説します。すなわち問1、問2、問4を選択します。合格率は26.3%
2016年問1:正規分布と推定量
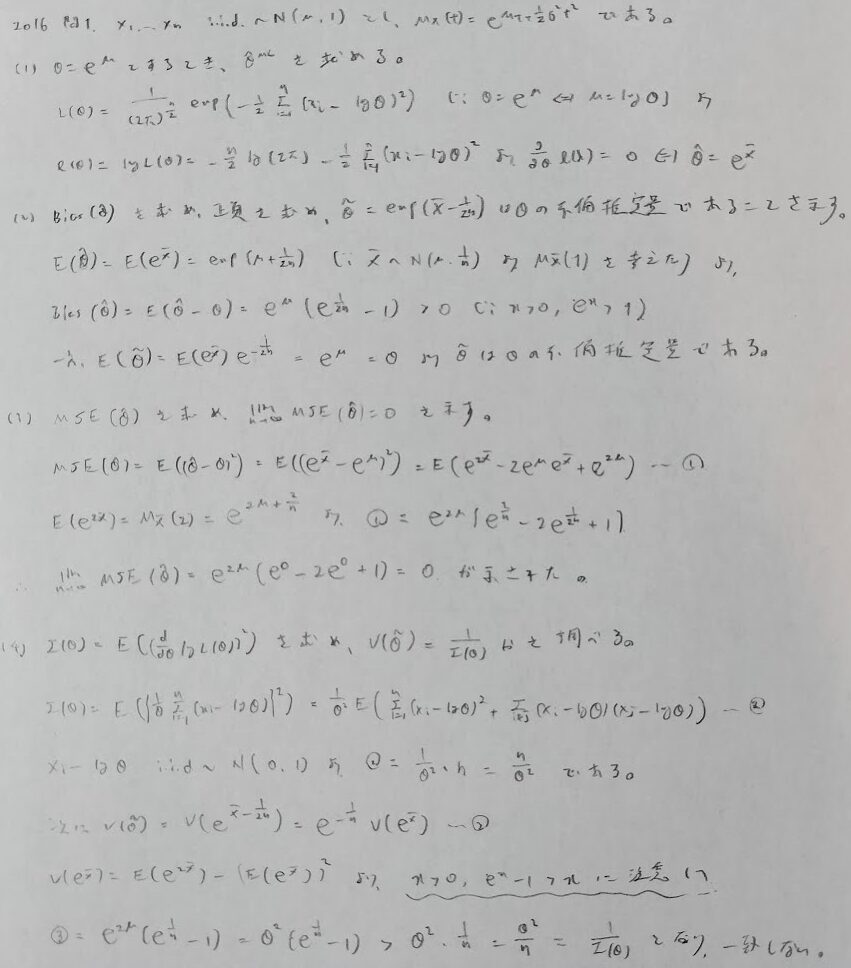
バイアスは新出です。2015年度と難易度は全く違いますが、いろいろな事柄を問うという出題背景は変わっていないですね。
最後の問の波線の有名不等式(指数関数のマクローリン展開の1次近似)を用いるところが難しいですが、気付けなくても強引に証明(確認)は可能です。
2016年問2:ガンマ分布と推定量

最後の問は積分区間のミスに注意です。
別解としてモーメント母関数から考える方法もあります。
2016年問4:モンテカルロ法
今後大事になりそうな重要問題です。一様分布との関係性を理解しましょう!
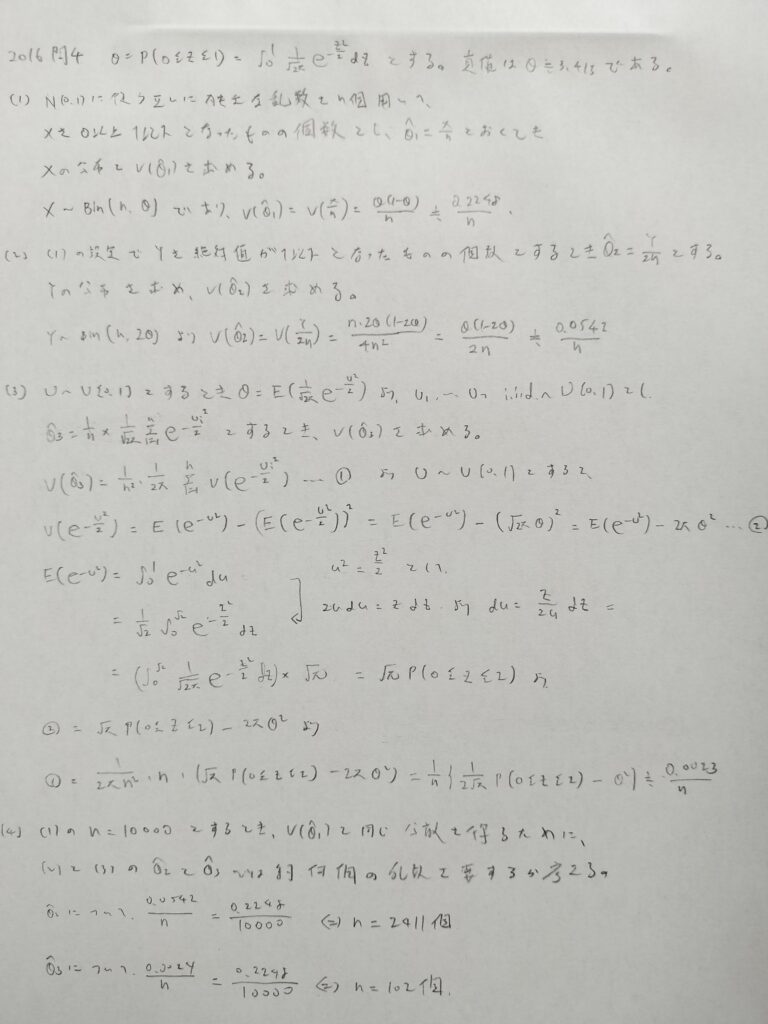
かなり面白い問題です。最後の設問で精度を保つために必要な乱数の個数の桁数が異なる結果が興味深かったです。
今後の統計検定1級の統計数理でも狙われそうなパターンになりそうですね。モンテカルロ法は『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』にいくつか例が載っていてわかりやすいです。
統計検定1級「統計数理」の過去問:2017年
前年と引き続き易化傾向です。今年度の問題は問1〜問5すべての問題が易しい(2015年度のような最難関の年度と比べてです)という現象が起きました。そういった意味でどの3問を選択するか悩むところです。最後の小問が確実に取れるか?で判断しましょう。1問1問の問題が演習問題として最適なのですべて取り上げます。各大問の最後の問題の難易度を考えると高得点を狙う場合は問1〜問3を選択すべきでしょう。合格率は24.5%
2017年問1:歪度と尖度

頻出の計算ですが、初見だと手詰まる可能性のある問題です。試験問題として十分な役割を果たしていると思います。

歪度と尖度は0に近いほど正規分布っぽいと考えます。これについては『統計学入門 (基礎統計学Ⅰ)』がわかりやすいです。
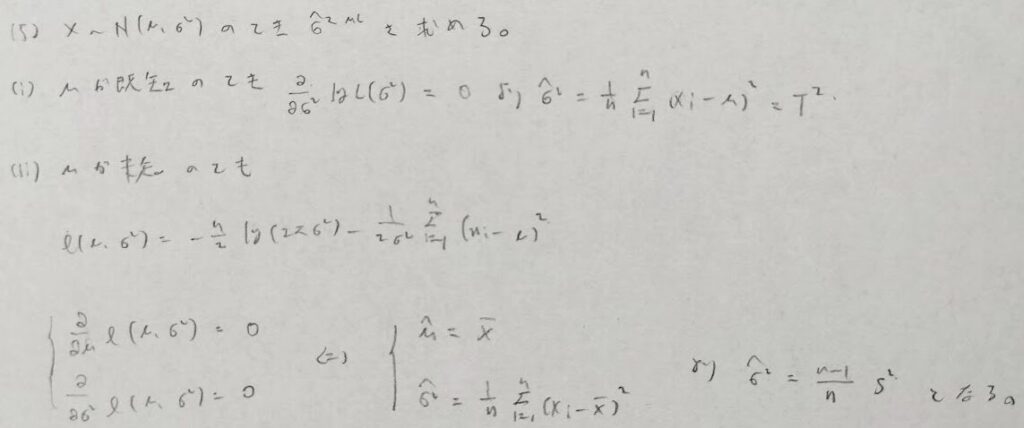
最後の問題が絶妙に時間を足りなくさせている感じですね笑
2014年度と2015年度(特に2015年)が難しすぎるだけで、この問題も十分にレベルは高いと思います。
2017年問2:一様分布
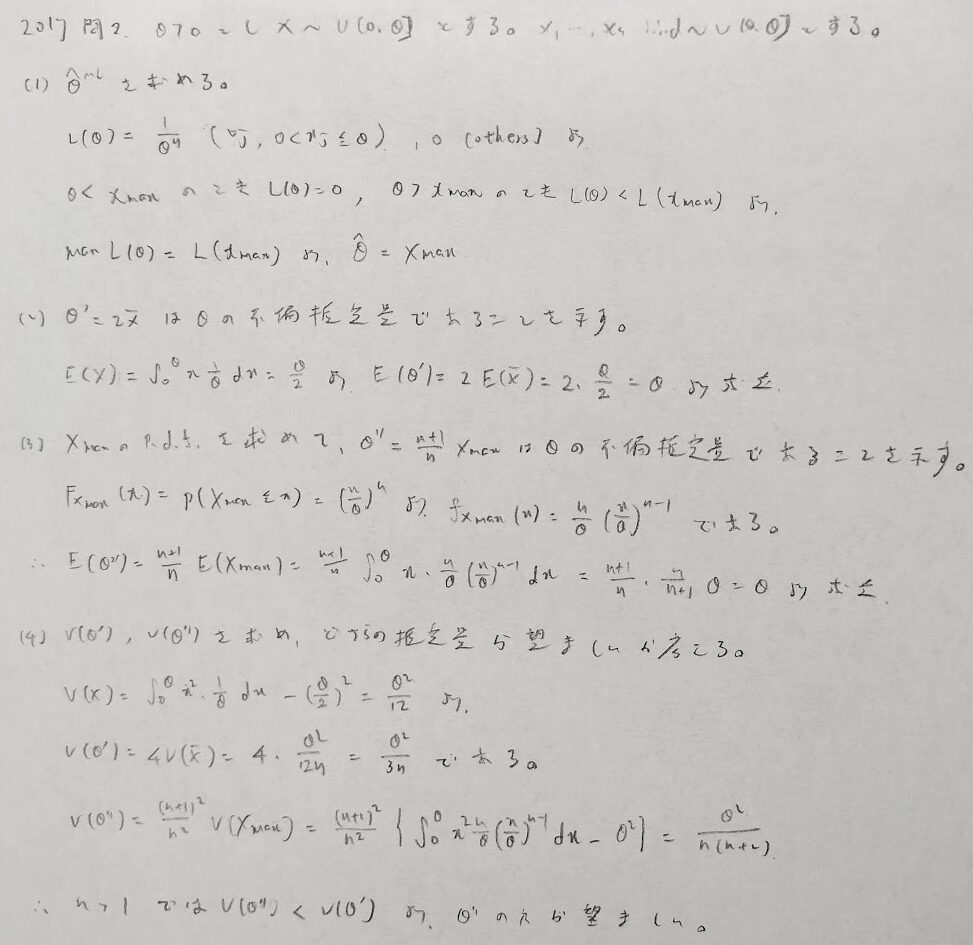
2017年問3:ポアソン分布

最後の問題はマクローリン展開を使うのがポイントです。マクローリン展開を知らないと解けない問題です。
テイラー展開などの細かい内容は『確率統計キャンパス・ゼミ』がおすすめです!かなり詳しく書かれています。
2017年問4:条件付き分布
今回のセットの中では最も合否を分けそうな問題です。最後の問題をすぐに反応できるかで勝負が決まります。逆に最後の問題が解けそうにない場合は選択しないほうが良いでしょう。
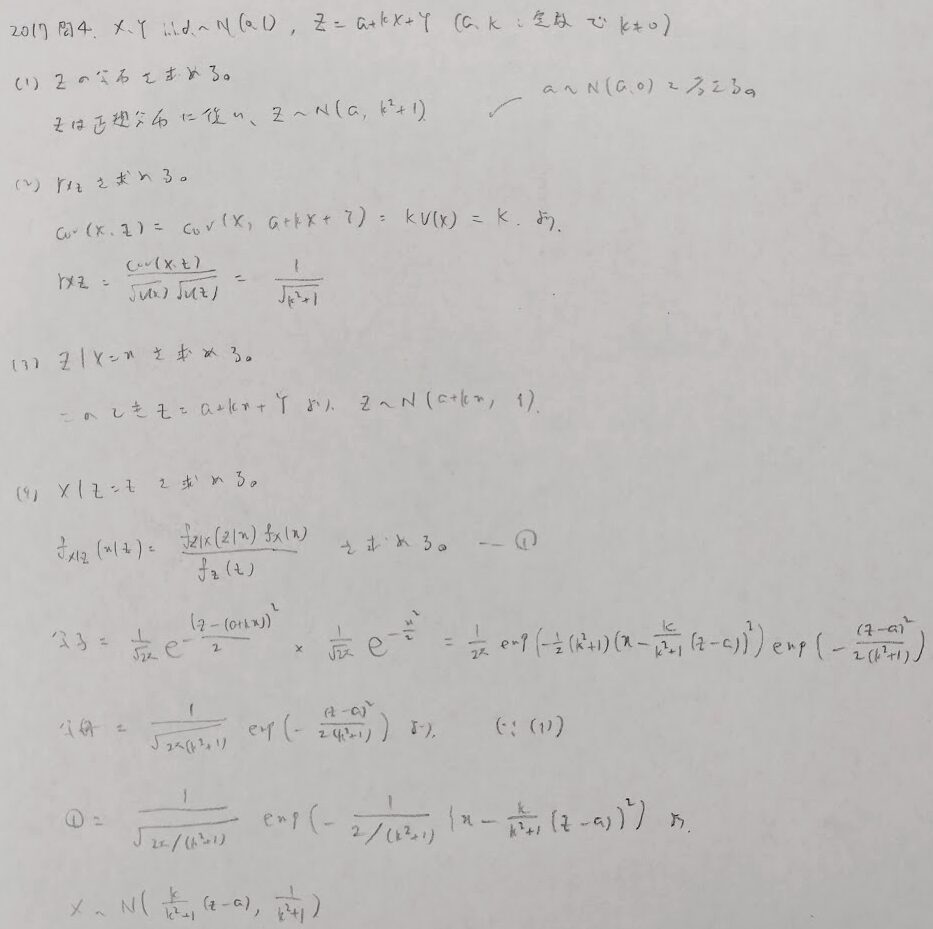
最後の最後で平方完成する理由について気づいたでしょうか。
2017年問5:変数変換
このレベルの問題が2023年付近の統計検定1級で出題されています。しっかりとスラスラと解きこなせるようにしておきたいですね。
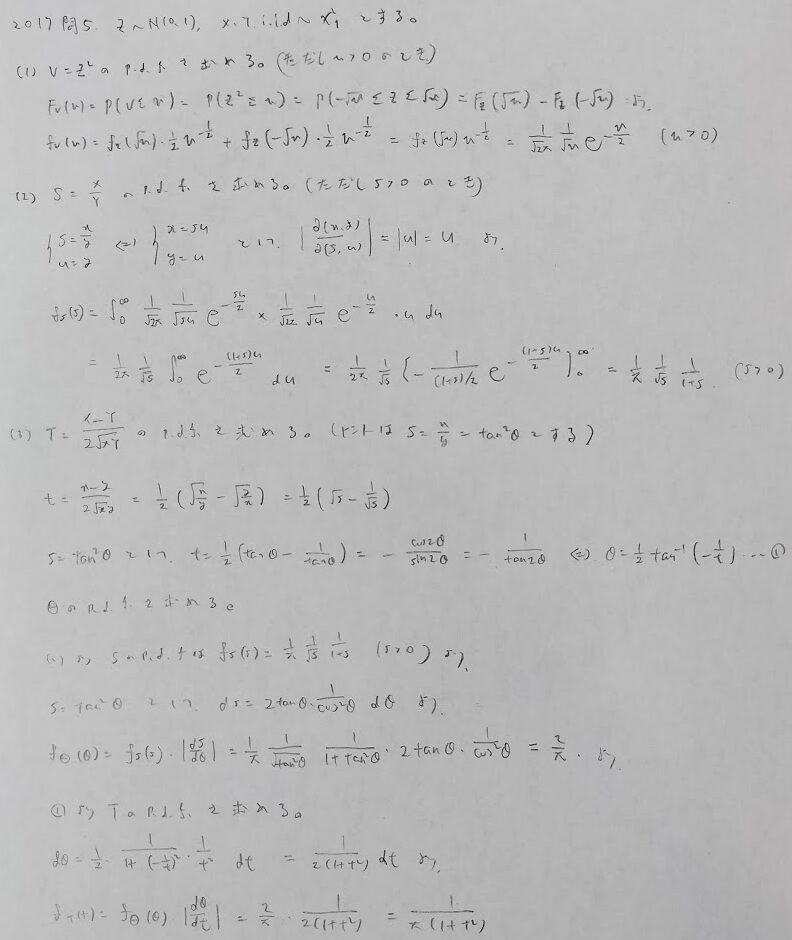
本問は逆三角関数の微分公式を知らないとアウトです。『微分積分キャンパス・ゼミ』で丁寧に学べます。
2017年度の統計検定1級の統計数理の問題の中では問5の最後の問題が一番難しいと思います。全体的により大学数学(の微積分)を意識してきている感じがしました。
統計検定1級「統計数理」の過去問:2018年
全体的な難易度が大幅に上がり近年の難易度になりました。ただし2015年度のような試験にならないような難しさではありません。最も難しい問題は問4のマルコフ性の問題です。近年に狙われそうな問題は問1のテイラー展開を用いる問題、問3のモーメント法の問題、問5の順序統計量の問題です。そのためこの3問を学習します。問4は超幾何分布ですが計算量が多いので今回のセットは除外します。全体的に条件付き分布の多い年だなという印象です。各問の最後の問題以外をしっかりと解ききれれば十分合格ラインでしょう。合格率は20.9%
2018年問1:カイ2乗分布
統計検定1級の統計数理頻出のデルタ法の本質に関する問題が最終問にあります。テイラー展開を用いて導出していますが、根本的には確率変数Xが不偏性を持つことを仮定しています。
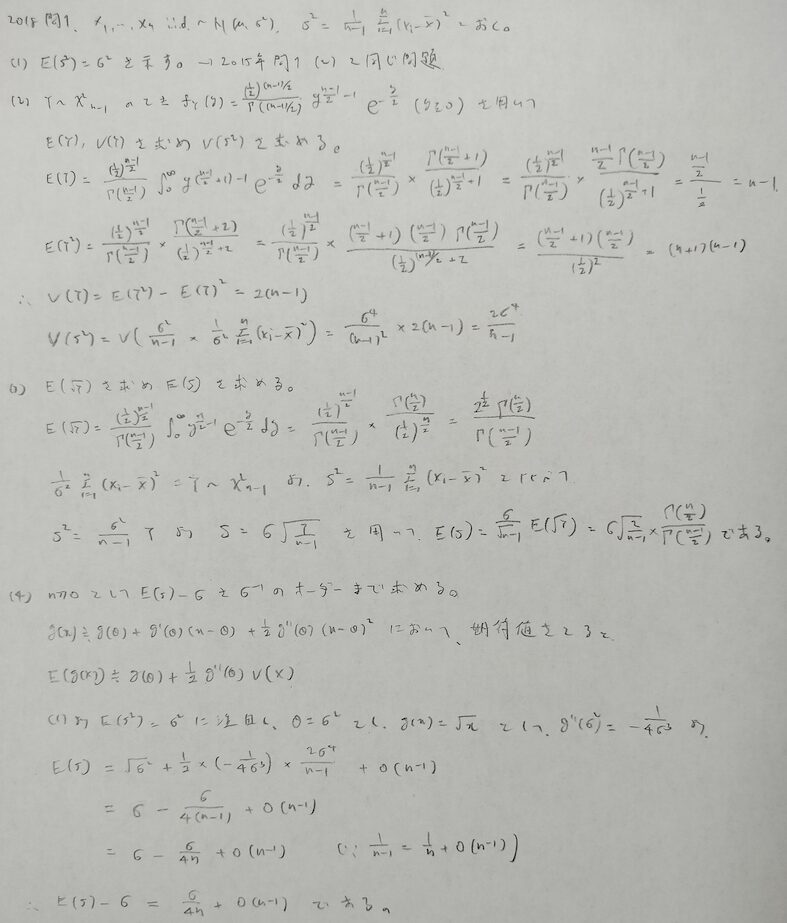
本問の学習事項はテイラー展開の部分です。決してトリッキーな発想ではなく定石手段だと意識することが大切です。ただそれでも最後の最後でのn-1をnに直すことに気づくことはかなりの難易度です。
2018年問3:二項分布と条件付き期待値
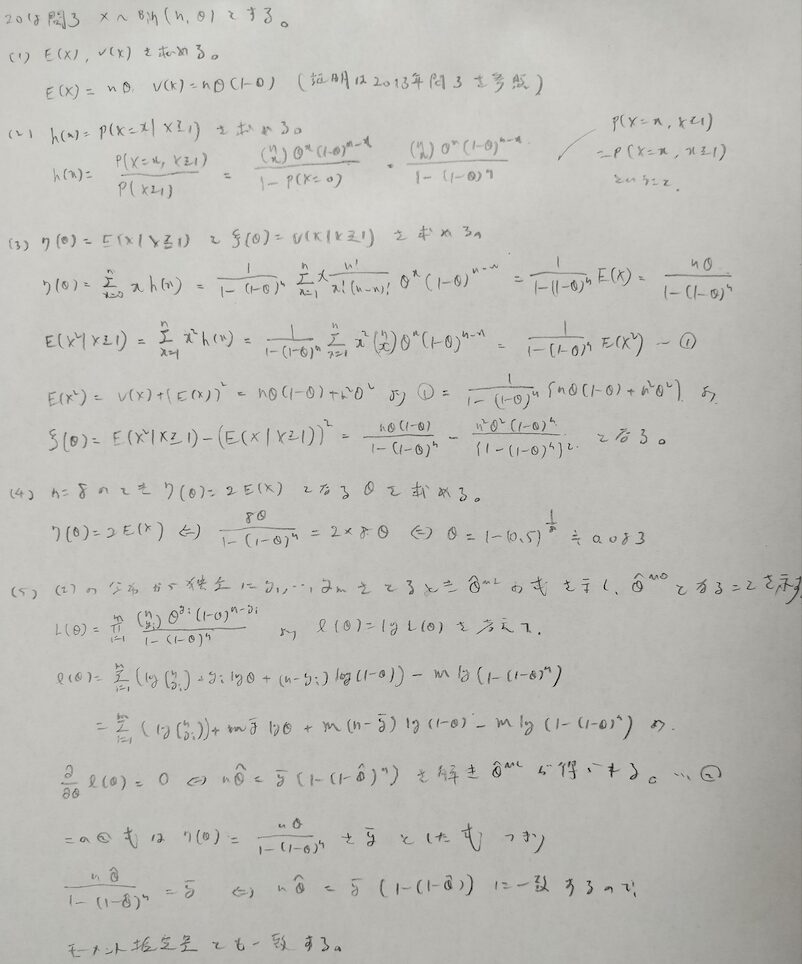
かなりの良問です。とくに最後のモーメント推定量は、どの期待値について注目しているか?を見失うと解けないようになっています。
意外と(2)の分子で手が止まってしまう人がいるかも知れません。分子は単純に考えればOKです。その思考の役割は分母が担っています。
2018年問5:一様分布と順序統計量
この問題の最後の問題まで解き切れれば最優秀賞でしょう。なかなか類題が見つからない素晴らしい良問です。

順序統計量の体系的な公式の導出(減点されない)はこちらに詳しく書いています。もしくは『現代数理統計学の基礎』でしっかりと学びましょう!
統計検定1級「統計数理」の過去問:2019年
難易度が下がりました。2017年度〜2019年度の難易度を比較すると、2017<2019<2018になります。今年度は問5のラプラス分布の問題の最後の2題がかなり難しいので選択肢から除外します。残りは問1〜問4ですが、問3は小問が6問あり、重たい問題もあるので選択肢から除外し、問1、問2、問4を選ぶことになります。ただし問3は今後出題が予想されるので学習べき問題としてチョイスします。合格率は23.0%
2019年問1:二項分布と確率母関数
2023年の統計検定1級の統計数理に類題が出題されています。重要問題です。

2019年問2:指数分布
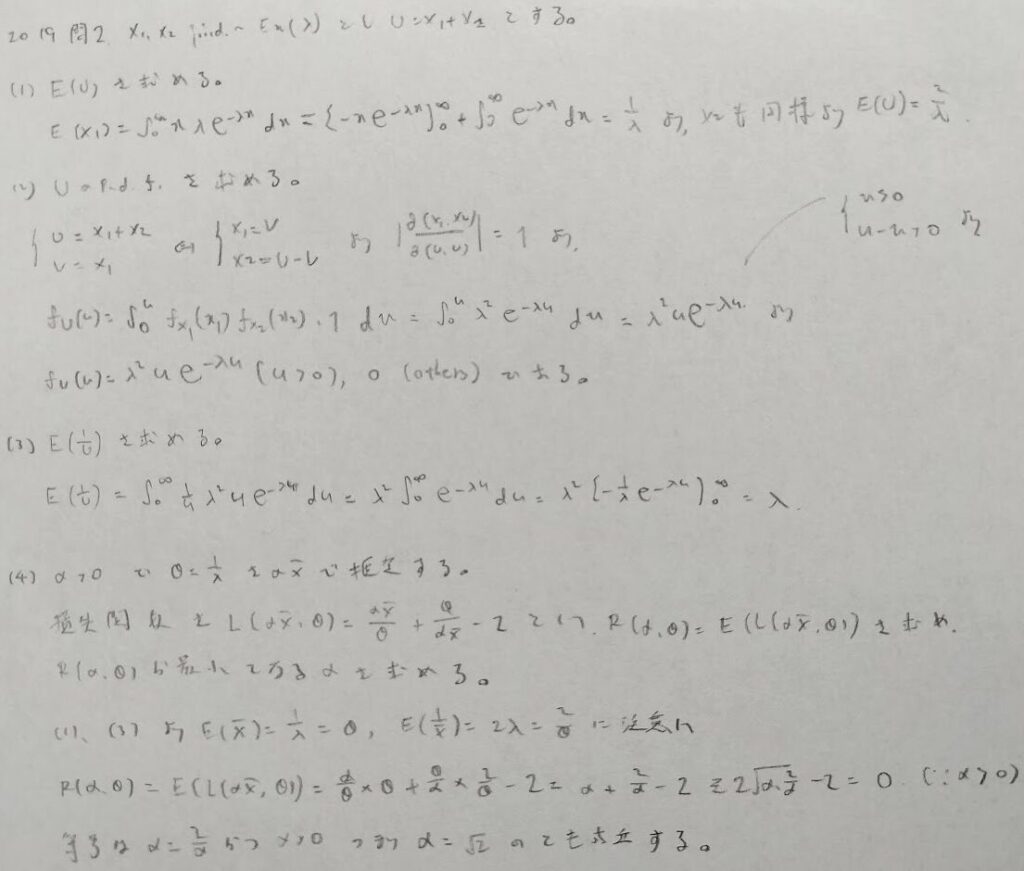
2019年の統計検定1級の統計数理の中で最も簡単な問題ですので、素早く完答しましょう!
2019年問3:一様分布と順序統計量
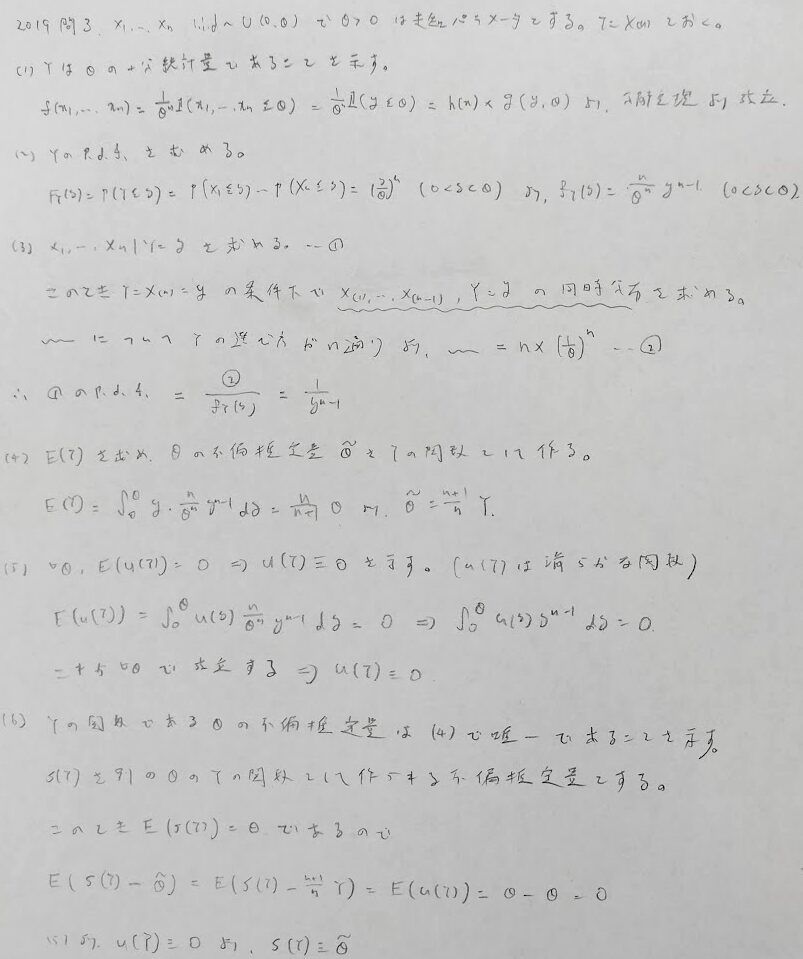
(3)は別解があります。条件付き分布の式をまず書きます。そしてそのまま直接計算する方法です。当然答えは違ってきますが、公式解答はそちらでもOKとすると書かれています。
本問では(3)の難易度が浮いています。本番で(3)が解けなくても以降の設問には影響しません。
統計検定1級あるあるですよね。わからない場合は次の問題を見てみると意外と解けちゃったりすることが往々にしてあります。
2019年問4:検定のサイズ
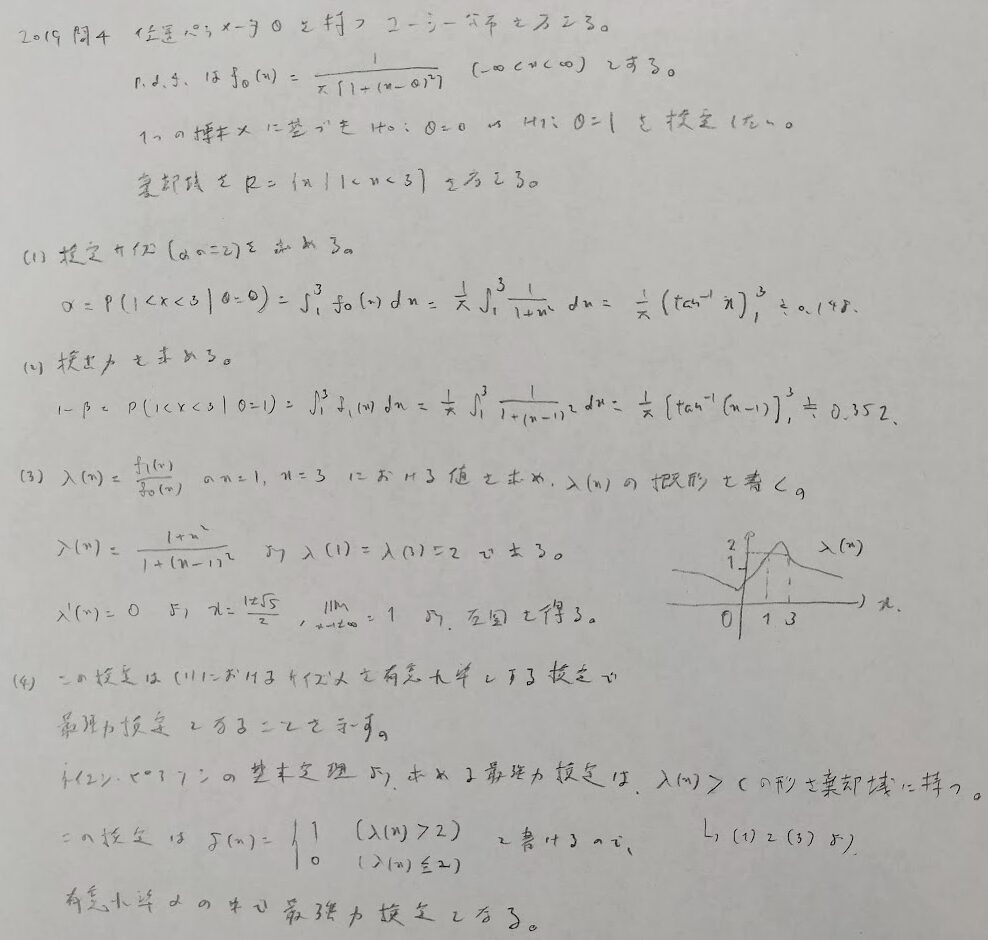
通常は有意水準αが与えられて棄却域を求める流れですが、本問では棄却域が与えられていてαに相当する量(検定のサイズ)を求める問題でかなりの盲点です。
検定のサイズについて統計検定1級のバイブル『現代数理統計学の基礎』にとてもわかりやすく掲載されています。
最後の問題も理解していれば一瞬で終わる問題ですね。統計検定1級は基本的な内容をしっかりと理解しているか?が問われる資格試験だと思います。
統計検定1級「統計数理」の過去問:2021年

統計検定1級の統計応用の一部の分野と統計検定準1級と統計検定2級において急激な難化があった統計検定界隈では有名な2021年のセットです。しかし実際は2019年度より難化(計算量が大幅に増加している)しているものの、統計検定1級の統計数理は難化の煽りをさほど受けておりません。問5は明らかな難問なので除外します。それ以外の問1〜問4までの問題は演習問題として価値が高いのですべて学習用教材として扱います。実際は問4は序盤のトリッキーさに気付けないと選択すべきではありませんので、実質問1〜問3を選択するのが無難です。ちなみに統計検定1級の統計数理の最難関のセットは2015年で次いで2014年度もかなりの難関です。合格率は25.8%
2021年問1:変数変換

アクチュアリー数学の小問の問題が連続したような問題でしたね。この問題は絶対に完答したいレベル感ですね!
最後の問題で、Y~U(0,1)に注目しないと解けないようになっているので、かなりの良問だと思います。
そうですね。明らかに2015年より先の問題の品質が上がっている気がしますね。十分差がつく出題だと思います。
変数変換で頭が混乱する方は岩沢先生のリスク本『リスクを知るための確率・統計入門』が神がかっていてわかりやすく書かれています!
2021年問2:超幾何分布と事後モード

以前より出題されていた(が難問だった)ベイズ推定の問題の難易度が落ち着いてきました。とはいえまだ計算量が多めですので、今後ともバリエーションを増やしていく可能性が高いです。
最後の問題の事後分布の分母は正規化定数を考える際は必要ですが、事後分布がどういった分布か?を考えるだけの場合は分子のみの計算で見抜くことができます。ベイズ推定の練習は『データ解析のための数理統計入門』が具体例が多く最適です。
2021年問3:ポアソン分布と信頼区間
最後の問題だけ別格に難しいです。ごちゃごちゃ書くと蛇足になってしまいそうなので、ここでは素直な解答としておきました。

2021年問4:高次モーメントの処理
問1〜問4の中では序盤でトリッキーな問題が潜んでいる注意パターンです。また計算量も途轍もなく多いので、選択する場合は覚悟が必要です。(4)が鬼門です。
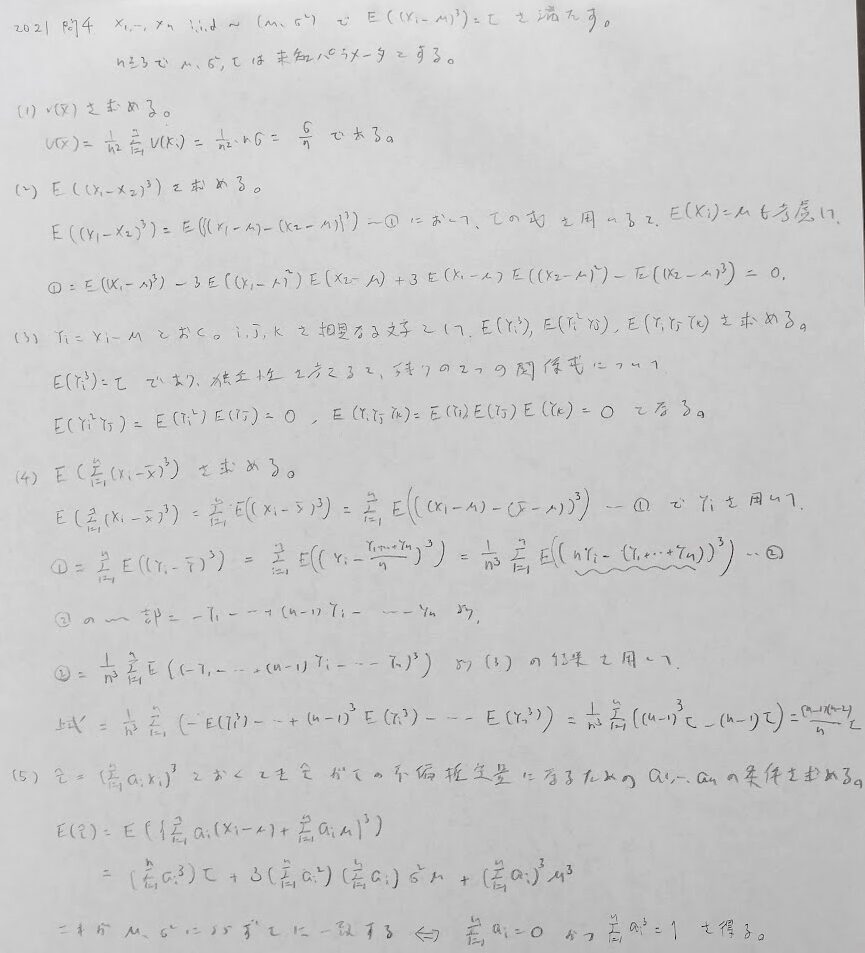
統計検定1級「統計数理」の過去問:2022年
合格のための難易度は前年度よりも下がりましたが、問1で新傾向問題が出題。しかし2023年度では元に戻っているので2021年度に難しくしたことの配慮と思われます。問5は分散分析の出題で計算量と、答るべき問題が多いので選択しない方が良いです。問1はトリッキーな出題(前年度からの傾向か)のため合格のためには問2、問3、問4を選択するしか無くなるでしょう。合格率は22.4%
2022年問2:一様分布と条件付き分布
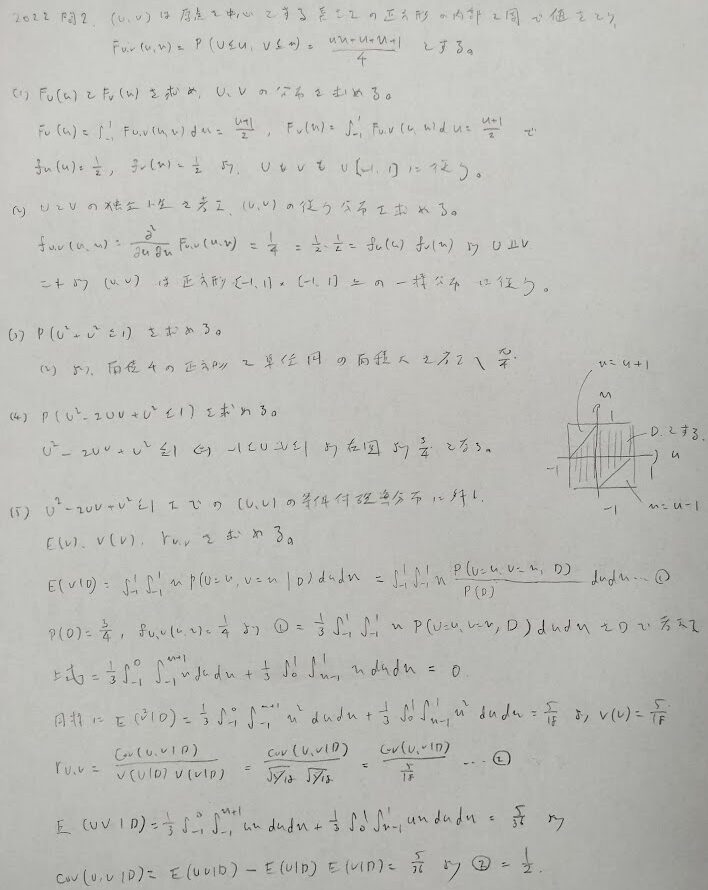
最後の問題だけ計算量が段違いです。
条件付き相関係数とはかなりの新傾向ですね。合格のためには最後は飛ばしても大丈夫そうです。他の問題の見直しに時間を回しましょう。
2022年問3:条件付き分布

2022年問4:変数変換

やはり全体的な難易度は下がっている感じがします。
いよいよ次が最新の2023年度です。傾向と対策をしっかりと行いましょう!
統計検定1級「統計数理」の過去問:2023年
明らかに問4と問5の難易度が難しすぎて浮いていますので、実質的に選択できるのは問1〜問3です。乱数の問題が新傾向です。ここ数年連続で新傾向を1つ出してきている傾向がありますが、『現代数理統計学の基礎』の演習問題を自力で解けるようになるなどのしっかりとした対策で対応可能です。また今年は過去問のパターンを問う問題が出題されています。今後この傾向は続いていくと思われます。確率分布が問題の大半を占める傾向は変わりません。合格率は22.5%
統計検定1級の2023年の過去問集は2024年9月現在はまだ未発売です。詳しい問題と解答は統計検定の公式ページからご覧ください。
お恥ずかしいことですが僕はこの回で落ちてしまっています。次回に向けての改善策などはこちらにて受験体験記としてまとめています。時間短縮を狙って結果のみを知っている状態から逆算した積分計算などは大幅原点になるようです。同じ失敗をされないように受験する方はご注意ください。
2023年問1:ポアソン分布と漸近相対効率
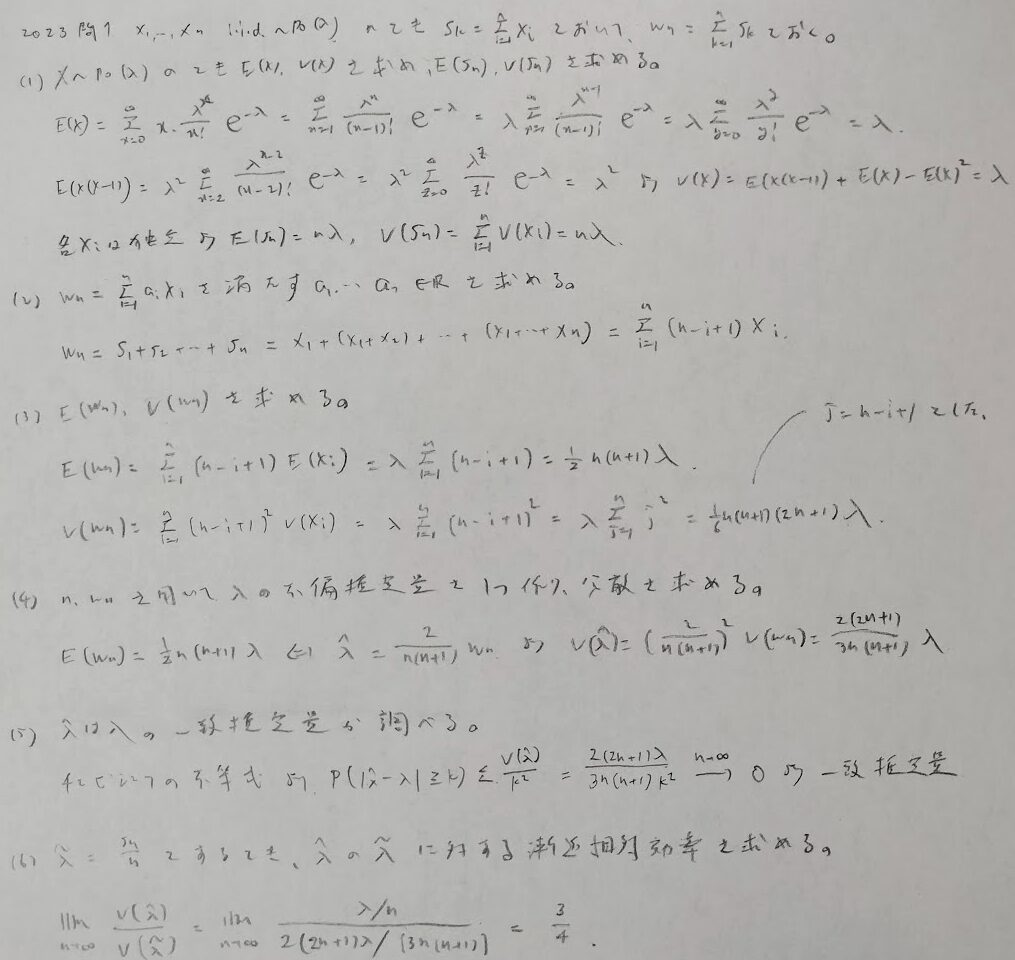
漸近相対効率は新傾向です。ひょっとしたら来年度に引き継がれるかも知れません。
漸近的な話題は『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』をご参照ください。この問題は実は試験範囲にしっかりと載っていますので、盲点的な問題でしたね笑
2023年問2:一様分布と乱数
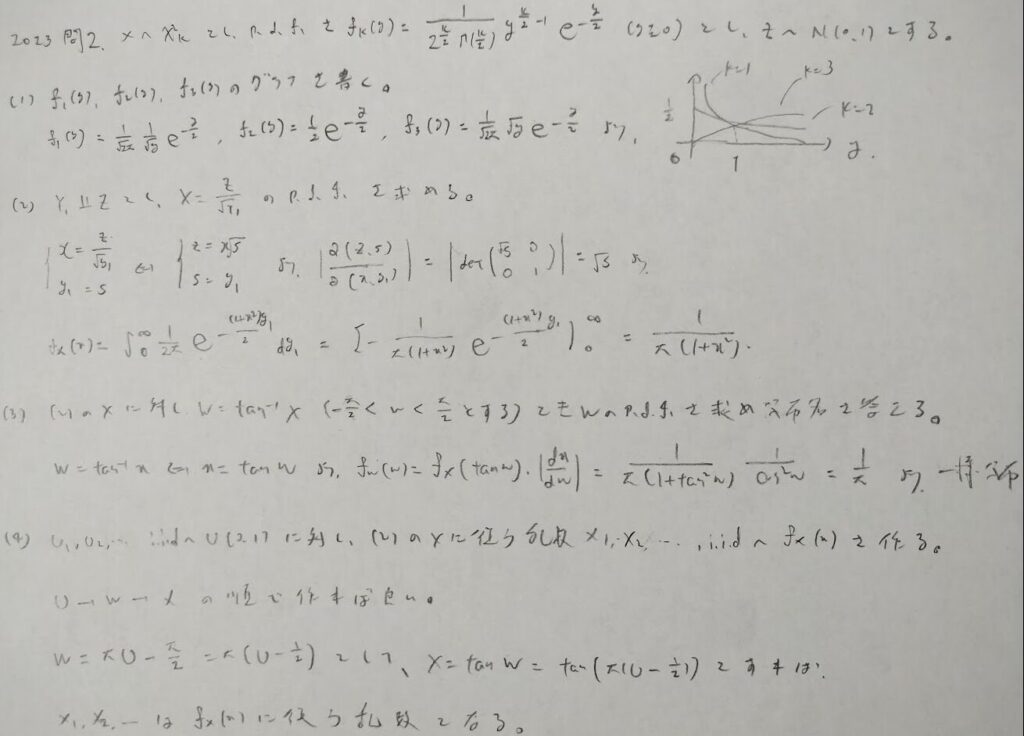
試験本番では(1)にとても時間をかけてしまって失敗しました。また(2)はt分布の公式を使って、自由度1のt分布としましたが全く点数が入っていない感じでした。統計検定1級では作問者の意図を汲み取って解答する技術が必要です。
2023年問3:指数分布とモーメント母関数
この問題が確実に合否を分けます。僕は(3)が解けずに以降が白紙になりました。試験後に過去問を見返したら解けました。過去問はとても大事だと身をもって痛感しました。

(5)の期待値を微分してみようという考えはなかなか思いつけるものではありませんが、問題文でhを場合分けさせているところから、期待値をhの関数と見るのかな?と思れば勝負アリです。
ここまでの演習でお気づきだと思いますがガンマ関数が絡む積分計算がかなり出題されています。置換積分を行なっても良いのですが、ガンマ分布の全確率1に帰着させる方が圧倒的にスピードが速いです。『弱点克服 大学生の確率・統計』に詳しい計算の仕方が掲載されており統計検定1級受験者は必見です。
統計検定1級の統計数理の傾向は前年度での内容を一部引き継ぐ傾向があることに気づきましたか?2024年度の統計検定1級の統計数理に向けては確率分布の内容をしっかりと学習しておくことが重要になります。過去問のリスト一覧を下記にまとめました。
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定1級 公式問題集[2016〜2018年]
日本統計学会公式認定 統計検定1級 公式問題集[2019~2022年]
過去問で大事な問題をしっかりと解けるようにし、統計検定1級のバイブル『現代数理統計学の基礎』で周辺の話題をきちんと取り入れておくことが合格へのキーポイントだと思いました!頑張りましょう!!
問題をパッと見て「解けそう!」でも時間切れで解けなかった。これが起こるのが統計検定1級です。本当に理解できているのか?を真摯に問いながら過去問や『現代数理統計学の基礎』や公式教材『増訂版 日本統計学会公式認定 統計検定1級対応 統計学』をしっかりと本質部分が理解できるように基礎固めを共に頑張っていきましょう!!
統計検定1級の統計数理の過去問解説→このページ
統計検定1級の統計応用の共通問題の過去問解説→こちら
統計検定1級の統計応用の人文科学の過去問解説→こちら















