2025年度の統計検定1級受験対策として統計応用の人文科学の過去問を解説します。共通問題の全過去問の解説記事はこちらです。また、統計数理の過去問解説記事はこちらです。
理工学ではないのですか?
理工学は2019年から難化してしまって実際2023年に受験して不合格になってしまったので、今年は次の観点から人文科学へとシフトします!
2024年の統計検定1級での人文科学は不合格でした。近年の共通問題は難易度が高くなっているので選ばない選択肢もありです。また、選択問題の落とし穴として、序盤が簡単でも終盤が難しい問題が固まっている大問を選ぶと不合格になります。ご注意ください。また≒ではなく、模範解答では≈(アプロクシメトリーと読み、外資系企業などで国際的に使われている記号)が使われているようです。
統計検定1級の人文科学を選択するメリット
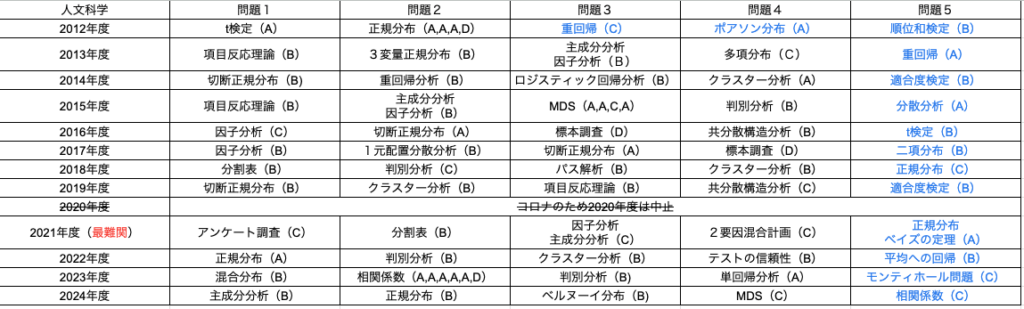
2012年〜2024年の人文科学の過去問を解いた感想では、統計検定準1級に合格しているならば統計検定1級の統計応用に最も合格しやすい応用分野は人文科学だと確信しています。
統計検定準1級に合格していれば人文科学はそのままの延長で対策可能です。
統計応用の中で計算ミスによる失点がもっとも少ない分野です。
人文科学は多変量解析を深めれば合格できます。
統計検定1級の他の統計応用分野との比較です。
理工学→最近は数理寄りの出題があるが計算量が膨大
社会科学→人文科学との共通問題もあるので補助教材としてOK
医薬生物学→もっとも人文科学とかけ離れた分野(心理学とは近い)
人文科学の過去問の類似度では社会科学→理工学(2018年の1題のみ)→医薬生物学になります。
それではいよいよ過去問の解説に入ります。人文科学を学習する際は次の点を意識していきましょう!
統計検定準1級内容の総点検をしましょう!
→『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』
多変量解析の説明を行列などを用いて0からできるようにしましょう。
→最適な参考書は『多変量解析法入門』です。
特に因子分析、主成分分析、クラスター分析は頻出です。
→『多変量解析入門――線形から非線形へ』がわかりやすいです。
統計検定1級で初登場する多変量解析の対策
→『Rによる多変量解析入門 データ分析の実践と理論』がおすすめです!
項目反応理論(過去問に難問は出てません)は2024年に出そうです。
→『項目反応理論[入門編]』の第2章までを学習しましょう。
最後に未出分野の対策もしましょう!
→公式教科書『統計検定1級対応 統計学』は統計応用で輝きます!
本記事では問題の著作権があるため、そのままの表現などを避けております。詳しい問題内容や模範解答を知りたい方は下記のリンクから詳しい内容をご確認ください。年度順にまとめておきました。最新年度の2024年は統計検定の公式HPからダウンロードできます。
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定1級 公式問題集[2016〜2018年]
日本統計学会公式認定 統計検定1級 公式問題集[2019~2022年]
日本統計学会公式認定 統計検定1級 公式問題集[2022~2024年]
統計検定1級「統計応用」人文科学の過去問:2012年

2012年問1:t検定

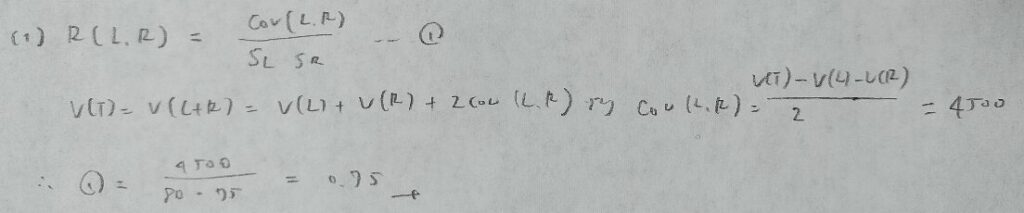
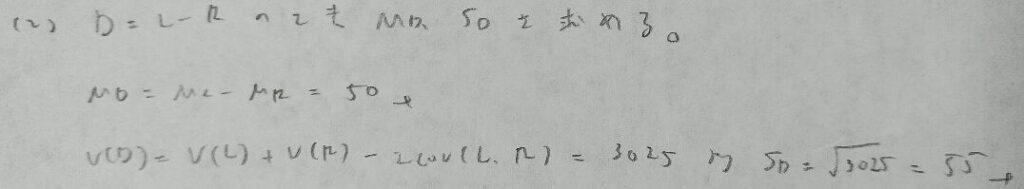

帰無仮説が何かを考えないと正解に辿り着けない良い問題です。
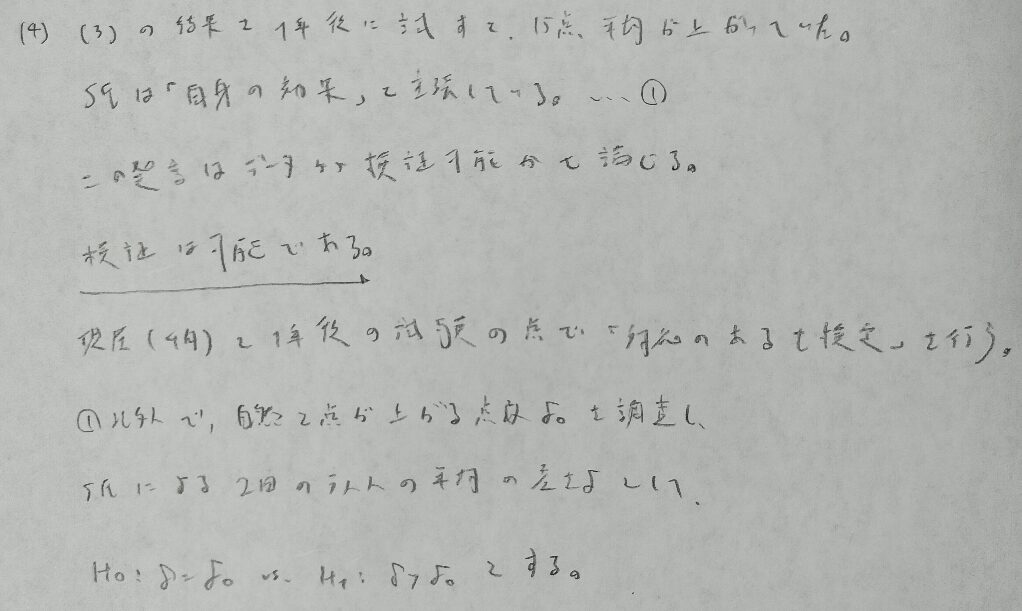
帰無仮説の設定が問われる良問です。
2012年問2:正規分布
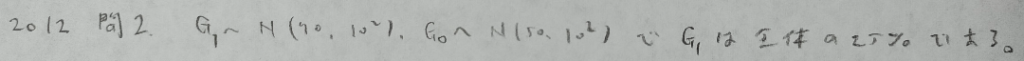
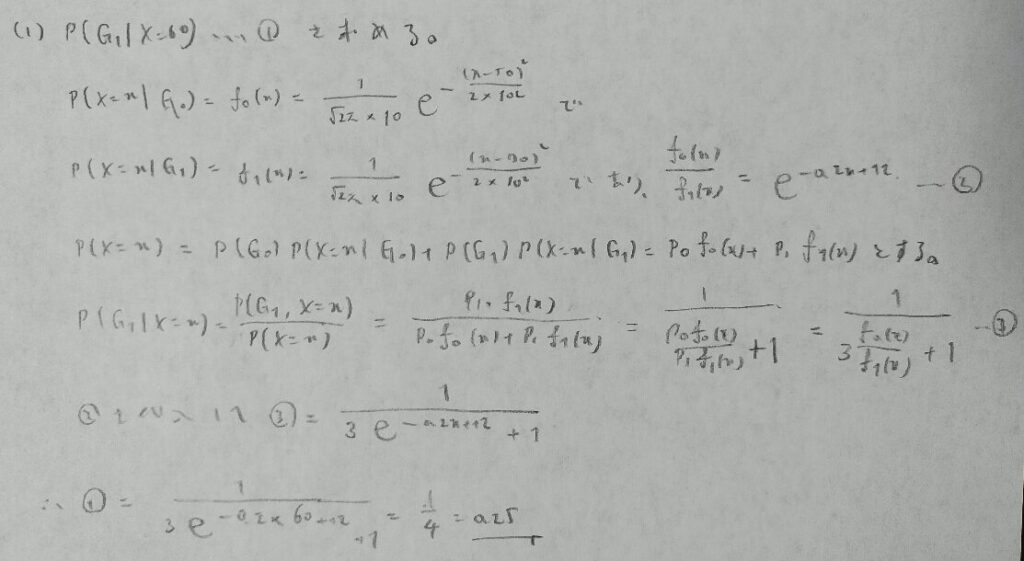
(1)をしっかり正解すると最後の問題の前までスッと完答できます。いかに(1)を先を見据えて解けるかが勝負です。
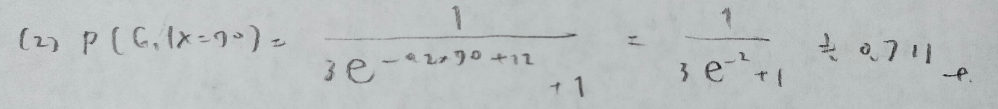
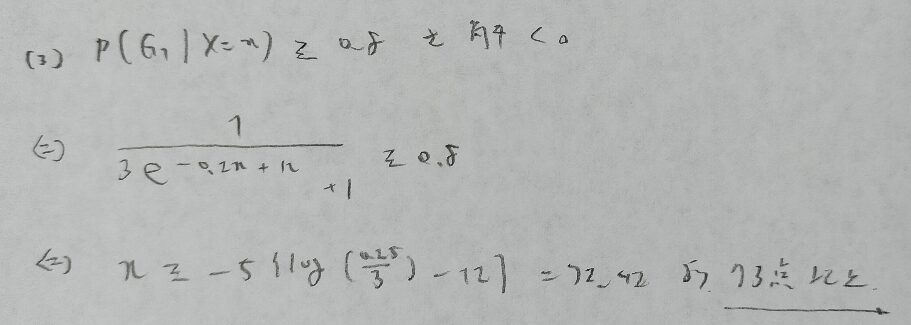
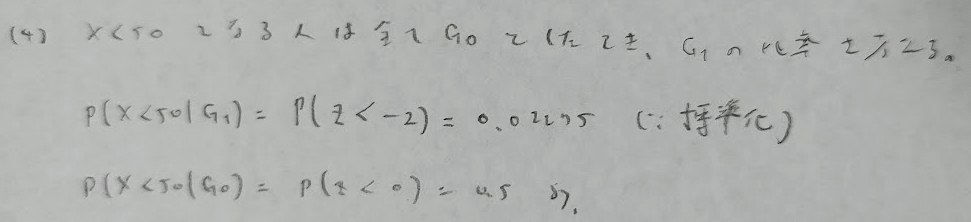
問題文の意図がわからず最後まで解ききれませんでした。最後の答えまで行かれた方は解き方のご教授をお願いいたします。
統計検定1級「統計応用」人文科学の過去問:2013年

2013年問1:項目反応理論
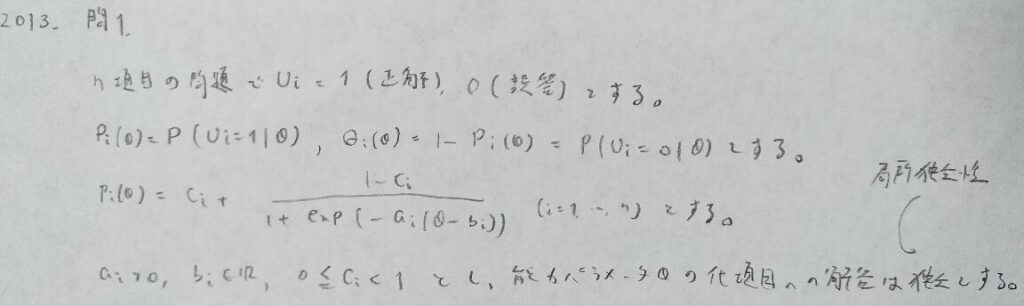
統計検定1級の統計応用の人文科学の項目反応理論の学習は『項目反応理論[入門編]』でOKです。
『項目反応理論[入門編]』の第2章まで学習すれば解けますので是非とも購入して頑張りましょう!
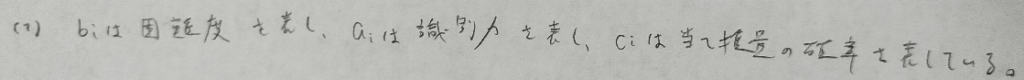
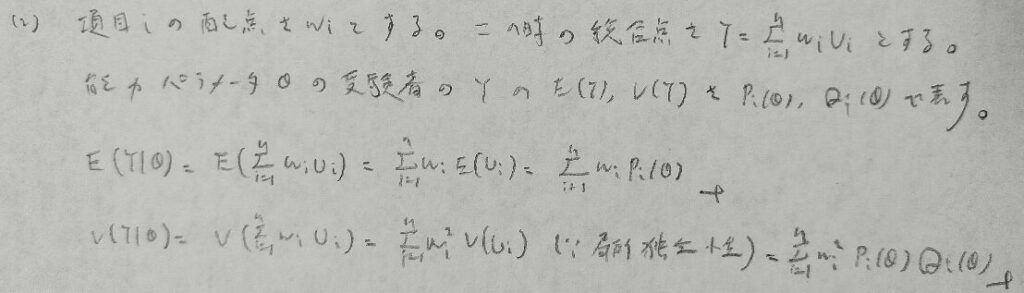
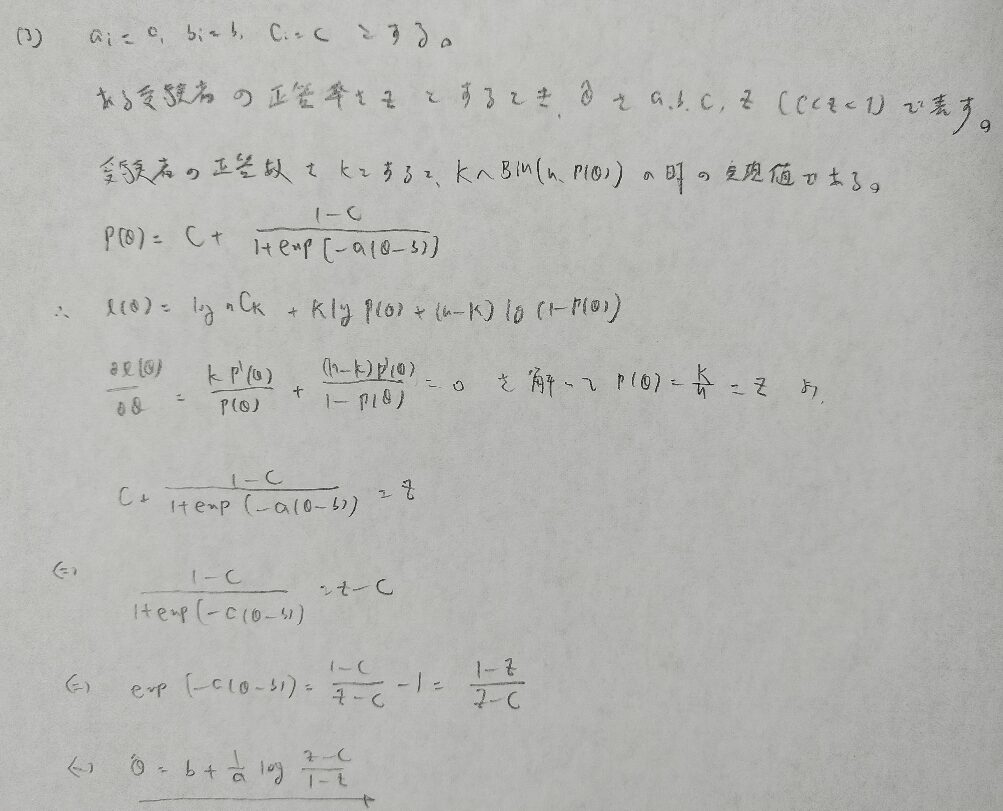
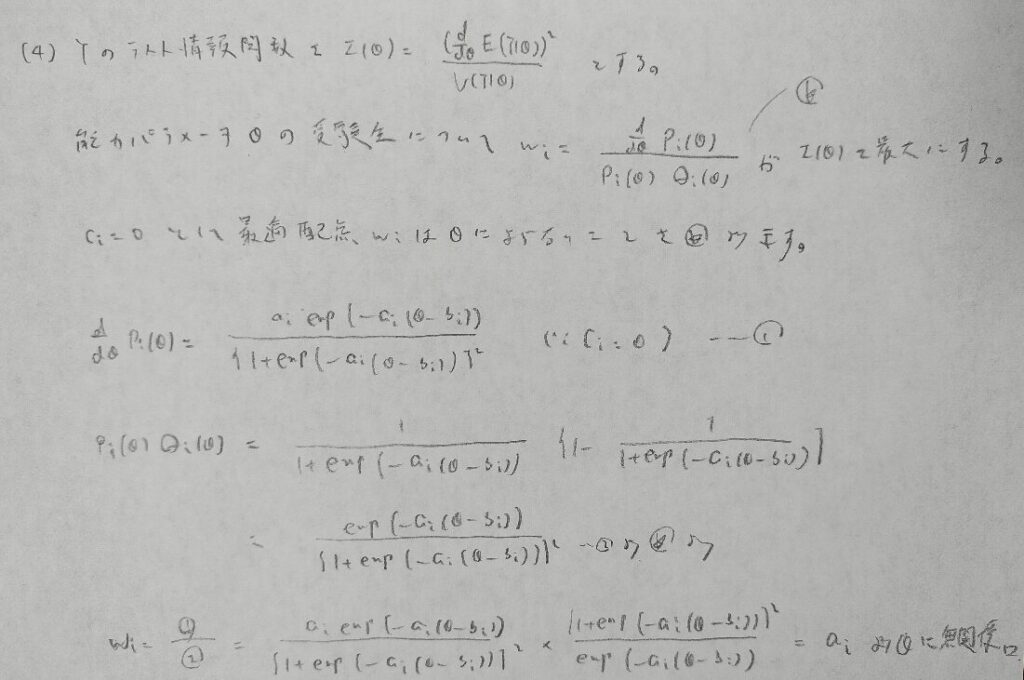
どの問題も基本をおさえて誘導に乗れば完答できます。項目反応理論の基本内容は別記事にてまとめています。
2013年問2:3変量正規分布
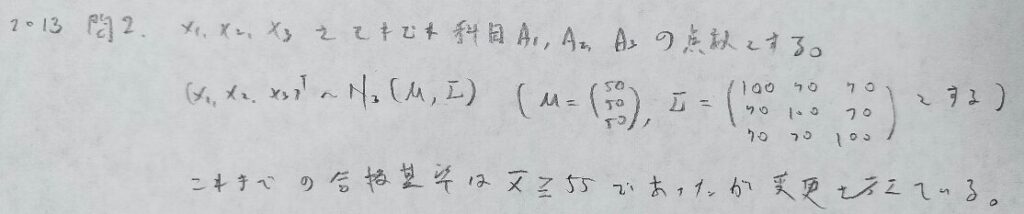

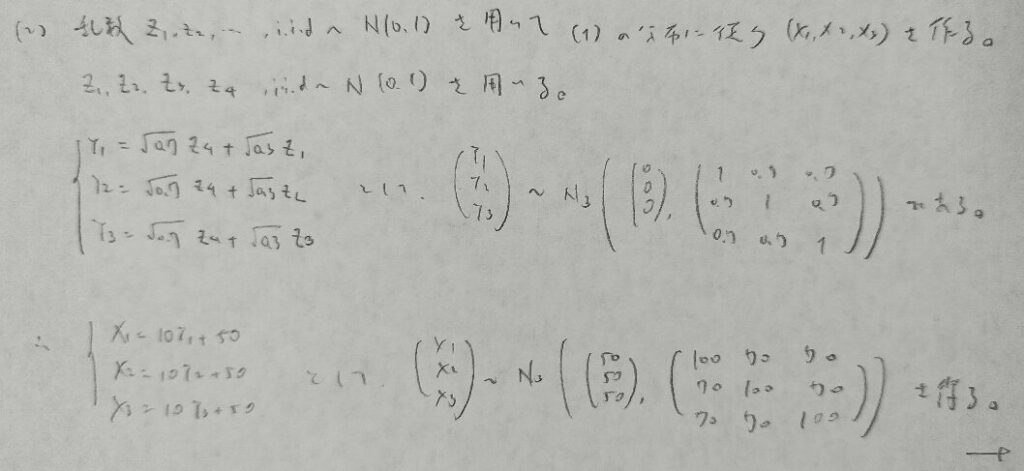
今後出される可能性がありますが難問です。

標準誤差とは、標本平均の標準偏差のことです。
2013年問3:主成分分析と因子分析
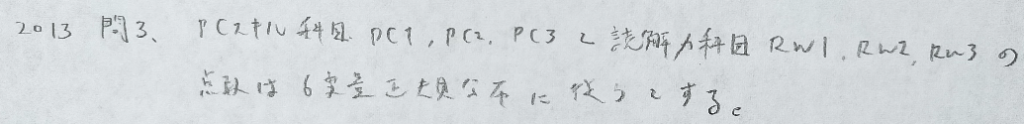
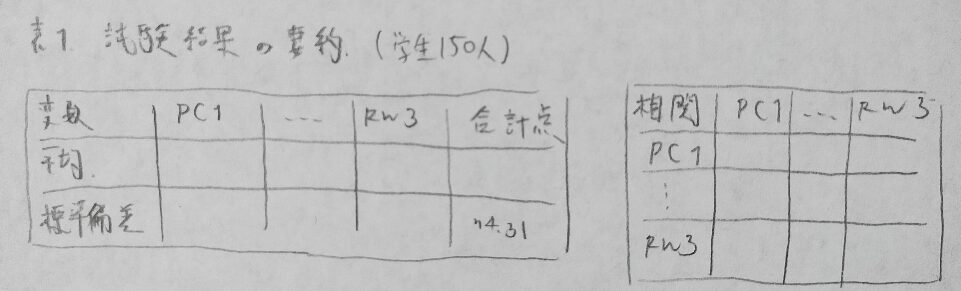
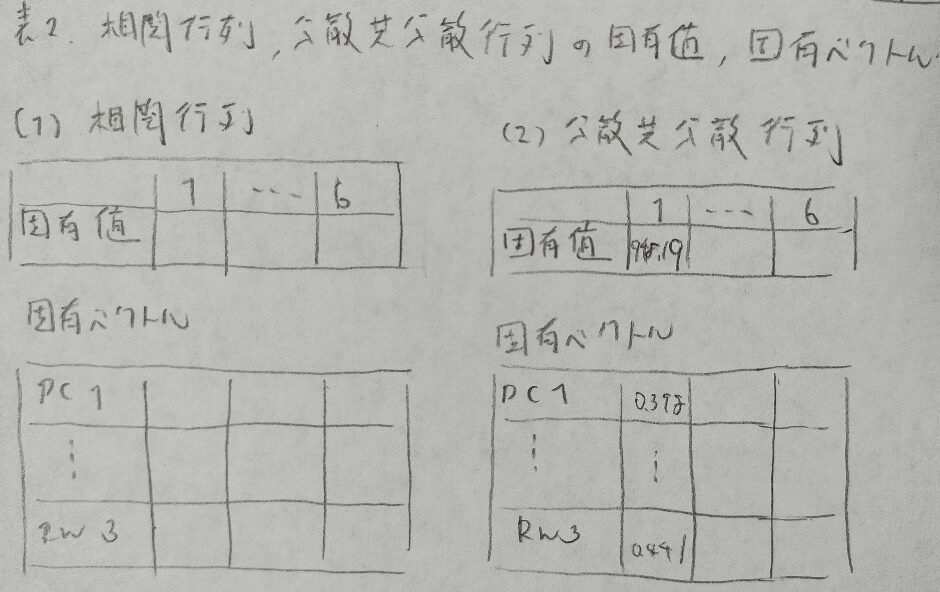
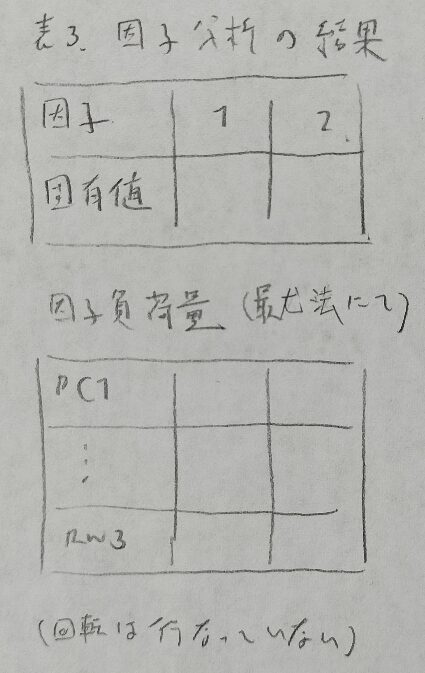
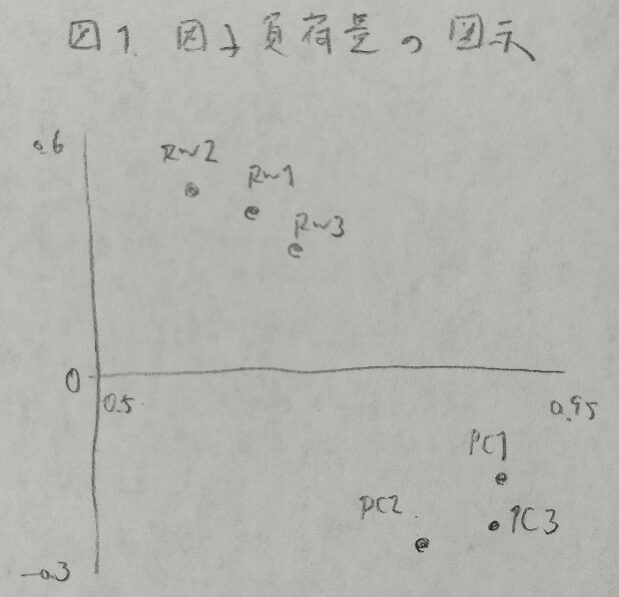
回答に必要な部分だけ書き込みました。

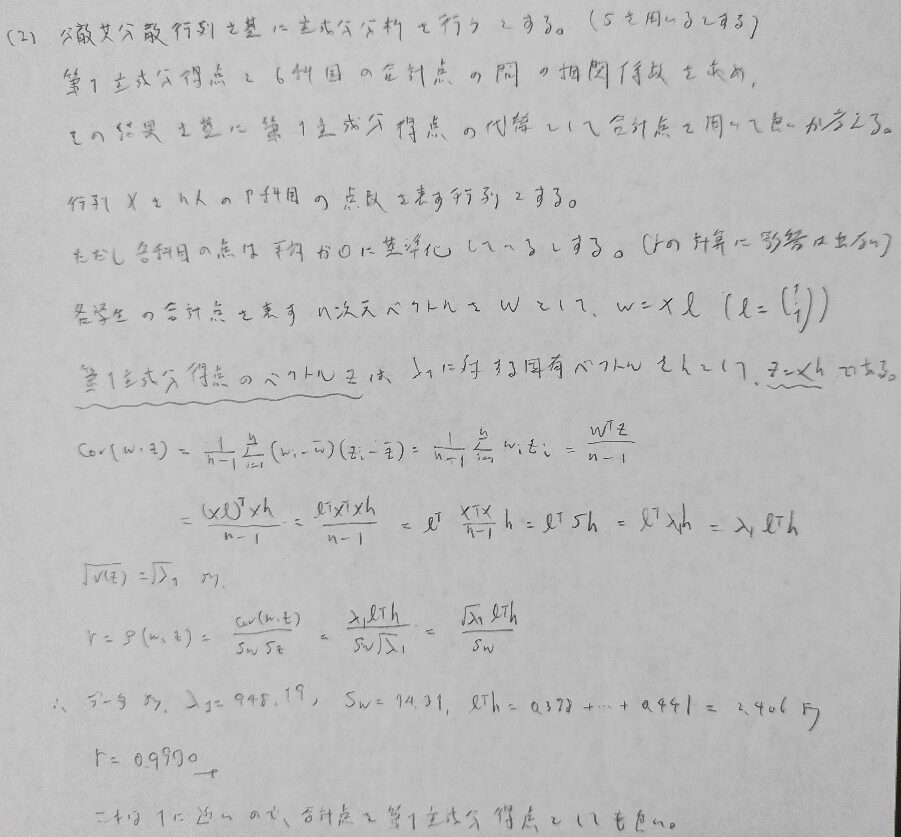
主成分負荷量の計算の流れを真似た解答を作ってみました。多変量解析は『多変量解析法入門』をおすすめします!
問3はこの問題が解ければ完答は近いです!


2013年問4:多項分布
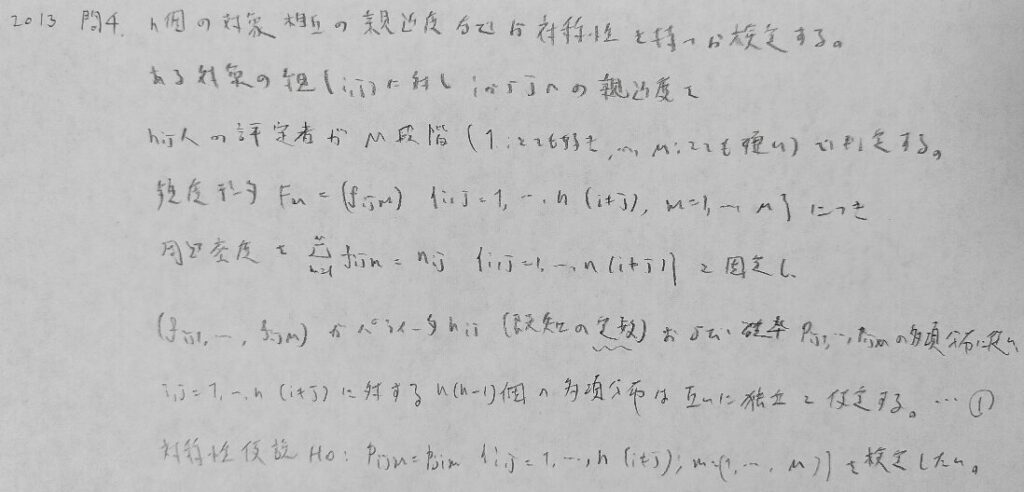
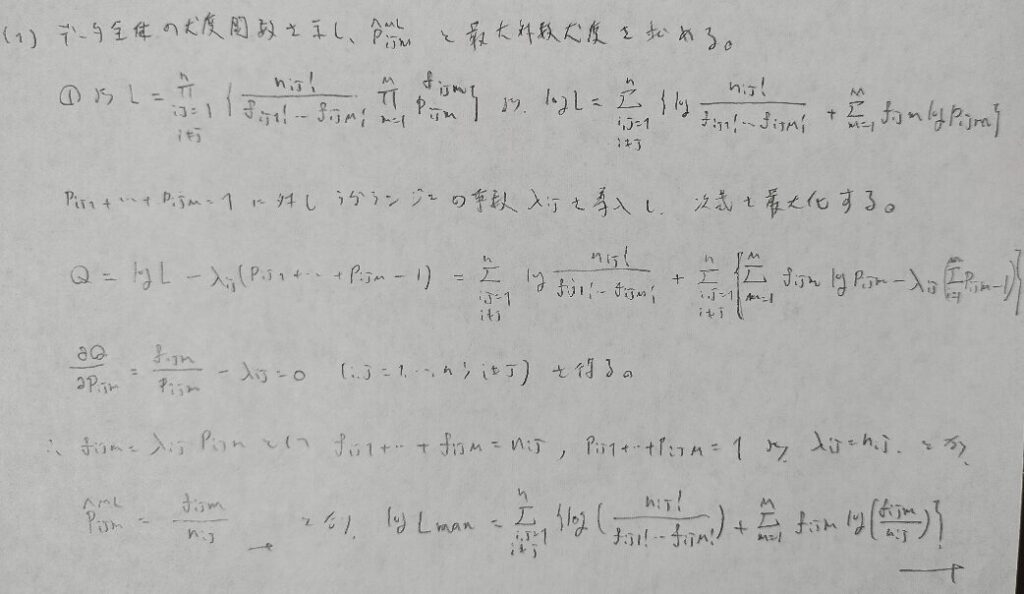
偏微分すると定数部分が消えてしまうのではじめからQは定数を抜かして考えて良いと考えます。
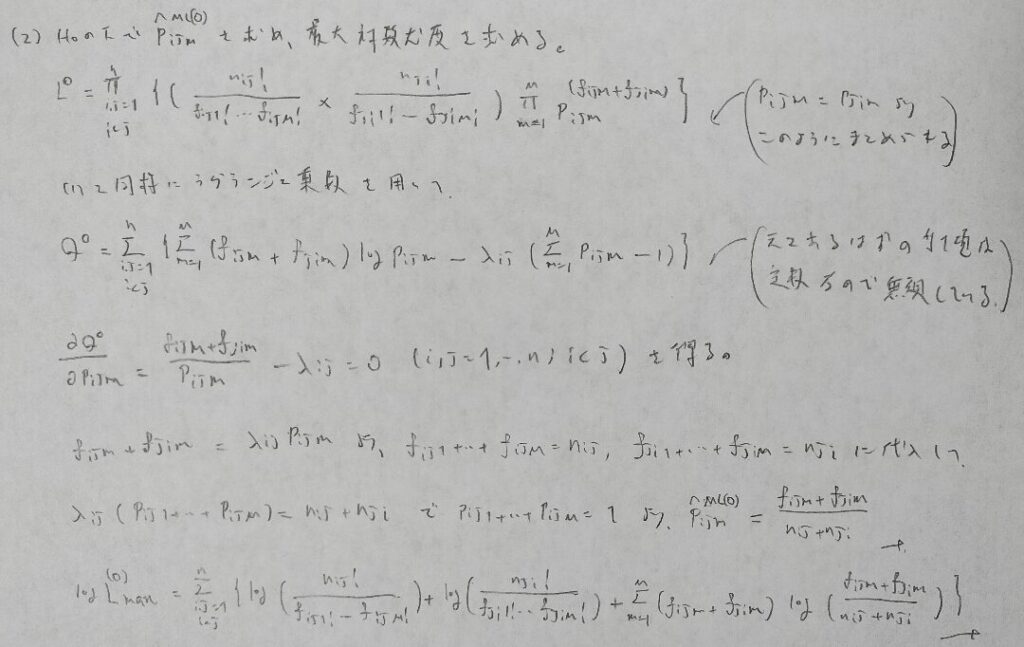
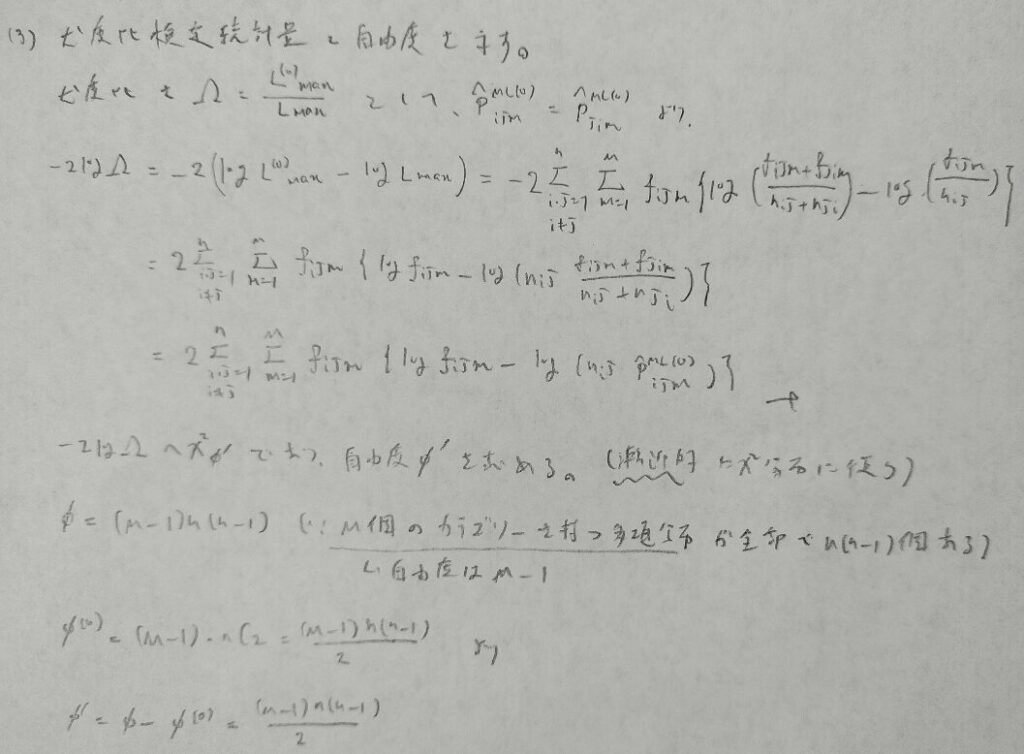
時間内に終わらない計算量のため難問です。ただし導き方は理解しておきたいところです。
統計検定1級「統計応用」人文科学の過去問:2014年

2014年度の詳しい問題内容は『日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年] 』をご参照ください。
2014年問1:2変量正規分布
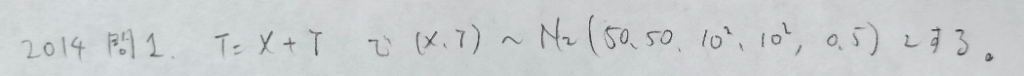
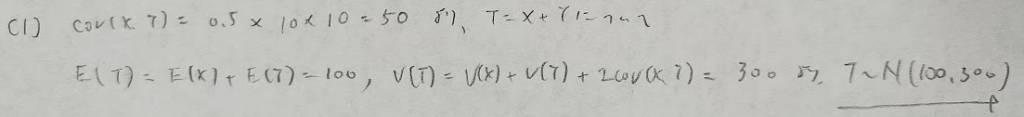
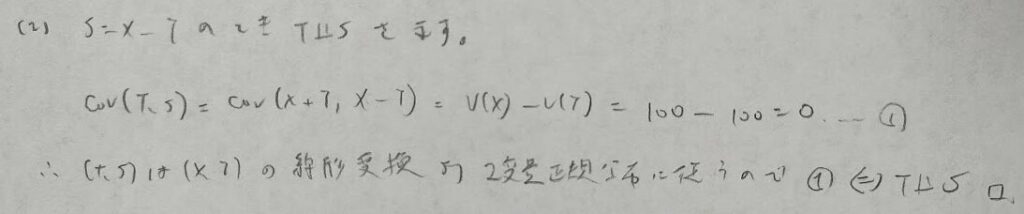
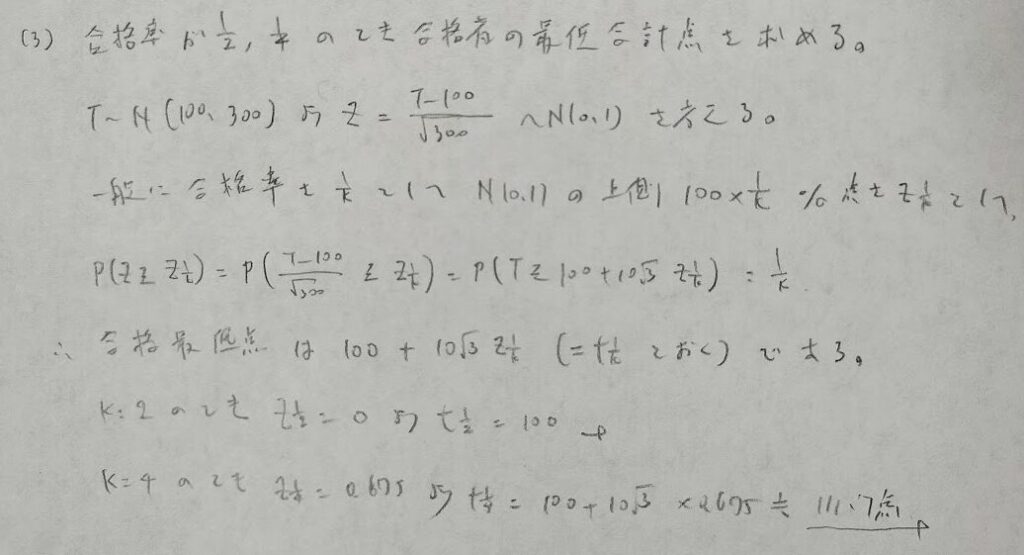
初見だと気付きにくいですが、かなりの良問です。
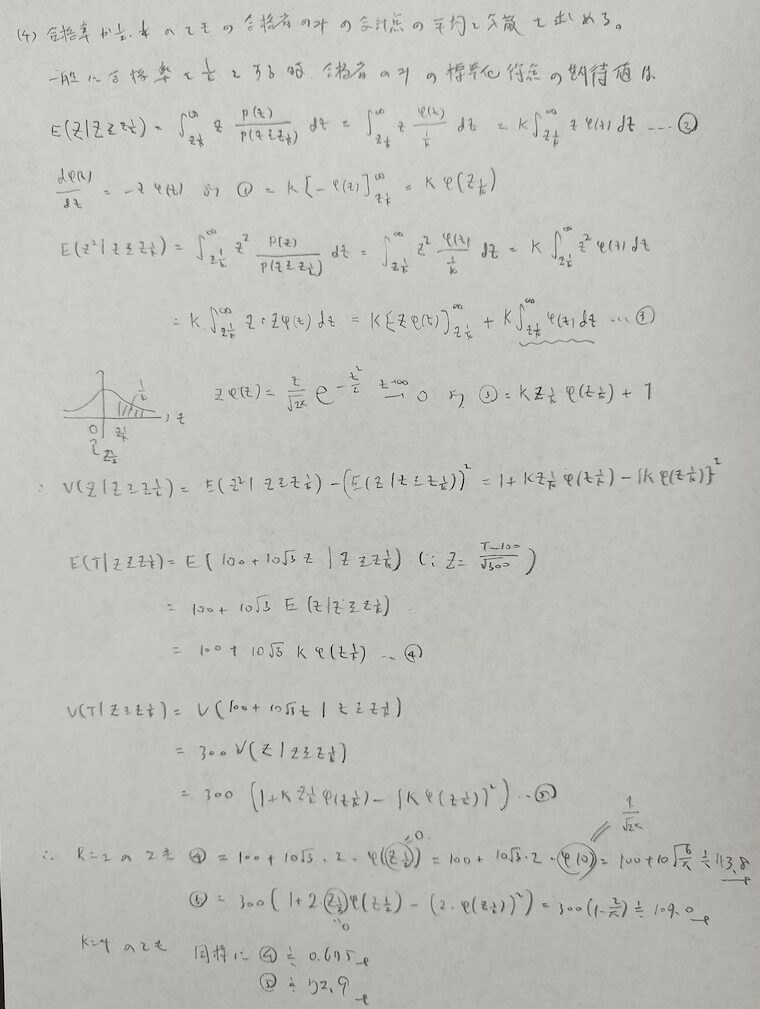
初見では難問ですが頻出問題ですので素早く処理できるようにしておきたい問題です。
2014年問2:単回帰分析
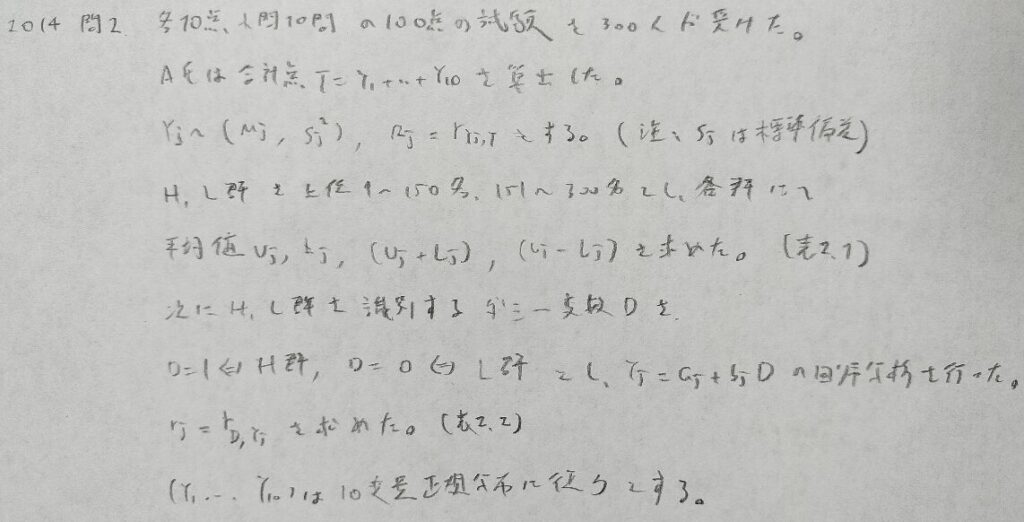



相関係数に注目することがポイントです。
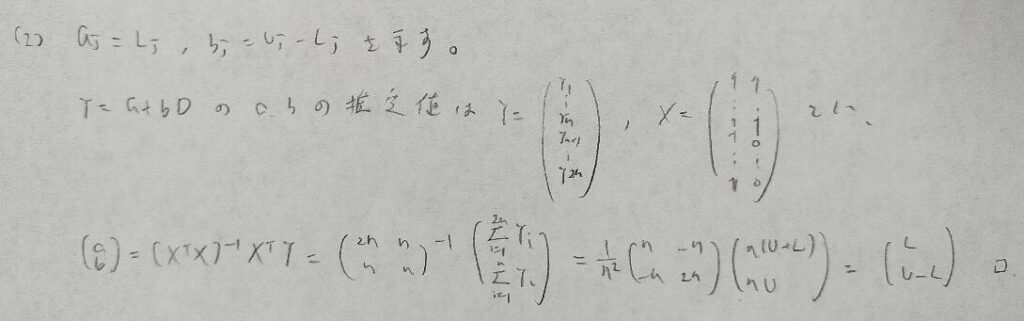
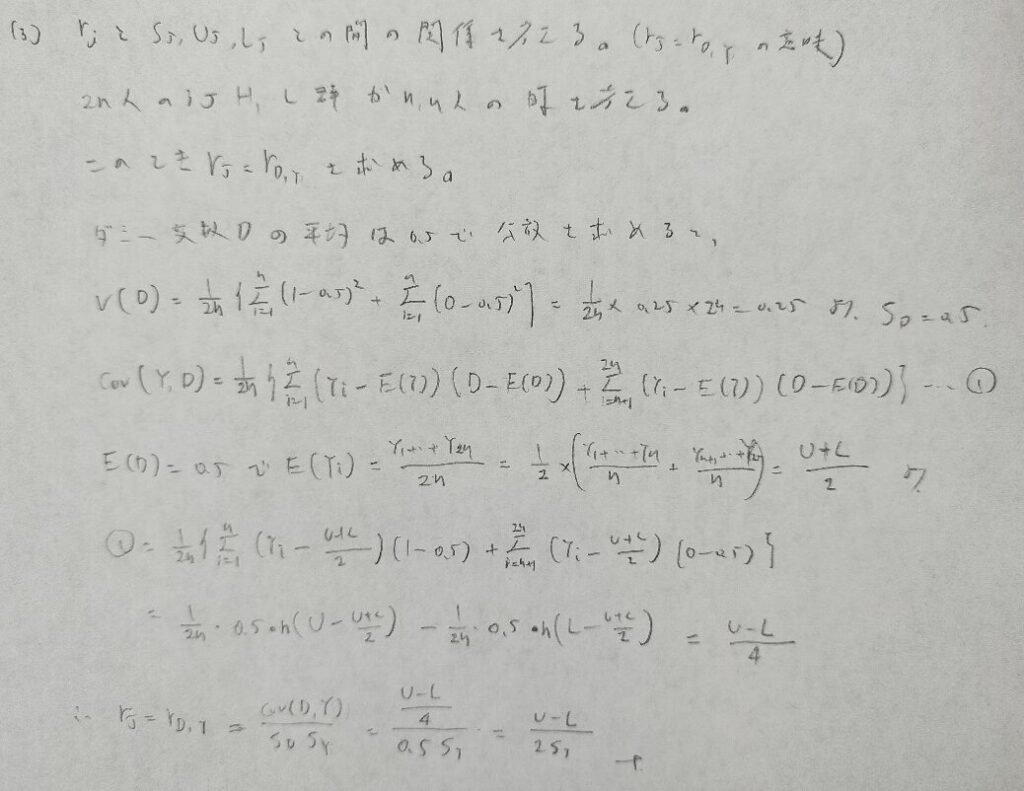
2014年問3:ロジスティック回帰分析
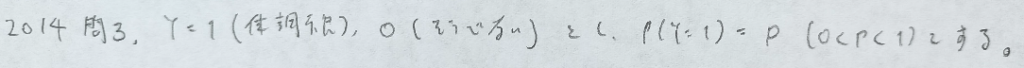


二番目の方のオッズの説明は、単に差という言葉で説明しても良さそうな気がします。


p値は、その変数の係数が0を帰無仮説とする考えで行うので、モデル選択におけるp値は値が大きいとその変数は削除することになります。
P値、AIC、ロジスティックモデルの改善点を書けばOKです。
2014年問4:クラスター分析
『多変量解析法入門 (ライブラリ新数学大系 E20)』に懇切丁寧に解説されています。
クラスター分析はこちらの記事でも詳しく説明しています!
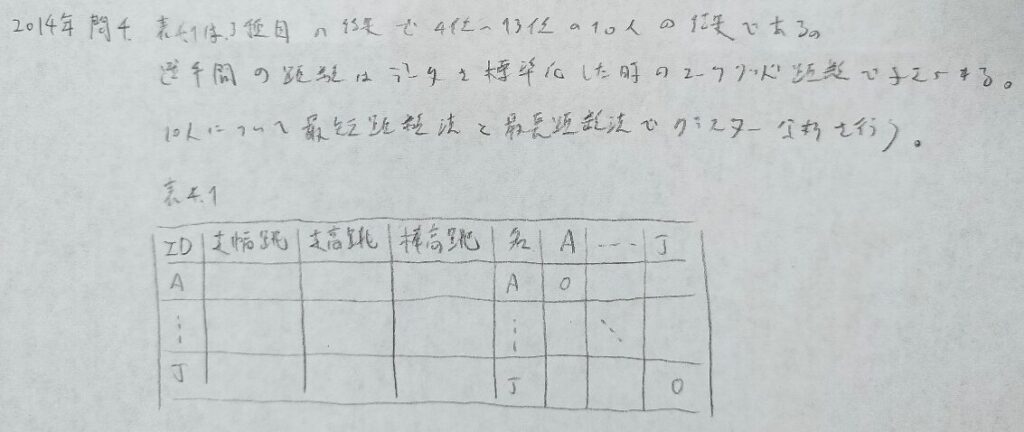


いきなりデンドログラムは書けないので、まずは考えやすい最短距離法から考えます。
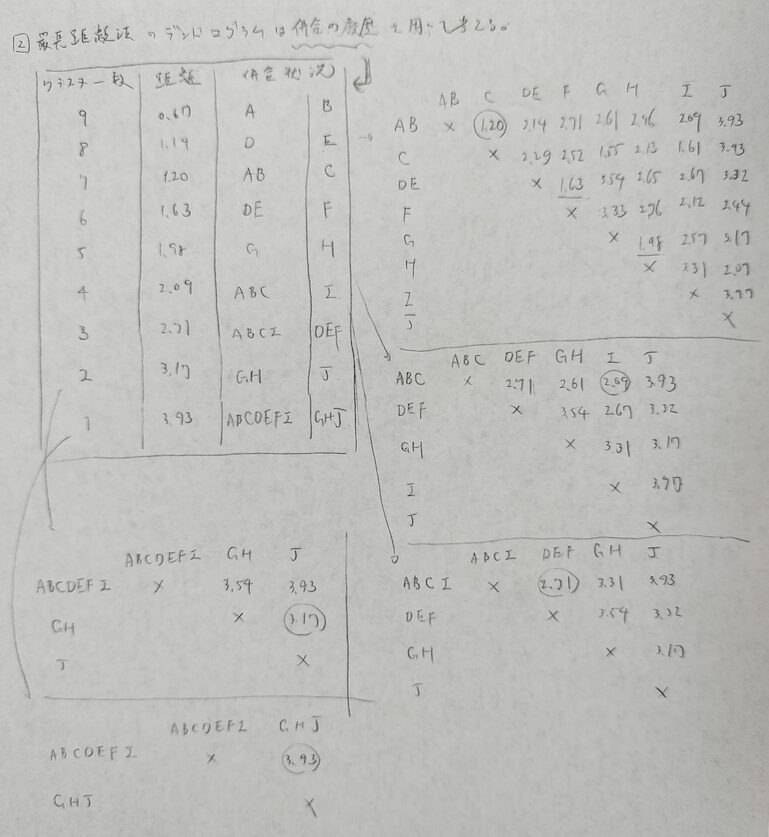
一つ一つ併合の様子を表で考えた方が安全です。
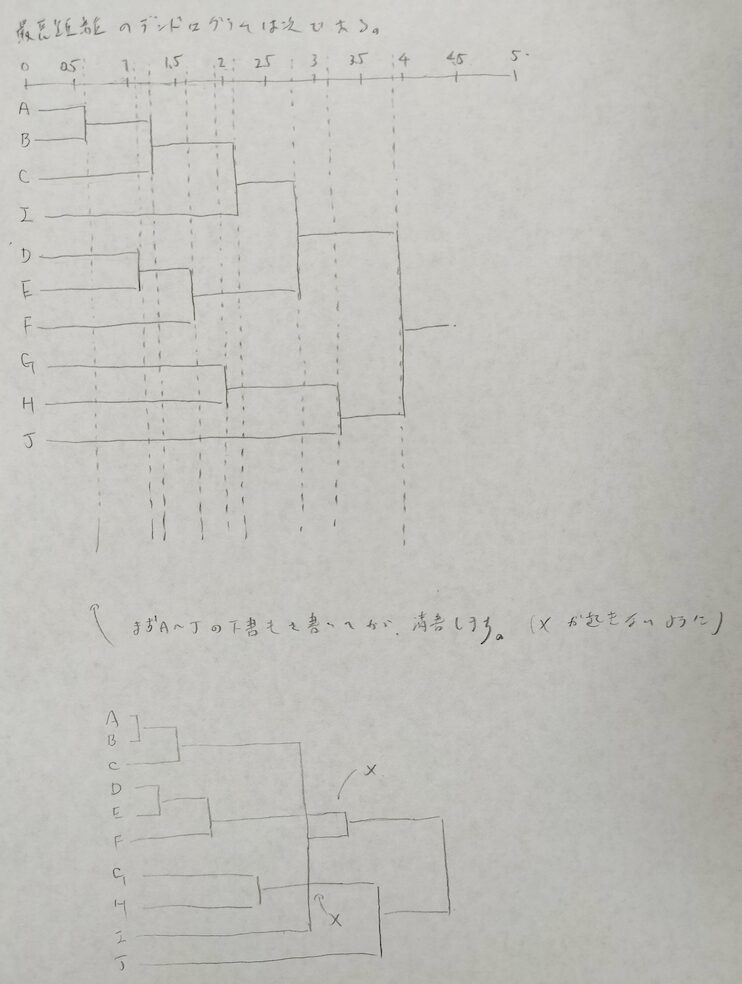
なるほど。下書きをしてみたら清書は素早くできますね!
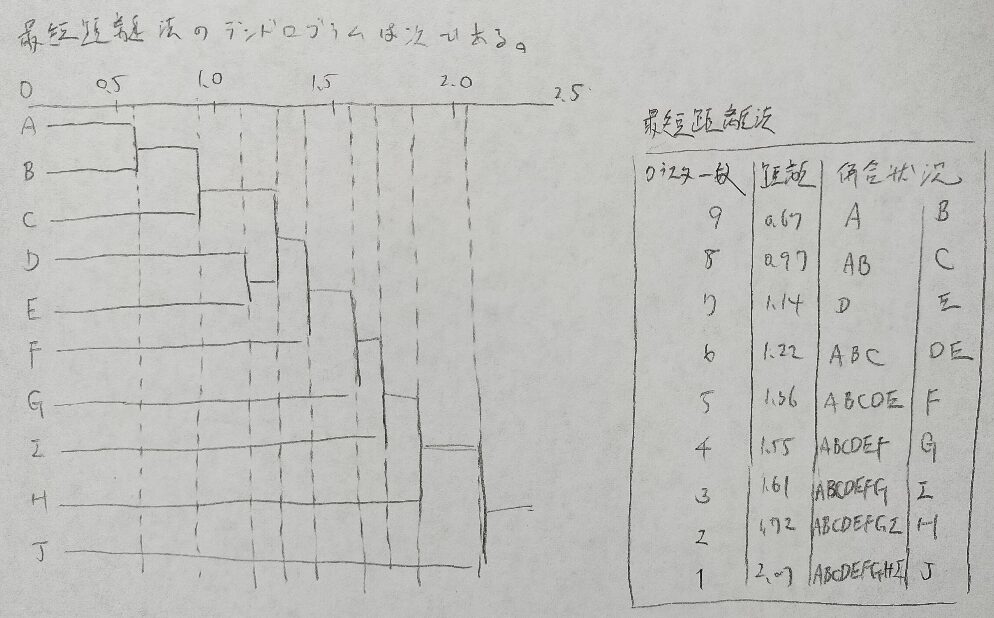
左図の点線は模範解答では書かれておりません。
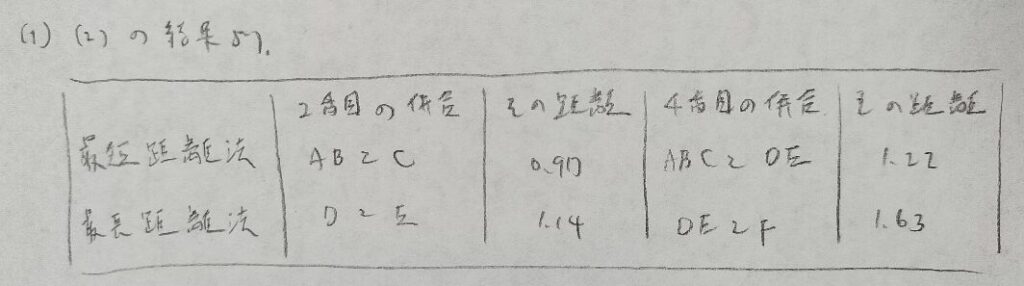

この解答ではアンバランスさをクラスター数が3の例を用いて説明しています。
統計検定1級「統計応用」人文科学の過去問:2015年

2015年問1:項目反応理論
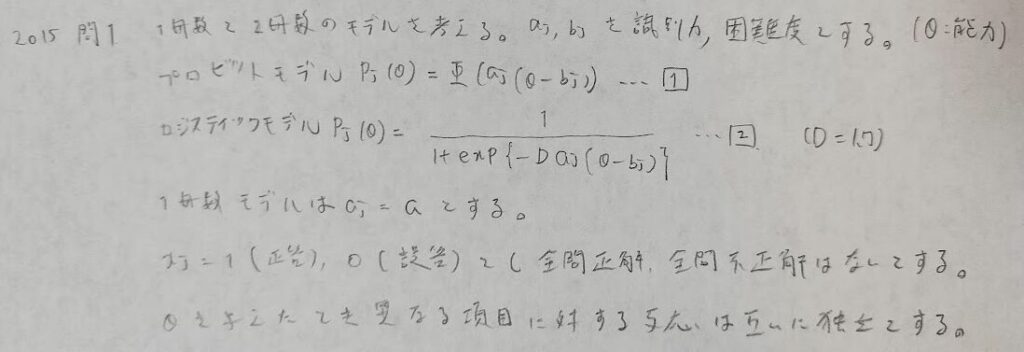
本問はひっかけがありますので次の2点に注意しましょう。
正解確率がどのように表されるか?
母数は問題によって異なるのか?
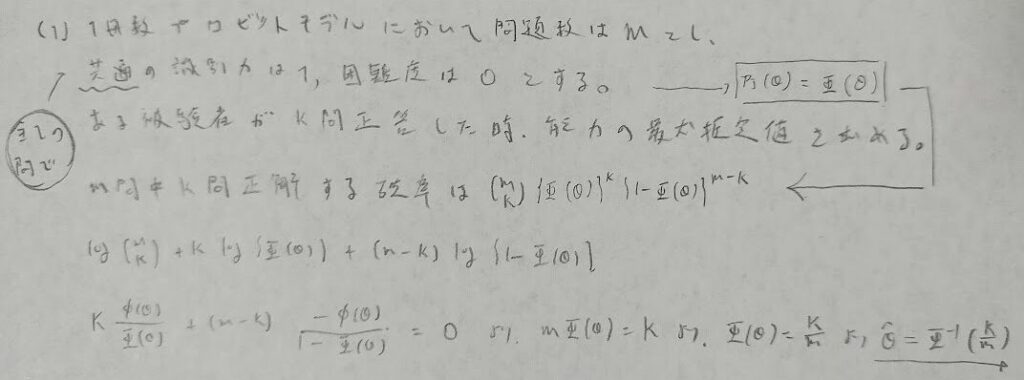
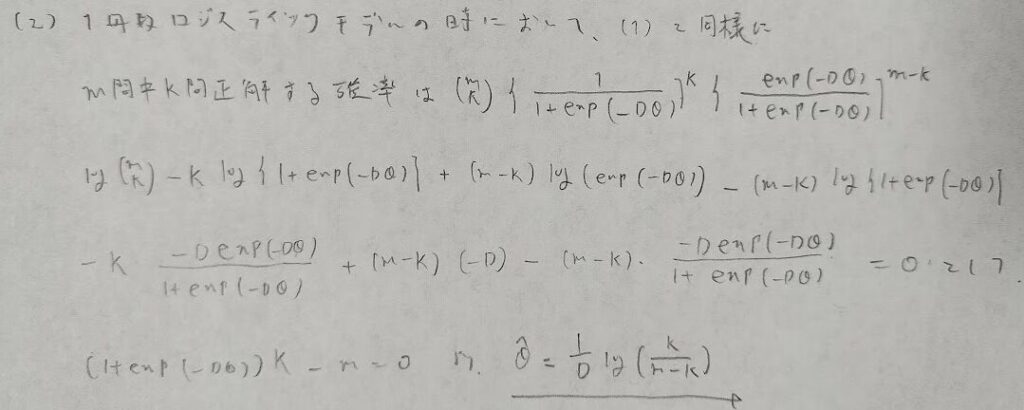
尤度関数からの最尤法は頻出ですね!
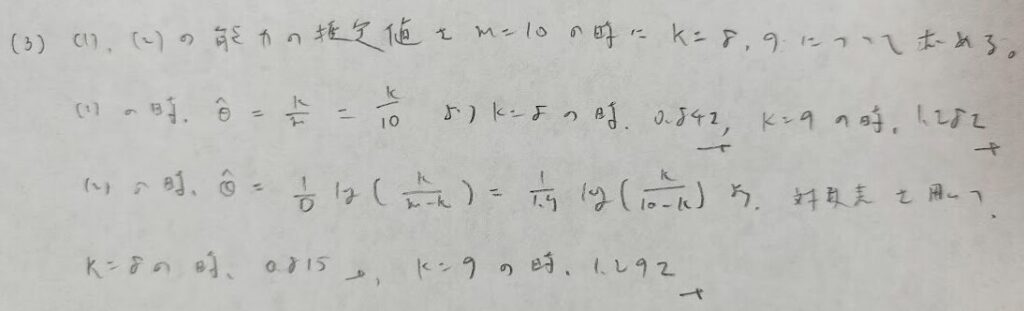
プロビットモデルもロジスティックモデルも、どちらから求めた値もほぼ一致していることが計算から確かめることができます。
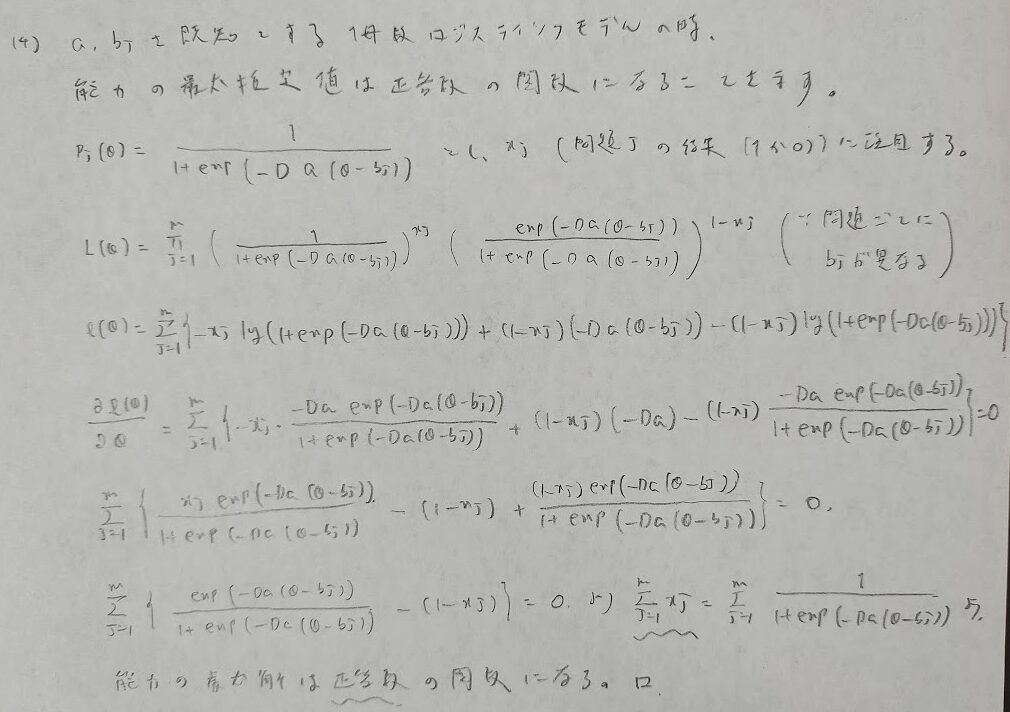
本問のメイン部分です。最後の変形をするように問題文にヒントが与えられています。尤度の作成で注意が必要です。二項分布としたらNGです。

問題文の独立の部分をよく読めば期待値を使うことに気が付くと思います。
統計検定1級の人文科学の項目反応理論は『項目反応理論[入門編]』の第2章まで学習すれば完答できる可能性が高まります。
2015年問2:主成分分析と因子分析

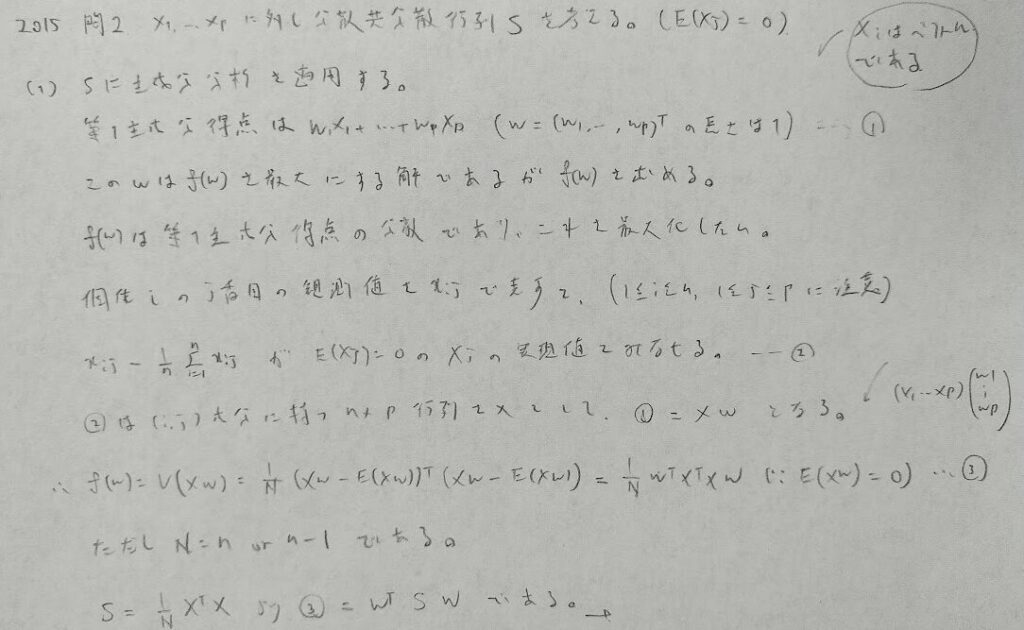
この問題は『多変量解析法入門 (ライブラリ新数学大系 E20)』よりも公式の教科書『統計検定1級対応 統計学』もしくは小西先生の『多変量解析入門――線形から非線形へ』を参照された方がわかりやすいと思います。
統計検定1級の教科書のほぼそのままの問題ですが、参考程度に小西先生の本(永田先生の本よりも難しい)に移るのが良いと思います。

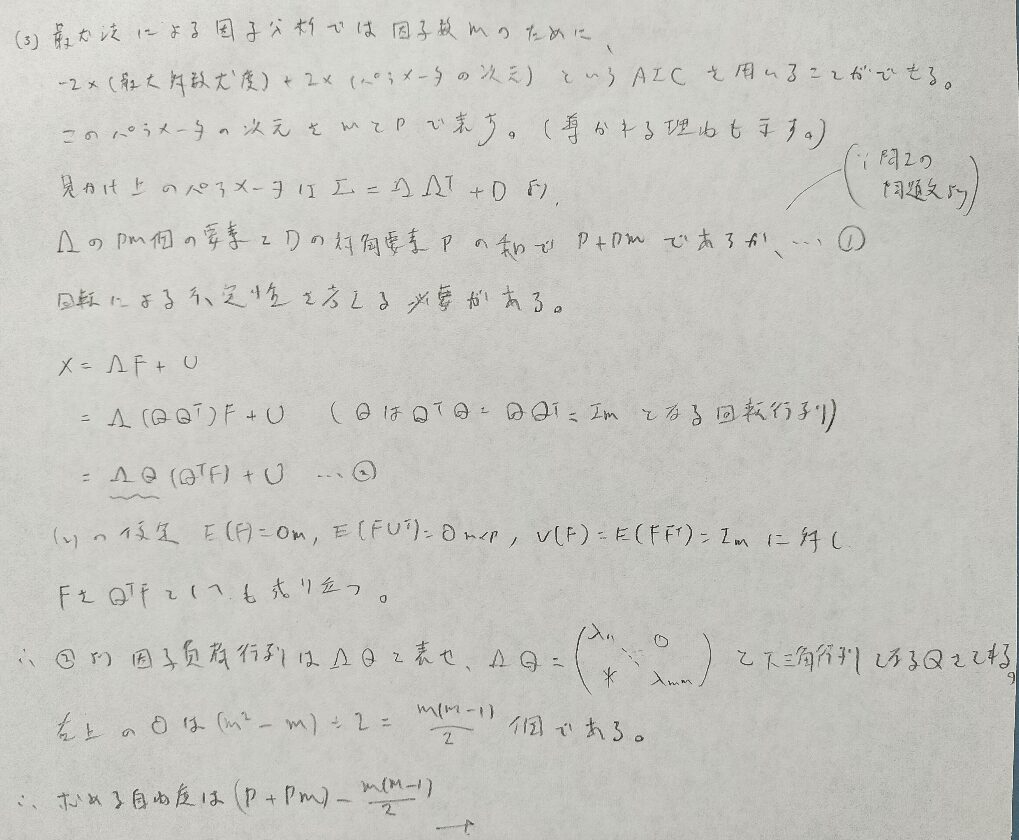

2015年問3:MDS
問3がずば抜けて難問です。時間内に解き切るのは厳しいでしょう。
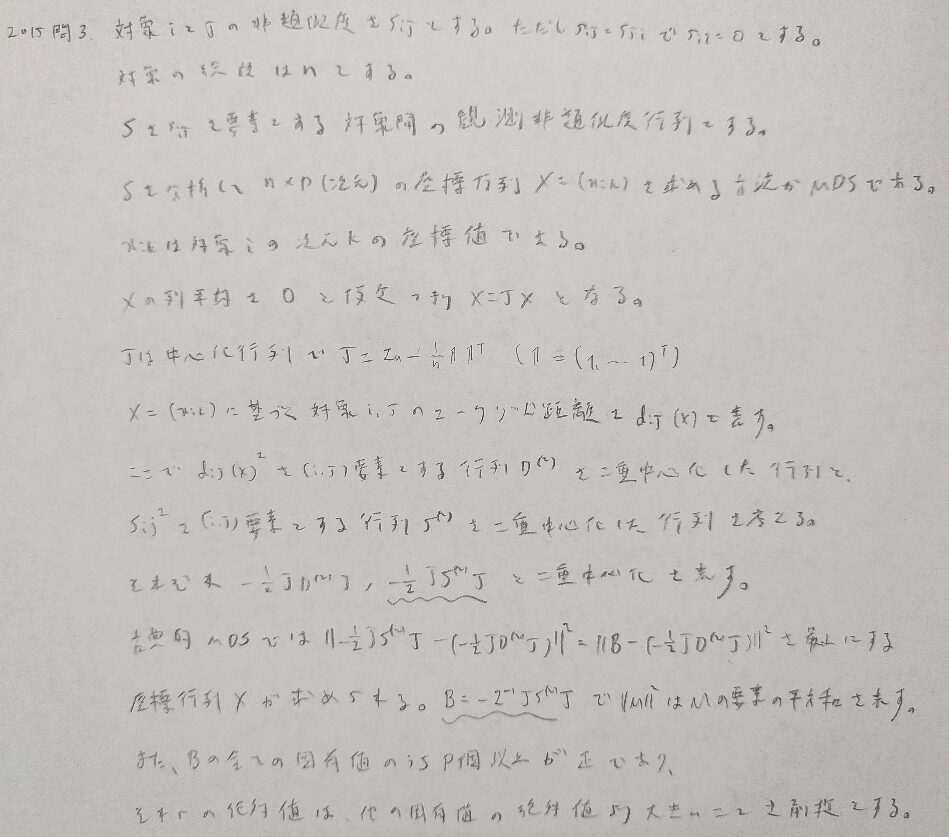
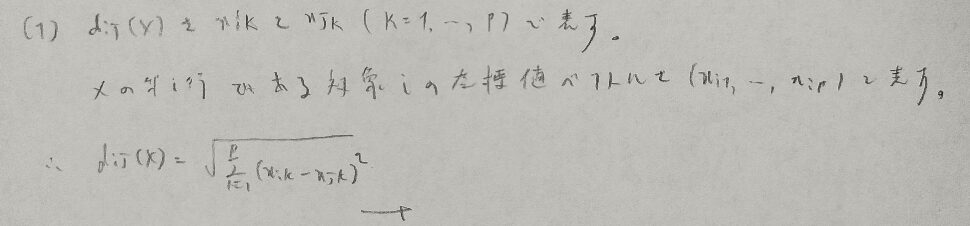
問題文をよく読めば座標が決定できるので距離は簡単に出せます。
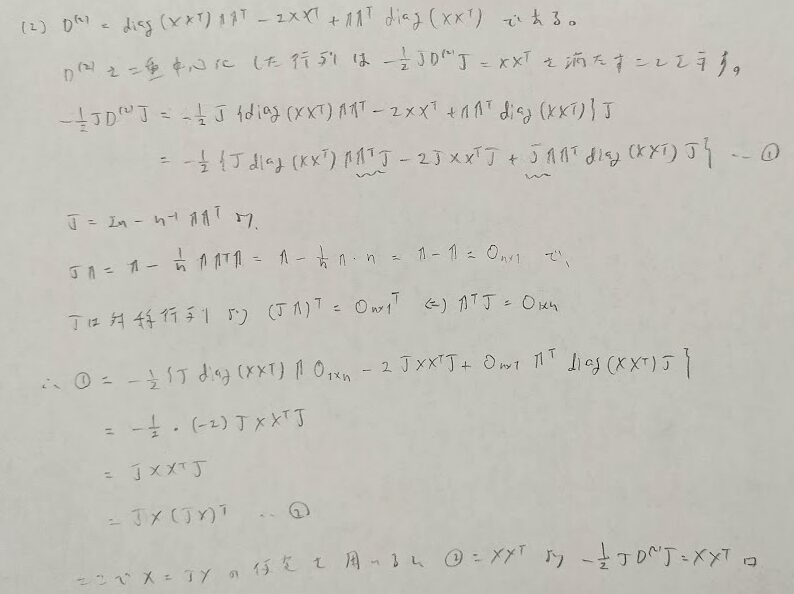
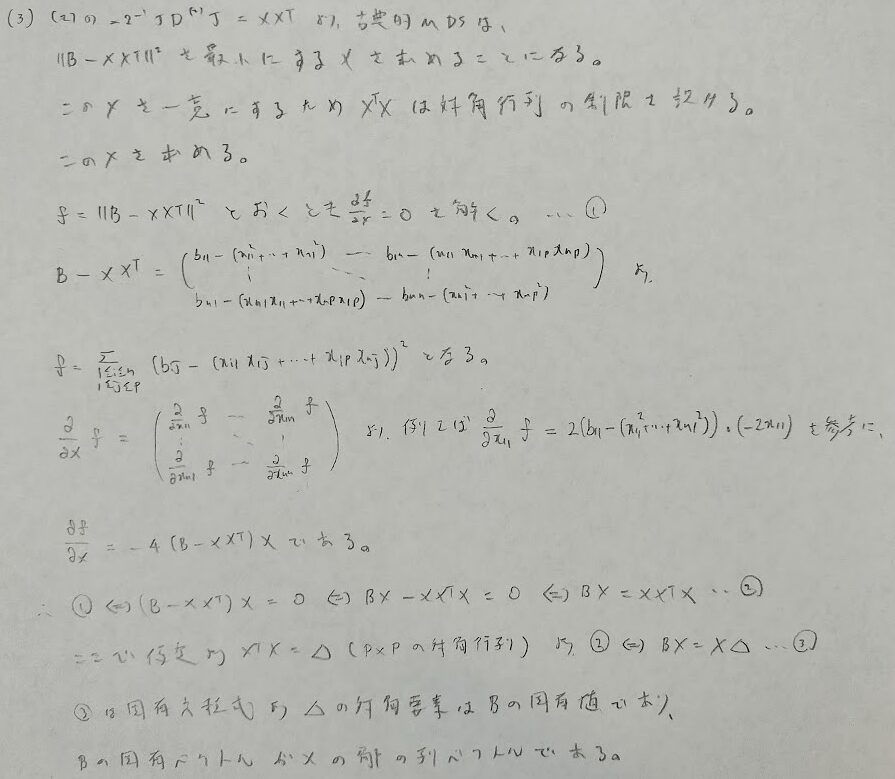
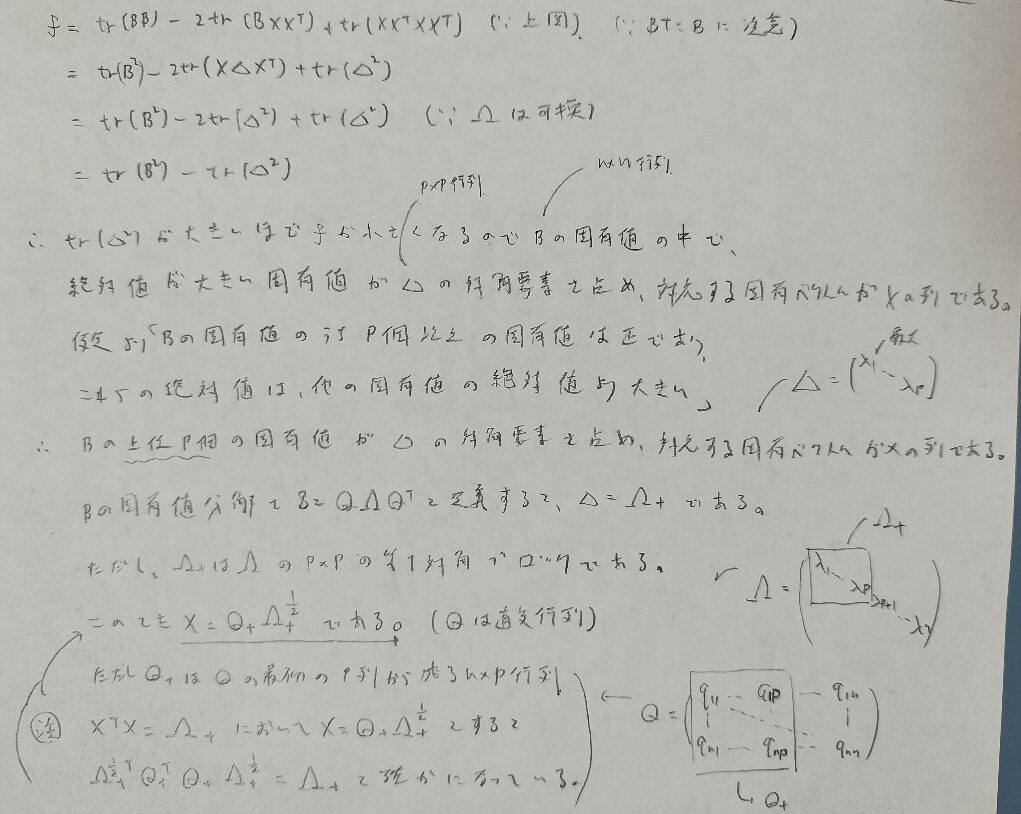
スカラーを行列で微分するなど開始から難しい難問でした。

2015年問4:判別分析
本問は『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』に類題が載っています!
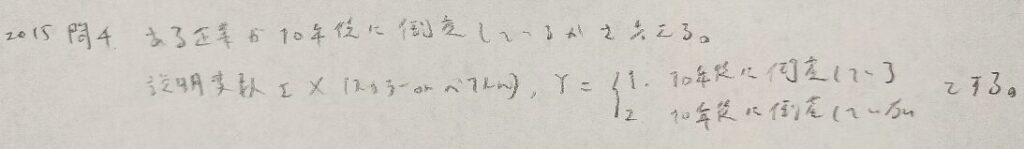
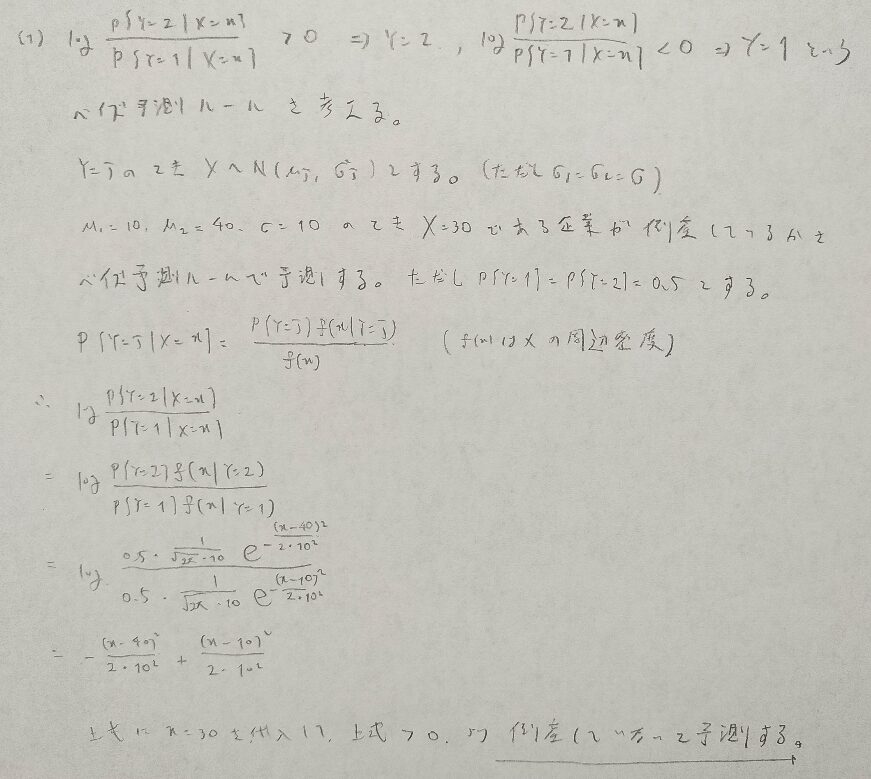
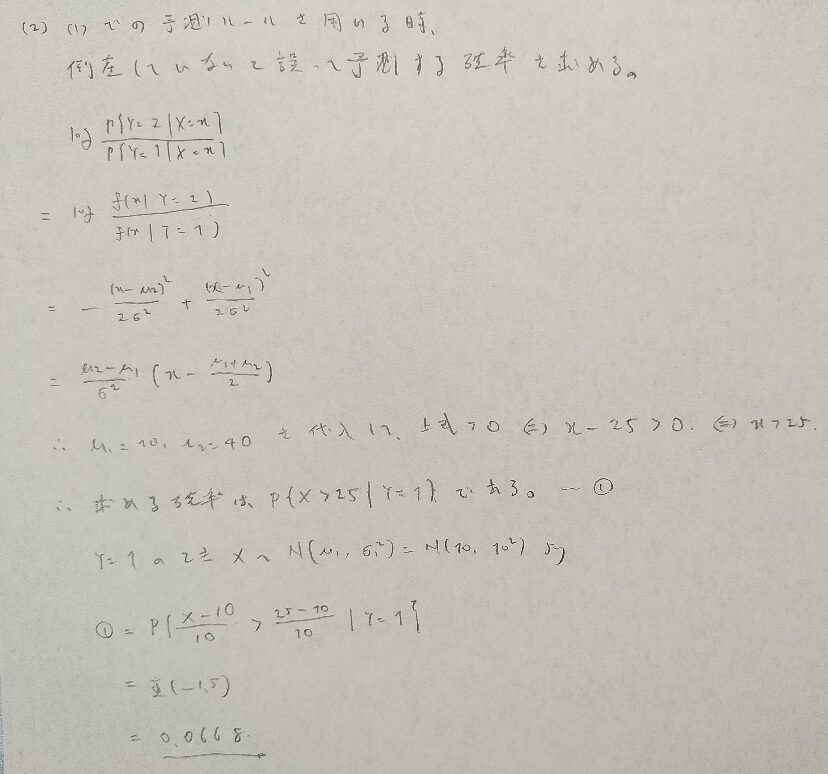
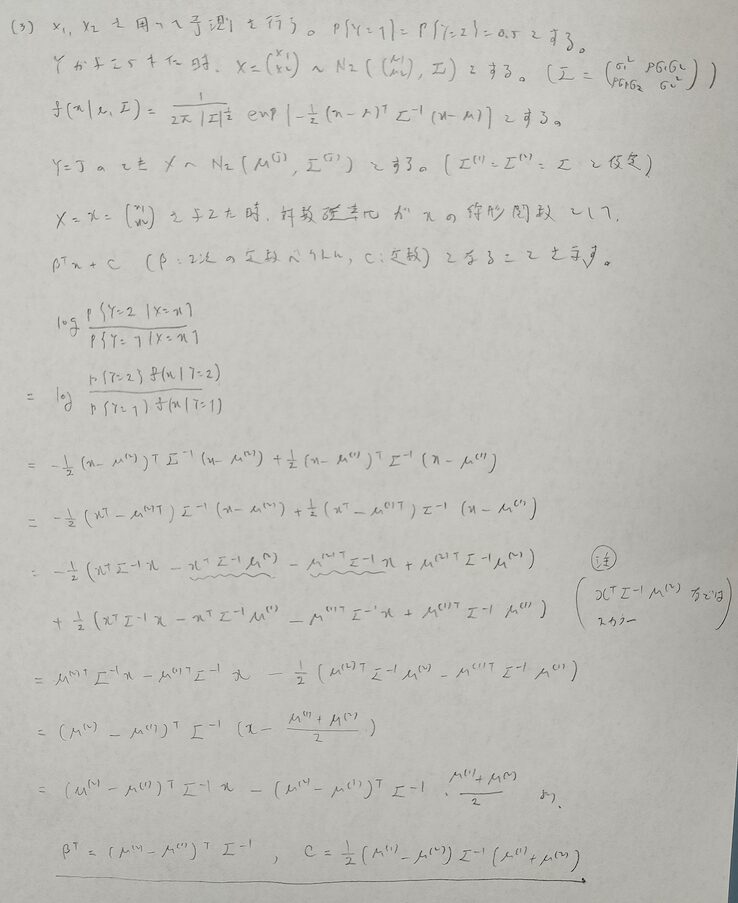
行列の計算は困ったら1つ1つ書き出してみれば先に進めます。
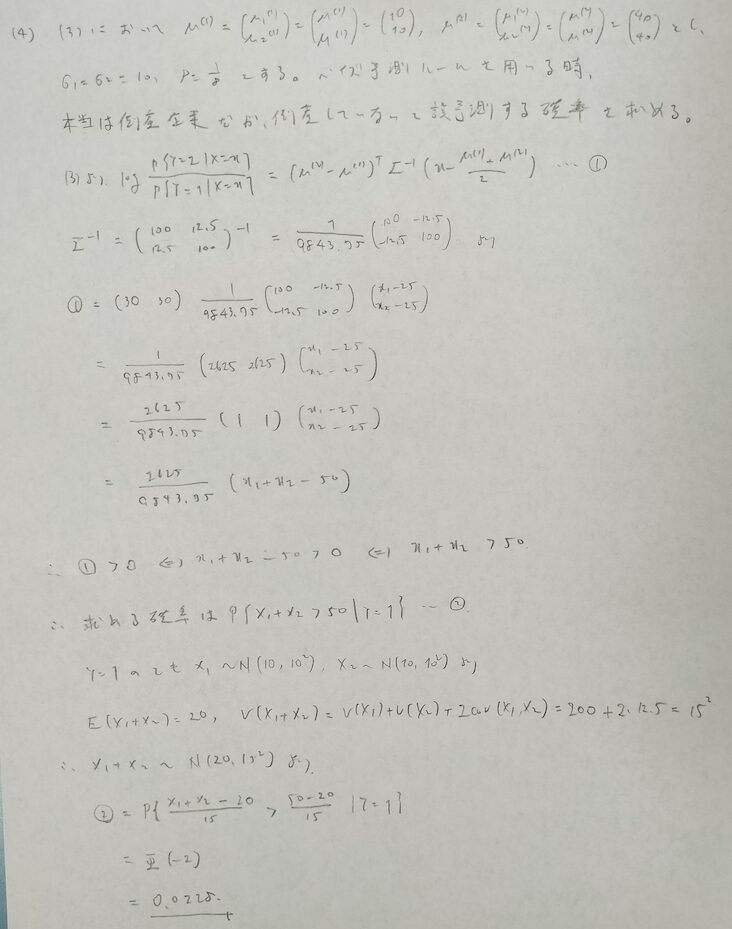
(4)は具体的な数値を代入するより、文字式のまま式変形を進めた方が良さそうです。
2015年度の人文科学は行列計算が大変な年でした。
統計検定1級「統計応用」人文科学の過去問:2016年

この年から大問に標本調査の問題が出題されるようになります。
登場頻度が低く、計算量が膨大で時間内に解き切れる可能性が低くなるため、過去問対策はおすすめしません。
2016年問1:因子分析

『多変量解析法入門』に載っている問題は因子間の相関がない前提の内容ですが、本問はそこにも相関がありますのでご注意ください。

表1の詳しい値については『日本統計学会公式認定 統計検定 1級 公式問題集[2016〜2018年] 』をご参照ください。

本問も次の問題もただの行列計算ですが、なぜこのような式になるのか?が問われています。
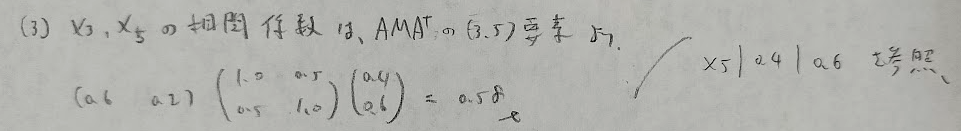
最後は回転に関する理解を問う問題です。

直交は内積0つまり無相関と考えれば覚えやすいですね。
2016年問2:切断正規分布

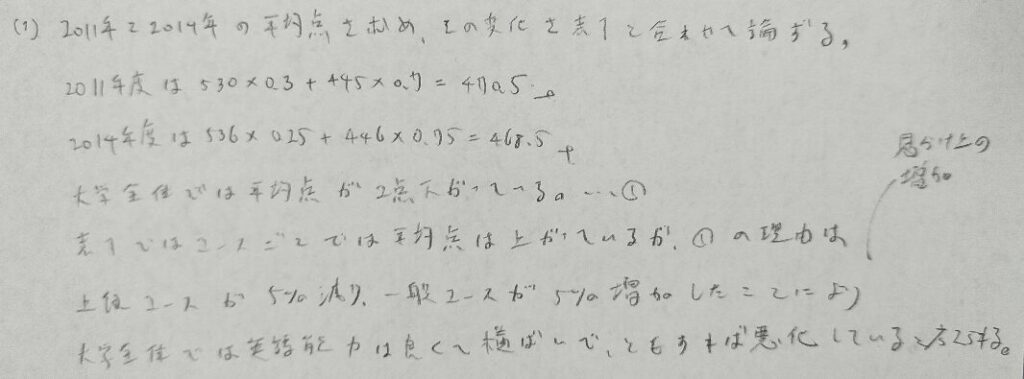

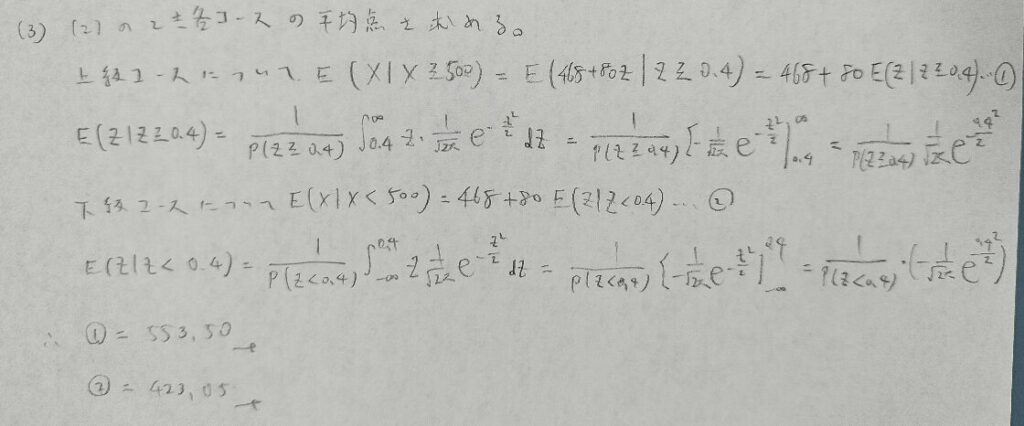
切断正規分布はテンプレ化されている感じですので、本番で出てきたら必ず解き切りたい問題ですね!
2016年問3:標本調査
標本調査に関する問題は時間内に解ききれないと判断して対策からは除いています。対策書は『概説標本調査法』が良いとの評判です。
2016年問4:共分散構造分析

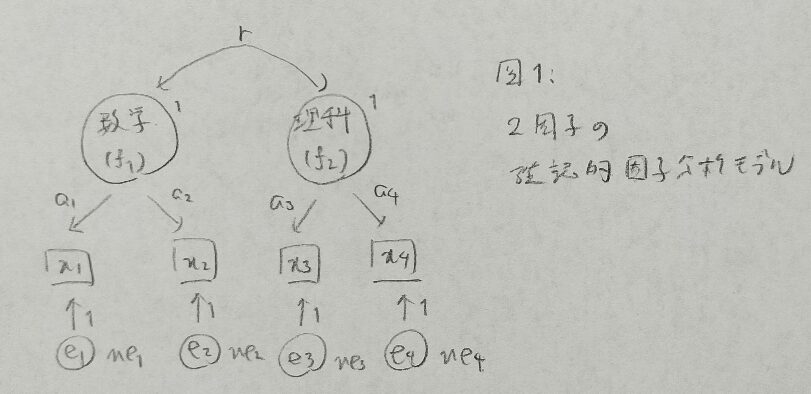
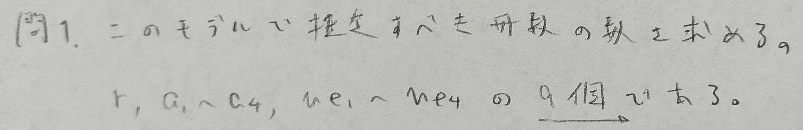

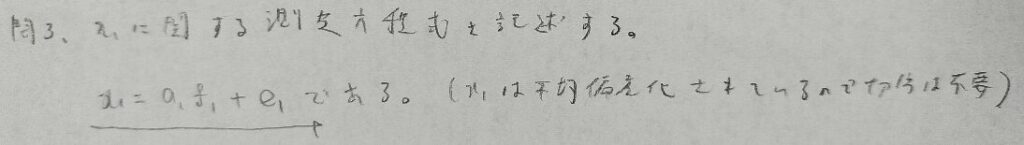
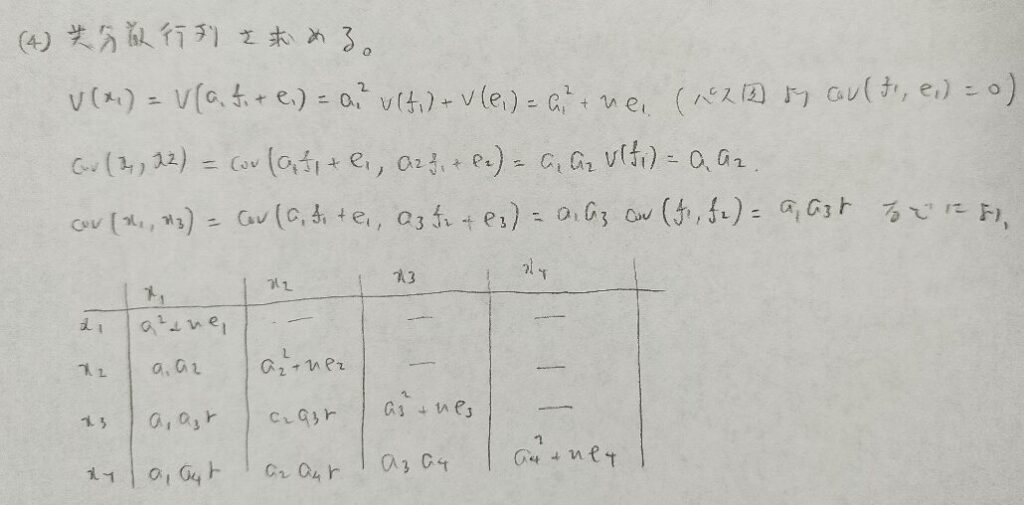

自由度が正以外なら識別不可能です。
統計検定1級「統計応用」人文科学の過去問:2017年

2017年問1:因子分析




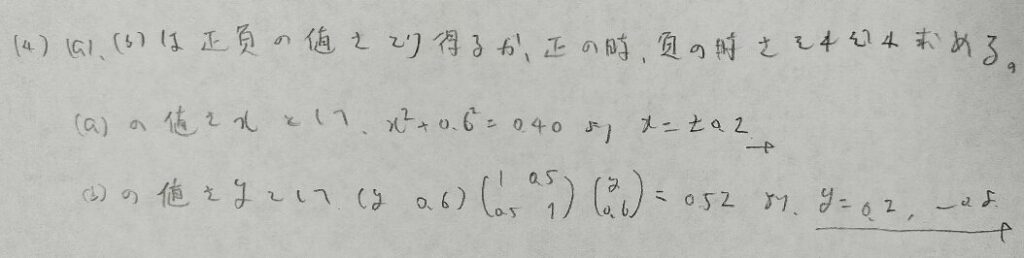

因子分析はモデル化できることが大切です。
2017年問2:一元配置分散分析

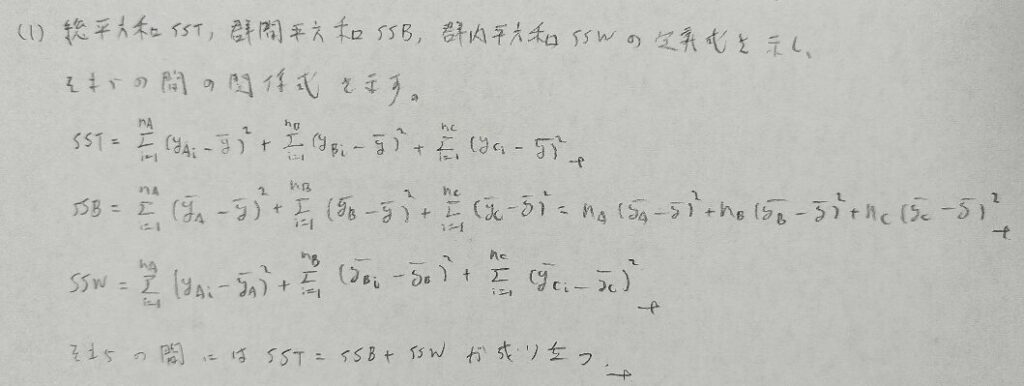
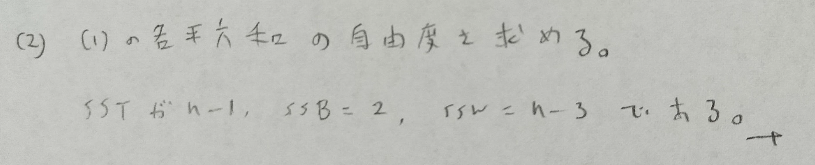
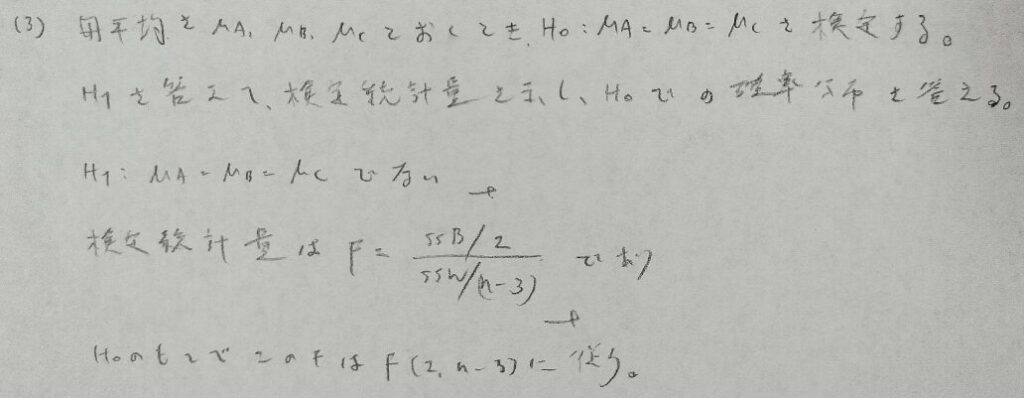
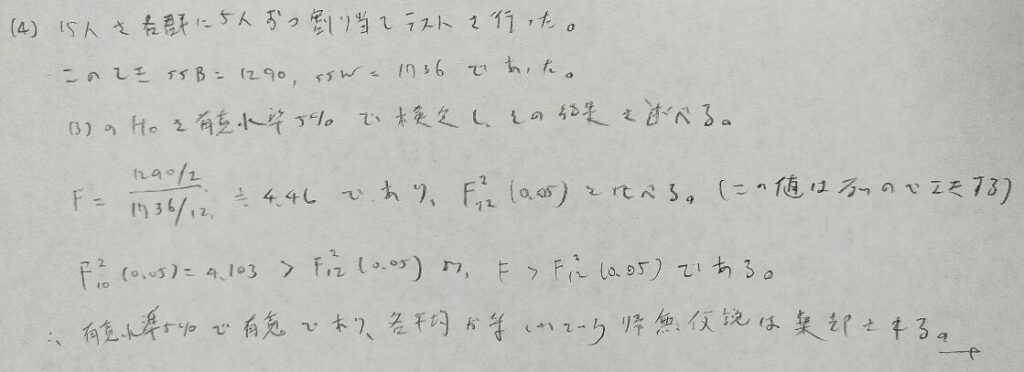
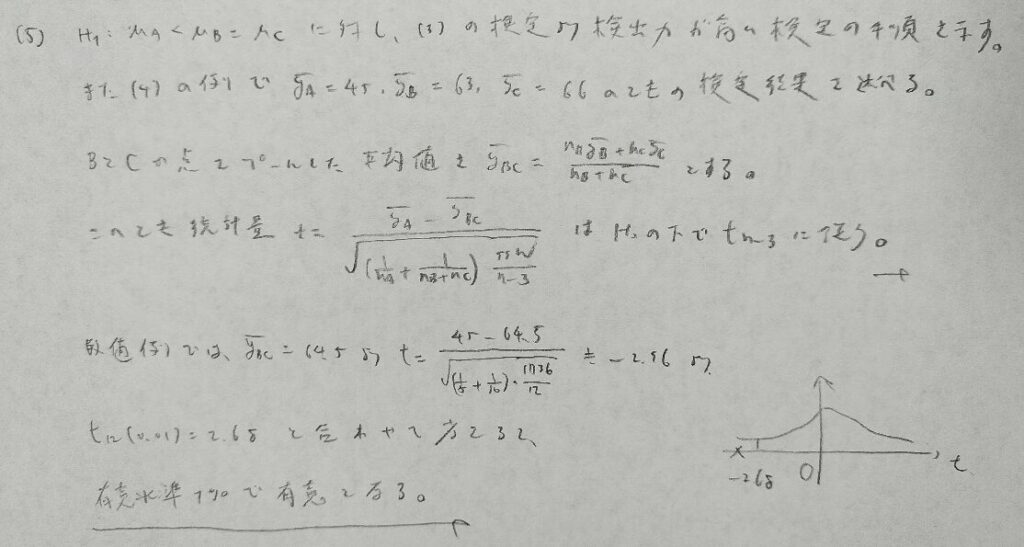
t統計量の分母でプールされた分散の推定値において、群間平方和でなく郡内平方和の方に注目している理由は、3つの母集団の中での各平均との差を考えているためです。もしくは通常のt検定の考え方の応用と考えても同じ結果が出てきます。
分散分析で用いる検定はF検定だけではありません。最後の問題は今後も出題されると予想します。
2017年問3:切断正規分布
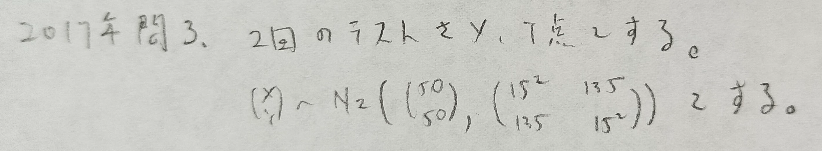
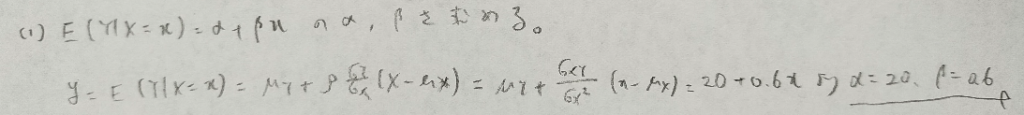
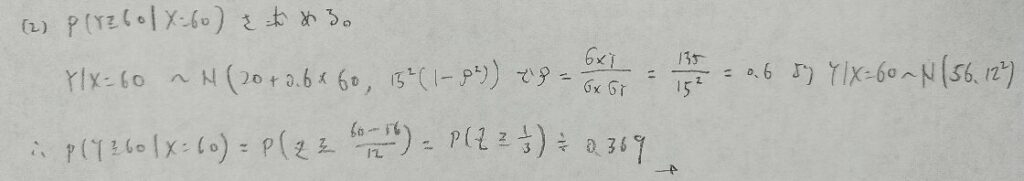
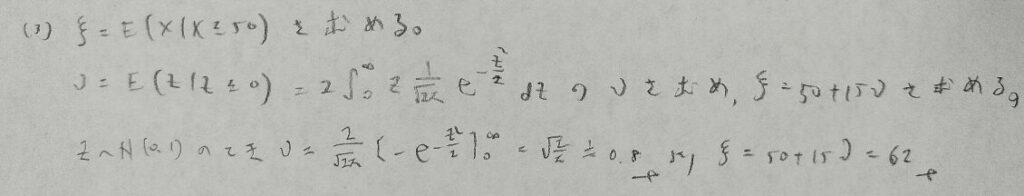
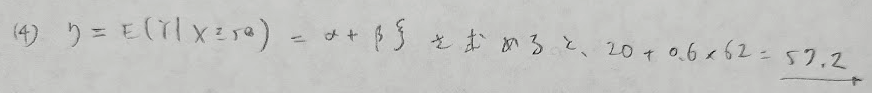

(4)はあれこれ考えずに素直に誘導に乗りましょう!
2017年問4:標本調査
標本調査に関する問題は時間内に解ききれないと判断して対策からは除いています。対策書は『概説標本調査法』が良いとの評判です。
統計検定1級「統計応用」人文科学の過去問:2018年

2018年問1:分割表

定義域は今後も聞かれる可能性があります。
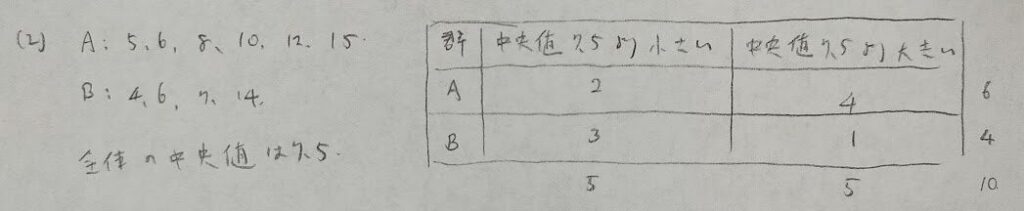

ファイ係数の絶対値がクラメールの連関係数です。
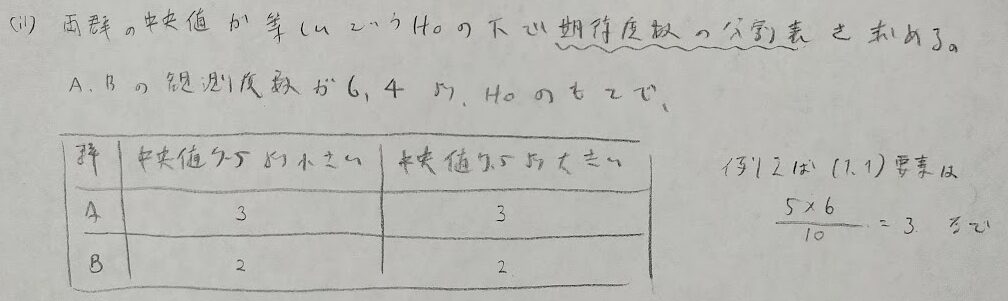
この期待度数の問題は統計検定準1級で学習しているので必ず正解しましょう!
本質的にはAとBが独立の時という意味ですね。
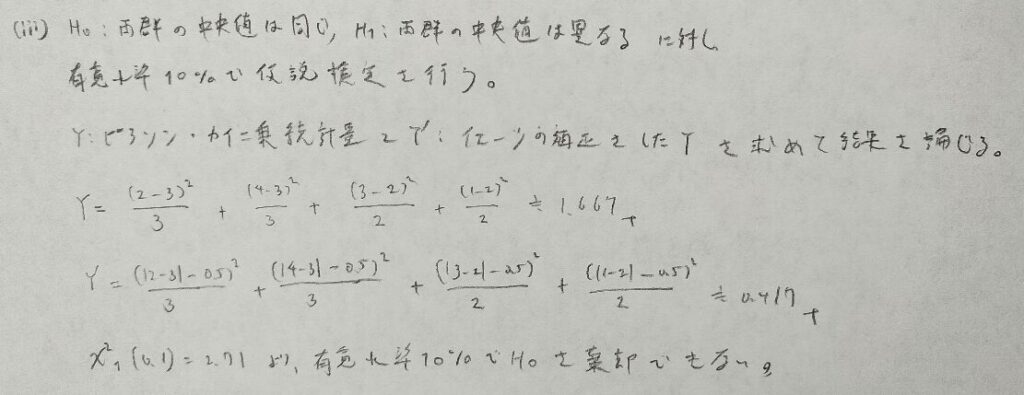
アクチュアリー数学と違って、統計検定1級では和の形で書き下せた方が良いです。

フィッシャーの正確性検定のp値とは、(両側検定は)起こりうる全ての表を考えたのちで実際に確率を計算した後で、両側検定の場合は観測値のときの確率以下の確率の和であり、片側検定は注目しているセルの度数以下(または以上)となる確率の和として定義されます。
2018年問2:判別分析



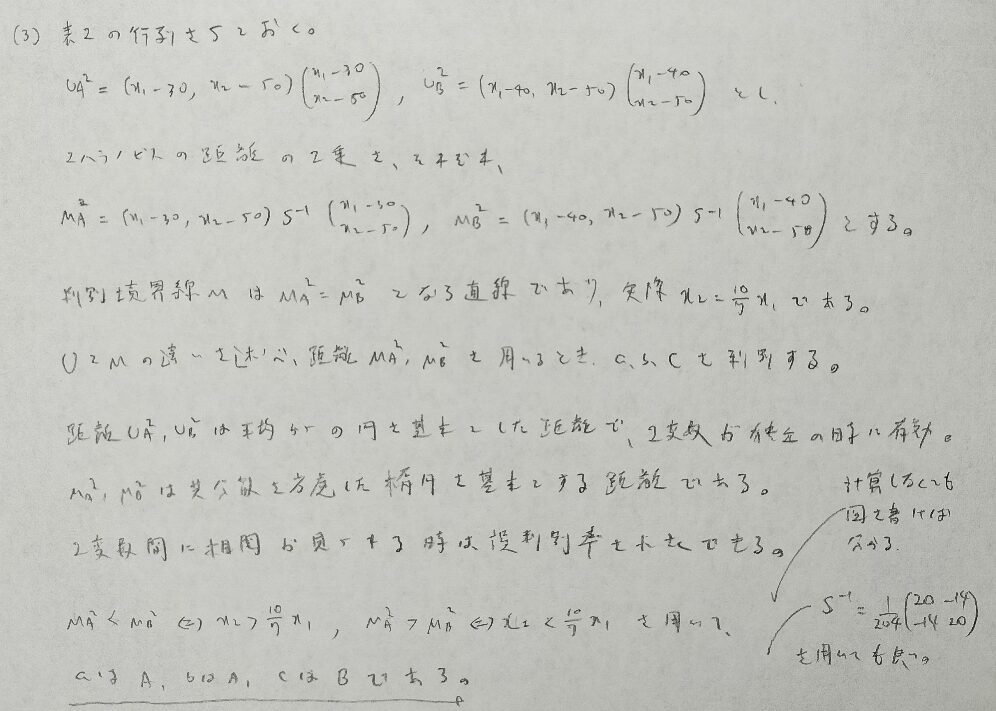
内積表示を行うとマハラノビスの距離への理解が深まります。マハラノビスの距離には楕円が関係しています。
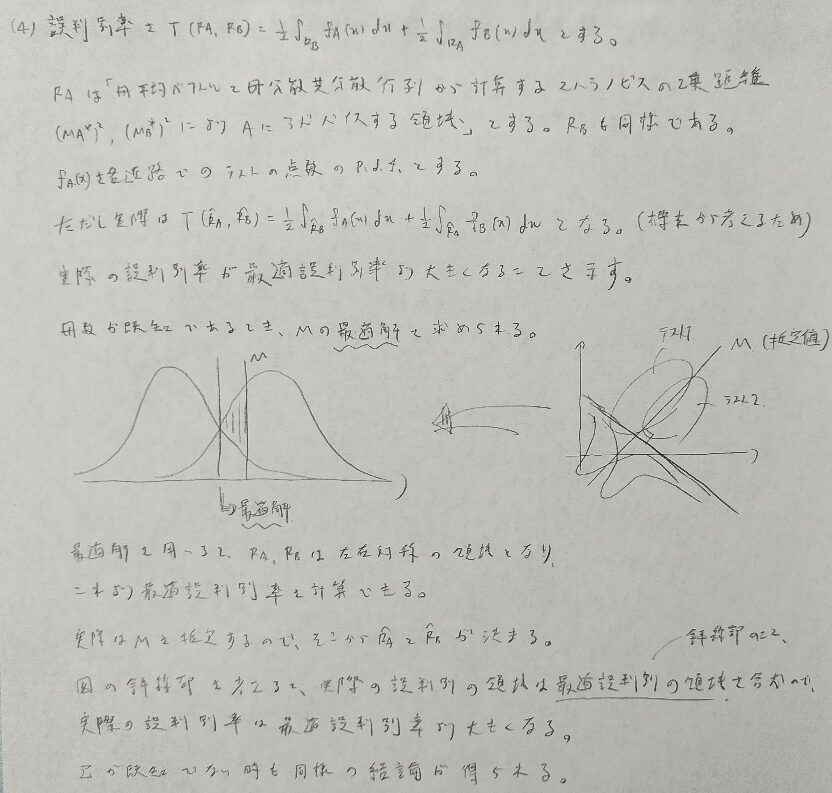
難問ですが、積分する関数と、積分する領域をしっかりと理解すれば部分点をもらうことはできますね。
2018年問3:パス解析
本問のパス解析は『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』に類題が詳しく掲載されいています。統計検定1級の統計応用の人文科学の対策本として素晴らしい名著です。

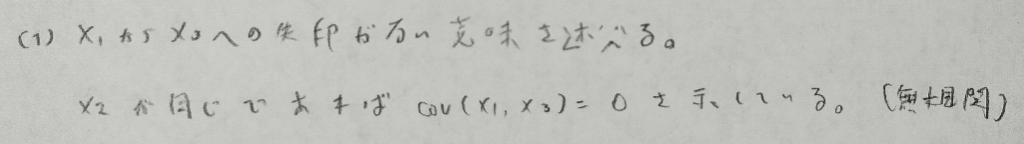
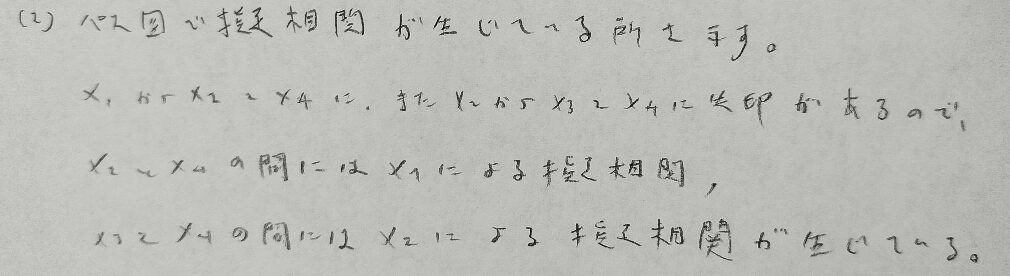

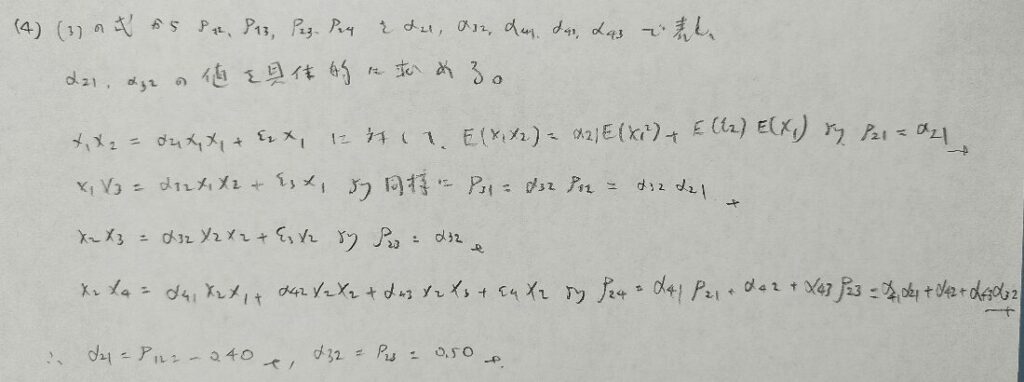
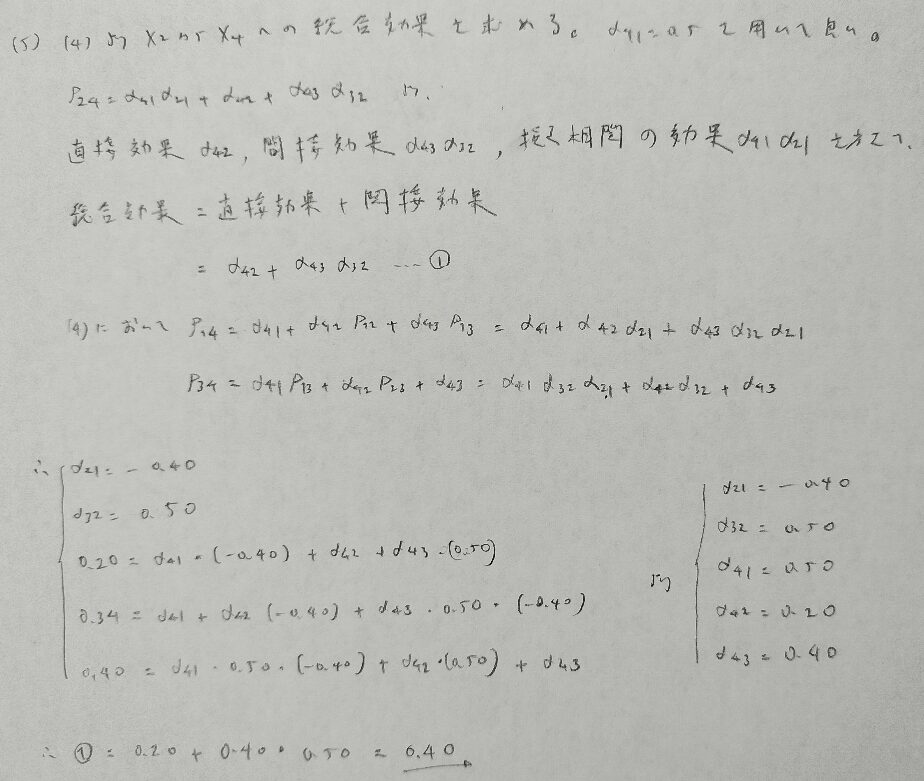
2018年問4:クラスター分析

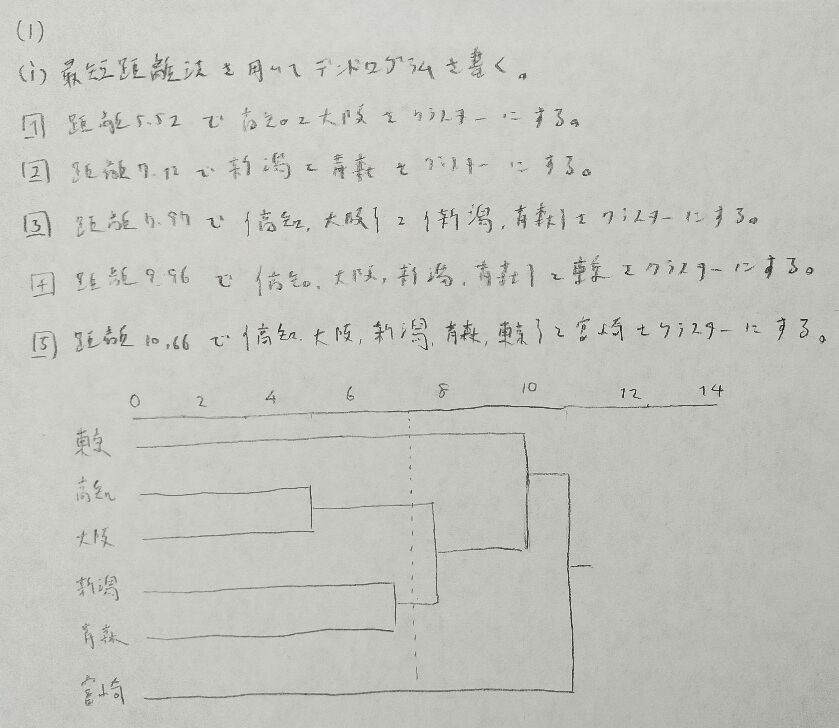

こういう問題は好きな距離で区切ってクラスター数を出した後に、元データまで遡ってクラスターの解釈を行えばよい。

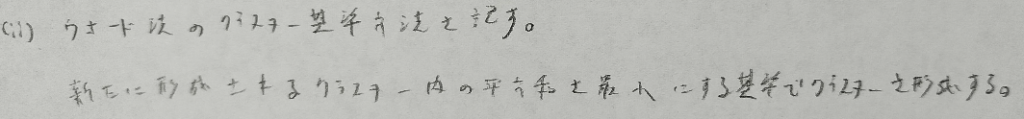

統計検定1級「統計応用」人文科学の過去問:2019年

2019年問1:切断正規分布

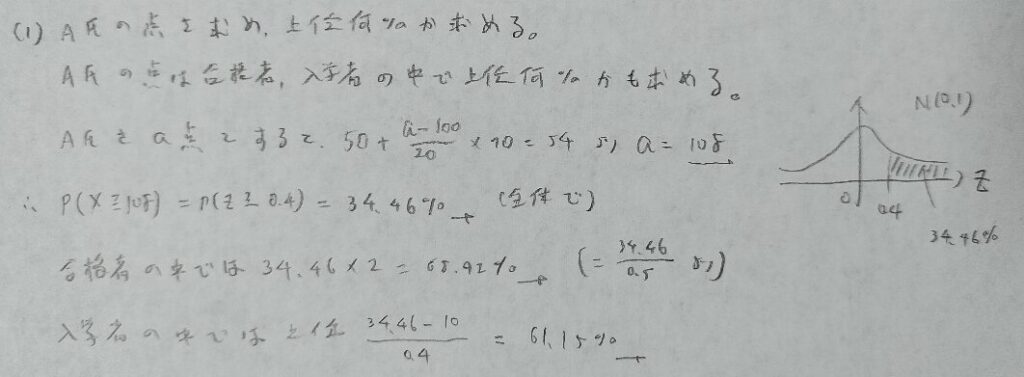
後半の2つの問いは条件付き確率の問題になります。場合によっては(2)が先に求まるかも知れません。

正規分布は対称性があるので、期待値と中央値と最頻値が一致します。
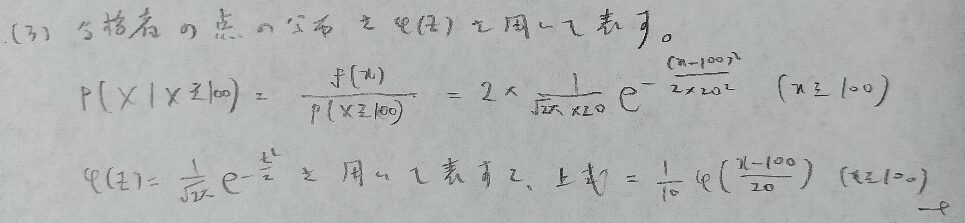
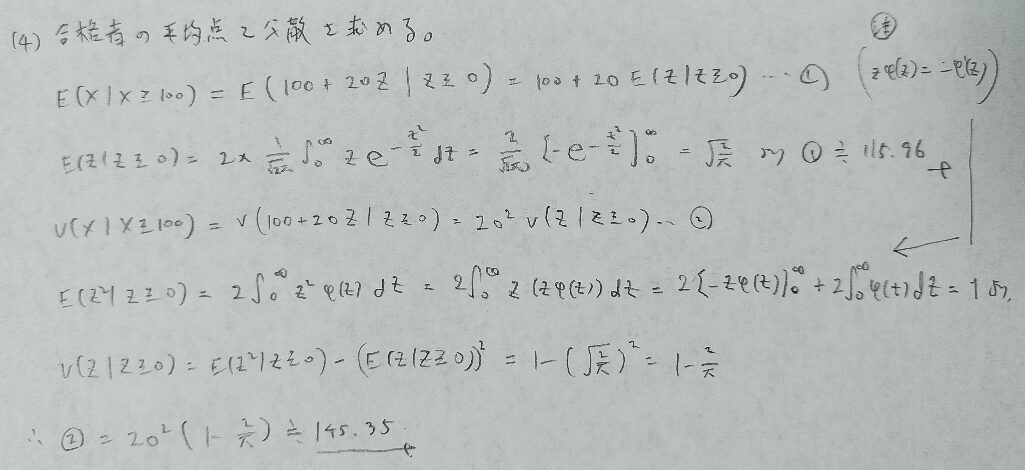
右上の注の内容は標準正規分布の部分積分でよく用いる公式として覚えてしまいましょう!
2019年問2:クラスター分析

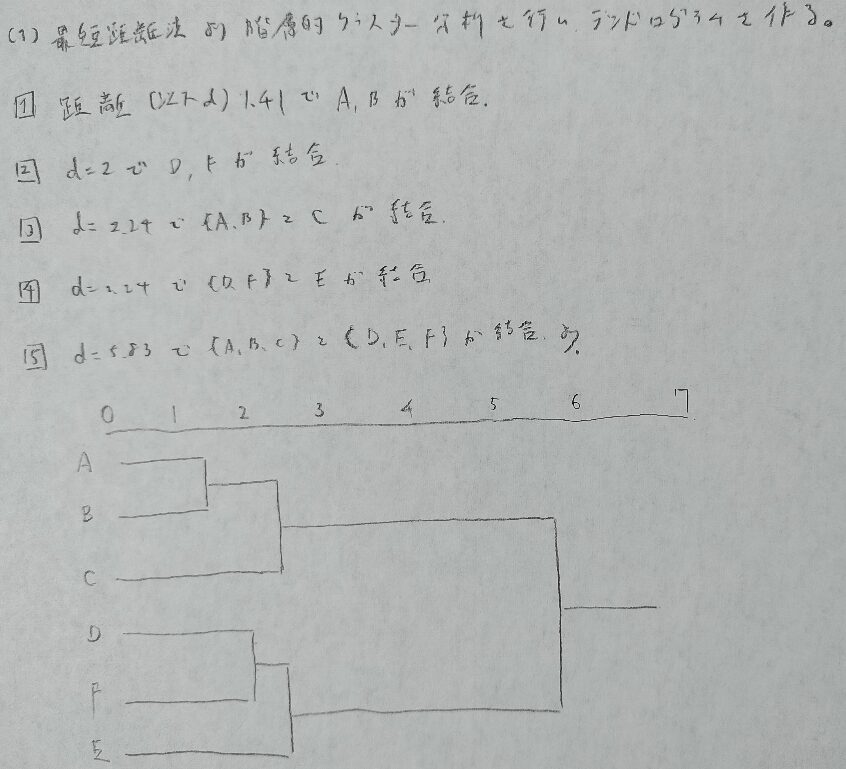
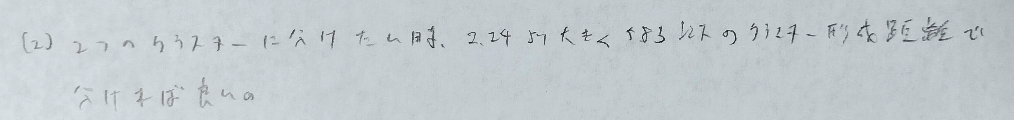
(3)の1行目は断層的→階層的の書き間違いです(皆さんもご注意を!)
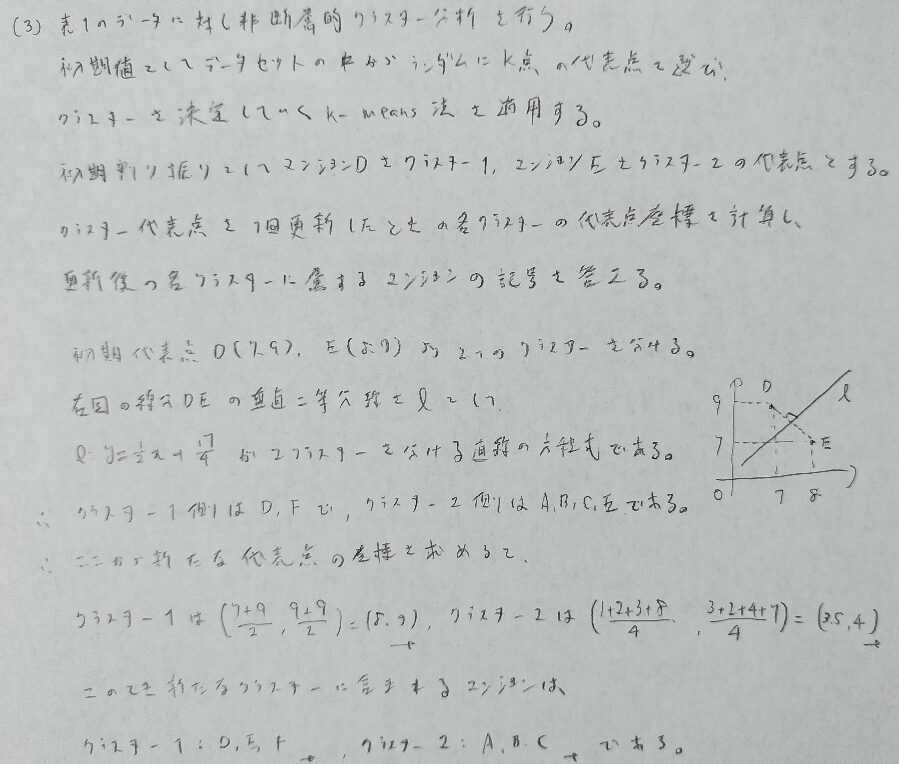
階層的クラスター分析(最短距離法など)に対して
非階層的クラスター分析(k-means法など)はあらかじめクラスター数を決めておく方法です。

2019年問3:項目反応理論
統計検定1級の人文科学の項目反応理論は『項目反応理論[入門編]』の第2章まで学習すれば完答できる可能性が高まりますが、本問では公式の教科書『統計検定1級対応 統計学』まで読んでおかないと完答ができないので注意です。しかし前著だけでも十分な点数は取れます。
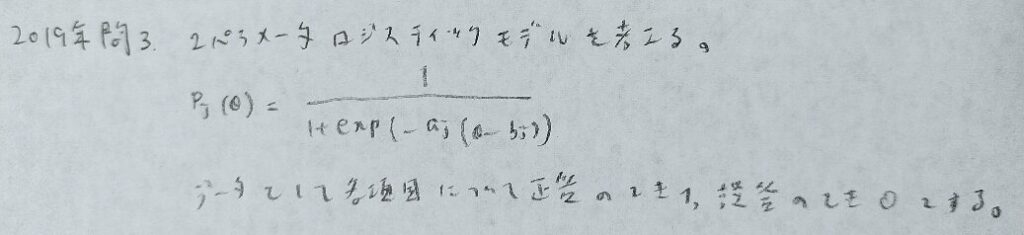

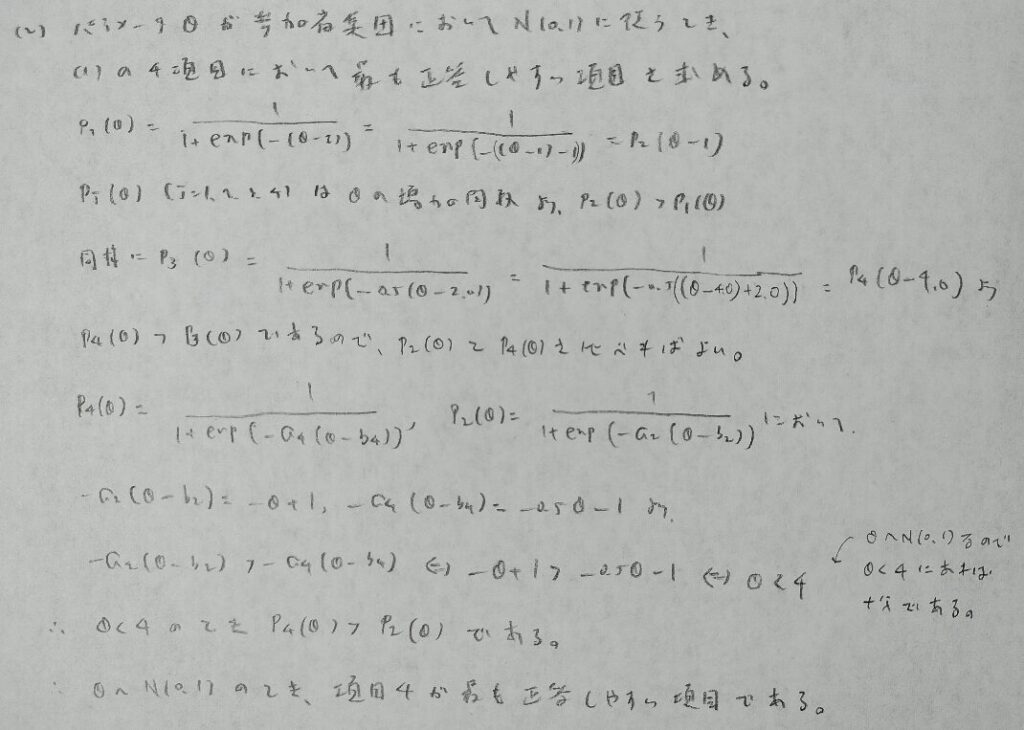
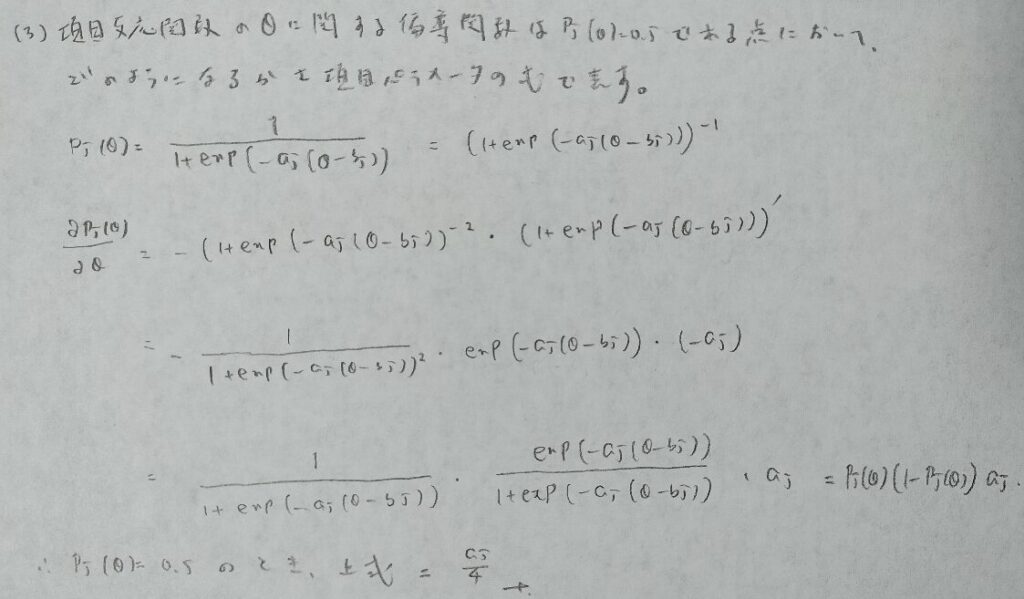

項目情報関数は『統計検定1級対応 統計学』に詳しく載っています。

2019年問4:共分散構造分析
年度が最近になるにつれパス解析系の内容の難易度も上がってきています。『Rによる多変量解析入門 データ分析の実践と理論』などで全体の概要をおさえておく必要性を感じます。
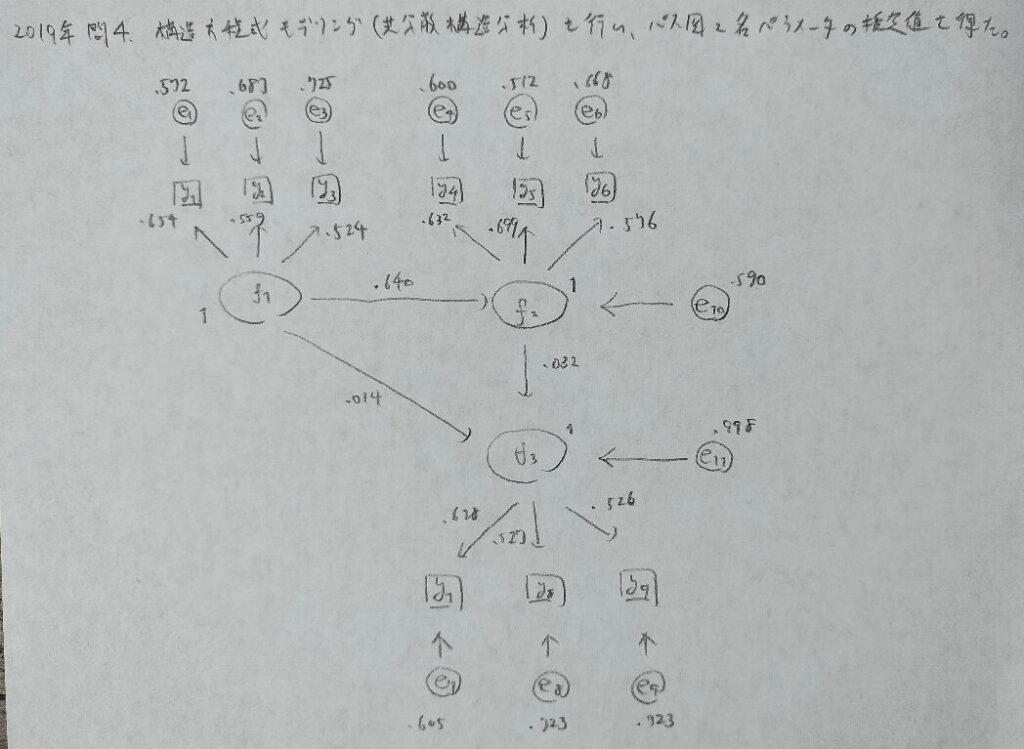
eの部分の数字が分散を表し、それ以外の数字は標準偏差を意味します。

(1)は公式の教科書『統計検定1級対応 統計学』には非掲載なので、『Rによる多変量解析入門 データ分析の実践と理論』で背景知識を入れておく必要があります。



構造方程式をピックアップして書かせる問題は今後頻出になっていくと考えます。

統計検定1級の統計応用人文科学は多変量解析の内容が主軸であると確信しました。一冊の本だけではなく複数の本からさまざまなパターンを頭に入れておくことが大事だと考えています。
統計検定1級「統計応用」人文科学の過去問:2021年

統計検定1級の統計応用の人文科学は2021年が最難関です。統計検定2級や統計検定準1級や統計検定1級の理工学でも2021年が最難関なので全体的に意識の変化があったのかと思われます。
2021年問1:アンケート調査
アンケート調査は新傾向の問題です。今後の出題も予想されます。







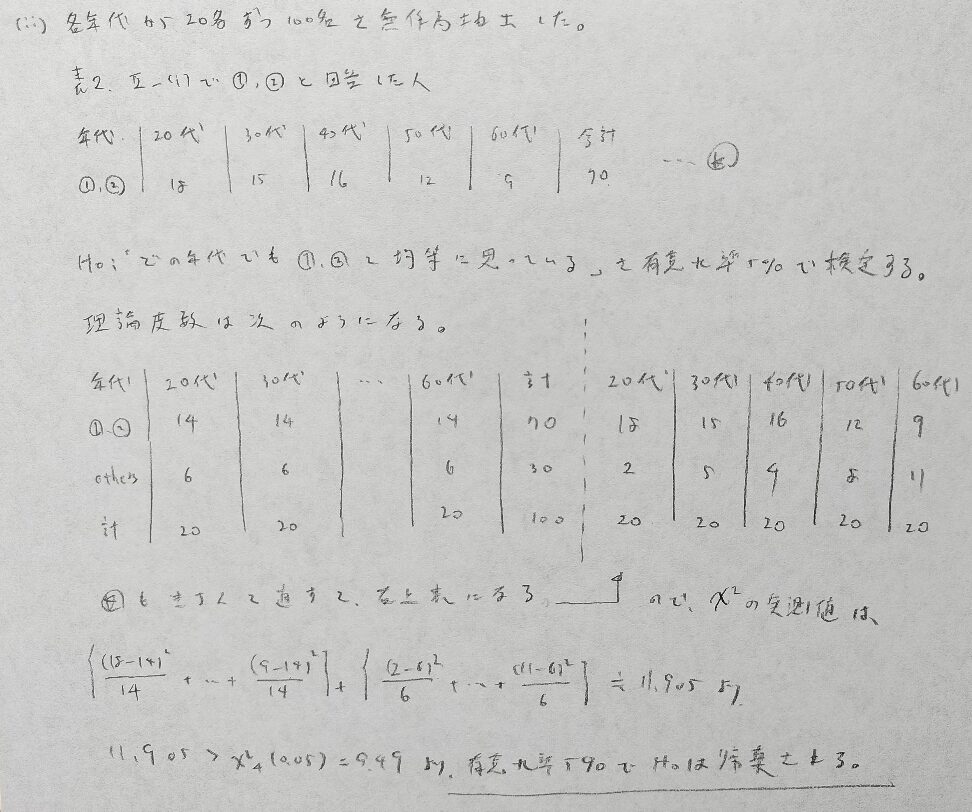
本問の立式がひっかけなので難しいと感じました。
2021年問2:分割表
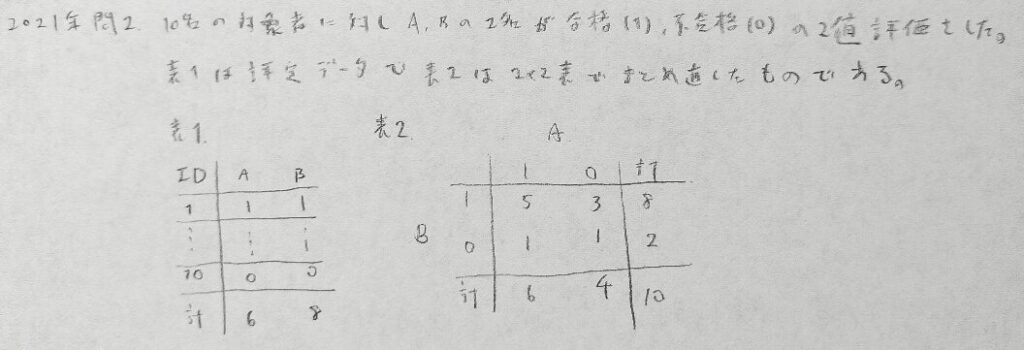

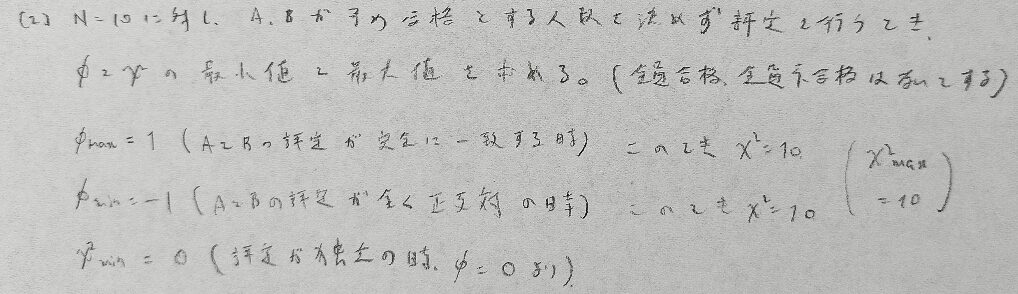
こういった最大最小の意味づけを与える問題は近年のトレンドかと思われます。
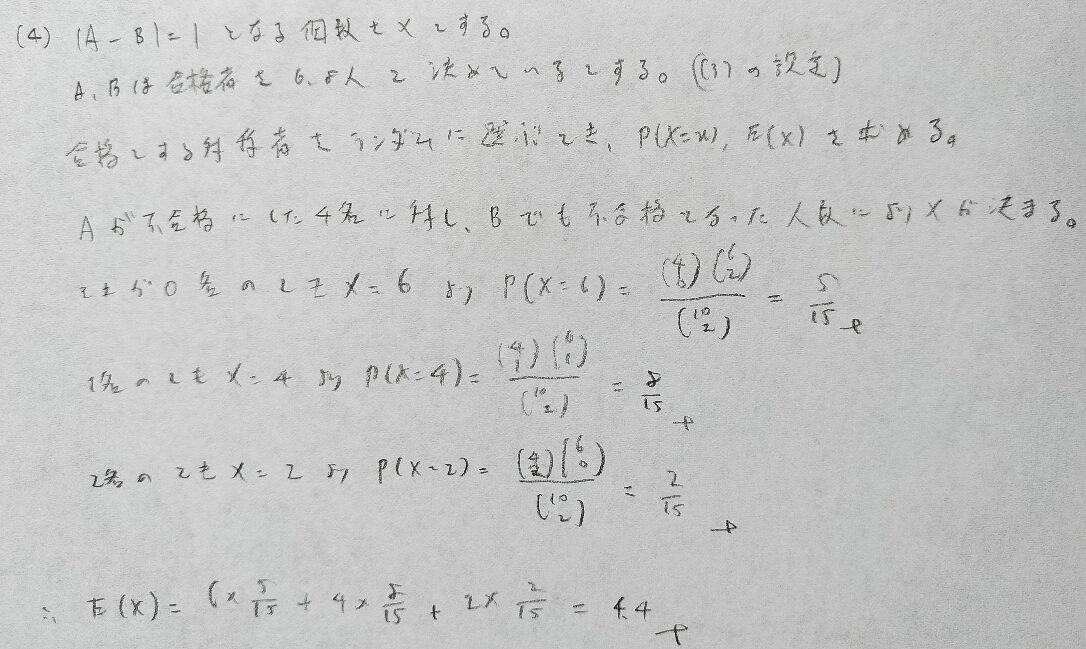
2021年問3:因子分析と主成分分析

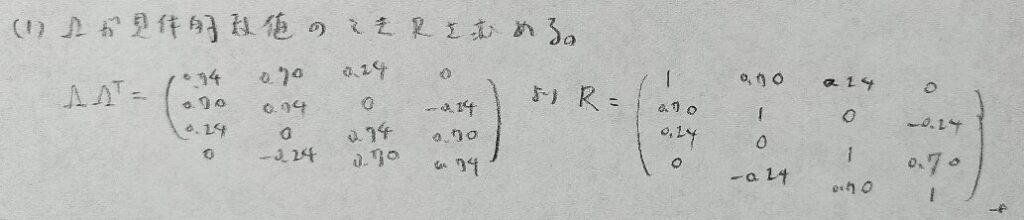

難問です。本問を解ききれればかなりのアドバンテージになります。


2021年問4:2要因混合計画
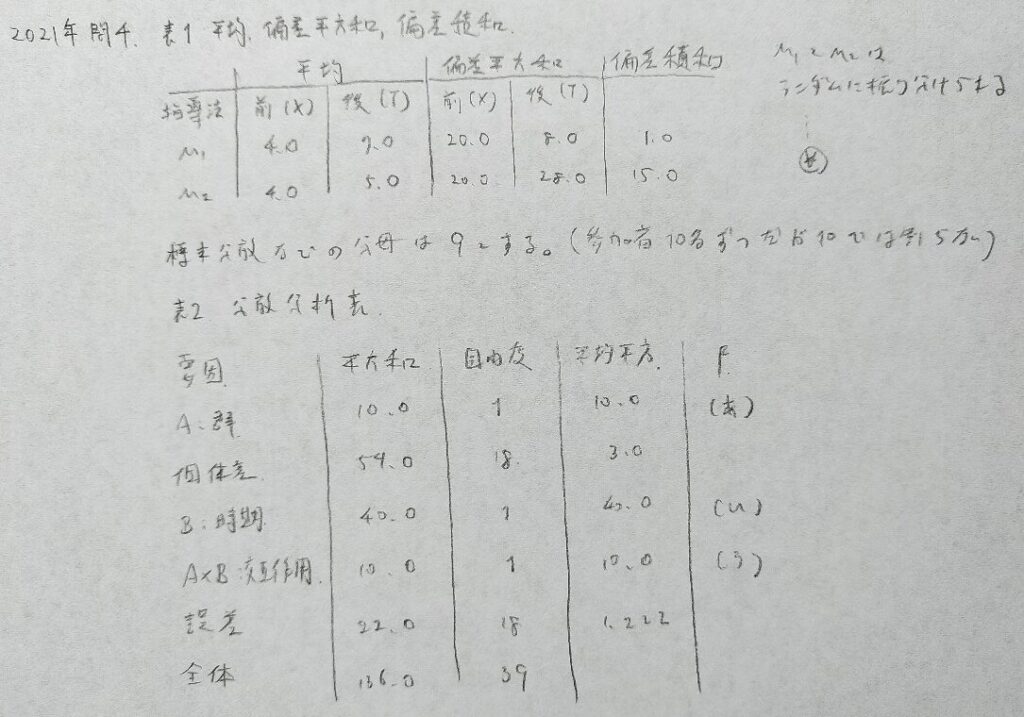


(使用状況は限られますが)分からなかったらt表から求めるのも手です。


平方和で???となったら実際に書き出してみると分かることが多いです。
2021年以後の問題でこうした傾向が見られます。

最後の設問が難問です。試験中に気づくのはかなり厳しいでしょう。
統計検定1級「統計応用」人文科学の過去問:2022年

2022年問1:正規分布

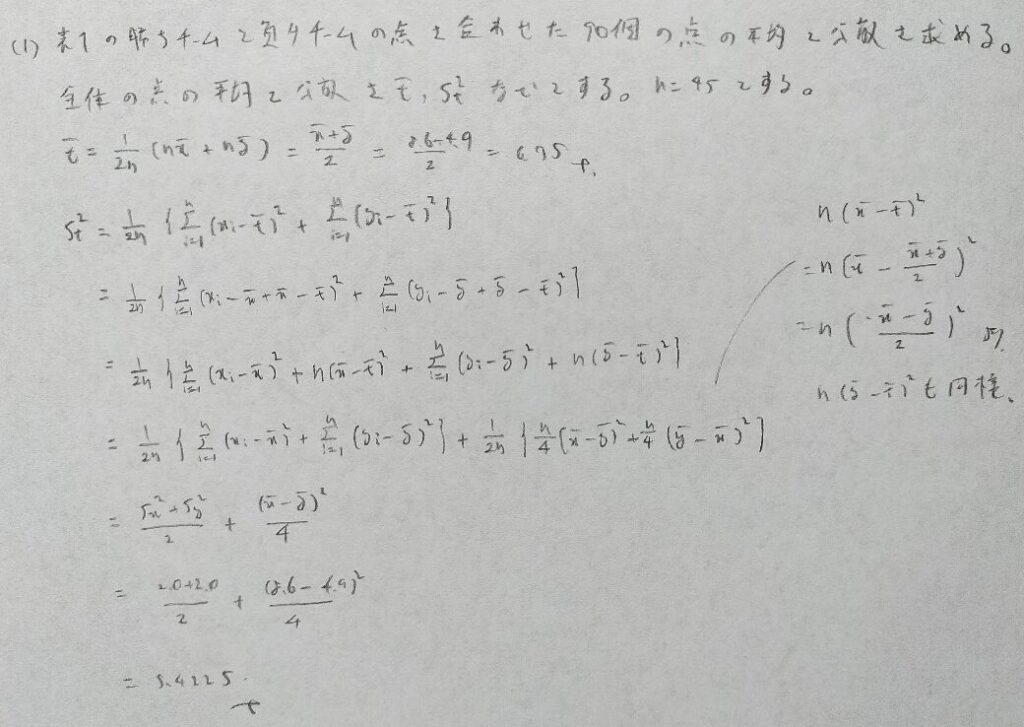
本問は長文問題ですが長文を読まなくても答えることが可能です。

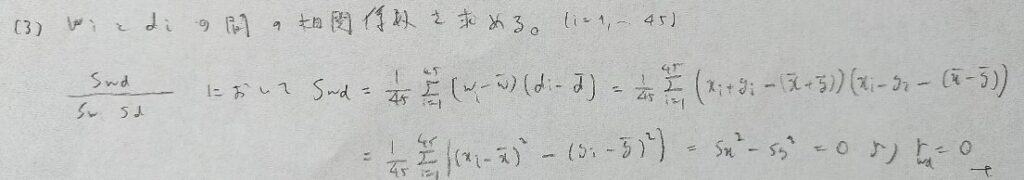
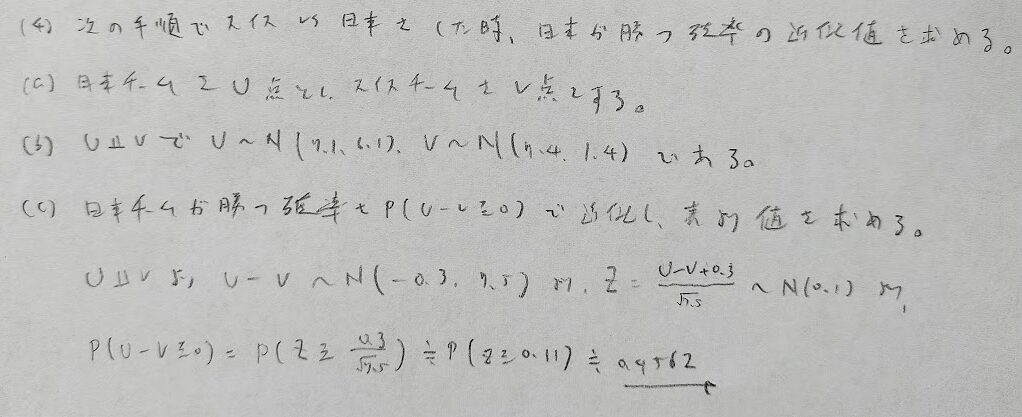
2022年問2:判別分析
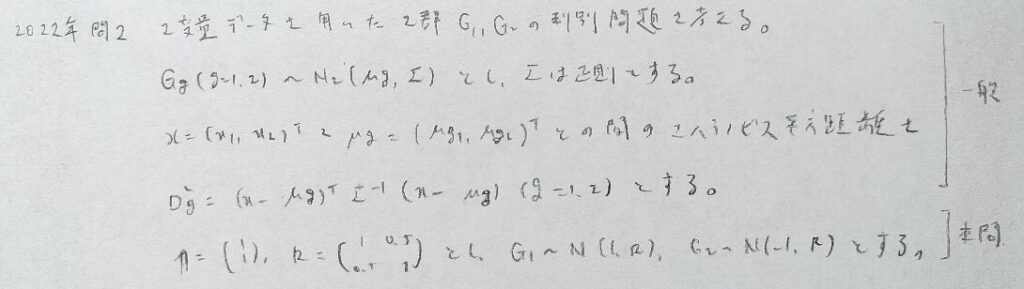

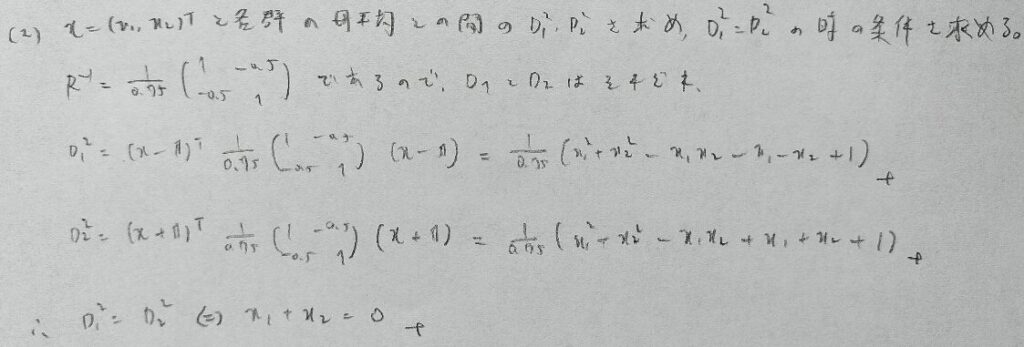
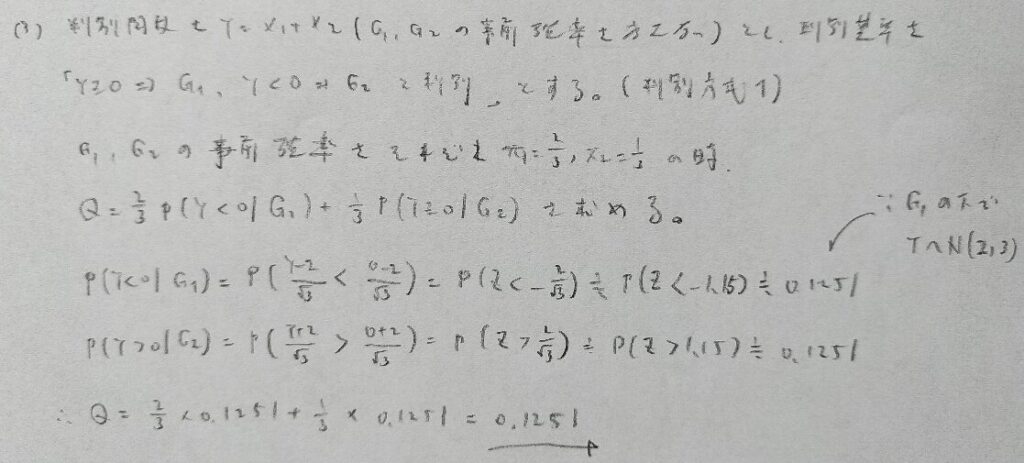
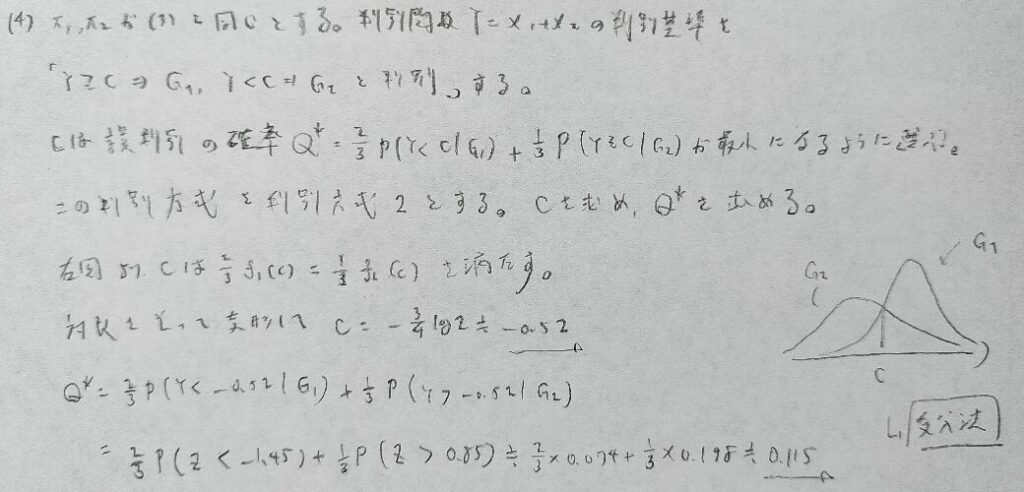
大掛かりな計算をせずに図の状況から最小性を考えるテクニック(変分法)を使えるようにしておきましょう。
2022年問3:クラスター分析

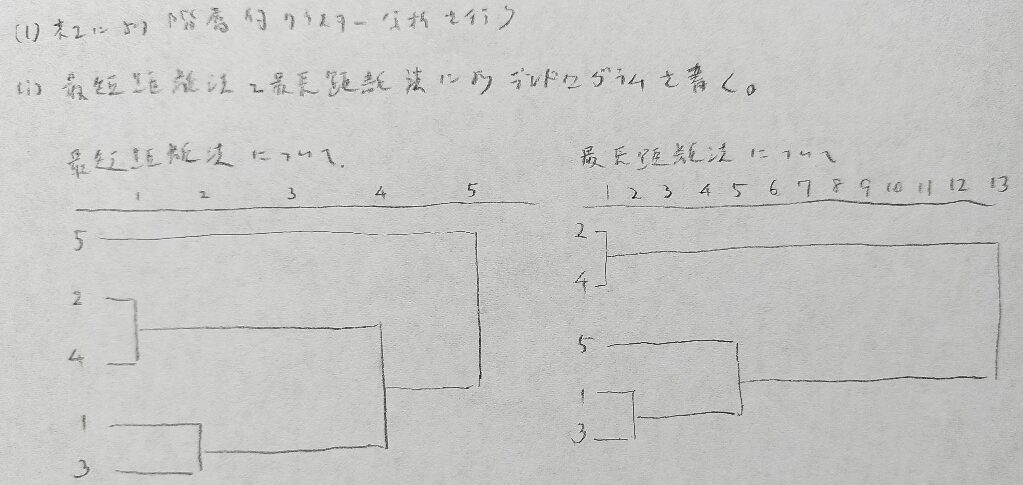
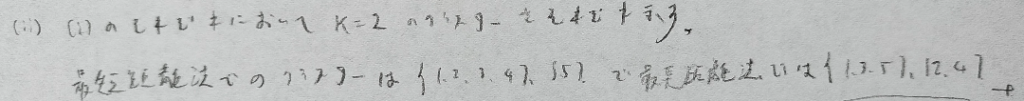
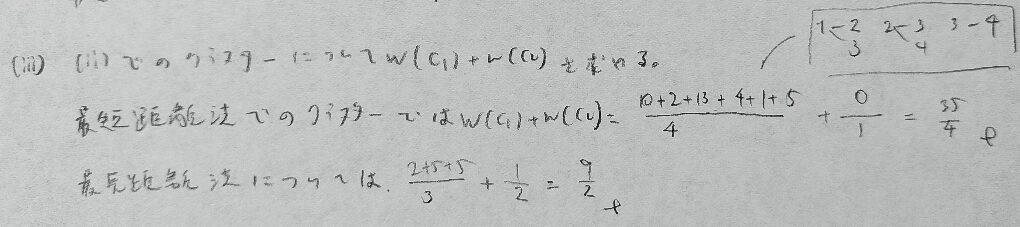
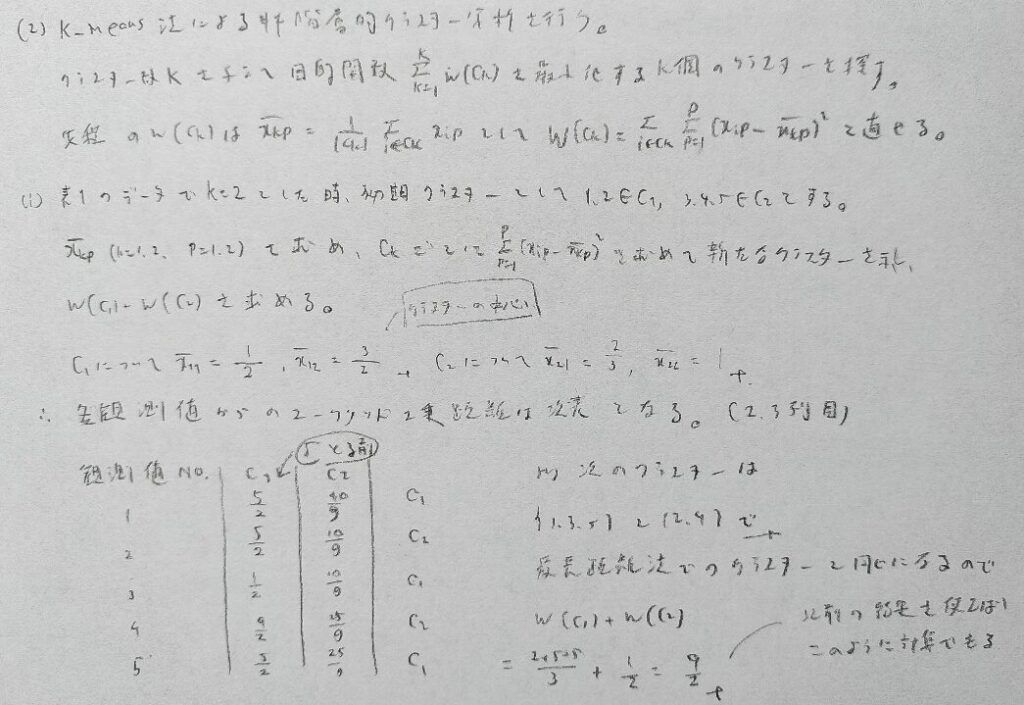

2022年問4:テストの信頼性
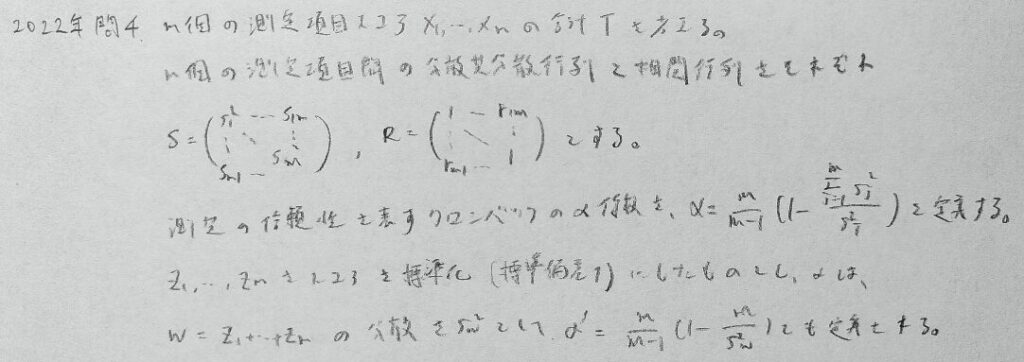

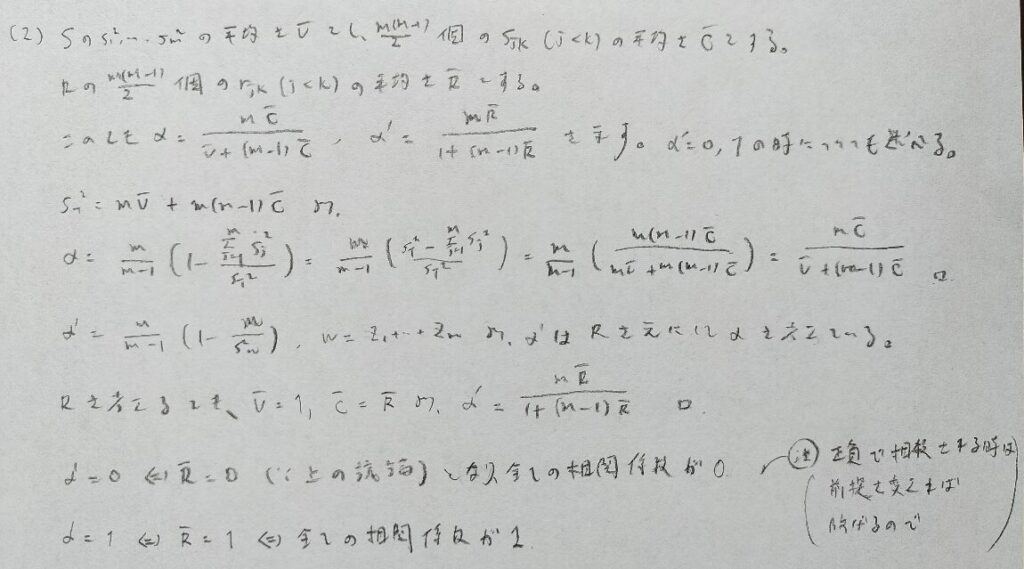

クロンバックのαの2通りの値が一致するためには各分散の値が等しいことが条件です。
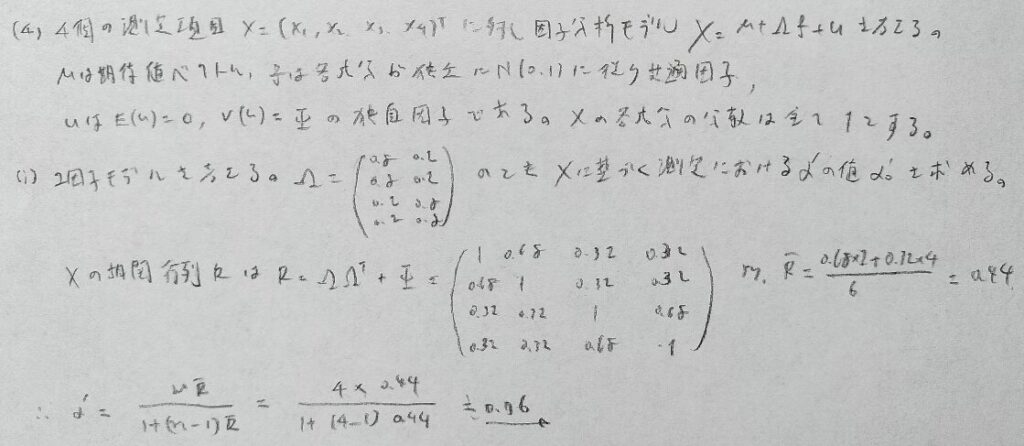
因子分析と融合されて驚きますがRを求めることが最優先です。Rは過去問でも頻出ですので過去問学習が大切なことがわかります。
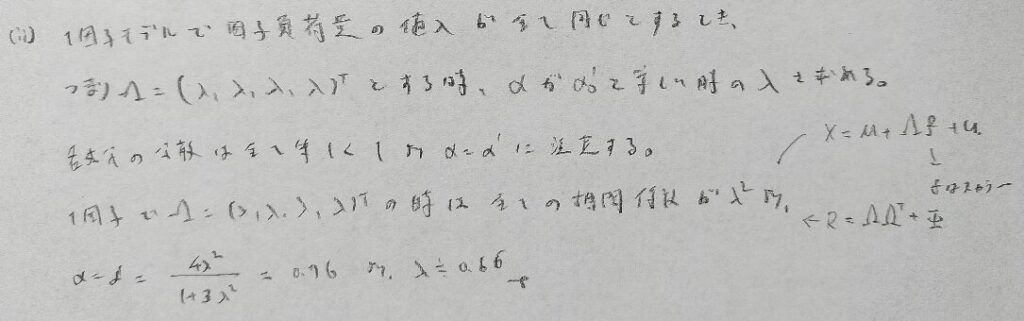
統計検定1級「統計応用」人文科学の過去問:2023年
2023年問1:混合分布

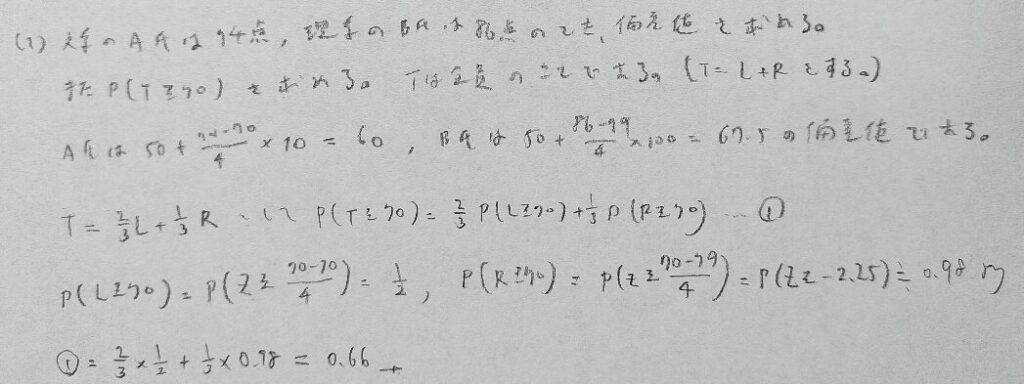
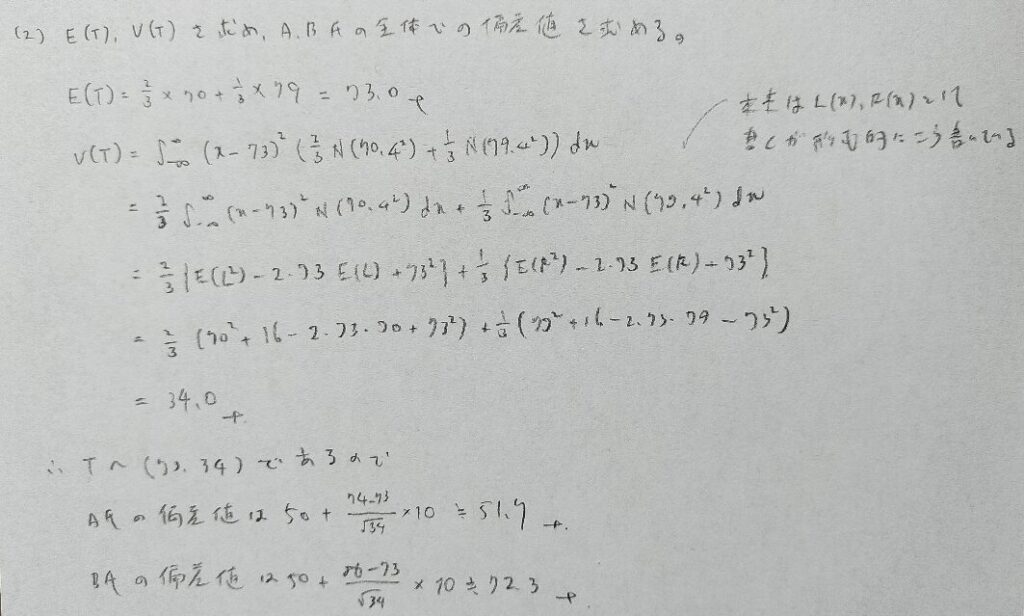
分散を出すところで差がつきます。統計検定1級の統計応用の理工学の2018年の問5に類題が出題されています。
統計検定1級の統計応用の人文科学は2021年が最も難しく、2022年からは以前と似たような傾向に戻っていると考えられます。

期待値の位置
分散による幅に注意
混合比による頂点の高さに注意しましょう
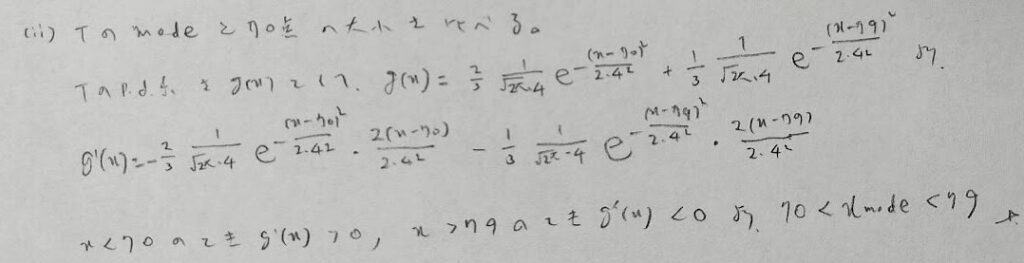
2023年問2:相関係数
最後の問題だけ未解決です。それ以外はとても簡単です。
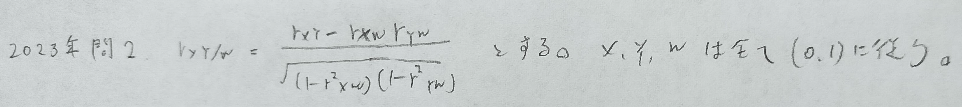
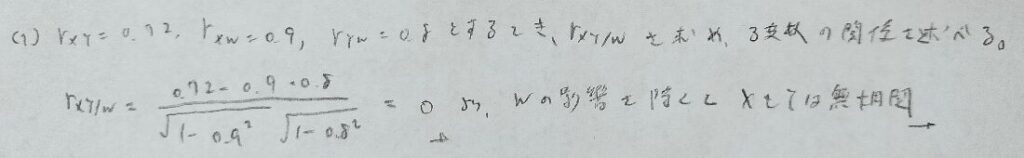
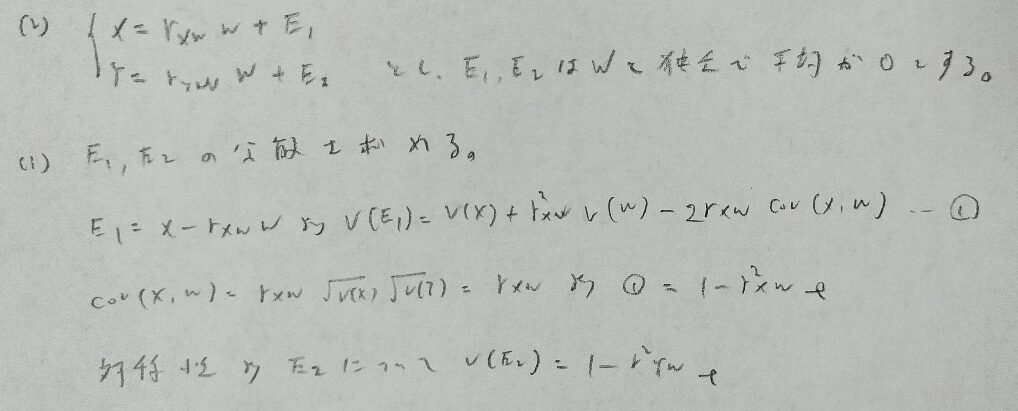
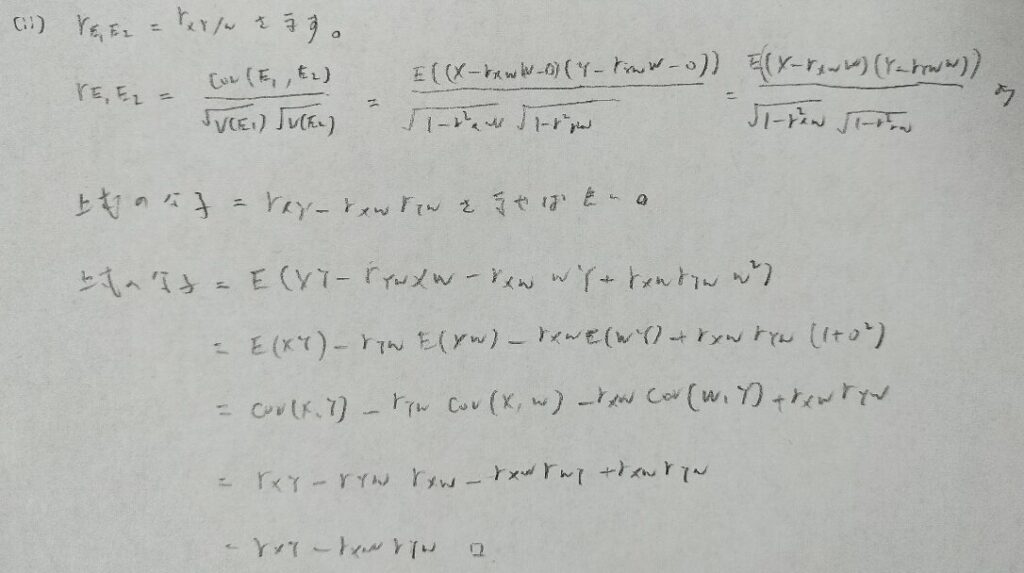

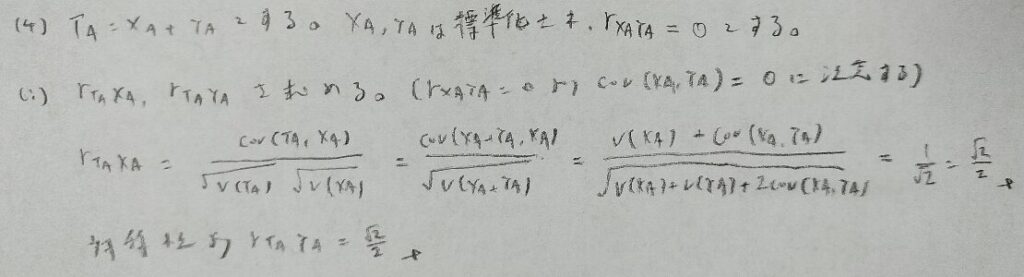
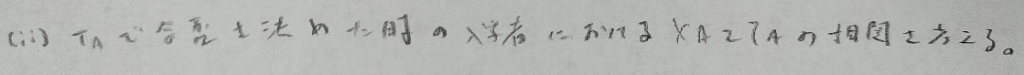
最後の問題が解けません。
2023年問3:判別分析
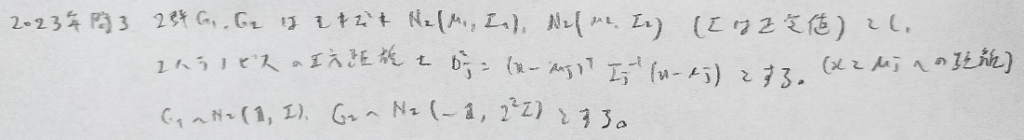
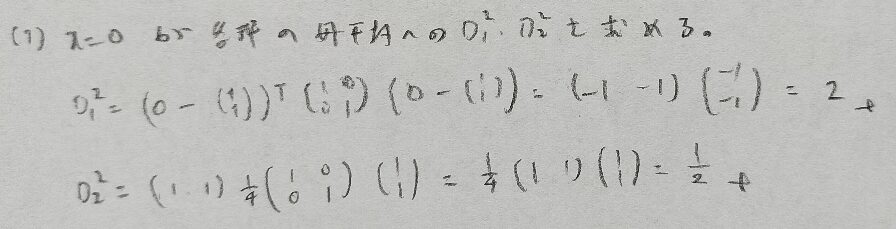
マハラノビスの平方距離などでは分からなくなったら成分計算に持ち込めばOKです!
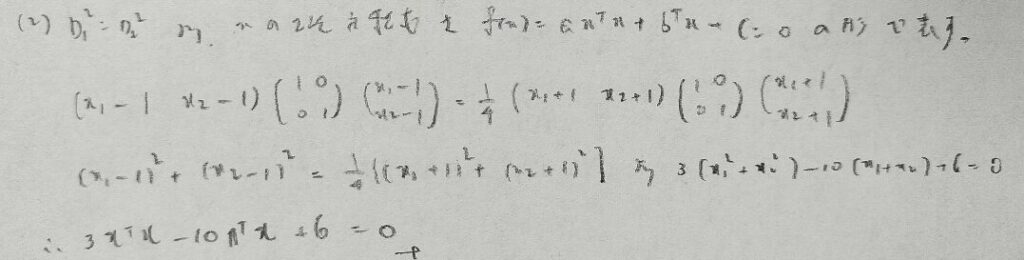
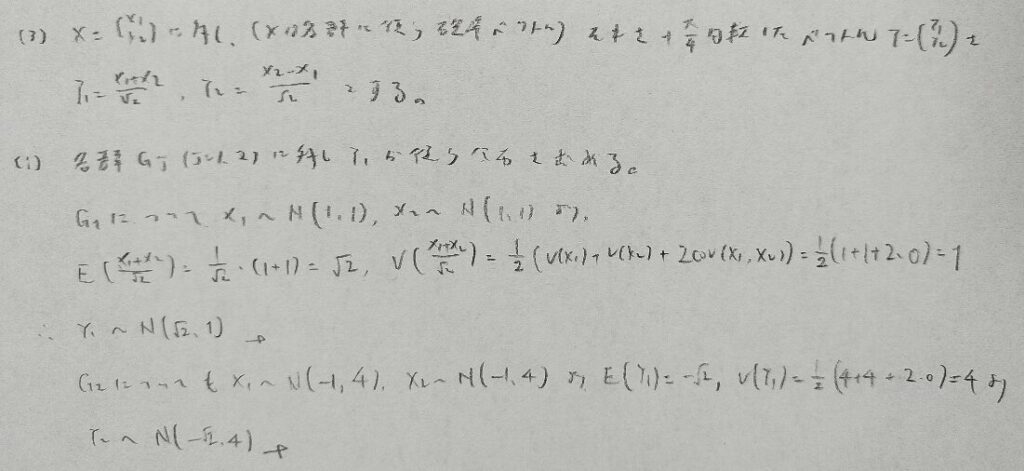
混合分布のときとは異なるので注意です。

やはり統計検定1級の人文科学の問題の難易度はここ数年で下がってきていると実感します。
2021年が難しいだけだったのかも知れませんね。

過去問で何度も誤判別率に関する問題が出ています。今後も出題が予想されますので要注意です。
2023年問4:単回帰分析

残差分散が与えられていますが解答では使いませんでした。

これは良い問題ですね。明らかに差があるとわかります。

この方法を自力で考えるのは難しいですが、問題文で誘導があるので、それに従って計算するだけです。
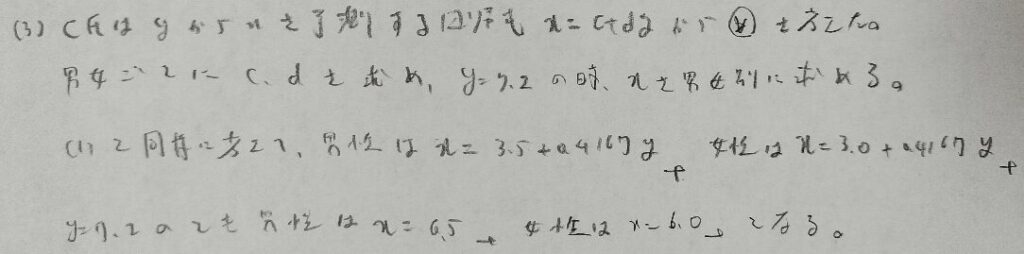

統計検定1級「統計応用」人文科学の過去問:2024年
2024年問1:主成分分析
本問の出来が合否を分けたと思います。解き直したら、本番でケアレスミスを連発していたようです。しかしとても良い問題で、さすが統計検定1級だと感心しました。

2024年問2:正規分布
最後の設問のみ、本番で解けませんでした。新出問題です。
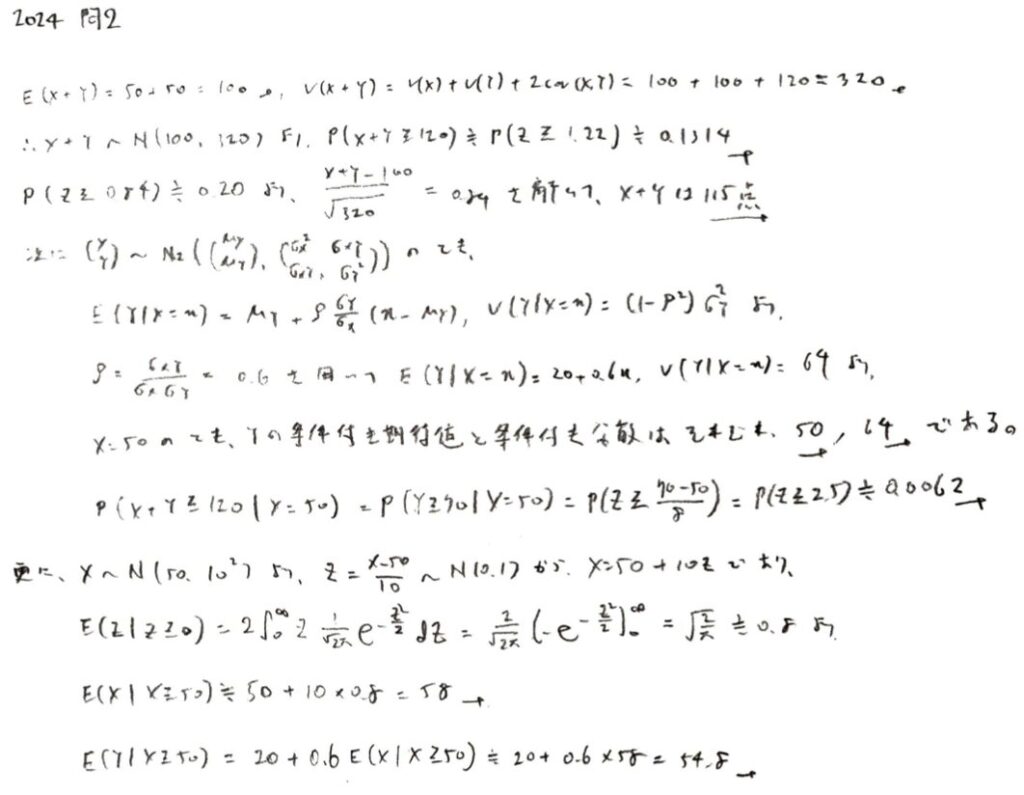
2024年問3:ベルヌーイ分布
本番では選択しなかったことが不合格の原因の1つだと思います。本問は確率変数が独立ではないので期待値などを求める際は同時分布で考えます。盲点を突いてきています。
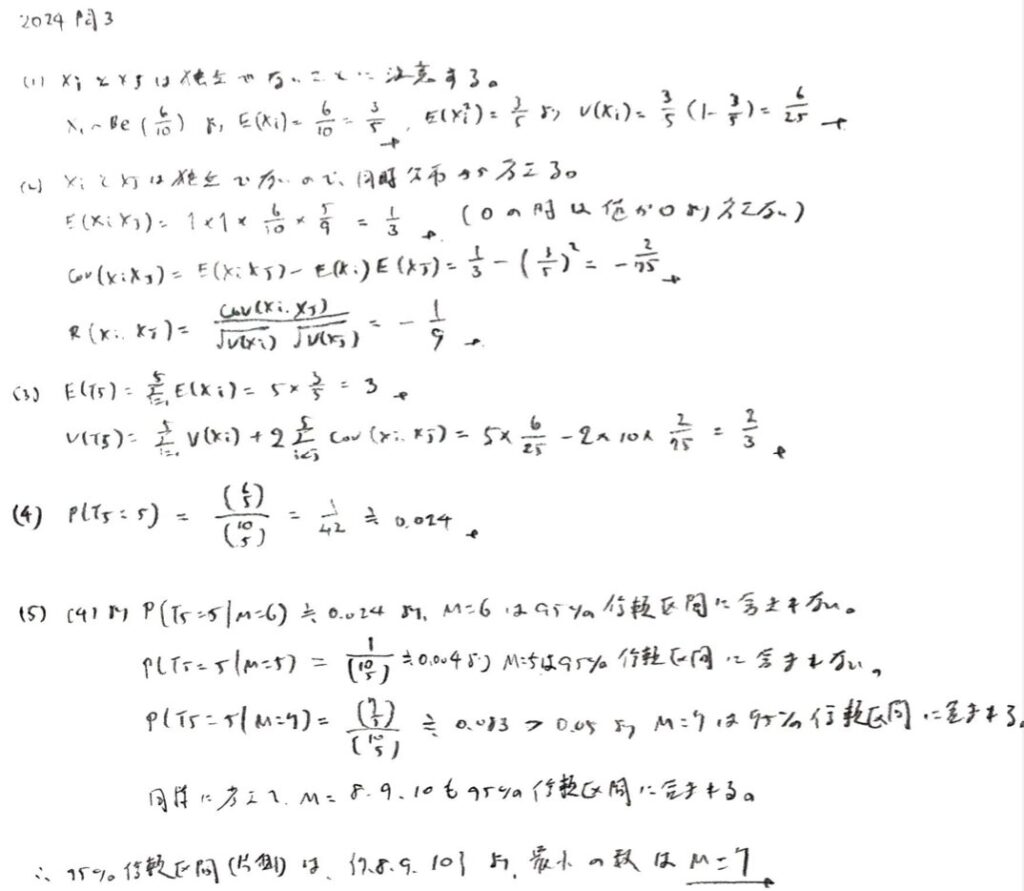
統計検定1級の統計応用(人文科学)の過去問の解説は以上になります。
単に回を増すごとに難易度が上がっているとは言えない試験ですね。
理工学の場合はここ最近難しいのですが、人文科学はまだまだ過去問が通用する難易度だと思います!
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定1級 公式問題集[2016〜2018年]
日本統計学会公式認定 統計検定1級 公式問題集[2019~2022年]
日本統計学会公式認定 統計検定1級 公式問題集[2022~2024年]
統計検定1級を目指す方々、ともに合格を目指して頑張りましょう!共通問題の全過去問の解説記事はこちらです。また、統計数理の過去問解説記事はこちらです。


-scaled.jpg)













