統計検定１級の統計応用の人文科学の過去問解説についてはこちらの記事をご覧ください。また統計数理の過去問解説の記事はこちらです。
本記事では問題の著作権の問題を考慮し、そのままの表現などを避けております。詳しい問題内容や模範解答を知りたい方は下記リンクから詳しい内容をご確認ください。確認しやすいように年度順にまとめております。最新年度の2023年は統計検定の公式HPからダウンロードできます。
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定１級 公式問題集［2016〜2018年］
日本統計学会公式認定 統計検定１級 公式問題集［2019～2022年］
統計検定１級「統計応用」共通分野の過去問：2012年
ポチップ
2012年問１：重回帰分析
最後の2題は以後出題されておりませんし、統計検定１級の教科書『統計学』にも記載されておりません。しかし統計学は統計応用の学習にとても素晴らしい本のため過去記事（内容はこちら）に学習しやすいように内容順を再編集したものを解説しています。
ポチップ
本問題の模範解答が公式の過去問集で誤植があったと思われるので、上の解答では訂正をいれています。
2012年問２：適合度の検定
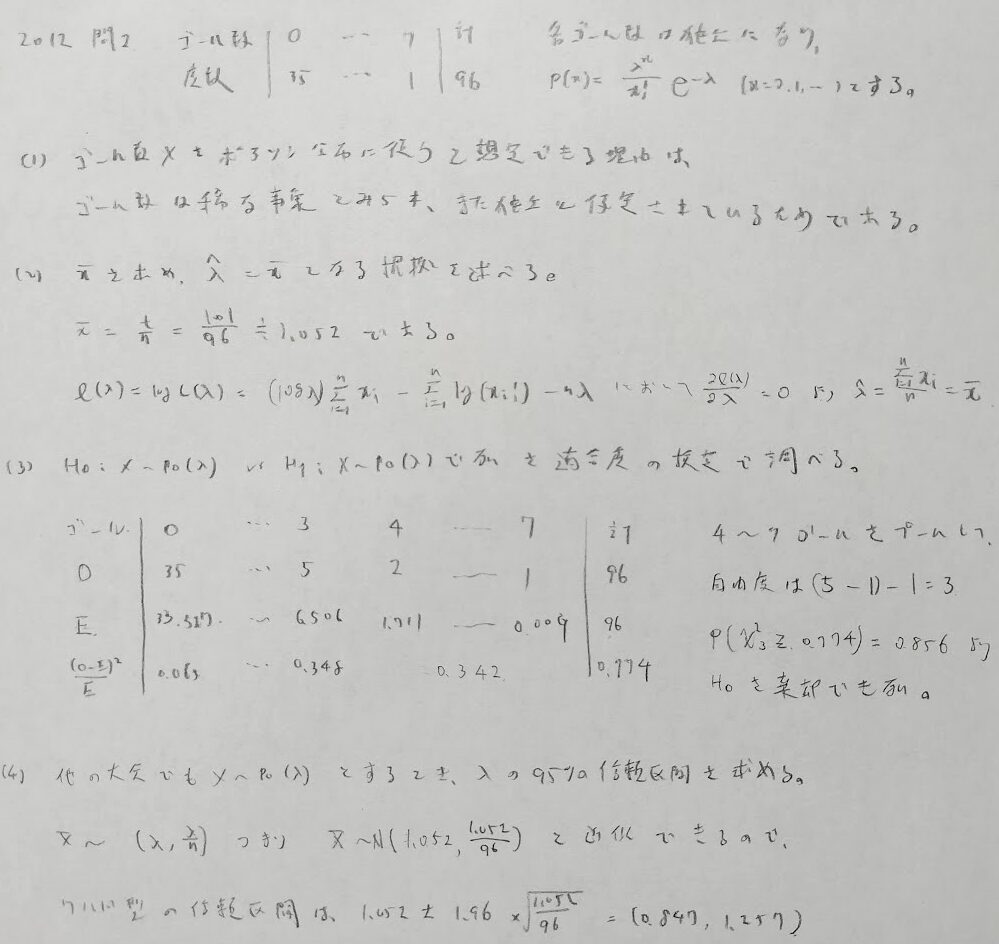
2012年問３：ウィルコクソンの順位和検定
本問については統計検定準１級の教科書『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』がとても参考になります。ノンパラメトリック検定を総浚いしておきたいですね。
ワークブックの内容はこちらにて詳しく解説していますのでご覧ください！
ポチップ
統計検定１級「統計応用」共通問題の過去問：2013年
ポチップ
次の問題では重回帰分析から得られた分散分析表から単回帰分析の残差平方和を求める際に注意をしましょう。
2013年問５：重回帰分析
重回帰分析における偏回帰係数は、その変数以外の変数によってyを予測した残りの部分（残差）に対するその変数の寄与分を表しています。
また（記述をしなければ減点にはならないと思いますが）（２）での平常点における係数のp値が0.003と低い（係数の値が大きく外れることは極めて少ない）ことからも、この変動がyの変動の説明に有用であるとの根拠の見方も大切ですね。
これらのポイントはかなりの盲点で、統計検定１級として流石の良問だと思いました。以後未出のですね！
統計検定１級「統計応用」共通問題の過去問：2014年
ポチップ
2014年問５：適合度検定
（２）がかなりの洞察力が必要な問題です。要するに前提の主語がどちらか？によって意味・無意味が変わってきます。
正規化定数をどこまで用いるのかをしっかり吟味したい問題です。
本問と似たテイストの問題が指数分布族の問題として統計検定１級2023年の理工学で出題されています。
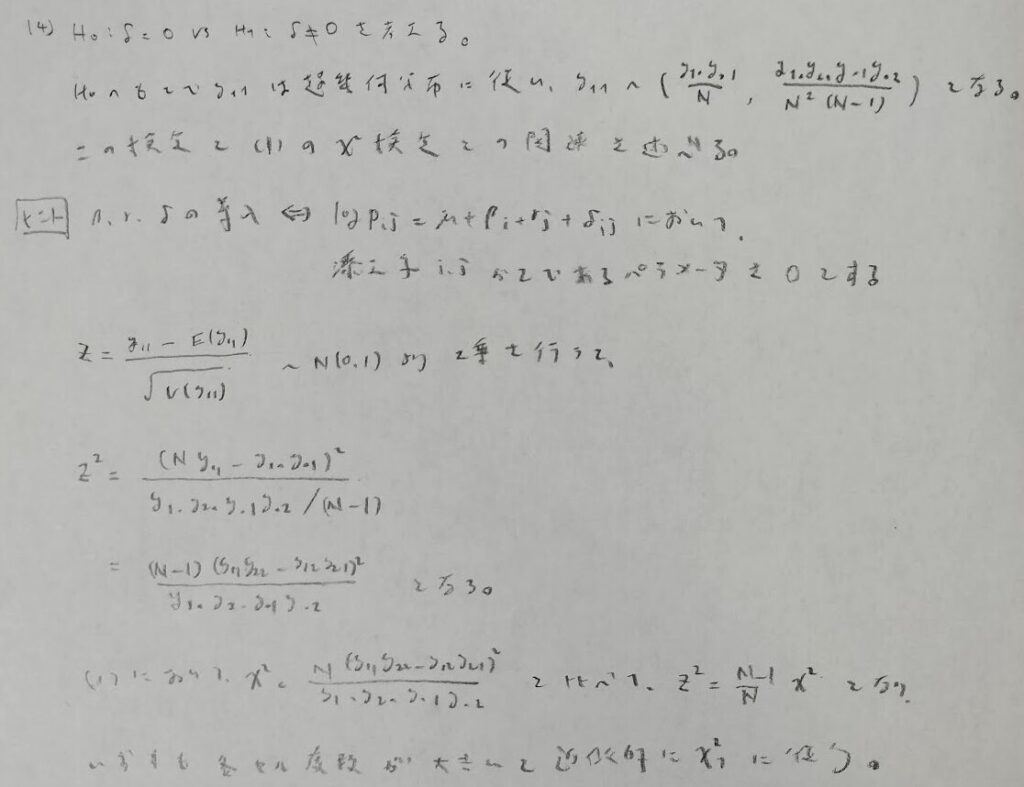
2013年度と比べて明らかな難化が起きています。計算量の増加が顕著です。
統計検定１級「統計応用」共通問題の過去問：2015年
ポチップ
2015年問５：実験計画法
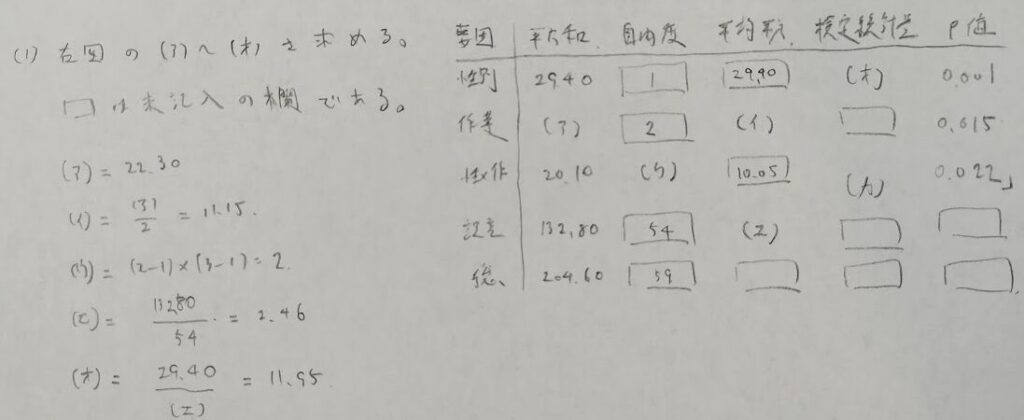
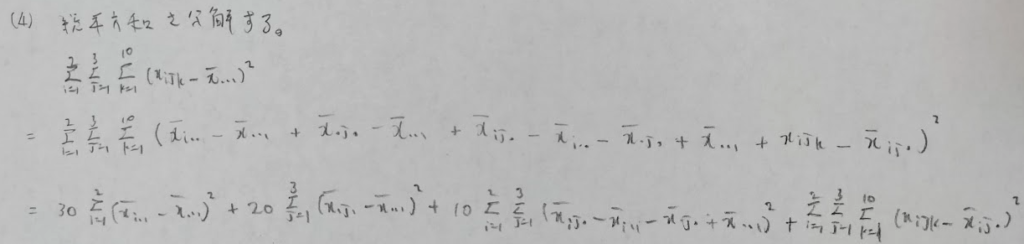
誤差分散の最尤推定量と不偏推定量は、誤差平方和を何で割っているか？による違いのみです。不偏推定量の方は誤差の自由度で割っています。対して最尤推定量の方は各水準数の積になります。
統計検定１級「統計応用」共通問題の過去問：2016年
ポチップ
2016年問５：２標本t検定
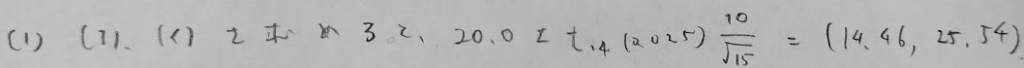
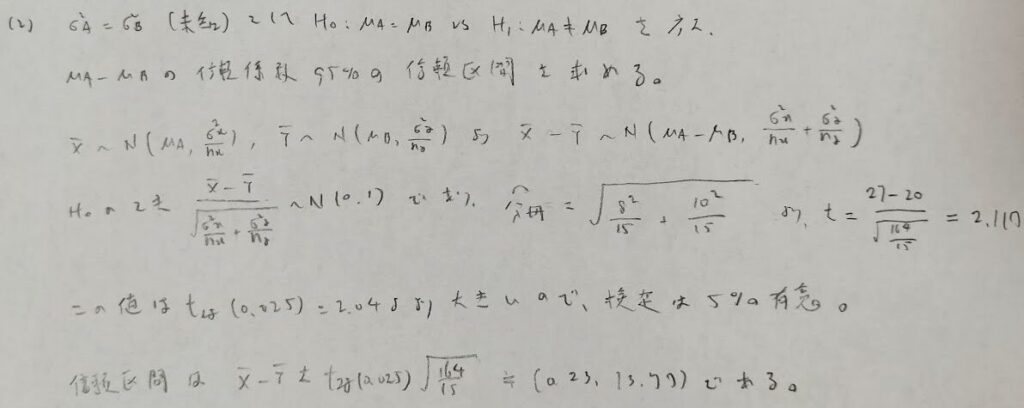
（３）はかなりユニークな出題でしたね！2024年の統計検定１級受験前ですが、類題は出題されていません。
標本標準偏差の定義を、通常とは異なる式（通常の意味での不偏分散の平方根）で用いていますので、しっかりと問題文を読みましょう！
最後の30%の箇所は記述が不明だったので『日本統計学会公式認定 統計検定１級 公式問題集［2016〜2018年］』を参照しました。解答の２行上まででも減点はないと思われます。
統計検定１級「統計応用」共通問題の過去問：2017年
ポチップ
2017年問５：正規分布
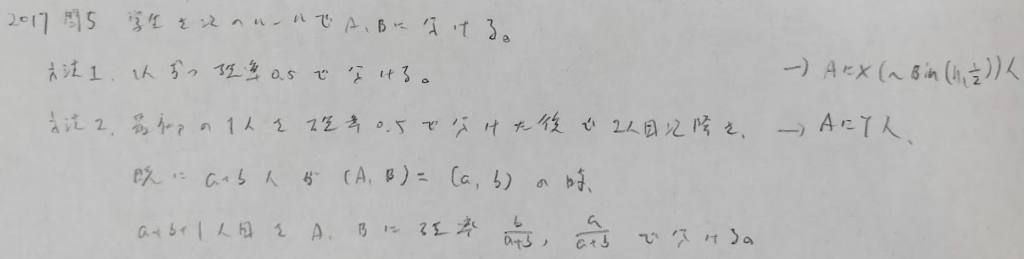
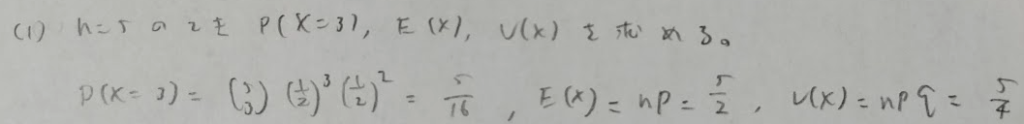
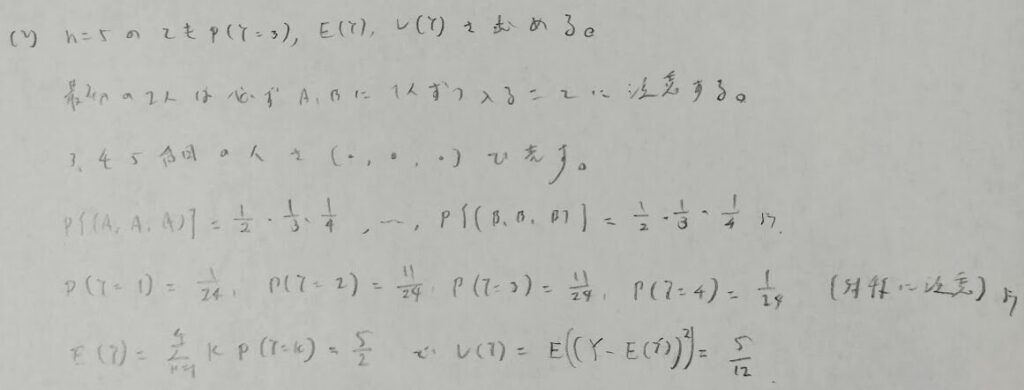
実はYの期待値は下の知識があれば一瞬で求まります。すなわち対称的な分布の期待値は中央値と一致する（最頻値も一致）という定理があります。
次の証明は数理統計の本には載っていなかったのでなんとか自力で証明をしてみたものです。
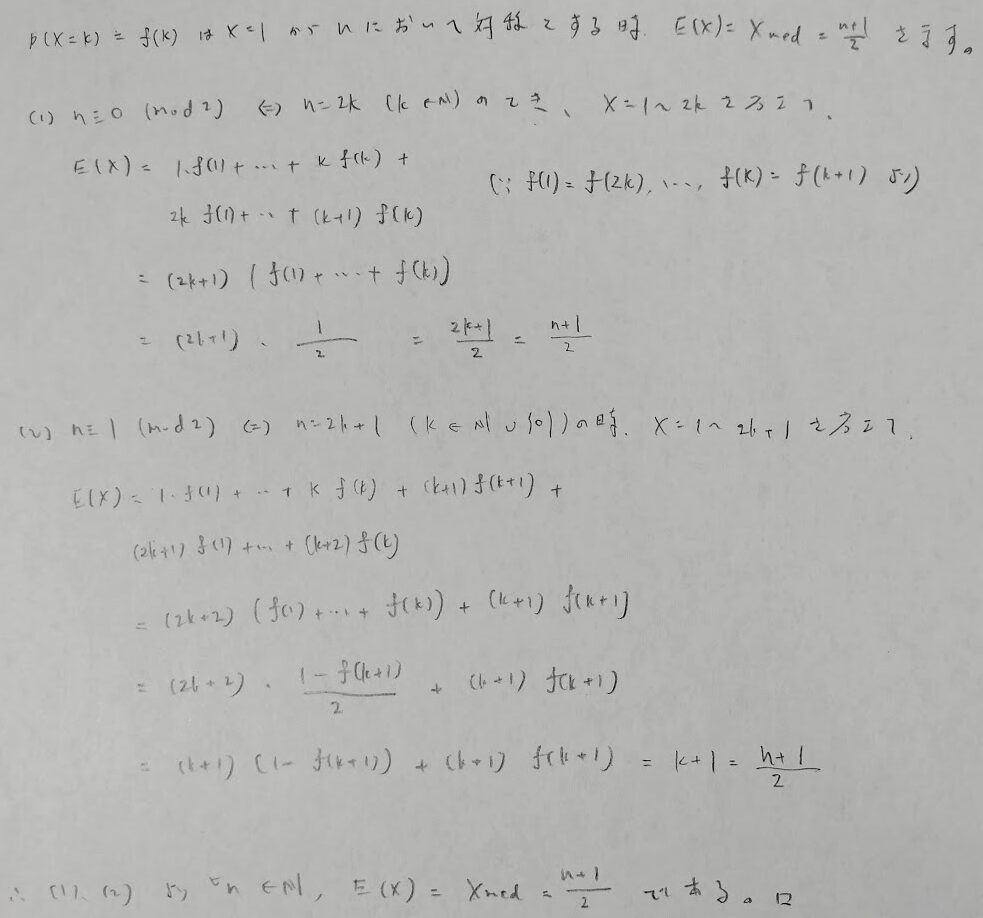
今回は離散確率変数ですが、連続型の確率変数の場合はどうやって証明するのですか？
『現代数理統計学の基礎』の第２章の問８に載っていますのでそちらを参照ください。積分を用いて示しますが、ポイントは中央値が原点にくるように分布を平行移動してから証明を開始することです。
ポチップ
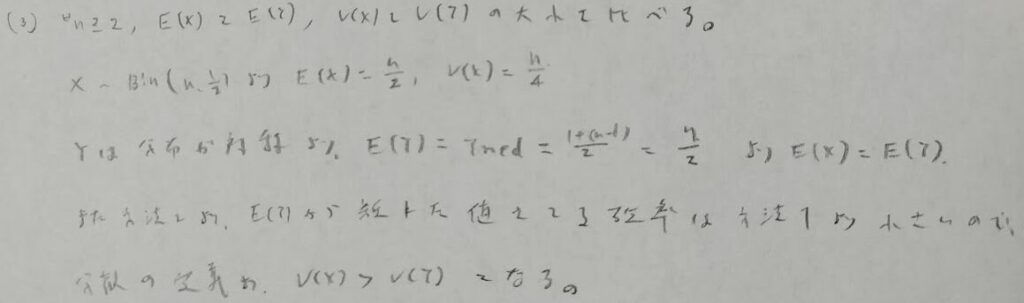
この小問が最も難易度が高いと感じます。
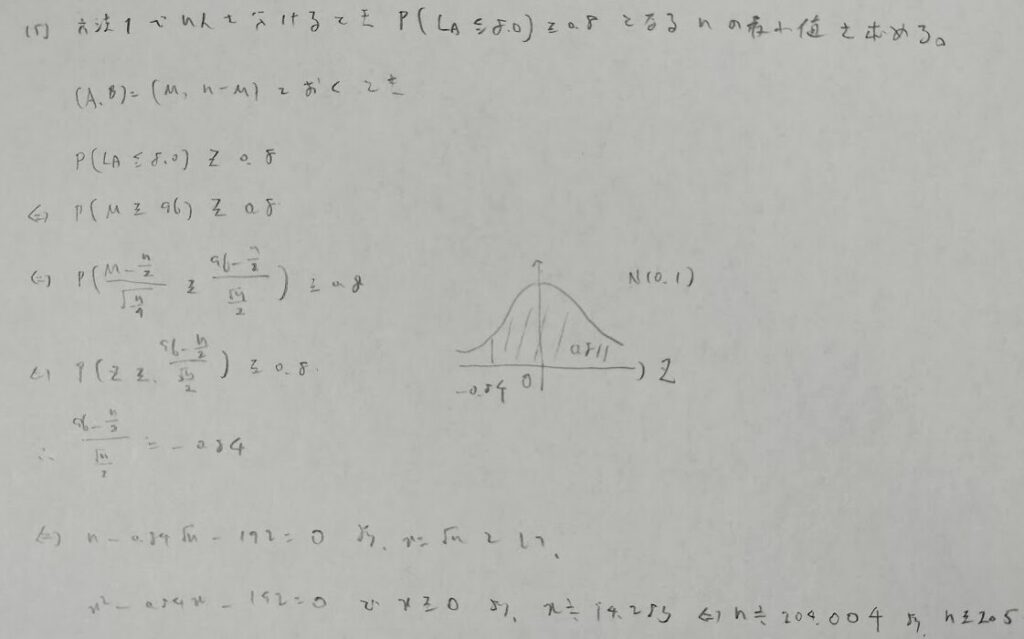
最初の立式をクリアすればなんてことはない問題ですが、最初の思いつきが難しいですね。
本問はさすが統計検定１級とうなりたくなるような、素晴らしい問題だと思います！
統計検定１級「統計応用」共通問題の過去問：2018年
ポチップ
2018年問５：正規分布
本問ではヒントが与えられていますが、今後はヒントなしでも解けるようにしておきたい問題です。（少なくとも（１）は）
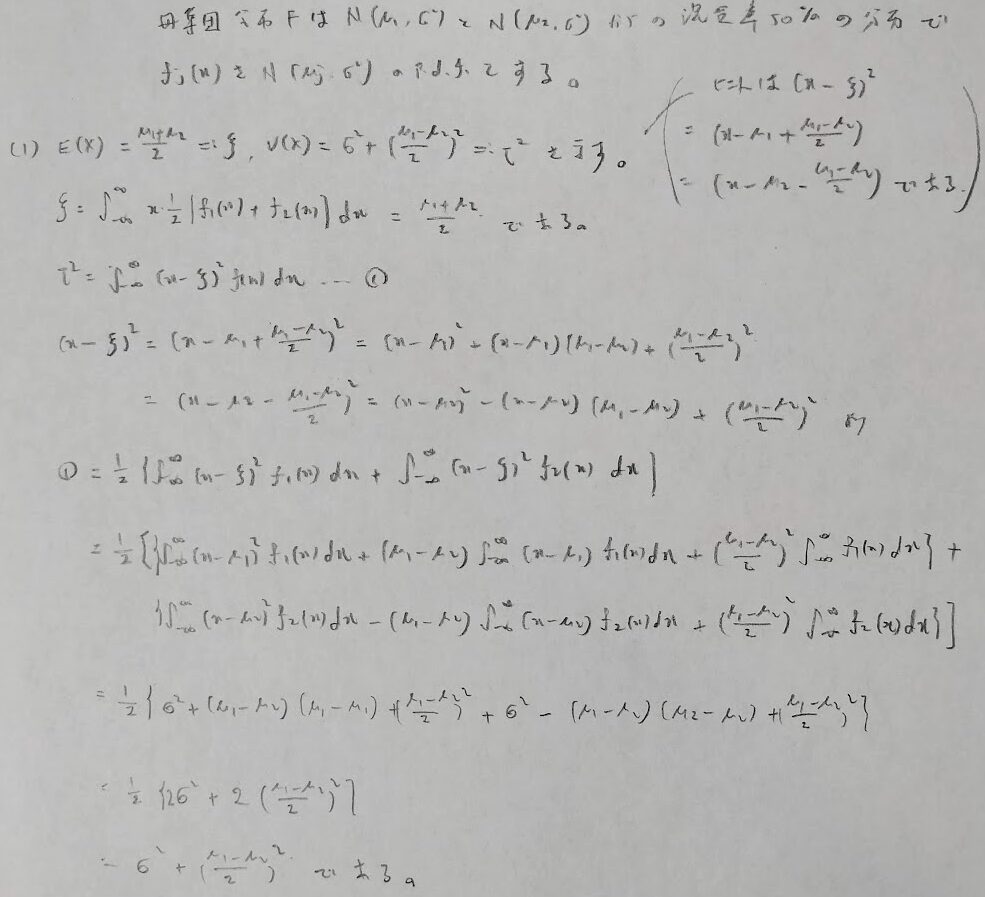
２つの期待値は異なるという条件が問題文に含まれていることにご注意ください。また（４）のヒントとなるパラメータを変えたときのFの図も書かれています。
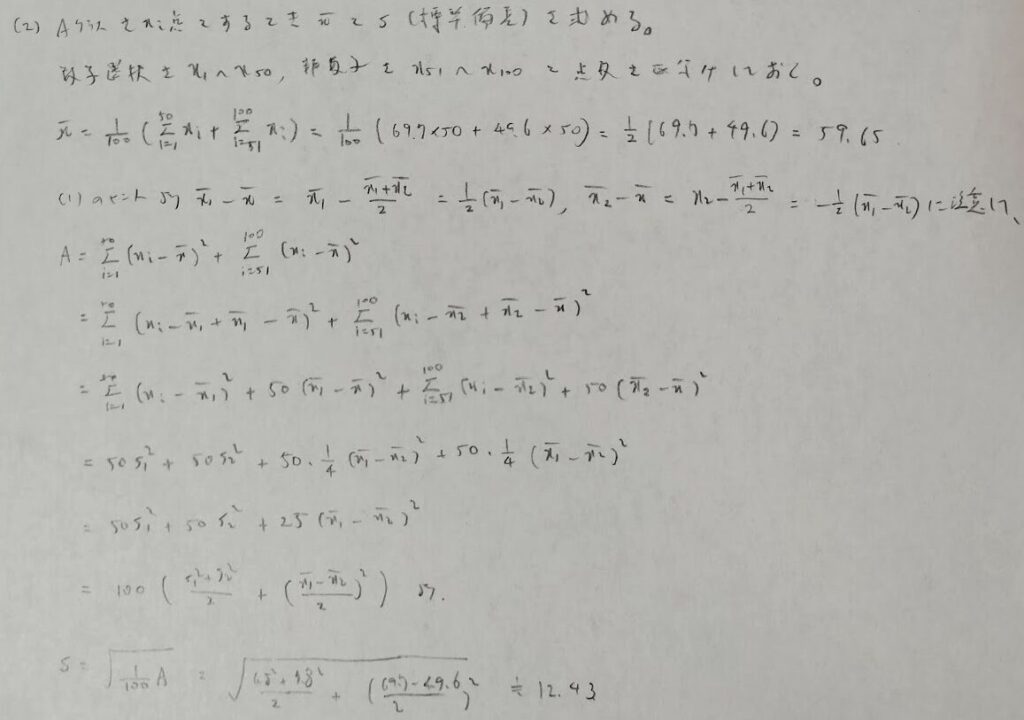
計算の工夫により処理にかかる時間が変わってきます。今回はsの計算の部分で計算の工夫をしています。
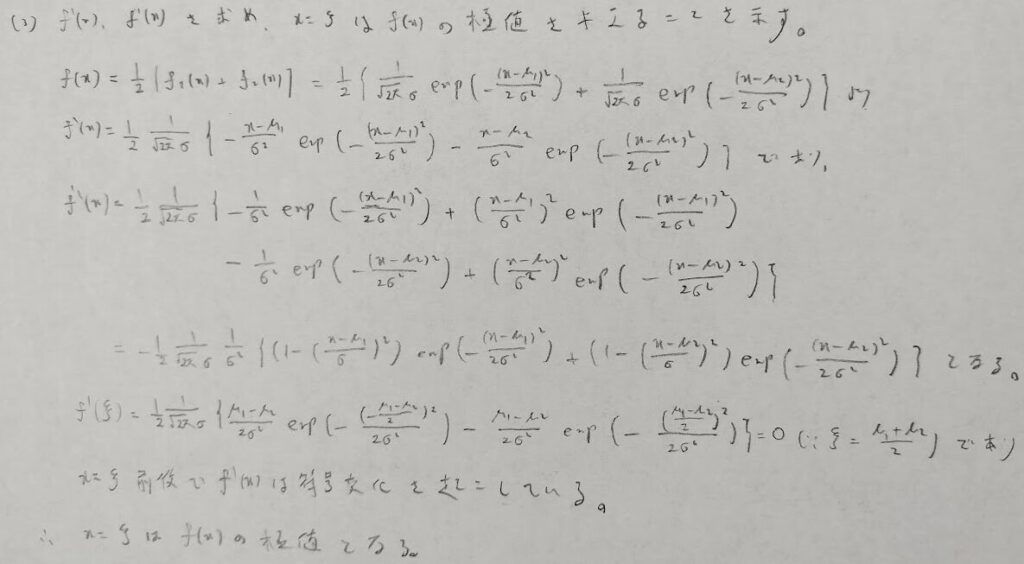
次の（４）はおそらく出題ミスだと思われます。正しくは「Fが２峰性以上を持つときの条件を求めよ」だと思われます。その理由は、原題のままだと厳密な答案を書くためにかなりの時間を消費することになり、試験としてのバランスが崩れるからです。そのため模範解答では１つの条件を調べただけで正解の判定のようです。
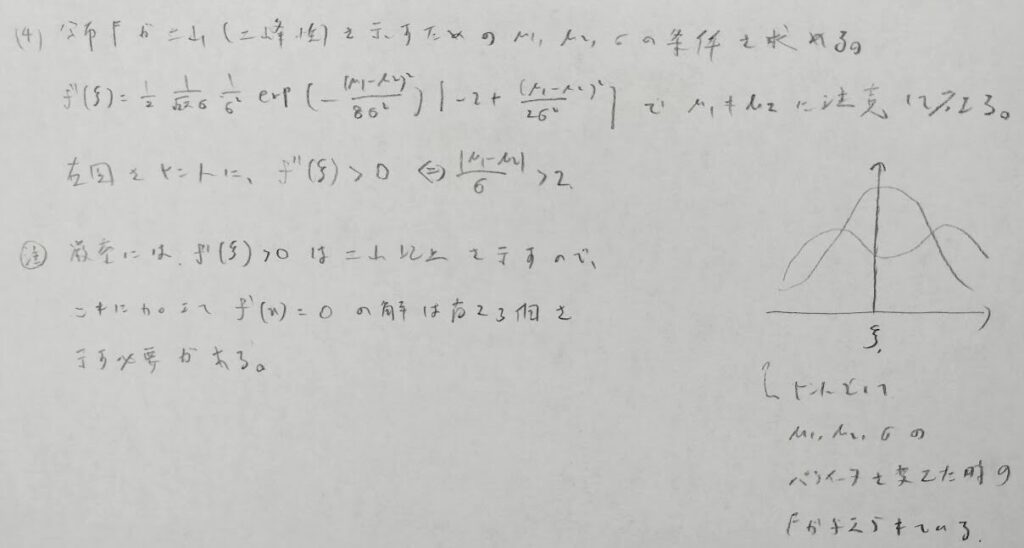
この問題が共通問題の中で最も難易度が高い問題なのでは？と思われる感じでした。
統計検定１級「統計応用」共通問題の過去問：2019年
ポチップ
2019年問５：適合度検定
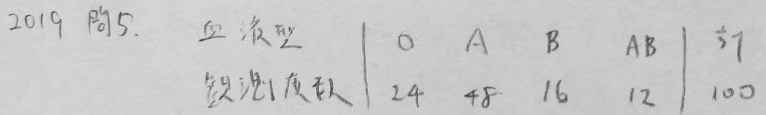
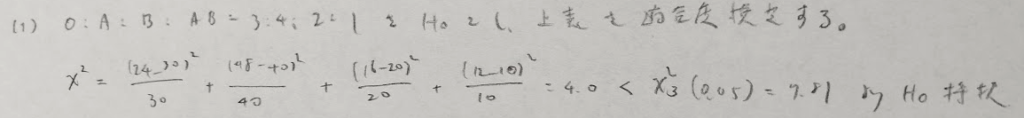
観測度数の値をすべてk倍するとカイ２乗統計量もk倍となります。
この証明のアウトラインは覚えておきましょう！ポイントは多項分布が多変量正規分布に近似できるという事実です。
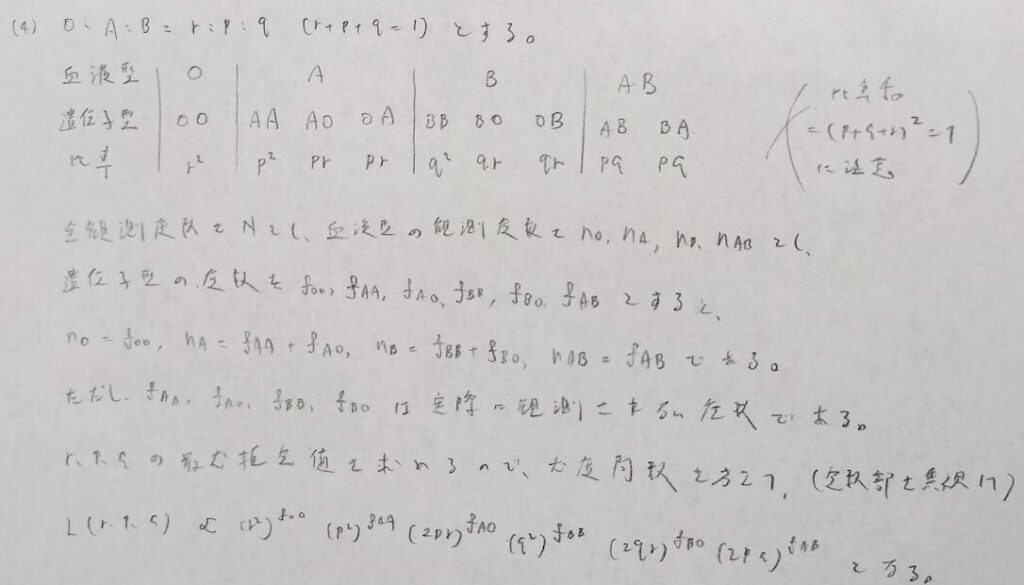
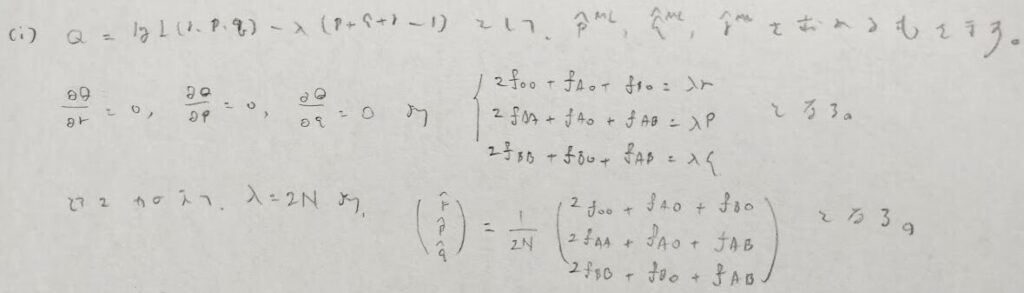
本問の背後にはEMアルゴリズムが潜んでいます。
統計検定１級「統計応用」共通問題の過去問：2021年
ポチップ
2021年問５：感度と特異度
ここら辺から問題傾向が明らかに変わっています。より世の中の（というより具体的あるいは有名問題的な）事例に即した問題へと変化しています。2023年現在でも同じ傾向が続いています。2020年度の中止の影響である予想に従うと、この傾向は以後しばらく続くと予想されます。
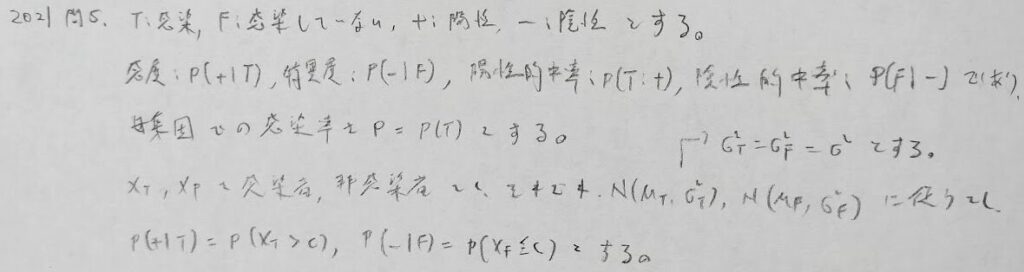
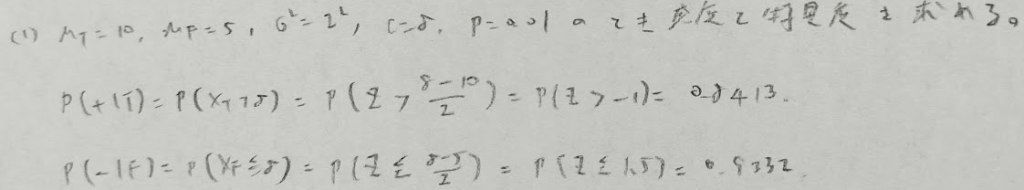
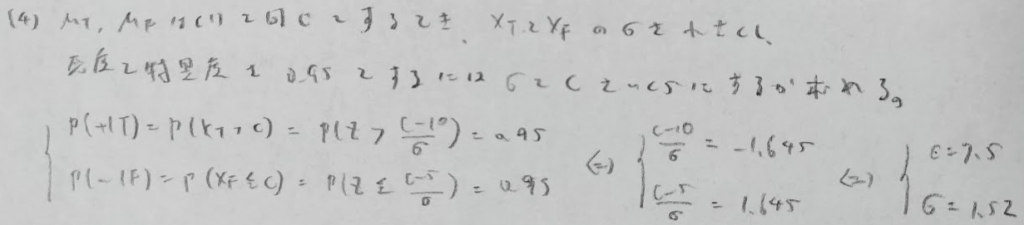
ここまではかなりのサービス問題ですので、しっかりと得点したいところですね。
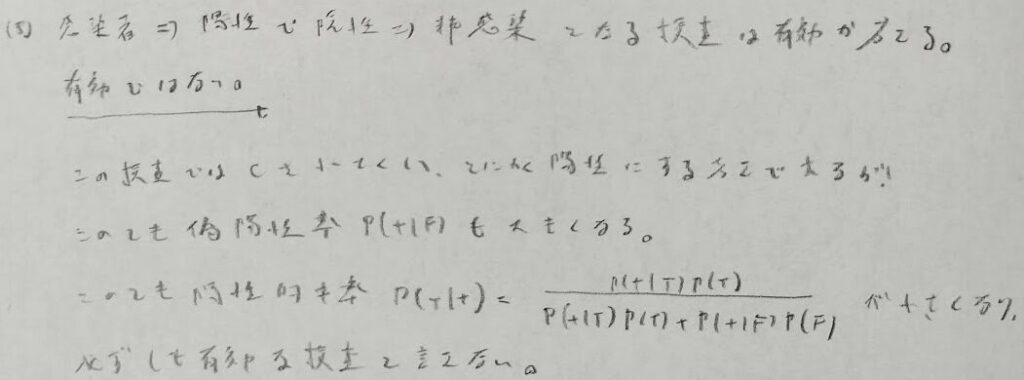
本問はかなりの難問です。時間がたくさんあっても思いつけるような単純な問題ではありません。
統計検定１級「統計応用」共通問題の過去問：2022年
ポチップ
2022年問５：平均への回帰
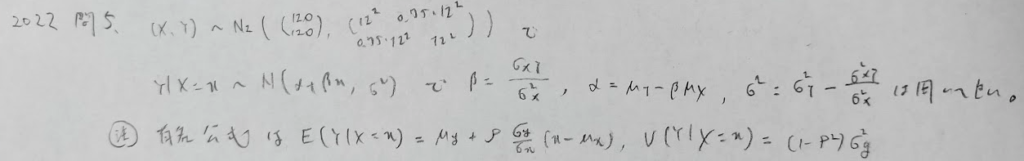
条件付き分散の第２項目の分子が２乗であることに注意しましょう。かなり盲点です。
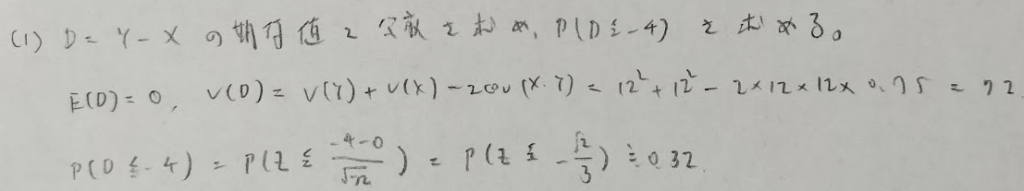
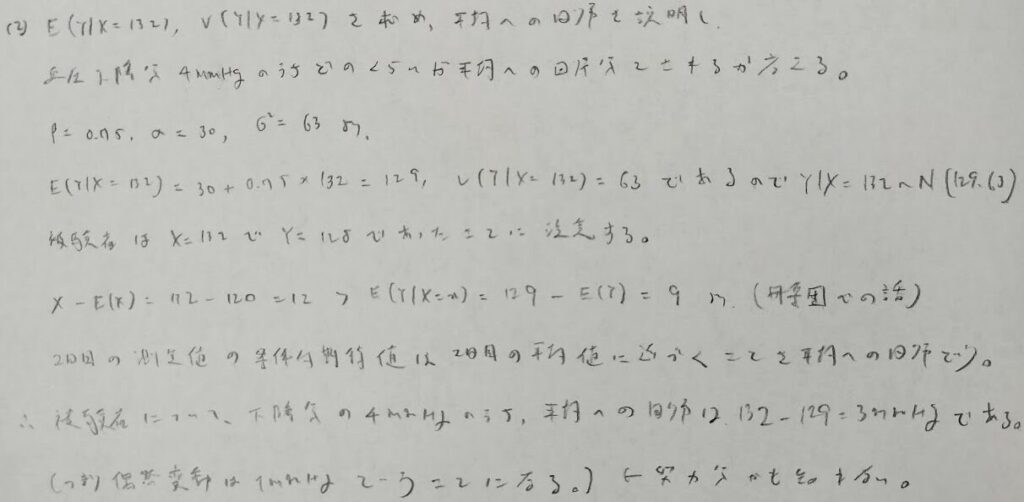
本人の努力分が統計的に出されるなんて、かなり面白い問題ですね！
以下に続く小問のために次のモデルを考えます。
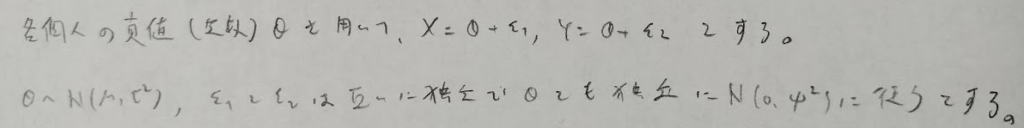
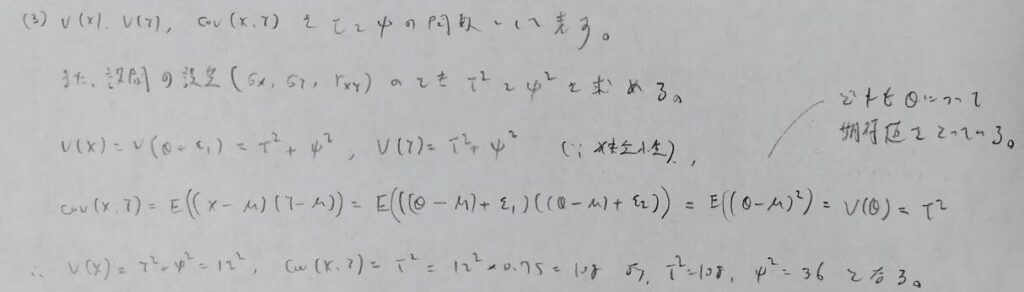
問題文をみないとどの文字について期待値をとるのか混乱するという、かなりレベルの高い問題です。
（４）は（３）の設定が保存されているようです。そうでないと処理不能になるので、細かい部分ですが問題文に配慮が欲しいなと思いました。今後の統計検定１級の出題で困ったことがあったら「前の問題の設定を使ってみる」ことが必要かも知れません。
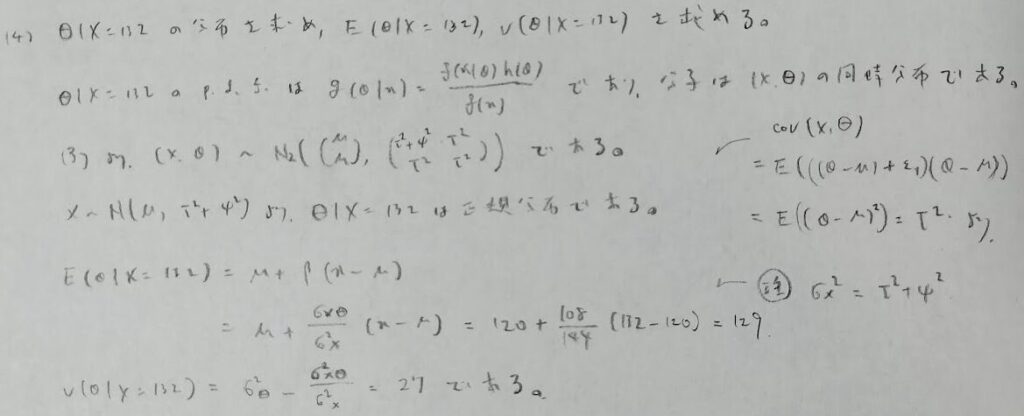
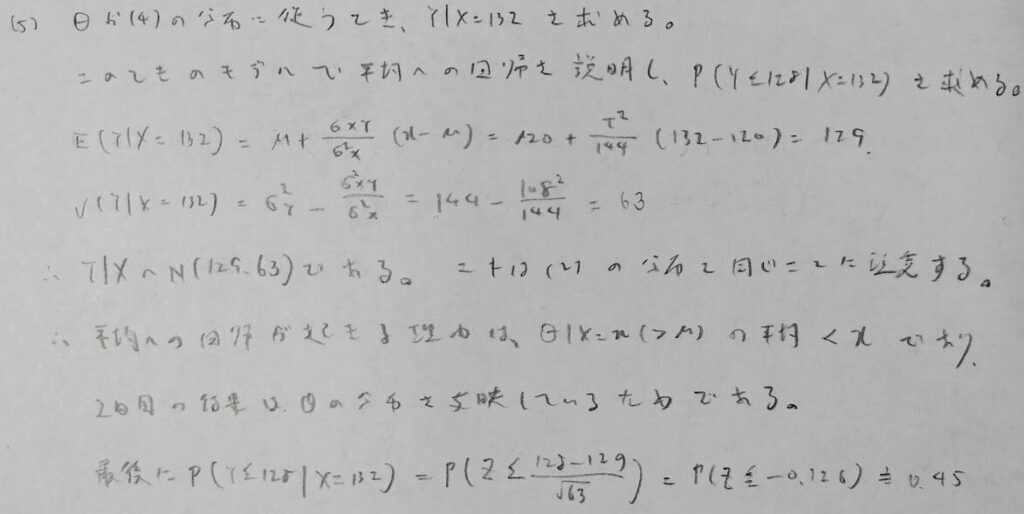
前年度と比べるとかなり得点しにくい問題です。本番では選択しない方が無難です。
明らかに2021年付近の統計検定１級の難易度が高いと思われます。そろそろ沈静化して欲しいと願います。
近年の統計検定１級の共通問題は必ずしも選択する必要はありません。選択問題の中で確実に得点できる分野を選択する方が懸命だと思われます。『増訂版 日本統計学会公式認定 統計検定１級対応 統計学』の応用分野の必須問題の章をよく読み込むことが対策としてはまだ有効だと考えられます。本書について詳細に解説した記事はこちらです。
統計検定１級「統計応用」共通問題の過去問：2023年
ポチップ
2024年9月現在、2023年度の統計検定１級の過去問は販売されておりません。そのため統計検定の公式ページから過去問をご覧ください。
2023年現在、モンモールの問題はアクチュアリー数学でも未出です。今後狙われる可能性が高いです。しかし統計検定１級としては２年連続での出題は限りなく低いと
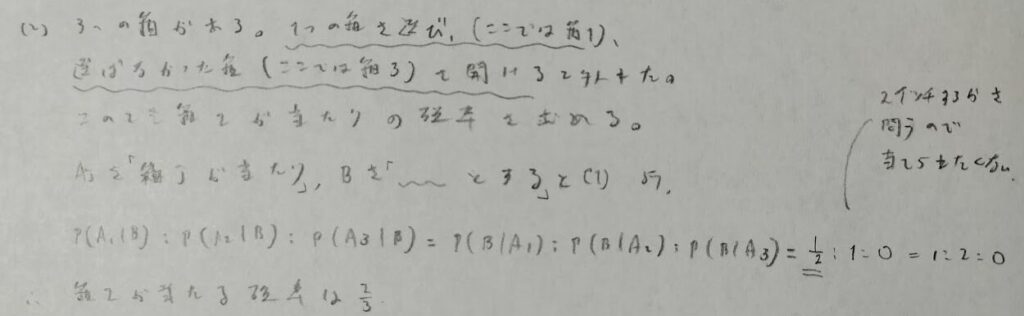
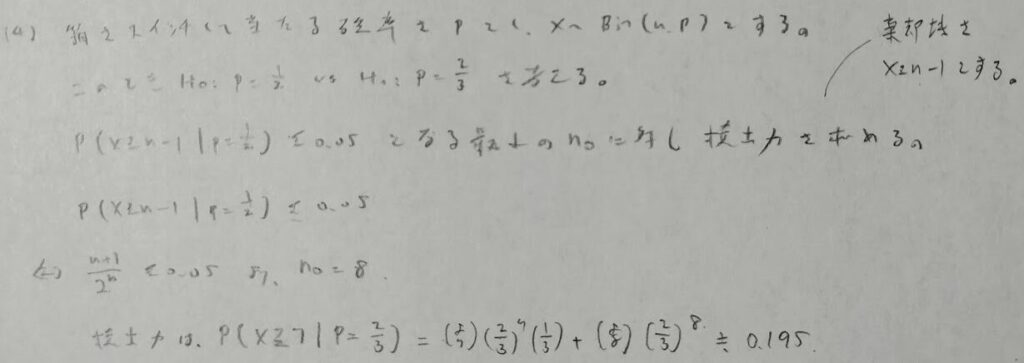
最後の問題はモンモールの問題の答えが0.5だと思っている人へのアンチテーゼですね。Xはn回の試行でスイッチして当たった回数を表すので二項分布です。
8回中7回スイッチして当たる確率が5%以下（滅多に当たらない場合なので）モンモールの確率の答えだと思い込んでいる0.5を棄却するときの検出力が約20%と少ないことがまた皮肉っぽい問題だと思います。単に試行回数が少ないからだと思いますけどね笑
このように統計検定１級の統計応用で高得点を取れるか？はかなりの運ゲーになってきています。まずは過去問に出ている問題を解けるようにして、各分野の対策に転じた方が統計検定１級の統計応用の合格に近づいていきます。共に頑張って合格を目指しましょう！最後に過去問集のリンクを掲載しておきますので問題の詳しい参照にご活用ください。
ポチップ
日本統計学会公式認定 統計検定 1級 公式問題集[2012〜2013年]
日本統計学会公式認定 統計検定 1級 公式問題集[2014〜2015年]
日本統計学会公式認定 統計検定１級 公式問題集［2016〜2018年］
日本統計学会公式認定 統計検定１級 公式問題集［2019～2022年］
統計検定１級の人文科学の過去問解説はこちらです。また、統計数理の過去問解説記事はこちらです。一緒に復習を頑張りましょう！
