統計検定1級で出題される離散型確率分布のラスボス的な存在は超幾何分布です。
超幾何分布は名前も難しそうだし、期待値や分散も覚えにくいし、証明も難しいのでラスボス的ですよね。
超幾何分布は難易度が高いのですが『現代数理統計学の基礎』『データ解析のための数理統計入門』『現代数理統計学』などの有名参考書ではサラッと流されている感じがしました。確かにポアソン分布などと比べると重要度は落ちるので仕方ないですね。
そこで超幾何分布の代表的な3つの性質についての導出の計算方法を詳しく紹介したいと思います。
組み合わせの記号Cについての計算公式と言い換え

超幾何分布のいろいろな性質を考えるときに受験数学でも登場した組み合わせCについての慣れが必要です。
上の図で知らないカッコがありますが、それはなぜ使うのですか?
組み合わせの記号でCを使わずにカッコを使うと、組み合わせのいろいろな公式を覚えやすくなります!
数学的にはnを自然数以外に拡張するときに用いる正式な記号です。
確かに!負の二項分布を勉強したときに証明で使っていましたね!
超幾何分布の内容を理解するときに必要な組み合わせの公式は2つです。
まずは大学受験でもおなじみのこの公式です。統計検定1級などではこのような公式はサッと出てこないといけないかなと思います。
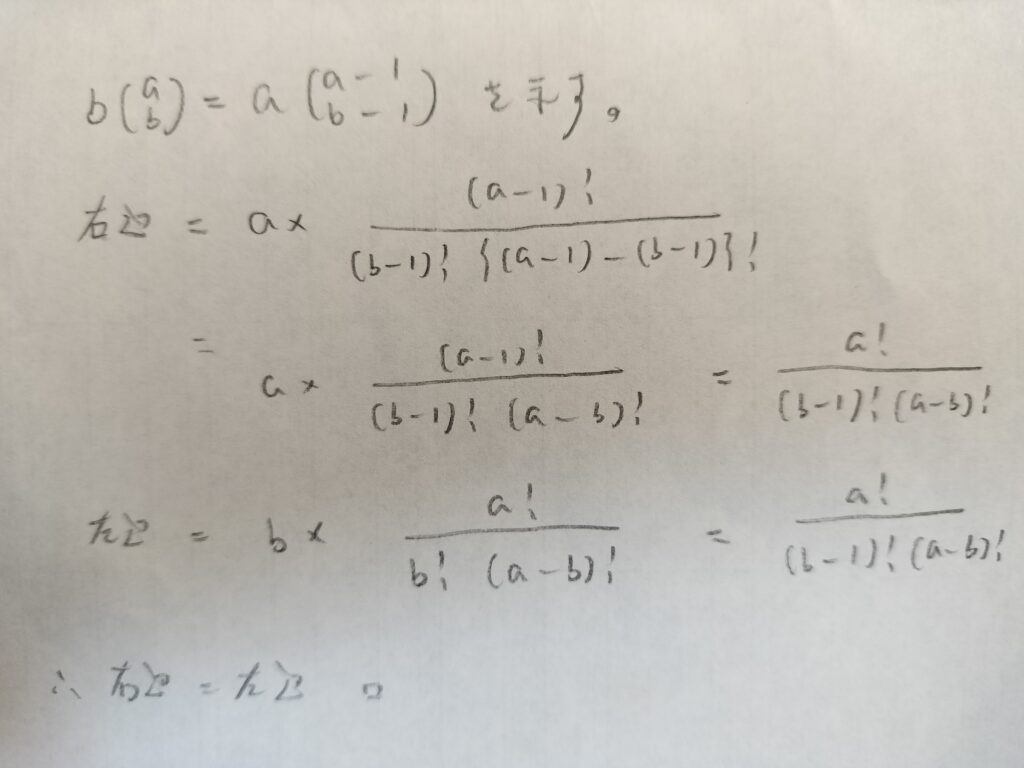
あともう1つの公式もありますね!
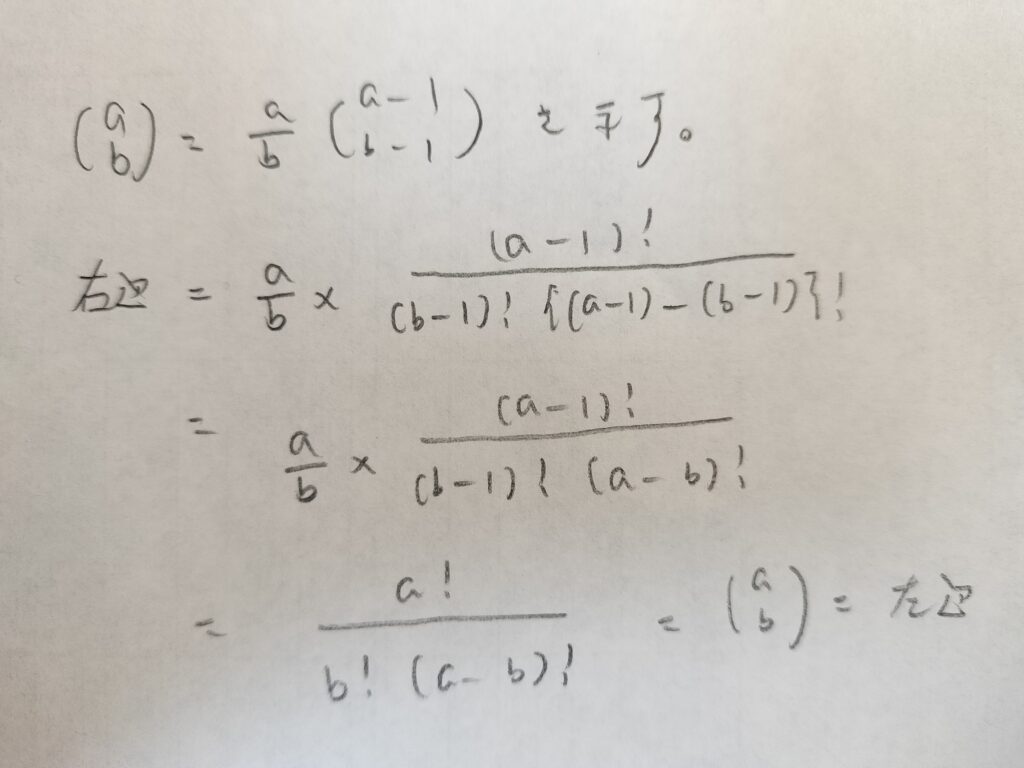
この公式は数学が得意な方なら「当たり前!」と感じる公式かも知れません。実際に組み合わせの記号をCではなくてカッコを使って書くと、当たり前さが伝わると思います。
どの記号を使っていくか?は大事なのですね!
組み合わせCの言い換えなどの公式は『アクチュアリー試験 合格へのストラテジー 数学 第2版』に綺麗にまとめられています。アクチュアリー数学を考えている方は是非ともチェックしてみてください!
超幾何分布の確率和1の証明
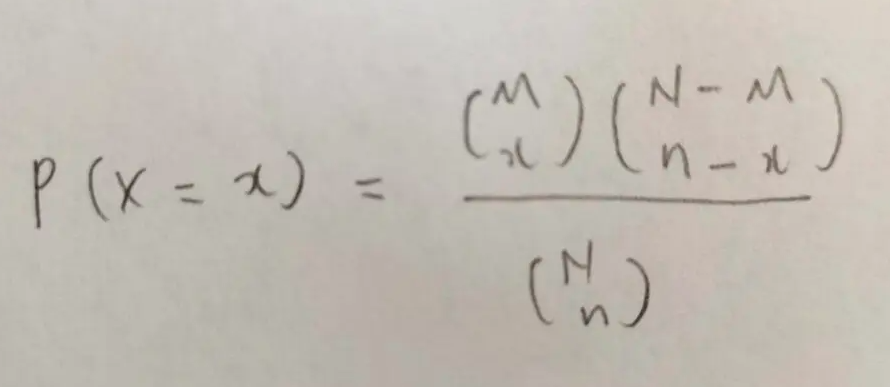
これが超幾何分布の確率関数です。
複雑すぎて覚えられません!
超幾何分布が難しいのは、この確率関数の形にも原因があります。そこでこの式が何を意味するのかを考えてみましょう。
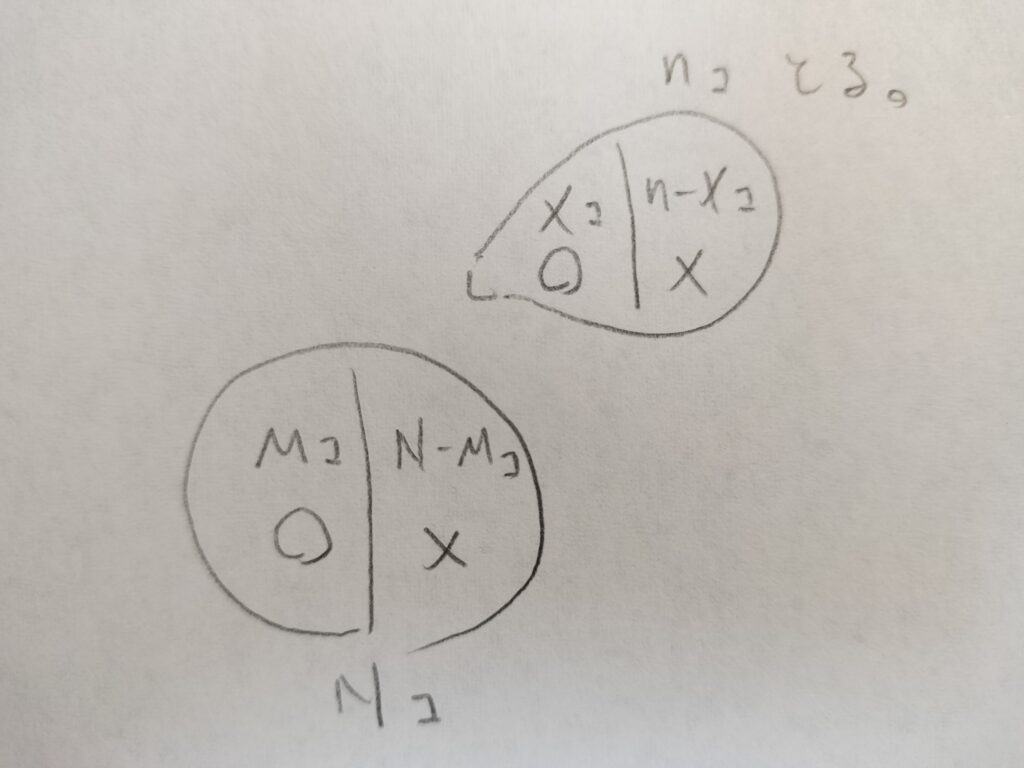
N個の中に当たりがM個あります。そこからn個を取り出します。n個の中にはX個の当たりがあります。Xを確率変数とするときに、Xは超幾何分布に従います。このことをX~H(N,M,n)と表現します。(H記号は例えば『リスクを知るための確率・統計入門』で使われています。)
この確率関数の和が1になるのか疑問ですので証明をお願いします!
まずはX=kが動く範囲の上限がMとnの小さい方であるということに注意します。別にここがわからなくてもシグマの上を書かなければ良いことなので計算上は問題ありませんが、記述ならば書かないとダメだと思います。
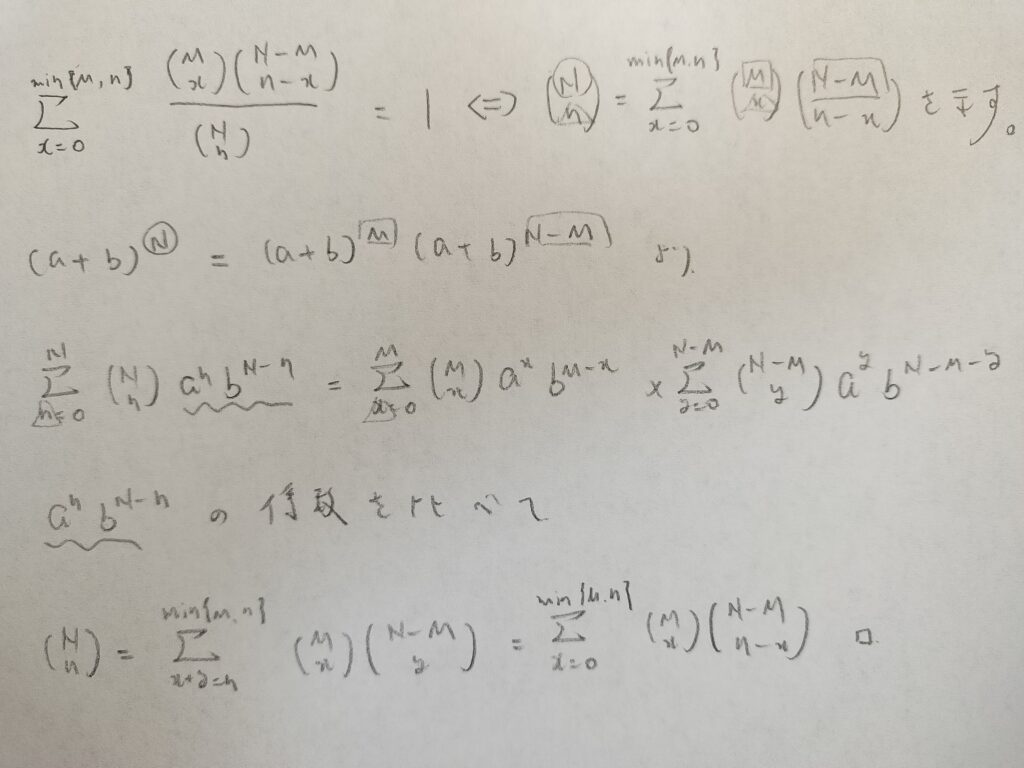
パッと見はやっぱり複雑ですが、書いてくれた記号を見ながら式を追っていくとなるほどなと感じます。
この証明のポイントは係数を比較するという発想を知っているかどうかで決まるので、初見ではかなり難しいでしょうね。
2023年時点では統計検定1級での出題歴はありません。しかしアクチュアリー数学では昭和63年に出題されています。この年はその後に超幾何分布の期待値と分散を求めよとなっていました。
超幾何分布の期待値の計算
超幾何分布の期待値の証明を初めてご覧になる方は、まずは結果だけを覚えておくことをおすすめします。覚え方は後半で書きます。
いよいよ中盤です。超幾何分布の期待値を計算します。ここでは組み合わせCの公式を2つ使いますので頑張りましょう!
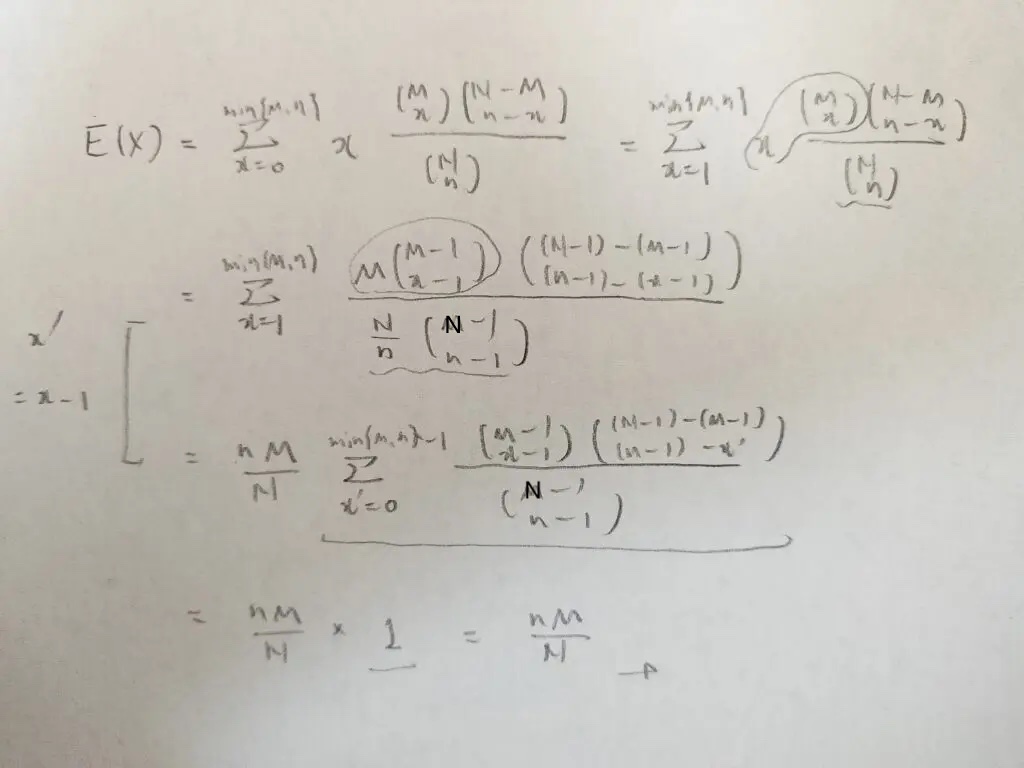
やっぱり複雑ですよ!笑
ポイントは3つあります。
①分子と分母でそれぞれ組み合わせの公式を別々に用いる
②下から2行目の式の下線部分を作るようにシグマの動く変数を0スタートにする
③確率和1を利用する。
最後の③がピンと来ないので説明が欲しいです!
この図を図をみて下さい。対応する部分が変わる様子を赤で書き直しました。
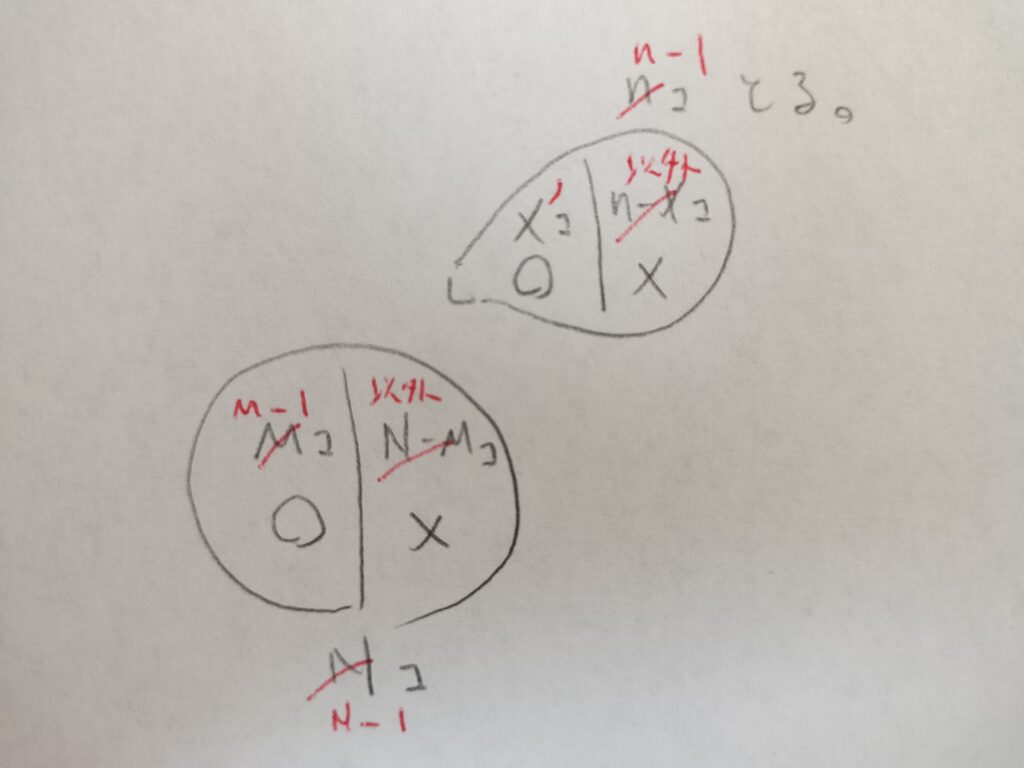
この図を参考にすると③の内容が理解できると思います。
超幾何分布の分散を計算する方法
きっと分散も難しいのでしょう。覚悟して証明を見てみます。
先にポイントを教えておくと、分散の証明は「いかに期待値の形を作り出すか?」がポイントです。
まずはX(X-1)の期待値を計算します。
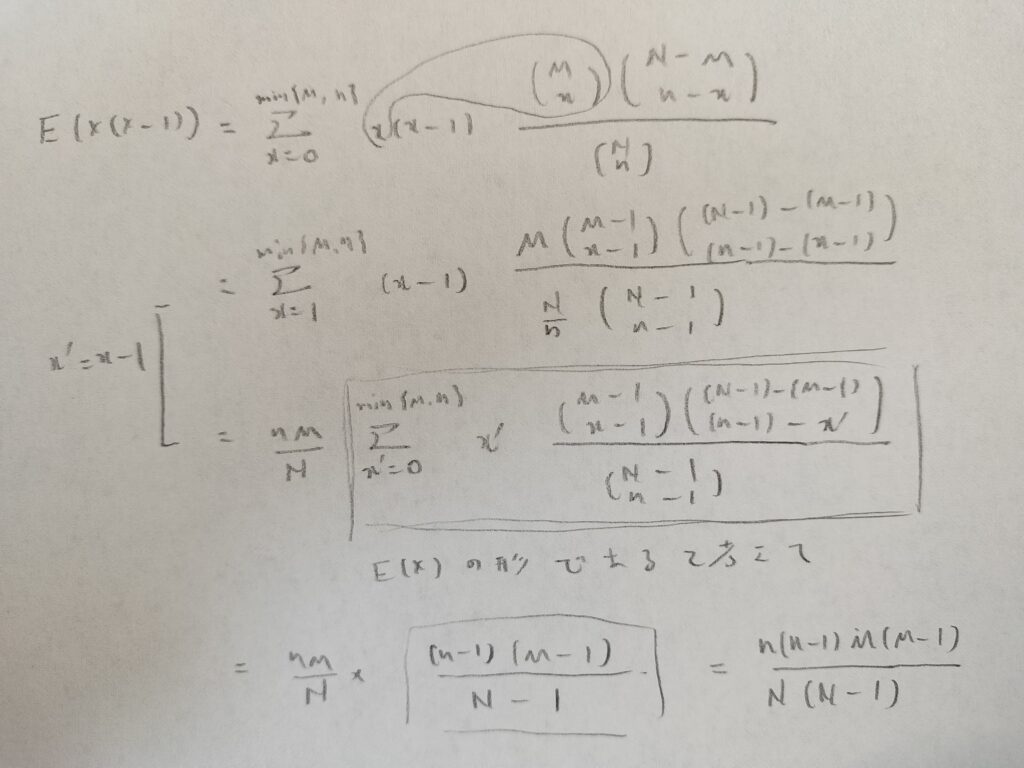
あれ?最後の結果は何か法則性を感じます。
そうですね。X(X-1)(X-2)の期待値の結果も類推できるのではないでしょうか。参考に今まで勉強した確率分布の期待値をまとめておきます。法則性を感じますね。
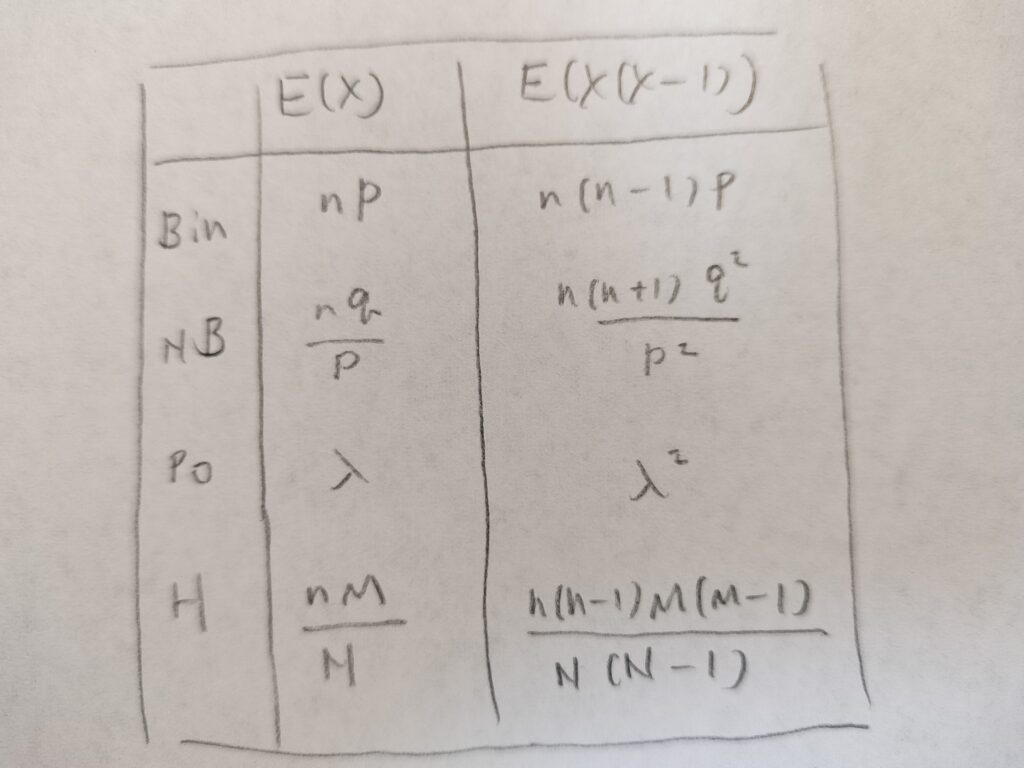
XとX(X-1)の期待値に法則性が見られるのは、二項分布、負の二項分布、ポアソン分布、超幾何分布が離散型確率分布でシグマをもとに期待値が計算されるからだったのですね!
では最後に分散を出しましょう。公式に代入するだけなので、すぐに終わります。
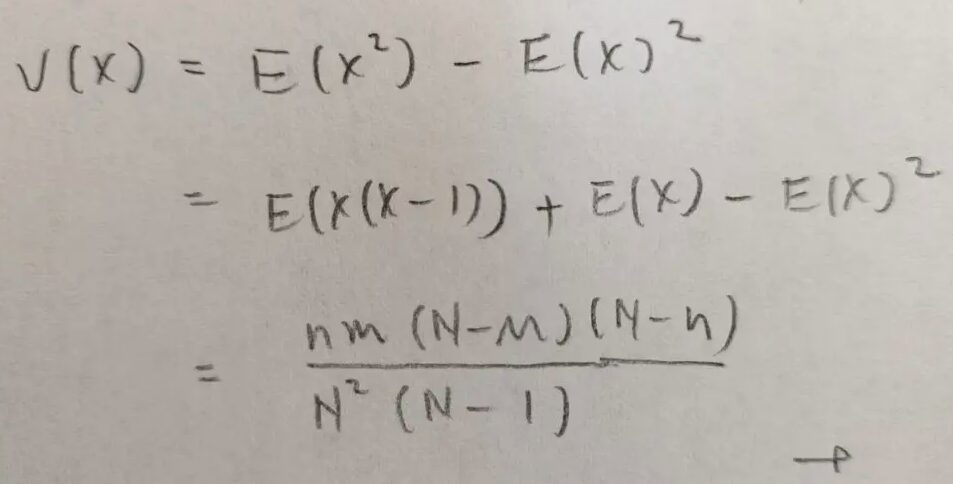
答えは出ましたけど、これを覚えられる自信がありません。
実はスッと覚えられる方法があります。
超幾何分布の名前の由来と二項分布との関係
超幾何分布は幾何分布との関係はなく、実は微分方程式と関係があります。ある常微分方程式の解が超幾何関数という関数で表現できる事実があります。超幾何分布の確率母関数がこの超幾何関数と関わるため、超幾何分布という名前がつけられました。
常微分方程式は数学検定1級で頻出です。『常微分方程式キャンパス・ゼミ』がとても分かりやすくおすすめです!
超幾何分布は二項分布から派生した分布とも考えられます。
超幾何分布の確率関数を作る背景を思い出すと、もともとN個の中から当たりがM個ある集団からn回取り出すと考え直してみると、当たりの確率が一定と考えたとき二項分布の考えに帰着できます。

期待値は確かに!なるほどという感じです。でも分散のところの有限修正係数というのがわかりません。
これは有限母集団という考えを使ったもので今後登場しますのでお楽しみに。
最後にこの記事で登場した参考書を紹介します。
常微分方程式はこれ1冊で数学検定1級レベルまで到達できるコスパ抜群の本です。演算子法も収録されています。なんとピカールの逐次近似法まで掲載されています。
超幾何分布関連では組み合わせCに関する公式の部分で参考にしました。アクチュアリー数学の公式が大量に掲載されています。最近改訂版が登場してさらにパワーアップしました。ボックスマーラー法も載っています。
確率分布の由来がとても丁寧に解説されています。小さいところですが本の重さが軽く持ち運びしやすい点が気に入っています。後半はコピュラが紹介されています。
統計検定1級以上の内容が体系立てて掲載されています。前半の確率の部分は懇切丁寧に書かれています。演習問題は後述の『現代数理統計学の基礎』よりも難しいです。
本書の演習問題は統計検定1級の予想問題として大変有用です。後半部分は概念的な説明が多い印象です。ポアソン過程などまで掲載されています。
統計検定1級の統計数理、統計応用のどちらにも有用な最強の教科書です。後半部分の内容がとても分かりやすく、今後読み込んでいきたいNO1の本です。








