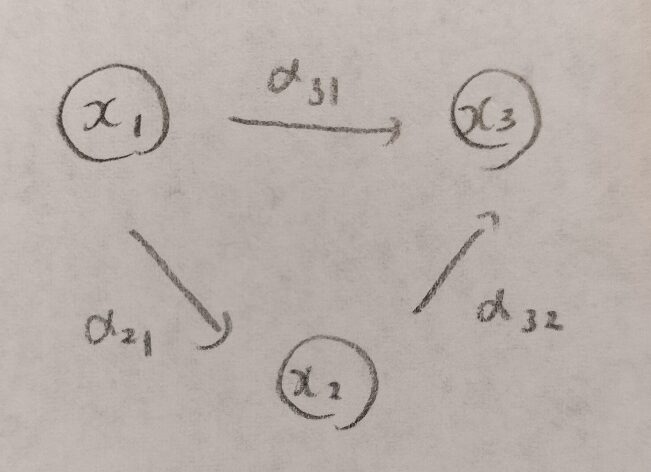前回のパス解析では相関係数が色々な要素で絡み合っている内容を勉強しました。
しかしパス解析で登場した偏相関係数は2変量のものでした。これを3変量以上で考えると一体どのようになるのでしょうか。
とても複雑そうなのでパス解析のようなグラフィカルな分析手法があるのでしょうね。
多変量の偏相関係数の独立性になるのかをグラフィカルに表現した独立グラフの扱いができるようになることを本記事の目標にします!
それでは1から解説していきます。
母相関係数行列と母偏相関係数行列の関係
母相関係数行列から母偏相関係数行列への変換
前回のパス解析では標本偏相関係数がメインでしたが、前回の記事の証明の中でもあったように母偏相関係数でも問題はありません。この記事では母相関係数や母偏相関係数を扱います。
まずは母偏相関係数行列がどのように計算されるのかを見ていきます。
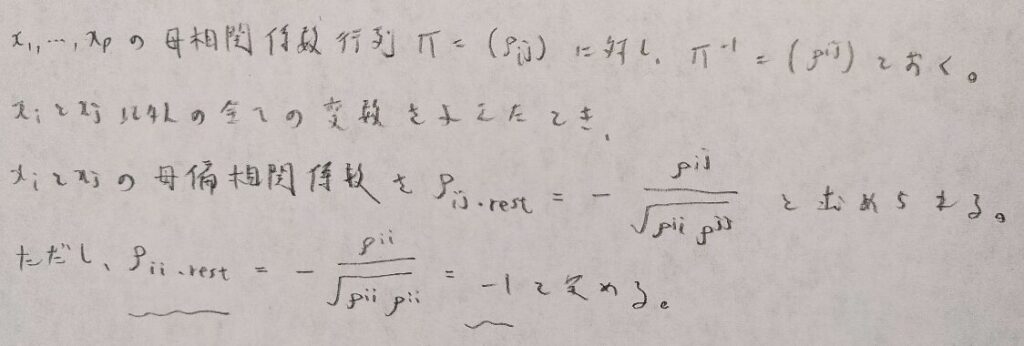
restは残りの全ての変数ということなので、3変量以上の母偏相関係数も定義できるのですね!でも4変数以上になるとrestの解釈が大変になりそうです。
母相関係数行列も母偏相関係数行列も、どちらも対称行列であることにご注目ください。記事の後半で役に立ちます。またrestの扱いについては記事後半の独立グラフで丁寧に説明します。
図01の最終行の内容はほとんど意味をなさないものですが、形式的に−1と定めています。
母偏相関係数行列から母相関係数行列への変換
今度は逆の変換について考えます。図02のような変換を通して母偏相関係数行列から母相関係数行列への変換ができます。
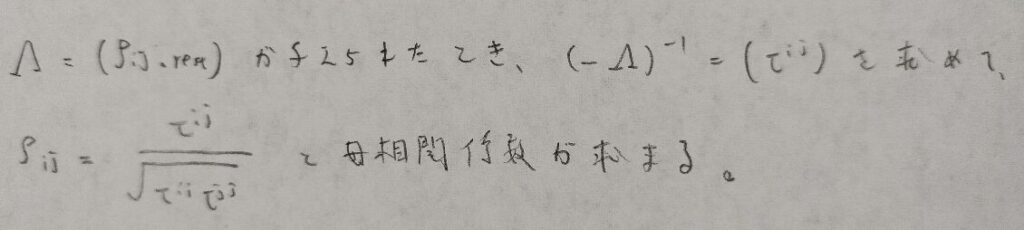
図02の1業目で定められる行列を各対角成分で割ることによって基準化したものが相関係数行列の成分になると考えれば、式の意味がしっくり来ると思います。
独立グラフを考えて母偏相関係数の条件部分の意味を解釈する
今回のタイトルにあるグラフィカルモデリングとは一体どういう意味ですか?
多変量正規分布を仮定したもとで、条件付き独立の関係をグラフを用いて表現することをグラフィカルモデリングを行うといいます。そして今回は量的変数の具体例を通して説明します。
多変量正規分布の内容の応用というわけですね。
多変量正規分布では独立性と無相関が同値であるという重要な内容を用います。グラフィカルモデリングでは3変数以上も扱えるので大変便利です。
独立グラフ(3変数)
具体例として3変数の多変量正規分布を仮定して、各変数間の条件付き独立の考え方を紹介します。
図03の母相関係数行列Πが与えられているとします。このときに母偏相関係数行列Λを求めます。
対角成分のーはどういう意味ですか?
−1という意味です。先ほどもお伝えしましたが、−1であることの本質的な意味はないのでーと表記をすること、そして母偏相関係数行列であることを明確にするためにーにしているという主張もあります。

各変数が離れているということは、互いに影響を受けない(独立=無相関)ということです。
母偏相関係数が0のときは、独立グラフにおいて変数間を線で結びません。
線で結んでいるということは偏相関係数が0ではないということです。
離れていれば影響を受けないという考え方はとてもわかりやすいです。
次の4変数の例で考えると、そのわかりやすさが明確になります。
独立グラフ(4変数)
4変数の独立グラフを用いた条件付き独立の関係性を考えます。
ここでも4変量正規分布を仮定していることにご注意ください。
多変量正規分布では独立性と無相関が同値であるからですね!

今回は4変数ですので、例えば変数2と変数3のrestは変数1と変数4です。しかし4変量の独立グラフを見ると変数1が中継地点になっています。そのため変数2と変数3のrestは変数1と考えても(多変量正規分布を仮定すれば)問題ないということになります。
なるほど!restの意味が少し漠然としていましたが、このように独立グラフを書くというグラフィカルモデリングの手法を用いると、どことどこが条件付き独立かが判明してくるのですね!
その通りです。ちなみにこの4変量の具体例では、変数1を固定すると(つまり動けなくするので変数1が消えるイメージです)変数2と変数3と変数4の行き来する経由地点(変数1)が消えて機能しなくなる(固定していて動かない)ので変数2と変数3と変数4の間に関係がなくなります。
今回の具体例では永田先生の『多変量解析法入門』を参考にさせていただきましたのでご紹介いたします。本書は統計検定1級の多変量解析部分をほぼ網羅しており、大変貴重な1冊となっております。
共分散選択をする理由
今回の例では母偏相関係数が0になる例でしたが、一般的なデータだと母偏相関係数が0になることはあまりなさそうですよね。その場合は独立モデルでの独立性がほぼなくなってしまうと思いますが、その場合はどうしますか?
そのような状況のときは0とみなして考えることになります。そのような考えを共分散選択をするといいます。
共分散選択を行い、得られたモデルの妥当性を評価しながら適切なモデルの選択を行うことがグラフィカルモデリングの真髄となります。