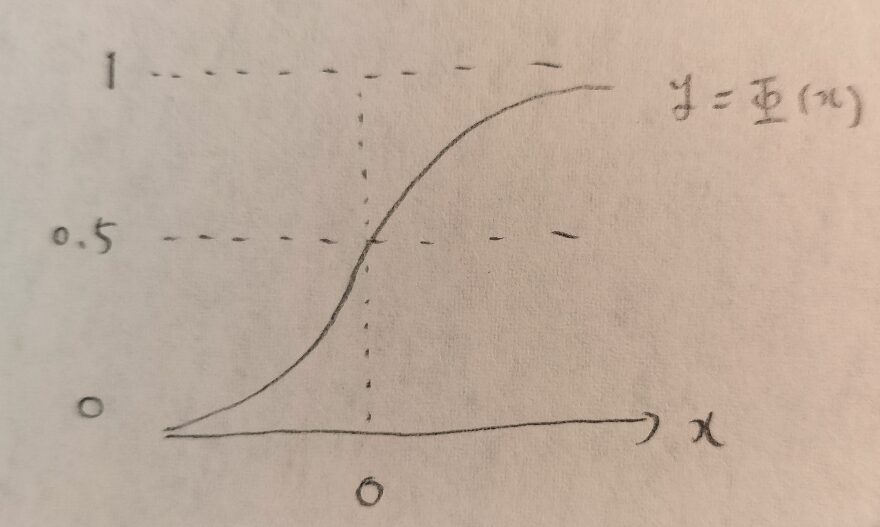ロジスティック回帰モデル(ロジットモデル)、プロビットモデルと回帰分析の応用を解説してきました。
今回はより一般化された内容を踏まえた上で、その特例であるポアソン回帰モデルを詳しく解説します。
ポアソン回帰とはポアソン分布と共変量(xなどの独立変数)との関係を調べるための回帰モデルのことです。
またこの記事では初めて統計学の緑本と言われる名著『データ解析のための統計モデリング入門』の内容も参考にさせていただきました。
一般線形モデルをわかりやすく解説
重回帰モデルの一般化をした概念を紹介します。のちに取り上げる分散分析モデルも一般線形モデルに属するモデルです。
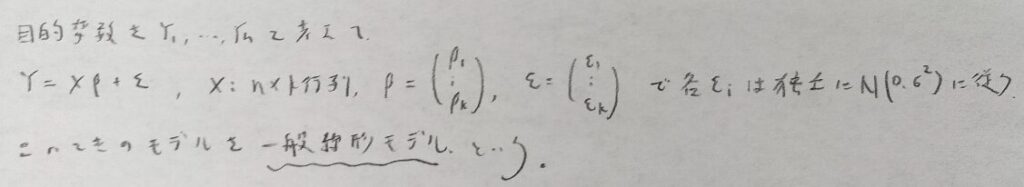
主に行列Xをどのように考えるか?によってさまざまなモデルが作り出されます。
一般化線形モデルをわかりやすく解説
次により一般化されたモデルである一般化線形モデルを紹介します。
以前の記事であるロジスティック回帰モデルやプロビットモデル、そして今回扱うポアソン回帰モデルはすべて一般線形モデルの一例です。

リンク関数はロジットモデルやプロビットモデルでも登場しましたね。線形予測子がいまいちわかりません。
線形予測子は『データ解析のための統計モデリング入門』に明確な説明が載っていまして、与えられたデータの次元数によって設定が変わります。例をみていきましょう。
一般化線形モデル(ロジスティック回帰モデル)
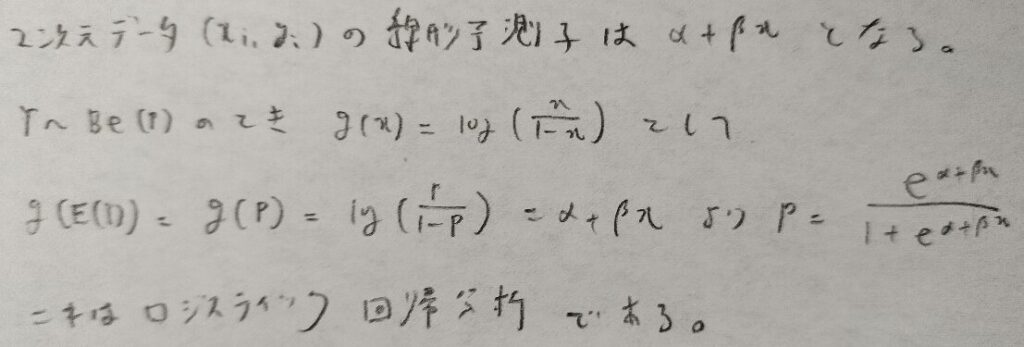
なるほど2次元データのときの線形予測子はお馴染みの形になるのですね。
その通りです。今回はyが取る値は0と1の2値なのでベルヌーイ分布を扱うわけです。
一般化線形モデル(プロビットモデル)
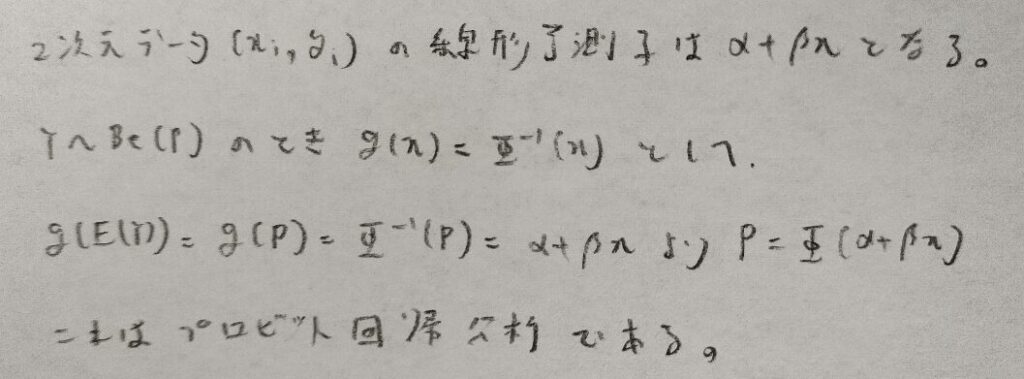
ロジスティック回帰モデル(ロジットモデル)と違うのはリンク関数をどのように設定するかだけですね!
その通りです。前回のプロビットモデルの記事とあわせて理解すると素晴らしいと思います。
一般化線形モデル(ポアソン回帰モデル)
ポアソン回帰モデルの1例を一般化線形モデルの1例として紹介します。

ここでは2次元データで、ポアソン分布のパラメータであるλが単純な形であることにご注意ください。
ポアソン回帰分布の推定量の求め方と検定をわかりやすく解説
一般的なポアソン回帰モデルを解説します。この章では久保川先生の『データ解析のための数理統計入門』の演習問題を参考にさせていただきました。
ポアソン回帰分布の推定量

先ほどの例とは異なり次元数が多く、ポアソン分布のパラメータも複雑であることにご注意ください。
リンク関数を技巧的に設定することで、先ほどの例との整合性を持たせているのですね!
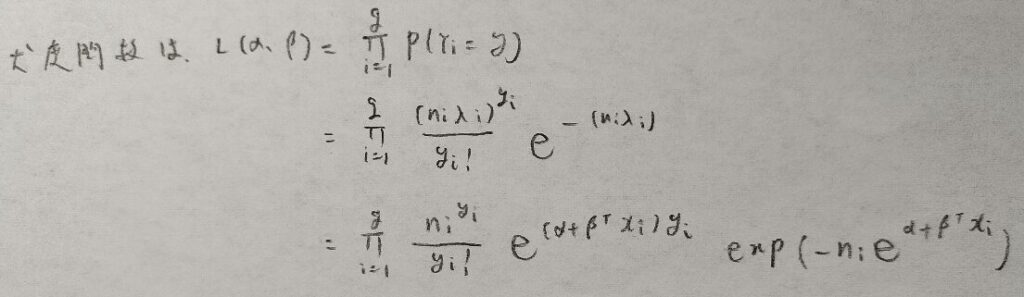
次に対数尤度関数を求めます。
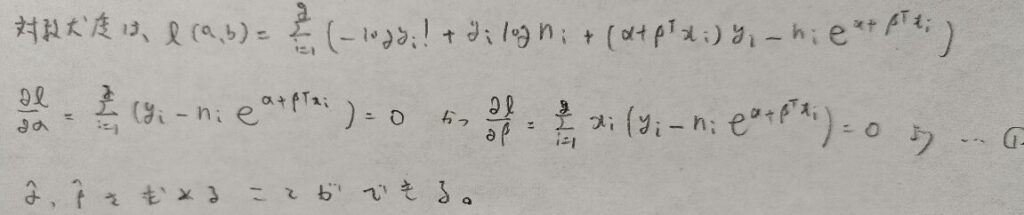
ポアソン回帰モデルの尤度比検定
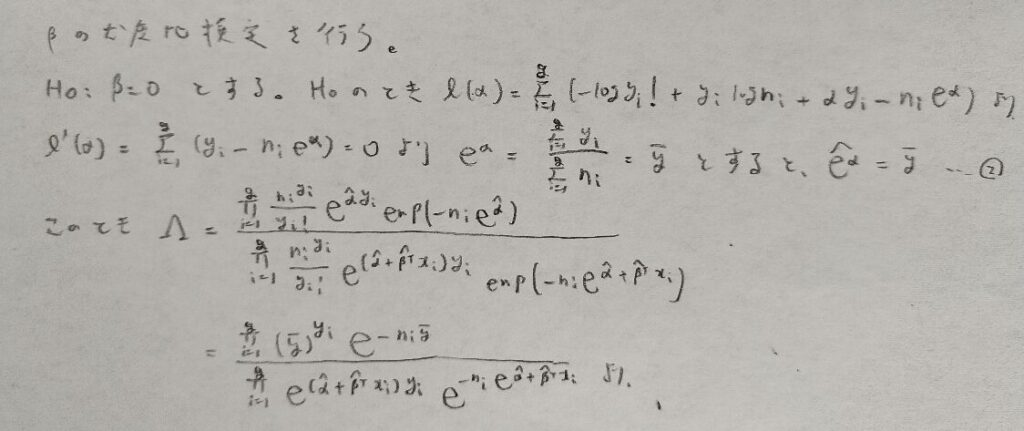
次に尤度比検定量を求めて棄却域を求めます。
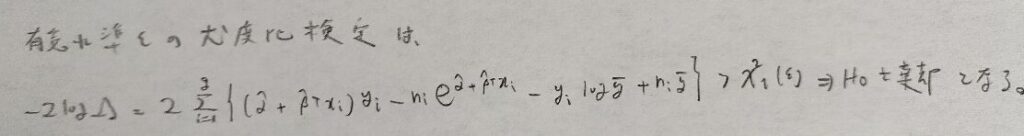
尤度比検定統計量とカイ2乗分布については『現代数理統計学の基礎』の説明がわかりやすくおすすめです!
本書は統計検定1級受験者にとっての教科書のような存在です。受験者は購入をご検討ください!
この本の演習問題がかなり素晴らしく、一緒に何周もがんばりたいですね!
このブログ記事でも本書の問題の解説がすでに登場しています。今後増やしていきますので、今後ともよろしくお願いします!