『現代数理統計学の基礎』の第5章の問題を解説していきます。本章では近似についての問題がメインとなります。
前回の第4章の内容とも関係しておりますので、未読の方はこちらからよろしくお願いします!
この近似については統計検定準1級の公式本『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』にてサラッと載っていますが、統計検定1級のバイブルである『現代数理統計学の基礎』ではその内容がほぼ1章分として構成されています。
確率収束・平均2乗収束・分布収束の3点を意識して取り組むと良いですね。
確率収束を示したかったら平均2乗収束を示せば良い。
分布収束を示したかったら分布関数を意識した変形を行えば良い。
統計検定1級やアクチュアリー数学を受けるにあたって、このような大事な気づきが第5章を解いていくことによって得られます。『現代数理統計学の基礎』を片手に一緒に頑張りましょう!
現代数理統計学の基礎『第5章』例題5.22

最後に微分方程式を解くことになりますが、ただ積分をするだけです。しかし逆三角関数の積分は盲点だと思います。
このような大学1年生で学ぶ微分積分は『微分積分キャンパス・ゼミ』がおすすめです!
現代数理統計学の基礎『第5章』例題5.23

統計検定準1級で学習したデルタ法の発展形が分散安定化変換ですね!
現代数理統計学の基礎『第5章』例題5.27
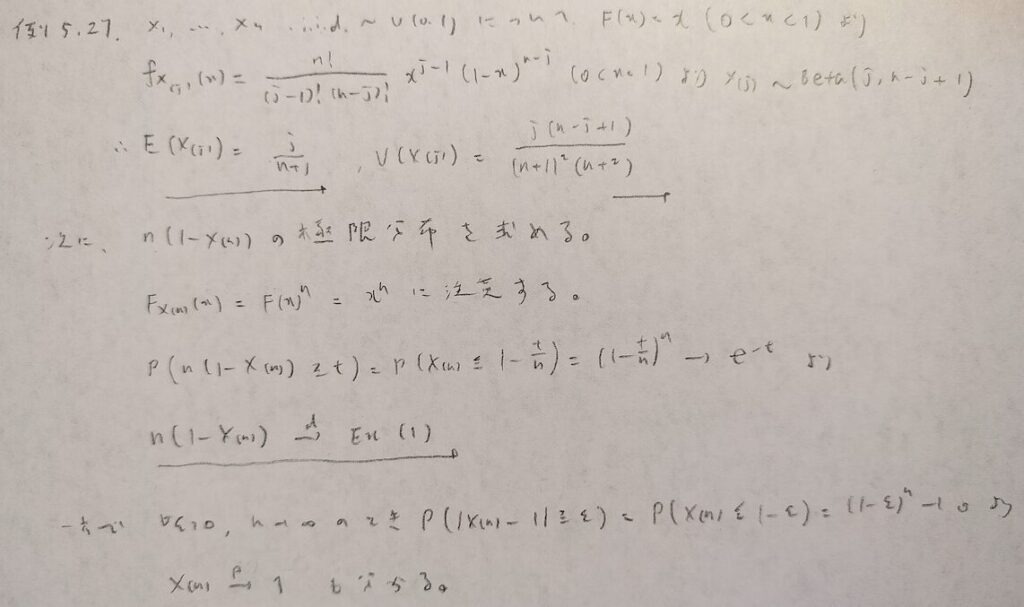
順序統計量は多項分布と関係しています。未学習の方はこちらをご一読ください!
現代数理統計学の基礎『第5章』例題5.28
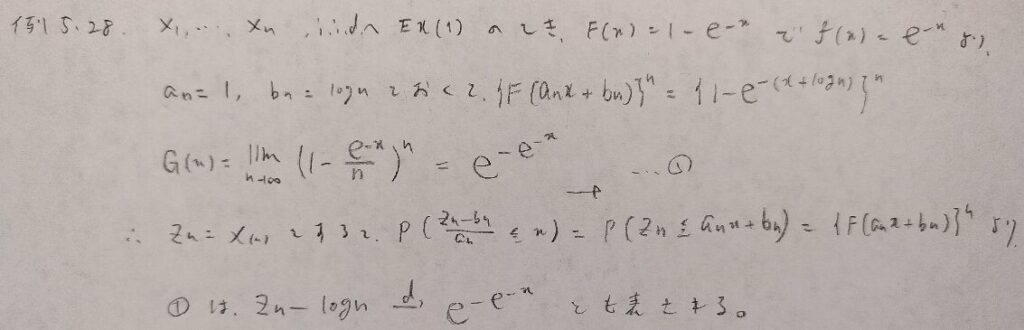
現代数理統計学の基礎『第5章』例題5.35
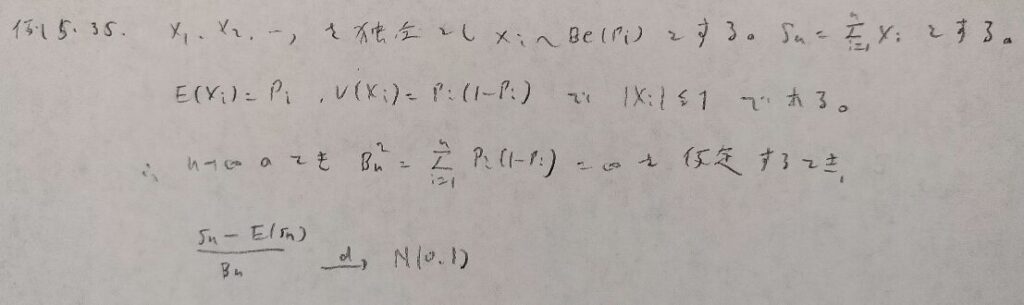
本問は発展としての紹介のため統計検定1級には出題されないと思われます。
現代数理統計学の基礎『第5章』問1
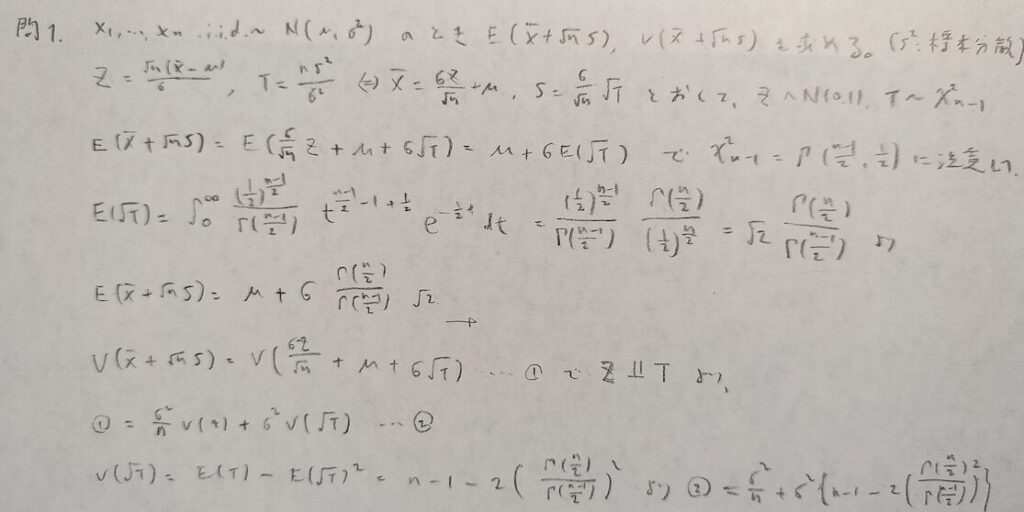
第1問から複雑な問題です。適宜変数を置き換えて対処しましょう!
現代数理統計学の基礎『第5章』問2
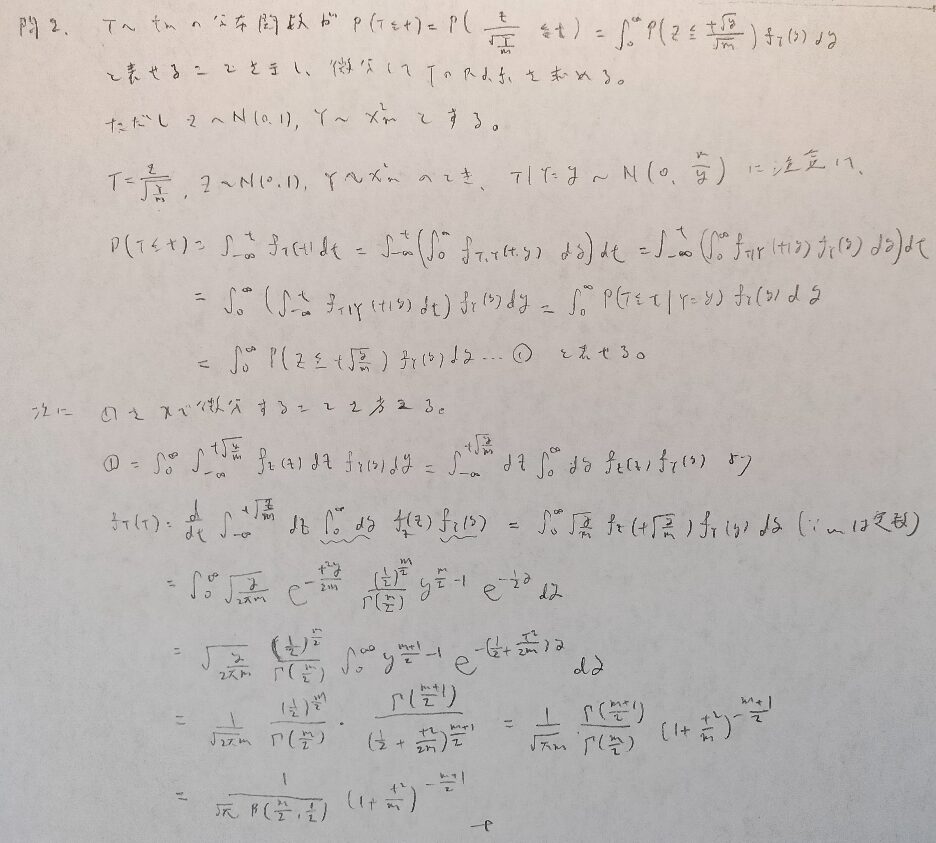
t分布の確率密度関数を混合分布の考えを用いて導出する素晴らしい問題です。
この導出の仕方は有名な参考書の中だと『現代数理統計学の基礎』にのみ掲載されていると思われます。
現代数理統計学の基礎『第5章』問3
前半の難問です。思考力+計算力が要求される問題です。
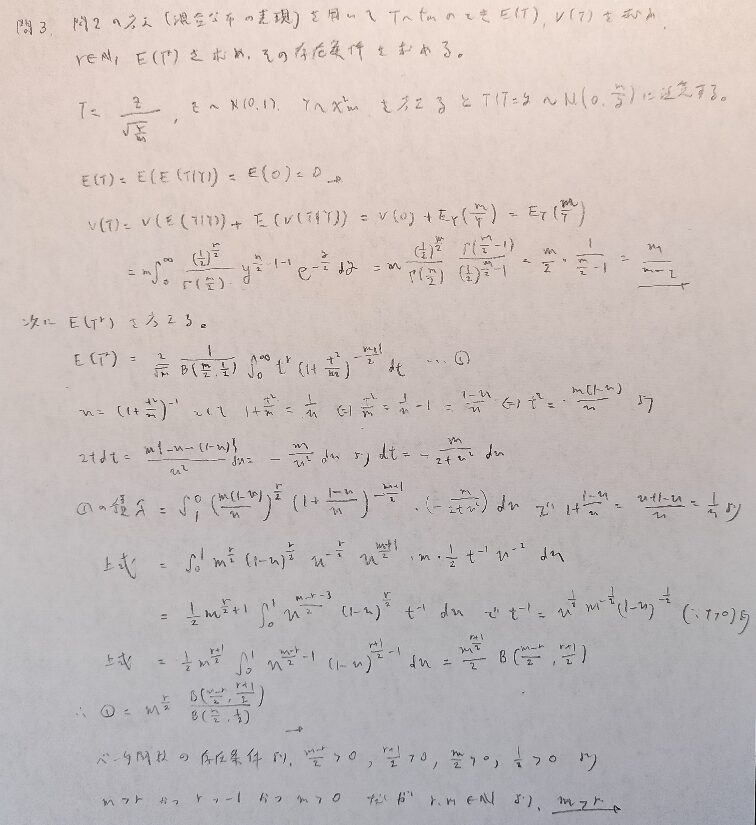
ベータ関数の存在条件が鍵になります。
とにかく置換積分が長かったです笑
現代数理統計学の基礎『第5章』問4
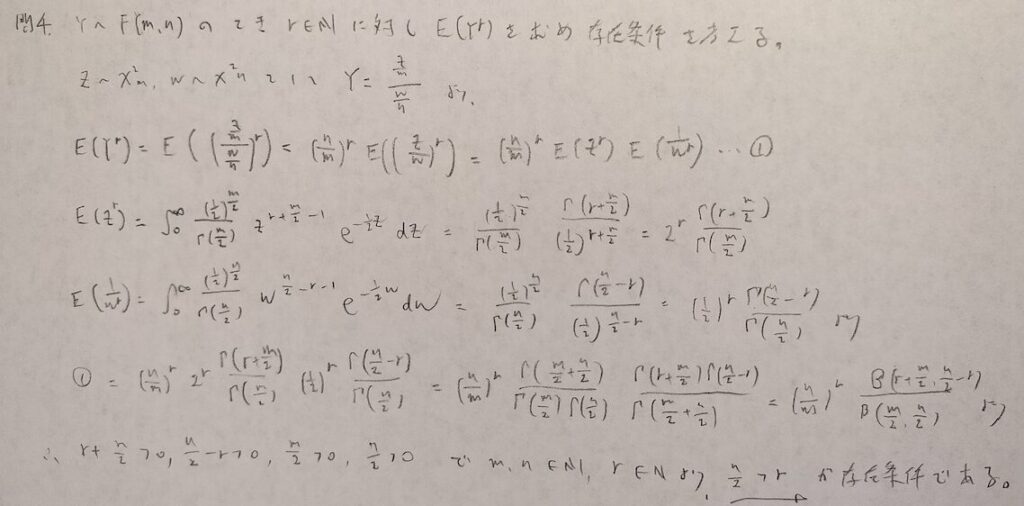
F分布に関する問題ですが前問と比べると計算量はまだ少ないです。
現代数理統計学の基礎『第5章』問5
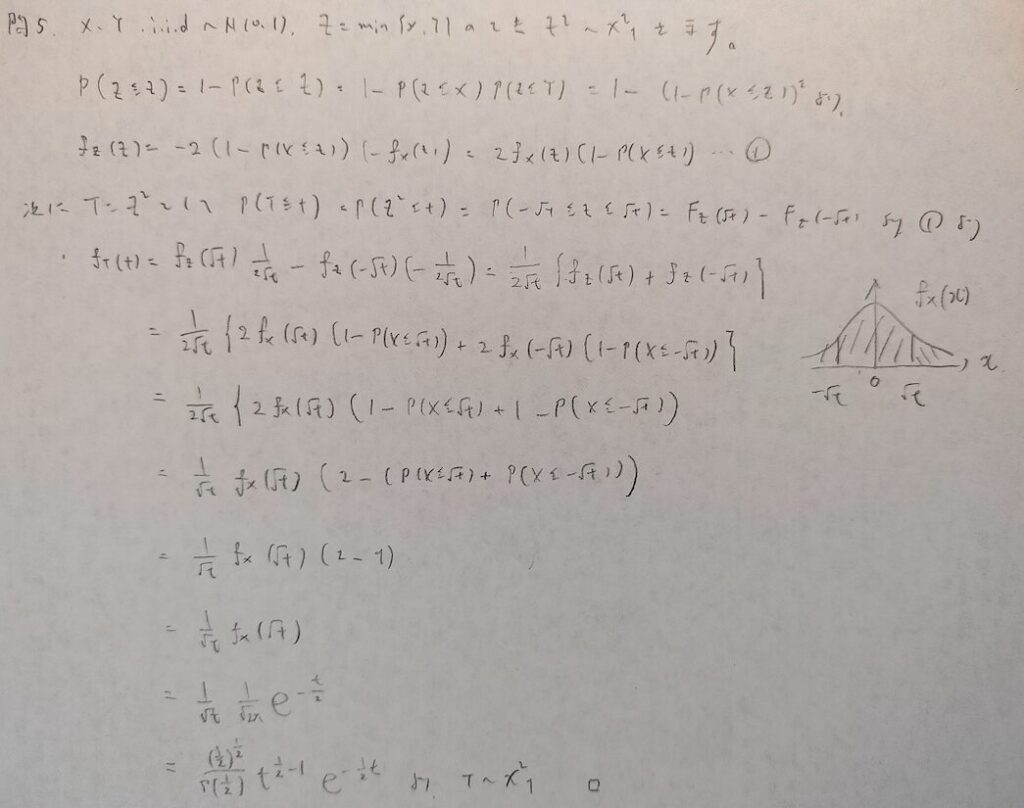
現代数理統計学の基礎『第5章』問6
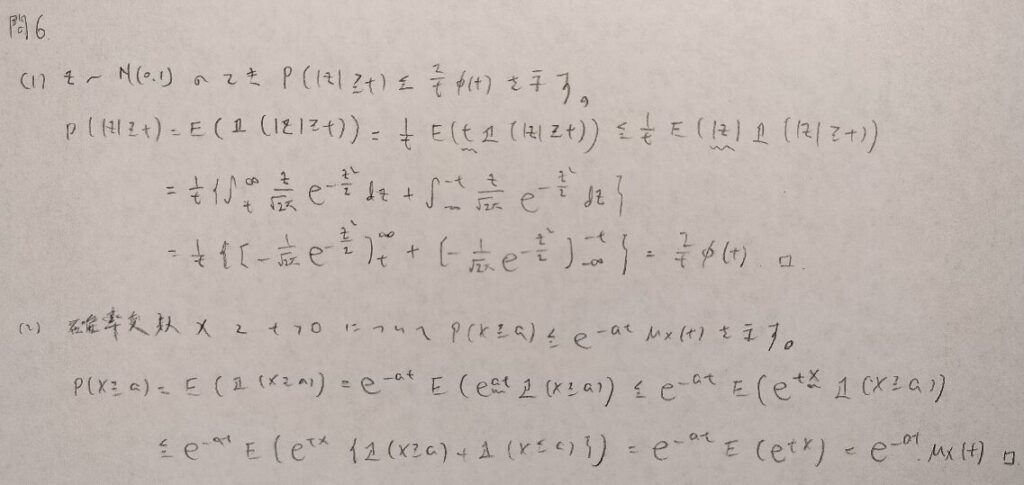
マルコフの不等式の証明などで用いる定義関数(恒等関数)を利用する問題です。よくあるパターンのため解法を覚えてしまいましょう!
現代数理統計学の基礎『第5章』問7
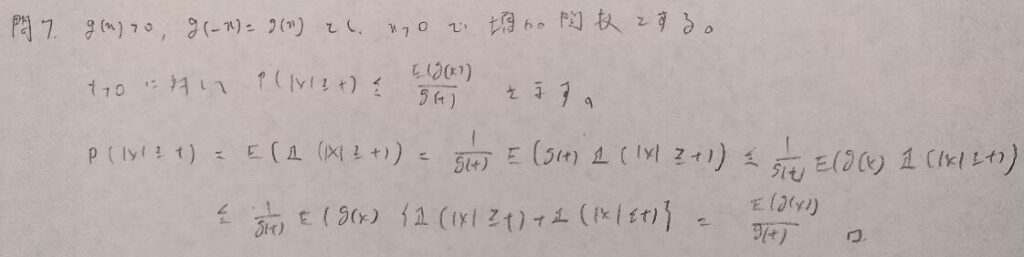
現代数理統計学の基礎『第5章』問8
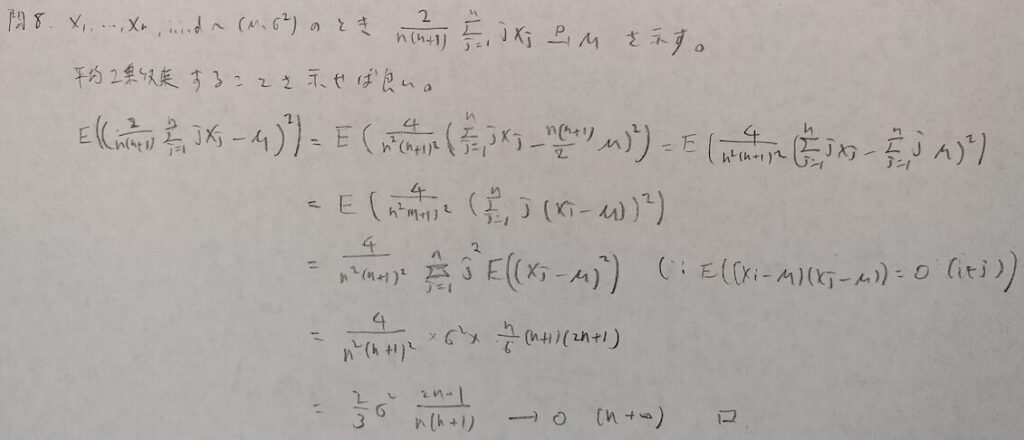
確率収束を示したい時は平均2乗収束を示せば良いので期待値計算を行う問題となります。
現代数理統計学の基礎『第5章』問9
難問です。(2)の3行目の式を思い浮かばなければ処理不能となります。
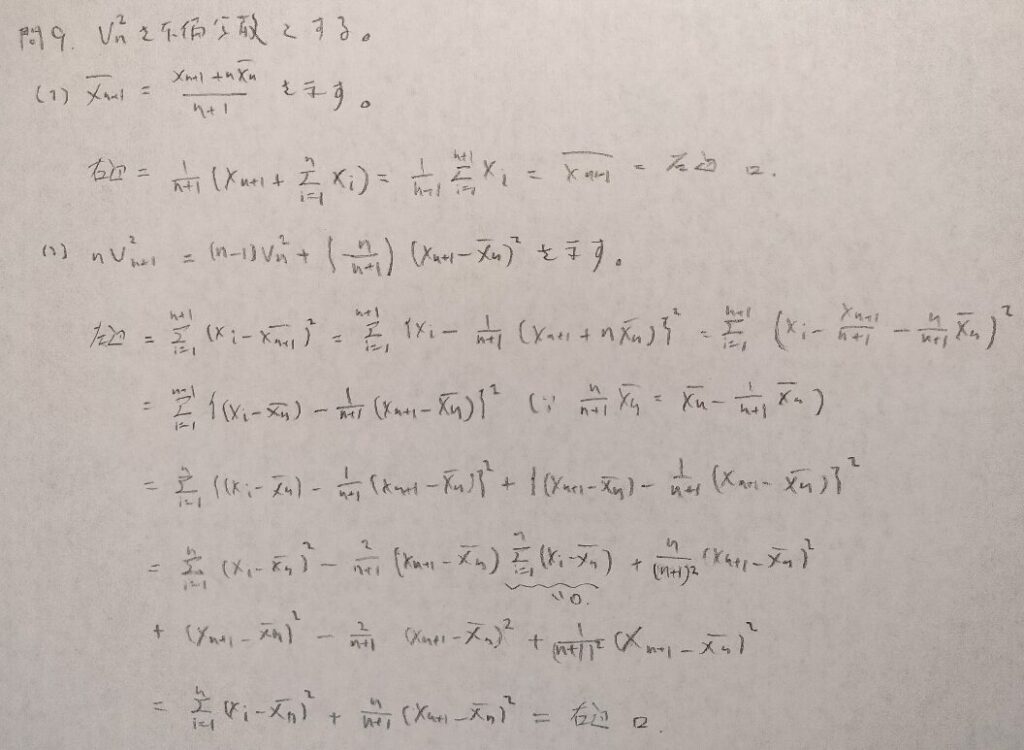
現代数理統計学の基礎『第5章』問10
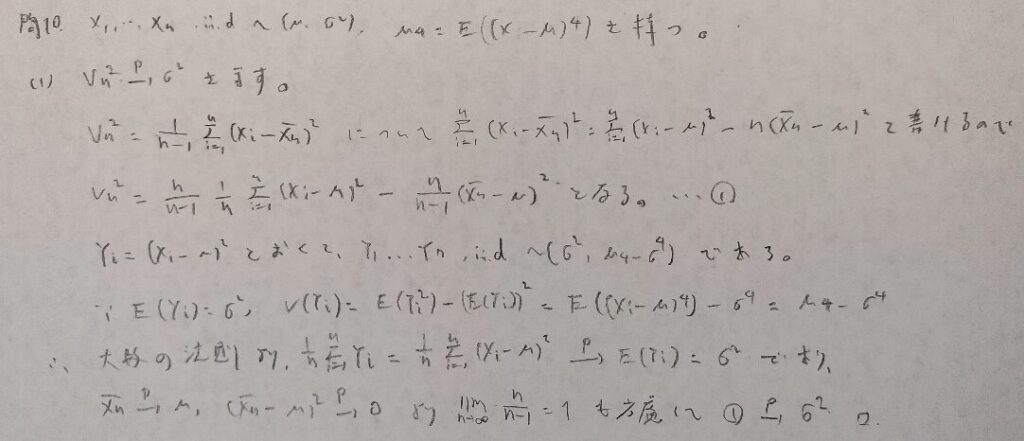
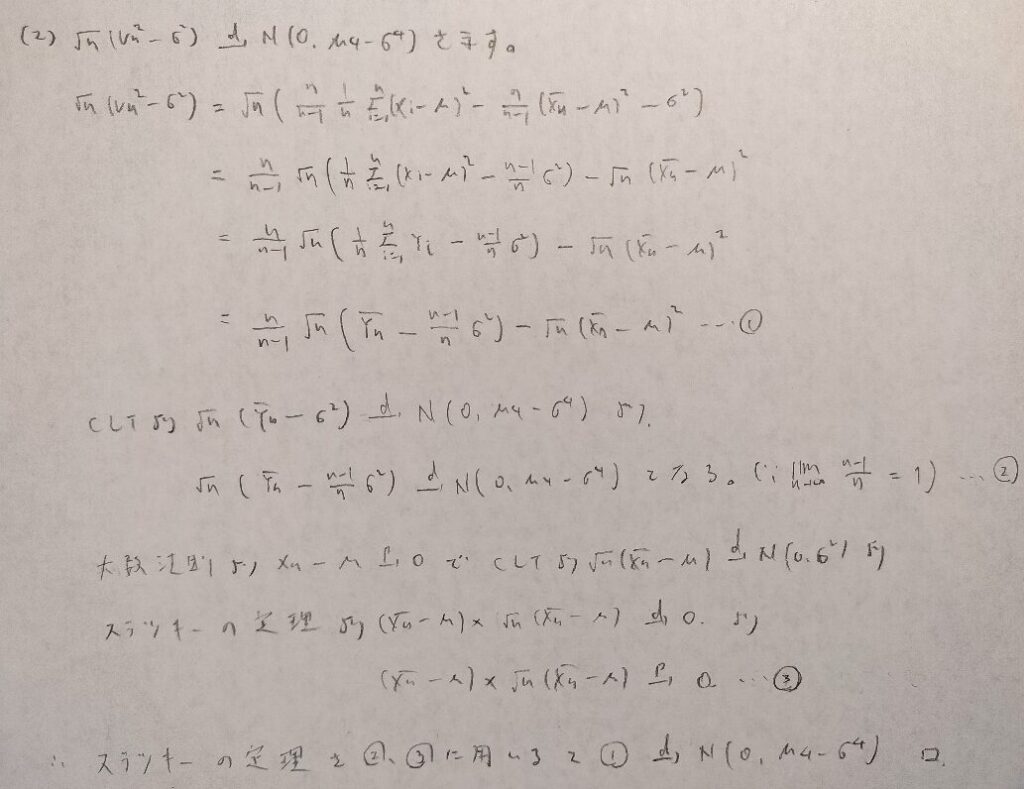
スラツキーの定理を用いる問題は基本的に難しい問題が多いです。
現代数理統計学の基礎『第5章』問11
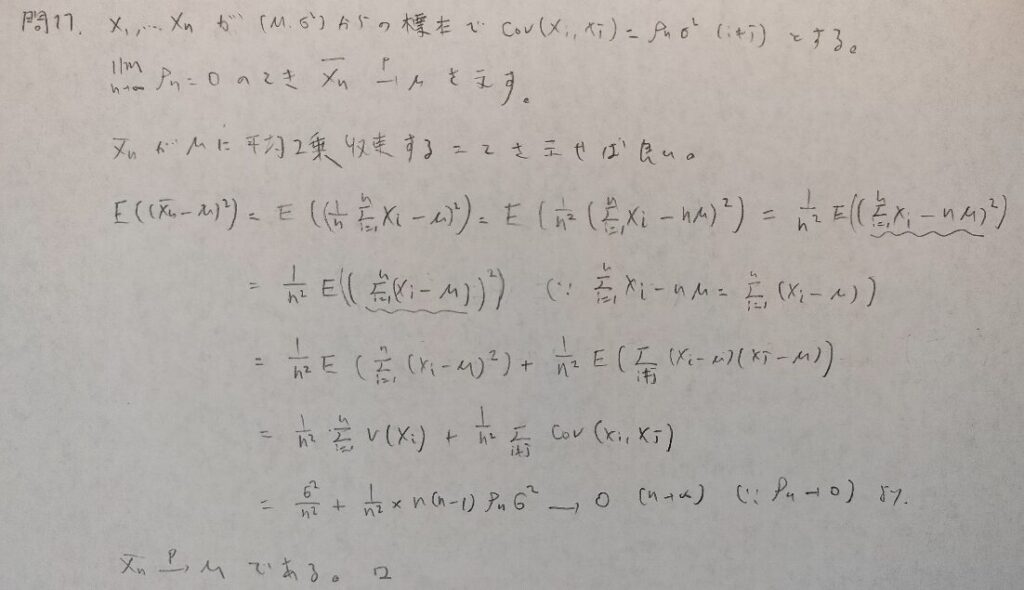
現代数理統計学の基礎『第5章』問12
第5章で最も難しい問題です。
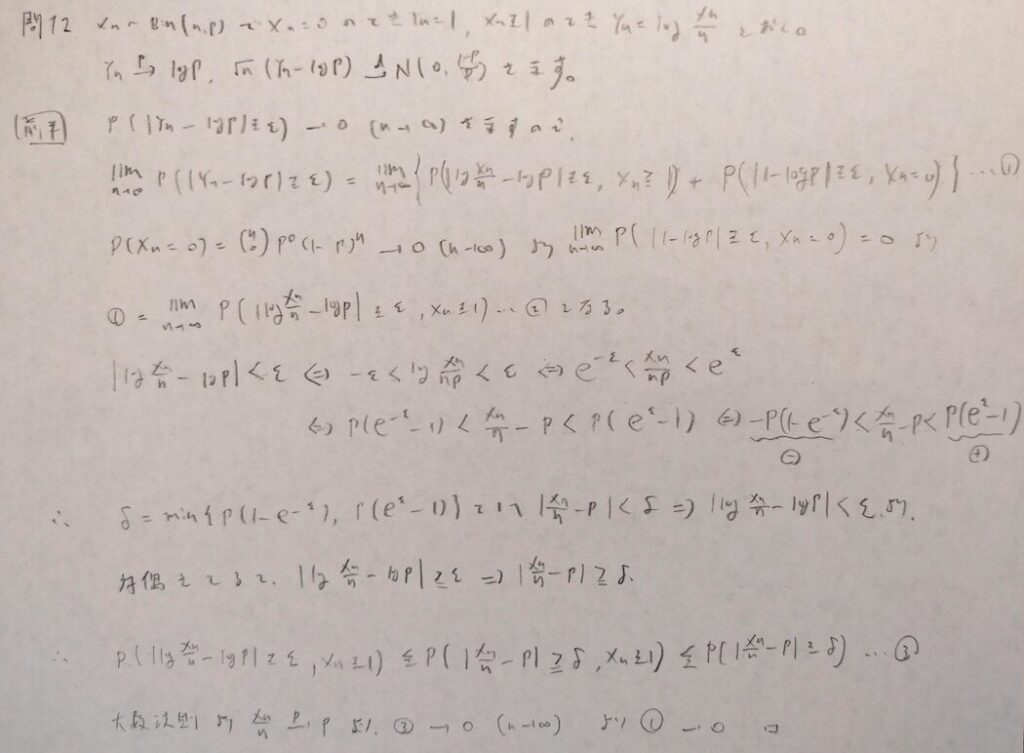
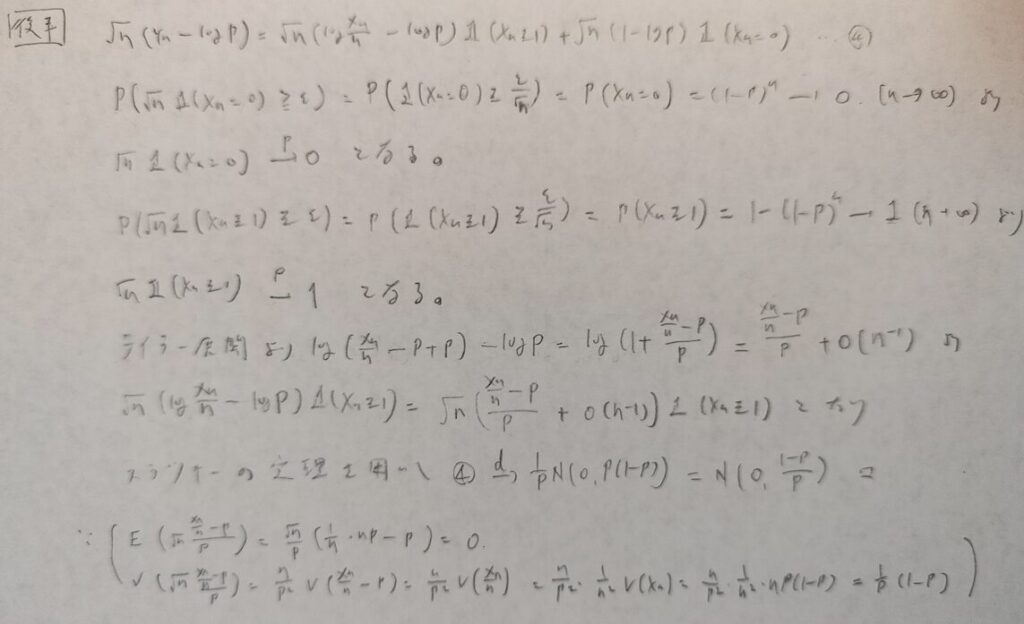
色々な要素がごちゃ混ぜになった難問でした。
この問題だけ突出して難易度が高いですよね笑
現代数理統計学の基礎『第5章』問13
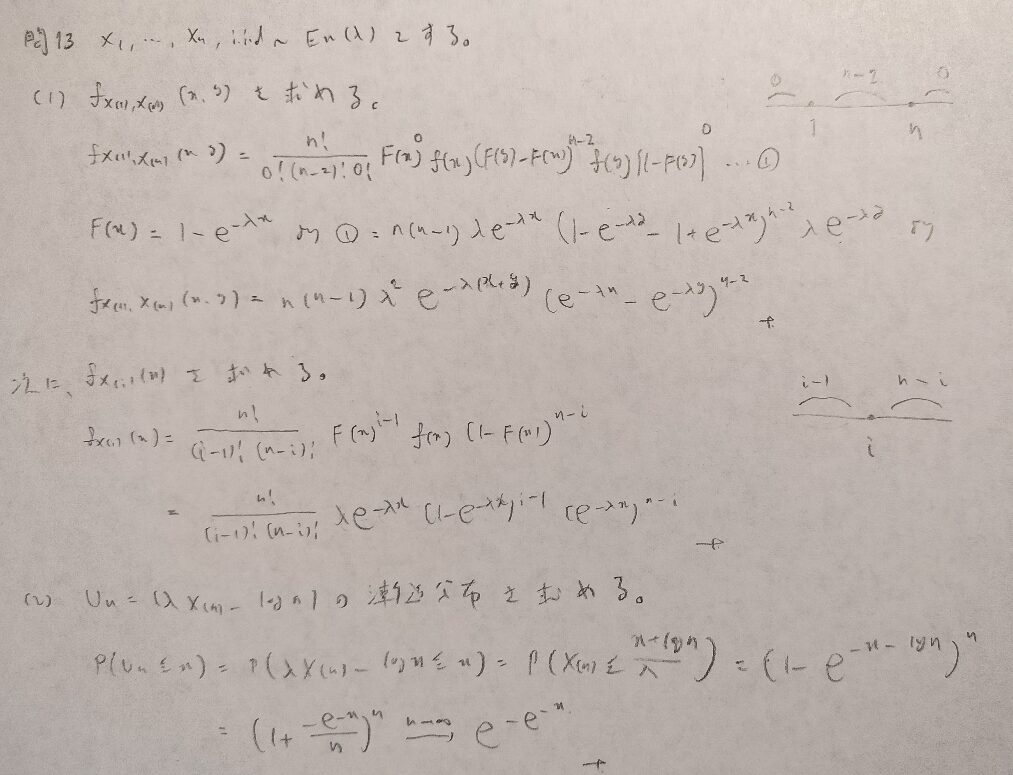
現代数理統計学の基礎『第5章』問14
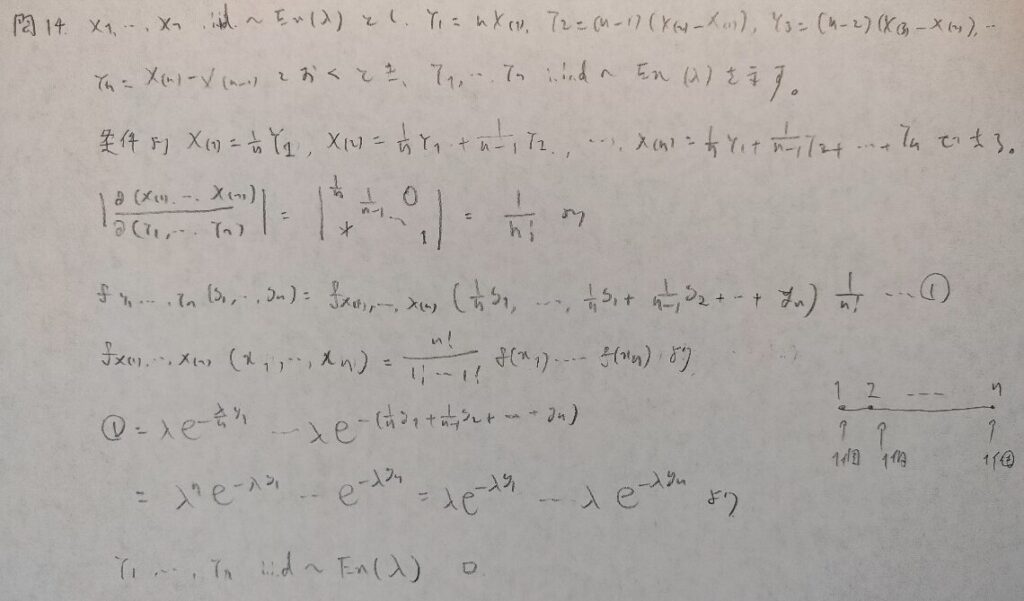
現代数理統計学の基礎『第5章』問15
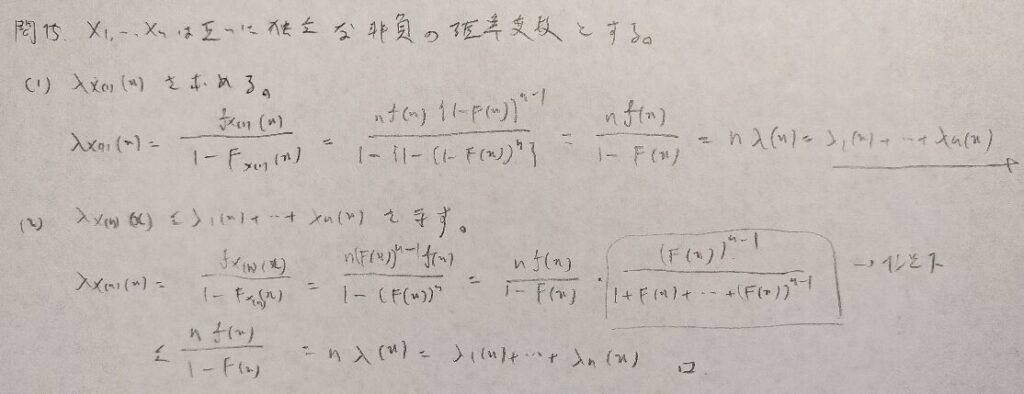
この問題はハザード関数を評価する問題です。(1)の最後の式や(2)の1以下の部分に気づくことが大事です。
現代数理統計学の基礎『第5章』問16
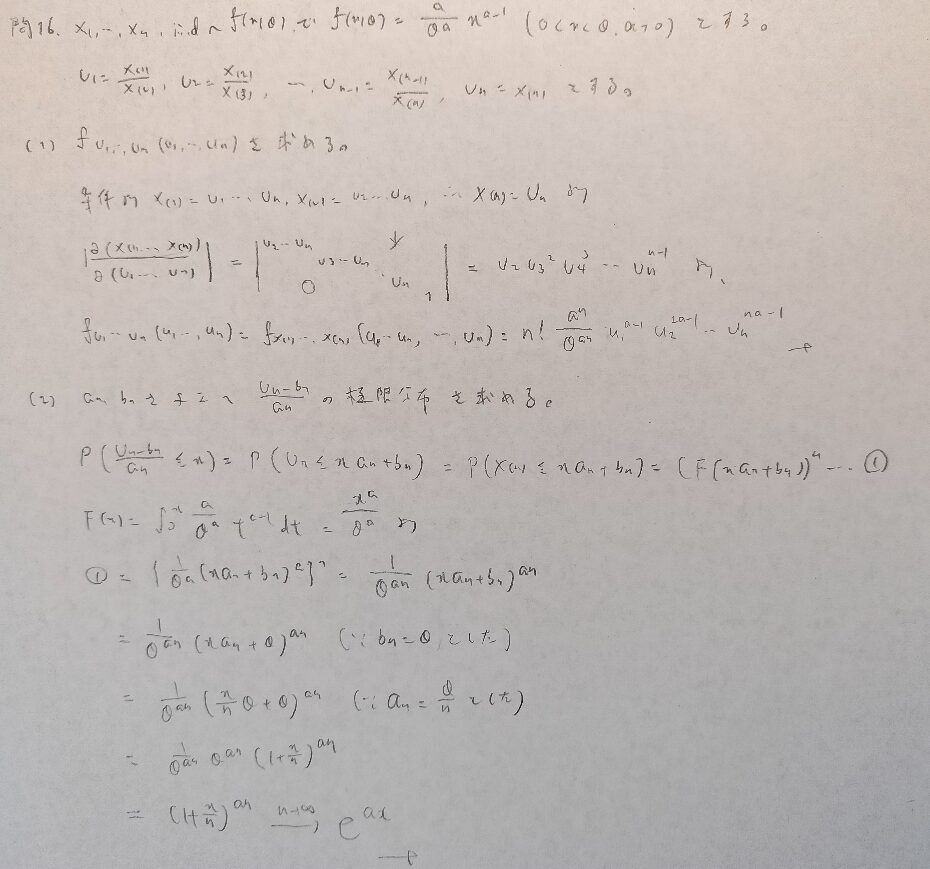
現代数理統計学の基礎『第5章』問17
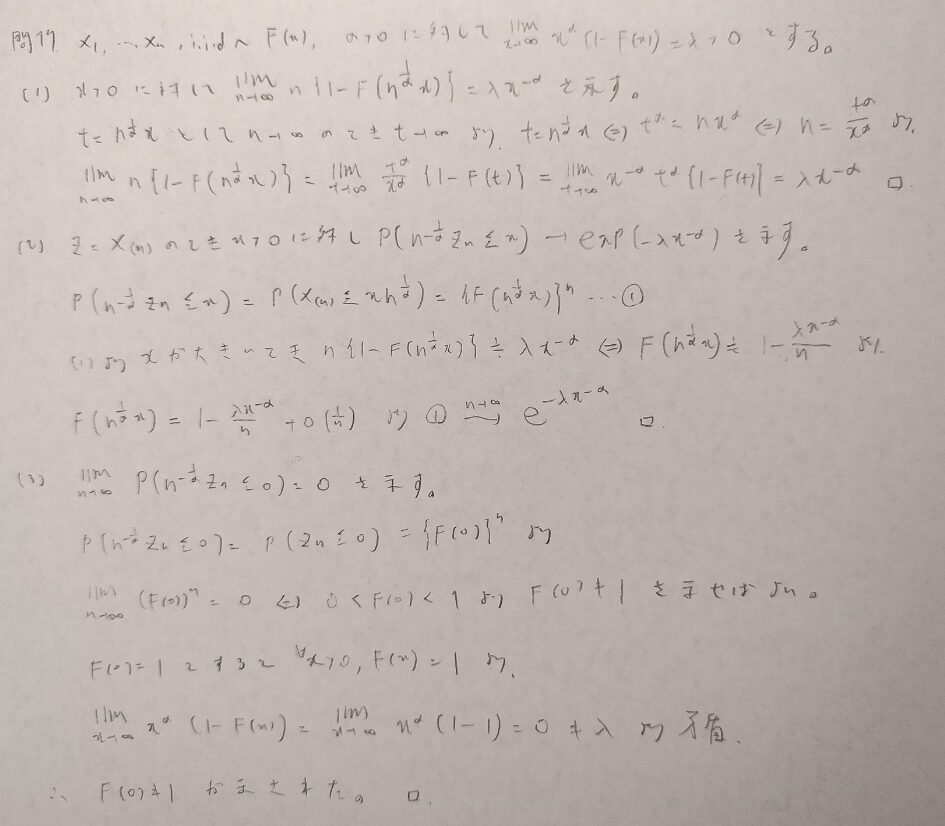
現代数理統計学の基礎『第5章』問18
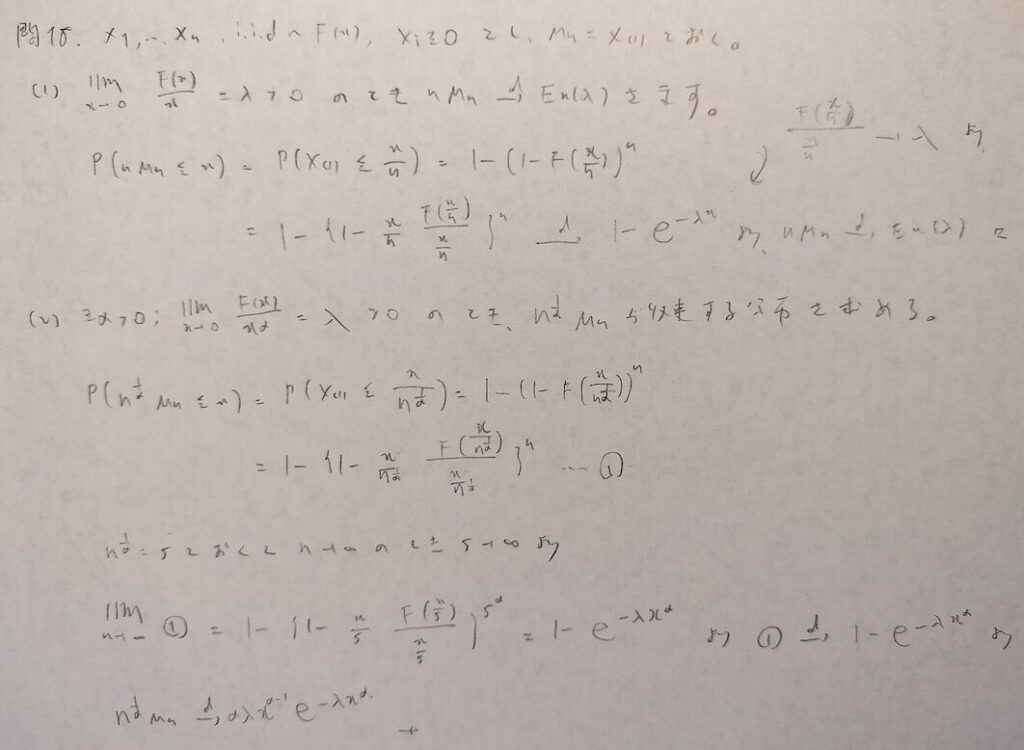
これでお終いですね!とにかく中盤が難しかったです!
お疲れ様でした。そうですね。終盤はすんなり解ける問題が多かったのではないでしょうか。とにかく『現代数理統計学の基礎』は名問が多いですね!
次回の第6章も一緒に頑張りましょう!




