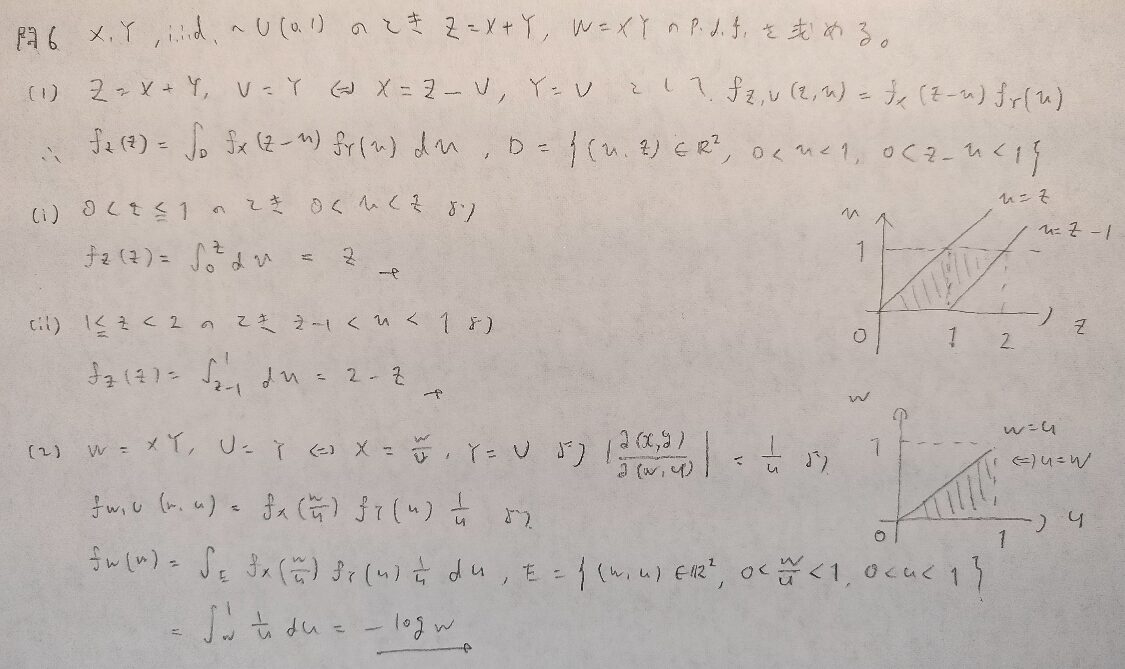統計検定1級の合格者のバイブルである『現代数理統計学の基礎』の多次元確率分布に関する内容になります。
当然ながら多変量の確率変数の問題は前回の第3章の内容よりも難易度が上がります。
変数変換でヤコビアンを用いる問題が増えることによって計算量が増えてしまうことも難点ですね。
その通りです。そのため第3章にはなかった例題が多数用意されています。本記事では例題の解説も行いますのでご安心ください!
しかし難しい問題にもポイントが必ずあります。本記事では問題ごとにポイントを提示していくことにより、問題内容を理解できるような構成になります。統計検定1級合格を目指してともに頑張りましょう!
現代数理統計学の基礎『第4章』例題4.1

離散量の確率変数では確率密度関数ではなく確率関数を考えます。
現代数理統計学の基礎『第4章』例題4.2

今回は確率密度関数の問題ですね!
現代数理統計学の基礎『第4章』例題4.4
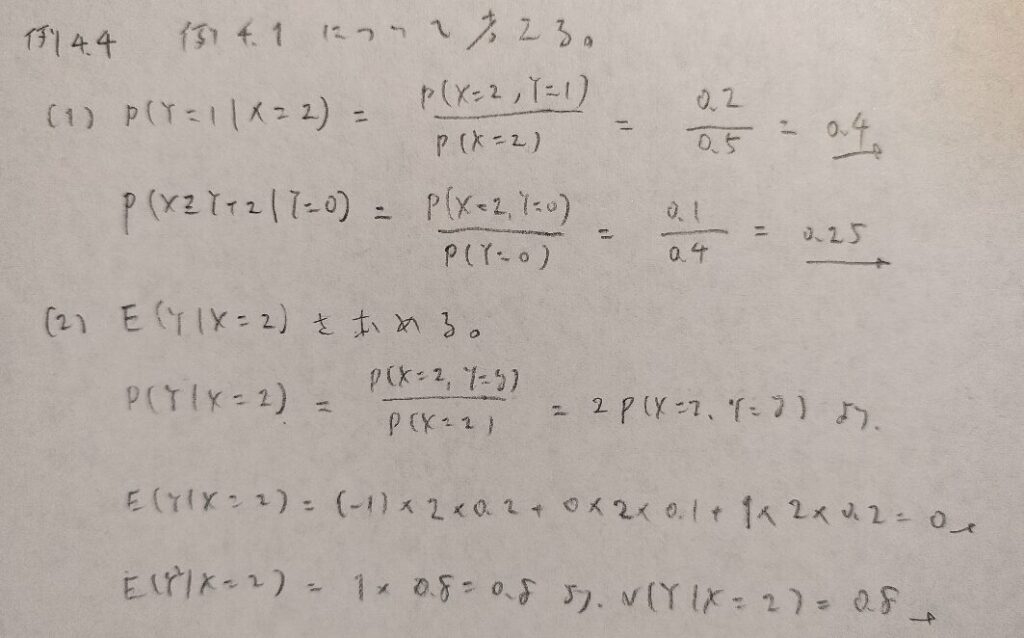
離散変数バージョンの問題です!
現代数理統計学の基礎『第4章』例題4.6
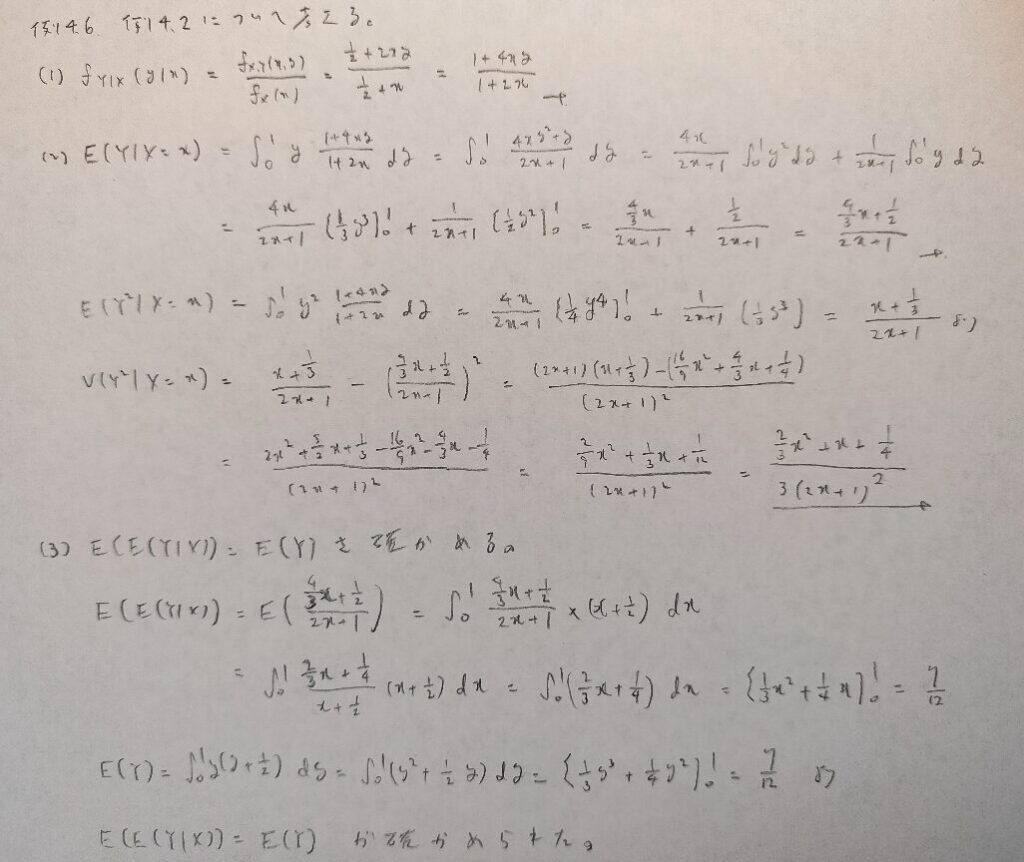
連続変数のバージョンで前問よりも聞かれている内容が多くなっています。
現代数理統計学の基礎『第4章』例題4.8
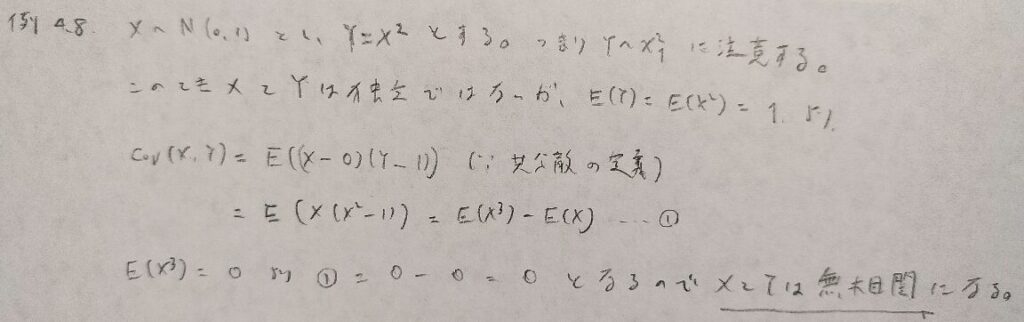
独立ならば無相関ですが一般的に逆は成立しませんが、正規分布の場合は独立と無相関は同値になります。
現代数理統計学の基礎『第4章』例題4.9

条件付き分布の定義を思い出せばすぐに解ける問題です!
現代数理統計学の基礎『第4章』例題4.10
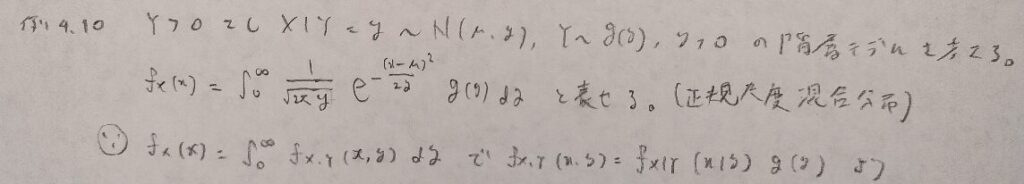
難しそうな名前ですが構造を捉えれば条件付き分布と本質的には同じ問題です。
現代数理統計学の基礎『第4章』例題4.12
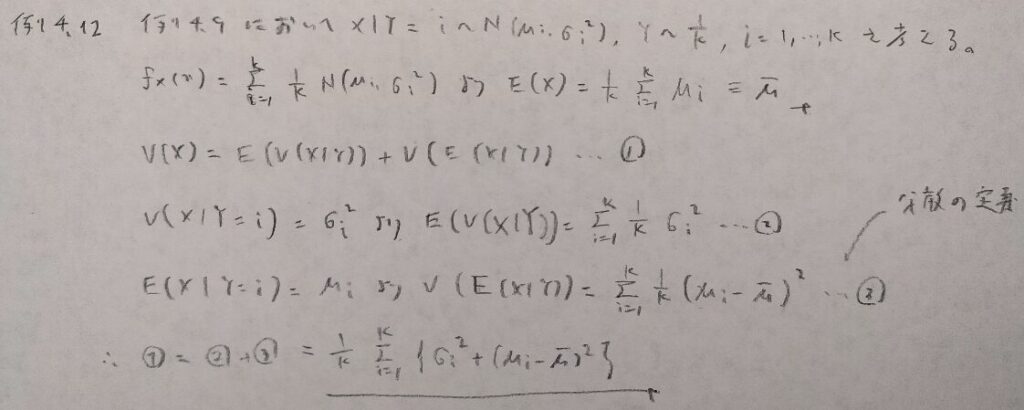
統計検定1級でもアクチュアリー数学でも全分散の公式は頻出ですので覚えておきましょう!
現代数理統計学の基礎『第4章』例題4.13
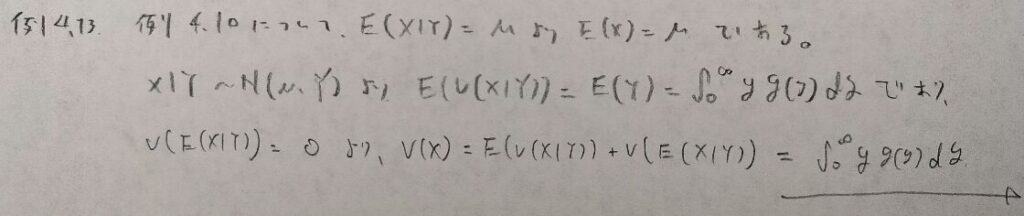
現代数理統計学の基礎『第4章』例題4.14
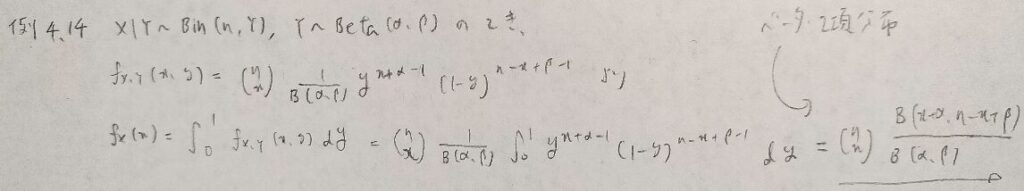
現代数理統計学の基礎『第4章』例題4.15
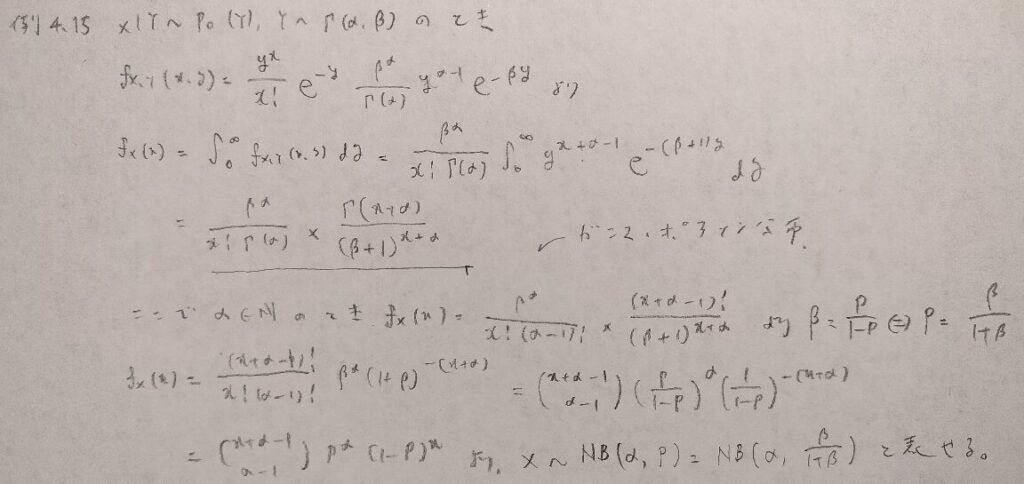
難問です。負の二項分布を導出する部分でpに相当する部分を技巧的に算出しています。
現代数理統計学の基礎『第4章』例題4.16
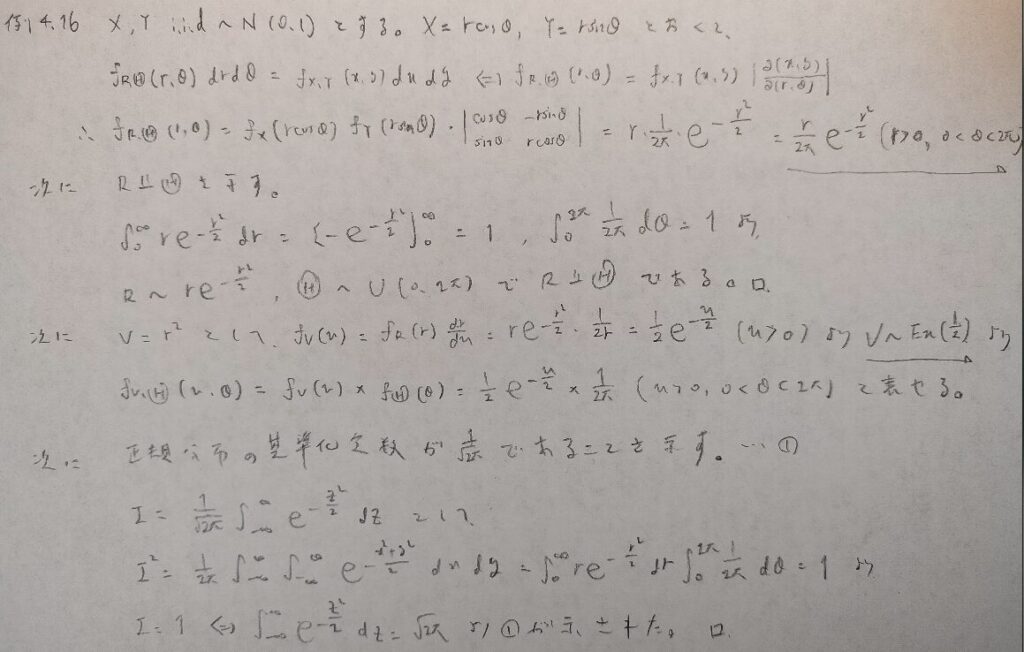
1変数の場合と違い2変数の変換の場合はヤコビアンに絶対値をつけましょう!
現代数理統計学の基礎『第4章』例題4.17
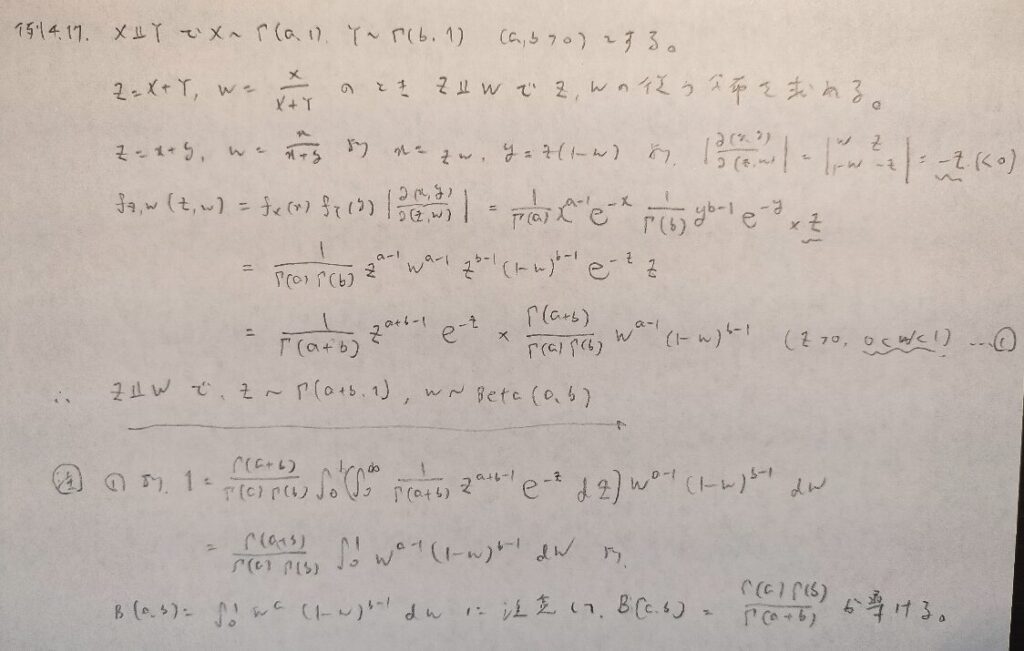
最後のB(a,b)の式でwの指数はa-1の間違いです。お読みの際はご訂正をお願いいたします。
現代数理統計学の基礎『第4章』例題4.18

アクチュアリー数学で頻出です!
現代数理統計学の基礎『第4章』例題4.19
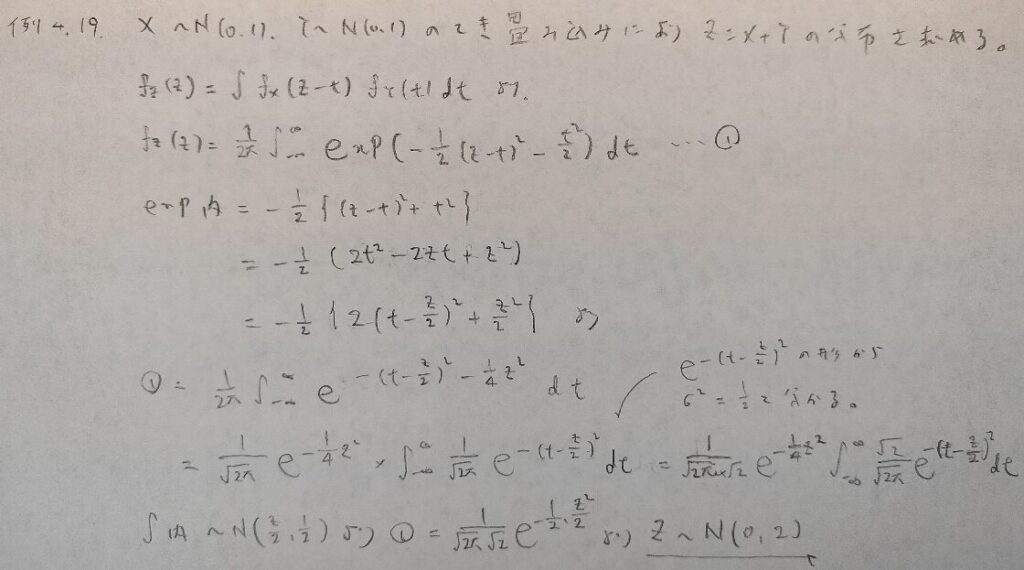
正規分布の形から期待値と分散を読み取れるようにしましょう!
現代数理統計学の基礎『第4章』問1
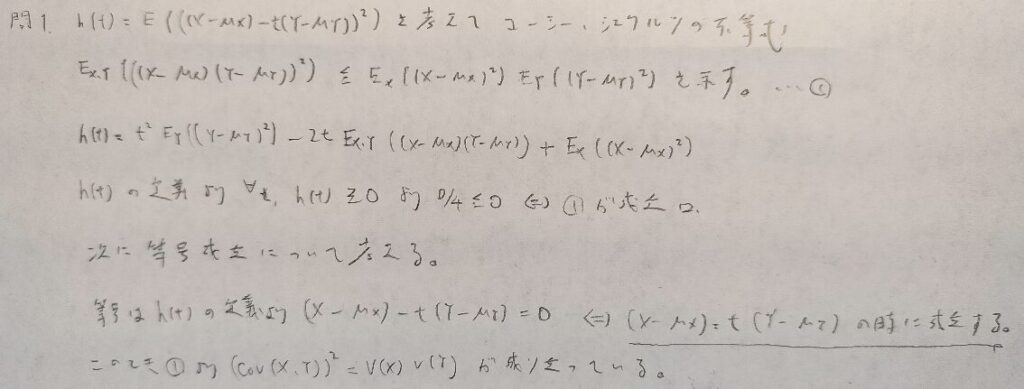
現代数理統計学の基礎『第4章』問2

かなり特殊な問題です。本問の類題は本書以外には見当たりません。素晴らしい問題です!
現代数理統計学の基礎『第4章』問3
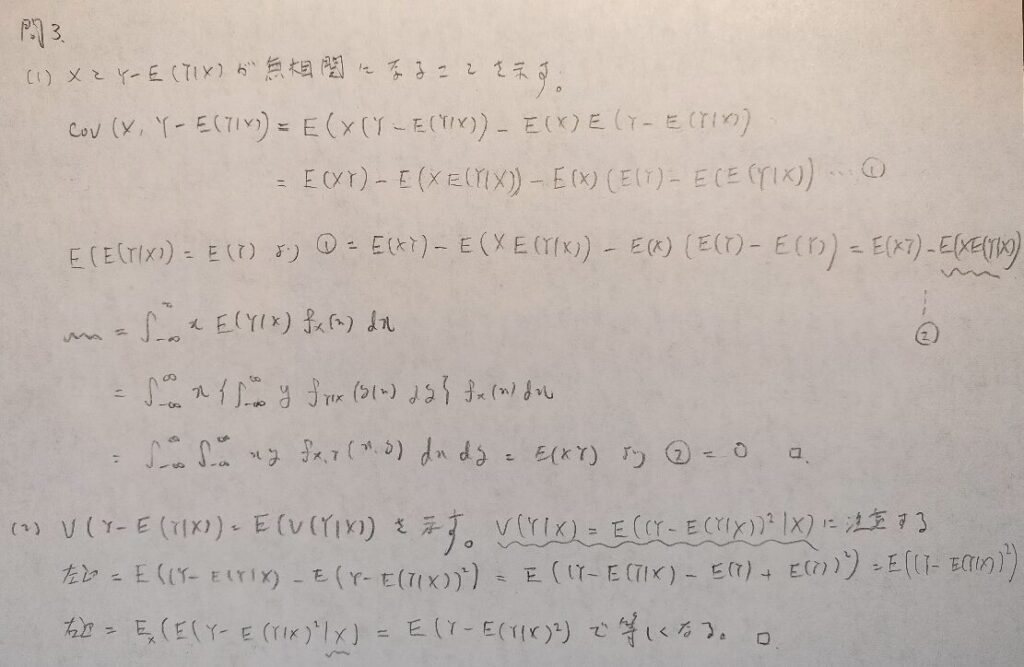
難問です。1つ1つの式変形をしっかりと追っていきましょう!
現代数理統計学の基礎『第4章』問4
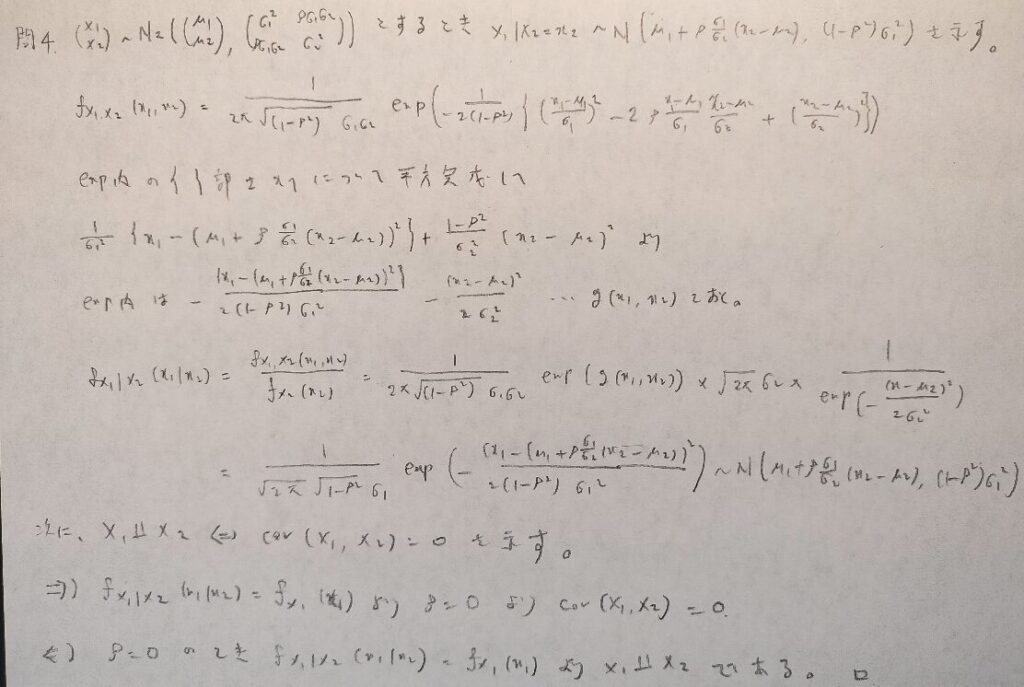
多変量正規分布に関する性質の証明問題です。
現代数理統計学の基礎『第4章』問5
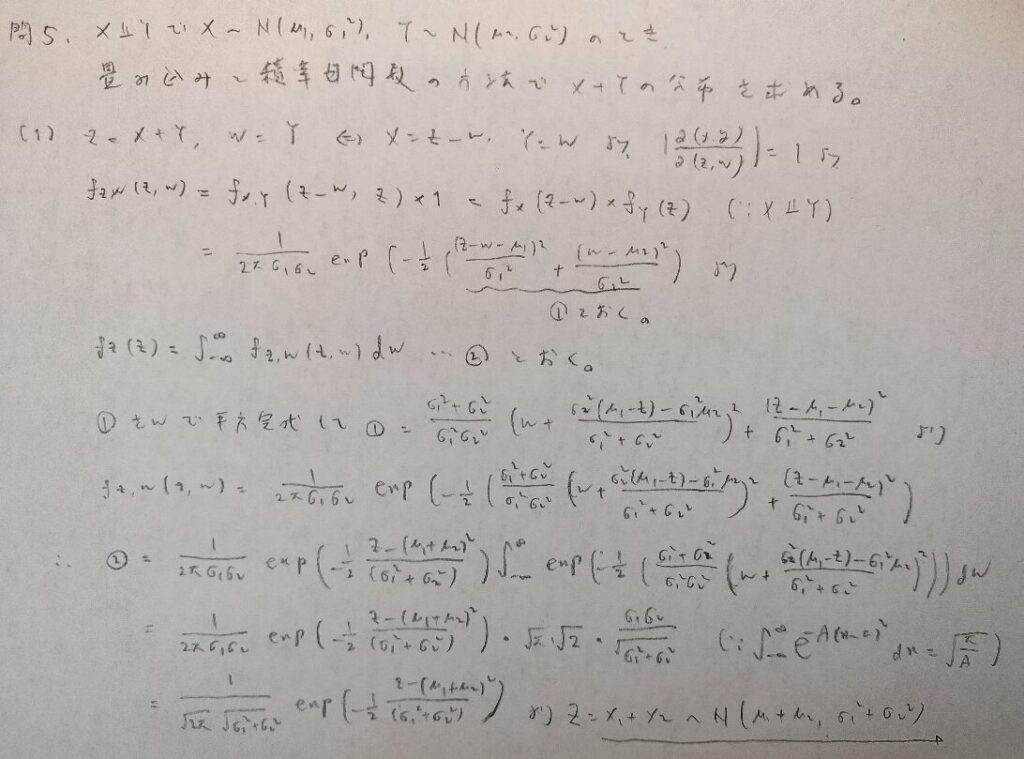
積率母関数を使えない場合は計算が厄介になることがお分かりいただけたと思います笑
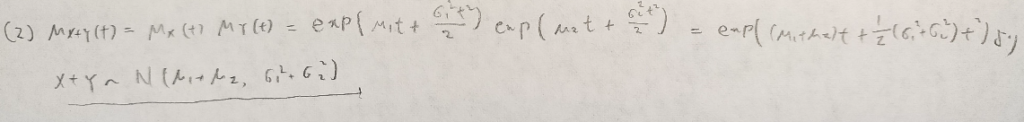
やはり積率母関数を用いた証明は鮮やかですね!
現代数理統計学の基礎『第4章』問6
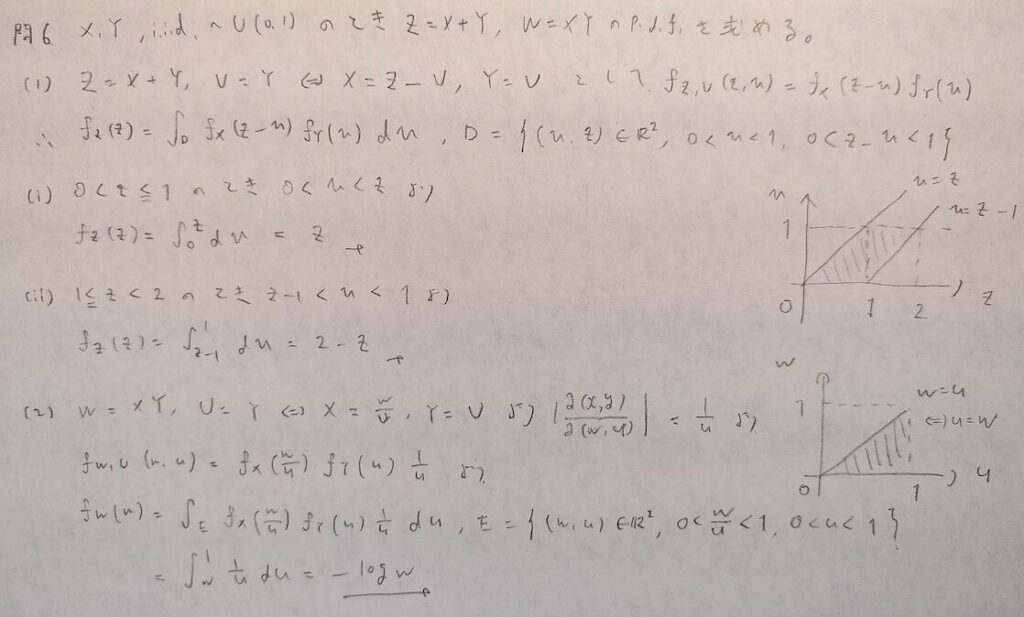
こういった標準問題に慣れることが大事です!
現代数理統計学の基礎『第4章』問7
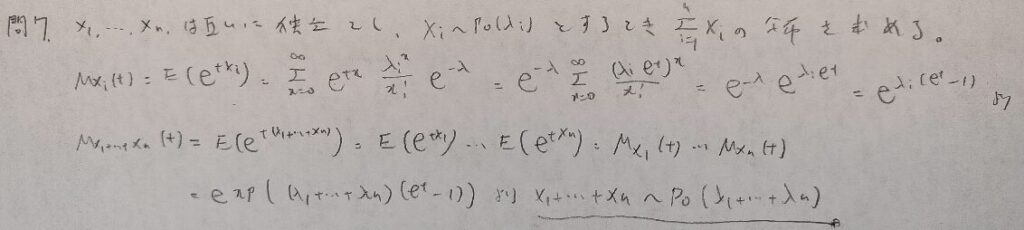
現代数理統計学の基礎『第4章』問8
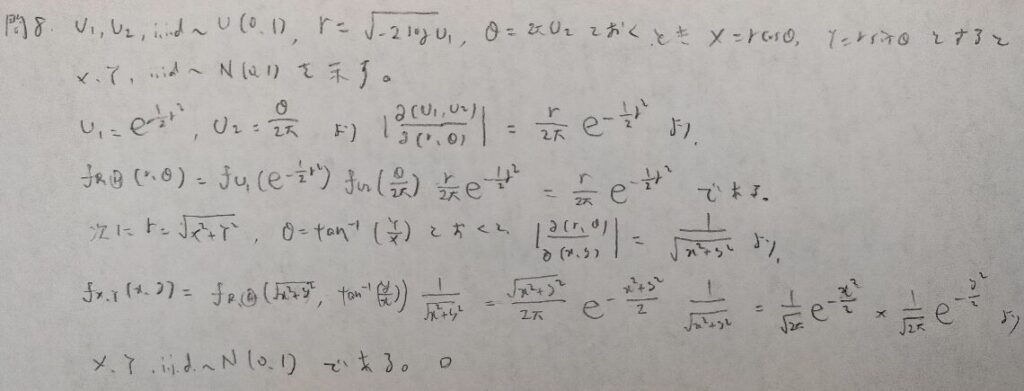
標準一様分布から標準正規分布を作るための変換です!
現代数理統計学の基礎『第4章』問9
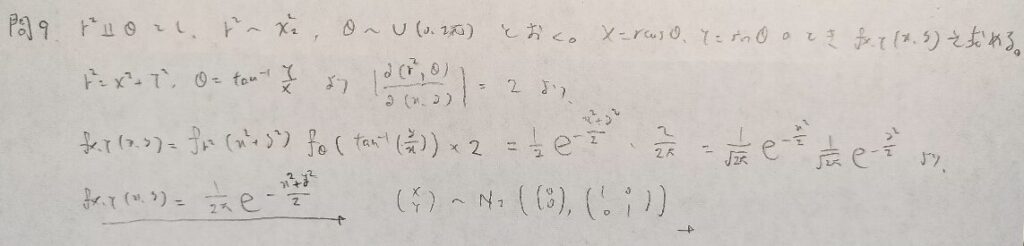
現代数理統計学の基礎『第4章』問10
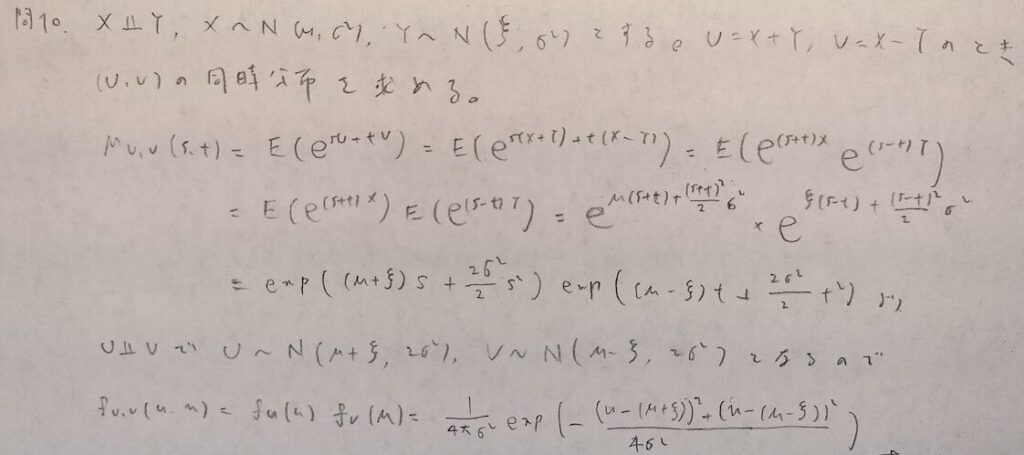
変わった問題ですが良問です!積率母関数の意外な使い方に関する内容です。
現代数理統計学の基礎『第4章』問11
難問です。ヤコビアンを用いる場合は1対1対応になることを確認してから用いましょう!
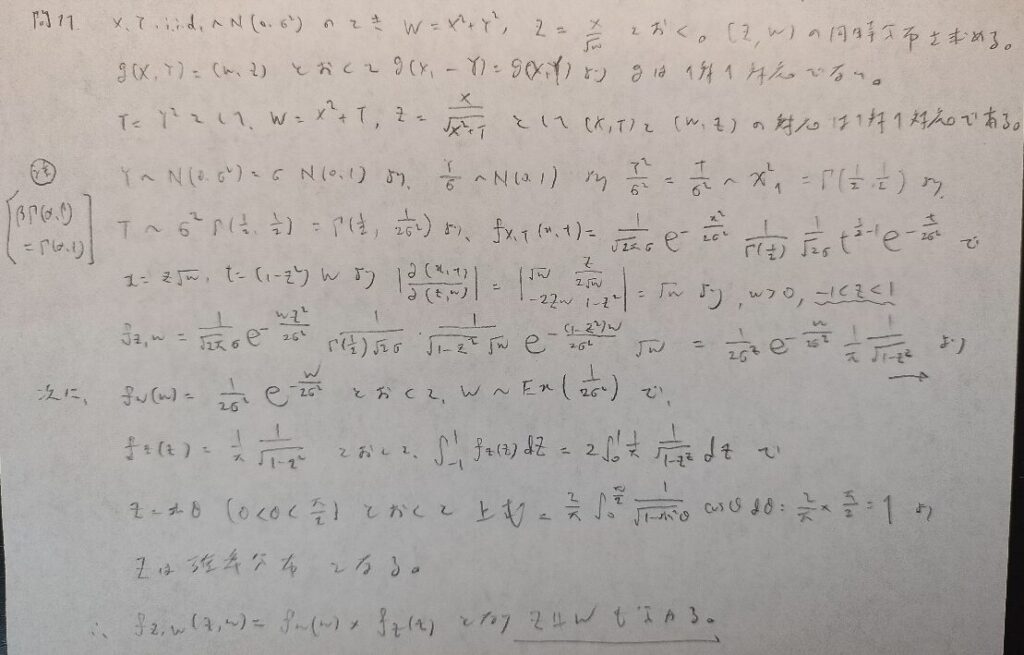
この後に数題登場する周辺分布の独立性の問題です。
左上に書いてあるガンマ分布の公式は初めて見ました!
アクチュアリー数学の神本で有名な藤田先生の『弱点克服 大学生の確率・統計』にて詳しく紹介されています!
現代数理統計学の基礎『第4章』問12
第4章で最も難しい問題です。

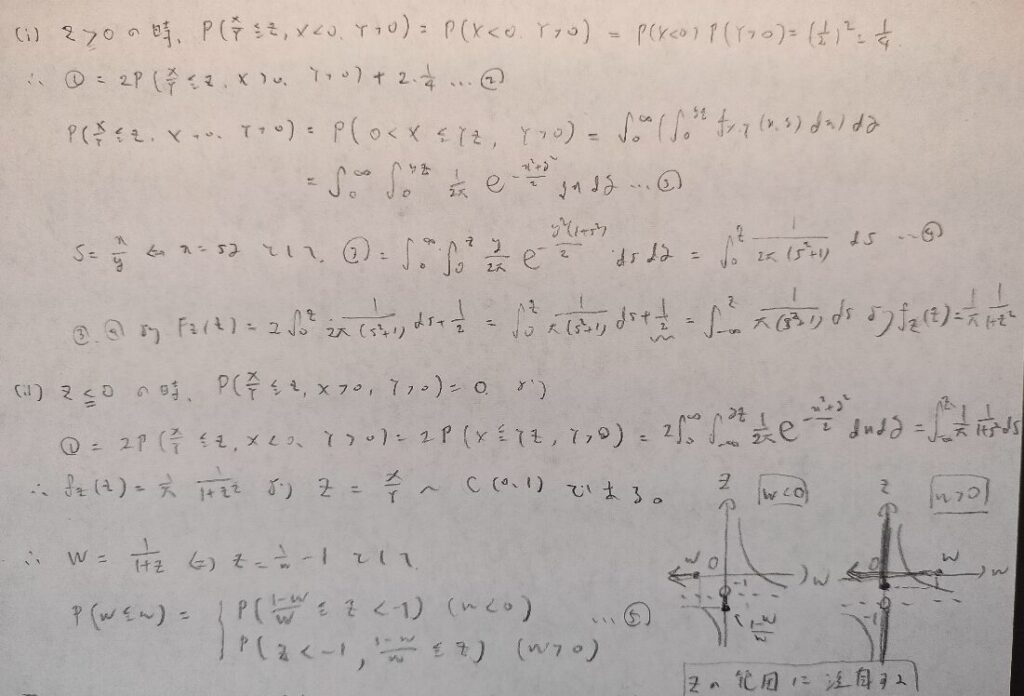
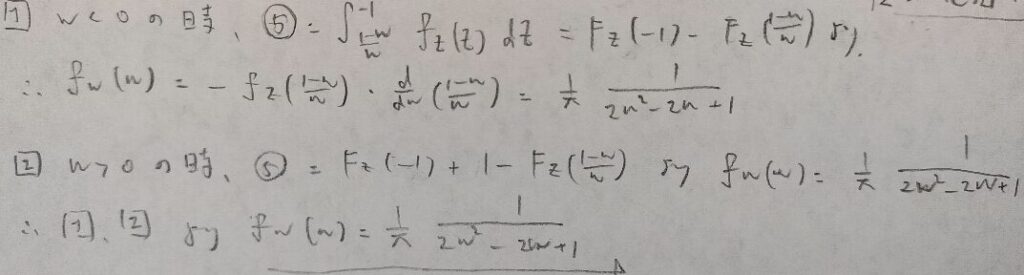

非常にボリューミーな問題でしたね。
現代数理統計学の基礎『第4章』問13
難問です。確率密度関数を求めるのに分布関数のような式を用いる不思議な問題です。
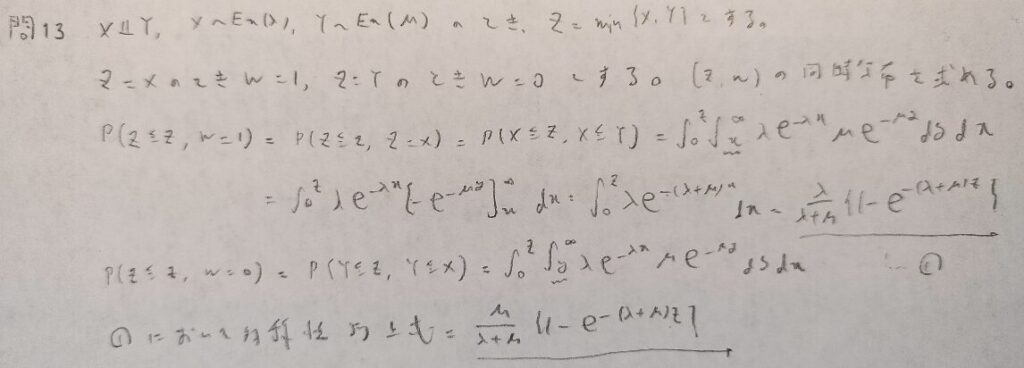
現代数理統計学の基礎『第4章』問14
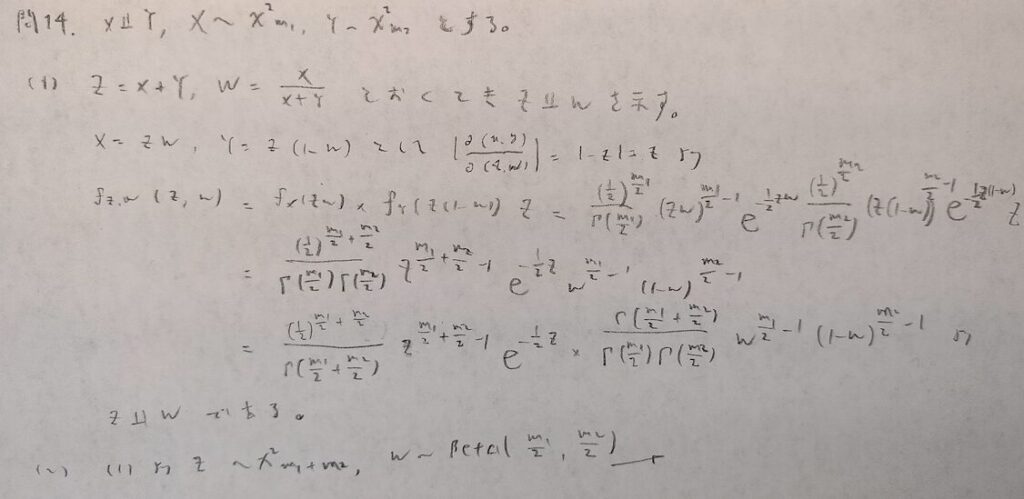
ガンマ分布とベータ分布間の関係式も似たものがあります。こちらをご確認ください。
現代数理統計学の基礎『第4章』問15
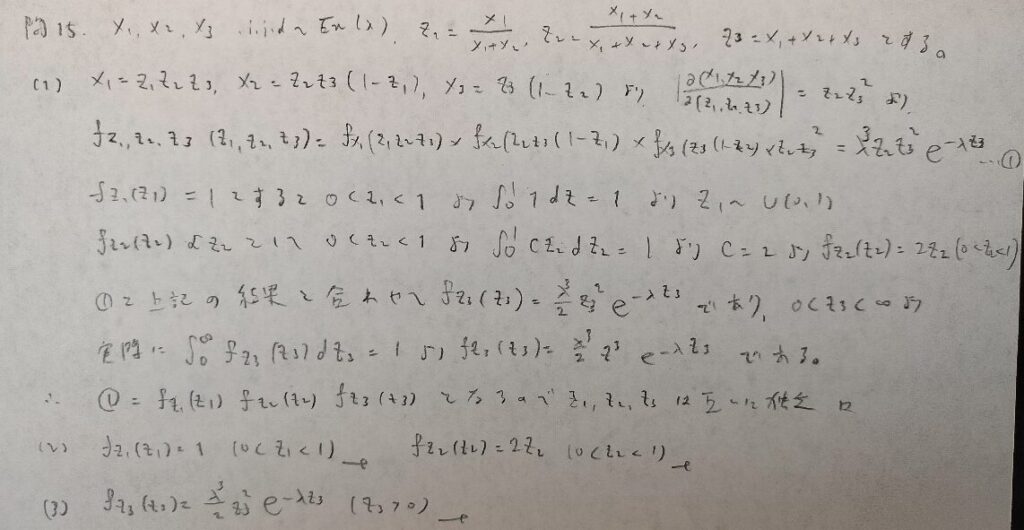
現代数理統計学の基礎『第4章』問16
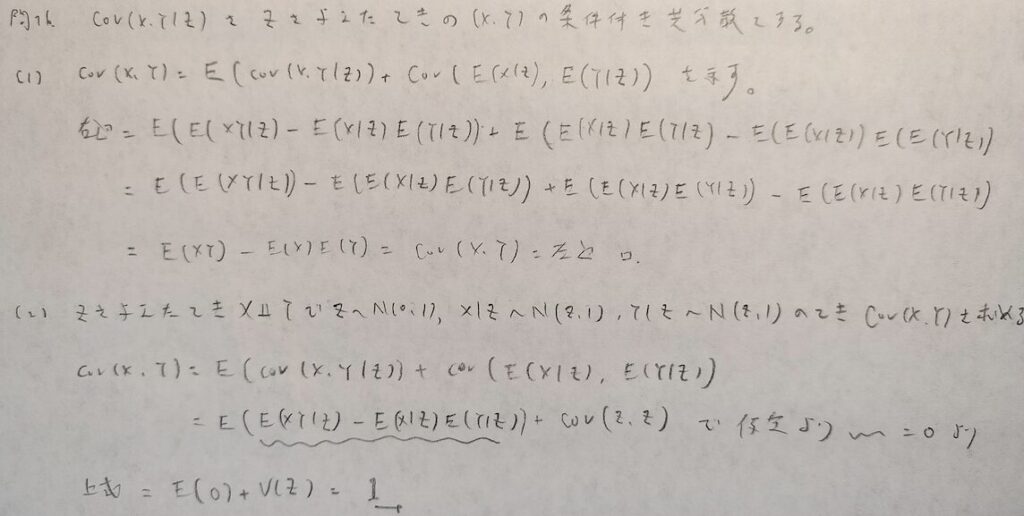
なかなか珍しいタイプの問題です。統計検定1級に出題されるかも知れません。
現代数理統計学の基礎『第4章』問17
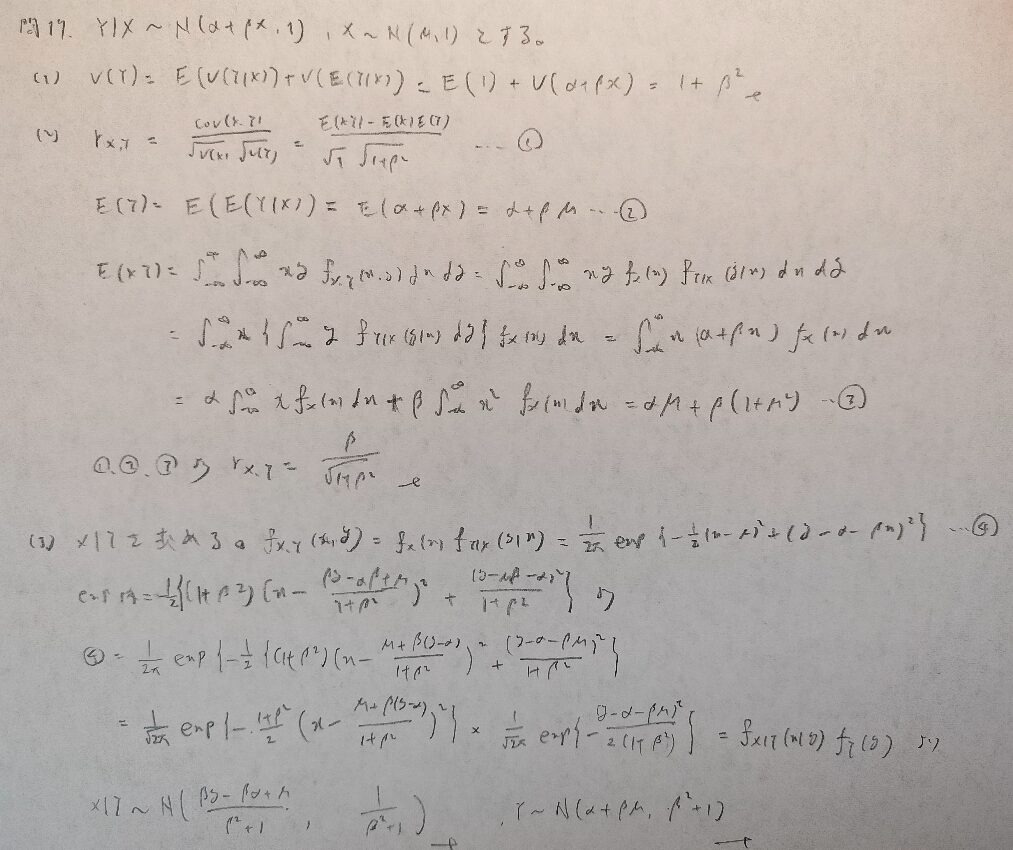
現代数理統計学の基礎『第4章』問18
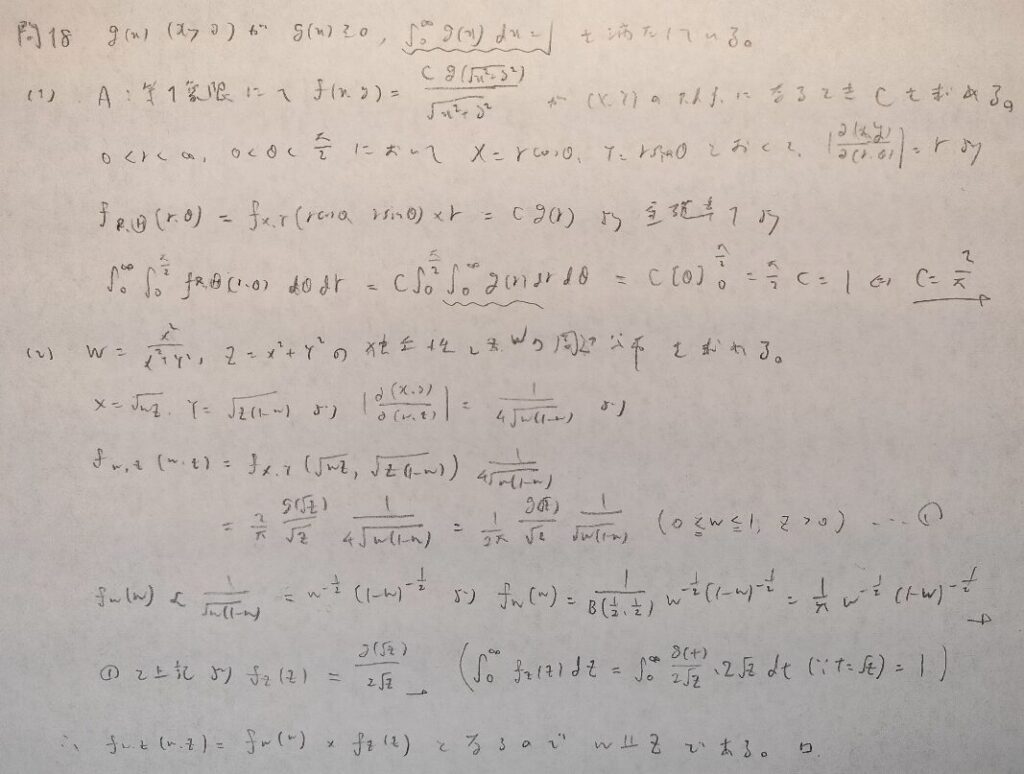
相似記号を用いると式変形が楽になります!
現代数理統計学の基礎『第4章』問19
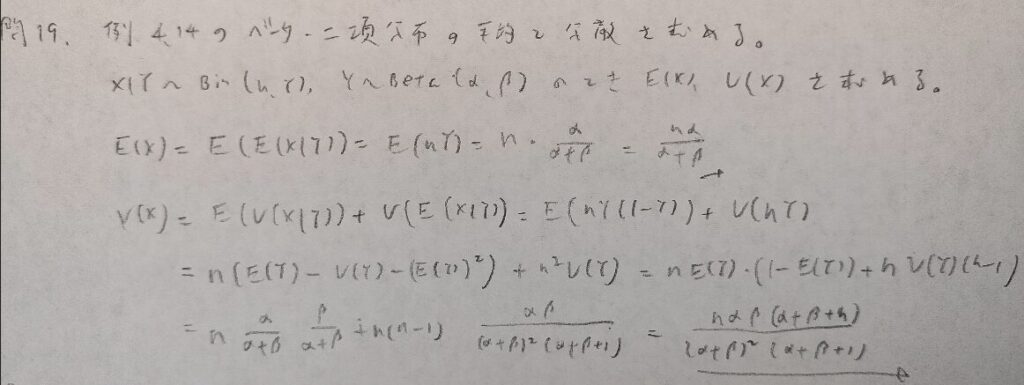
現代数理統計学の基礎『第4章』問20
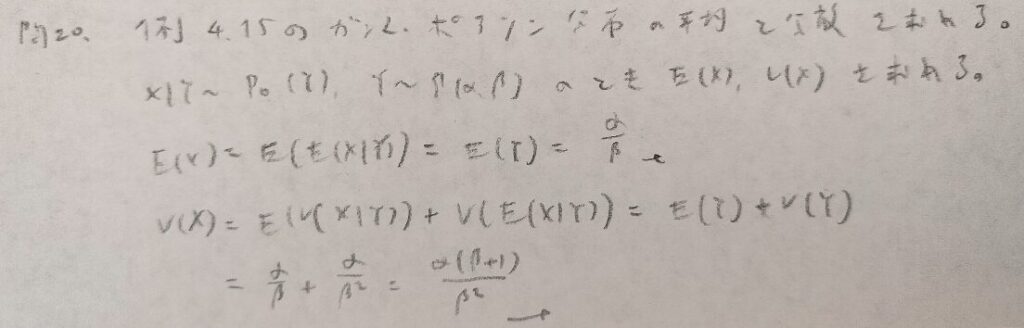
現代数理統計学の基礎『第4章』問21
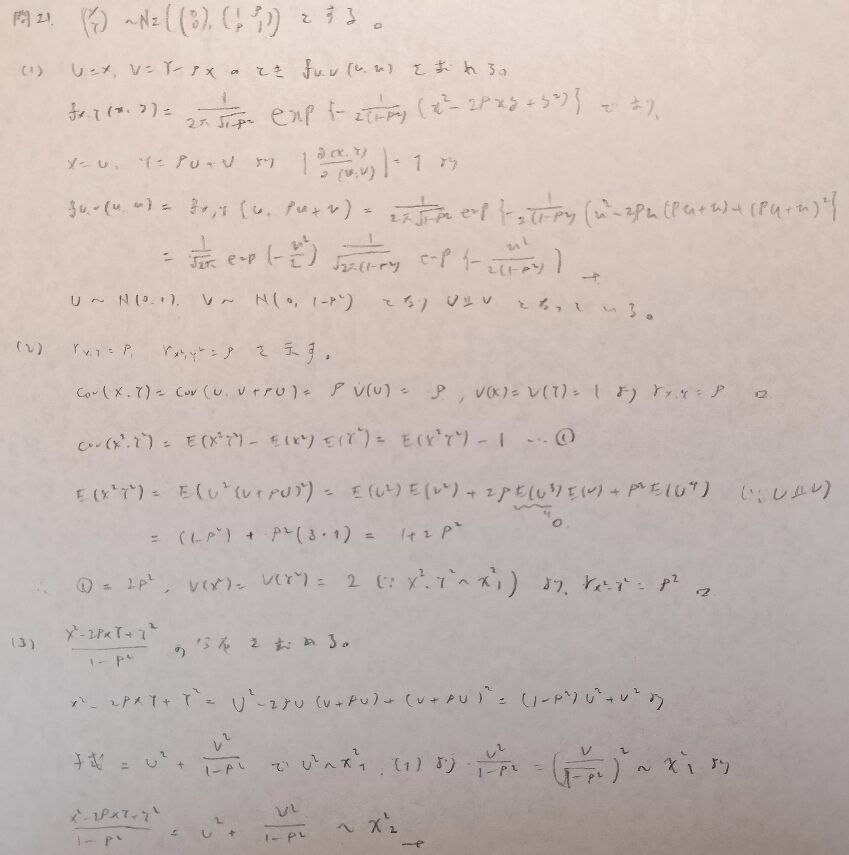
現代数理統計学の基礎『第4章』問22
難問です。記述量も多いです。積分計算の式変形で特殊な方法を用いています。
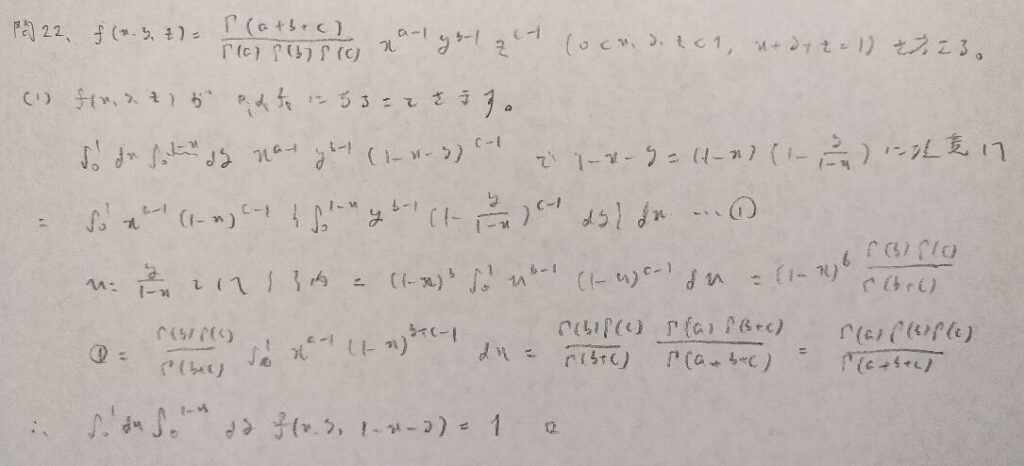
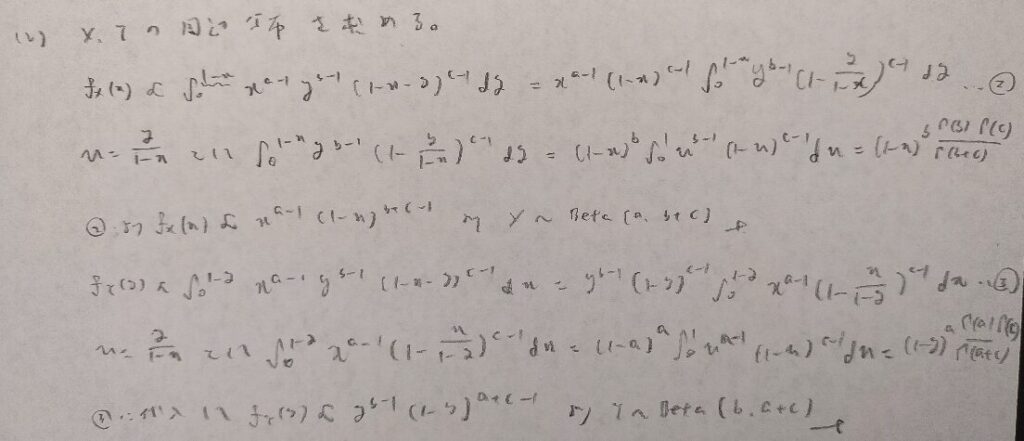
この結果はアクチュアリー数学で頻出です!
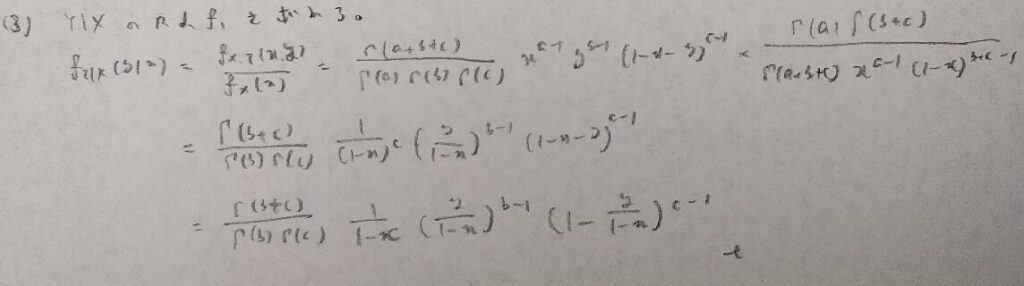
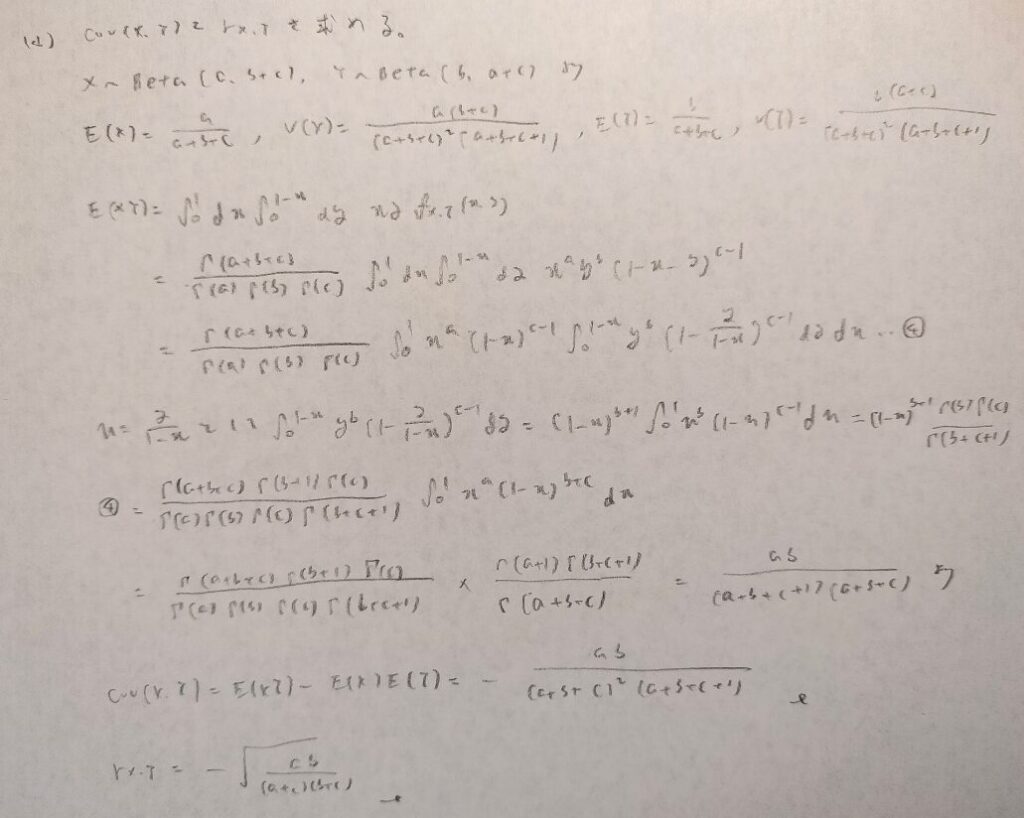
現代数理統計学の基礎『第4章』問23
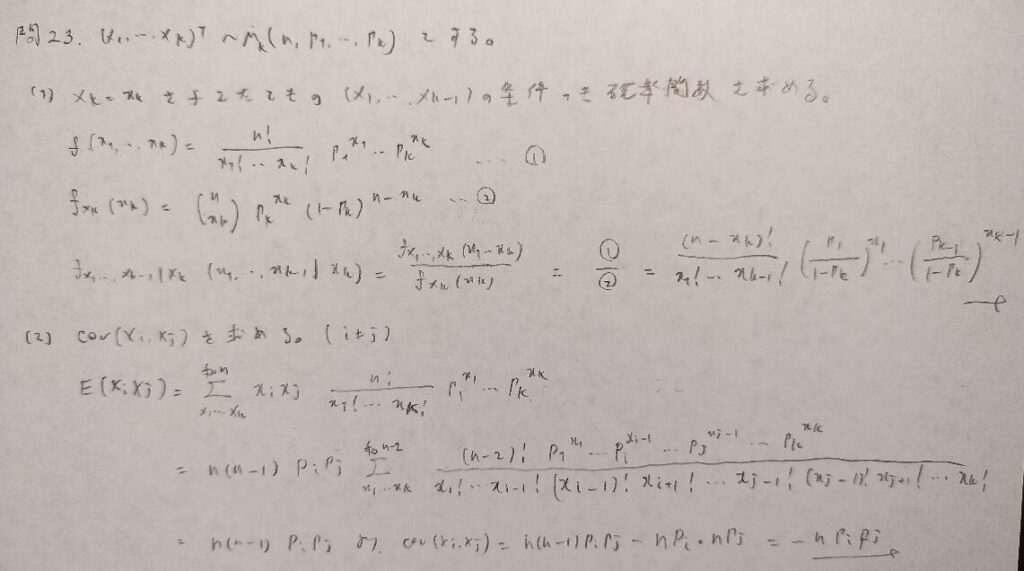
現代数理統計学の基礎『第4章』問24
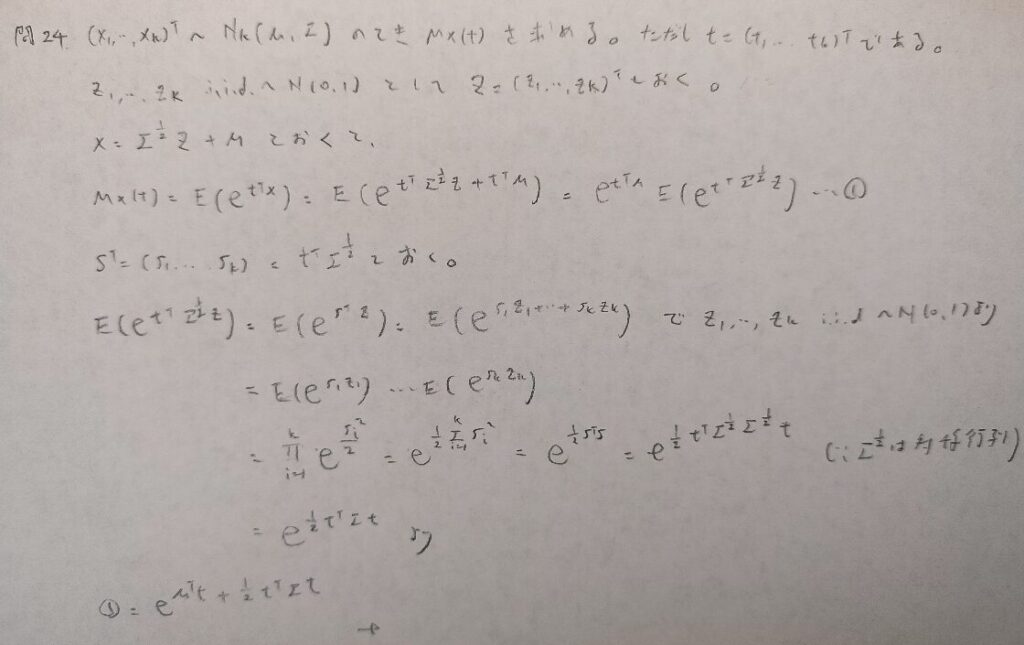
よく見ると1変量の場合とそっくりなことに気づきましたか?
以上で『現代数理統計学の基礎』の第4章は終了です。難問も複数あり例題と合わせてかなりのボリュームでしたね。次回も一緒に頑張りましょう!次の第5章はこちらです!