統計検定1級の統計数理分野のバイブルである『現代数理統計学の基礎(共立講座 数学の魅力 11)』の第3章の例題と演習問題の解説を行います!
第2章『確率分布と期待値』について未学習の方はこちらにて解説をしております。
第3章は多次元の確率変数を除く主要な確率分布を扱います。そのため解説部分に例題はなく命題としてページが割かれています。
つまりこの記事では第3章の演習問題の解説を行うことになるわけですね!
第3章の演習問題は次の4つのポイントを意識しましょう!
①離散確率変数の期待値と分散は確率母関数からの方が求めやすい
②マクローリン展開とランダウの記号のダブルコンボ
③ガンマ分布に結びつけて積分計算を省略する
④重積分に持ち込んで積分順序の入れ替え
第3章では様々な確率分布が登場します。そのため各問ごとに関連する記事がある場合はリンクを貼るなどして丁寧な解説を心がけます。
現代数理統計学の基礎『第3章』問1
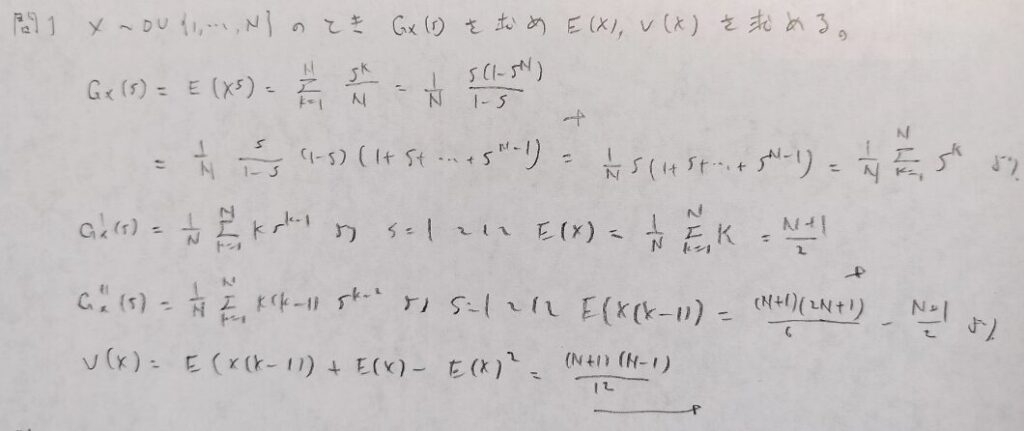
一様分布に関する問題です。離散型確率変数の場合は、一般的に言われているように積率母関数を経由するよりも、確率母関数を経由して期待値や分散を求める方が計算量が少なくて済みます。
現代数理統計学の基礎『第3章』問2

二項分布が関係します。証明は小問をヒントとして経由して帰納法にて解決していきます。
この解答では組み合わせの記号Cを使わずに書いています。
負の二項分布など用いられるように一般化二項係数に対応するためですね!
現代数理統計学の基礎『第3章』問3
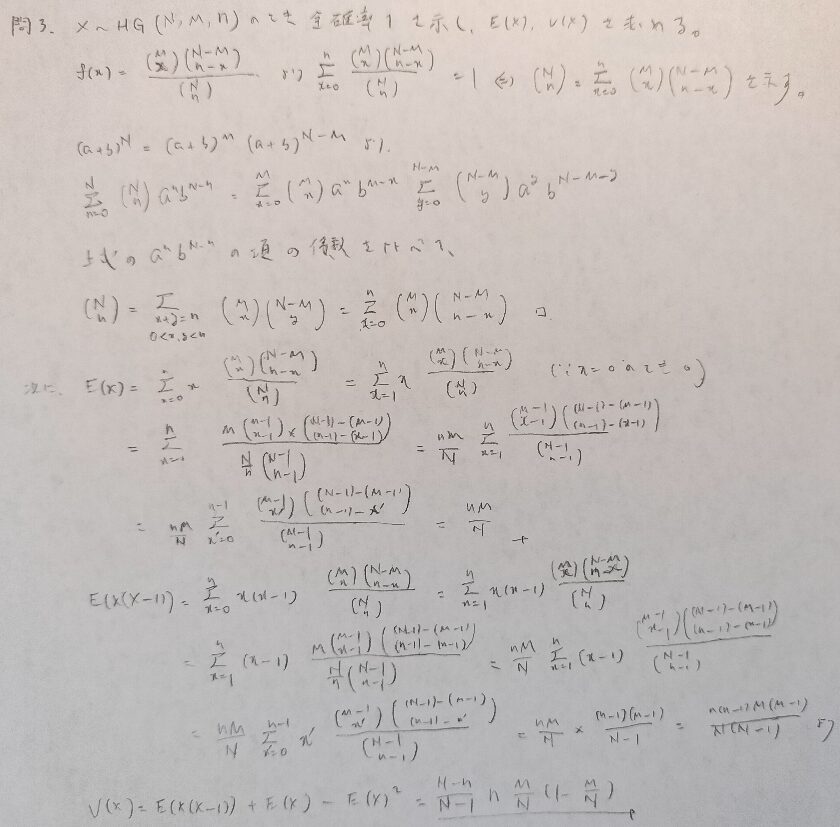
超幾何分布の期待値と分散を求める問題です。シグマ計算では前問に登場した組み合わせCに関する定理を用いていきます。
現代数理統計学の基礎『第3章』問4
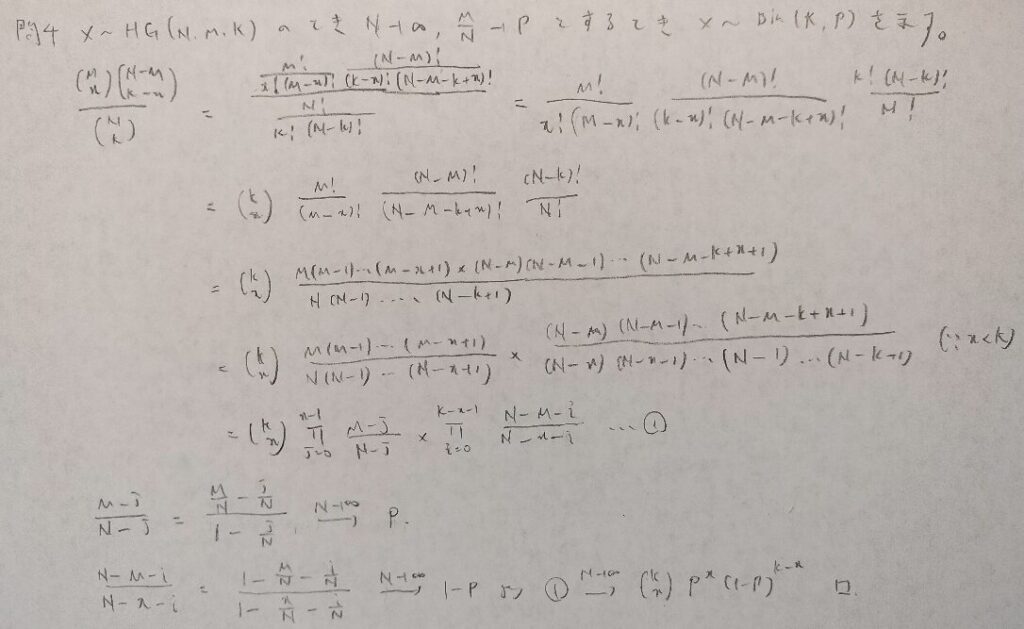
超幾何分布の期待値と分散は本問の結果を考えれば暗記できます!
現代数理統計学の基礎『第3章』問5
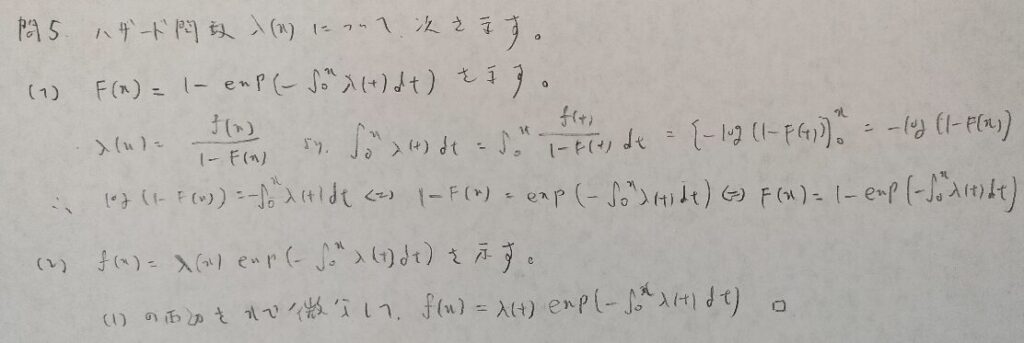
ハザード関数については『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』にて丁寧に解説されています。
本問の(2)のは統計検定準1級では公式として覚えておきたい内容です。
現代数理統計学の基礎『第3章』問6
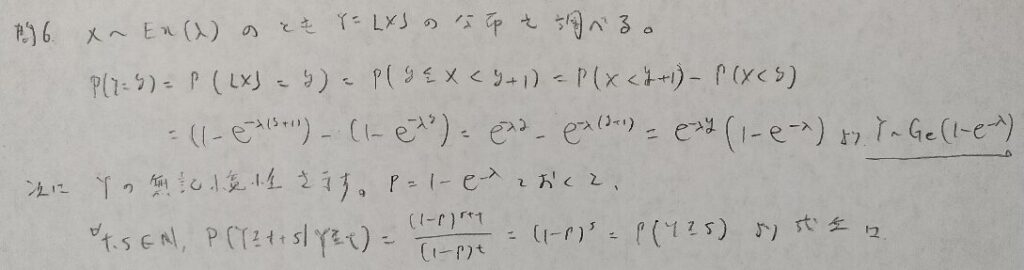
指数分布の離散版が幾何分布になるという有名な問題をガウス記号を用いて書かれた問題です。
指数分布と幾何分布は無記憶性という性質でつながり合っています。
現代数理統計学の基礎『第3章』問7
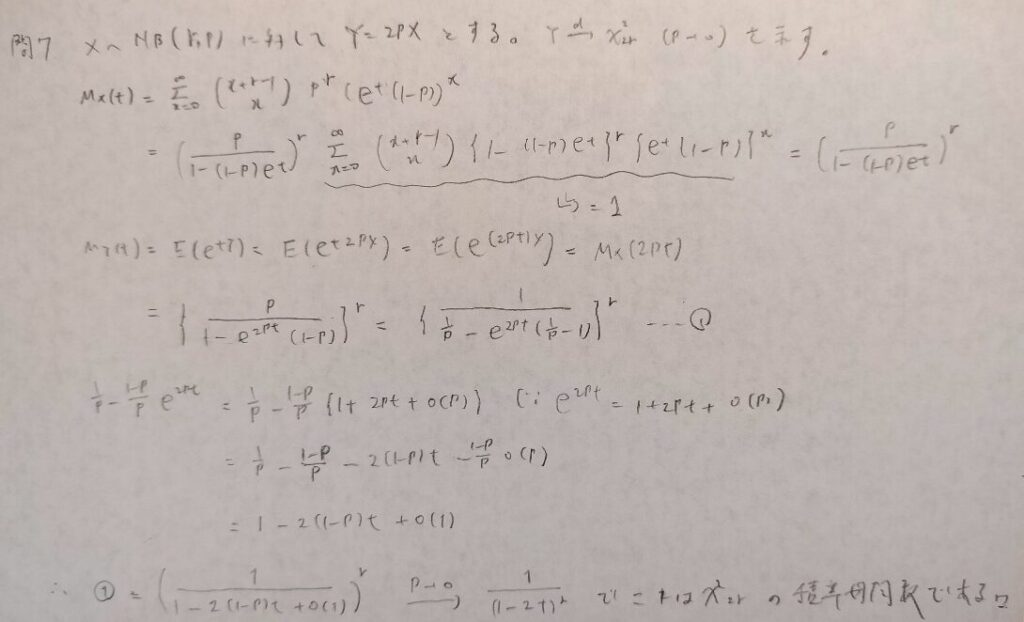
負の二項分布とカイ2乗分布が分布収束という形でつながっている面白い問題です!
この問題からマクローリン展開からのランダウの記号のコンボ問題が登場してきます。
現代数理統計学の基礎『第3章』問8
難問のため2つに分けました。マクローリン展開を2回用います。またランダウの記号の使い方がテクニカルです。
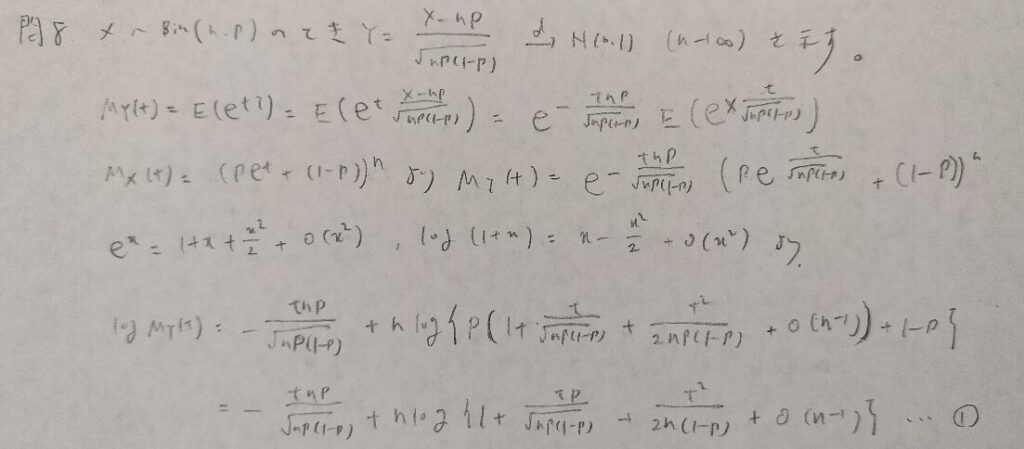
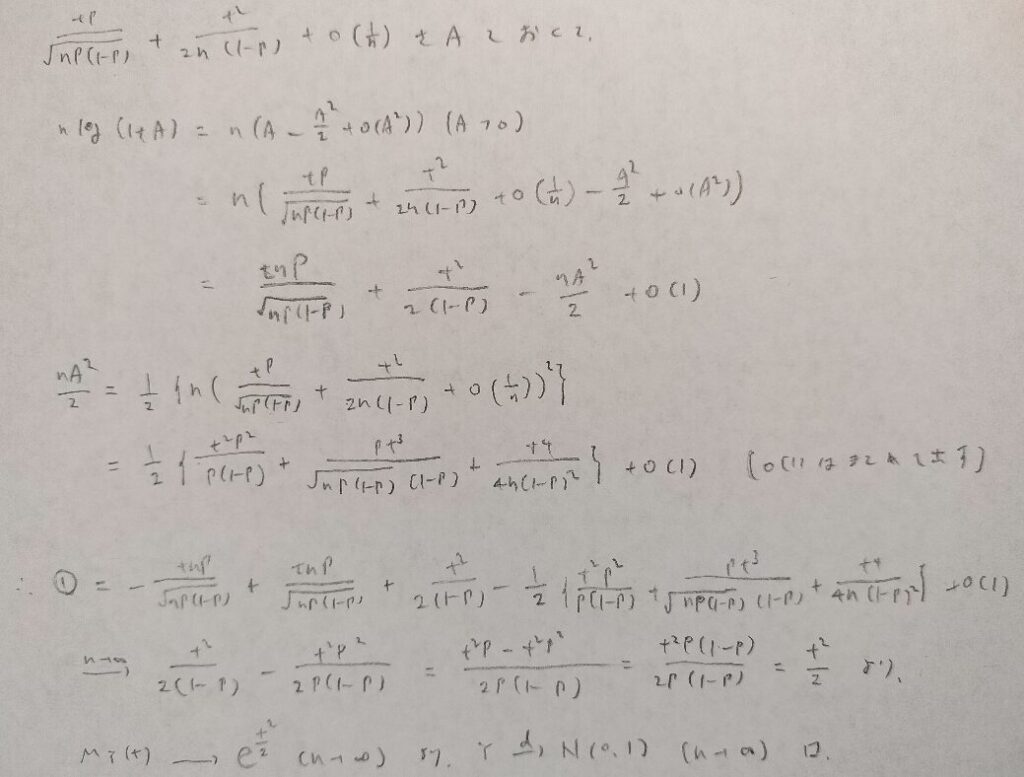
中心極限定理については『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』に体系的に解説されており参考書としてもおすすめです!
デルタ法への流れが綺麗ですよ!
実はこの内容を最もわかりやすく解説している本が『確率統計キャンパス・ゼミ 改訂8』です。ただし内容が長すぎて数ページに及ぶ証明になっています。
現代数理統計学の基礎『第3章』問9
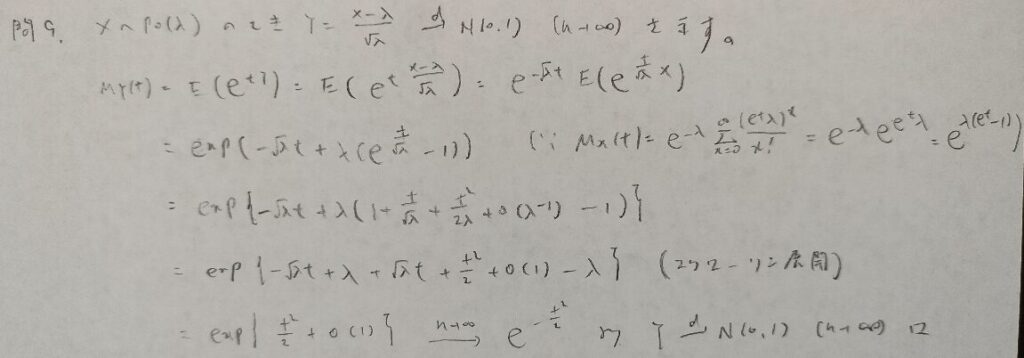
難しかった前問の類題です。ポアソン分布が絡んだCLTの内容です。
現代数理統計学の基礎『第3章』問10
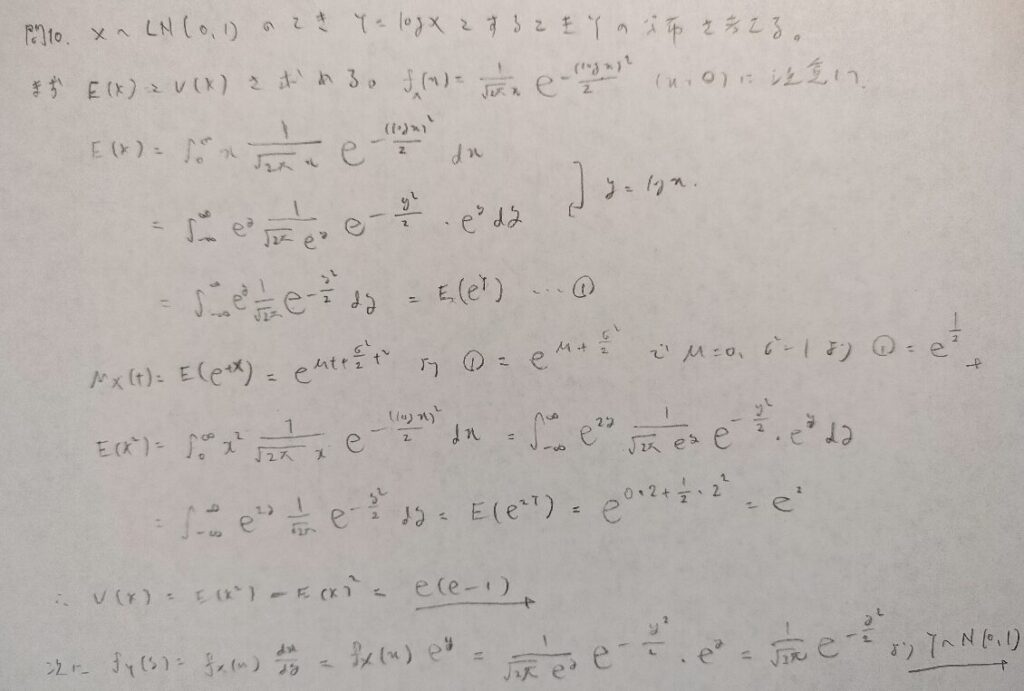
対数正規分布に関する有名問題です。
現代数理統計学の基礎『第3章』問11
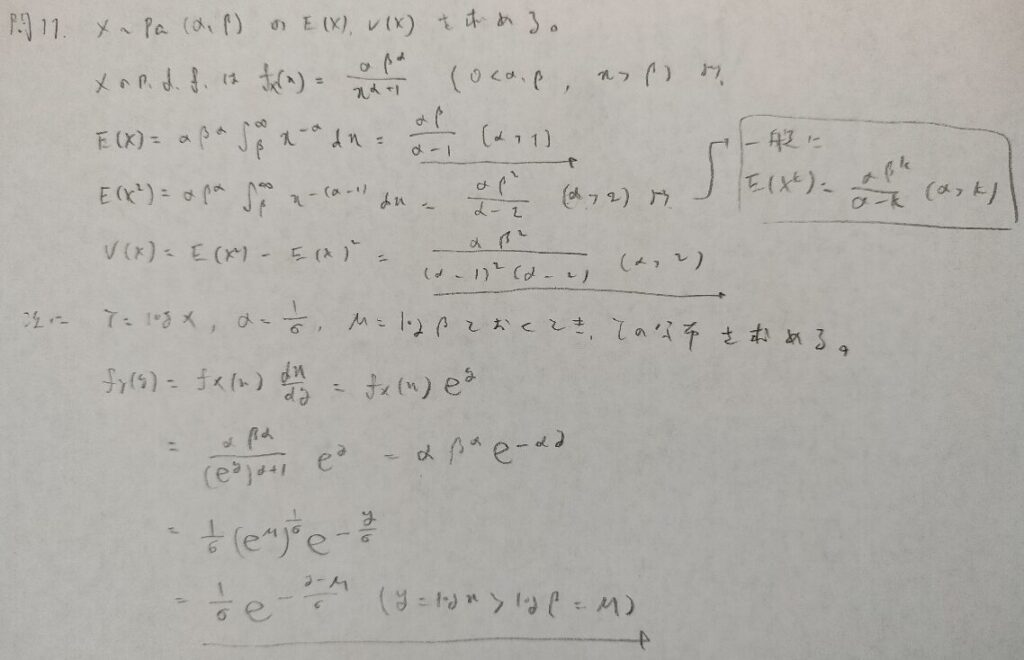
パレート分布は統計検定1級でもアクチュアリー数学でも頻度がかなり低い問題です。
現代数理統計学の基礎『第3章』問12
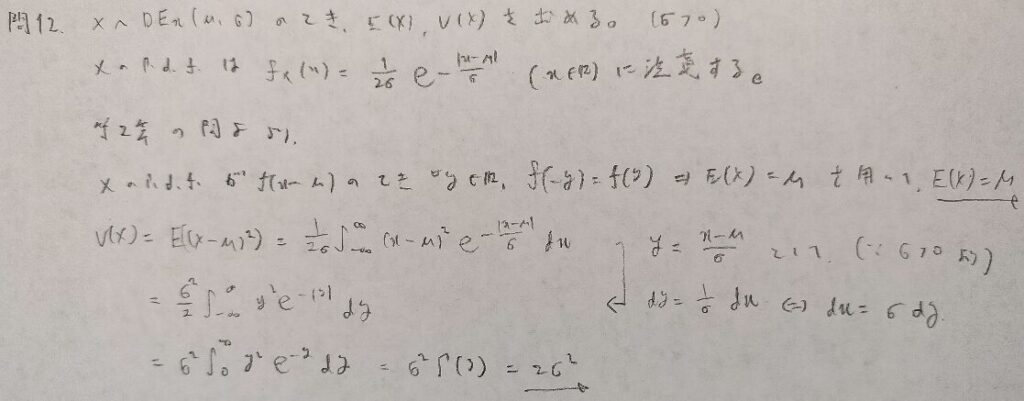
ラプラス分布の記号は2重指数分布の頭文字から来ています。
両側指数分布とも言われます!
現代数理統計学の基礎『第3章』問13
本問は1問1問が重たく意味を持っています。そのため分割をしています。
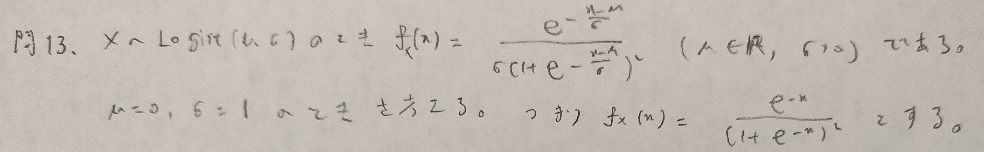





現代数理統計学の基礎『第3章』問14
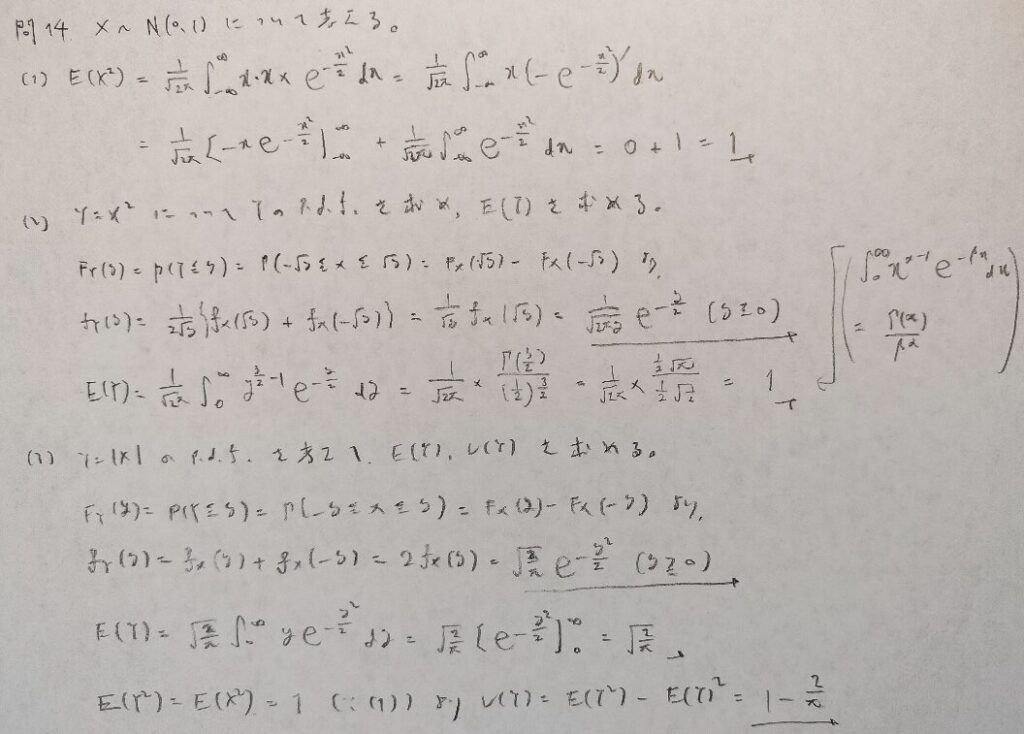
標準正規分布に関する問題です。高次モーメントはアクチュアリー数学では高頻出です!
現代数理統計学の基礎『第3章』問15
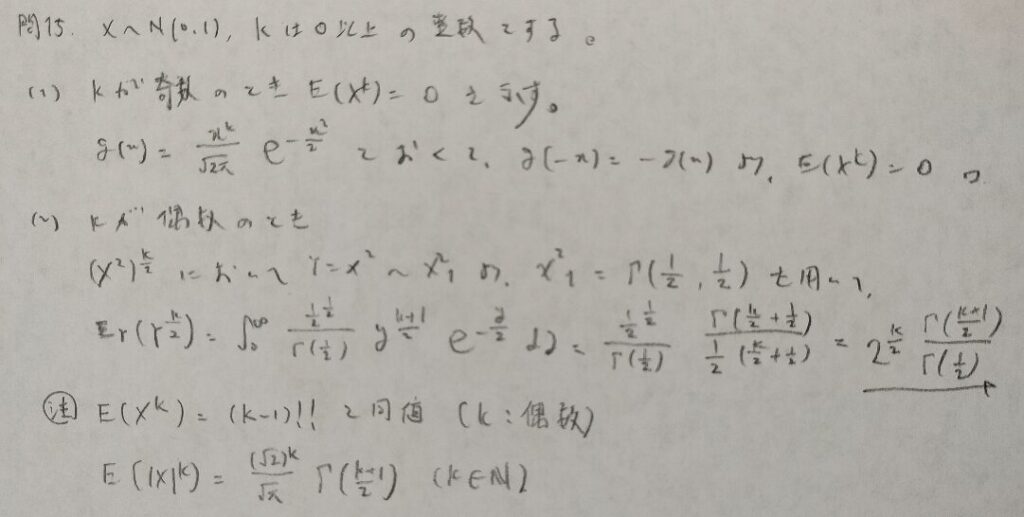
前問の追加問題です。こちらの方が有名な公式となっています。
現代数理統計学の基礎『第3章』問16

正規分布の怒涛の嵐の最後の問題ですね!笑
こういう問題でも躊躇なく出題してくるのが統計検定1級です。
現代数理統計学の基礎『第3章』問17
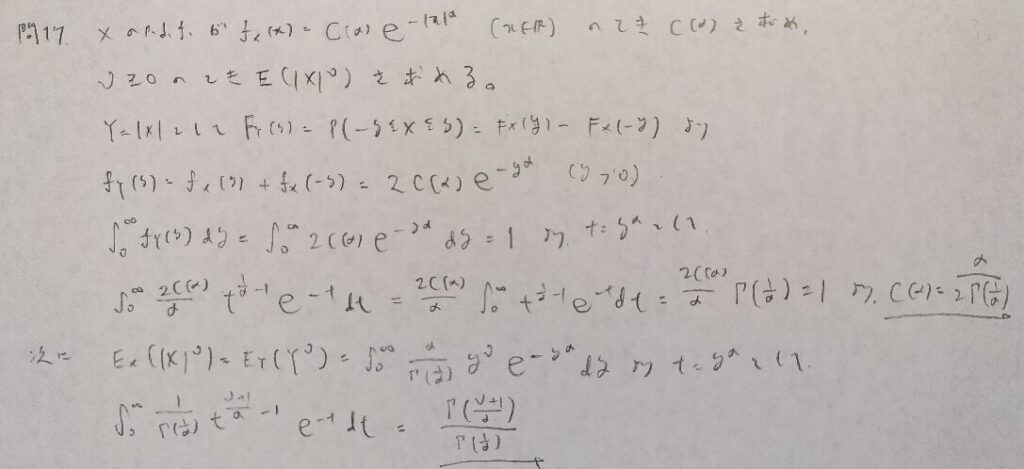
積分計算はガンマ分布との関係を即座に見抜いて対処をしましょう!
現代数理統計学の基礎『第3章』問18
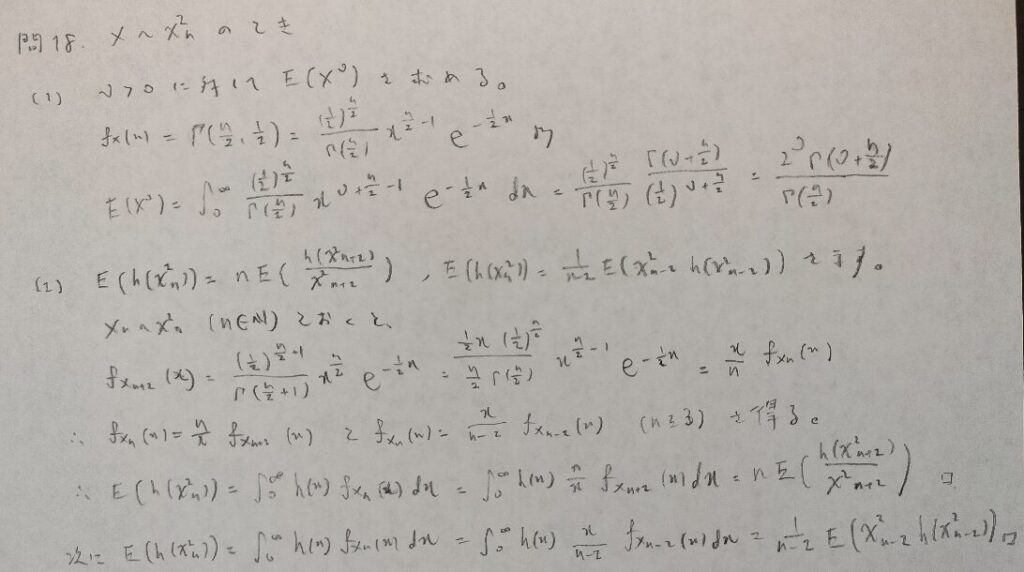
カイ2乗分布に関する期待値の漸化式の問題です。統計検定1級での出題歴がないため要チェックの問題です。
現代数理統計学の基礎『第3章』問19
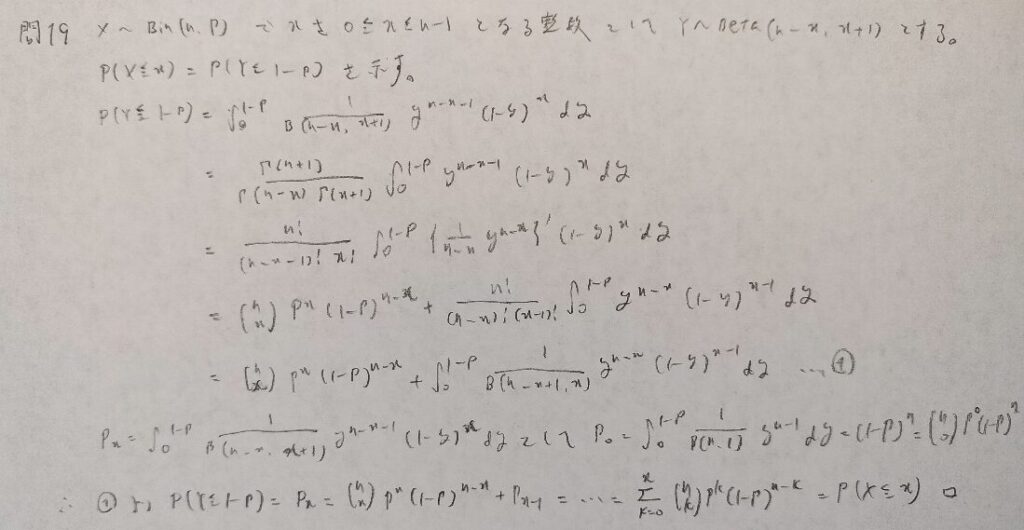
本問は超有名問題ですね!
どの本にも掲載されているタイプの問題ですね!『明解演習 数理統計 (明解演習シリーズ 3) 』が分かりやすい解説でした!
現代数理統計学の基礎『第3章』問20
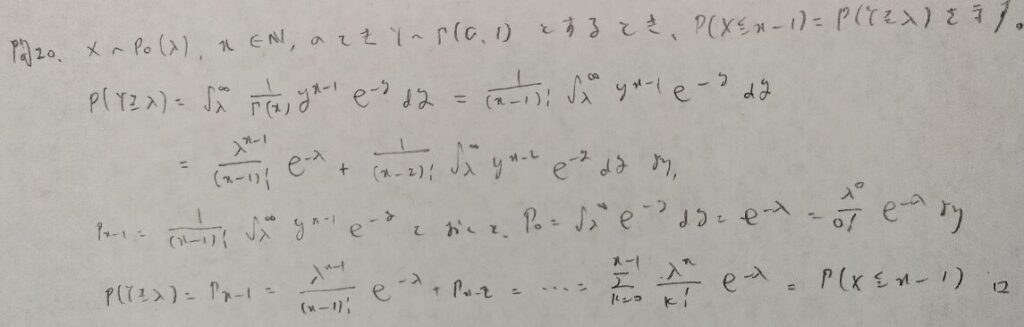
前問の類題でポアソン分布とガンマ分布の有名問題です。こちらも『明解演習 数理統計 (明解演習シリーズ 3) 』の解説が詳しかったです!
現代数理統計学の基礎『第3章』問21
難問です。重積分に持ち込んで積分順序の交換を意識しましょう!
3行目の最後の式で(x-t)を書くのを忘れています。お読みの際は補ってくださいますと幸いです。
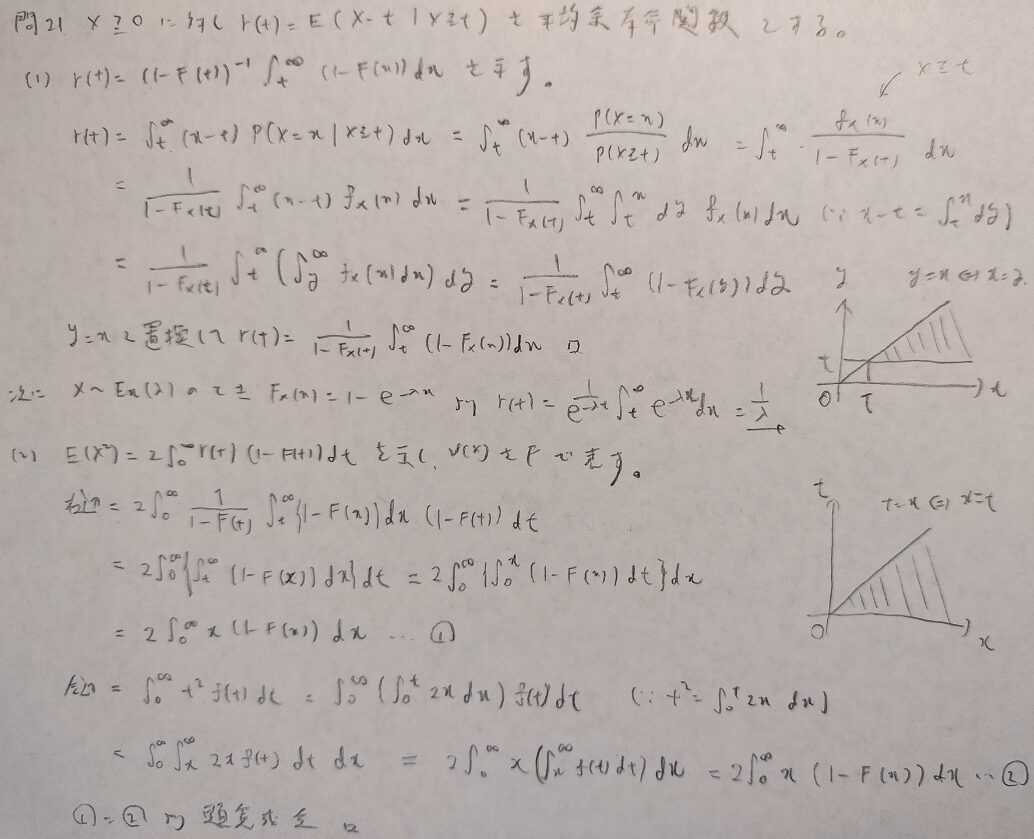
現代数理統計学の基礎『第3章』問22
統計検定2級で主に登場するジニ係数を厳密に計算していく問題です。実用的には(3)の結果を用いて不平等度を判断していくことになります。


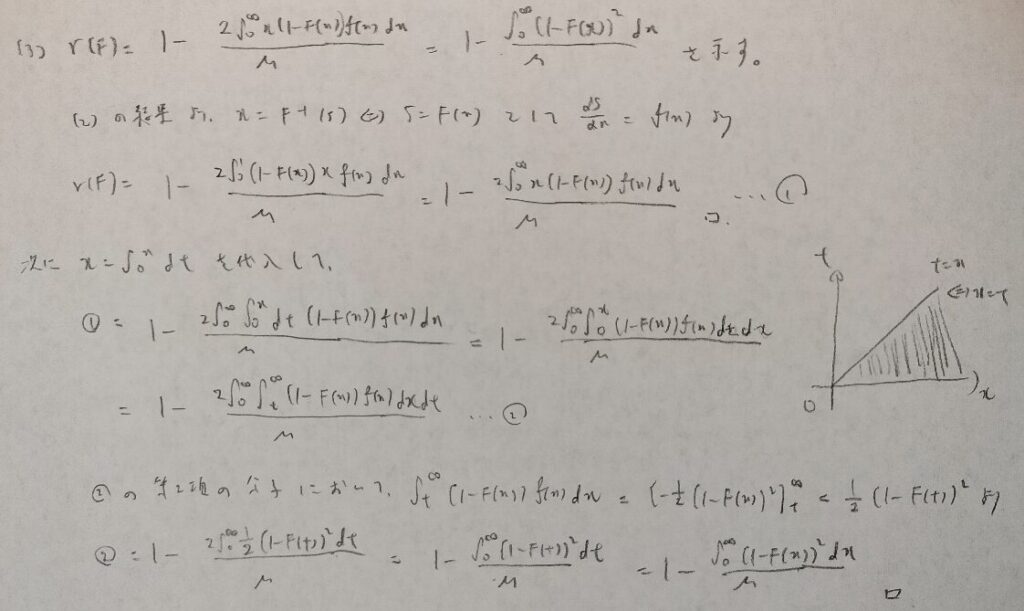

最後の問題の結果には考えさせられるものがありました。
第3章は全22問をもって解説を終了したいと思います。
第4章(こちらです)も『現代数理統計学の基礎(共立講座 数学の魅力 11)』を片手に一緒に頑張りましょう!

















