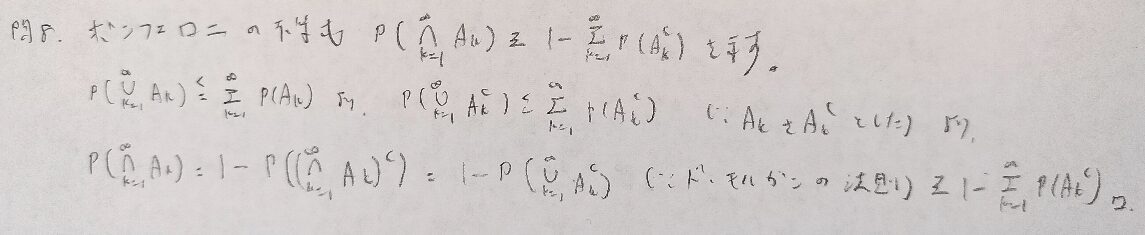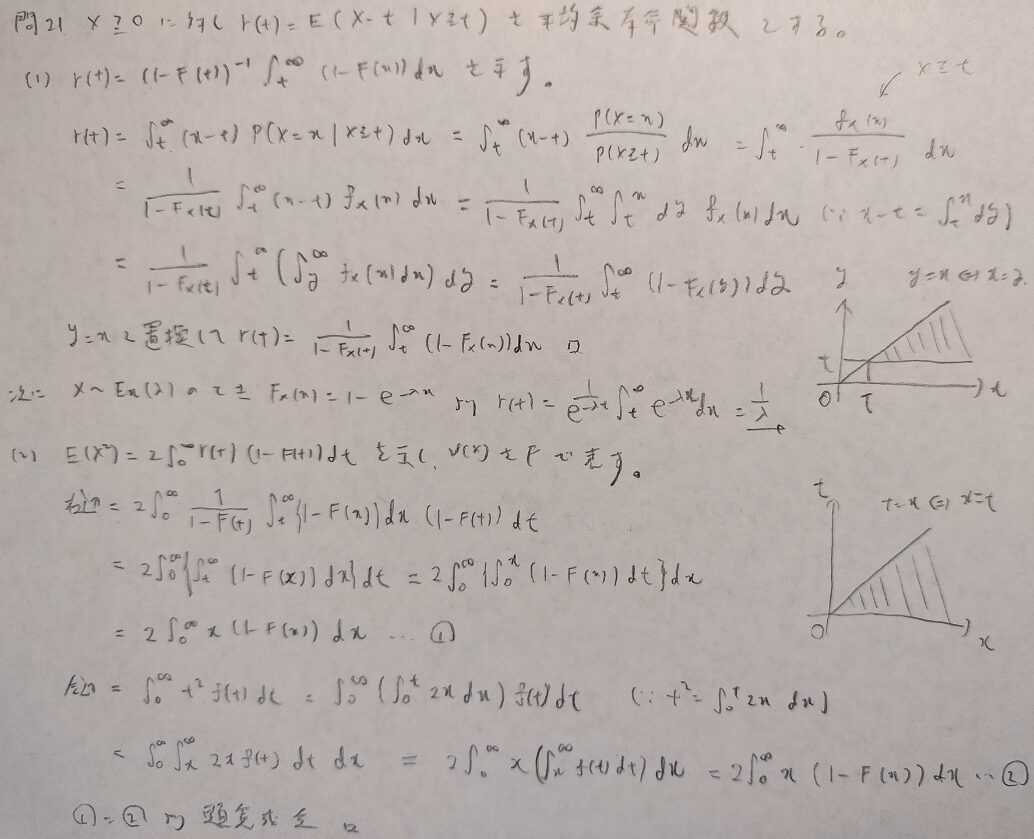本記事では統計検定1級のバイブル書『現代数理統計学の基礎(共立講座 数学の魅力 11)』の第2章にある例題と演習問題の解説を行なっていきます。
この第2章から8章までが統計検定1級の統計数理の実質的な範囲になりますよね!
第2章では第1章と比べると例題と演習問題の難易度のギャップが大きいです。
演習問題を行う際には次の3点に注意してください。
①問6と問7の期待値に関する難問が基本となって後の問題の解法につながる流れである。
②積率母関数を微分していく問題などでマクローリン展開を頻繁に行うことがある。
③代入計算ができない場合は極限計算で対処する(ロピタルの定理を高確率で用いる。)
第1章を未学習の方はこちらからよろしくお願いします!
現代数理統計学の基礎『第2章』例題2.1
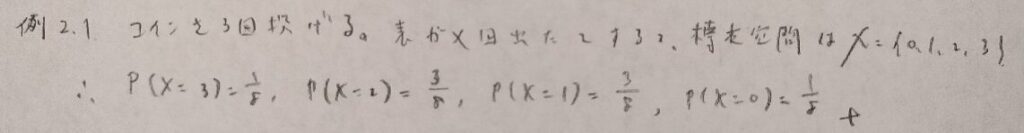
現代数理統計学の基礎『第2章』例題2.5
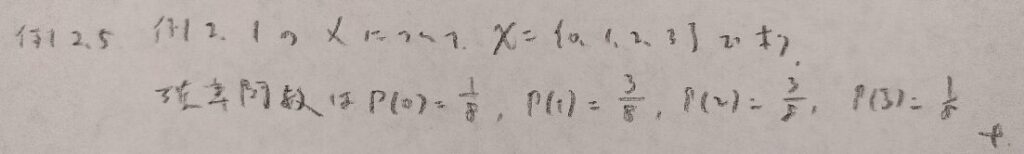
確率関数はp.m.f.と表します。
現代数理統計学の基礎『第2章』例題2.7
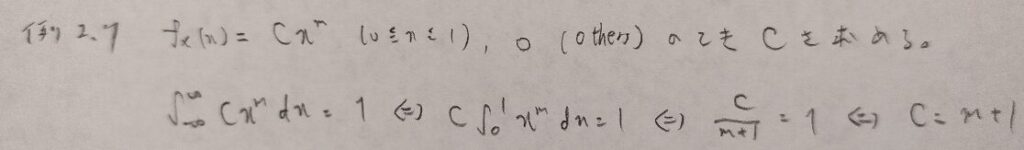
現代数理統計学の基礎『第2章』例題2.10
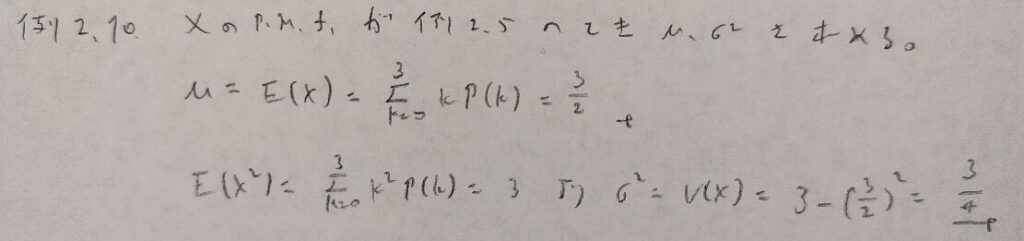
現代数理統計学の基礎『第2章』例題2.11
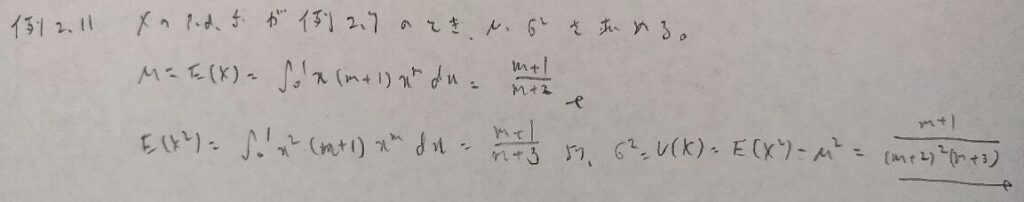
確率密度関数はp.d.f.で表します。
現代数理統計学の基礎『第2章』例題2.12

現代数理統計学の基礎『第2章』例題2.15
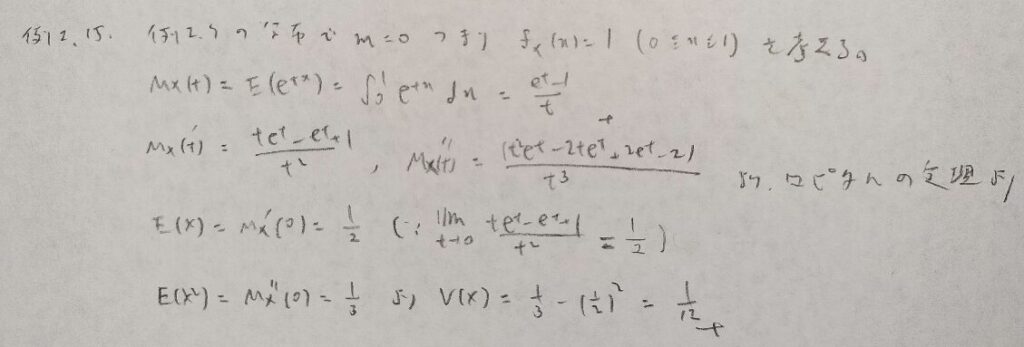
現代数理統計学の基礎『第2章』例題2.22
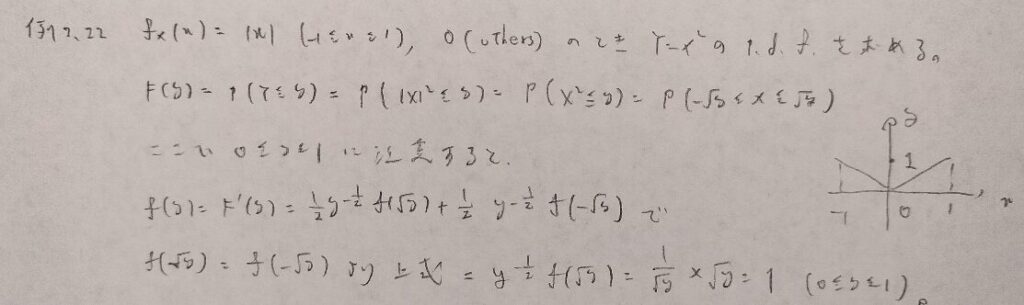
現代数理統計学の基礎『第2章』問1
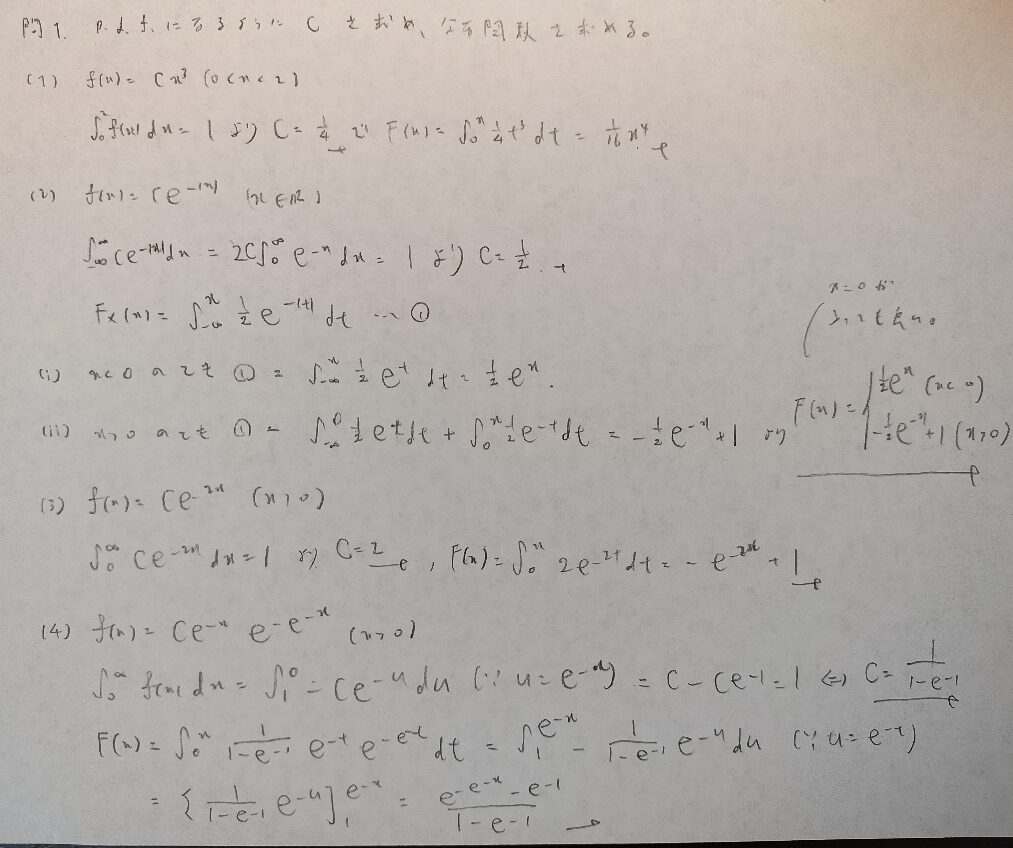
現代数理統計学の基礎『第2章』問2

分布関数であることを示すには次の3つを言います。
①単調増加
②右側(無限大)に飛ばすと1に収束
③左側(マイナス無限大)に飛ばすと0に収束
現代数理統計学の基礎『第2章』問3
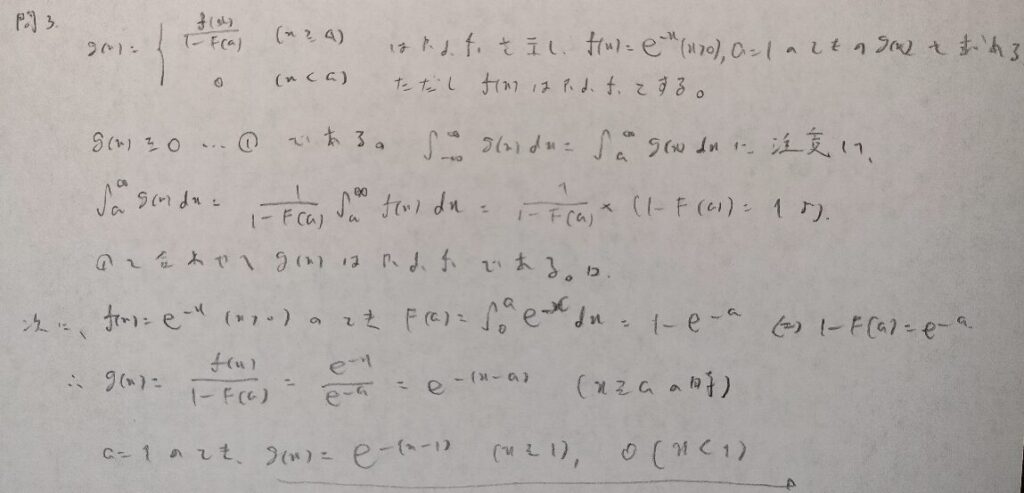
現代数理統計学の基礎『第2章』問4
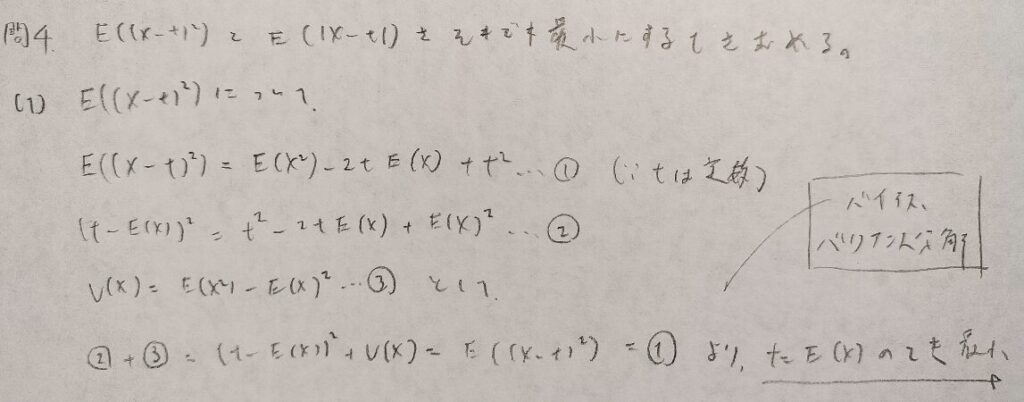
統計検定準1級の公式本『日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック』でも解説されている分解法ですね!
平均2乗誤差(MSE)関連の内容として解説されていましたね!
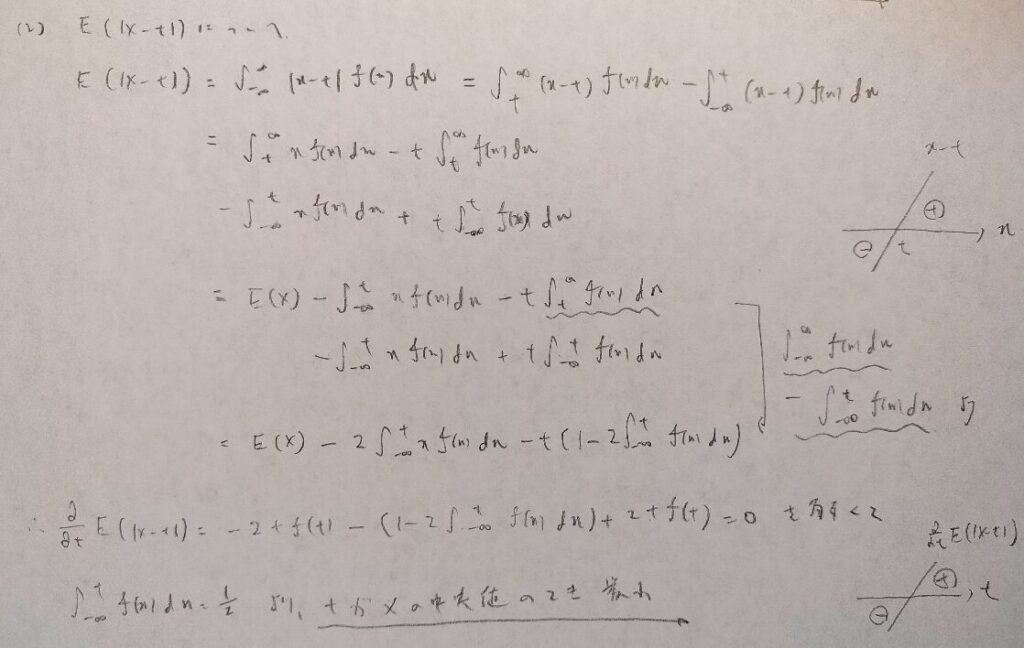
現代数理統計学の基礎『第2章』問5
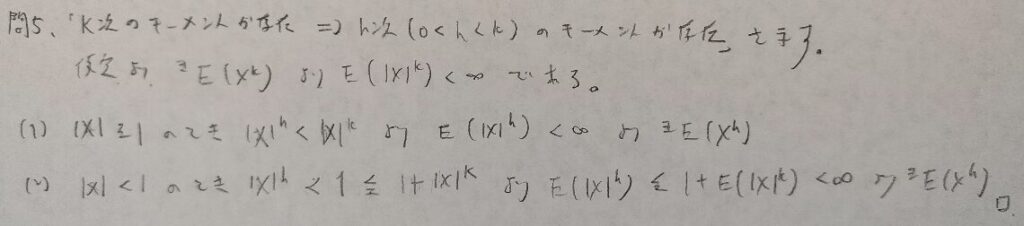
現代数理統計学の基礎『第2章』問6
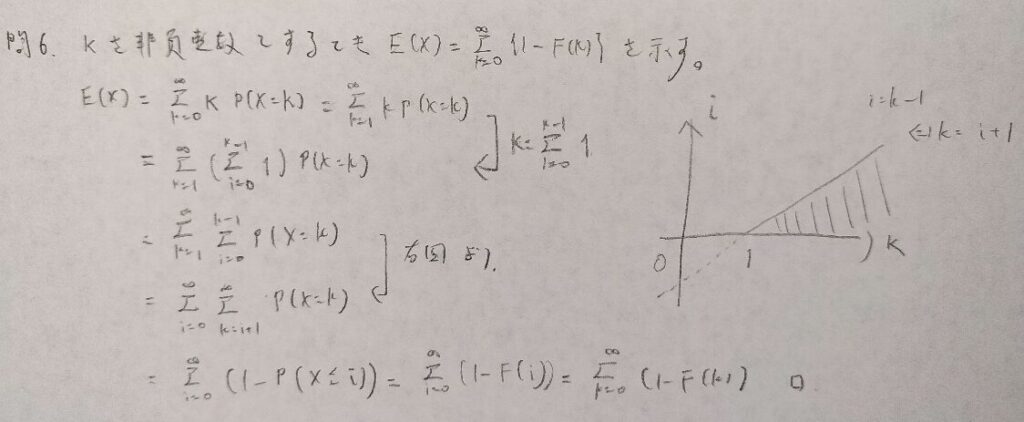
次の問7と合わせて第2章の中核をなす問題です。
kをシグマで表現するところがものすごく技巧的ですね!笑
現代数理統計学の基礎『第2章』問7

(1)の最後の下から2行目の式の中括弧の中の式が間違っているので証明すべき方の式にご訂正ください。-∞の処理で計算ミスをしています。
この問題は問6の連続バージョンです。
この問題もxを積分で表すところがテクニカルすぎます!笑
現代数理統計学の基礎『第2章』問8

確率密度関数は常にf(x)と表示されるわけではないことに注意を払う良問です。
現代数理統計学の基礎『第2章』問9
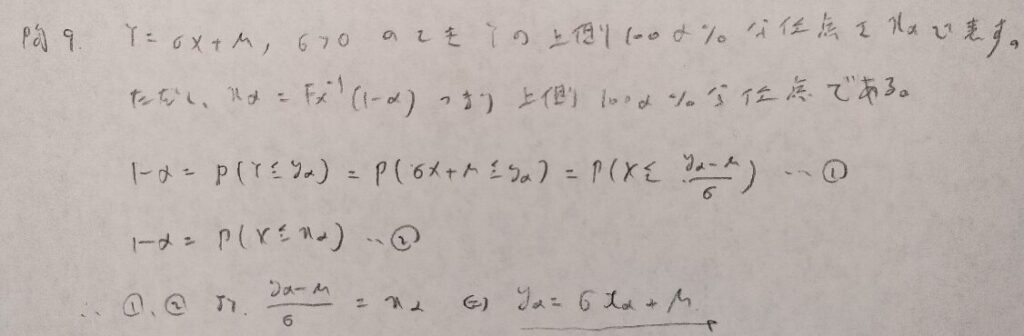
比較がポイントです!統計検定3級などでも類題がある典型問題です!
現代数理統計学の基礎『第2章』問10
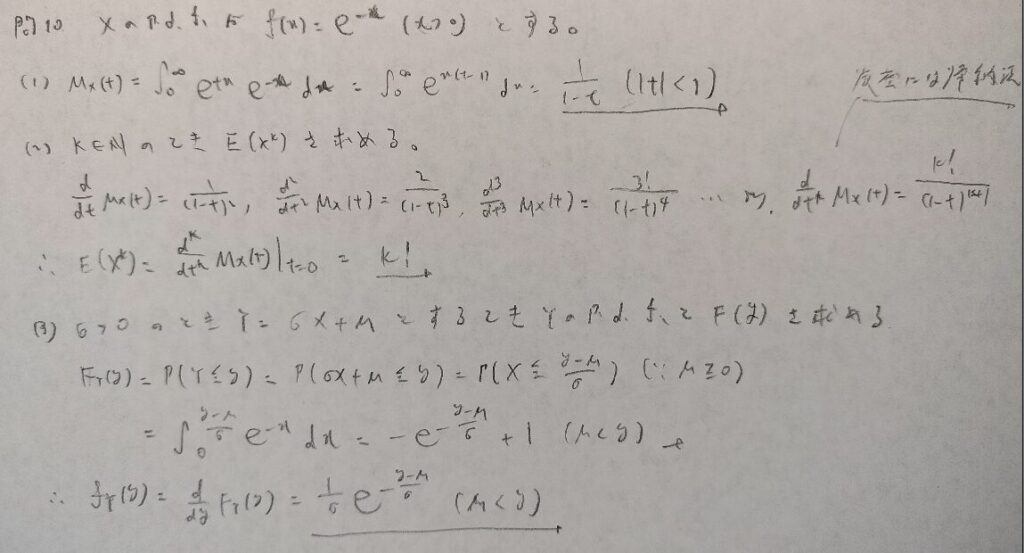
現代数理統計学の基礎『第2章』問11
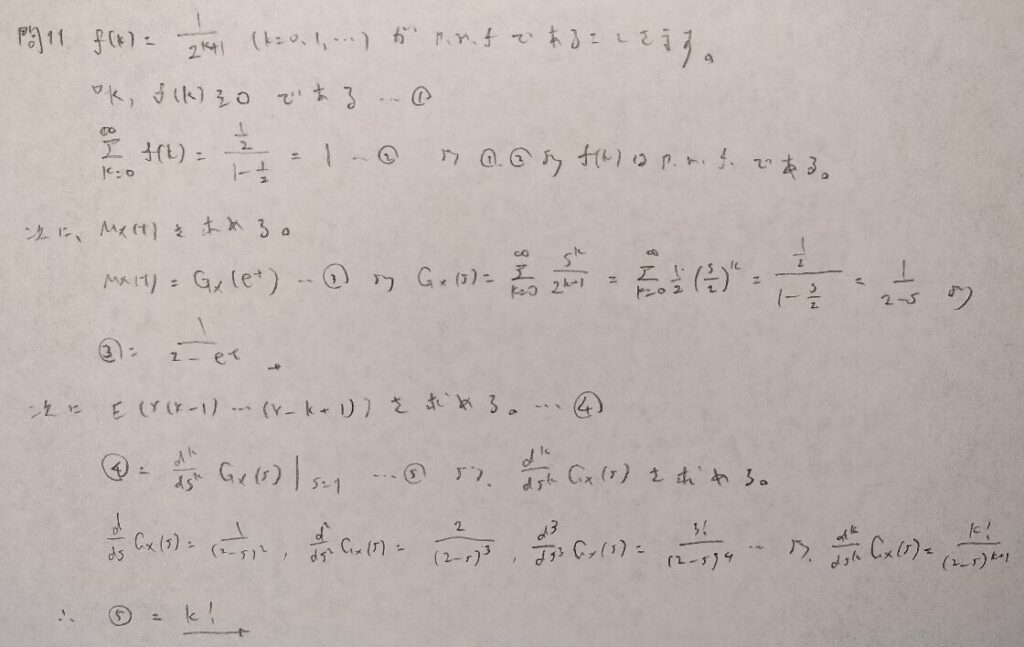
階乗モーメントは確率母関数と相性抜群です!
現代数理統計学の基礎『第2章』問12
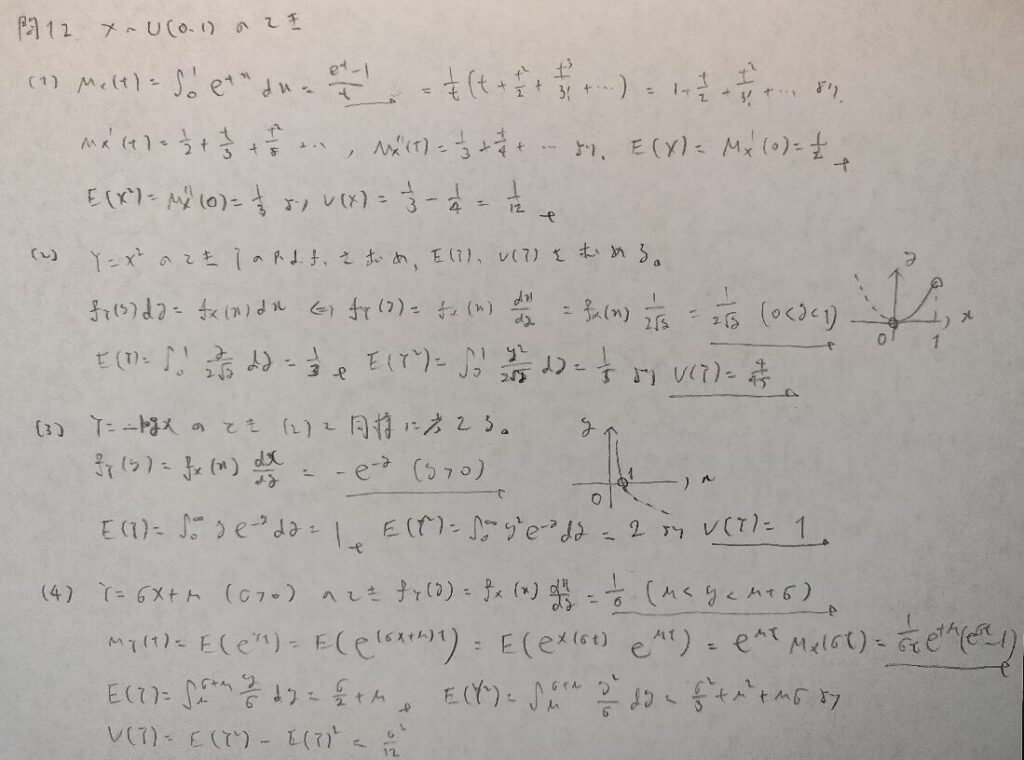
マクローリン展開を用いることにより項別微分に持ち込むテクニックです!
現代数理統計学の基礎『第2章』問13

現代数理統計学の基礎『第2章』問14
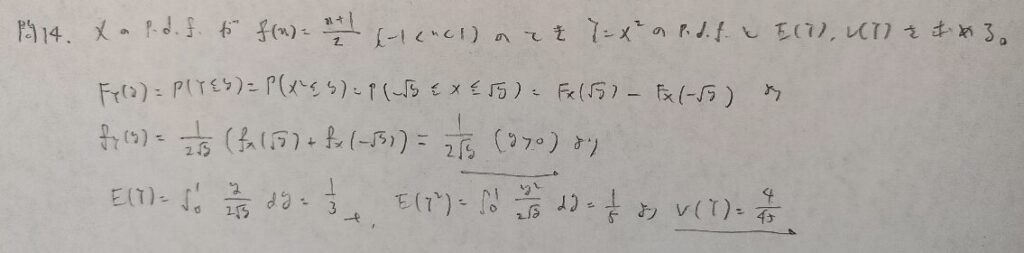
1対1でない場合は分布関数から求める方法が無難です。
微分を経由する方法が早いだけにもどかしい気持ちになりますね笑
現代数理統計学の基礎『第2章』問15
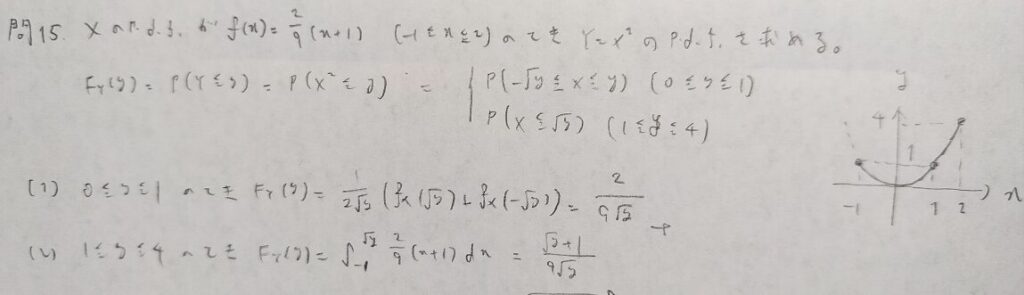
グラフを書いて1対1に対応している部分としていない部分に分けることが大事です!
本問はアクチュアリー数学の有名参考書『弱点克服 大学生の確率・統計』に詳しい記述があります。
早速チェックしてみます!
現代数理統計学の基礎『第2章』問16
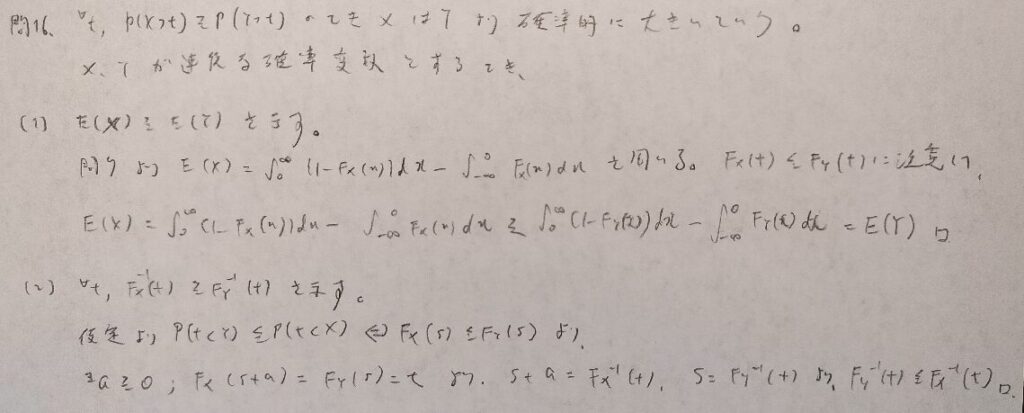
本問は問6や問7の理解がベースとなっている難問です。
現代数理統計学の基礎『第2章』問17
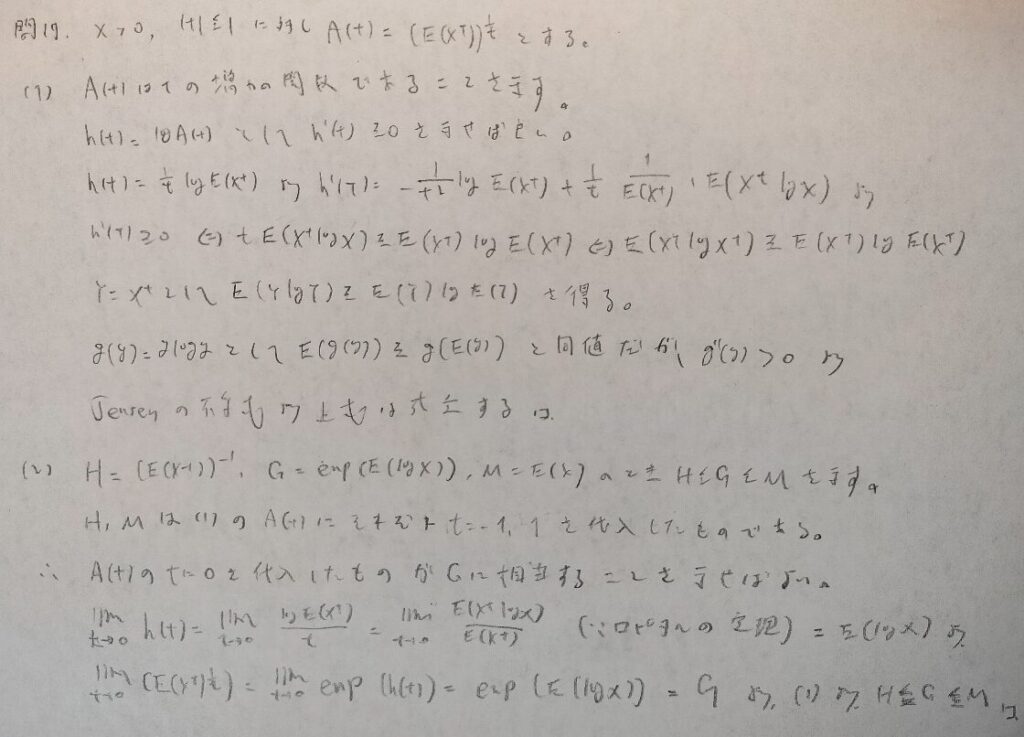
現代数理統計学の基礎『第2章』問18

以上になります!次の第3章ではいよいよ様々な確率分布が登場する回になります。
第2章はとにかく期待値関連のトリッキーな問題が目立ちましたね。次回も楽しみにしています!