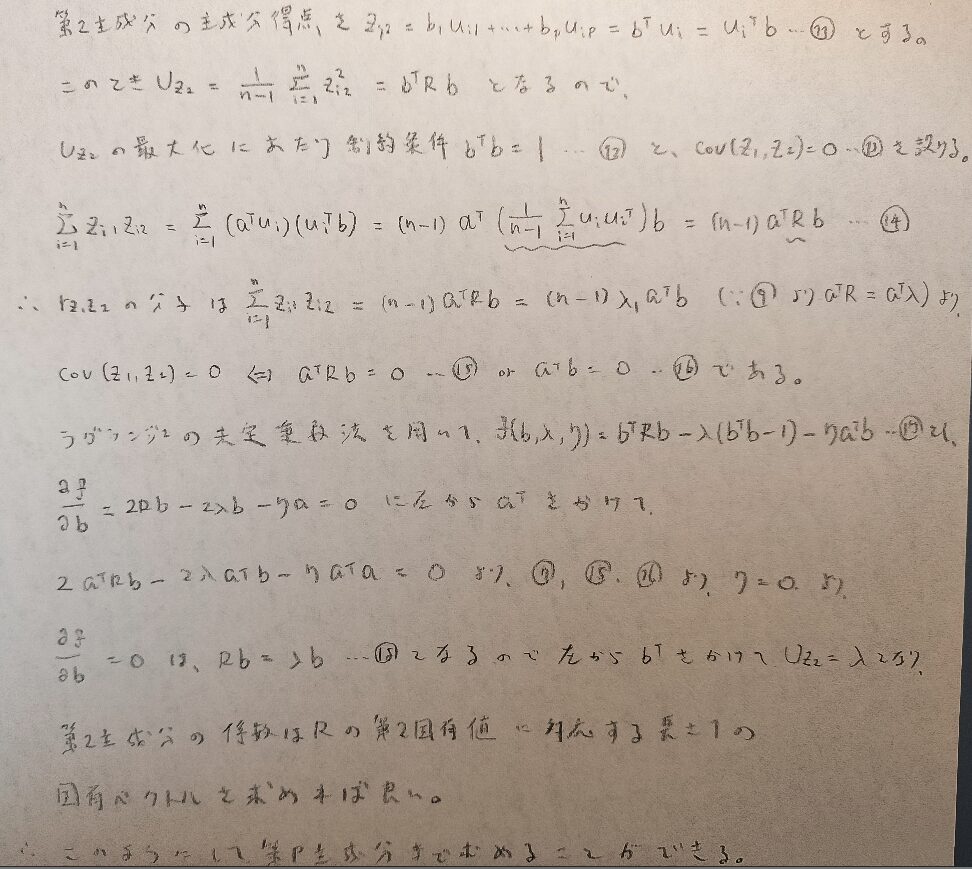多変量解析の中の集大成的な難易度である因子分析を解説します。
まとめという感じですね。どのような感じで難しいのでしょうか。
因子分析は主成分分析と似ているところがあります。そして変数を標準化するというパス解析的な考えもあります。また、回転をさせるところで判別分析的な考えも出てきます。当然、重回帰分析の内容も出てきますので、多変量解析の集大成的なレベルとなります。
ここでいう多変量解析とは永田先生の『多変量解析法入門』を指しています。本書は統計検定を考えている方に強くおすすめできる素晴らしい教材です。
因子分析と主成分分析との違い(ともにエクセルで用います)
因子分析について説明していきます。まず因子分析は主成分分析と似ている考えが多いので、主成分分析について未学習の方は、こちらの記事をおすすめいたします。
主成分分析では、多くの変数の情報をできるだけ少ない次元で解釈することを目的とし、観測変数の1次結合の形をした主成分を構成しました。
因子分析では、多数の観測変数の背後に少数の潜在因子を想定し、それによる観測変数間に相関関係が生じていると考え、それをモデル化して解析を進めます。
「潜在因子を想定すること」、「モデル化して分析すること」が主成分分析との違いなのですね!
因子分析(pythonでも用います)のモデル化
まずは生の変数を標準化した量uが与えられたとします。
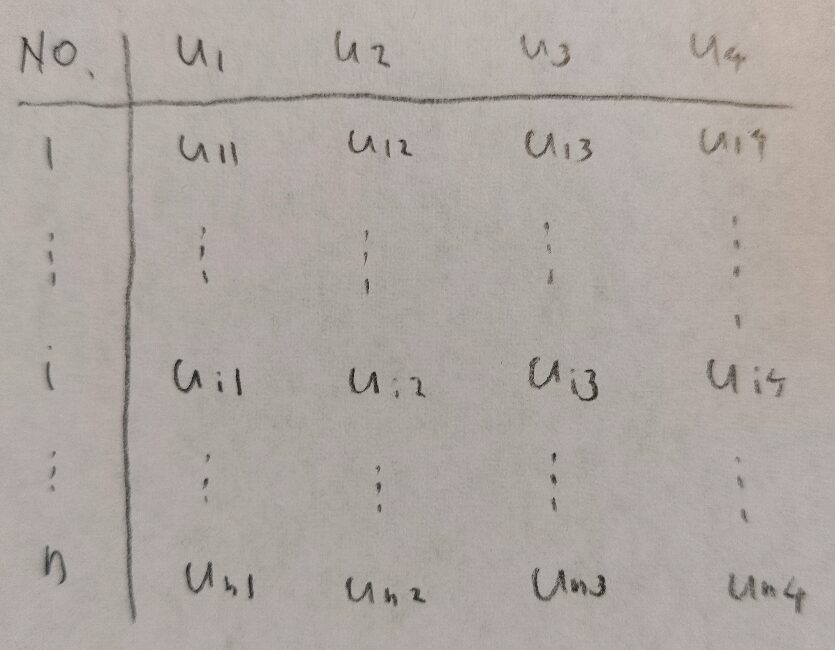
このデータで次のモデルを想定します。これを因子分析のモデルといいます。
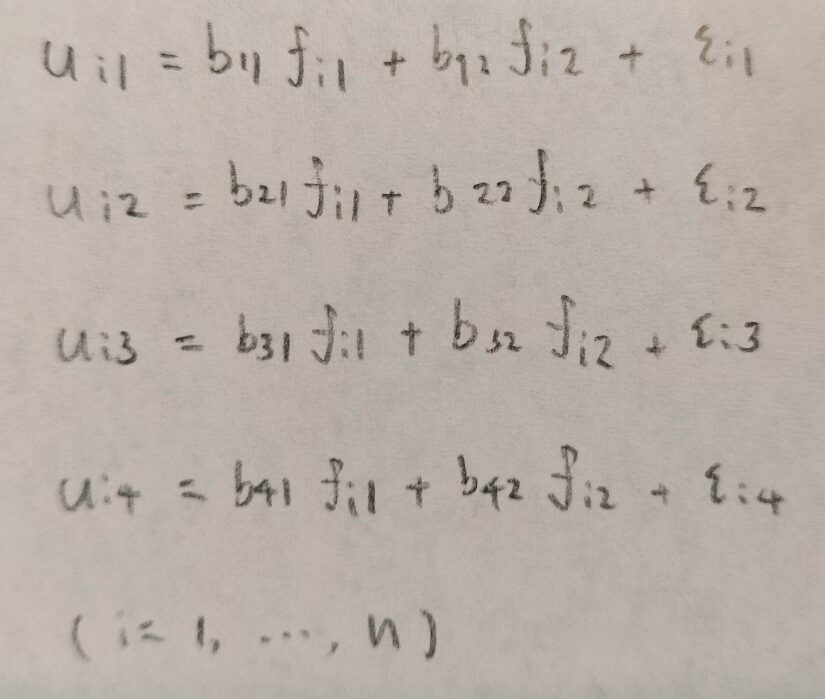
ただし、因子分析では記号の使用について注意点があります。それはサンプル番号によって記号が異なるか、それともサンプル番号によらずに記号が同一かということを考える点です。

サンプル番号によらない記号は、まずは共通因子です。共通因子とは例えば、理系によるか、文系によるかなどの因子のことです。また共通因子に負荷を与えている定数のことを因子負荷量といいます。これは定数です。
サンプル番号に依存する記号は、まずは因子得点です。これは上での共通因子に対応する概念です。そしてεはサンプル番号に依存するので独自因子といいます。誤差のようなものです。
ここで大事な注意点がありますので、お読みください。標準化や無相関の仮定をここで入れます。
共通因子はすべて標準化しています。
独自因子のそれぞれの期待値は0で分散はdの2乗と変数によって固定されています。
共通因子間、独自因子間は無相関です。
共通因子間と独自因子間も無相関とします。
因子分析での目標を教えてください。
因子分析の目標は、因子負荷量の推定や、因子得点の推定を行うことです。そして因子の解釈を行うことです。
そのために記号間での関係を1つ導いておきます。この結果が後でとても大事になります。

すなわち因子負荷量は標準化された変数と共通因子が分かれば算出できるということです。
因子分析(rでも用います)の共通性と独自性
次に因子分析を行列表示して考えていきます。それにより、因子負荷量や因子得点の推定ができるようになります。そしてここがメインとなります。
先ほどの図04の母相関係数とは意味が異なりますのでご注意ください。図05は各成分が因子負荷量で構成される母相関係数行列を作るためのものです。
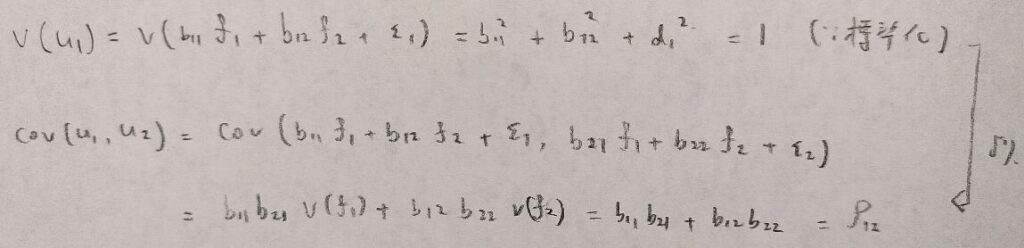
このようにして各母相関係数を並べた母相関係数行列Πを作成します。
Πの成分はすべてbで構成されるものになりますので、図06の右にある行列Bと対角行列Dを用いて表現します。この式は後でとても大事になりますので覚えておいてください。
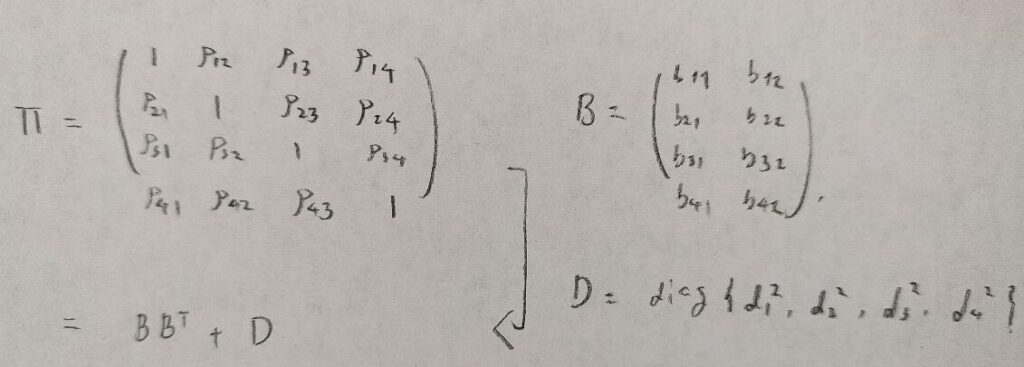
ここで共通性と独自性という概念が登場します。まずは図07をご覧ください。
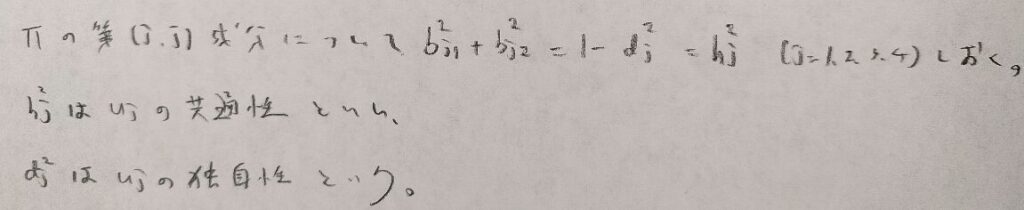
ここで図07の説明を補足します。母相関係数行列Πの対角成分に注目します。変数hは変数uの変動のうち共通因子によって説明できるので共通性と呼びます。
またdの方は共通因子では説明できないばらつきの大きさなのでuの独自性といいます。
因子分析(英語はfactor analysis)における因子負荷量の推定
ここから難易度が上がります。適宜、主成分分析の記事を参照しながらお読みください。
共通因子の個数の設定
図02では共通因子の個数を2としましたが、実際の解析では共通因子の設定が第1に行われます。それにより因子分析のモデルが定めるからです。共通因子の個数の設定は主成分分析のときと同様に考えて、標本相関係数行列(つまりΠの推定量)の1より大きな固有値の個数とします。
因子負荷量の推定(主因子法)
因子負荷量の推定はさまざまな方法がありますが、この記事では主因子法を紹介します。
この方法はΠーDの対角成分の推定精度を高め、かつ、ニュートン法のように感覚的にもわかりやすい方法であるからです。
直接、対角成分を推定しにいくと精度が悪くなります。そのため図06で登場した行列の関係式を用いることを考えます。
それでは主因子法を詳しく説明します。ここが本記事のメイン部分となります。図08の中盤の式(ΠーDの推定)で行列のスペクトル分解の知識を用いています。
行列の階数についてrank(A)≧rank(AB)の知識も用いて、①の右辺の階数が2であることを導いています。
行列のここら辺の内容をしっかり理解するための参考書としては『線形代数学』がおすすめです。線形代数の書籍として理解のしやすさと到達点の高さを考えるとかなり完成度が高い本です。
それでは図09をご覧ください。

これで行列B、つまり因子負荷量を推定できました。それと同時にΠーDの対角成分も推定できたことになります。
固有値が大事な因子分析における因子の解釈
因子分析の難しさは、因子の解釈があるせいともいえます。いよいよ記事の終盤です。判別分析で行なったように回転の考えを導入します。
回転を行なって何が変わり、何が変わらないか?を意識して読み進めてください。結論は図12に載せます。

この段階で☆の式に注目してください。とても大事です。
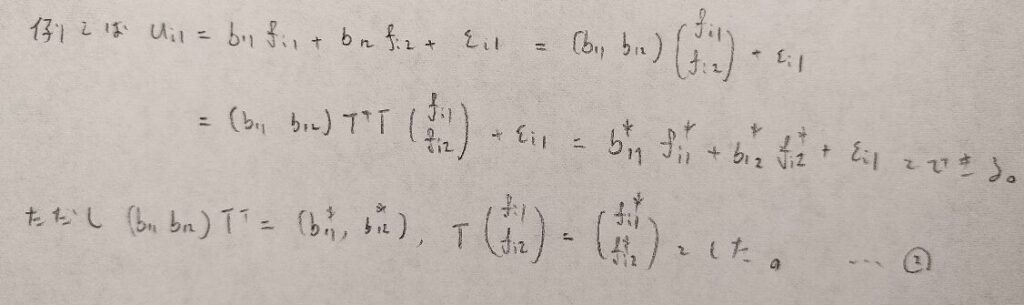
図10を頼りに、回転後の各文字の性質を調べます。

ここで図04で学んだ各変数間の関係が回転後にも成り立つかを吟味します。そのためには回転前のときの前提条件が成立していればOKです。
なるほど!だから図09~12までの流れがあったのですね!
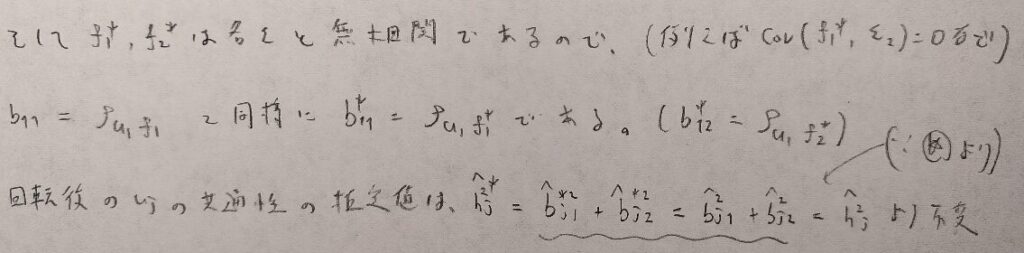
つまり因子分析では回転を行なっても因子の解釈(共通性の推定値は回転によって不変(図09の☆の式より))には影響がないということです。これは判別分析のときと同様に軸を回転させても因子の解釈は変わらないことは自然と分かると思います。ということはどのような回転を行うと、因子の解釈がしやすいか?という問題になります。
詳しい回転の内容は『ようこそ「多変量解析」クラブへ 何をどう計算するのか』にて解説されており、おすすめです。
この問題は図13に示すバリマックス基準によって解決されます。バリマックス基準によれば、因子負荷量がゼロに近いものとゼロから大きく離れるものに分離できるためです。
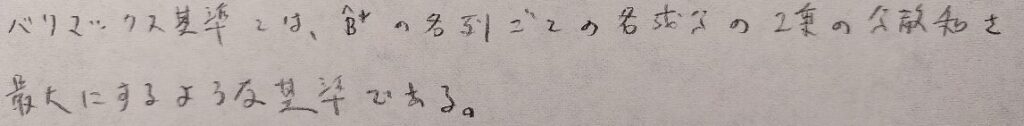
因子得点の推定
因子得点を推定するには重回帰分析の知識を用います。

この最後の行列のSの説明をお願いします。具体的にどう計算するのですか?
了解です。図15にて説明します。注意点として主成分分析のときの流れを踏襲して、不偏分散を考えているので、いろんな場面でnー1で割っていることにご注意ください。
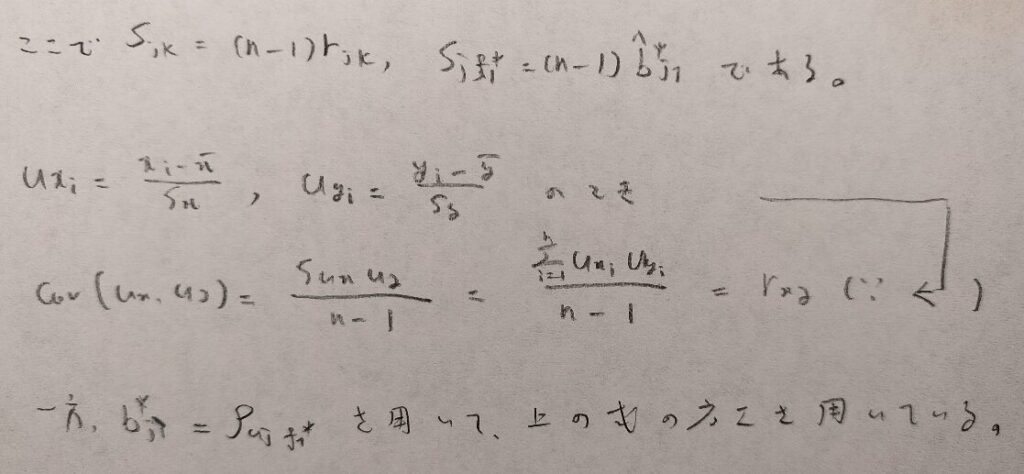
このようにして偏回帰係数を求めることができました。そのようにして求めた予測式(図14の①式など)の各uに各サンプルの観測値を代入すれば、因子得点を推定することができます。因子得点の利用の仕方は、主成分得点の利用と同様です。
因子分析の寄与率と累積寄与率
先ほどの回転のお話に戻るのですが、回転によって変わってしまうものの例はありますか?
わかりやすいのが寄与率と累積寄与率の話です。このうちのどちらかが回転によって変わってしまいます。
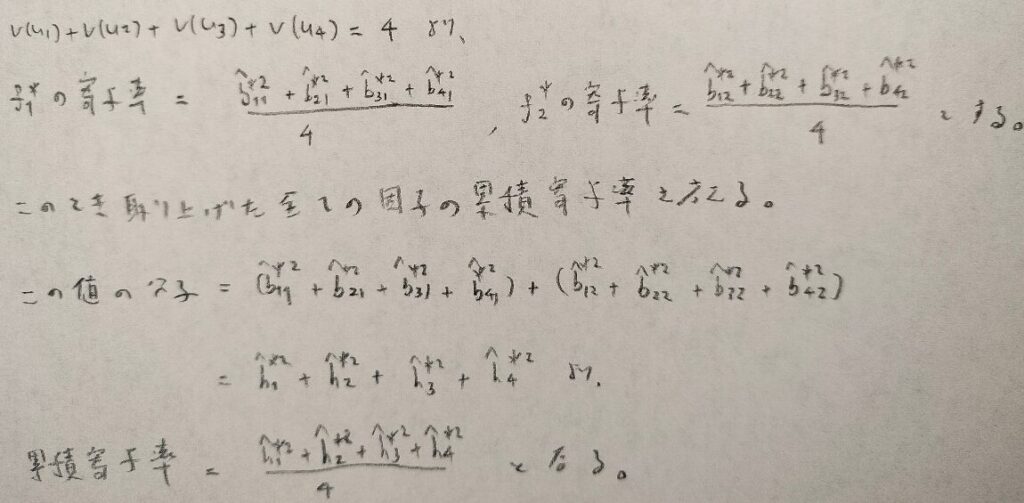
なるほど!寄与率は回転によって変わってしまいますが、図12の結論を思い出すと累積寄与率は回転によって変わらないですね!
回転によって変わるものと変わらないものがありました。因子分析はとても難しいので、何度も読み返してくだされば幸いです。