標本分布の代表例としてカイ2乗分布→t分布と学んできました。そしてついにこの流れでのラスボスのF分布に突入します。
カイ2乗分布は標本の偏差平方和が従う分布でt分布は標本平均を不偏分散で標準化した値が従う確率分布でしたね。
F分布とは標本分散の比が従う分布のことで、F分布を用いると分散分析(実験計画法へと続くので奥が深い)が可能となります。(『統計学大百科事典 仕事で使う公式・定理・ルール113』より)
これら3つの分布(カイ2乗分布、t分布、F分布)を学べば推定・検定の内容が理解できますので一緒に頑張りましょう!
F分布の確率密度関数
F分布の確率密度関数の導出
まずF分布を定義します。F分布は単なる2つのカイ2乗分布の比で定義されないのでご注意ください!
F分布は自由度がm,nの2つありますね。そして表現方法も使用時の状況に応じて2通り覚えておくと便利です。
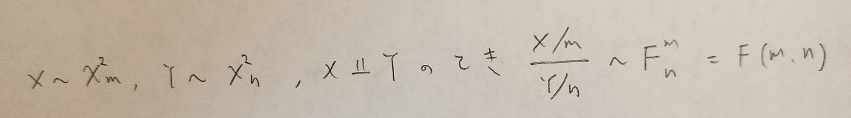
自由度(m,n)のF分布の確率密度関数を求めてみましょう。方法はt分布のときと同じですが、置き換えが難しいです。そのため2段階の置き換えで乗り切りましょう!
最終的にはUが従う確率分布を求めています。途中でZが出てきますが、このZは後に関連するベータ分布との関わりで大事ですので残しておきます。式としては③に注目してください。
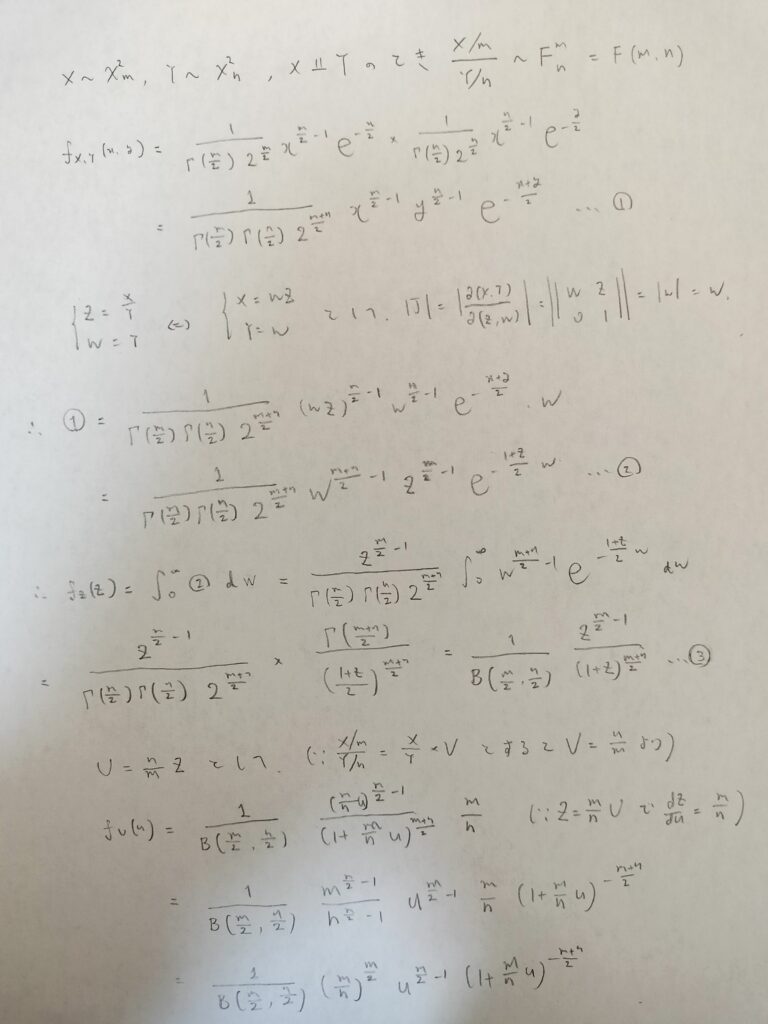
2段階での置き換えは初見では難しいですね。この式を見ながら計算を頑張りたいと思います。
この結果を見て何か気づきませんか?
ベータ分布が入っています!
ということはF分布はベータ分布と相性が良さそうですね。
F分布がベータ分布とどのような関係があるのか楽しみです。ここでいったんF分布の確率密度関数の結果をあらためて書いておきますね。
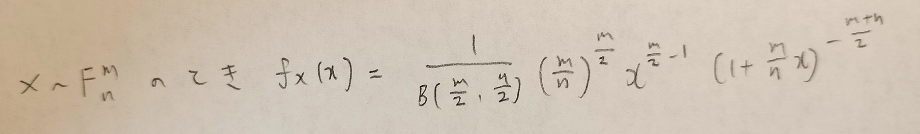
F分布の全確率1の証明
F分布は確率分布なので当然、全確率1を満たします。これを証明します。

またベータ分布が出てきました!というよりこの証明の本質部分はベータ分布な感じがします!
その通りです。ベータ分布との関わりはたくさんあって複雑なので、記事の後半から順を追って説明します。お楽しみに!!
F分布の期待値と分散
F分布の期待値と分散を求めましょう。途中式まで詳しく解説します。
多くの書籍ではF分布の期待値と分散までは掲載されていません。しかしアクチュアリー数学では公式として出題されますので、受験者は覚えておいた方が良いです。『アクチュアリー試験 合格へのストラテジー 数学 第2版』に公式のみ掲載されています。
F分布の期待値
まずは期待値から求めましょう。
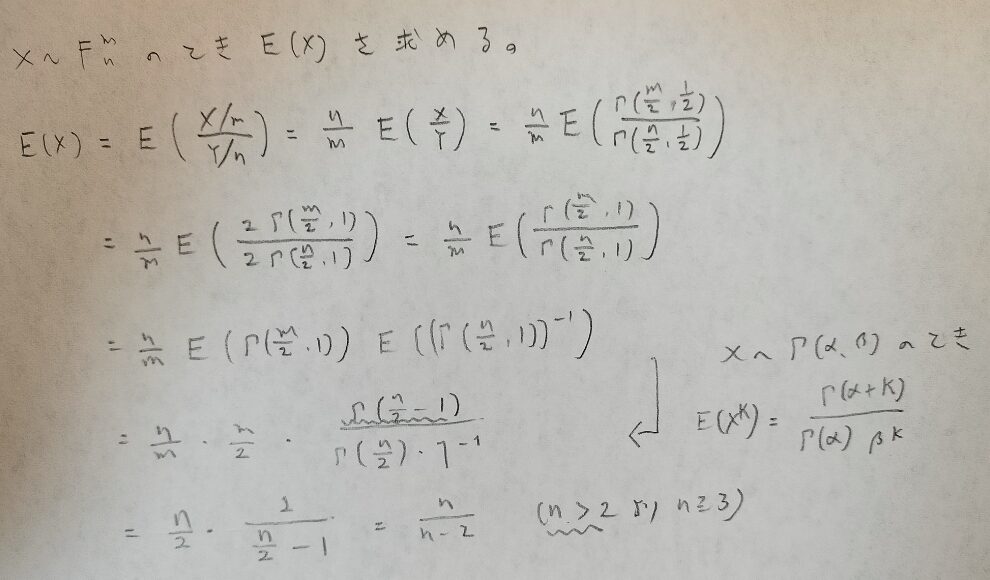
なんと!t分布の分散と同じ結果が出てきました!
その理由は記事の最後の方で解説します。t分布とF分布には関連性があるからです。
期待値の導出ではガンマ分布のk次モーメントの公式が本質な感じがしました!
期待値が存在するnの条件はガンマ関数の定義域が正の数であることから導いています。
F分布の分散
次にF分布の分散を求めます。
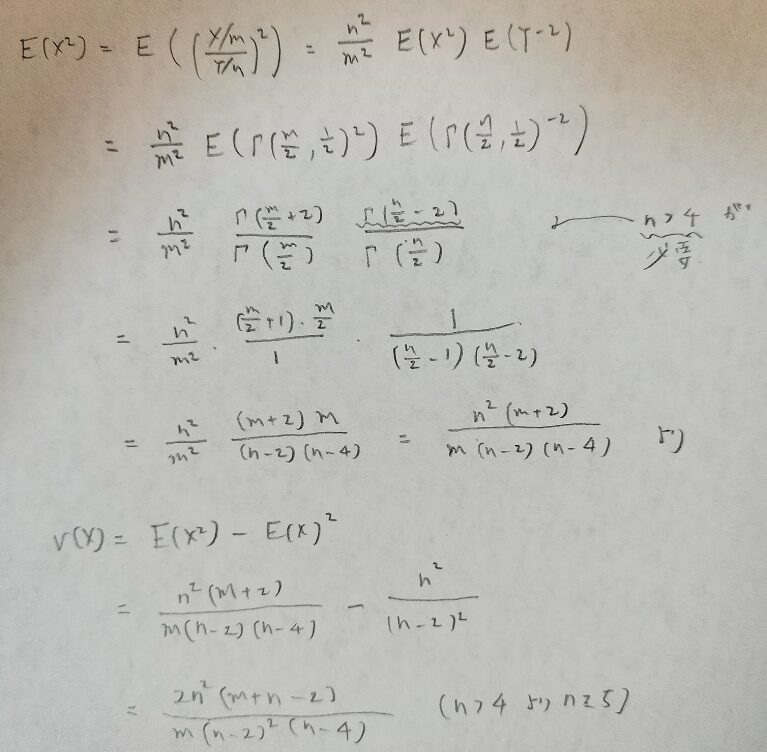
期待値のときはnが3以上で存在して、分散は5以上で存在するのですね。なんか複雑ですね笑
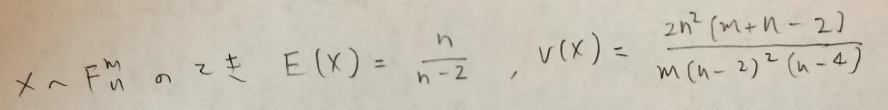
アクチュアリー数学では公式としてこれを覚えていないといけないので覚え方を教えます。
基本的にnは分母にくる。
登場する数字は2と4のみ。
それ以外はmは下でnはnorthで北なので分子にくる。
F分布とベータ分布との関係
F分布にも慣れてきたと思いますので、そろそろF分布の中核部分に入ります。
カイ2乗分布の比とベータ分布の関係
唐突にベータ分布が出てくると混乱すると思いますので、まずは記事の序盤で出てきたF分布の確率密度関数を導出する式から始めましょう。
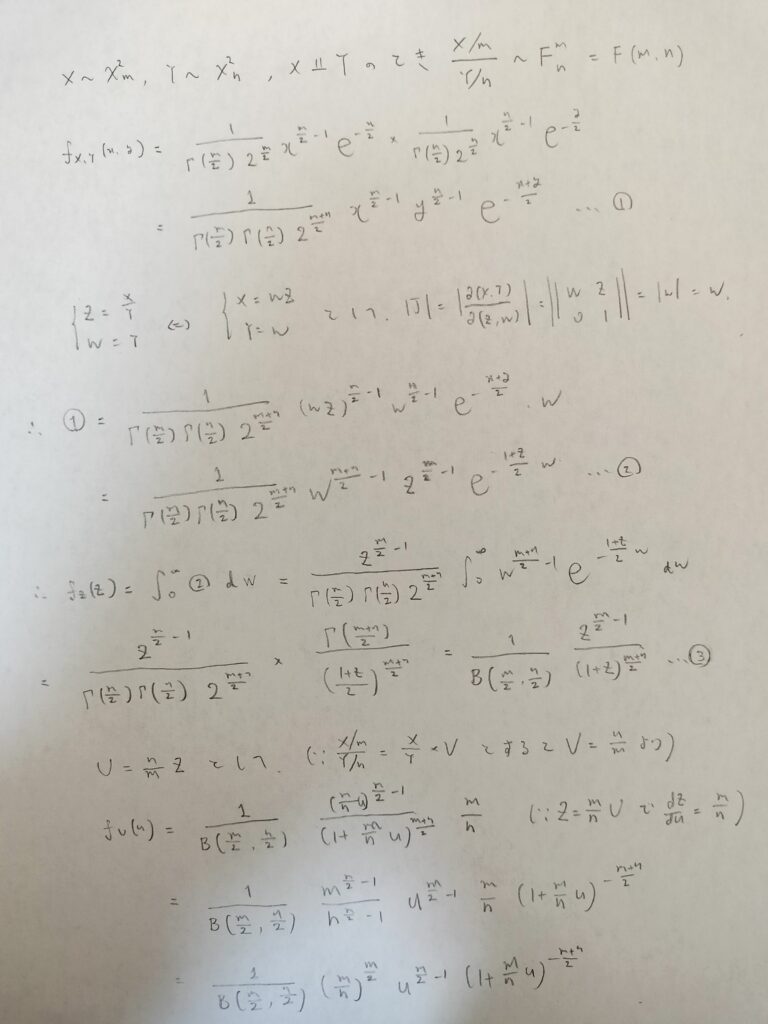
この③式から開始します。
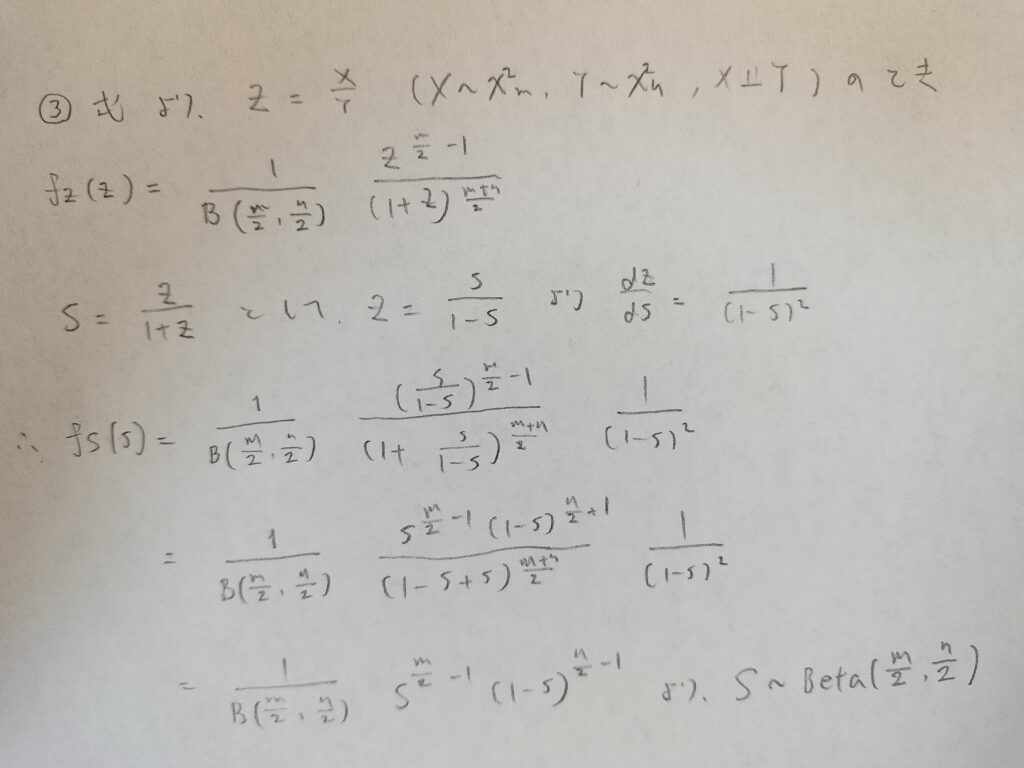
ZはF分布に従う確率変数ではないのでご注意ください。Zはカイ2乗分布の比に従う確率変数です。
なるほど。Zがどんな確率変数かをしっかりと理解しないと確かに混乱しそうですね。
ここで得られた結果をまとめます。
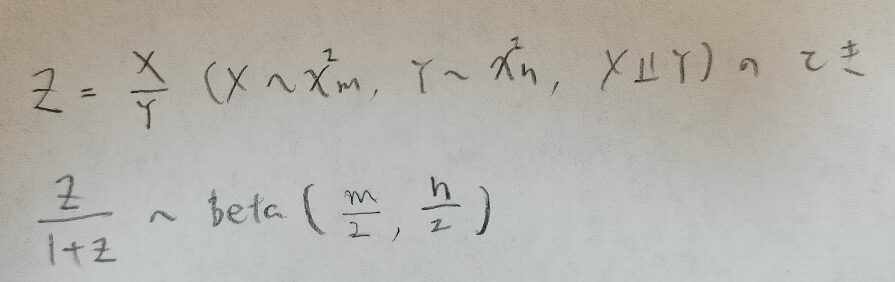
F分布とベータ分布の関係
いよいよF分布とベータ分布を結びつける関係式を紹介します。
多くの書籍ではカイ2乗分布の比とベータ分布の関係式、F分布とベータ分布の関係式のどちらかしか掲載されておりません。このことが混乱の元になっています。この記事では2つ同時に紹介しますので、頭が混乱しないように配慮して説明をしていきます。
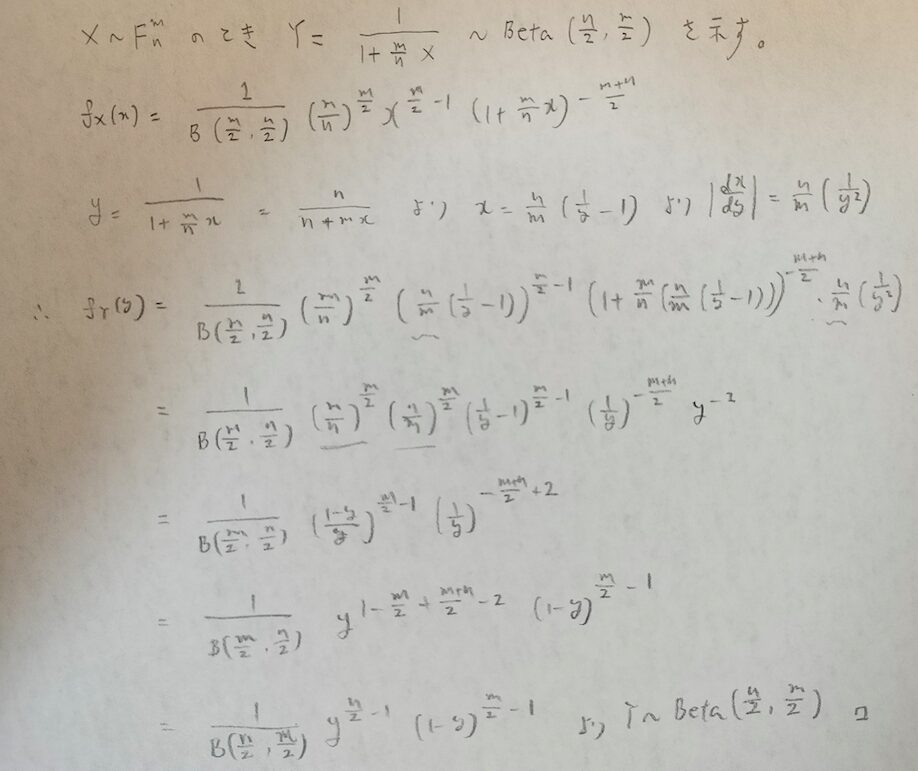
さっきの関係式と似ていますね。これは混乱しそうなのは納得です笑
カイ2乗分布の比とベータ分布の関係式、F分布とベータ分布の関係式をまとめておきます。
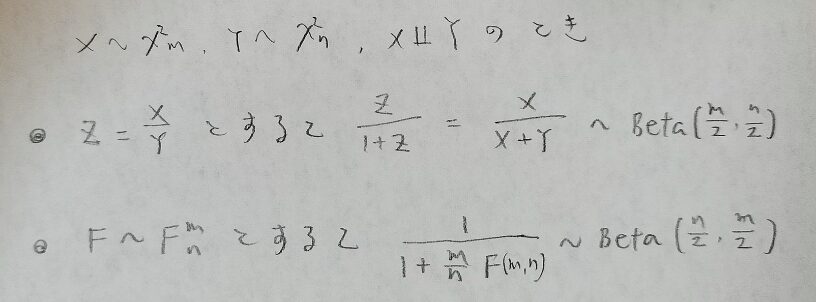
特に下のF分布とベータ分布の関係式が覚えにくそうなので、覚え方を紹介します。左側の分子1から分母の1へ目を移して次はm/nの分母nから分子mへ目を移してF(m,n)の中のmからnへ目を移し、右側に移ってBeta(n/2,m/2)でn/2→m/2へと視線を移していきます。目線の動きを覚えれば公式を暗記できます。
表で大切!F分布とベータ分布の上側ε点との関係
さらに混乱しやすいところへ移りますが、図と共に理解しましょう!
F分布とベータ分布の関係式をさらに深掘りするのですね!頑張ります。
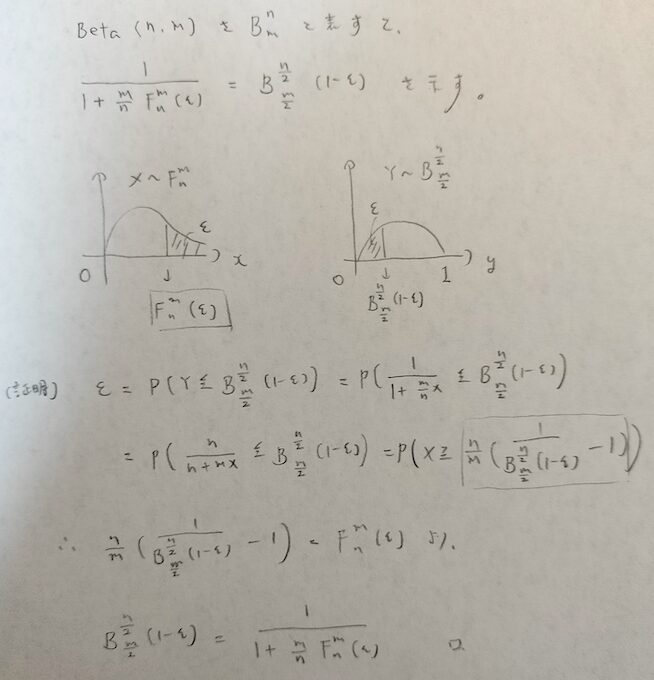
左辺と右辺で左辺が下側ε点で右辺が上側ε点になっています。逆になる!と覚えてください。
F分布とt分布の関係
F分布の期待値がなぜt分布の分散と等しかったのかを説明します。
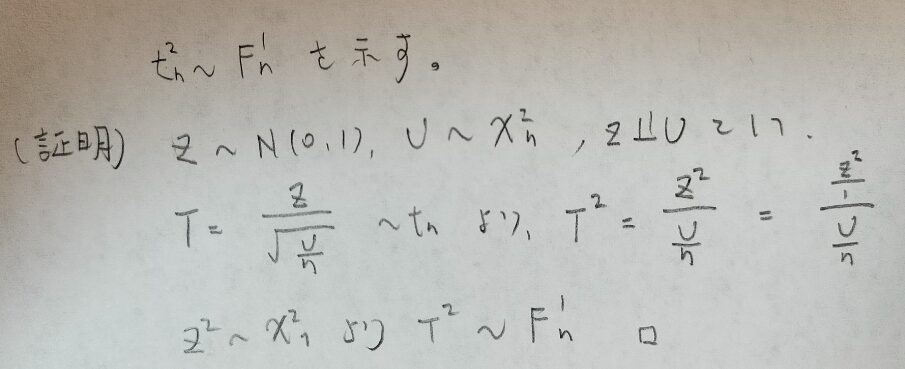
なるほど!t分布の定義とF分布の定義から導いたのですね!t分布の2乗がF分布のイメージを持っておきます!
標準正規分布の2乗→カイ2乗分布
t分布の2乗→F分布
F分布とベータ分布と標準一様分布(順序統計量)と負の二項分布と二項分布の関係
ここで一気に各分布が繋がるんですね!
ここは感動しますので、一緒に頑張りましょう!
F分布の自由度についての公式
F分布の逆数は自由度が反転します。
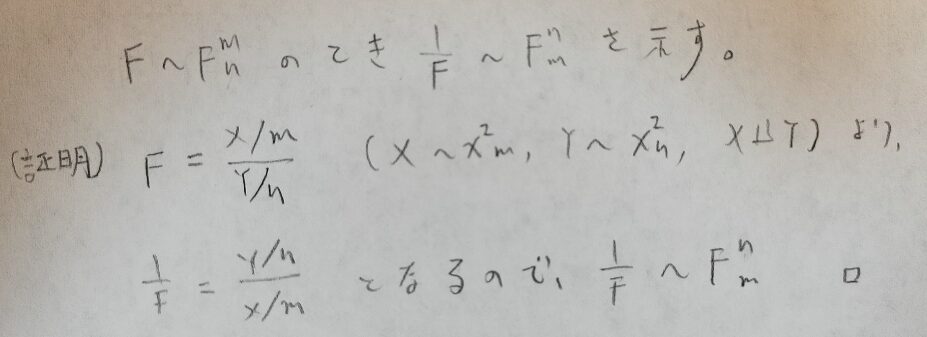
上側ε点はどうなりますか?
逆になります!さっきのF分布とベータ分布のときと同じイメージです。
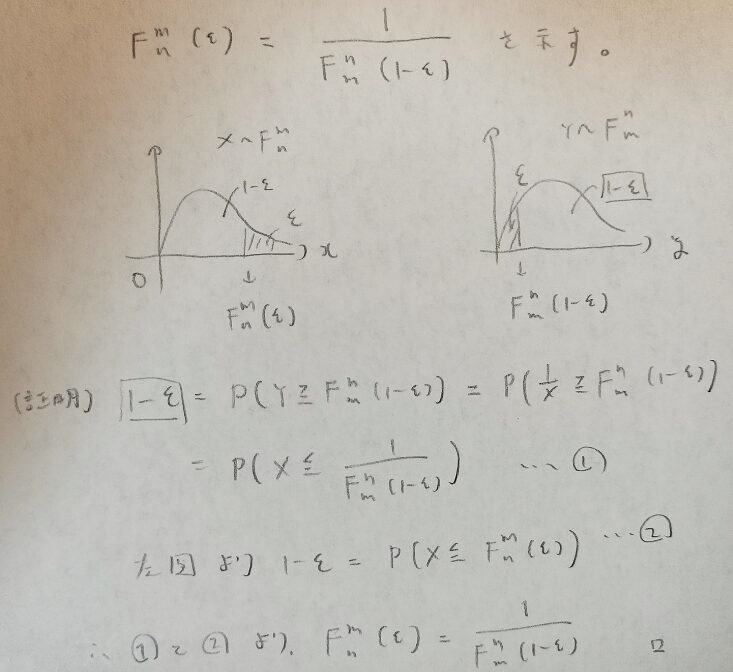
この証明はわかりやすいですね。1-εから始めると最後までスムーズにいけますね!
この記事でのメイン部分のF分布とベータ分布の関連性を3つまとめます。
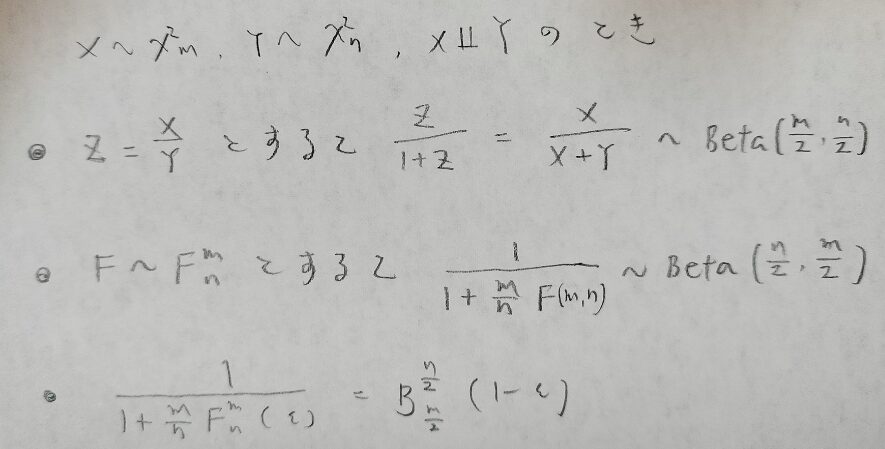
最後に二項分布→負の2二項分布→標準一様分布(順序統計量)→ベータ分布→F分布の関係性をまとめます。
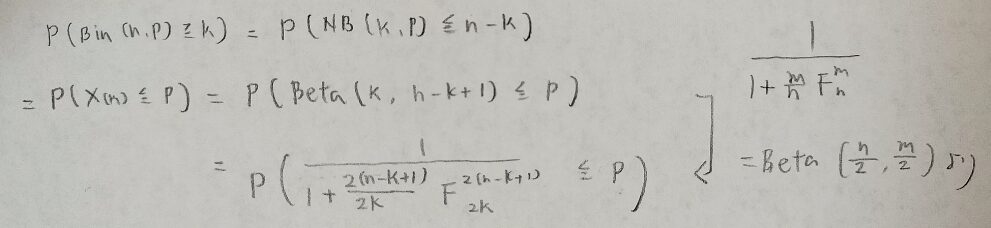
今まで勉強してきた分布が結びついて感動しました!ありがとうございました。





