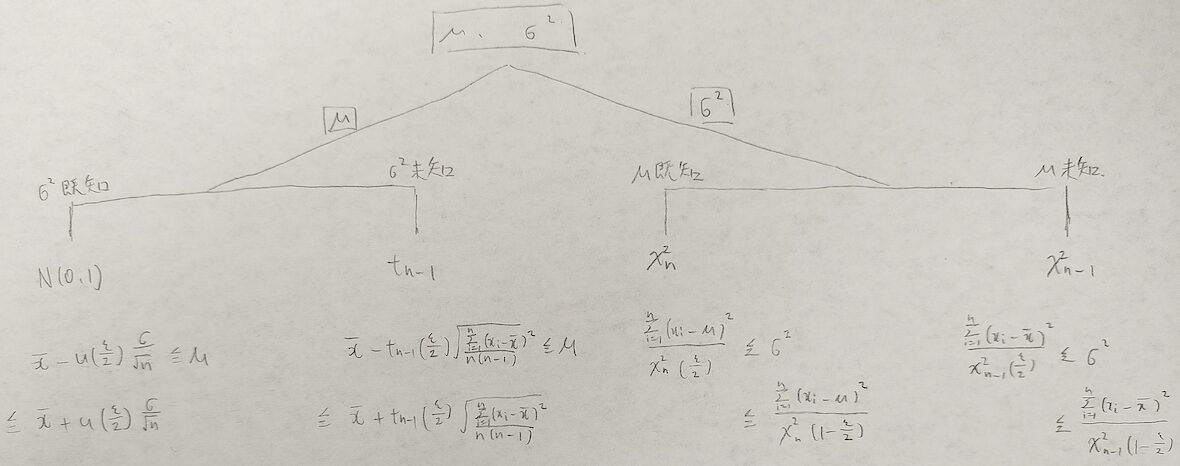
寿命などでよく用いられる指数分布の母平均μの区間推定について解説します。機械の故障問題などでも指数分布は用いられるので、指数分布の母平均の区間推定はとても実践的な話題です。
この記事では指数分布のいろいろな性質は学習済みとしています。未学習の場合は、次の記事をご覧ください。
この記事の最後ではひょっとすると信頼区間の結論に対してビックリするかも知れません。結末は記事の終盤の図16をご参照ください。
指数分布の母平均を最尤法で求める
前回の記事で詳しく学習した区間推定における信頼区間の求め方を復習しておきます。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
信頼区間の出し方でなぜ最尤推定量から出発するのか疑問の方は次の記事をご覧ください。
母平均μを持つ指数分布についてμの最尤推定量を求めます。
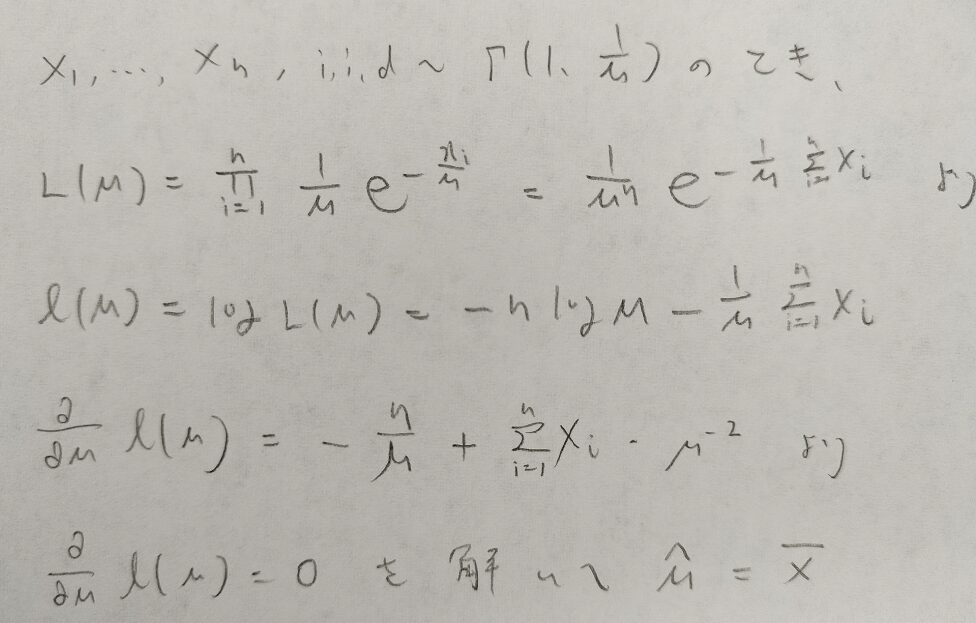
では、この標本平均をもとにして統計量Tを求めていきます。
ちょっと待ってください!
はい。どうしましたか?
前回の記事での正規母集団では母平均の最尤推定量が標本平均だったのは感覚的に納得できました。でも指数分布の母平均がなぜ標本平均と一致したのか感覚的にわからないので、教えてください。
了解しました。それでは点推定の1つであるモーメント法を説明します。モーメント推定量を考えれば感覚的に納得できるはずです。
モーメント推定量は今回の指数分布の母平均の信頼区間の結果には関係ありません。指数分布の母平均の最尤推定量が標本平均になることの感覚的な理由を感じたい方は次の章を飛ばして先にお進みください。
指数分布の母平均をモーメント法で点推定する
モーメント法を説明します。モーメント法は期待値と分散がメインになるので、確率分布の特性値に強い方ならすぐに出すことができます。
モーメント法を支えるのは大数の法則です。まずはモーメント法の概要をご覧ください。大数の法則を理解してからモーメント法に戻り、具体例として指数分布の母平均のモーメント推定量を求めてみます。
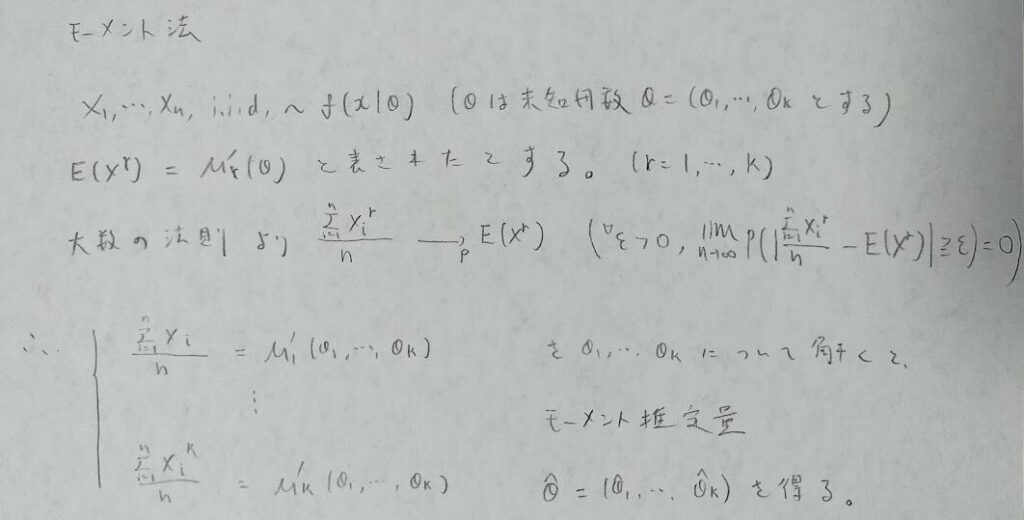
これはさっぱりわかりませんので、大数の法則の説明をお願いします。
大数の法則を示すためには、チェビシェフの不等式を用います。そしてチェビシェフの不等式を示すにはマルコフの不等式を使います。
マルコフの不等式→チェビシェフの不等式→大数の法則の順番で示します。
マルコフの不等式
マルコフの不等式は生存関数を上から大雑把に評価するための不等式です。
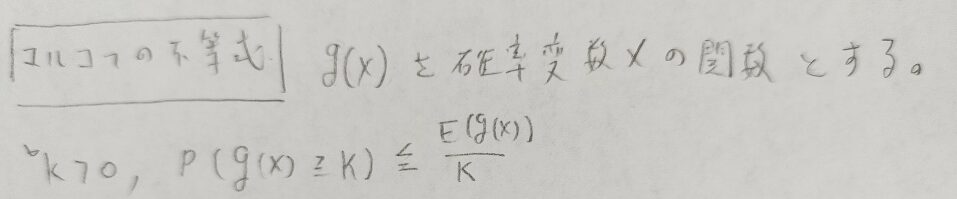
マルコフの不等式を証明するために定義関数を用います。定義関数を用いると確率分布の表現が簡素化されるので便利です。
定義関数に関する注意点や使用法などは『現代数理統計学の基礎』に詳しく掲載されております。
この本は統計検定1級のためのバイブルですよね!

チェビシェフの不等式
チェビシェフの不等式はアクチュアリー数学や統計検定1級などで登場する一致推定量の議論で用いる頻出の不等式です。
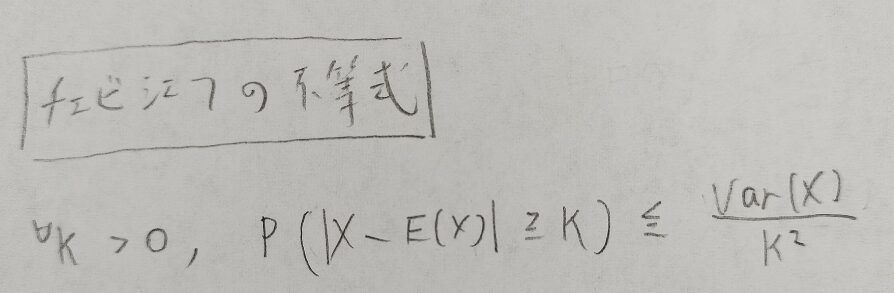
チェビシェフの不等式はマルコフの不等式から導けます。
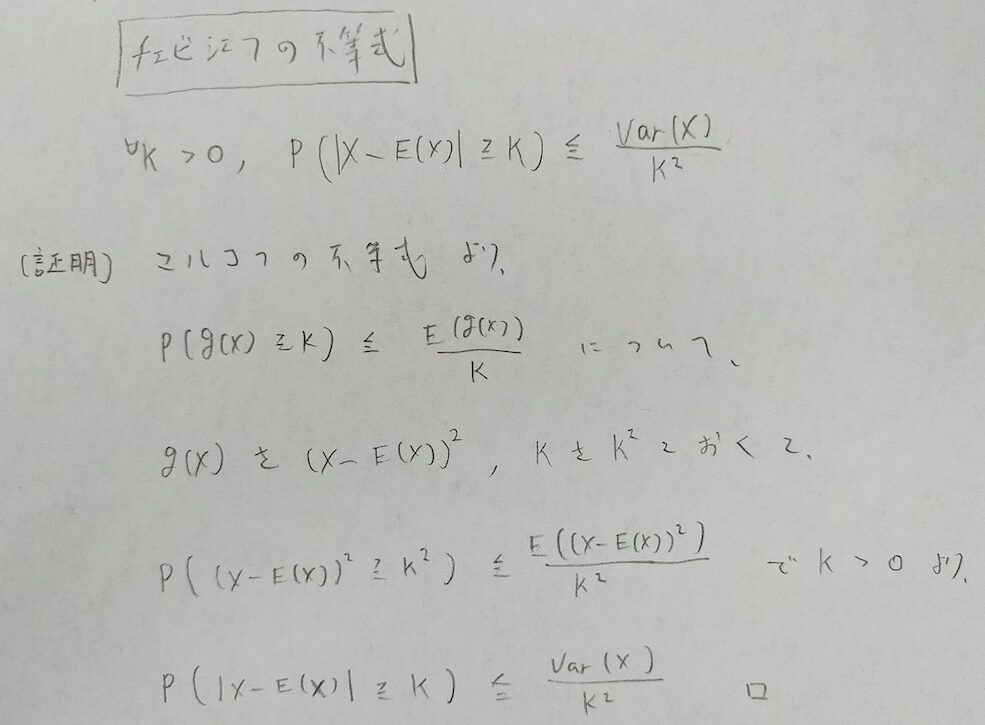
大数の法則(大数の弱法則)
いよいよ大数の法則を証明します。モーメント推定法に関わるのは大数の法則の高次バージョンですが、まずは有名な方を示します。
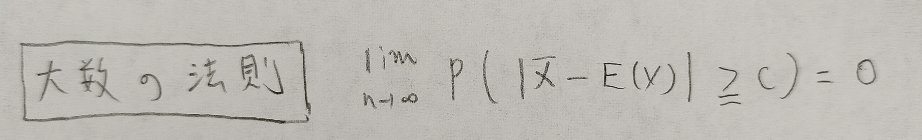
このときに、標本平均はXの期待値に確率収束するといいます。→pという記号で表現します。
「確率収束することを証明せよ」といわれたら、極限の式を立式して考えれば良いですね。
その通りです。そして大数の法則はチェビシェフの不等式を用いれば証明できます。
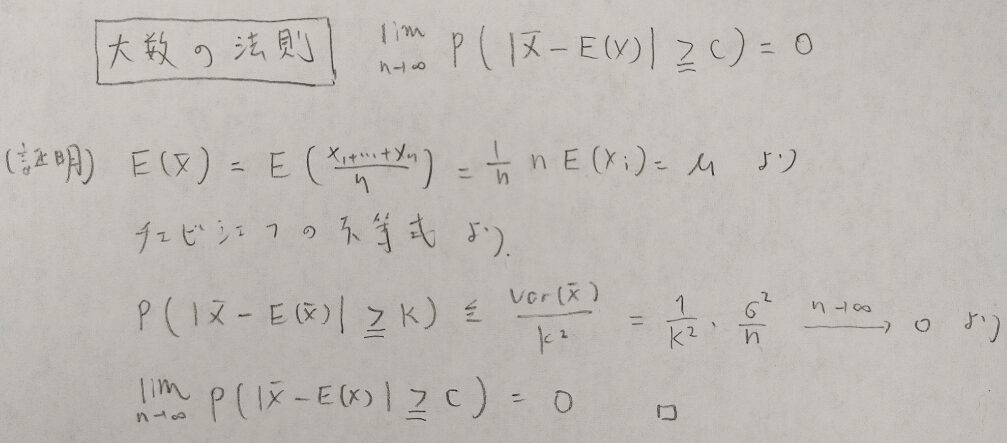
それではいよいよモーメント法に戻りましょう。
モーメント法
それでは具体的な問題設定でモーメント推定量を出してみましょう。
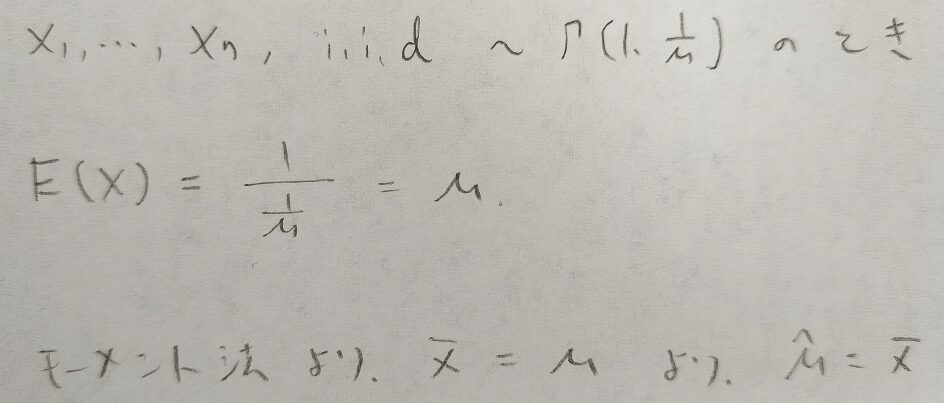
え?これでおしまいですか?笑
その通りです。この例では1次モーメントのみで完結しました。つまり標本平均と期待値がイコールとして母平均の推定量を出しました。
推定量が2つある場合は2次モーメントまで持ち出して、分散も持ち出せば理論上は答えが求まるのですね!
それではモーメント法の概要をもう一度出します。言っている内容が理解できるはずです。
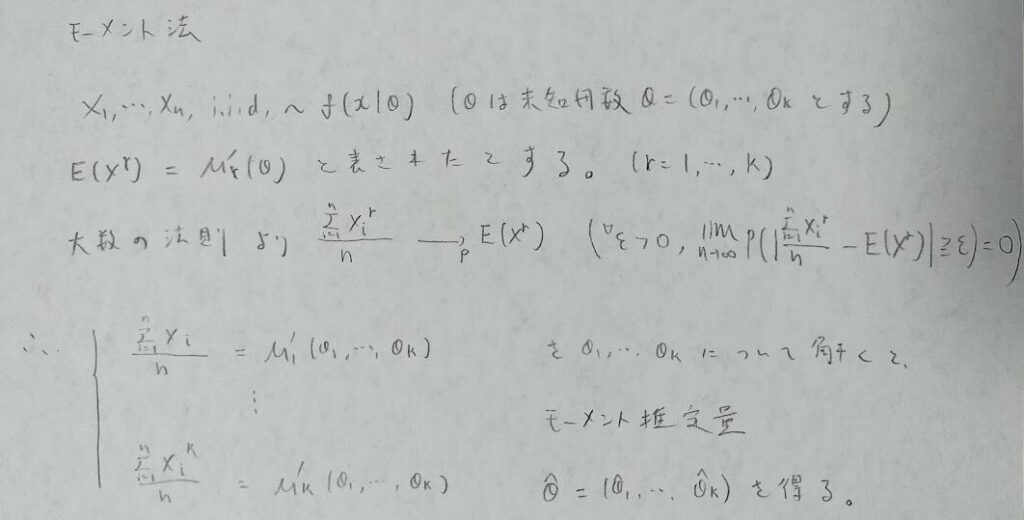
途中で大数の法則より〜と書いている部分の証明が書籍に載っていないので証明をお願いします。
了解しました。チェビシェフの不等式から証明してみましょう。記号に慣れるため確率収束の記号を用いています。
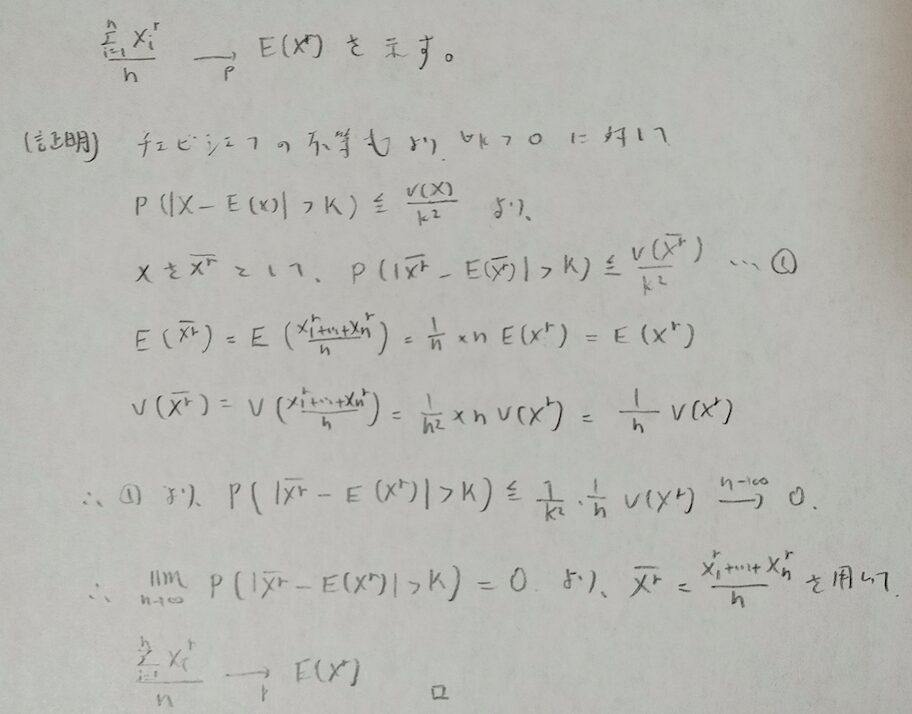
長くなりましたが、指数分布の母平均の最尤推定量が標本平均になることは、モーメント推定量を考えれば納得できたのではないでしょうか。
指数分布の母平均の区間推定(打ち切りなし)
打ち切りという概念が登場します。打ち切りとは観測を①回数で打ち切る定数打ち切りと、②ある値で打ち切る(定時打ち切り)の2種類があります。まずは打ち切りがない状態での母平均の区間推定を考えます。打ち切りの名前は『確率統計演習 2 統計』を参考にしています。
この本はアクチュアリー数学の指定教材です。アクチュアリー数学に限らず数理統計学全般に対応した問題集です。
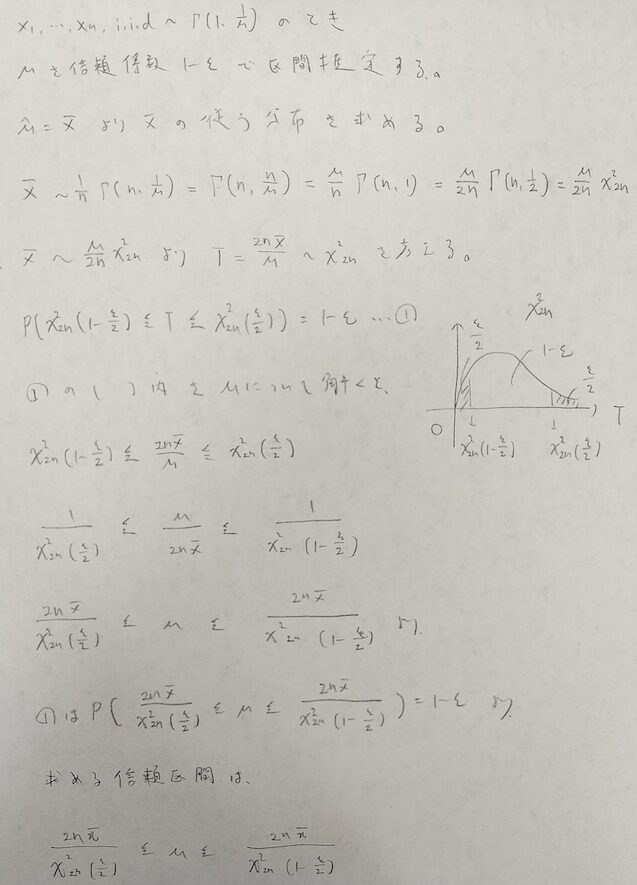
統計量Tの出し方がなんだかスッキリしません。
別の角度から説明してみました。
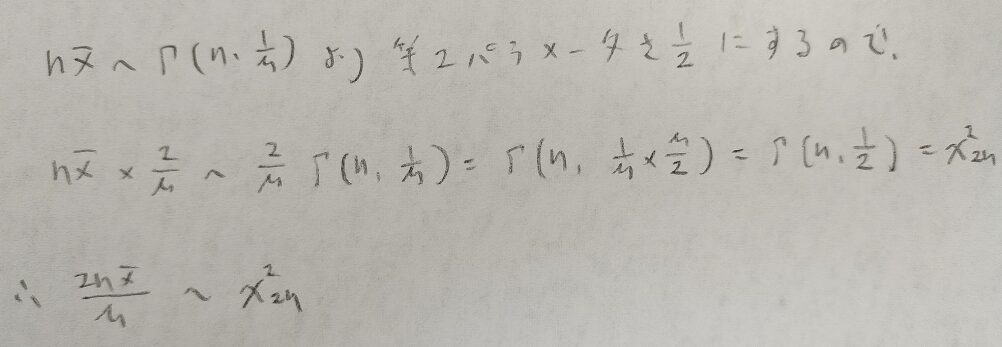
これから打ち切りがある場合を考えますが、母平均の信頼区間の結果は3つとも同じです。違うのは最尤推定量のみになります。そのため最尤推定量をどのようにして求めるのか?という観点でこの先をお読みください。
指数分布の母平均の区間推定(定数打ち切り)
定数打ち切りは順序統計量の考えを用います。未習の方はこちらをご覧ください。
説明では定数打ち切りの定義を考えて順序統計量を用いていますが、例えば『確率統計演習 2 統計』では順序統計量を使用していません。また上の記事と関連づけるため順序統計量を用いています。

ここからの流れは図12の後半部とまったく同じです。違うのは最尤推定量のみです。
指数分布の母平均の区間推定(定時打ち切り)
定時打ち切りの場合は、ある時点で観測を止める方法です。

あれ?さっきの結果と似てますね!
素晴らしい。よく気づきました。今回のXの部分のみ異なるだけであとは一緒です。そして信頼区間も図12の後半部からの流れは全く一緒です。異なるのは最尤推定量のみです。図16に詳しくまとめました。

指数分布の母平均の最尤推定量の法則は、打ち切りがない場合(つまり標本平均)をベースにし、分子について残りのN-n個の観測されない(打ち切られた)データを追加したものを観測数nで割ればOKです。このように考えれば3つの最尤推定量がなぜこのような形になるのかが感覚的に理解できます。
こうなると商品の信頼性という考えが大事だと痛感します。
実は数学では信頼度という概念を定義できます。最後に信頼度の紹介をして終わりたいと思います。
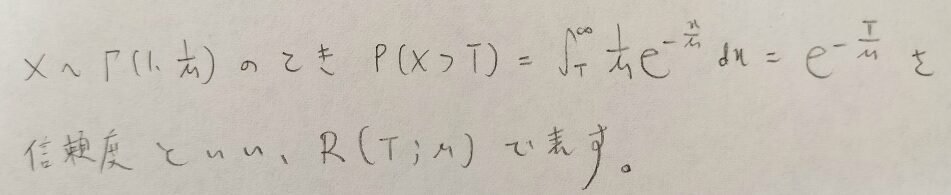
製品や人がある一定時間以上動き続ける確率を信頼度というのですね。
実はこの信頼度とは生存関数のことです。気づかれましたか?生きることと信頼がつながって感動しました!