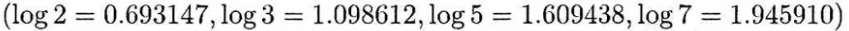連続確率分布の一様分布の次は指数分布になります。
正規分布だと思っていました。なぜ指数分布を選んだのですか?
指数分布は「どれくらい待てば良いかの確率」や「地震の発生する確率」など、世の中での生活での応用が効く例が多く一様分布以上に身近な分布です。
指数分布を使えれば便利そうことがわかりました。さっそく勉強していきたいです!
一体なぜ、それらの状況が指数分布で説明できるのか?そして指数分布とはどういった数式なのか?など理解のしやすさを優先して、分かりやすく説明していきますね。一緒に頑張りましょう!
目次[非表示]
累積分布関数と生存関数(テイル確率)
指数分布を学ぶにあたり、累積分布関数と生存関数(テイル確率やしっぽ確率とも呼ばれます)をおさえます。
累積分布関数は分布関数とも呼ばれます。
まずは分布関数F(x)から定義します。大文字で表記することがポイントです。
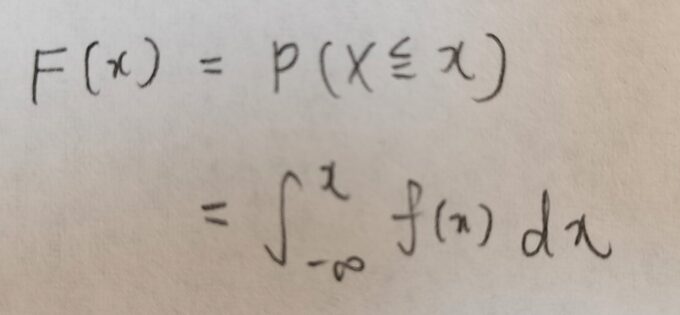
離散確率分布ならシグマ計算に対応しますね。
次に生存関数S(x)を定義します。たぶん生存の英単語がsurvivalなので、その頭文字を取ったのかな?と考察しています。
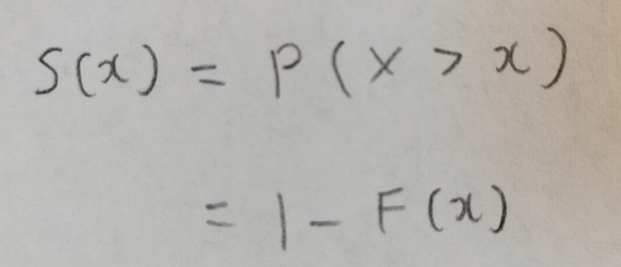
ポイントは離散確率分布の時にも定義できるように、等号を抜いているところです。ここら辺の説明は『弱点克服 大学生の確率・統計』を参考にしました。この本では生存関数のことをしっぽ確率と呼んでいます。
生存関数の特徴はどういったものがありますか?
上での定義からS(0)=1です。そしてxが∞になるにつれて値は0に近づきます。
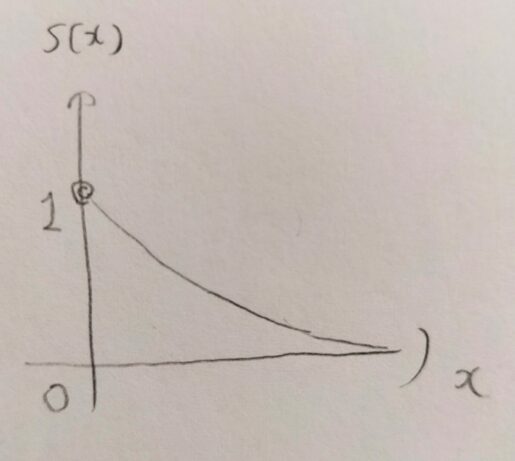
S(x)のイメージはこのような感じです。S(0)での微分係数は負であることに注目してください。
確かに!グラフが減少しているからですね。
無記憶性を満たす唯一の連続分布が指数分布
指数分布を特徴づける事柄を学び、その副産物として指数分布を導出します。
タイトルにある無記憶性ってどういう意味ですか?
無記憶性とは下記の数式を満たす性質のことです。アバウトに言えばすでに経験した記憶を無くした状態で居続ける性質ということです。
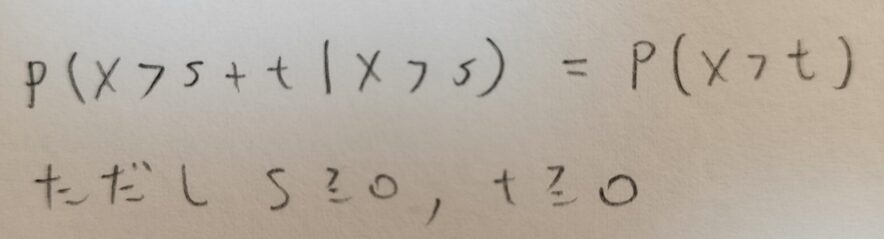
Xが連続確率変数のとき、無記憶性を持つときに、Xはどのような確率分布に従うかを計算で示してみましょう。
式の途中で出てくるλが正、つまりλ>0であることを意識しましょう。次の証明にはその根拠も述べられています。途中の式で両辺からS(s)を引くとという記述がありますが、正しくはS(s)/tを引くになります。
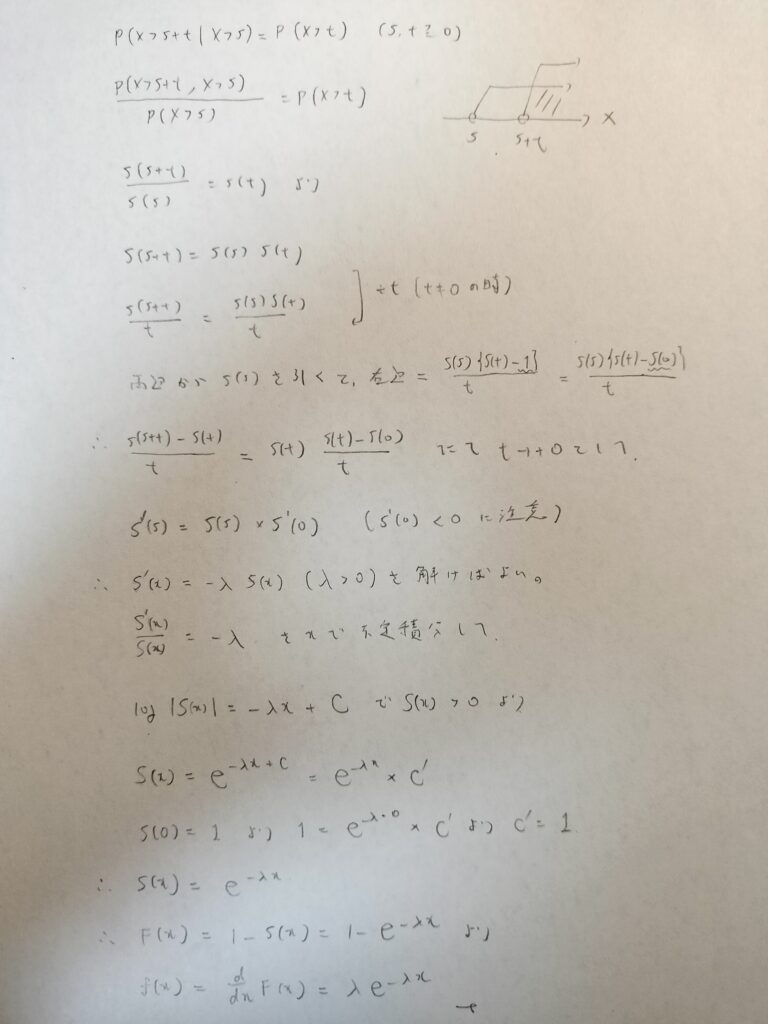
微分方程式を導いてそれを解く流れで証明を行いました。この微分方程式は変数分離型と呼ばれるタイプです。常微分方程式の知識は『常微分方程式キャンパス・ゼミ』で仕入れることをおすすめします!(説明がとても分かりやすいので)
最後に出てきた自然対数の底eを用いた式がXが従う確率分布ですね!
そうです!この分布を指数分布といいます。x≧0かx>0かは本によって異なりますが、この記事では説明の都合上x>0としておきます。
『リスクを知るための確率・統計入門』ではx≧0
『弱点克服 大学生の確率・統計』ではx>0としています。
そしてこの結果から次の事実が導かれます。これこそが指数分布を決定付ける特徴です。
無記憶性を持つ連続確率分布のことを指数分布といいます。
指数分布と幾何分布とファーストサクセス分布との関係について
指数分布は幾何分布とファーストサクセス分布と無記憶性で繋がっています。
離散確率分布で無記憶性を持つ分布は幾何分布とファーストサクセス分布のみになります。
こちらも証明を知りたいです。お願いします!
まずはXが自然数という条件のときに無記憶性を持つ分布はファーストサクセス分布のみであることを証明します。
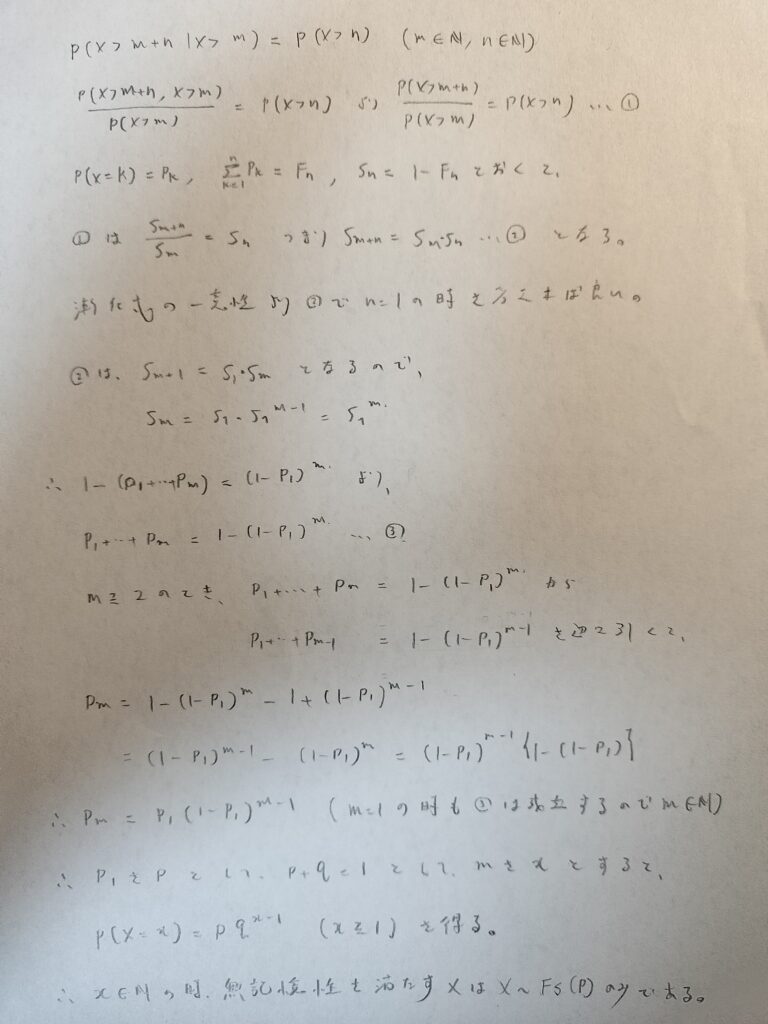
この証明ではmとnが両方動くと難しいので微分方程式の一意性を用いています。これを使うとmを固定してn=1として解いた結果が所望の結果であるという論理で考えました。
次にXが0以上の整数という条件のときに無記憶性を持つ分布は幾何分布のみであることを証明します。こちらの方が難易度が高い証明です。
(結局は上の証明と同じことをしているのですが)最初の式では上の証明で用いたXが自然数のときの流れを用いたいので、無記憶性の式に調整を加えています。

長すぎますね!笑。でも幾何分布やファーストサクセス分布にも無記憶性があると知って驚きました。
実はこれは無記憶性の意味を考えれば納得のいく結果なのです。
無記憶性とは、すでに経験した記憶を無くした状態で居続ける性質ということです。幾何分布やファーストサクセス分布は、初めて成功する事象を違った角度から見た分布です。これらの反復試行は互いに独立なので無記憶性を持つことは自然と理解できると思います。
指数分布とはどういった確率変数を持ちその確率変数が従う式(指数分布の確率密度関数)はどのような意味を持つのかイメージできますか?
無記憶性を持つような連続分布なので、幾何分布やファーストサクセス分布の考えを連続的にすれば良いのですよね?わかりそうでパッとした例が思いつきません。
指数分布のハザード関数
そのモヤモヤ感はハザード関数を定義すれば一気に解消します。
ハザード関数…なんか危険な感じがするお名前ですね。
ハザード関数とは「x時間まで動いていてΔx(一瞬の後という意味です)時間後に止まる確率」を数式化したものです。
それでは分かりやすく数式で変形してハザード関数の正体に迫りましょう!
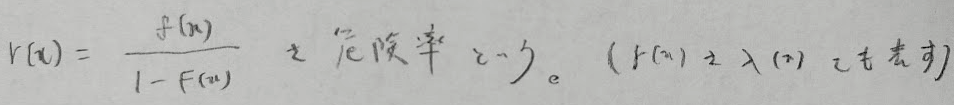
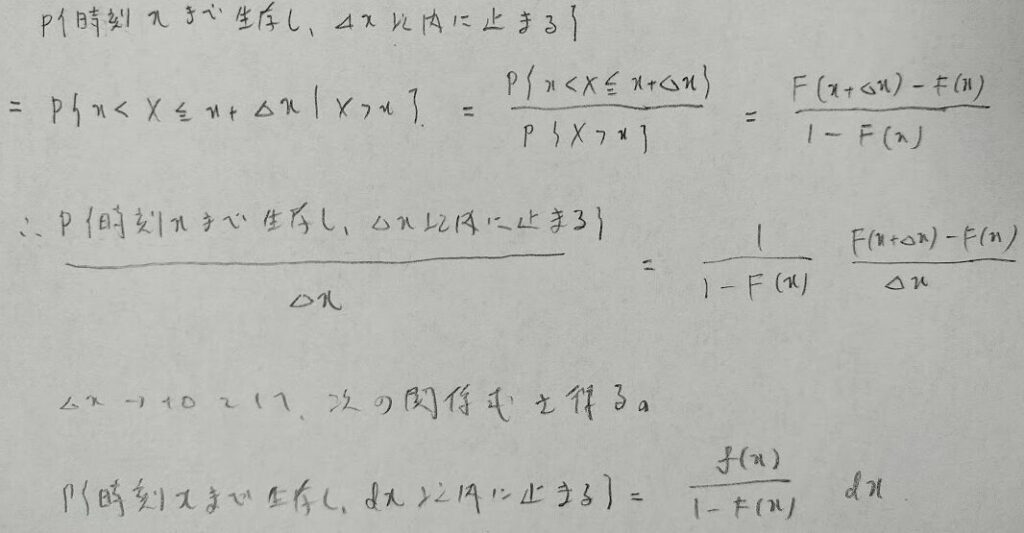
上の導出ではP{ }が確率密度関数×dx(つまり微小時間に生じる確率)という意味で進めています。本によってはP{ }が確率密度関数(確率0)という意味で進めているものもあります。
なんと分布関数と確率密度関数を用いて表現できちゃいましたね!
ハザード関数とは確率密度関数と生存関数の比の値のことだったのです。
指数分布はハザード関数とどのように関係しているのですか?
良い質問です!ハザード関数を一定としたときのf(x)の正体を暴いていきましょう!
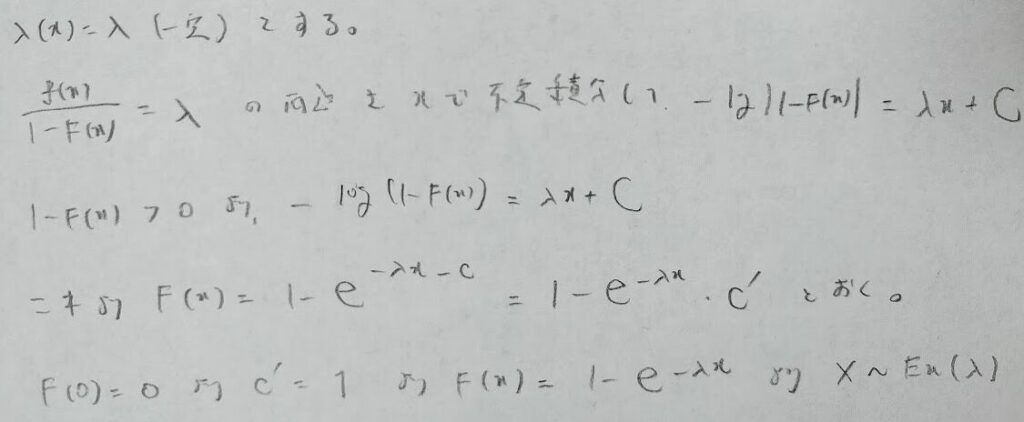
ええっ?!なんと指数分布が出てきましたよ!
ビックリしますよね!それでは指数分布はどのような意味を持つ分布だと思いましたか?
指数分布とは無記憶性を持つ唯一の連続確率分布です。そしてハザード関数が一定値λ、つまり「x時間まで動いていてΔx(一瞬の後という意味です)時間後に止まる確率」が一定値λという特徴を持つ確率分布です。つまり指数分布とは間隔(時間)を確率変数に持ち「劣化せず(無記憶性を持ち)停止は偶発的なイベントで発生」する確率分布ということになります。そのため指数分布は寿命や機械の故障間隔などをテーマにした分布として用いられることがあります。
とても納得しました。λの持つ意味もわかりました。λが正の値である理由もきちんとした根拠があったのですね!
イベントという表現を使いました。イベントには良いイベントと悪いイベントがあります。そしてイベントは発生するものです。イベントの発生といえばポアソン分布とも関連しそうです。その話題は記事の終盤で深掘りします。
指数分布の期待値と分散をガンマ関数を用いて分かりやすく計算します
指数分布は連続確率分布なので当然全確率1を満たすはずです。
さっそく証明しましょう!
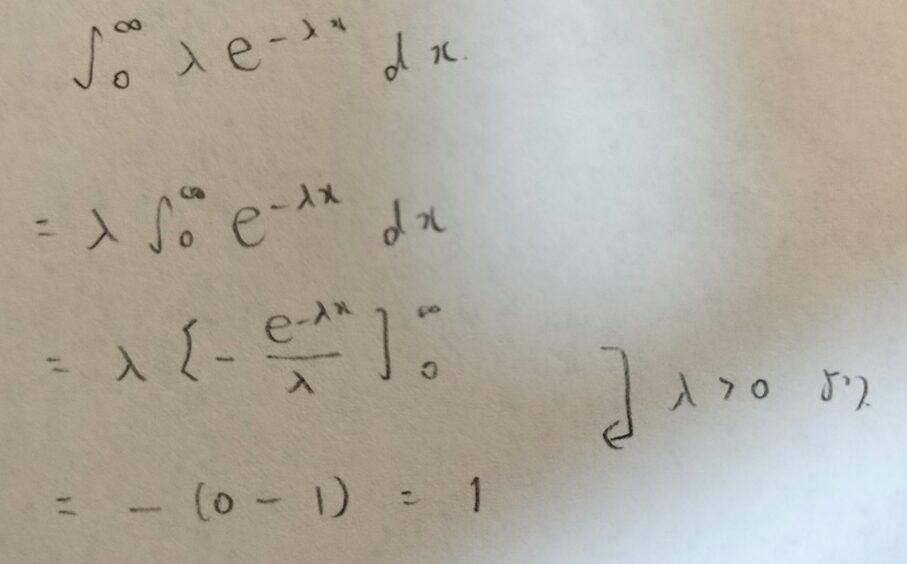
λ>0という条件がここで活用されましたね!
次は期待値と求めますが、その前にガンマ関数の計算ができるようになっておくべきです。
ガンマ関数を用いなくても計算できますが、計算量が爆発します。『弱点克服 大学生の確率・統計』の著者の藤田先生もガンマ関数は使えるようにすべきとおっしゃっています。
次の数式を満たす関数をガンマ関数といいます。
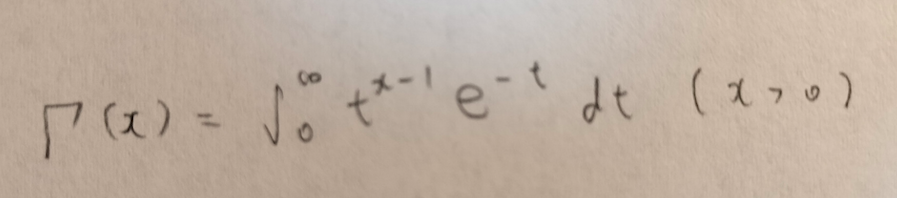
これは覚えにくいですが、数学検定1級でも頻出なので、大学教養数学を勉強をされた方は馴染みがあると思います。
確かガンマ関数って階乗と関係ありましたよね?ガンマ関数に直せると階乗計算ができるから一瞬で計算が終わって便利だった覚えがあります。
まずはガンマ関数の有名性質を導いてみます。
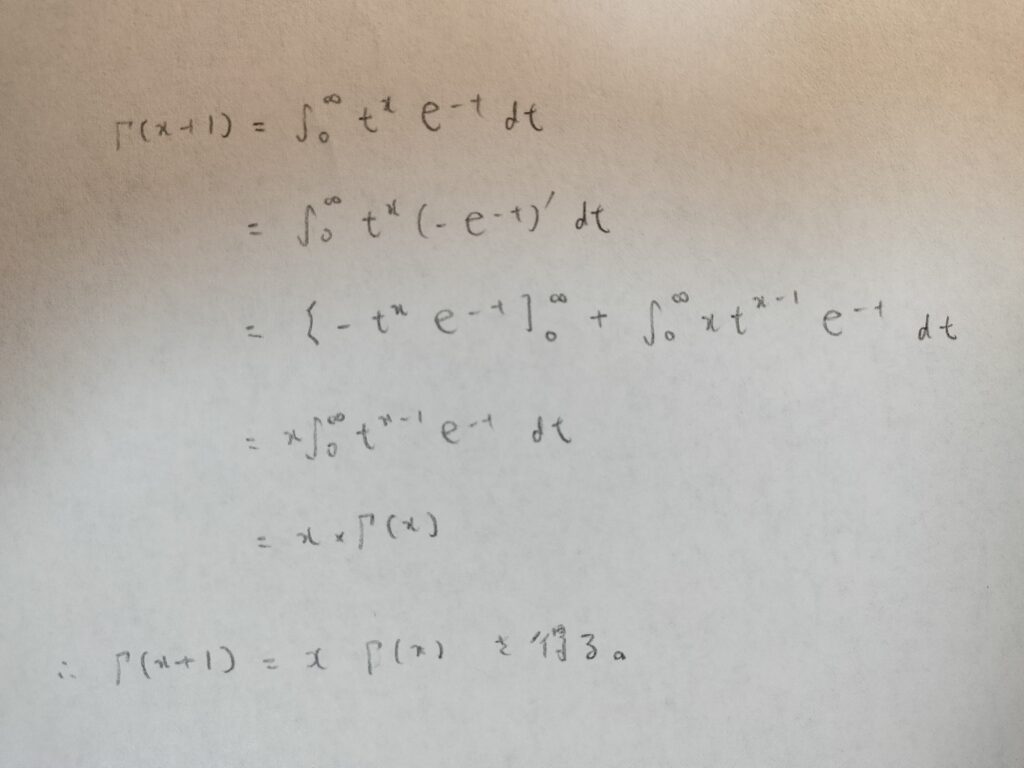
次にx>0を自然数nと考えたときの処理をしていきます。
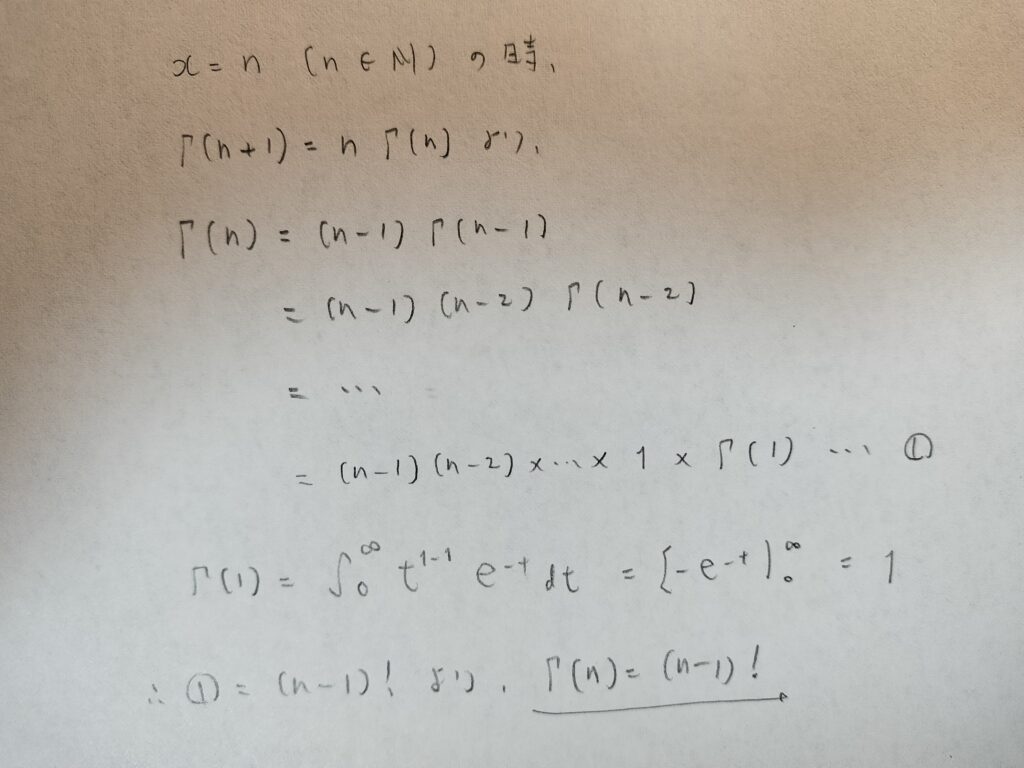
nが自然数のときという条件のときに証明をしました。つまりガンマ関数とは階乗の一般化だったのです。ガンマ関数を使うととても便利!という表現は『確率統計キャンパス・ゼミ』では計算がGAMEOVERになるという表現をするなど、いろんな本の随所からガンマ関数の便利さが伝わってきますね。
では指数分布の期待値の計算をしましょう!
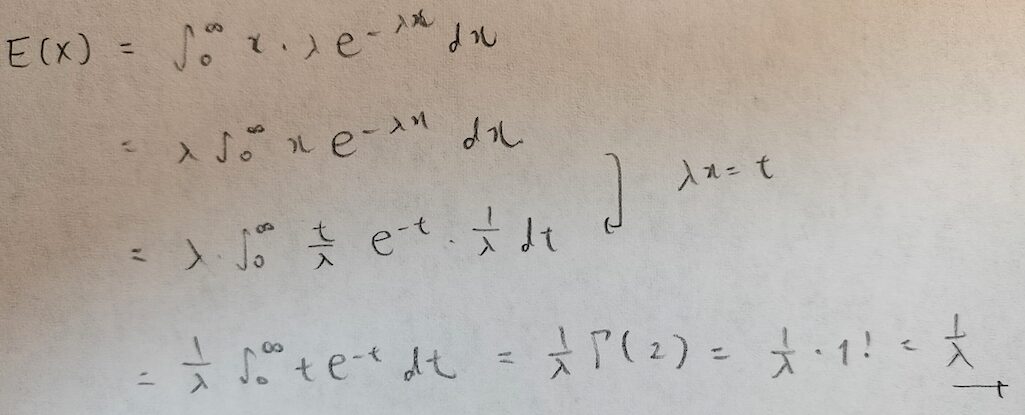
Γ(2)などスラスラ使えるとかっこいいですね!
次に指数分布の分散を計算します。まずはXの2乗の期待値からです。
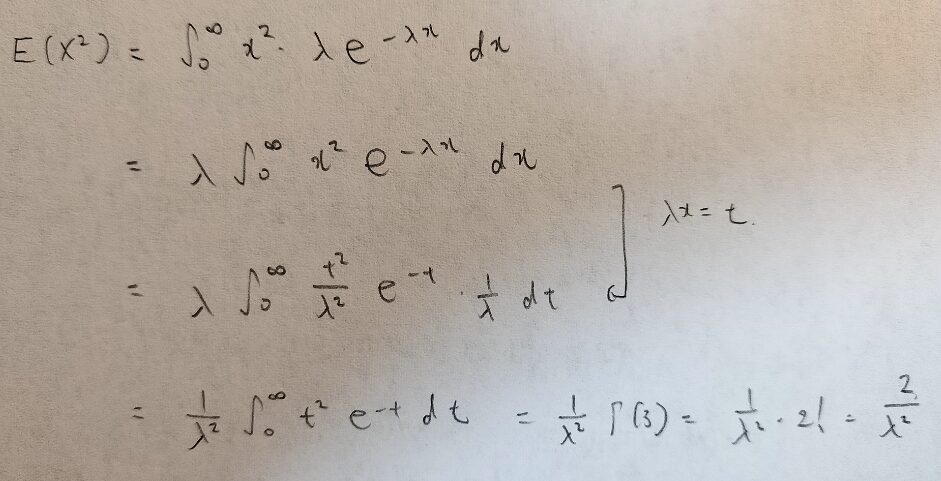
では分散の計算をしましょう。
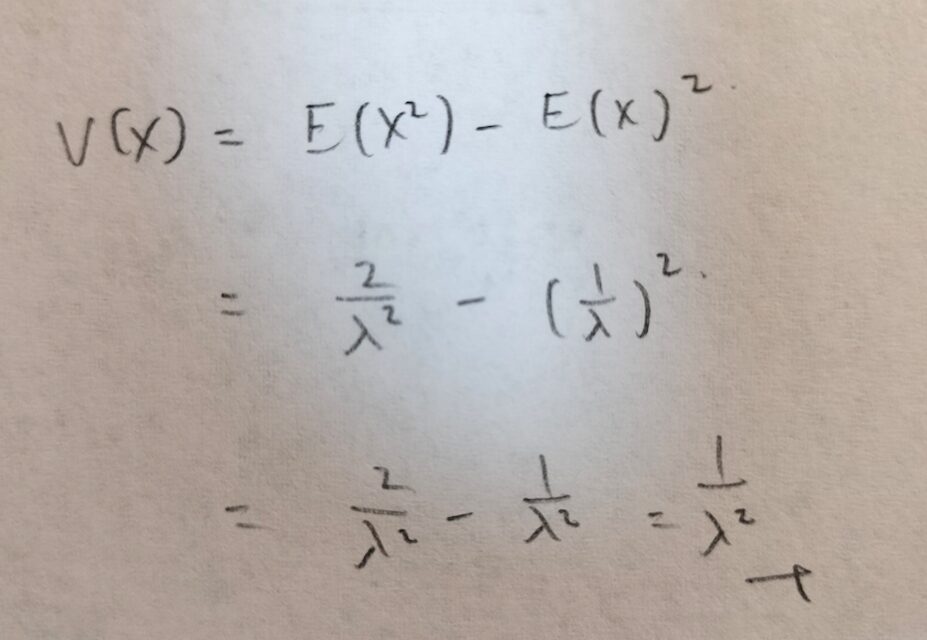
指数分布のパラメータはλの1つですので、期待値も分散もλを用いて表現できることは自然な流れだと思います。
期待値がλの-1次式。分散がλの-2次式なので覚えやすいですね!
指数分布の例
指数分布がどのような問題として使われているのかを2つの例を用いて説明します。
イベント発生の確率
100年に1度起こるイベントの発生間隔をXとおく。このイベントが10年以内に起こる確率を求めてください。
『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考にしました。
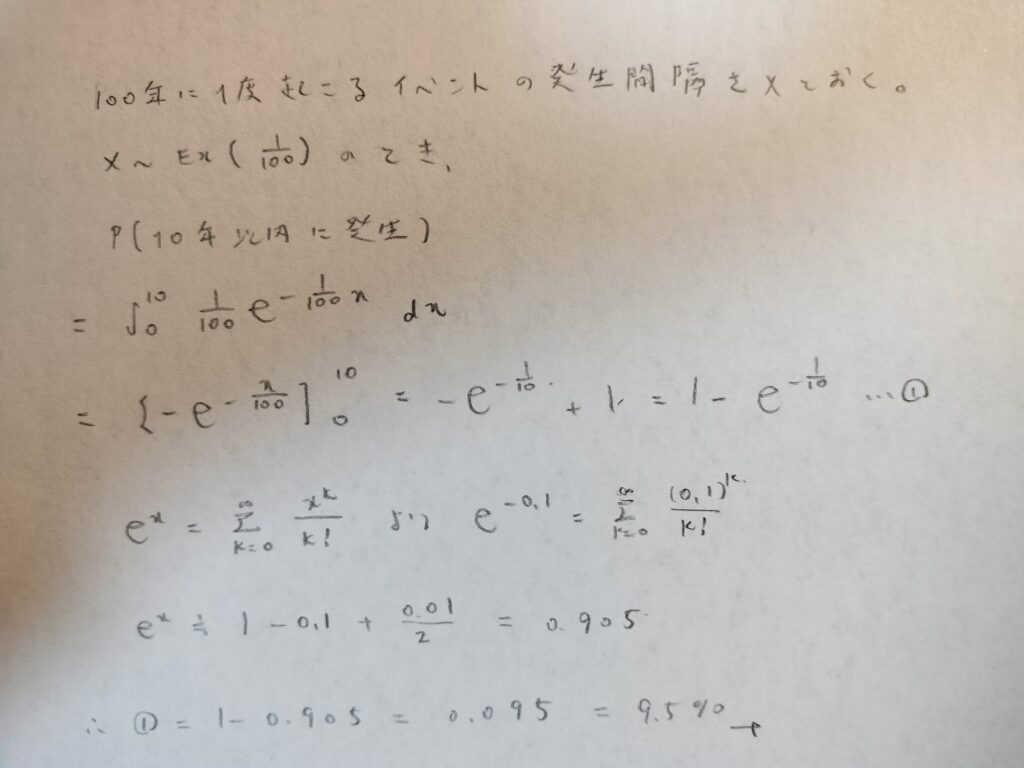
イベントとは色々あります。悪い意味でのイベントは日本語ではイベントとはあまり言わないため、指数分布を使うと判断しずらいようです。例えばこの問題は地震の発生確率の問題としても扱えそうです。実際は地震の発生分布はきちんとした分布がありますが、今回はアバウトに指数分布に従うと仮定しています。
9.5%って思ったより低くて安心しました!
記憶の忘却問題
次の問題は人の記憶の忘却に関する問題です。忘却とはネガティブな単語ですが、これもイベント発生と読み替えてください。
人間の記憶が残存する時間は指数分布に従うとし、30分以内に記憶が失われる確率は1/2であるとする。このとき、記憶の平均残存時間を求めよ。
アクチュアリー数学(平成9年)
求める値は期待値であるということに気づけるかどうかがポイントです。そのためには指数分布の期待値を知っていないといけません。
指数分布の期待値はパラメータλの逆数です!
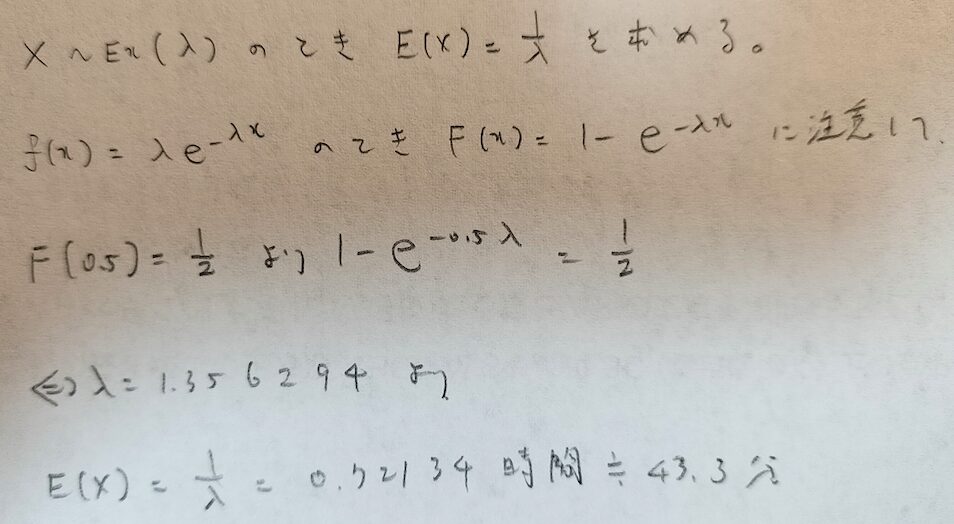
なんと1時間もない結果でした。復習することの大切さが伝わる素晴らしい問題ですね。
指数分布の期待値がパラメータλの逆数になっていることに注意してください。
後述するポアソン分布ではパラメータがλで期待値も分散もλと全部一緒です。
なぜλが共通しているのか?いよいよ指数分布の記事も終盤です。
指数分布とポアソン分布のλで結ばれた関係
いよいよ指数分布とポアソン分布との関係を深掘りします。
ここがとても混乱していまして。分かりやすく教えてください!
目標はポアソン分布から指数分布を導くことです。二つの分布はλという定数で結ばれています。
アクチュアリー数学で頻出の箇所です。難易度が高いですが頑張りましょう!
イベントが平均的にλという時間の間隔で発生する状況のとき、イベントが起こってから経過した間隔を確率変数Tとしたとき、Tはパラメータλの指数分布に従います。
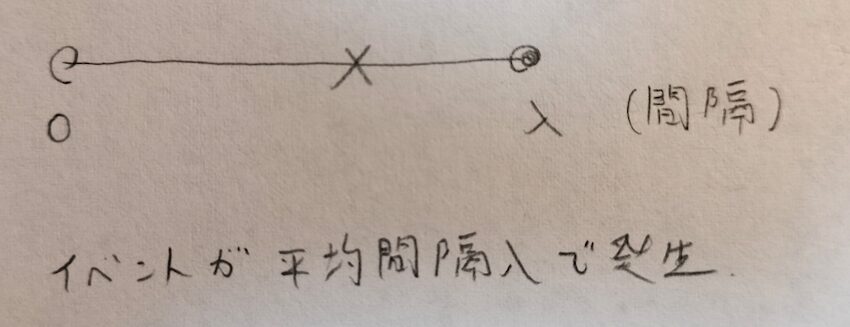
今度はイベントの発生回数について考えます。間隔は単位時間(1という長さの間隔)にします。その1という間隔でイベントが平均してX回発生するとします。このときXはパラメータλのポアソン分布に従います。左端の0は含まれていませんので白丸としています。
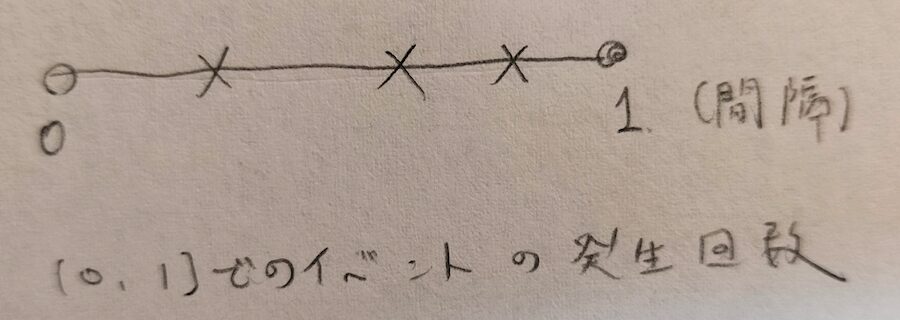
これらが指数分布とポアソン分布がパラメータλで結ばれた関係であることの説明です。要するにイベントが発生するという事象をどの角度から見ているかの違いです。
最後にポアソン分布から指数分布が導かれる様子を紹介します。今回の指数分布の記事の内容の総まとめ的な内容ですので頑張りましょう!
ポアソン分布から出発するので単位時間を設定すると思います。しかし今回は時間感覚tという変数を結果の式に出したいので計算間隔をtまで広げて進めていきます。左端の0は含まれてないので白丸としています。
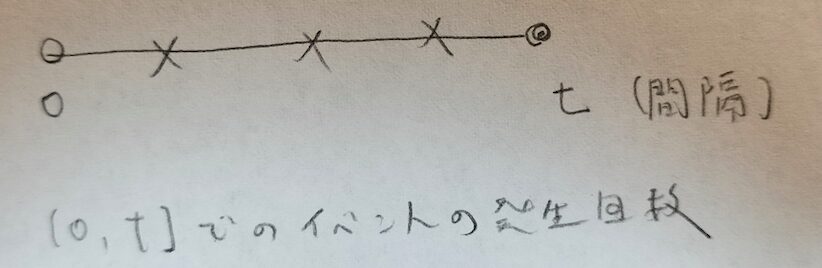
それでは指数分布の式が登場する様子をご覧ください。
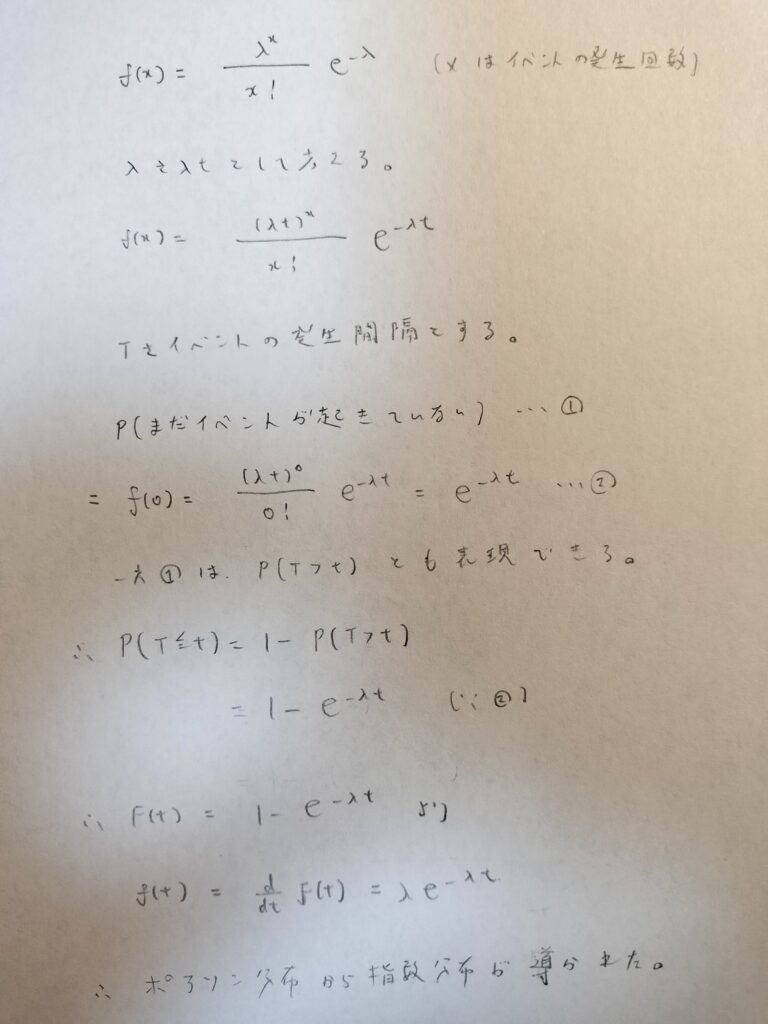
生存関数の意味を理解できているか?が問われていると感じました。難しいですが、とても勉強になりました。
同じ事象を異なる視点から考える問題はアクチュアリー数学2022年のコーシー分布の問題で出題されています。コーシー分布は期待値が存在しない変わり者の分布で面白いので後ほど記事にします。しばしお待ちください。
指数分布と一様分布の違い
指数分布についてかなり深く理解できました。勉強をしていくうちに一様分布も似て非なるものだと感じました。最後にこれらの分布の違いを教えてくれますか?
ではこの記事の最後のまとめとして、機械の故障ということになぞらえて、一様分布と指数分布の「止まること」についてまとめます。
一様分布は「ある時間後に確実に止まるけど、いつ止まるかは不明である」
指数分布は「劣化せず(無記憶性を持ち)停止は偶発的なイベントで発生」
最後までお読みいただきありがとうございます!指数分布の記事で参考にした資料をまとめておきますね。
ガンマ関数の使い方がとても詳しく載っています。ポアソン分布についての説明も掲載されています。ただし指数分布についての記述は少なめです。
指数分布の無記憶性の説明部分で参考にしました。本書は指数分布の一般化であるガンマ分布の説明がとても詳しく、手元に置いておきたい一冊です。
変数分離型の微分方程式の解法部分で参考にしました。ベッセルの微分方程式も掲載されております。偏微分方程式は別の本として販売されています。
ガンマ関数を使え!使えないとダメだ!などの喝が伝わってくる熱い本です。アクチュアリー数学に向けた演習書ですが、確率分布に関しての網羅度が高いです。
指数分布の例として100年に1度という問題の原型は本書の地震発生の確率を計算する問題から引用しました。本書は統計検定1級の内容に対応しています。