指数分布からの流れでラプラス分布とパレート分布を学習してきました。ラプラス分布とパレート分布はともに2つの指数分布から作られる分布でした。
次はどのような分布ですか?
指数分布を複数個集めたガンマ分布を考えます。まずはガンマ分布の作り方から説明します。
ガンマ分布が登場する背景
前回の議論によってべき関数をベースとした分布をもとにパレート分布が導かれました。べき関数は単項式の一例です。そして指数分布は指数関数がベースとなっています。今回はべき関数と指数関数を合体したもので確率密度関数になるものを見つけよう!というところから出発します。参考『リスクを知るための確率・統計入門』
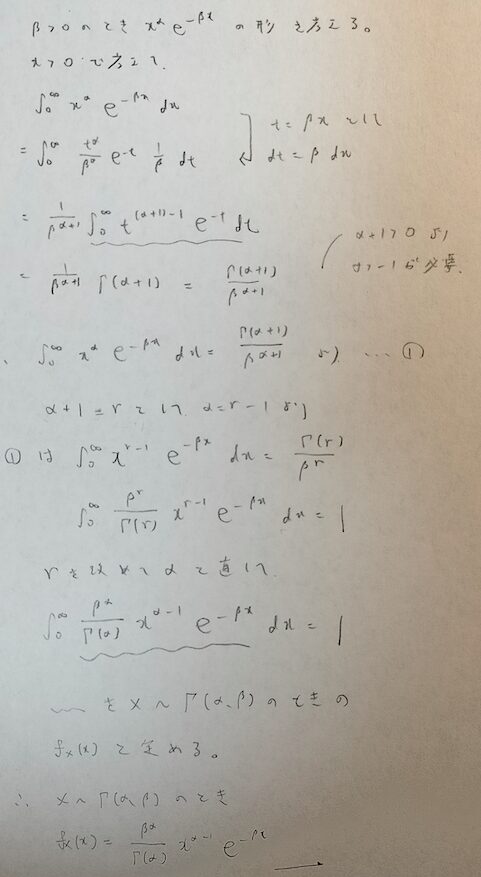
最後の結果を2つのパラメータα,βをもつガンマ分布といいます。αを第1パラメータでβを第2パラメータと呼びます。意味的にはαは形状パラメータでβはスケールパラメータ意味します。上の説明の波線部分の式はガンマ分布の全確率が1の式となっています。
β>0は指数分布からの流れでOKですが、αは自然数ではなく正の実数なんですね!
実はαを自然数nとするガンマ分布をアーラン分布と呼びEr(n,β)と表します。
本記事ではガンマ分布を主体として扱います。ガンマ分布で成り立つ公式はアーラン分布の公式として考えることもできます。書籍によって第2パラメータの表記が異なるのでご注意ください。
αを1としたものはどのような分布でしょうか?
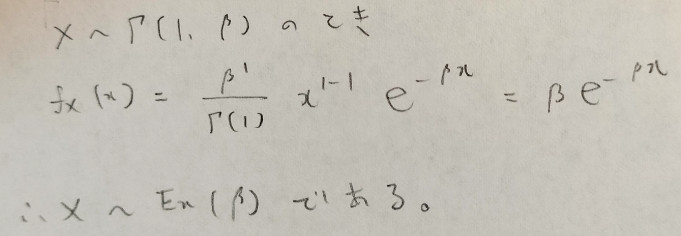
指数分布ですね!
ガンマ分布でαを1とした分布は指数分布です。指数分布を複数個集めた分布はガンマ分布になります。これは記事の後半で積率母関数を用いて証明します。
ガンマ分布は構造的にはべき関数と指数関数を合わせて作られる分布であり、意味的には指数分布を集めて作られる待ち時間(複数のイベントを待つというイメージです)を意味する分布になります。
ガンマ分布の期待値と分散の導出
『弱点克服 大学生の確率・統計』で使用頻度NO1のガンマ関数に関する有名公式をガンマ分布の全確率1の式を変形して導きます。
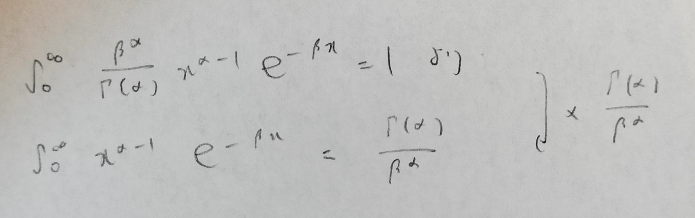
この公式はとても大事ですので、この公式から出発してガンマ分布の期待値と分散を導出したいと思います。参考『データ解析のための数理統計入門』
まずはガンマ分布の期待値からです!両辺をβで微分するというテクニックを使っています。微分したあとはガンマ分布の期待値の式になるように両辺に数式を掛けるだけです。
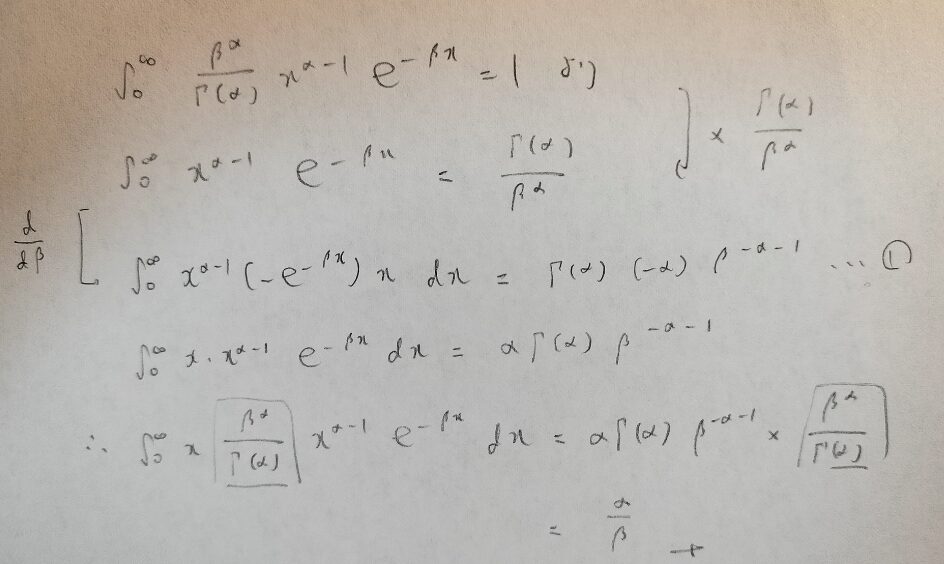
次はガンマ分布の分散を計算するためにXの2乗の期待値を求めます。
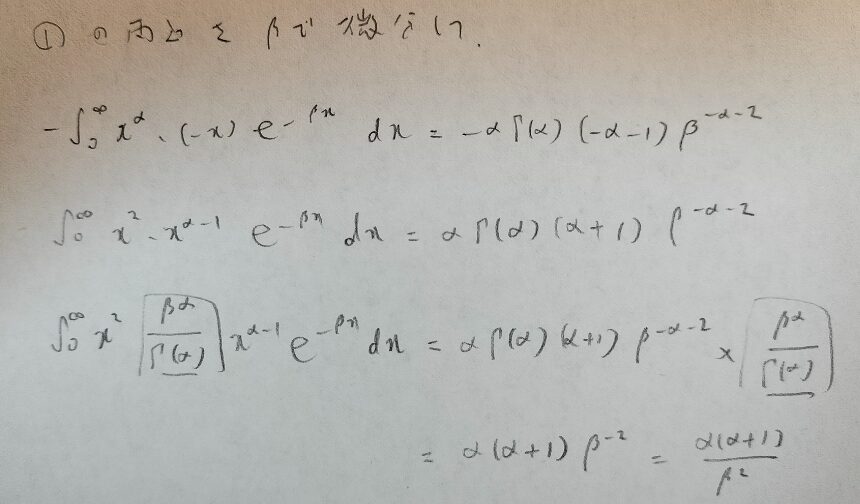
ここまでくればガンマ分布の分散はすぐですね!
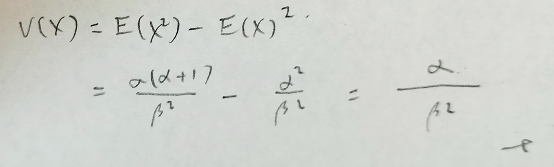
しかしこの方法では欠点が1つあって、原点周りの高次モーメント(Xのk乗の期待値のことです)を求めるために複数回微分する必要があることですが現実的ではありませんので、期待値の定義に従って求めてみます。
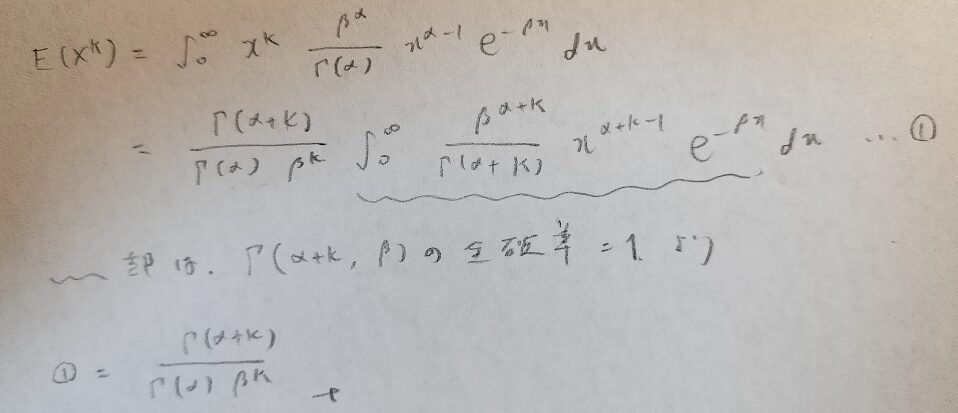
この結果はアクチュアリー数学で頻出です。覚えていないと時間切れになります。
波線部分がポイントです。全確率1を積極的に使えるようになれば、積分計算をしなくても答えが出るときがあります。
ガンマ分布の積率母関数
今までの確率分布の記事で積率母関数という言葉が出てきましたが、この記事で紹介します。
ここまで引っ張った理由を教えてください。
ガンマ分布は指数分布を集めたものであるということの証明に使うからです。またガンマ分布は積率母関数を使用すると便利な場面が多いためです。例えば先ほどの(原点周りの)高次モーメントの計算が便利になるときがあります。
確率密度関数と分布関数と積率母関数は1対1に対応します。すなわち確率変数X,Yの積率母関数が一致すればXとYは同じ分布であることになります。本質的にはラプラス変換を行っています。ラプラス変換の学習は『ラプラス変換キャンパス・ゼミ』がとてもわかりやすく高い到達点を誇ります。
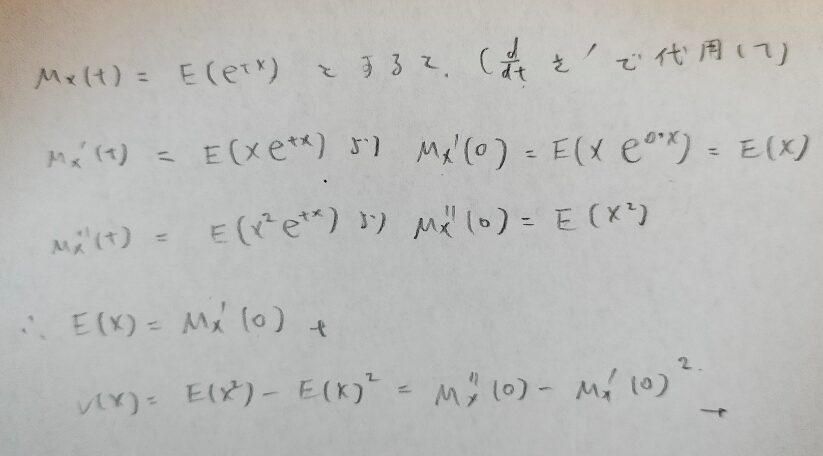
期待値の正体とは(原点周りの)1次モーメントです。分散の正体とは分散の定義を思い出すと(平均周りの)2次モーメントのことです。
積率母関数を用いて他に便利になることを教えてください。
確率変数が独立かどうかが判定できます。
確率変数XとYが独立であるための必要十分条件はs,tを実数としたときに以下で与えられます。左側の記号は独立記号です。左辺が同時分布の積率母関数を意味していることに注意してください。
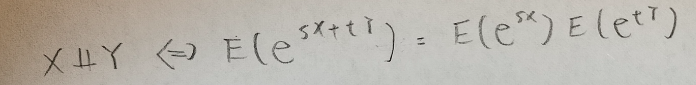
証明をお願いします!
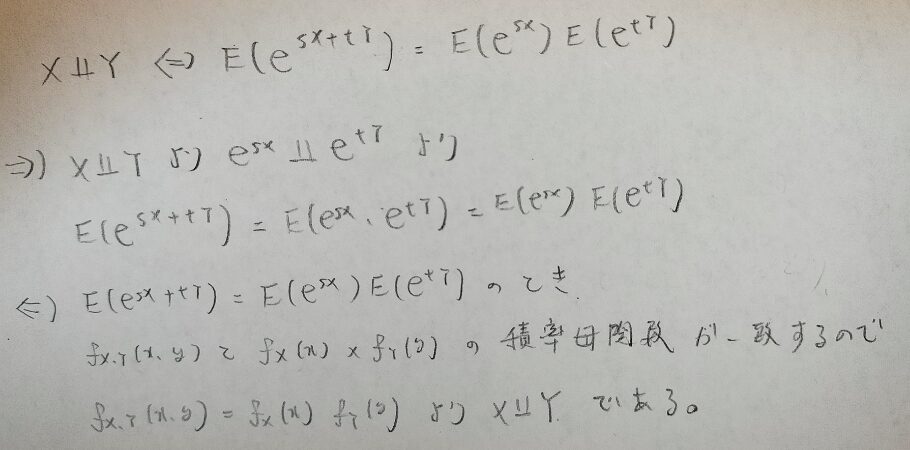
この証明には『確率統計演習 1 確率』を参考にしました。
ガンマ分布の積率母関数を計算しておきましょう!図の□の部分はこの記事の上にある使用頻度NO1公式を用いています。
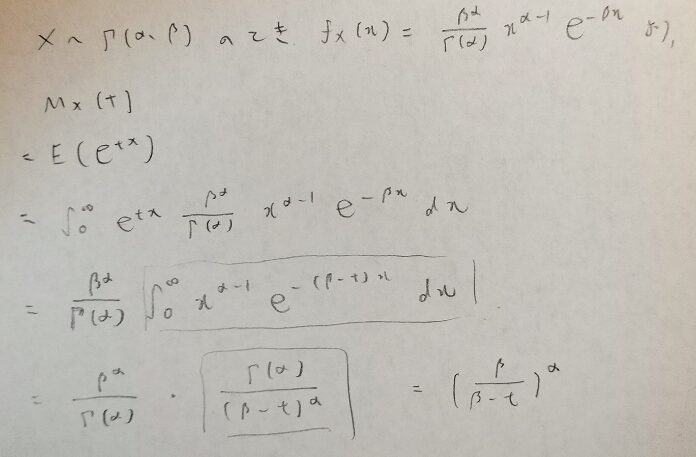
ガンマ分布と指数分布との関係
α個の互いに独立な指数分布の和はΓ(α,β)となります。
指数分布とガンマ分布の積率母関数を用いて証明します。
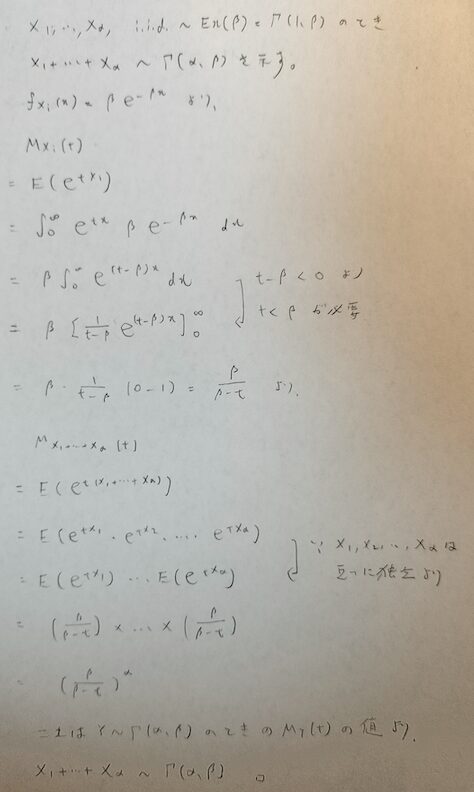
ガンマ分布の第1パラメータαは積率母関数の面で大事だと分かりました。では第2パラメータβが大事になってくる場面を教えてください。
ガンマ分布を道具として利用していく際に2つのガンマ分布同士を結びつける公式があります。カイ2乗分布を扱う際に高頻度の公式となっています。証明は確率変数の変換で考えます。
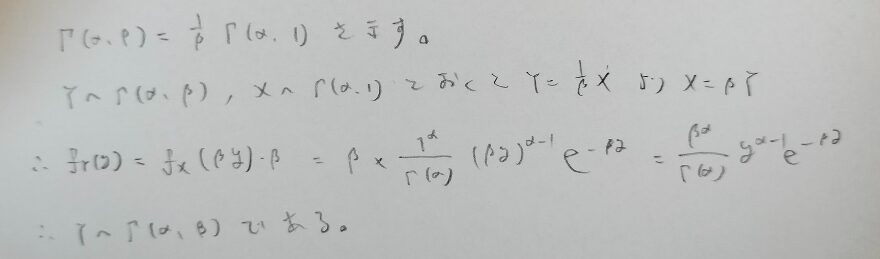
この公式の覚え方については次のtweetが参考になると思います!僕はこの覚え方に気づいて覚えられました!
ガンマ分布の再生性
X,Yが同じ種類の分布(例えばポアソン分布)に従うときに、X~Po(a),Y~Po(b)ならばX+Y~Po(a+b)が成り立つとき、ポアソン分布は再生性を持つといいます。
ガンマ分布の場合は第1パラメータについて再生性が成り立つことを証明します。積率母関数が大活躍していることに注目してください。
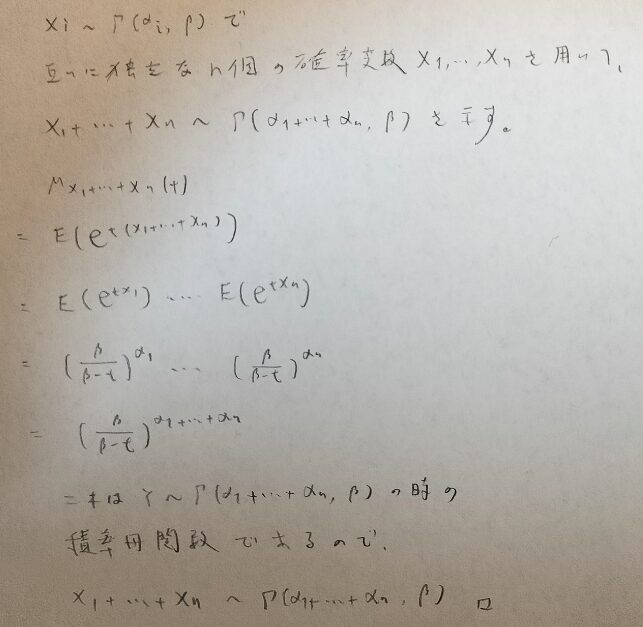
ガンマ分布、二項分布、負の二項分布などでも第1パラメータについて再生性が成り立ちます。
幾何分布や指数分布は再生性を持ちません。なぜなら再生性とは分布を足し合わせても同じ種類の分布になるということですので、幾何分布を足し合わせたら負の二項分布になり、指数分布を足し合わせたらガンマ分布になるので、それぞれ違う分布になってしまっているためです。
積率母関数は他にも使用場面はありますか?
多いに活躍します。たとえば二項分布においてnp=λとしてnを無限大にすると二項分布はパラメータλのポアソン分布になるというポアソンの少数の法則も積率母関数を使えば3分程度で証明できます。
ガンマ分布の分布関数の導出
後にポアソン分布とも関係するガンマ関数の分布関数を既存の知識のみで導出していきます。
ガンマ分布の分布関数はシグマを用いて表されます。そのため計算過程がやや複雑になります。
まずは補題として次の命題を示します。類題が第102回(2005年4月)数学検定1級の1次検定に出題されています。
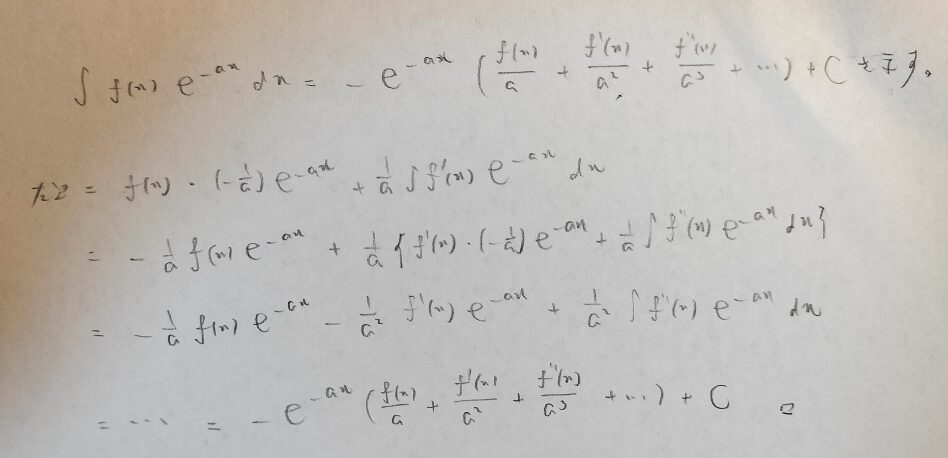
受験数学の数学Ⅲで勉強した置換積分の一般化ですね。
次にこの補題を用いてガンマ分布の分布関数をゴリ押しで計算します。
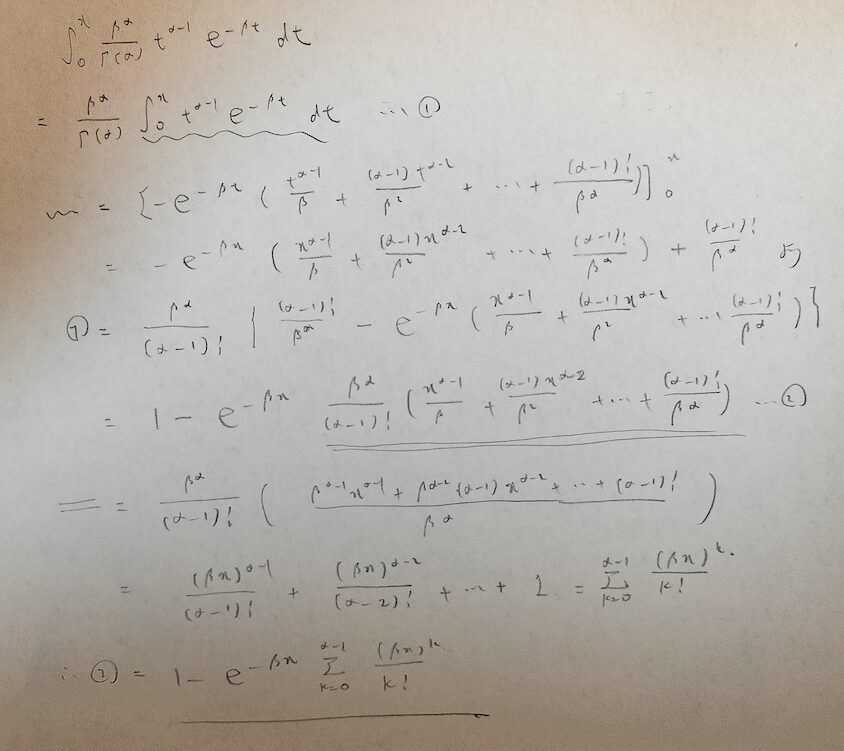
分布関数が綺麗な形で出てこない分布は他にもありますので、分布関数は必ず綺麗な結果になると思い込まない方が良いです。
最後にアーラン分布とガンマ分布の内容を作成するために使用した本を紹介します。
ガンマ分布がべき関数と指数関数の積で表現されるという内容について参考にしました。
ガンマ分布での使用頻度NO1公式は本書でたくさん出てきたので知らない間に暗記していました。アクチュアリー数学を受験する方は持っておくべき有名対策本です。
国沢統計で有名な本の確率版です。積率母関数を用いた独立性の証明で使用しました。
積率母関数を求めることはラプラス変換をしていることであるという説明で利用しました。僕が東大院試を受験したのときのラプラス変換の学習は本書が中心でした。本書の学習後の到達点は高いです。
本記事ではガンマ分布の期待値と分散の導出部分で使用しました。本書は2023年の秋に出版された新しい本です。理論面以上に具体的な例題が多いという観点からtwitterでも高評価の声が多く、2024年以降の統計検定1級を受験する際の統計応用の学習には特に必須になってくると思われます。







