多変量解析ではとても有名なクラスター分析について解説します。
前回の多次元尺度構成法よりも断然難易度が低いのでご安心ください!
クラスター分析はどういった分析法ですか?
クラスター分析とは、各サンプルをウォード法などを用いてクラスター(グループ)に分けて、各クラスターがどのようなサンプルで構成されるのか?そして各クラスターの意味について考える分析法です。
主成分分析と似ていますが、どのような違いがあるのですか?
素晴らしい質問です。この記事が進めば疑問も解消されていくと思いますので、時折その質問にも触れていきたいと思います。
具体例として変数は2変数として理解を重視していきます。クラスター分析では距離の計算があるのため、変数が少ないほど行なっている計算が「見えやすい」と判断したためです。具体例は『多変量解析法入門』を参考にさせていただきました。統計検定1級受験者の中でおすすめ書籍とされる多変量解析法の名著です。
クラスター分析(エクセルやrでも用いる)は最短距離法が直感的でわかりやすい
まずは最も理解がしやすい最短距離法でクラスター分析を行なっていきます。
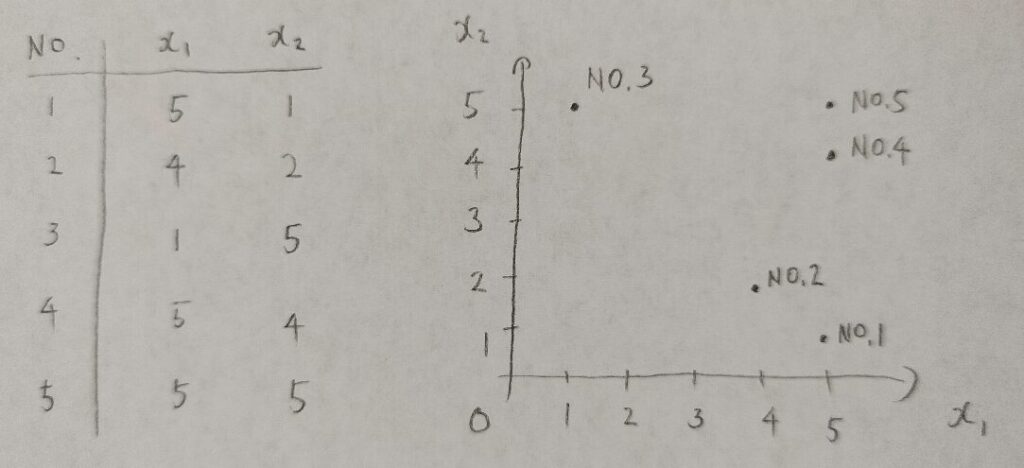
タイトルにもある最短距離法やウォード法などは、サンプルとクラスター間の距離をどのように計算していくか?のルールのことです。
サンプル同士の距離は通常のユークリッド距離を用います。
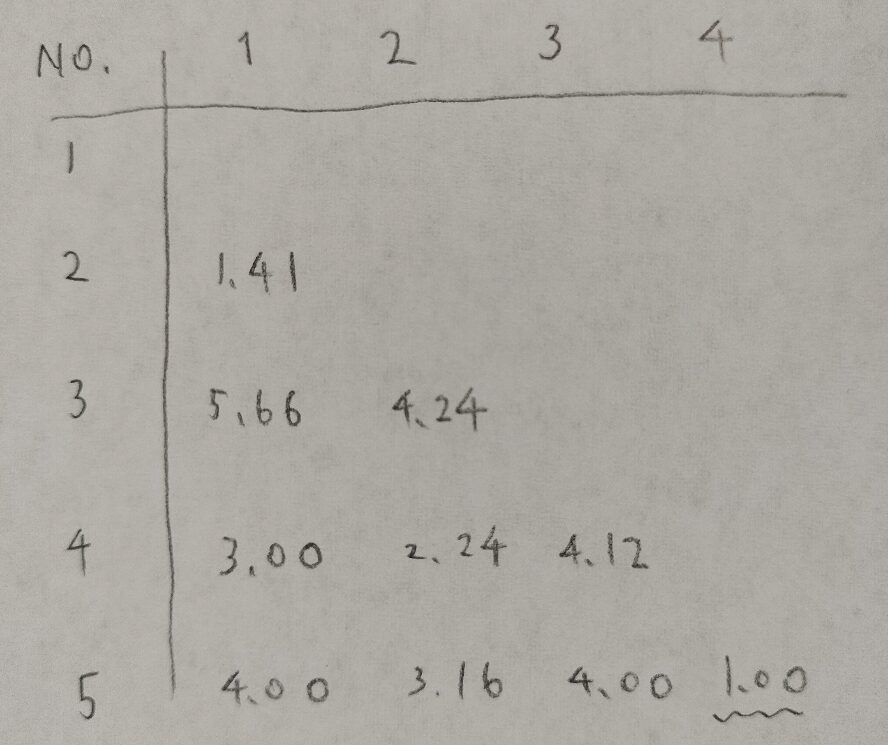
この表では4番と5番のサンプルの距離が最も近い(図01の座標からも明らか)ので4番と5番をクラスター1とします。
いよいよ最短距離法の出番です。たとえば1番とクラスター1との距離は、「1番と4番の距離」と「1番と5番の距離」のうち小さい方を1番とクラスター1との距離と定めるというルールです。
なるほど。確かに直感的でわかりやすい方法ですね。
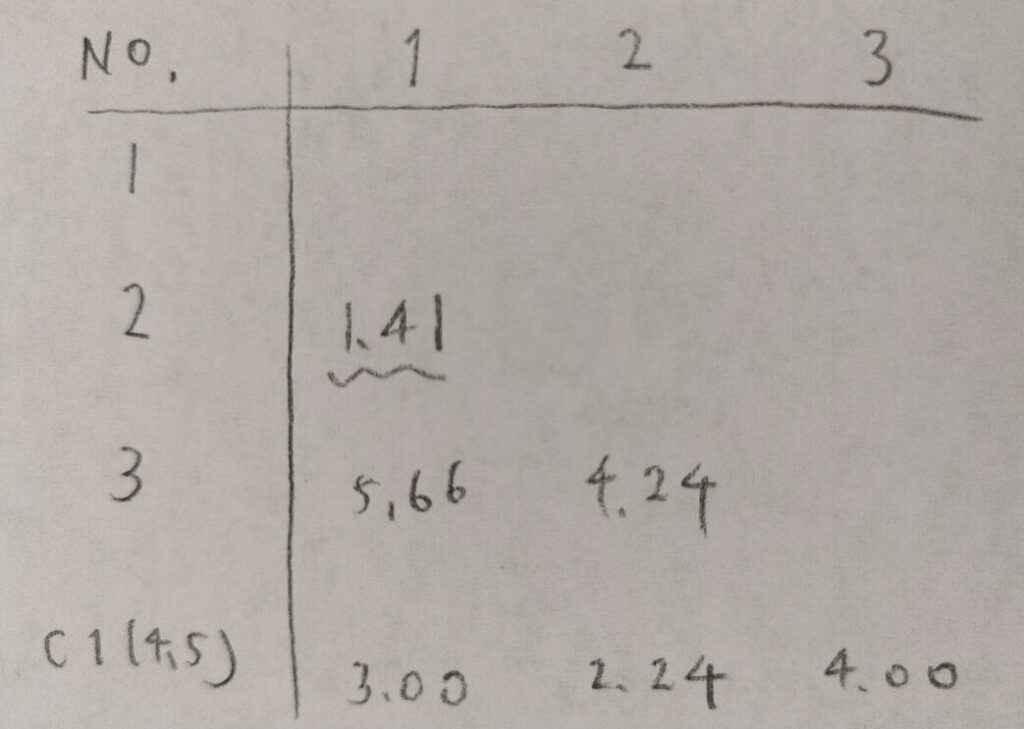
次に1番と2番の距離が最も短いのでこれをクラスター2とします。
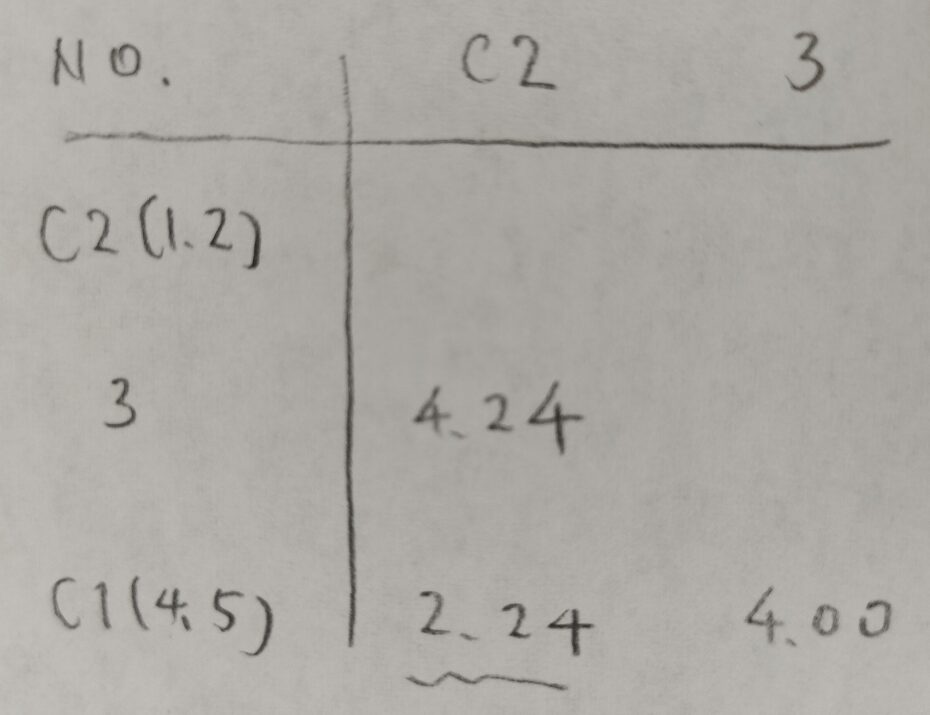
このようにしてどんどんクラスターを作成していきます。
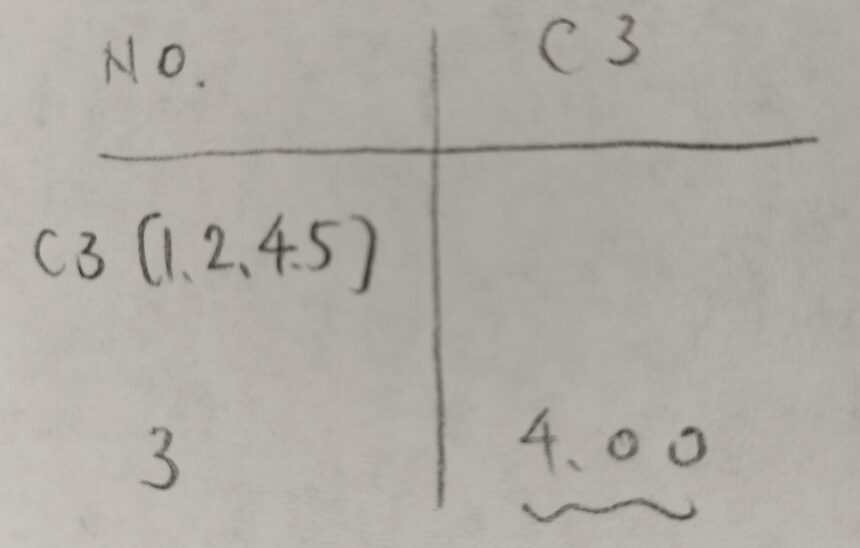
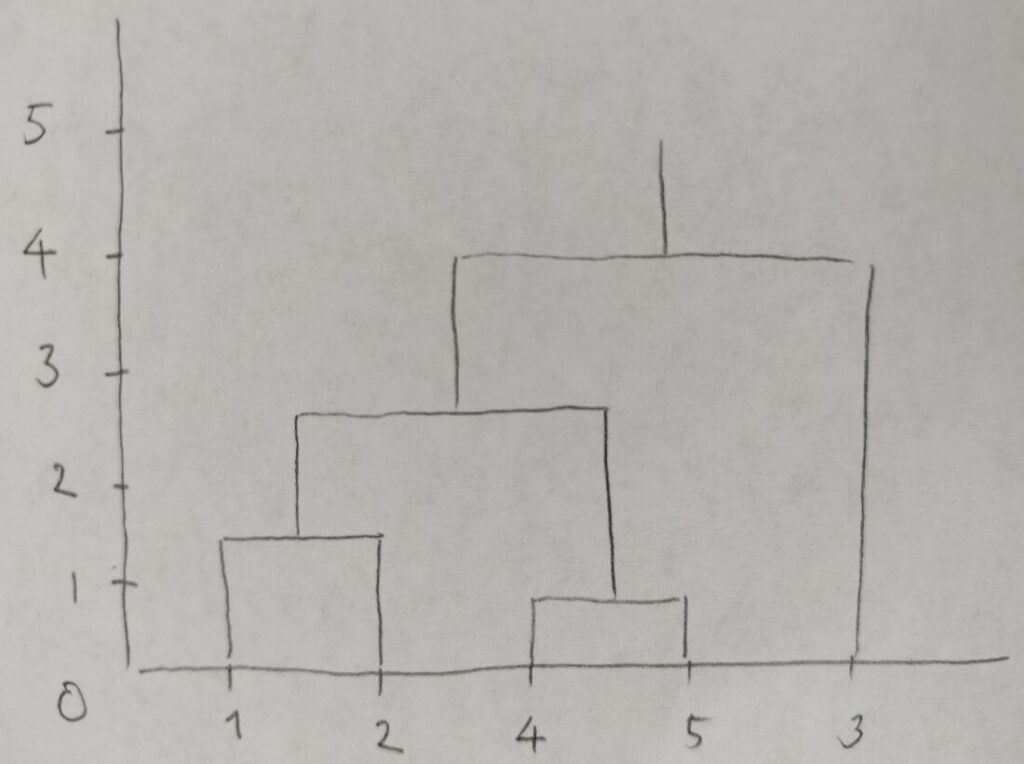
ここまでの情報をもとにデンドログラムと呼ばれる図06を作成します。縦軸に現れる統合時の高さに注目してください。
ここでこの3グループの解釈を行うというところまでがクラスター分析の内容です。
でもこの解釈の部分では解釈する方の主観が入りません?
その通りです。クラスター分析の欠点としてグループの解釈に解釈者の主観が入るというものがあります。
なるほどさっき私がした主成分分析との違いがわかった気がします。主成分分析でも第n主成分を散布図に書いたときに、主成分の解釈に対して解釈者の主観が入りますよね。
そうですね。主成分分析もクラスター分析も解釈者の主観というものがキーワードになりますね。
最短距離法は理解しやすい内容ですが、デンドログラムで鎖効果(ある1つのクラスターに対象が順に1つずつ吸収されてクラスターが形成されていく現象)がウォード法と比べて起きてしまいやすい欠点があります。そのため最短距離法は理解しやすいですが、実用性が高いとは言えません。
クラスター分析(spssやpythonでも用いる)で鎖効果が起きにくいウォード法
クラスター分析で最短距離法を勉強しましたが、他にはどのような方法がありますか?
『多変量解析法入門』によると最短距離法、最長距離法、群平均法、重心法、ウォード法などがあります。最短距離法の時と同じ例題を用います。
その中でも実用性が高いウォード法を解説していきます。
図07をご覧ください。1番と2番を1つのクラスターとみなしたときに、そのクラスター内での平方和を考えます。
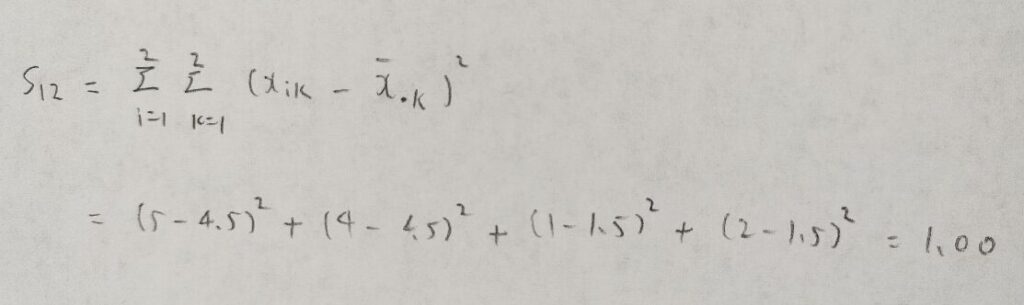
これらを各サンプルで計算していきます。
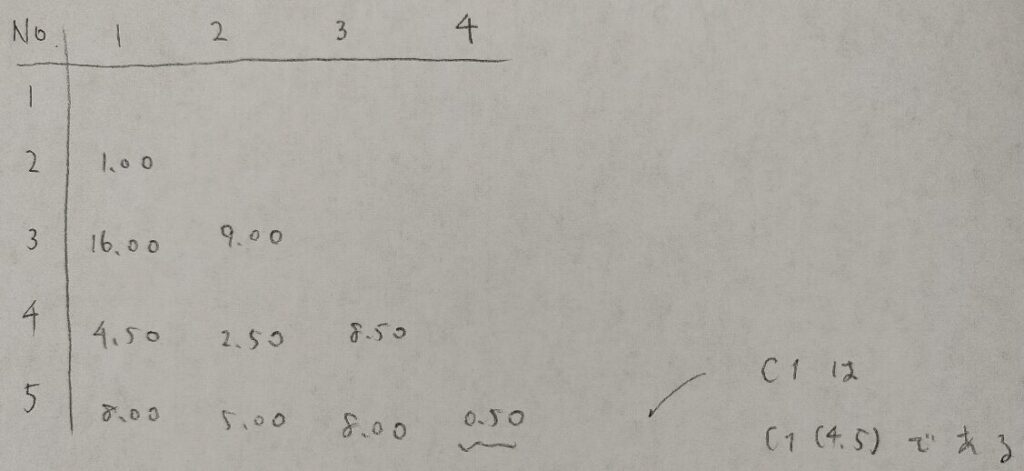
この作業を繰り返したいのですが、各サンプルとクラスター間の距離をウォード法ではどのように計算するのか?を明確にしないと先に進めませんので、計算法を定義します。
具体例としてクラスター1と1番との距離を定義します。ここでも平方和がポイントです。
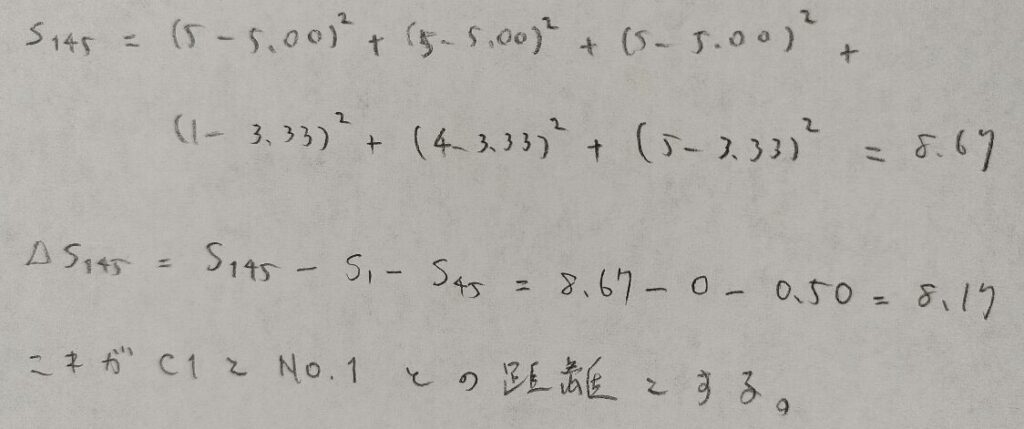
この作業を繰り返していきます。計算量が多くなるので、実際はエクセルやr、spssやpythonなどを使用していくことになります。
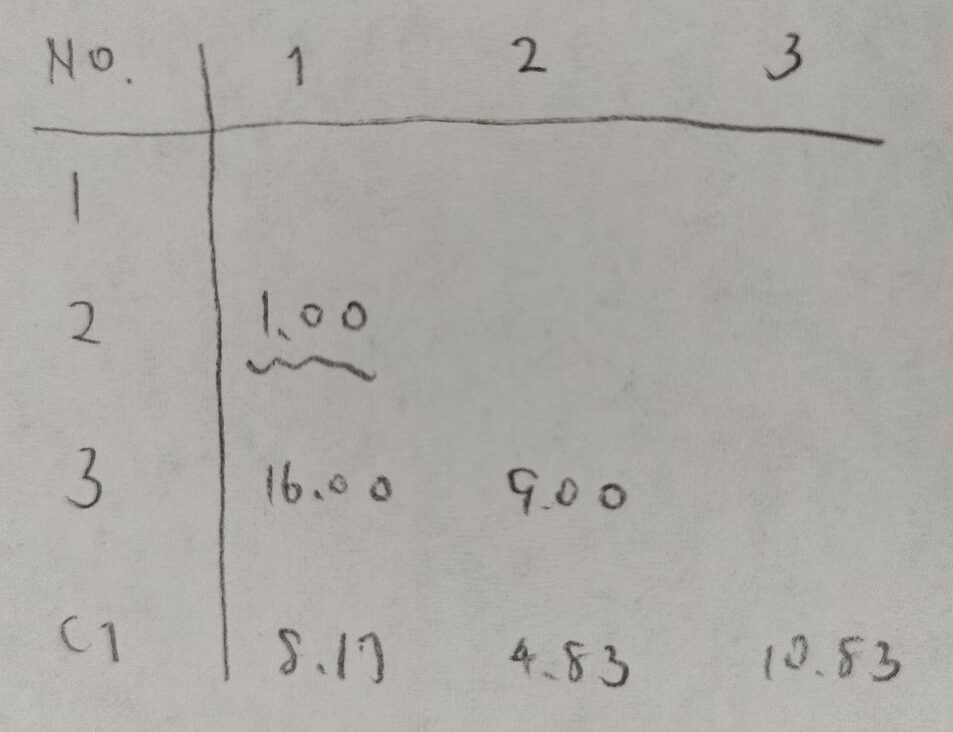
さらにまとめていきます。
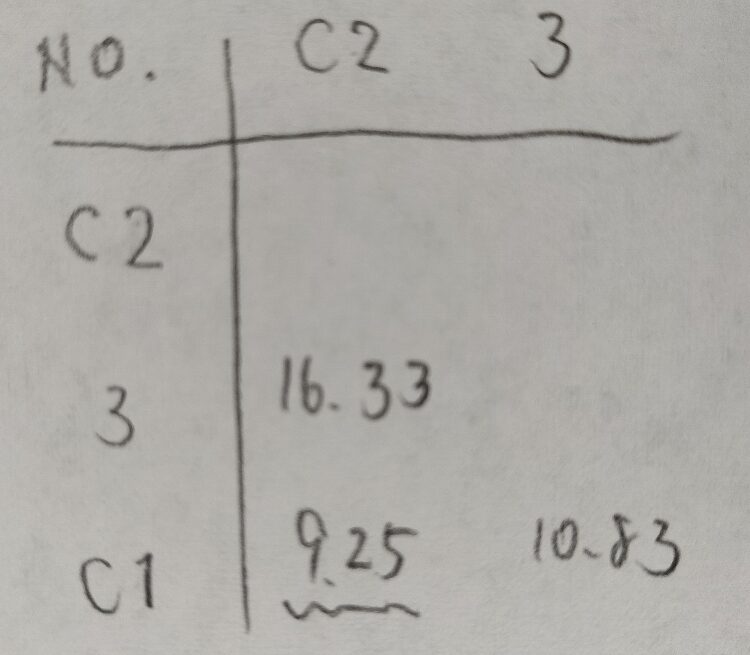
表側や表頭は東大出版の有名な『統計学入門 (基礎統計学Ⅰ) 』に定義されています。大事な概念だと思うのですがなかなか解説されている書籍が少ないのが現状です。
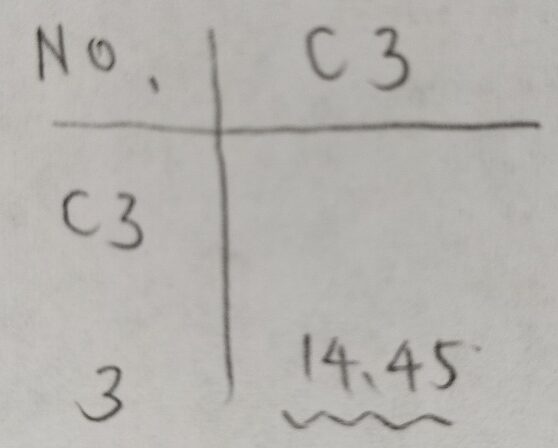
ここまで集まったデータを用いてデンドログラムを作ります。
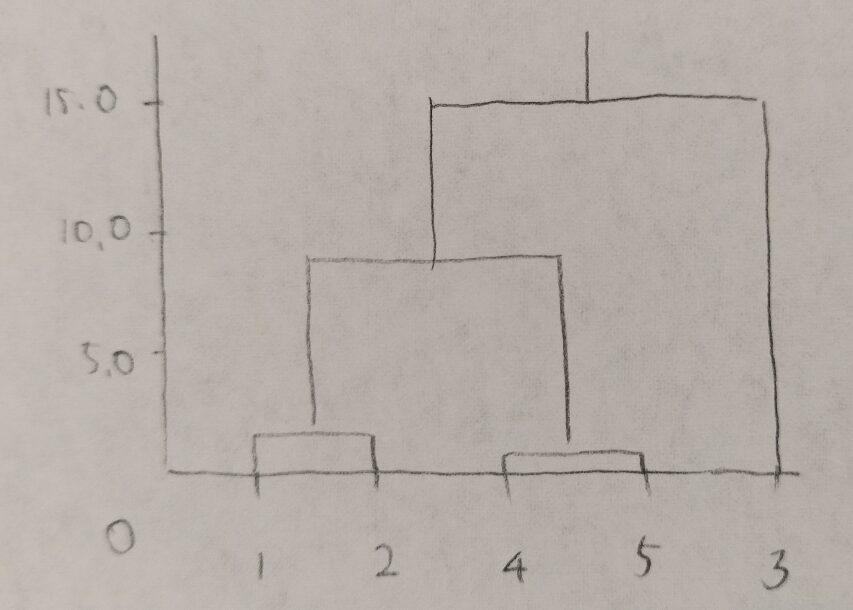
最短距離法の時よりも縦軸の数値が大きいですね。分類がしやすそうですね!
その通りです。これについては永田先生の『多変量解析法入門』にて、ウォード法は経験的に鎖効果が起きにくく実用性が高いと評されています。
実際に分析をしてみて、ウォード法の便利さが伝わってきましたでしょうか?クラスター分析は難しい手法が多い多変量解析の中ではわかりやすい手法です。身近な例でクラスター分析を行なって、自分なりの解釈をしてみると面白いですよ。
先ほど紹介で出てきた東大出版の『統計学入門 (基礎統計学Ⅰ) 』は東大出版の中では、万人受けの内容です。要するにとても難しい本ではなく、僕が1冊目として最もおすすめする『確率統計キャンパス・ゼミ』を読まれたあとの2冊目としてちょうど良いレベル感と内容です。その後に統計検定1級のバイブルである『現代数理統計学の基礎 』などへ進のが王道だと感じています。


