カイ2乗分布が関係するピアソンの適合度検定を勉強します。
メンデルの法則などで有名な検定ですね。実生活での応用が多いと聞きます。
統計検定1級のバイブルになりつつある久保川先生の新作『データ解析のための数理統計入門』では、適合度検定で1つの章になるほど、実社会においてとても大事な検定のお話です。
身近な例では、適合度の検定はどのような状況で使えますか?
例えば理想的な6面サイコロはどの目も出る確率は等しく1/6のはずですよね。複数回の実験した結果、1〜6の目が出る確率が不均一だったとします。このサイコロは正しいサイコロであると判断できるか?などという問題で使います。
適合度検定とは母集団がモデルとする分布に適合するか否かということを検定するための方法です。またこれはカイ2乗検定の一種になります。
メンデルの法則やはじめとし、文理をこえたところで役に立つ検定ですので、理論面と計算面を同時に鍛えていきましょう!
カイ2乗検定(適合度検定)はエクセルと相性が良い
適合度検定を行うために、まずは表の見方を覚えましょう!カイ2乗検定は表を扱うので、具体例をエクセルに打ち込みながら行うと理解が深まります。
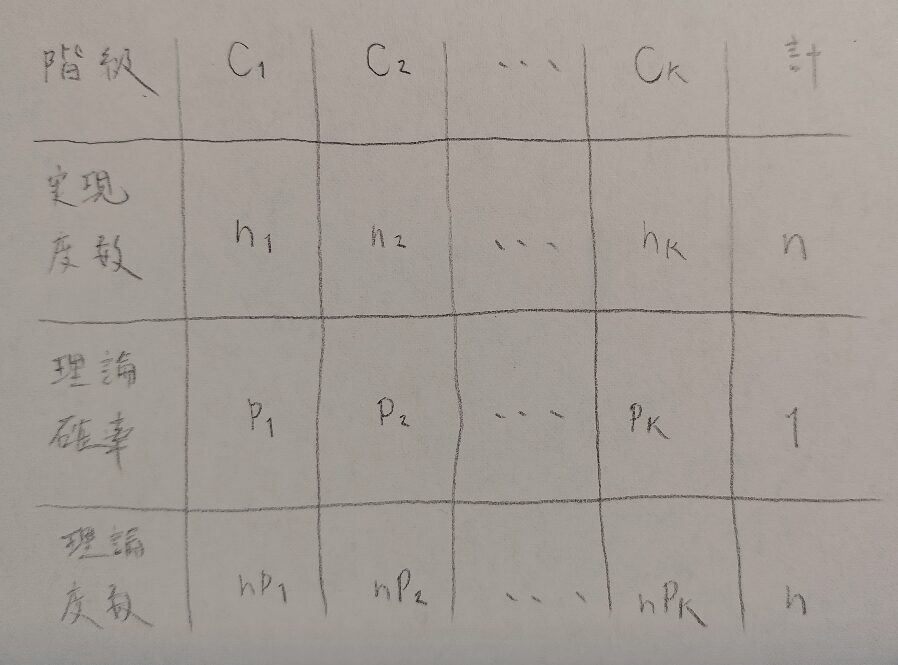
階級をまずは設定します。サイコロで例えると1の目、2の目、…などです。
階級の考えは多項分布のときの考えと似ていますね。
その通りです!適合度検定を理解するためには多項分布の理解が必須になります。
次に実現度数を見てください。これは観測度数(英語を考えてObservation frequencyの頭文字のO←オーで表す書籍が多いです)ともいいます。
実際に得られた値のことですね。
次に理論確率があります。これは理想のモデルにおける確率のことです。例えば理想的なサイコロの各目が出る理論確率は等しく1/6です。
それに伴い、理論度数(別名:期待度数)という理想的な量を計算して出します。
理想的な量と現実的な量とがどれくらいのギャップを持つか?というところから出発します。ギャップが多いほど適合していないとなりますよね。そのため適合度検定の棄却域は右側にとります。図03を参照。
カイ2乗検定(適合度検定)の計算方法
それでは適合度検定の計算方法を紹介します。
図02におけるTをピアソンのカイ2乗検定統計量といい、Tは自由度k-1のカイ2乗分布に従います。
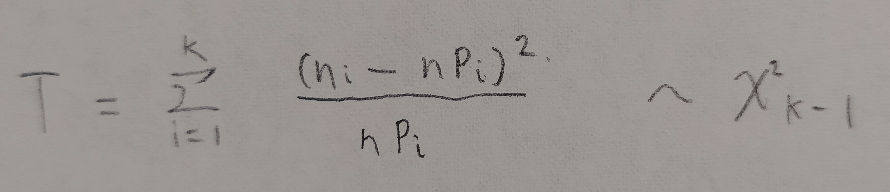
カイ2乗分布が出てくるイメージはTの分子の形が分散を想起させるからです。そもそもカイ2乗分布は2乗和が大きく絡む分布でした。
棄却域はこちらになります。右側検定であることをご確認ください。
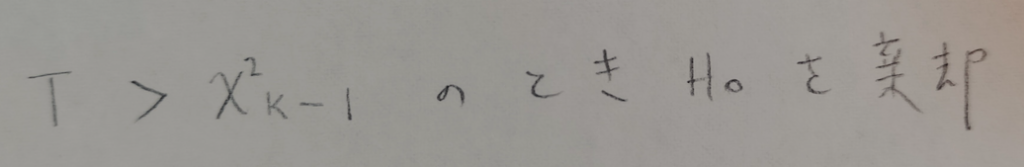
k=2のときのカイ2乗検定(適合度検定)の例
Tが本当にカイ2乗分布に従うのか疑ってます笑。確かめて欲しいです!
了解しました。例えば確率和1などの合計の値が定数であることにご注意ください。
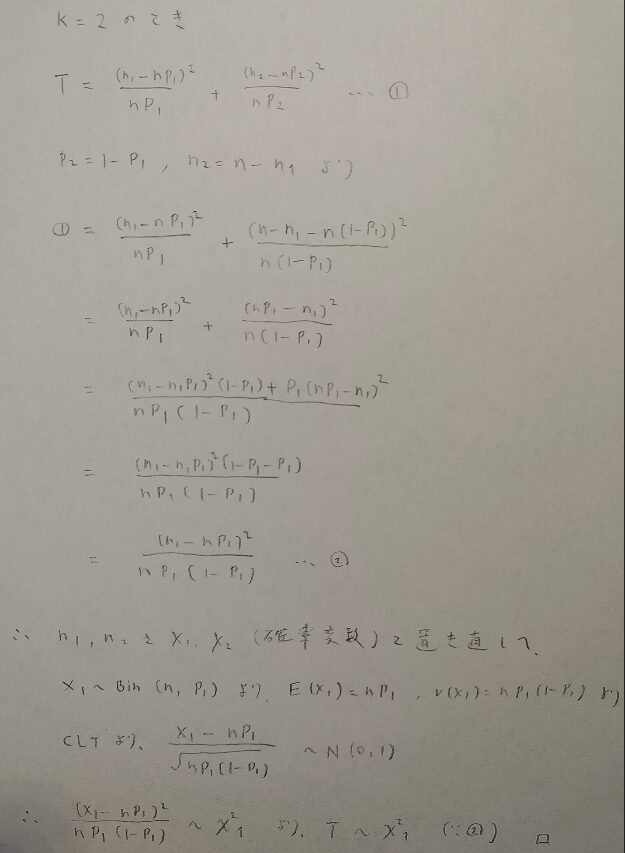
すごいゴリ押しですね!笑。でも確かにカイ2乗分布に従うことが確かめられてよかったです。
しかしk=2ではなく、より大きい一般の場合の証明はかなり難易度が高いです。そのため後述する尤度比検定を用いて考えます。
カイ2乗検定(適合度検定)の自由度が絡む計算をわかりやすく解説
まずは理論確率を求めて理論度数を求めるために、理論確率を多項分布による最尤法で求めましょう。その後に適合度検定の統計量(ピアソンのカイ2乗検定統計量)を求めますが、ここでは一般的な尤度比検定の考えを経由して求めていきます。
まずは最尤法を用いて理論確率を求めておきましょう。
理論確率は多項分布による最尤推定量でラグランジュの未定乗数法を用いる
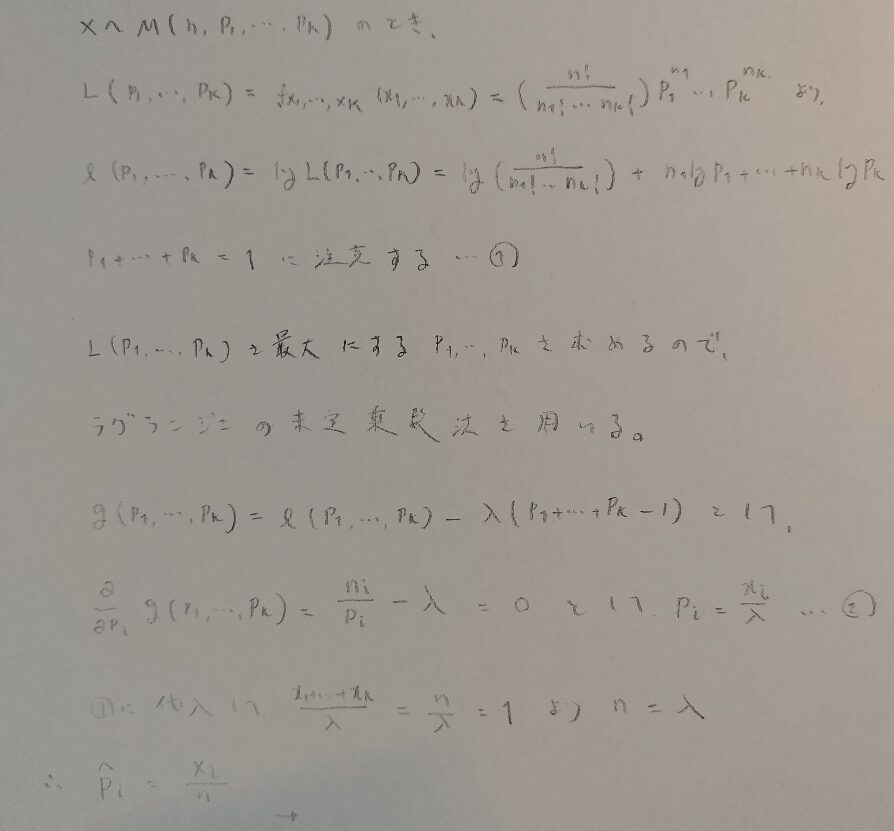
マクローリン展開やラグランジュの未定乗数法は『微分積分キャンパス・ゼミ』がわかりやすく書かれています。数学検定1級の対策書としても有効です!
ピアソンのカイ2乗適合度検定統計量Tがカイ2乗分布に従うことの証明は2通りあり、1つは真正面から示す方法で、もう1つは尤度比検定を経由する方法です。前者はとても難易度が高いので、この記事では後者を採用します。
尤度比検定をわかりやすく解説

尤度比検定からはさまざまな検定が導かれます。今回のカイ2乗検定(適合度検定)もその一例になります。
尤度比検定では棄却域はどのように定めるのですか?
尤度比検定はどちらを分母にするかで2通りの考えがありますが、一般にカイ2乗検定は自由度が絡むので、一貫して覚えやすいように図06を採用しました。それに伴い棄却域の形が変わってきます。

図08のように尤度比検定統計量に自然対数の−2倍(尤度比検定統計量の分母分子を逆にした場合は2倍)した量がカイ2乗分布に近似的に従います。この近似的という点が記事後半のポイントになります。
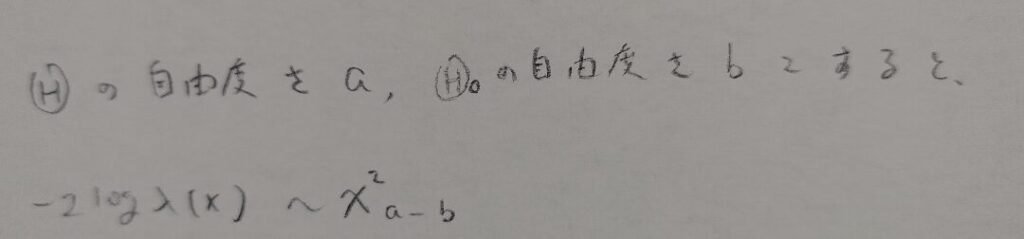
カイ2乗検定(適合度検定)では図08にあるような詳しい自由度の考察は不要です。注意点は次の2つです。
1.階級がK個の場合は、Tは自由度k-1のカイ2乗分布に従う。
2.未知パラメータがある場合は、その個数分だけ自由度から引く。
アクチュアリー数学では未知パラメータがある場合も多々あり、自由度の計算に気をつけないといけません。
カイ2乗検定(適合度検定)のp値の計算法
それではこの記事のメイン部分に進みます。Tが自由度k-1のカイ2乗分布に従うことの証明です。
帰無仮説は理想的なモデルに相当する確率が、観測するモデルで得た確率と等しいことを仮定します。対立仮説はその否定です。
まずはこのことを踏まえてご一読をお願いします。テクニカルな要素としては対数関数のマクローリン展開になります。またランダムのo記号を用いると証明をすっきりと書けます。
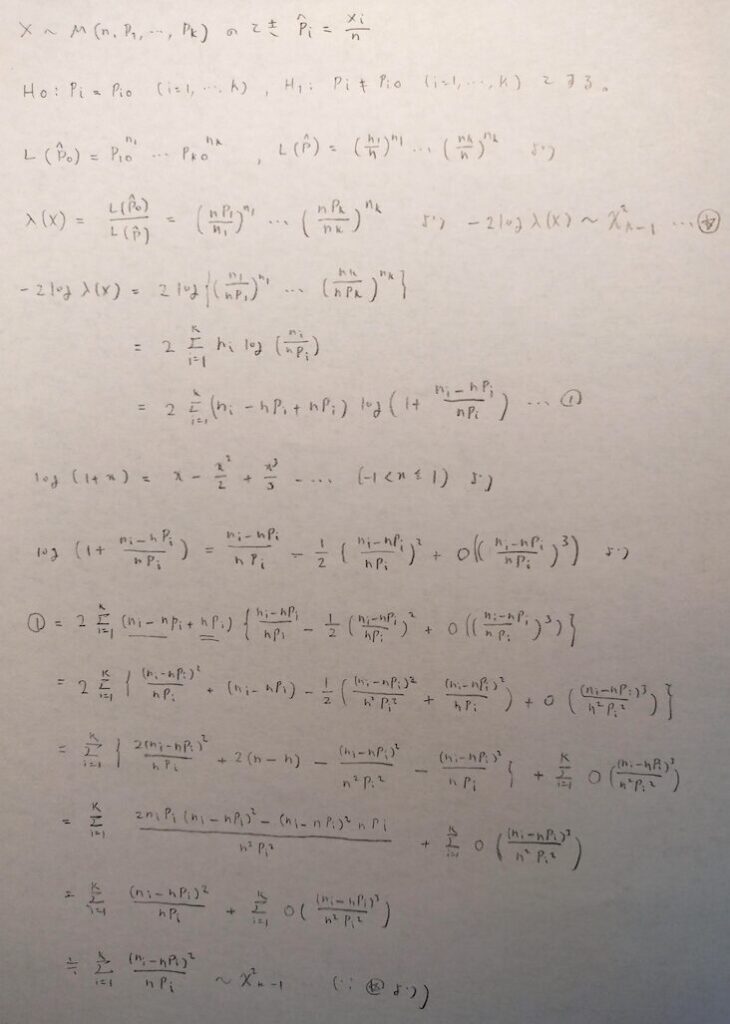
まずは1つ1つまとめていきましょう。マクローリン展開は数学検定1級の内容です。おすすめの参考書などはこちらの記事をご覧ください!
最後の行の≒つまり、近似的に自由度k-1のカイ2乗分布に従うとの結論ですが、適合度検定を使用するための条件はありますか?
適合度検定の使用条件は理論度数が全て5以上のときです。4以下のときは隣のセルと合わせて(プールして)全て5以上になるように調整(自由度の数がその分減ります)してから改めて、適合度検定を開始します。
このように標本の数が大きいときに良い近似ができることを数式を用いて説明しておきます。この考察では標本数nが大きいほど、確率piの最尤推定値の精度が良くなる考えをもとにしています。

以上からp値の計算法はピアソンのカイ2乗検定統計量Tに実現度数(観測度数)や理論度数(期待度数)を代入して計算した計算結果が起きる確率になります。このp値が小さいとTが計算した結果になることが起きる状況はあり得ないと考え、p値がεより小さいと帰無仮説は棄却されます。
カイ2乗検定(適合度検定)のまとめ
1.階級がK個の場合は、Tは自由度k-1のカイ2乗分布に従う。
2.未知パラメータがある場合は、その個数分だけ自由度から引く。
3.適合度検定の使用条件は理論度数が全て5以上のときです。
p値は得られたデータの希少性を表す数値が生じる確率なのですね。
p値は品質管理などでも耳にする言葉です。少しずつ慣れていきましょう。





