この記事は『統計学大百科事典 仕事で使う公式・定理・ルール113』などで書かれているカイ2乗分布が持つ意味を説明するために書きました。カイ2乗統計量が標本分散の定数倍に等しいことを順を追って導いていきます。標本という概念がところどころに登場しますので徐々に慣れていきましょう。
正規分布から導かれる分布について考えていきます。カイ2乗分布やt分布やF分布がありますが、この記事ではカイ2乗分布を扱います。
正規分布の記事を未読の方はこちらをご覧くださいね。
カイ2乗分布の確率密度関数
まずはカイ2乗分布がどのように定義されるかを考えます。
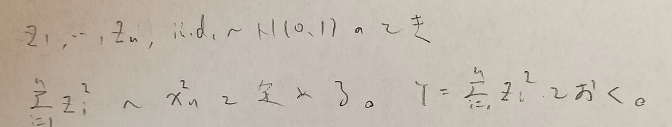
χ文字はX(エックス)みたいな文字ですが、この文字χはギリシャ文字の X(エックス)に対応する文字で『χ(カイ)』と読みます。Yは自由度nのカイ2乗分布に従うと読みます。
χの右下の小さいnは何ですか?
χの右下の小さいnは自由度と呼ばれるものです。自由度はdegree of freedomで略してd.f.と表現します。ギリシャ文字φ(ファイの小文字)を用いても自由度を表す記号です。d.f.記号は『確率統計演習 2 統計』の分散分析の章で主に多用されています。
自由度nのカイ2乗分布はガンマ関数の特例でもあります。

証明をお願いします!
ポイントは平方変換とガンマ分布の再生性です。
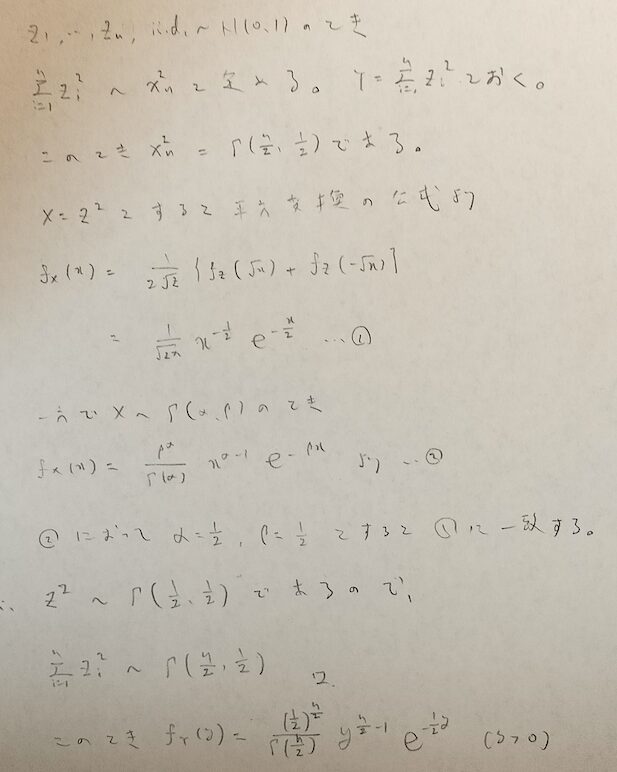
例えば『データ解析のための数理統計入門』によるとガンマ分布の特例としてカイ2乗分布を定義しているなど定義が異なります。この記事では正規分布を組み合わせた分布として定義します。
カイ2乗分布の期待値と分散と積率母関数と再生性の証明
カイ2乗分布はガンマ分布の特例なので期待値や分散などの特性値は自動的に求めることができます。例えば自由度nのカイ2乗分布はガンマ分布の特例のため当然、全確率1を満たします。
ガンマ分布の記事を未読の方はこちらからご覧ください。
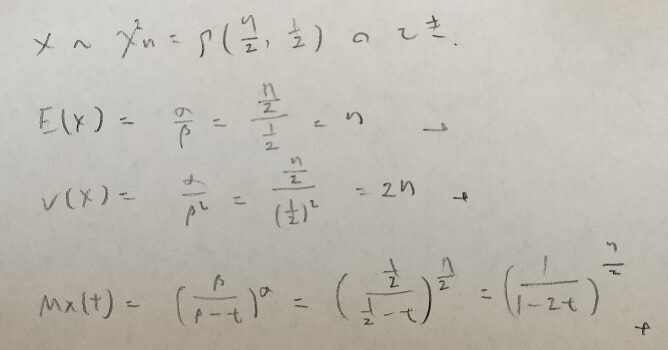
ガンマ分布が第1パラメータについて再生性を持つので、カイ2乗分布が自由度に関して再生性を持つのも当然ですね。再生性を証明したいのでm個のカイ2乗分布に従う確率変数は互いに独立であることにご注意ください。
m個の独立な確率変数と同じ意味ですが、m個の標本はある確率変数に従う(有限でなはない)母集団から独立に選んでおりますので、本によっては独立という部分が省略されているものもありますのでご注意ください。
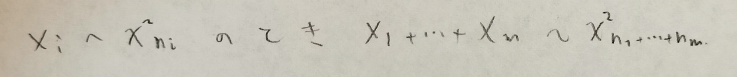
証明をやってみます!
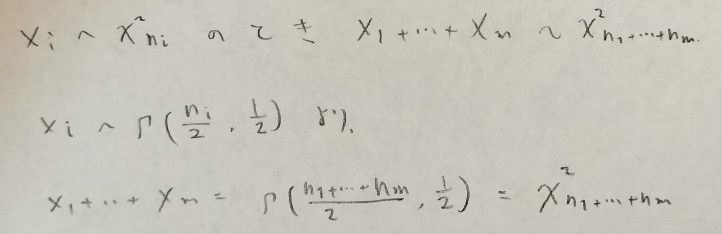
カイ2乗分布(カイ2乗統計量)の持つ意味
カイ2乗分布の期待値や分散や積率母関数を導出しました。次はカイ2乗分布に従う数式(=カイ2乗統計量)はいったい何を表すものなのかを考えていきます。次の図の1行目の数式はカイ2乗分布に従う統計量です。証明は正規分布に従う確率変数Xを標準化して標準確率変数に従う確率変数Zにする考えに沿って進めます。
n個のカイ2乗分布に従う確率変数は互いに独立であることにご注意ください。こちらも正規母集団からn個の標本(確率変数)を取ったと考えてください。
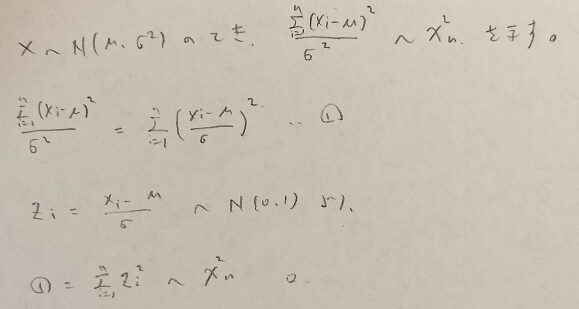
まずは上の図の1行目の数式をご覧ください。
この数式の分子に期待値記号をかぶせると分散の式になりますね!ひょっとしたらカイ2乗統計量は分散に近いものなのかも知れませんね。
次の例を考えるとカイ2乗統計量が分散をイメージさせるものだという認識に少し近づきます。下の図の1行目は自由度n-1のカイ2乗分布に従う統計量を表します。先ほどの自由度nのカイ2乗分布に従う統計量との違いは分子が期待値μではなく標本平均となっているので、標本分散に近い形をしていますね。
きちんとした証明は記事の後半で扱いますが、次のように考えれば下図の1行目の式がなぜ自由度n-1のカイ2乗分布に従うかが分かります。ポイントは期待値μを作り出すことです。
最後の行はカイ2乗分布の再生性を使っていますね。
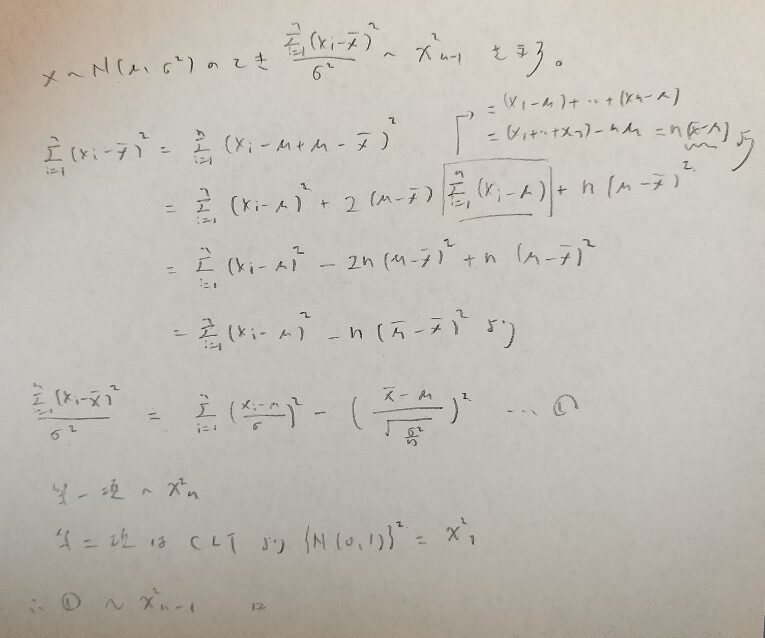
カイ2乗分布の性質と直交行列(ヘルマート行列)を用いた標本平均と標本分散が独立であることの証明
まずは標本平均と標本分散の定義を行います。
n個の確率変数を足してからnで割った値を標本平均といい、次のように表します。
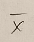
次の式を標本分散といいます。Sの右下にXがあるのはどのような確率変数で考えているかを明確にするためです。
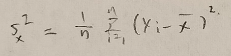
カイ2乗分布で最も難しいのは正規分布に従う互いに独立なn個の確率変数Xの標本平均と標本分散が独立であることの証明への応用です。こちらは事前準備が必要なので順に解説します。
直交行列Tの復習をします。
行列Tについて、「T(Tの転置行列)=(Tの転置行列)T=E」となる行列Tを直交行列といいます。det(T)=det(Tの転置行列)なので「」の関係式の両辺に行列式を取るとdetT=1または−1になります。そのためTの行列式の絶対値は1になります。直交行列関連について『線形代数学』がとても分かりやすく詳しく載っています。
まずは標準正規分布に従う確率変数Xについて考えます。
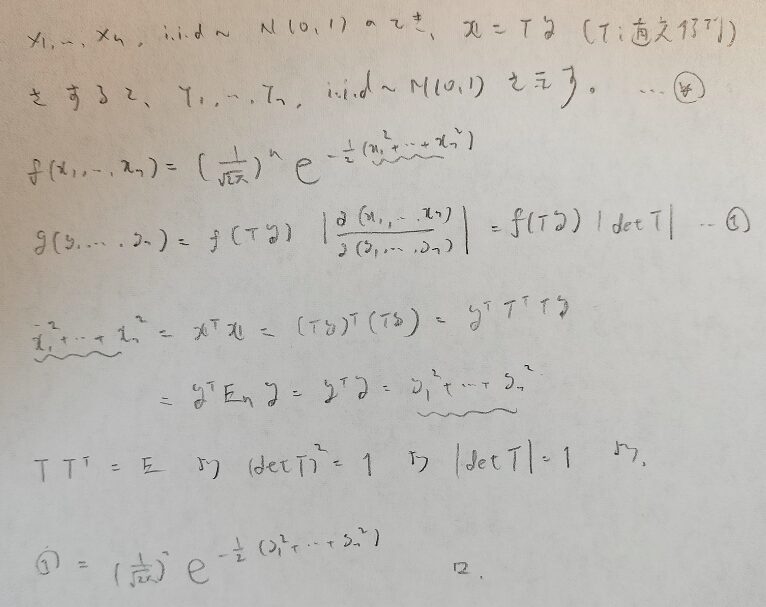
最後の結果はn個の独立な標準正規分布に従う確率密度関数に分けられますので題意が成立します。
次に正規分布に従う独立な確率変数についての独立性を示すために直交行列がどのように使われるのかを具体例で説明します。ポイントは正規分布を標準正規分布に標準化することです。
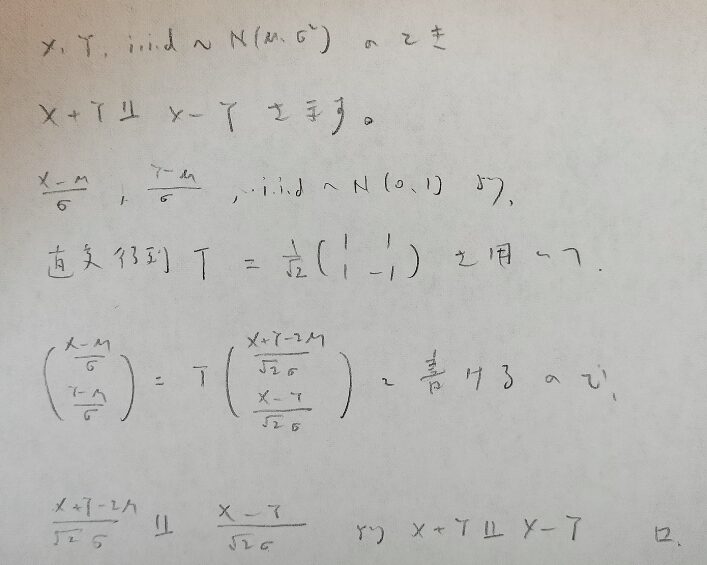
『明解演習 数理統計』を参考にしました。
準備が整ったので、いよいよ正規分布に従う互いに独立なn個の確率変数Xの標本平均と標本分散が独立であることの証明します。すなわち下の図の※を証明します。

証明には直交行列H(ヘルマート行列:英語名Helmert matrix)を用います。
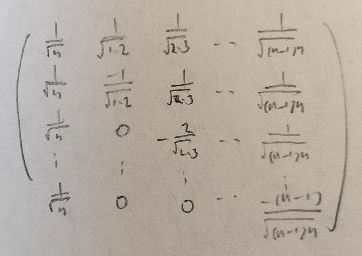
Xで考えると難しいのでまずは標準化したZで考えてからXへと戻ります。
この証明の中には標本分散を分散の2乗で割った値(=カイ2乗統計量)が自由度n-1のカイ2乗分布に従うことが副産物として得られています。
先ほど行った証明のより厳密なバージョンですね。こちらのヘルマート行列を用いた証明は『現代数理統計学の基礎』などで丁寧に解説されていますね。
証明中の□で囲った部分がこの証明の最後の部分の本質となる部分です。全体的に難易度が高い証明です。
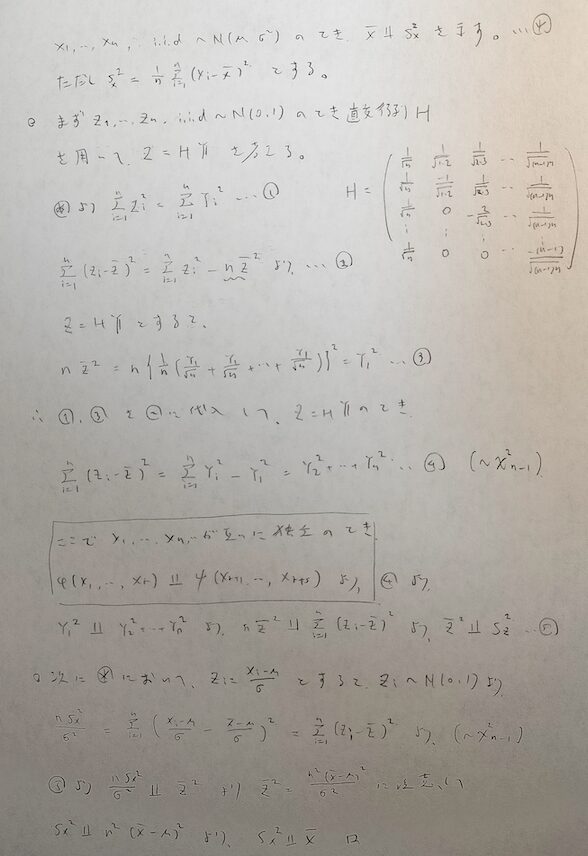
下から3行目においてXの標本分散の定数倍が自由度n-1のカイ2乗分布に従うことがわかります。
カイ2乗分布とは分散が関係した分布であり、カイ2乗統計量の意味とは標本分散の定数倍だったのです。
母集団が正規分布に従うとき、標本平均と標本分散が独立であることの証明がカイ2乗分布が絡んでいたことが分かって面白かったです。カイ2乗分布の『2乗』が標本分散を表していたこともよく分かりました!
最後にカイ2乗分布の記事で参考にした素晴らしい本たちを紹介します。
線型代数で僕が最もお世話になった本です。ジョルダン標準形までとても分かりやすく解説されています。練習問題も良問ばかりです。東大院試の線形代数は本書をしっかりと学習すれば対処可能です。数学検定1級にはお釣りがくるレベルです。
直交行列のところで参考にしました。アクチュアリー数学受験者にとって名前が必ず上がる有名な本です。
統計検定1級受験のためのバイブルです。ヘルマート行列の名前は本書からの抜粋です。
カイ2乗分布の定義のところで参考にしました。この本ではガンマ分布との絡めた定義として掲載されています。
カイ2乗分布の持つ意味について参考にしました。統計学の辞典としてもっともリーズナブルな本です。
カイ2乗分布の自由度のところで参考にしました。本書はアクチュアリー数学受験者のための指定教材となっております。










