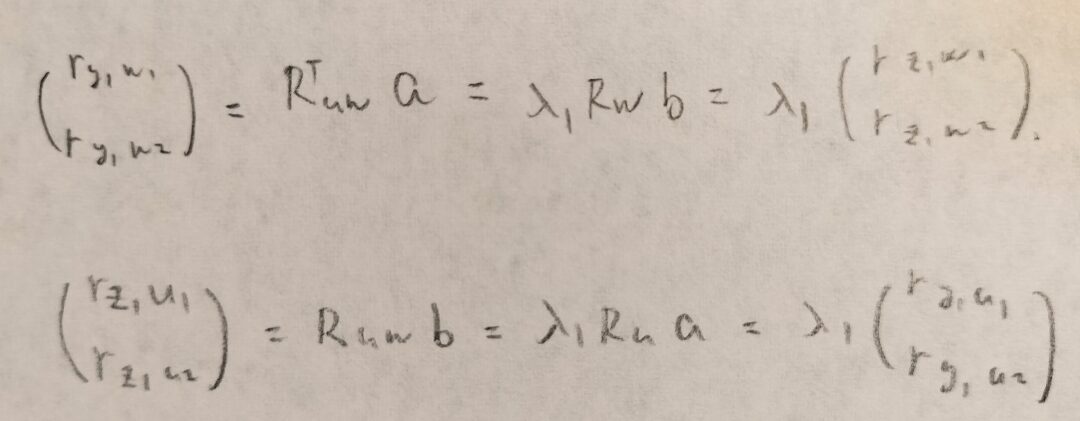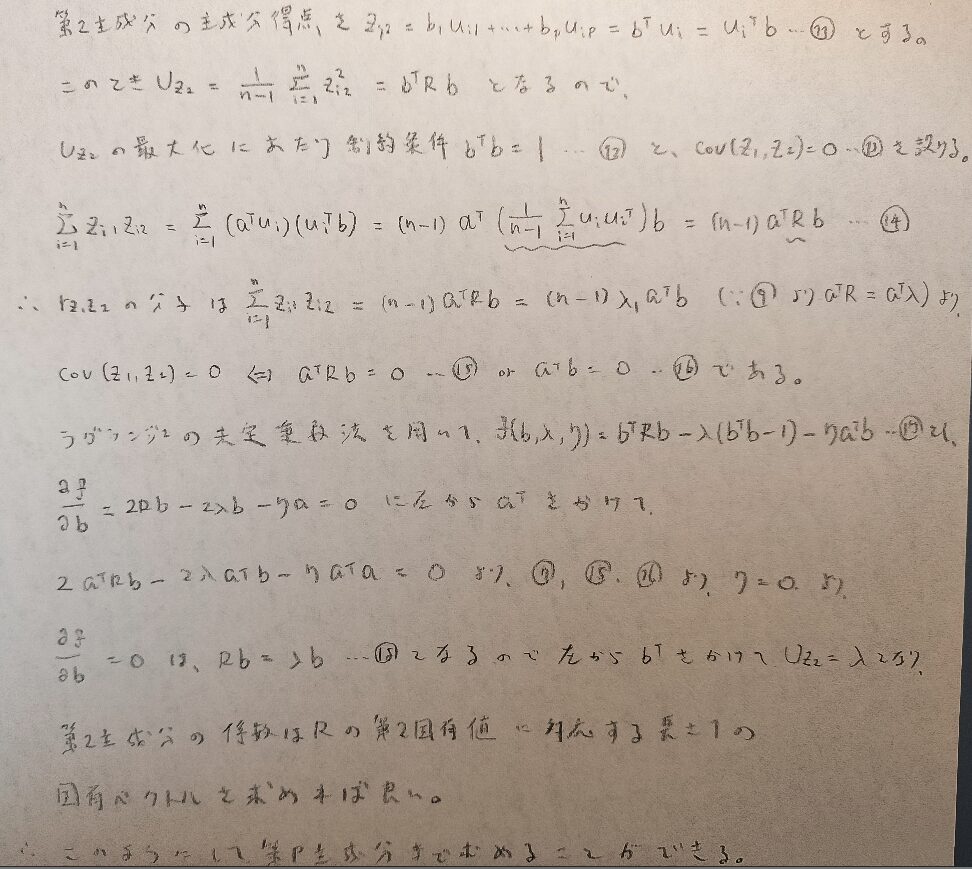変数が2つのグループに分けられている時、2つのグループの変数間の関連性を考える分析法を正準相関分析といいます。本記事では正準相関分析の目的と考え方を主成分分析の考えと照らし合わせながら考えていきます。
また多変量解析の参考書では『多変量解析法入門』がおすすめですので紹介しておきます。
正準相関分析の第1正準変数の設定
正準相関分析では2つのグループの変数間の関係を考えます。各変数は標準化されているとします。
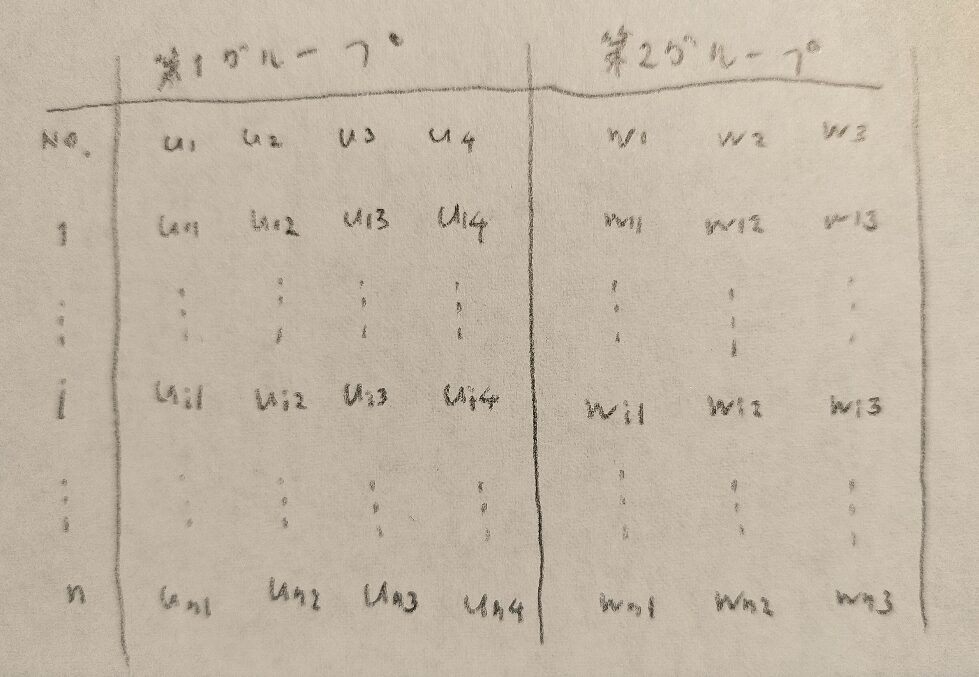
第1グループの変数に基づく合成変数と第2グループの変数に基づく合成変数を図02のように設定し、これらの相関係数が最大になるように定数を定めます。
詳しい定数については図02をご覧ください。
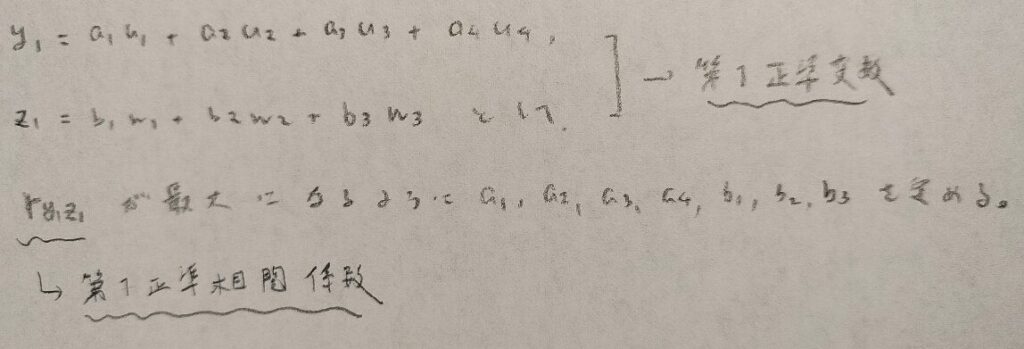
所望の相関係数のことを第1正準相関係数といいます。
正準相関分析と固有値問題の考え方
主成分分析などで何度か登場した固有値問題は正準相関分析でも登場します。
またか!という感じです笑
多変量解析の後半部分になるとほぼ毎回固有値問題が登場するパターンに気付きましたね!笑
第1正準変数などの求め方
ここでは理解を重視していくため、変数の量を減らして考えます。具体的には第1グループや第2グループに属する変数をそれぞれ2変数とします。
主成分分析のときと同じように相関係数行列を作り出すことを考えます。
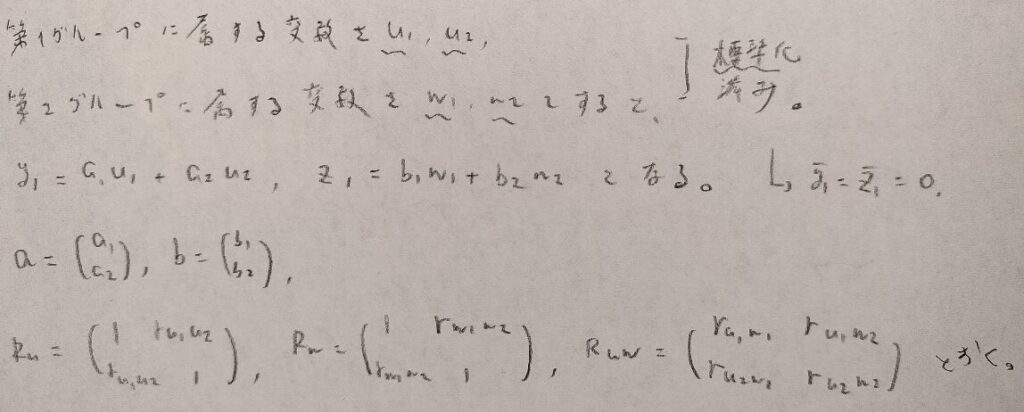
右側の行列を除く各相関係数行列の対角成分が必ず1になるのはなぜでしょうか?感覚的にはわかりますが、数式的な証明が欲しいです。
了解しました。図04をご覧ください。
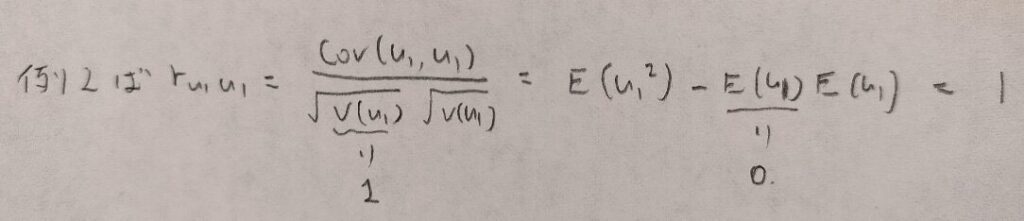
共分散の記号を用いていますが、実際は標本共分散のことです。後ほど混乱を避けるために別の記号を使用します。図05では標本分散ではなく不偏分散を用いているので、記号はVではなく、Uを用いています。
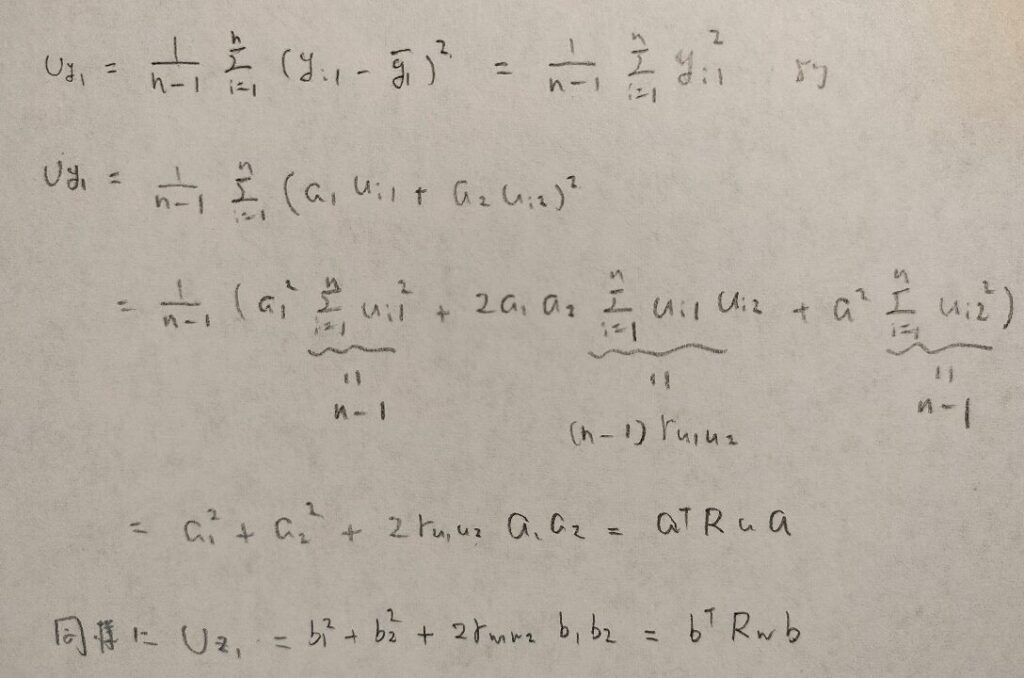
これで第1正準変数の不偏分散を二次形式で表すことができました。
主成分分析のときと流れがほぼ同じですね。
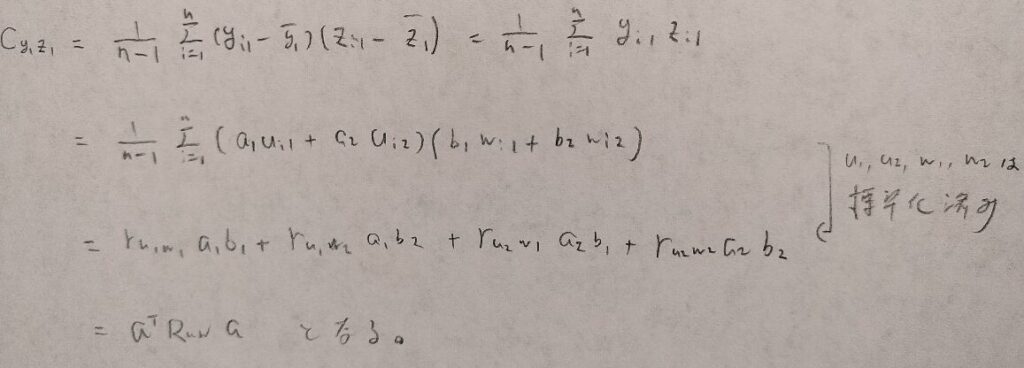
ここまでで第1正準変数を求めるための準備が整いました。

ここからは主成分分析などで何回も登場しているラグランジュの未定乗数法を用いて最大値問題を考えていきます。
進めていくと無事に固有値問題へと辿り着きます。

ここまで来れれば図02の定数が推定できるので、第1正準変数を求めることができます。
もしも第2正準変数も求めたい場合は主成分分析のときと同じような仮定を設ければOKでしょうか。
その通りです。2つのグループの変数間の説明が第1正準変数のみでは説明力が十分でない場合は、第2正準変数以降も考えます。
第2正準変数であるy_2、z_2を求めたいので、(変数が標準化されているため)それぞれの分散が1であることに加えて、y_2はすでに求めたy_1とz_1と無相関であり、z_2もy_1やz_1と無相関である条件のもとで、第2正準変数の相関係数を最大にしますので、図08の③や④式から固有値問題を考えて、2番目の固有値に対応する固有ベクトルに基づいて、第2正準変数の係数を定めれば良いです。
正準変数の解釈
例えば上で求めた第1正準変数の意味を解釈したいとします。この解釈は2通りの方法で考えていきます。
再び図02をご覧ください。グループ1とグループ2で考えた正準変数はそれぞれ、どういった文字が使用されているかをチェックしましょう。
またグループ1はuが、グループ2はwがもとの変数であることにも気をつけましょう。
正準負荷量
まずは各正準変数と同じグループに属するもとの変数との相関係数を考えます。これを正準負荷量といいます。
図09では具体的にその値を算出しています。今回の例では全部で4パターンあることを意識しましょう。
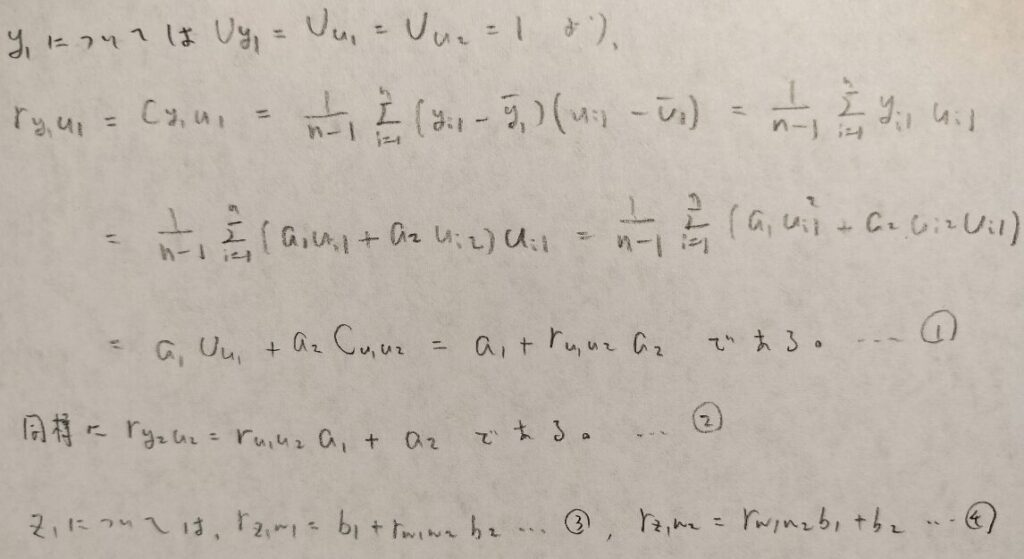
そして正準負荷量によって定められる寄与率の概念があります。
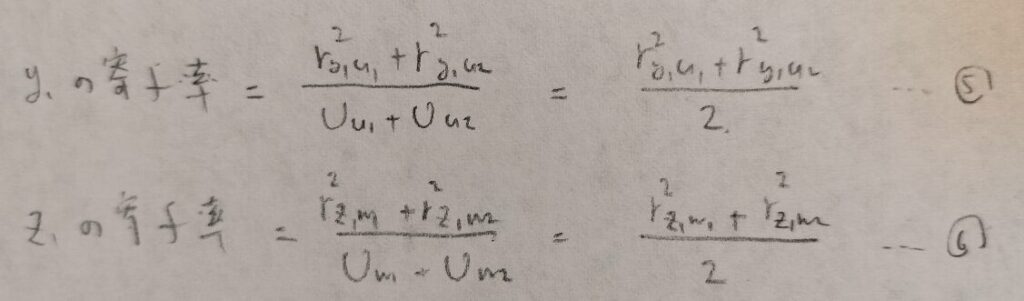
当然、累積寄与率の概念もあります。第2正準変数以降を考えるときは、各グループごとに寄与率を加えることによって累積寄与率が定義できます。
交差負荷量
次に正準変数ともう一方のグループに属するもとの変数との相関係数を考えます。これを交差負荷量といいます。
先ほどの正準負荷量の反対の概念ですね。
正準相関分析では2つのグループ間の変数の関係を考えるので、正準負荷量と交差負荷量の2つが存在するのは必然です。
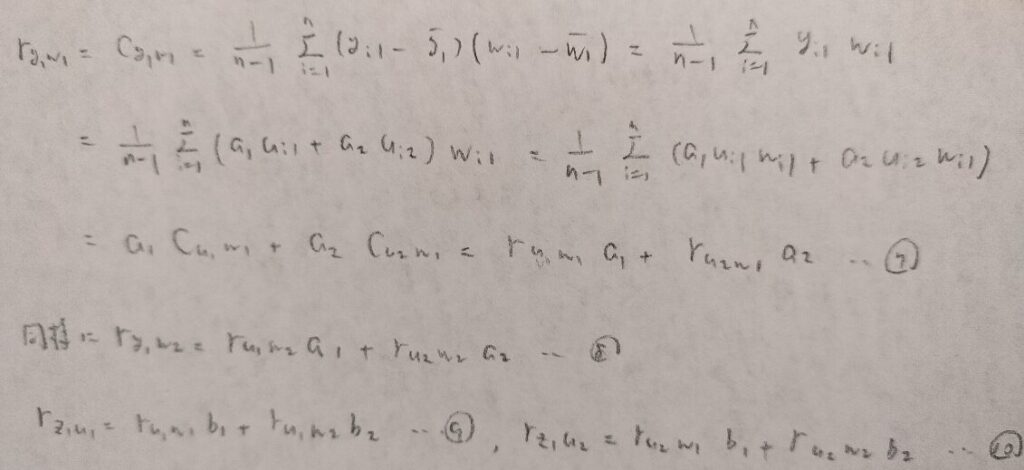
交差負荷量にも寄与率に対応する概念がありそうですね。
あります!それは冗長性係数という見慣れない名前のものです。ただしこれは寄与率の計算とほぼ同じです。
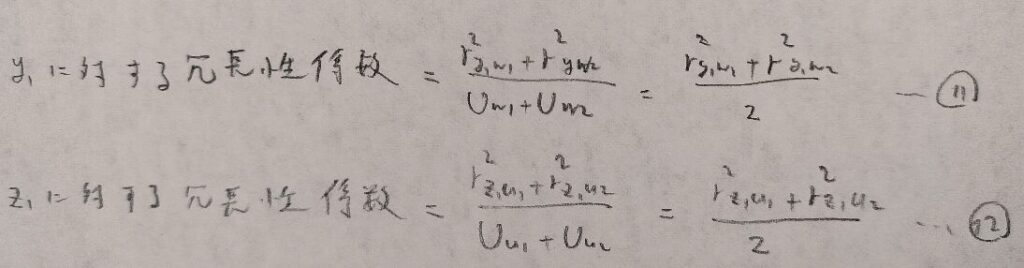
冗長性係数についても、各グループごとに冗長性係数を加えたものを累積冗長性係数といいます。
正準負荷量と交差負荷量は似ていますが、これらの間の関係性を表す公式はありますか?
ありますよ。最後にこちらを紹介しますね。
まずは図09と図11を見ながら図13をご覧ください。途中で出てくる行列の関係式は図08で既出の内容です。
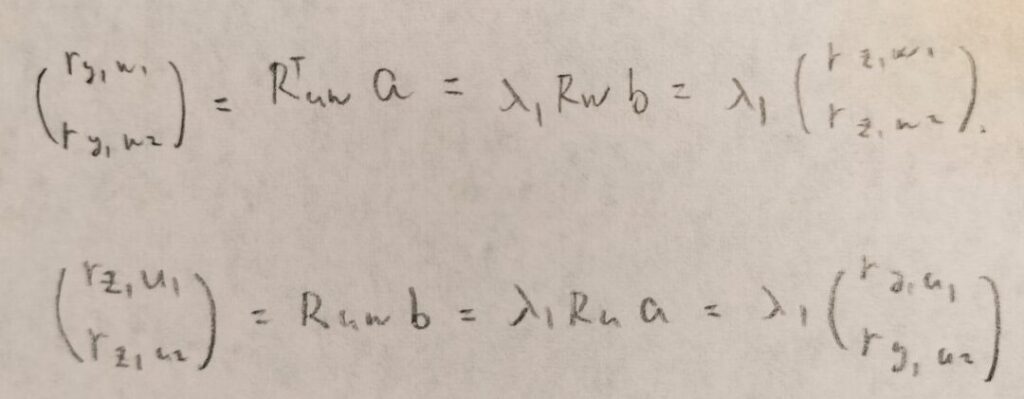
この公式は正準相関分析の総まとめ的な公式でしたね!
そうですね。正準相関分析は変数のグループを1つだけ考えて合成変数(主成分)を構成して解析していく主成分分析と違って、2つのグループごとに合成変数(正準変数)を構成して解析を進めていくことに大きな違いがあります。ただし根本の考え方や固有値問題が出てくる過程などは主成分分析が元ネタになっています。
2つのグループの比較は単純ではなく奥が深い内容でしたね。今回もお読みくださり、ありがとうございました。