本記事はアクチュアリー数学で最も難易度が高い公式である二項母集団の母比率(母百分率や母不良率ともいう)の区間推定の解説をします。難易度が高いため、F分布の内容をおさえた上でお読みください。
二項母集団の母比率の区間推定では近似法と精密法があります。
精密法は公式がたくさんありすぎて、丸暗記をするのはとても難しいです。何か覚え方のコツなどを教えて欲しいです!
ポアソン母集団の母平均の区間推定にも近似法と精密法はありました。その時の近似法は素直で簡単でしたが、二項母集団の母比率の区間推定で用いられる近似法の方が難しいです。そのため全体的に記事の難易度が上がります。
ただし、勉強の仕方をうまくすれば、暗記量を減らすことができます。
私たちと一緒に頑張りましょう!
二項母集団の母比率の最尤推定量
『リスクを知るための確率・統計入門』によると、区間推定では、どんなに難しい内容でも、まずは最尤推定量から考えていくとうまくいくことが多いです。
区間推定における信頼区間の求め方を復習しておきます。
信頼係数1-εの信頼区間の作り方(『統計学大百科事典 仕事で使う公式・定理・ルール113』を参考)
1.母集団のパラメータを用いて標本の統計量の分布を作る(この統計量をどうするか?がかなり大事!)
2.確率1-εとなる統計量の範囲を求める
3.統計量の実現値が入るとして2.の範囲をパラメータについて解くと信頼係数1-εの信頼区間が得られる。
今回の二項母集団の母比率の区間推定で用いる信頼係数は検定への応用を考えて1-εとします。
それでは二項母集団の母比率pの最尤推定量を求めましょう。ポイントはベルヌーイ分布を元に考えることです。いきなり二項分布から考えても良いですが、尤度関数が二項分布の確率関数そのままで良いことが分かりにくいので、ベルヌーイ分布を元に考えています。両者の結果は等しくなります。
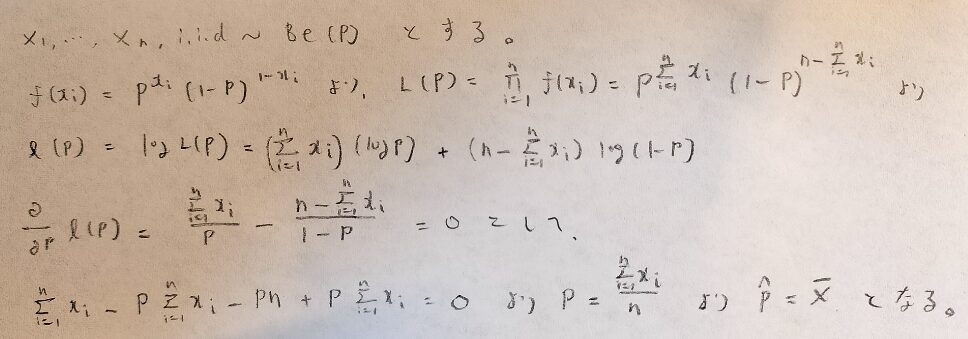
二項母集団の母比率の最尤推定量が従う確率分布
では次に最尤推定量が従う確率分布を求めます。
この内容はそのままアクチュアリー数学の過去問で出題されています。
二項分布の復習のためにn回中k回成功と書いていますが、区間推定の実際の場面ではk回失敗と考えるものが多いです。例えば『確率統計演習 2 統計』ではそれにならいpを母不良率ということもあります。
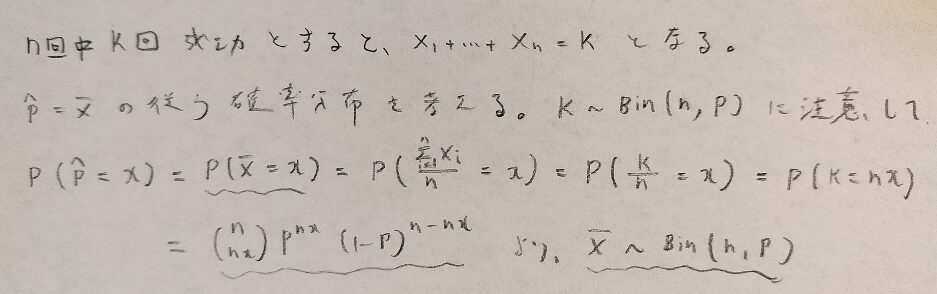
二項母集団の母比率pの区間推定では二項分布B(n,p)を元に考えていけば良いことが分かりました。
二項母集団の母比率の区間推定(精密法)
精密法の概要
いよいよ精密法に入ります。具体的に何をすべきか?の方針を先に示します。
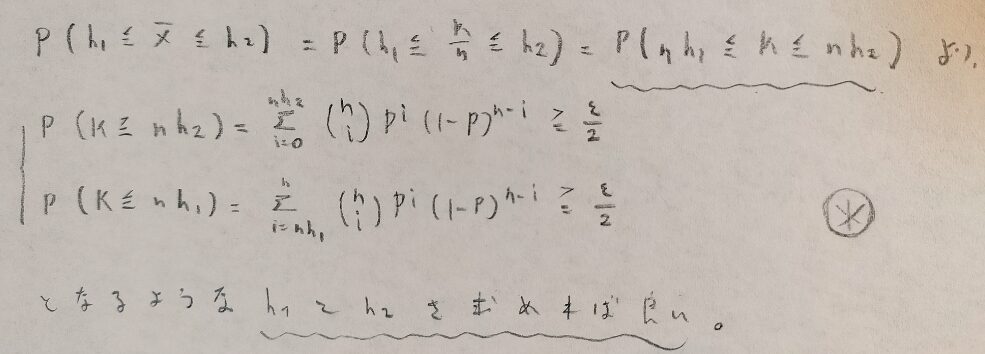
要するになんとかしてこのh1とh2を求めれば良いのですね。
ただしすぐには求まりませんので、二項分布とF分布の関係を考えることになります。そしてこの図03の※の式はまた後で再登場します。
二項分布とF分布の関係(二項分布の分布関数に相当するF分布の公式)
二項分布とF分布の関係式(☆)を証明していきます。kがどのような意味を持っているのか?を意識してください。今回は二項分布を足していく最後の項がk項目という意味のkです。
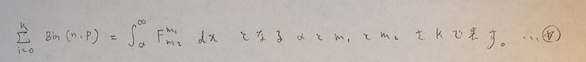
Bin(n,p)などをシグマや積分の中に書くのは厳密にはNGです。ただし、この記事では理解を優先しているため、理解がしやすいと判断した場合はこのような表記をすることがあります。
まずこの☆式の証明が今回でのメインの部分です。よってここが最も難しいです。
大きな方針を教えてください。
1.ベータ分布から出発する。
2.積分値を部分積分する方法と積分値を置換積分する方法が一致することを示す。
3.F分布の部分の自由度などがどのように表記されるか?が最も大事です。
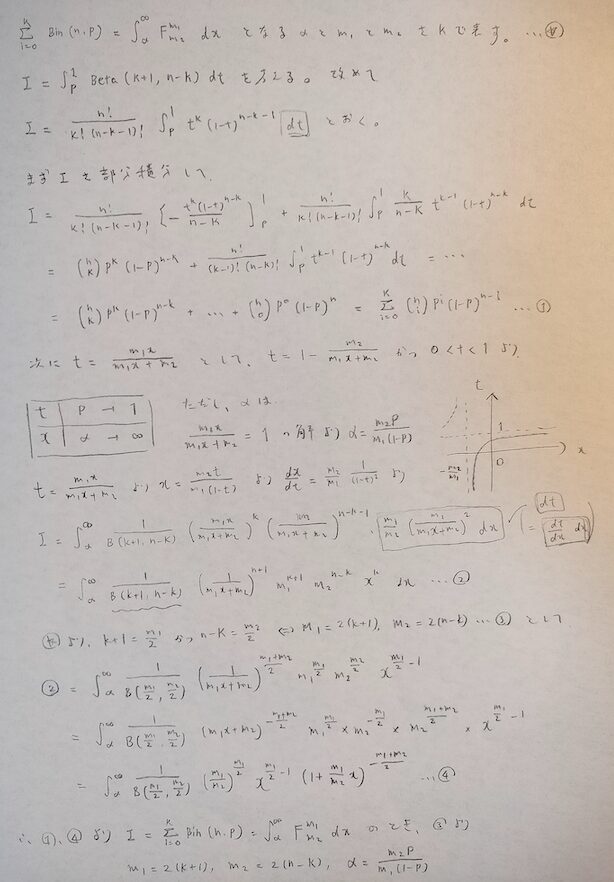
ポアソン母集団の母平均の区間推定のときと2.と3.は同じ方針なので、実質的には1.でベータ関数からスタートしようというところを知っているかどうかで証明できるかが決まります。
証明の道筋だけではなくて、途中計算がかなり複雑ですね。
m1やm2やαの値が複雑すぎて、こんなの暗記できない!と思うかも知れませんが、後で暗記のコツを教えます。今はこのまま次に進んでいきましょう。
今回は二項分布の分布関数に関するF分布の公式を求めたわけですね。
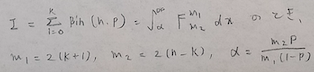
二項分布とF分布の関係(二項分布の生存関数に相当するF分布の公式)
次は図06の結論を変形して得られる二項分布の生存関数に相当するF分布の公式を導きます。
F分布特有の公式を用いています。F分布の逆数の分布は第1パラメータと第2パラメータがひっくり返ります。
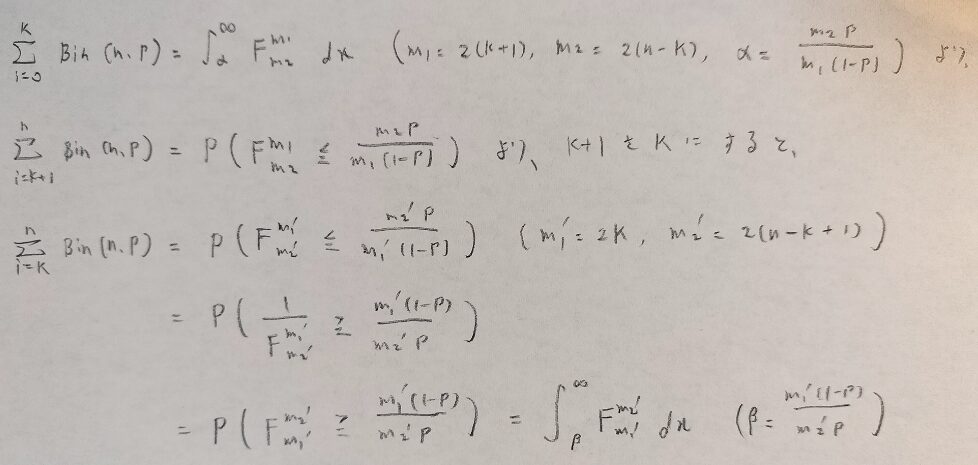
ここでの注意点は、F分布側の結果の不等号が同じ向きであることです。そうなるように式変形をしていったと考えます。m1とm2はk+1をkにしたことにより、少しずれています。ここも難しいところです。式を見失なわないように図07を丁寧に追っていきましょう。
ここまでに導いた二項分布とF分布を結びつける公式の一覧をお願いします!
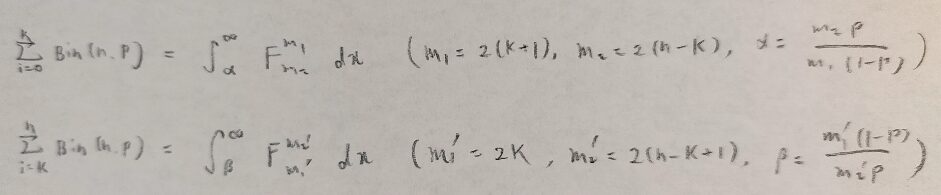
二項分布の母比率を区間推定する流れ
まずは記事の冒頭に紹介した、二項母集団の母比率を区間推定する流れをもう一度ご覧ください。
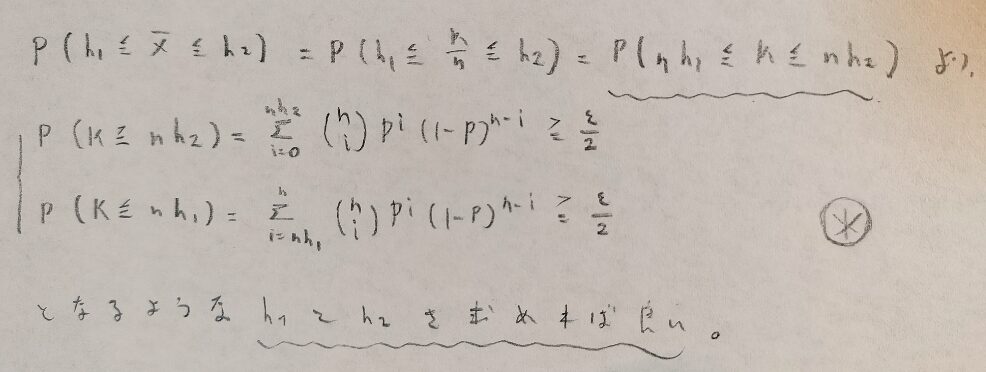
目標はh1とh2を出すことでした。そうすれば波線が信頼区間になりますよね。
ただし真正面からはh1やh2は出せません。その代わりとして先ほどF分布を用いて二項分布の分布関数や生存関数を表す公式を導いたのです。早速それを利用しましょう。
h1とh2は上側ε/2点を考えれば自然と求まります。感覚的にはnh1やnh2をkと置いて、図08の関係式を用いているだけです。
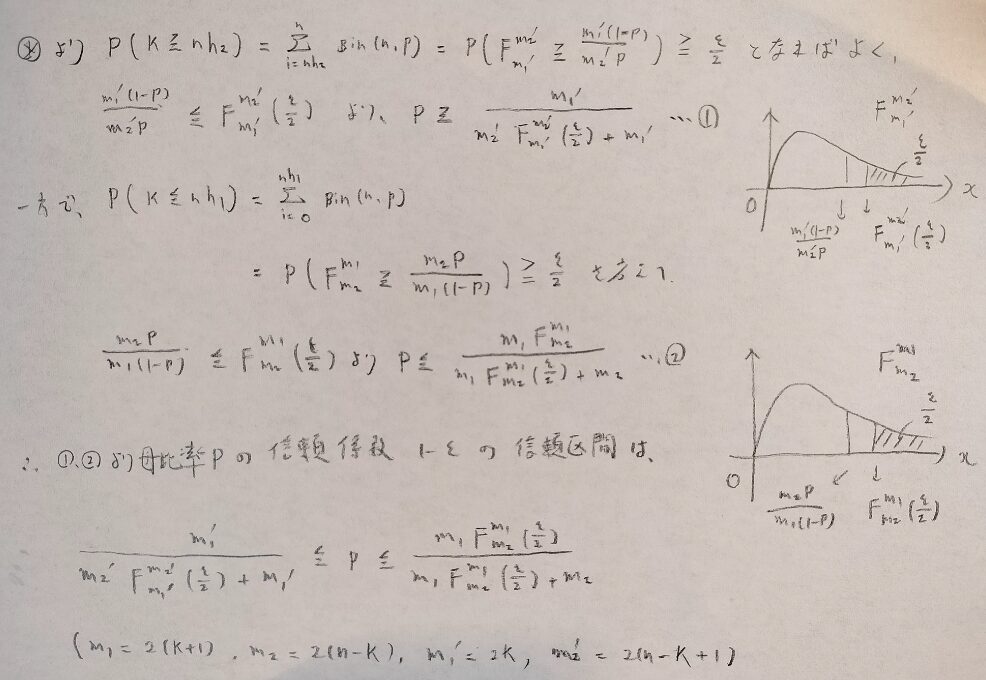
二項母集団の母比率の信頼区間の覚え方
二項母集団の母比率の信頼区間は導けましたけど、とてもごちゃごちゃしています!笑
確かにそうですね。この結果の式は、導出の自然さを意識したものなので、最終結果が綺麗にまとまっているか?と聞かれたら、覚えやすい形とは言えません。
二項母集団の母比率の信頼区間の忘れにくい覚え方を教えます。
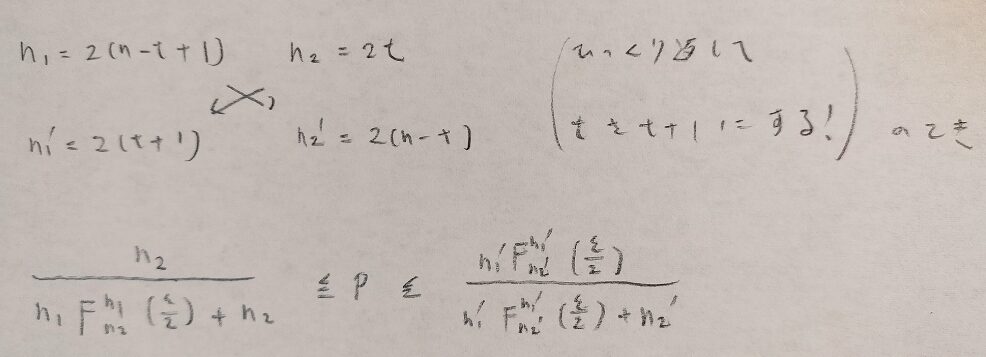
tは先ほどの図10の結果でkに相当する量です。意味的にはトータルの成功回数(n回中k回成功)(問題によっては不良個体数などの失敗回数を表すことも)を表します。そのため、このトータルの成功回数が少ないなら精密法、多いならば近似法を用いることになります。
二項母集団の母比率の区間推定(近似法)はワルド法で考える
精密法より理解が簡単な近似法のお話をします。
ポアソン母集団の母平均の区間推定のときに、中心極限定理を用いて標準正規分布に持ち込めたことを覚えています。今回も中心極限定理は使えますか?
もちろんCLT(中心極限定理)は使えます。まずは概要を紹介しましょう。その後に注意点を述べます。

図12の下から3行目の不等式を見てください。例えばポアソン母集団の母平均の区間推定を近似法で行った場合は問題はなかったのですが、今回の二項母集団の母比率の区間推定を近似法で行う場合、pそのものが未知(推定すべきもの)なのでこれ以上進むことができません。そのため、最後の行の実現値を代入する場面で、pには最尤推定値を代入します。この考えをワルド法(Wald method)といいます。(『入門 統計学(第2版): 検定から多変量解析・実験計画法・ベイズ統計学まで』より)
最尤推定量ではなくて、最尤推定値なことに注意ですね。
その通りです。信頼区間は実現値で表現できるからですね。


