高校生が一番先に習う確率分布は二項分布です。
そして一般的な数理統計学の教科書でも二項分布が初歩的な確率分布として紹介されています。
二項分布の期待値や分散の導き方がわかりません。教えてください!
二項分布の平均と分散の公式を計算することによって求め方を考えてみましょう。
二項分布の作り方をわかりやすく説明します
確率の和が1という点に注目をして多くの確率関数や確率密度関数が作れます。
例えば岩沢先生の『リスクを知るための確率・統計入門』にわかりやすく書かれています。
今回は二項分布という離散型確率変数なので確率関数を考えることになります。
二項定理が二項分布の出発点です!
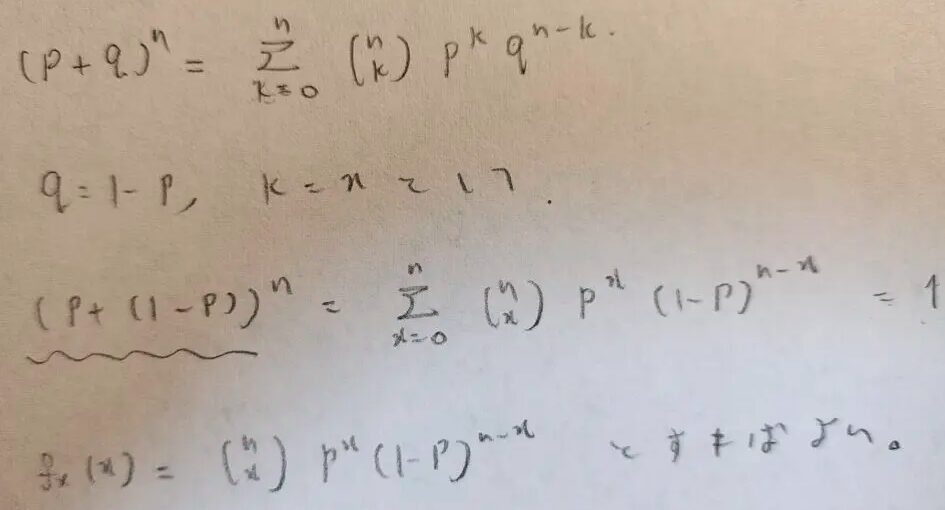
このようにして確率関数を作ります。この最終結果が確率変数Xが二項分布に従うときのXの確率関数となります。
二項分布はどのような意味があるのですか?
n回の試行を行ったときにk回成功する場合を考えています。このときのXが従う確率分布を二項分布といいます。
実はnに1を代入したときのXの分布をベルヌーイ分布といいます。
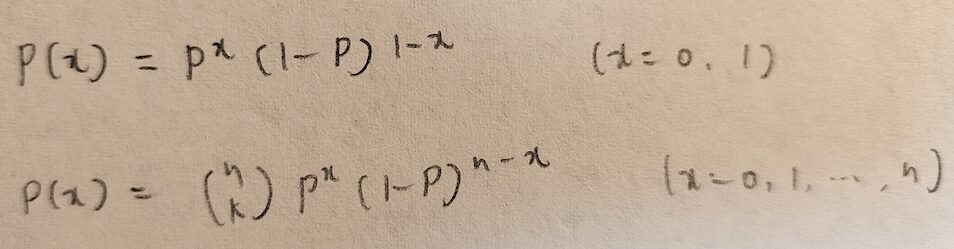
上の確率関数がベルヌーイ分布で下の確率関数が二項分布のものになります。
ベルヌーイ分布の確率関数は意外と掲載されていない参考書がありますので要注意です。
例えば久保川先生の『データ解析のための数理統計入門』に掲載されております。
二項分布の平均と分散の公式をわかりやすく計算して導きます
期待値と分散を計算する方法は2通りあります。
公式を暗記している方は、公式を用いて計算します。
公式を導けと言われたら、定義に従って計算します。
計算の際には離散型確率変数ならシグマ計算を、連続型確率変数なら積分計算をします。
今回は離散型確率変数なのでシグマ計算ですね。
まずは二項分布の期待値の計算からします。
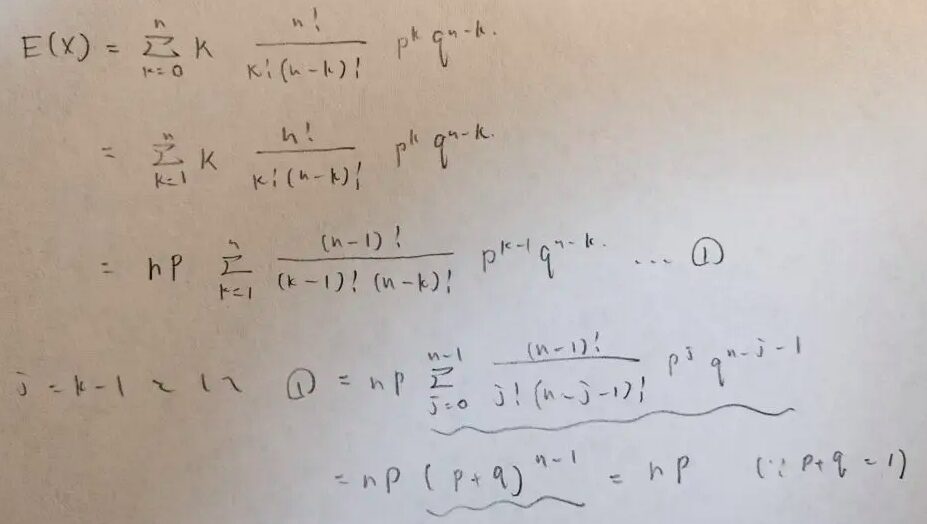
途中でなぜnpで括っているのですか?
答えがnpになることを知っているので、npを括った後のシグマの式(波線部)は1になるはずだというところから式変形をしています。
具体的には二項定理に持ち込んでいます。
他の例題も紹介ということで、今度はX(X-1)の期待値を出してみます。
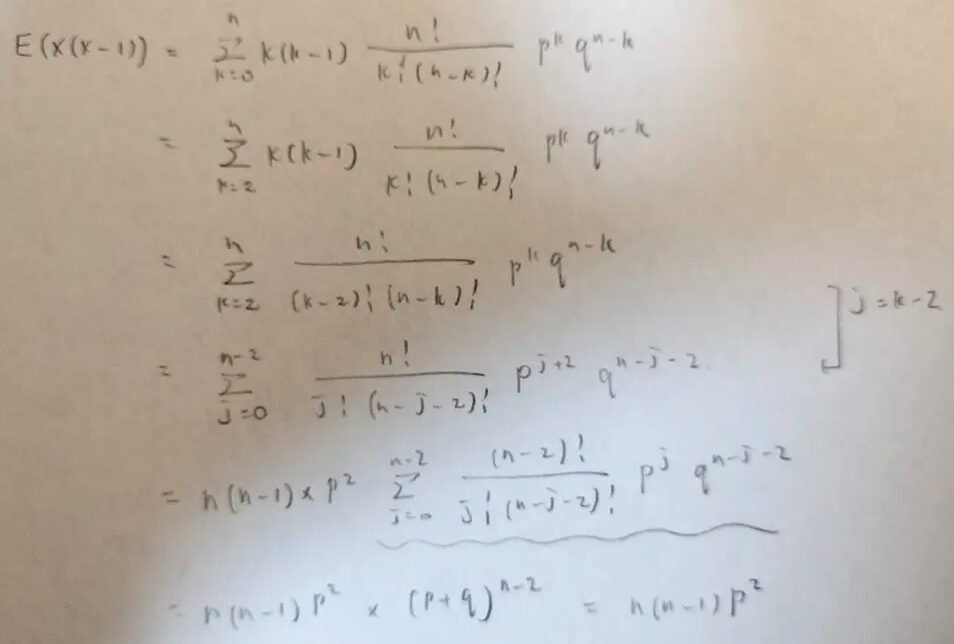
今回は答えがどうなるかは知らないので、二項定理に持ち込むことを目標に式変形をしています。
①kのスタート地点が0だと0項目が0になって和に影響が出ないので、1や2(上の例題では2)スタートにして見やすくする。
②改めて0スタートとして意味をなすようにjなどの新しい文字で変数を設定し直す。
③上の図の波線部のように二項定理に持ち込んで1になるように調整する。
期待値はわかりましたけど、分散はどうでしょうか?
分散は、2乗の期待値から期待値の2乗を引けば良いので、XとX(X-1)の期待値の結果をうまく使って出します。
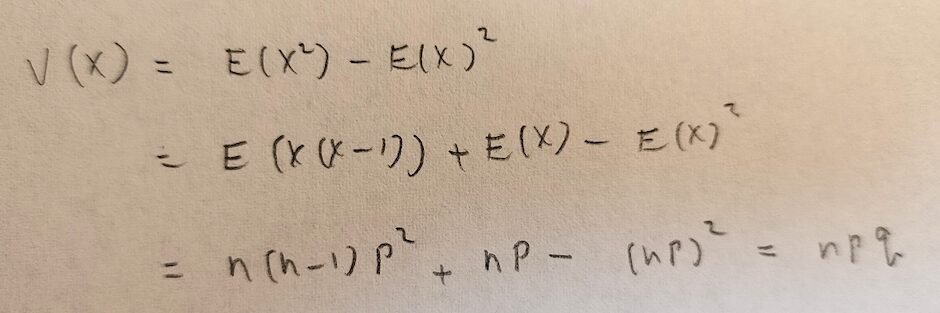
このようにして計算をして、二項分布の期待値と分散の公式が得られます。ただしq=1-pとしています。
二項分布の期待値はnpで分散はnpqです。
他の書籍たとえば『現代数理統計学』や『弱点克服大学生の確率・統計』でも同じ証明が載っています。
ちなみにX(X-1)の期待値の結果から、一般化してX(X-1)(X-2)(X-3)などの期待値も類推できそうですよね。
ベルヌーイ分布の期待値と分散をわかりやすく説明します
ベルヌーイ分布とは二項分布においてn=1とした分布です。
ということはベルヌーイ分布の期待値はなんでしょうか?
正確には確率変数Xがベルヌーイ分布に従うとき、Xの期待値を求める問題を考えています。
二項分布の期待値がnpなので、ベルヌーイ分布の期待値はpです!
ベルヌー分布の分散はなんでしょうか?
二項分布の分散がnpqなので、ベルヌーイ分布の分散はpqです!
これでベルヌーイ分布の期待値と分散が求まったので、結果を書きますね。
ベルヌーイ分布の期待値はpで分散はpqです。
ベルヌーイ分布の確率関数を求めてから期待値や分散を考えるよりも、二項分布で理解ができた段階で、その特殊な例として算出するのが良いと思います。
一応、計算では出せましたが、特に分散を出す計算が多すぎて大変ですね。もっと良い方法はありませんか?
いくつか方法はあります。例えば積率母関数というものを使って微分を行う方法です。
積率母関数関連はまた後日に紹介します。最後にこの記事で登場した参考書について紹介しておきます。
統計検定1級に関わっている1人である竹村先生の著作です。後述の久保川先生の本と比べてレベルが高いです。決定論にウェイトが置かれている数理統計学の本です。語り口調で書かれていることが特徴です。相性が良ければ最高の本だと思います。
統計検定1級対策で現時点でNO1だと思う本です。前半部の数理統計部分も説明が洗練されており、式変形などもわかりやすいです。本記事の証明部分とほとんど同じ説明になっております。本当におすすめです!
確率分布をどうやって思いついたのか?などの根本的な部分から解説しているわかりやすい本です。こちらは統計検定1級よりもアクチュアリー数学用の参考書で計算のテクニックが満載です。
アクチュアリー数学の対策で統計部分を除く確率とモデリングの部分で真価を発揮する問題集です。前半の確率分布の説明ではテクニックが満載されており、面白いです。しかし統計検定1級ではしっかりと式変形をして「自分は暗記に頼らずに式変形できますよ」とアピールすることが大事です。





