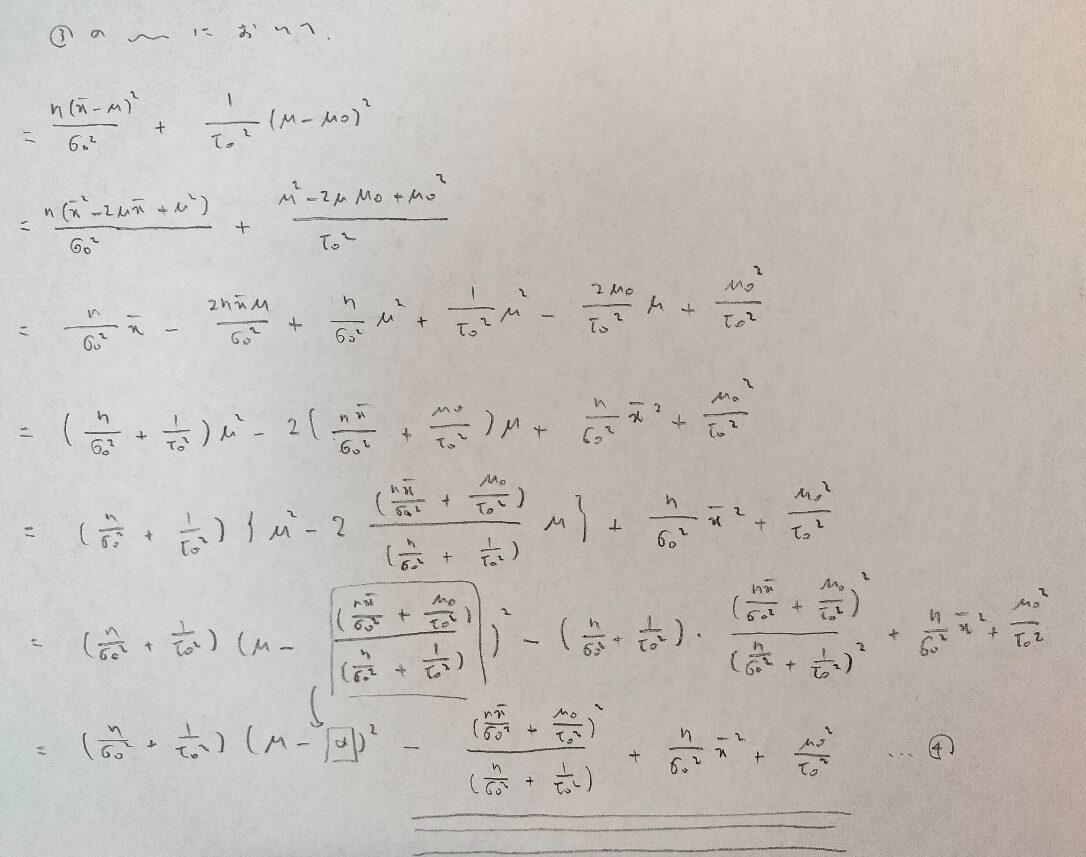今回の内容はベイズ統計でMCMCの前まで扱う関係のためとても長いです。少しずつお読みくださると幸いです。
ベイズ統計は広範囲になりますが、この記事では統計検定1級や統計検定準1級のベイズ統計(MCMC法の前まで)レベルの問題が解けることを目標にしています。
使用するテキストは『データ解析のための数理統計入門』です。記事の最後に『データ解析のための数理統計入門』に掲載されている演習問題を一気に解いていきます。『データ解析のための数理統計入門』の模範解答では途中式が省略されていますので、行間が埋められなくて困っている方に参考にしてほしいと思います。
本書は統計検定1級対策で有名になりつつある参考書です。このブログでも他記事にて演習問題を解いていますので、他のページもご覧くだされば幸いです。
事前分布、事後分布、ベイズ推定量、ベイズ信用区間、最高事後密度信用区間
まずはベイズ統計における用語の説明を行います。

のちに事後分布の期待値などの概念が出てきますが、アルファベッドの大文字、小文字については本書ではバラバラの基準になっています。そのため統計検定の問題を解く際は、問題設定にあるルールに従って記述すればOKだと思われます。
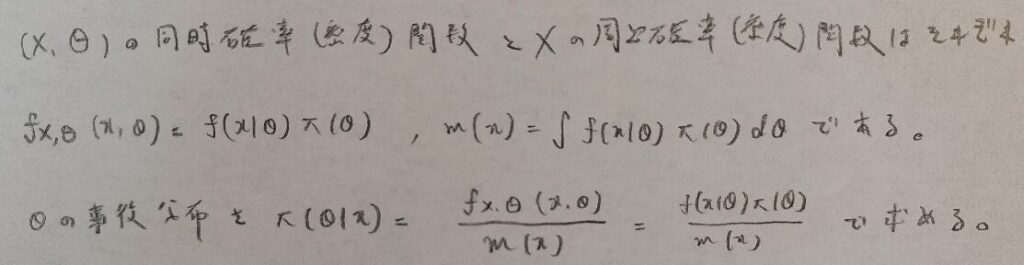
事後分布は同時確率(密度)関数を経由して求めます。ここら辺はのちの演習問題にて特訓しましょう!
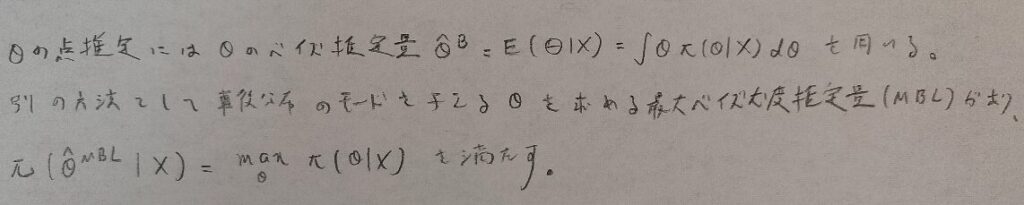
よく問題で問われるのはベイズ推定量の方です。最大ベイズ尤度推定量(MBL)の方は参考程度に捉えてください。

ベイズ信用区間はとてもよく出ます。事後分布を積分して考えることを意識しましょう!また信頼区間とは異なる概念ですので用語のミスにご注意ください。
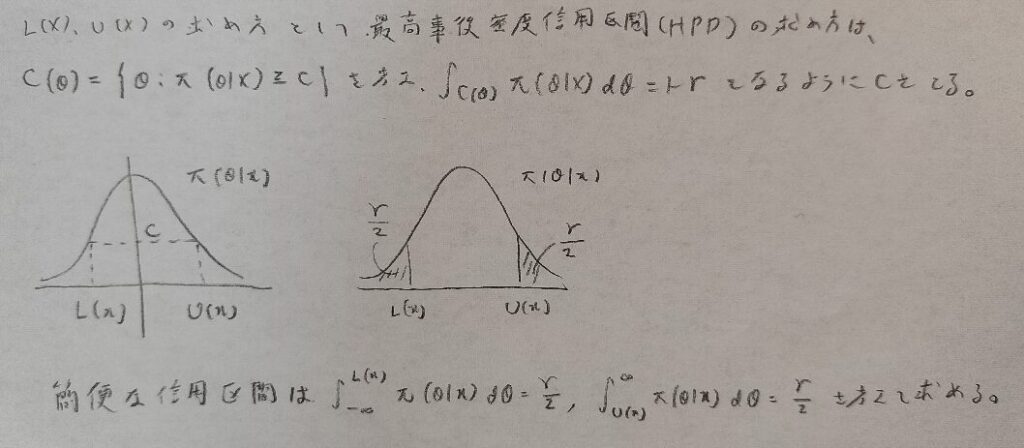
実際の問題では最高事後密度信用区間を直接出すことは少ないです。ガンマ関数などが絡む場合は簡便な信用区間を求めることになります。その理由はHPDを考えると数値計算になってしまうからです。
ベイズ信用区間を求める問題も本記事でたくさん扱っていますので、少しずつ慣れていきましょう!
最後に信用区間と信頼区間についてまとめておきます。統計検定のベイズ統計の問題を解く際はここまで細かい理解は不要です。
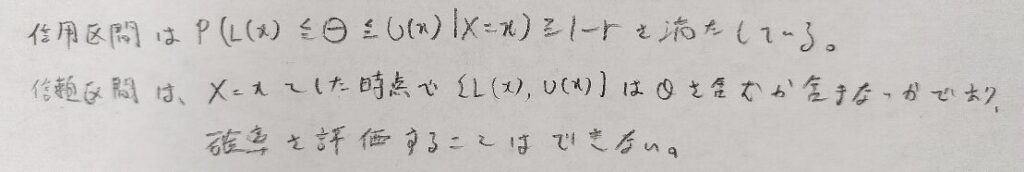
データ解析のための数理統計入門:第14章「演習問題」問1
事後分布は十分統計量の関数となることを示します。フィッシャーネイマンの分解定理を用います。

ベルヌーイ・ベータモデルとポアソン・ガンマモデルなどの有名モデル
それではここまで登場したベイズ統計の知識を用いて具体的なモデルを紹介していきます。
ベルヌーイ・ベータモデル
まずはベルヌーイ・ベータモデルの紹介です。このモデルを通してベイズ推定量の意味について考えていきます。これはベルヌーイ分布とベータ分布を合わせた分布です。
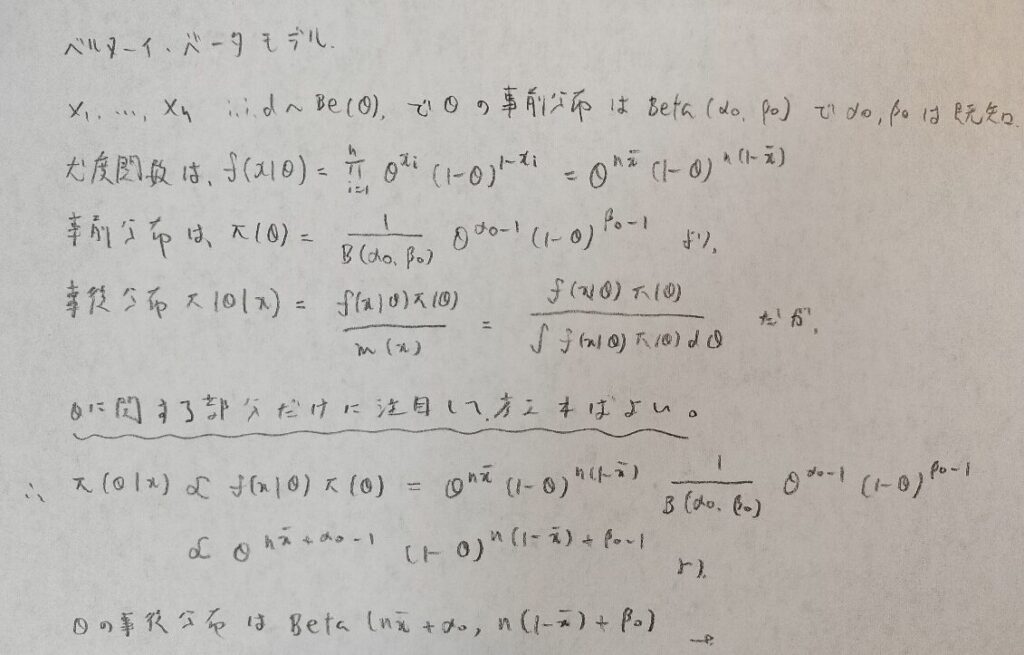
次にベイズ推定量を出します。
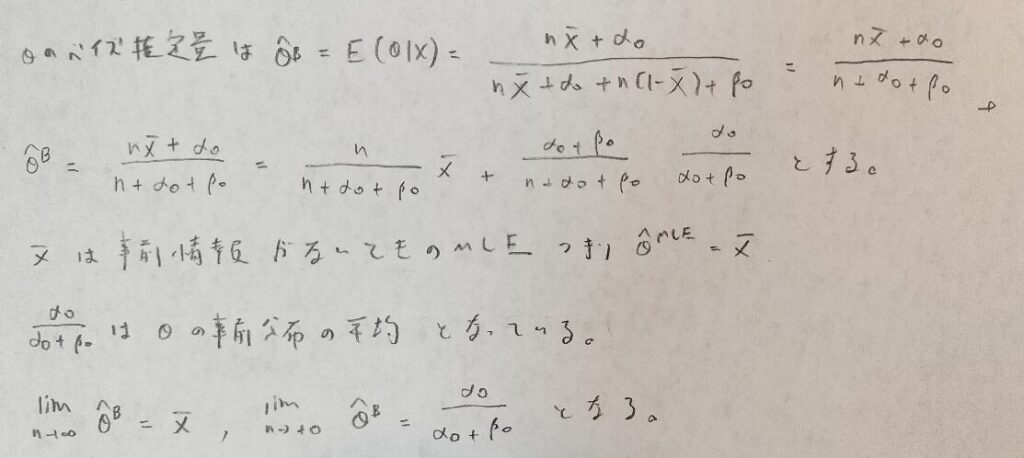
この例ではベイズ推定量は最尤推定量と事前分布の平均との加重平均の形で表されます。
サンプル数を増やせばベイズ推定量は最尤推定量に近づき、サンプル数が減れば事前分布の平均に近づきます。
なるほど。事前分布をどのように考えるかがベイズ統計では重要になってきそうですね。
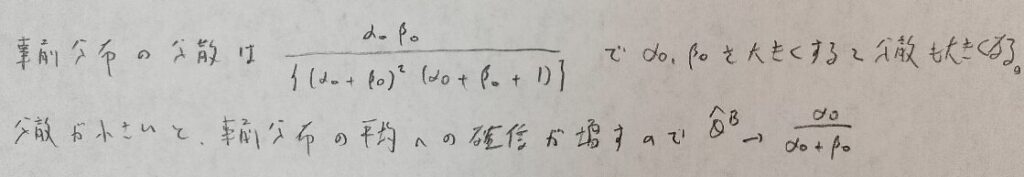
先ほどの説明を別の角度から捉えてみました。
ここまでで得られた結果を考察します。
信頼性の高い事前分布がないときは、一様分布のような曖昧な事前分布を設定した方が良いです。
そしてこのときのベイズ推定値とベイズ信用区間は(事前情報がないときの)最尤推定量に基づいた推定値と信頼区間に近い値となっています。
ポアソン・ガンマモデル
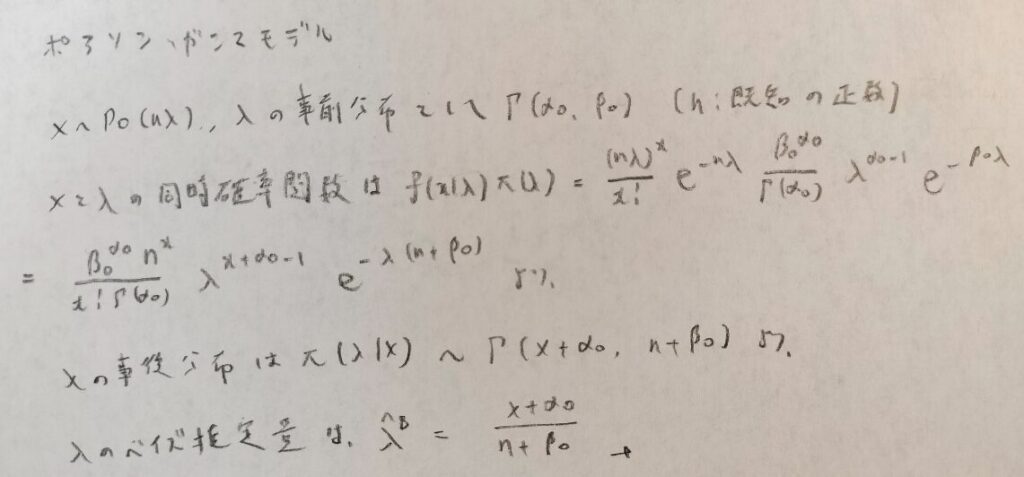
正規分布で分散が既知の場合(平方完成のやり方)
今までに見たことがないレベルの平方完成が登場します。平方完成は中学で学ぶ方もいますが、レベルがMAX付近になるとここまで難しくなる1つの好例として捉えても面白いと思います。
『データ解析のための数理統計入門』ではこの平方完成が絡む部分をほとんど省略されてしまっているので、私では理解できませんでした。
僕もパッと見ただけでは分からないので、実際に計算をしてみました。ご覧ください。
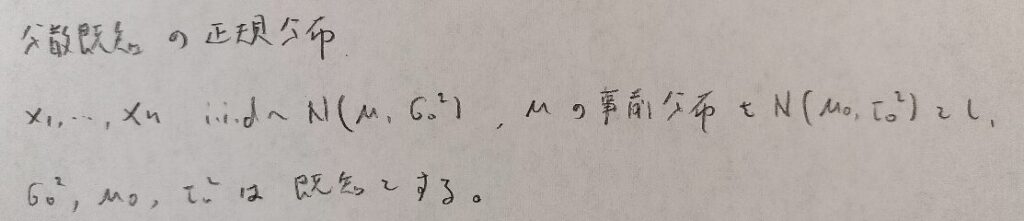
まず問題の設定はこちらです。今回は分散が既知とし母平均μが主役となります。
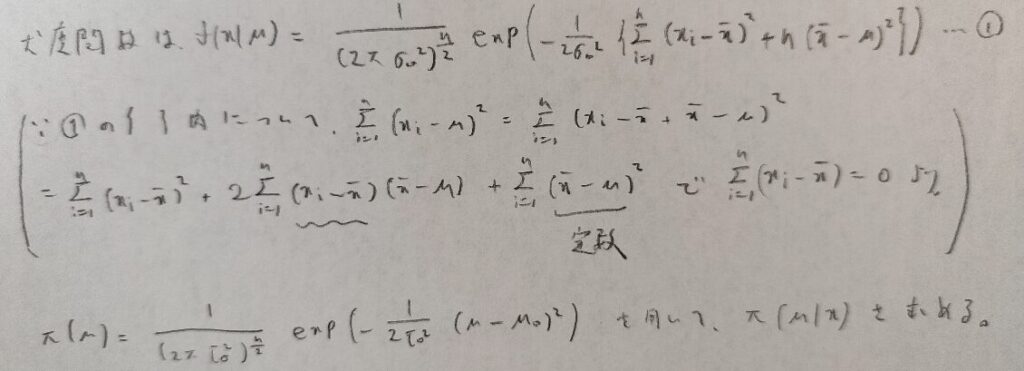
事後分布が求まればベイズ推定量などが分かりますから事後分布を考えるのですね!
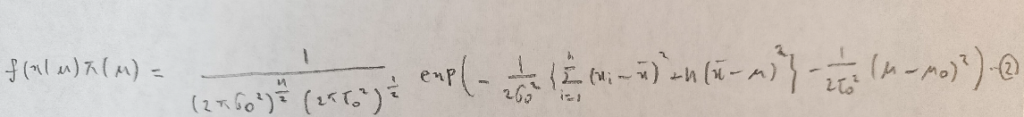
まずは同時分布を計算します。
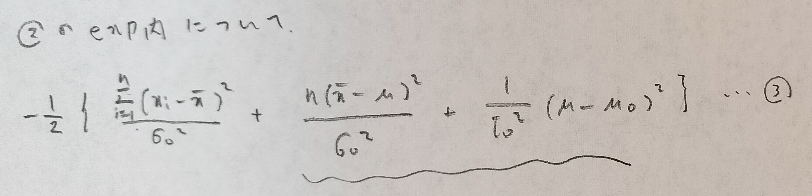
この波線部分を変形していきます。7行目の四角で囲った値がベイズ推定量になりますが、ここではまだそれが判明しないので、定数αと置いておきます。
『データ解析のための数理統計入門』ではいきなりベイズ推定量として扱っていますが、僕はこの段階ではそれが見抜けなかったのでただのαと置いています。
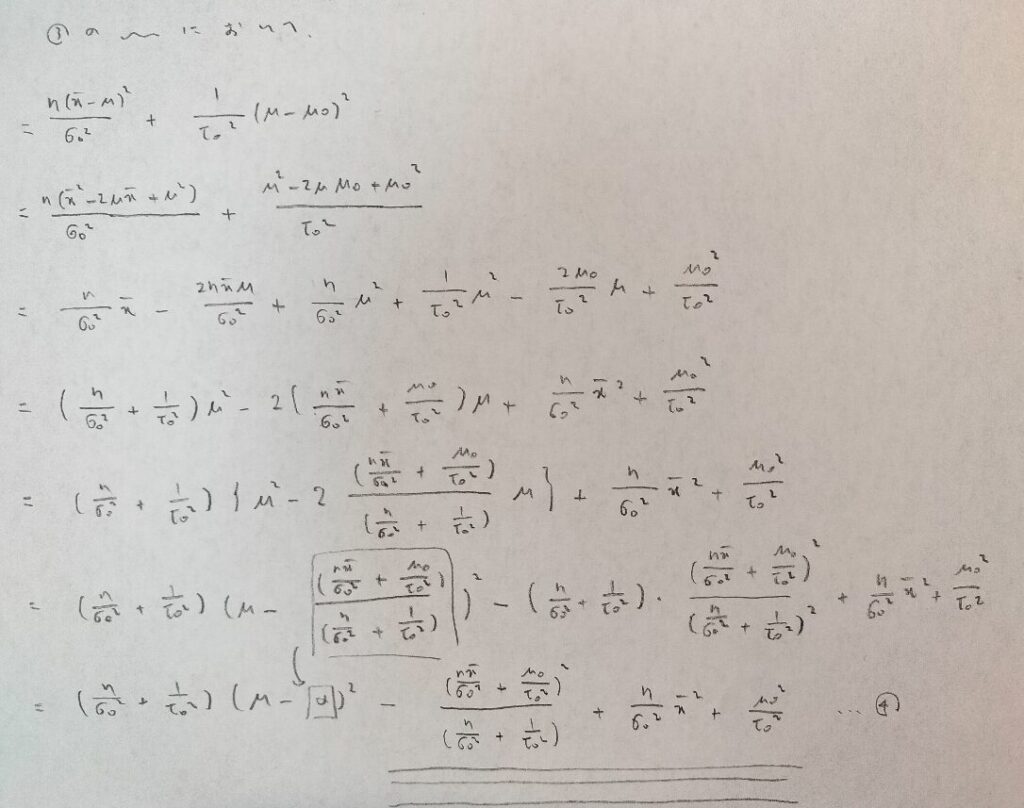
次にこの3本線の部分をまとめていきます。まだ終わらんのかい!と言いたくなりますよね笑
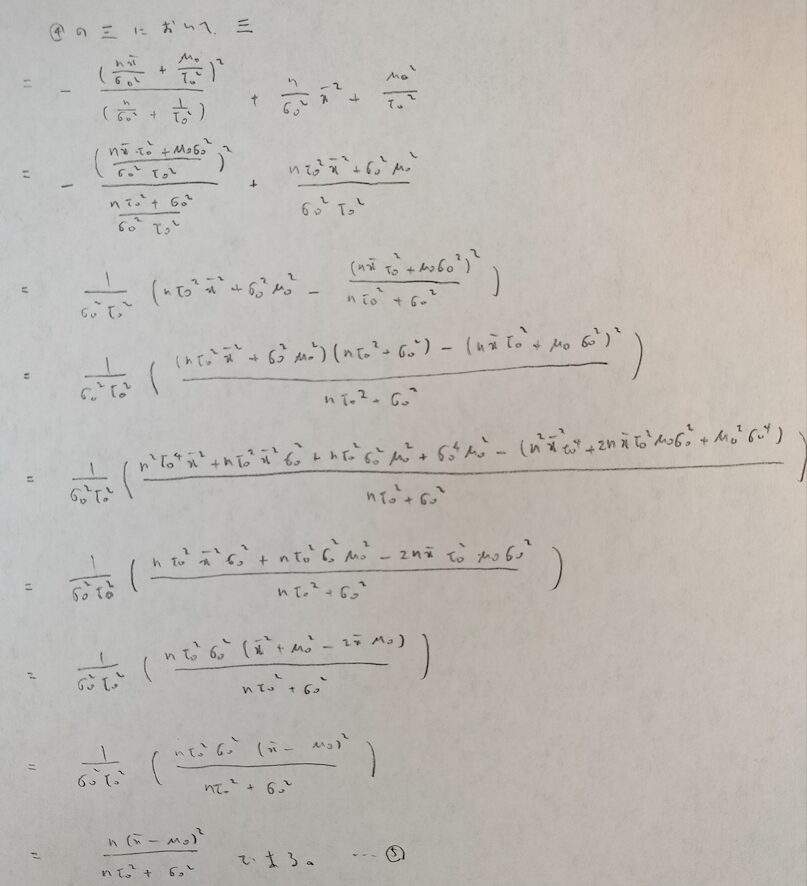
ようやく終わりが見えてきました。
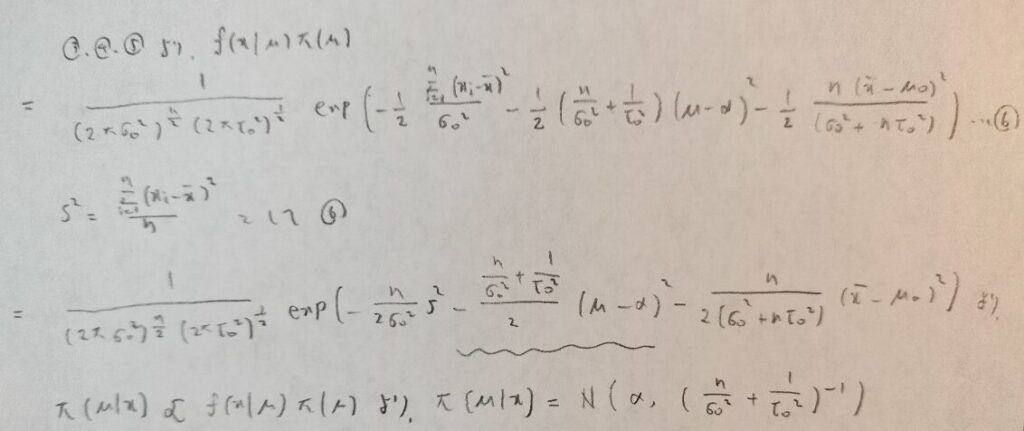
あ!やはりベイズ推定量はαだったのですね!
その通りでしたね。ではこの結果をまとめておきます。
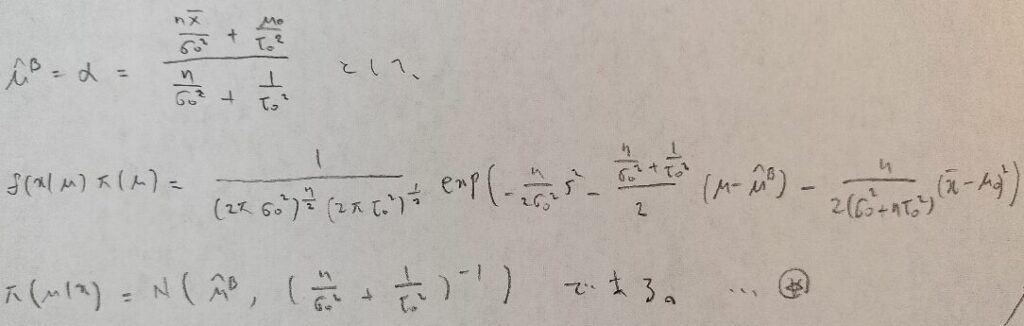
振り返ればとんでもない計算量でした。しかしこれが統計検定1級で要求される計算能力だと感じています。
それではベイズ信用区間などを調べていきましょう。
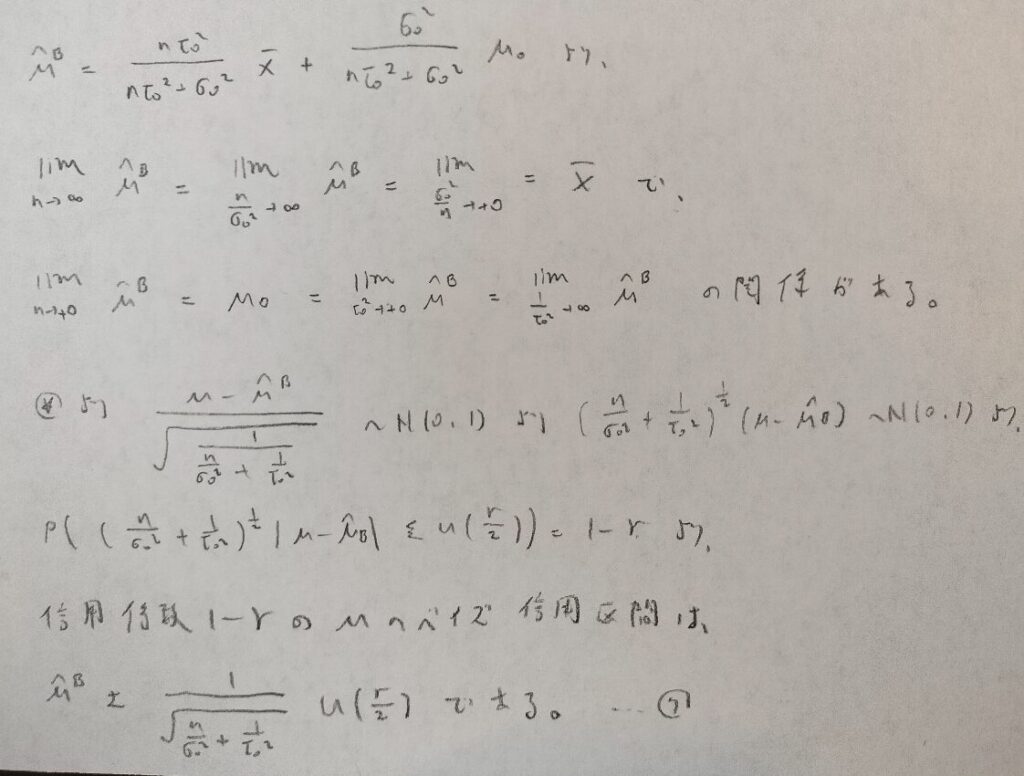
ここまでで得た結果を考察します。
事前分布が単峰で対称のとき、最高事後密度信用区間と簡便な信用区間は一致します。
ベイズファクターを用いた検定
ベイズ統計を用いた画期的な検定法を紹介します。この考えを応用したジェフリーズは検定の仮説の選択の度合いを数値で表現するという興味深い結論を出しています。
まずはベイズファクターまで行き着くためにいろいろな導入をします。以下の説明は一般論になります。
事後オッズ比を用いた検定

のちの演習問題でも定義関数を使用する問題があります。とくに一様分布関連の問題だとよく使用するイメージです。
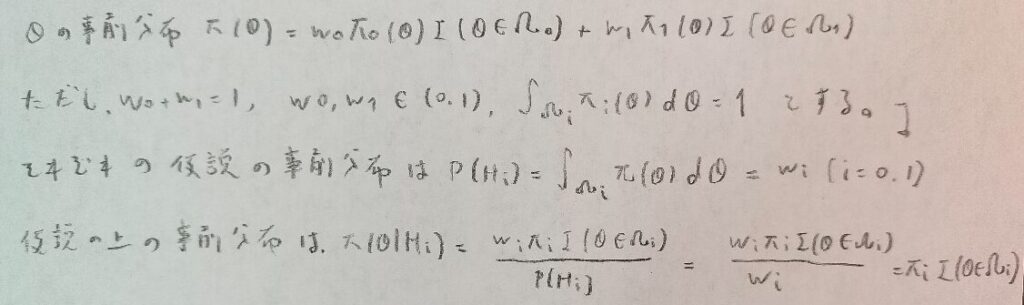
個人的にはここの内容は測度論に通じるためかかなり理解が難しい印象です。しかしここが分からなくても具体的な問題を解く際に影響はありません。
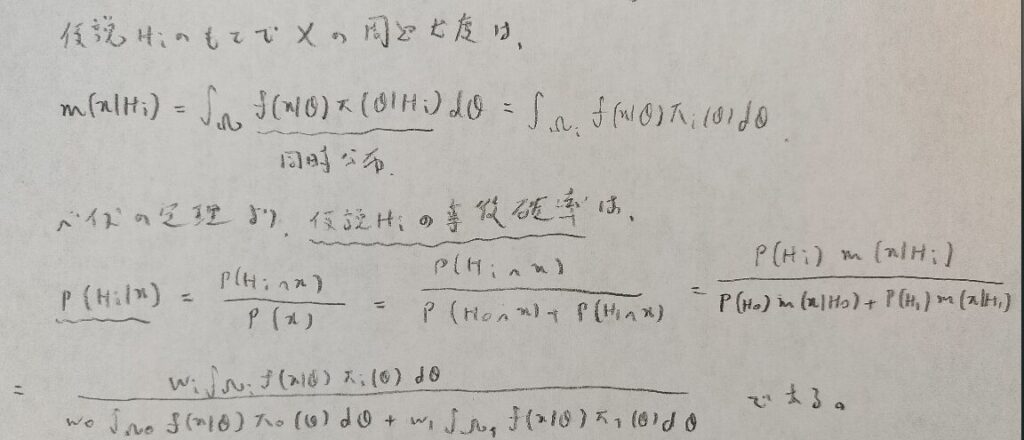
『データ解析のための数理統計入門』ではここの計算過程も半分くらいスルーされていましたので、補足しました。
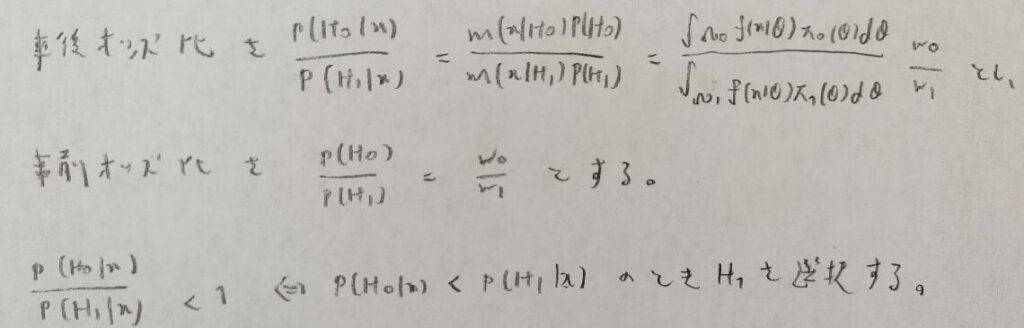
ようやく事後オッズ比を用いた検定の仕組みまで辿り着きました。
図24の最後の式で確率が大きい方を選択するという考えが直感的で納得できます。
ベイズファクターを用いた検定
ここまで色々と導入してきたので、ベイズファクターの定義自体はあっけないくらいです。
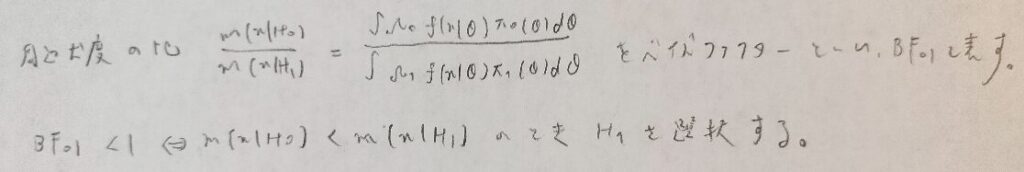
ここでは尤度が大きい方が採用されるという直感的な結果になりましたね。
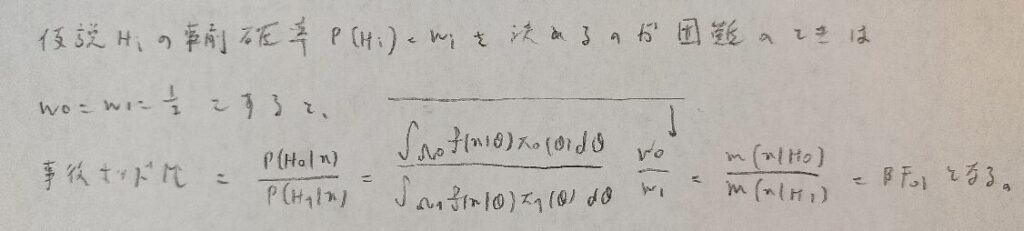
それぞれの仮説の事前分布を曖昧にすると事後オッズ比とベイズファクターは等しくなります。
ジェフリーズ考案のベイズファクターを用いた仮説の支持の程度の判断
ジェフリーズはベイズファクターの常用対数の値に基づいて仮説の支持の程度の判断を考えました。
LBFをベイズファクターの常用対数の値とします。
LBF>0のときH0を支持
-0.5<LBF<0のときH1を弱く指示
-1<LBF<-0.5のときH1を指示
-2<LBF<-1のときH1を強く指示
明確に数値で断言できるのはとてもすごいことだと思います!
ベイズファクターを求める例題
この例では先ほど学習した正規分布の例題が再び登場します。

まずは同時分布を求めます。そして周辺分布を求めます。

次にベイズファクターの計算になりますが、分子には要注意です。
ベイズファクターの分子の計算は同時分布にH0で与えられる1点を代入したものになります。
そうでない場合はあまり出ません(と言いながらこの例題です)がその場合はおとなしく積分をしましょう。
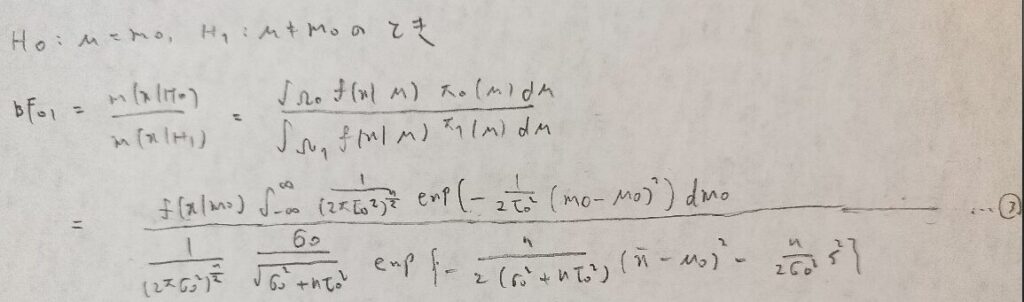
図30の第1行は滅多に起きない現象です。僕は初見の学習時にかなり混乱しましたので、乗り切り方をシェアしました。
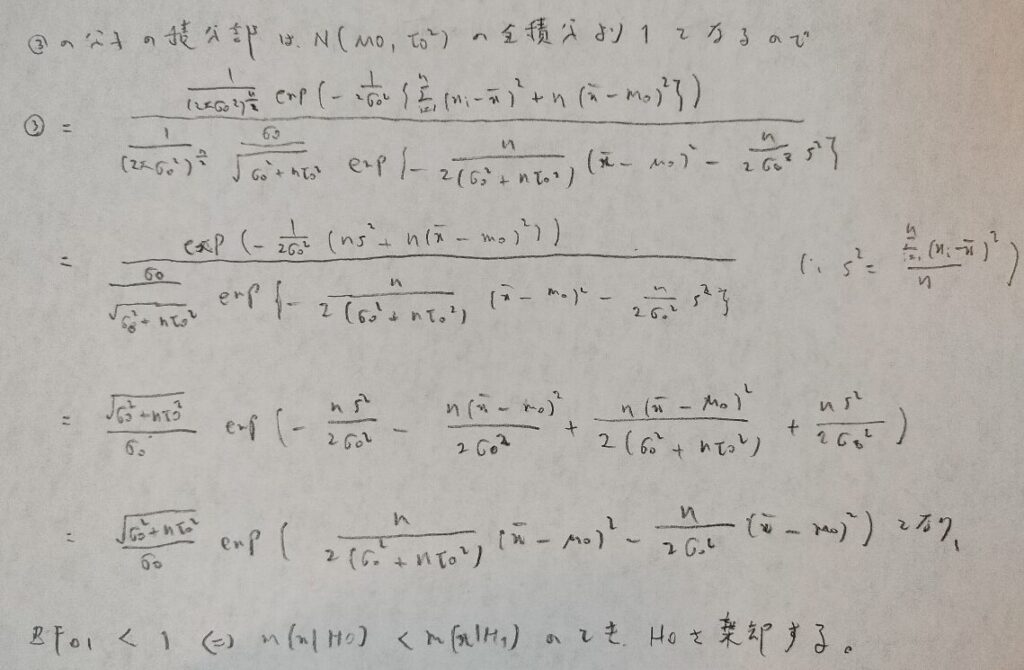
HPDを用いる場合は正規分布が単峰で対称性があることから、簡便なベイズ信用区間の結果と一致します。
HPDを用いずとも一般的にベイズ信用区間の反転を用いた検定方式も考えられます。

ベイズ統計を用いた検定の方法はいろんな種類があります。
事前分布の設定(超母数の利用)や共役事前分布やジェフリーズの事前分布と正則性
超母数
ここまでの内容から事前分布の設定がいかに大切かがお分かりいただけたと思います。ここでは事前分布の代表的な設定方法を学習します。

共役事前分布
そしてベイズ統計には共役事前分布という大事な概念があります。
実はこの共役事前分布の例はこの記事で何回も出てきたことにお気づきになられましたか?
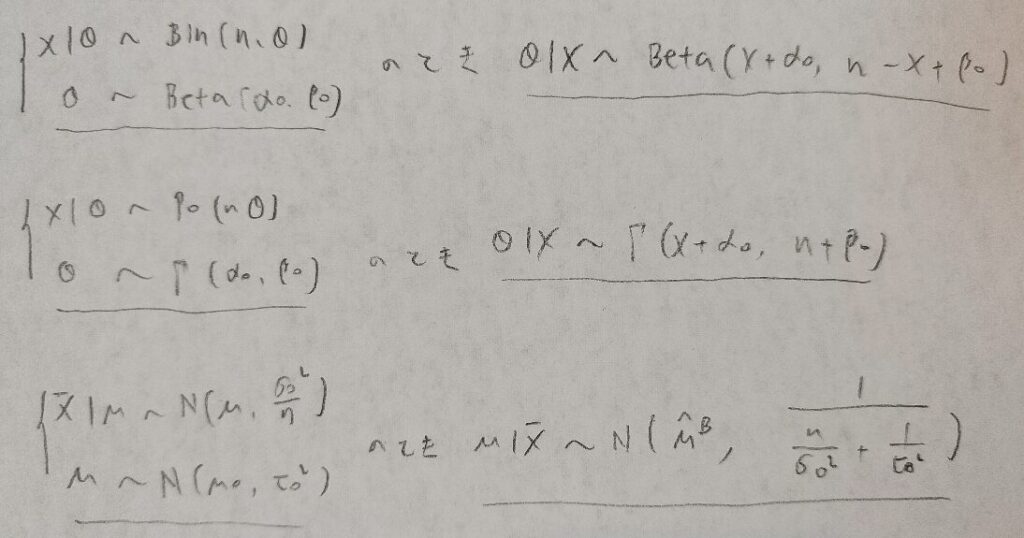
なるほど。下線が引いてあるところが同じ分布属になっていますね!
共役事前分布のメリットは、データの更新過程を同じ分布属の中で構成できることです。
ジェフリーズの事前分布(統計検定で大事)
『データ解析のための数理統計入門』の演習問題の後半でたくさん出てくる事前分布がジェフリーズの事前分布です。
主事前分布とは事前分布がわかっている設定(データが取られる前に設定)
客観ベイズ法とは事前分布の恣意性を緩和または排除する方法で例として無情報事前分布があります。
なるほど!その無情報事前分布の1つとしてジェフリーズの事前分布が下のようにして考えられるのですね!

とにかくジェフリーズの事前分布では定数倍は無視する原則に従ってください。またフィッシャー情報量(行列)を出す際はーのつけ忘れにご注意ください。さらに定数倍を無視するので尤度ではなく確率密度関数(確率関数)から出発した方が時短できる問題が多数あります。
事前分布の正則性
また事前分布には線形代数のときのような正則性の概念がありますので紹介します。
全範囲の積分が有限になる事前分布を正則な事前分布といいます。発散する場合は非正則といいます。
正則性が問われる問題も頻出ですので、統計検定で出題されたら確実に得点源にしたい箇所ですね!
ジェフリーズの事前分布の例題
とにかく大切なジェフリーズの事前分布です。いくつか具体例を通して慣れていきましょう!そのためには有名分布の期待値はすぐに出せるようにしておかないといけません。
二項分布
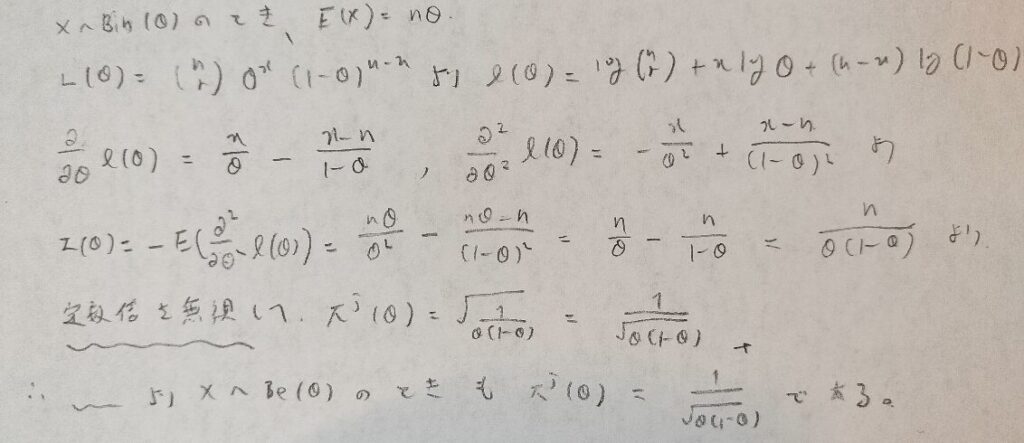
ポアソン分布
次はポアソン分布の問題です。
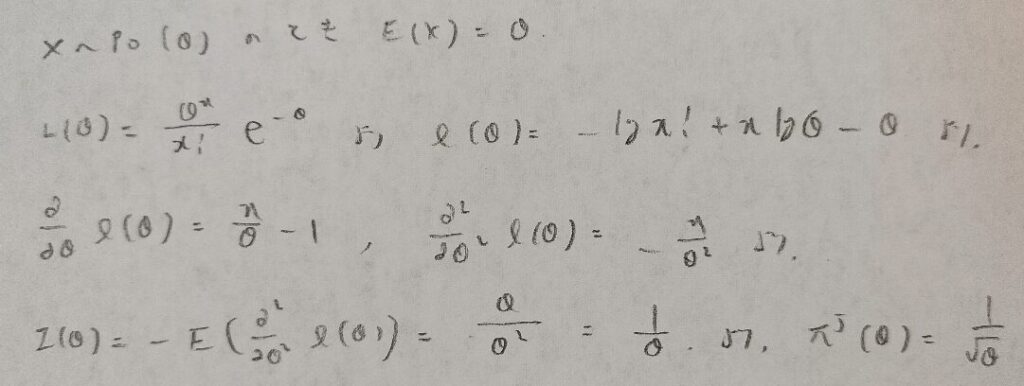
分散既知の正規分布
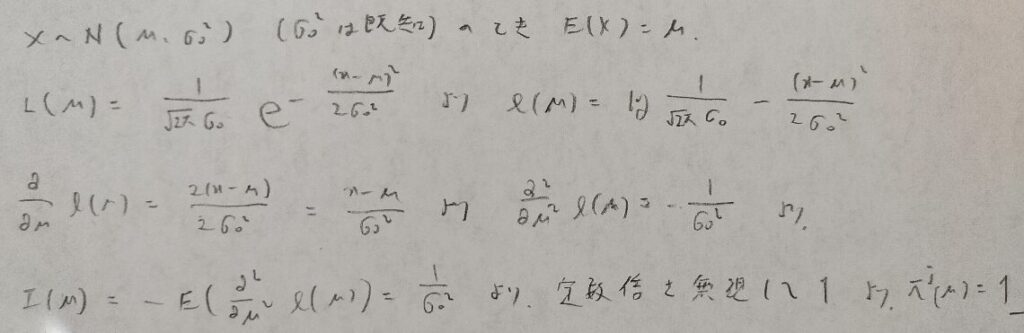
最後は定数倍を無視して1にするのが初見では間違いそうですよ!笑
分散未知の正規分布(フィッシャー情報量行列を求めるタイプ)
フィッシャー情報量行列はその定義から対称性に注目すると必ず対称行列になります。
次の問題は問われ方によってジェフリーズの事前分布が異なる結果になると気づいたので、2つ紹介します。
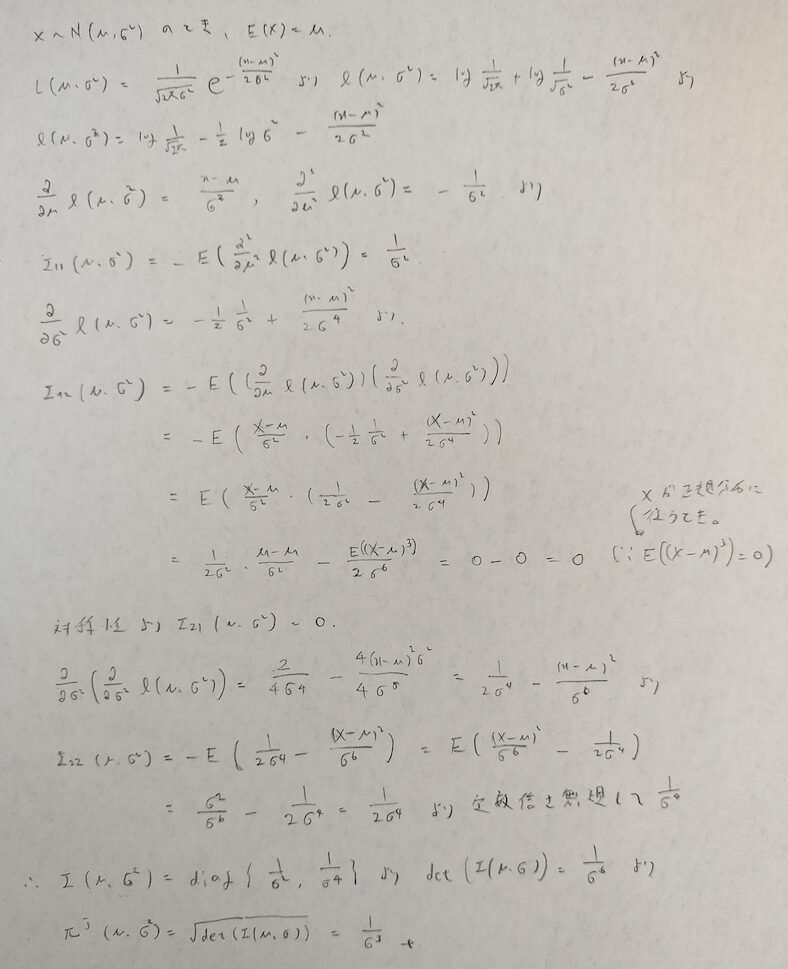
次に2つ目の問われ方に移ります。
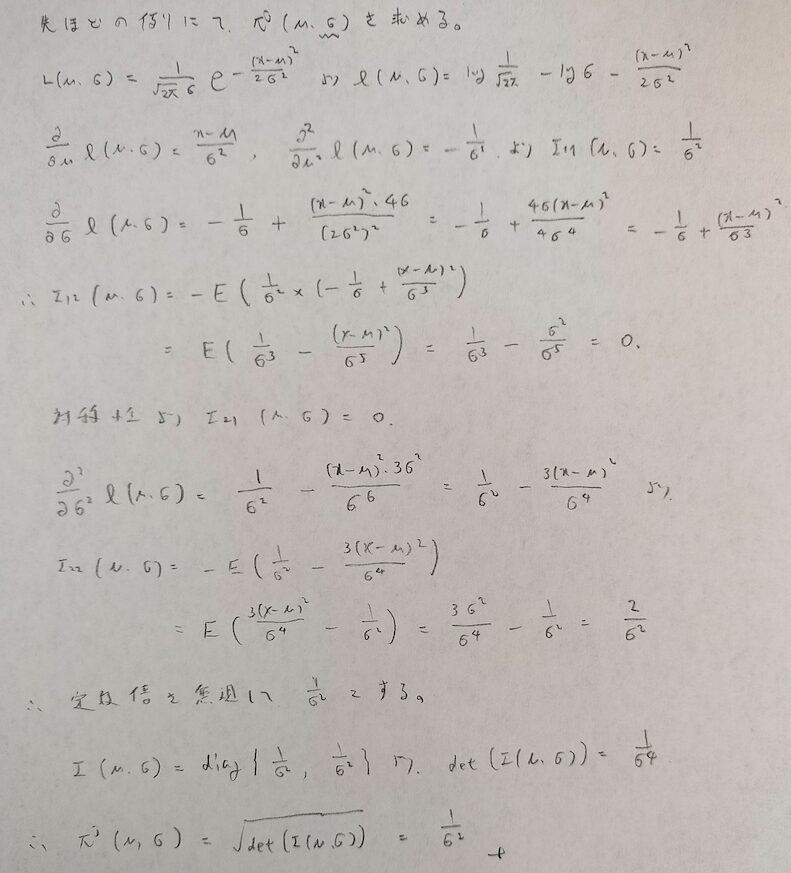
先ほどの平方完成に比べるとこちらの計算はまだ可愛い方だと思いませんか?
再び正規分布
ジェフリーズの事前分布の知識を用いて1つの例を考えてみましょう。事前分布が一様分布になることから最終結果が次のようになることに納得はできたのではないでしょうか。
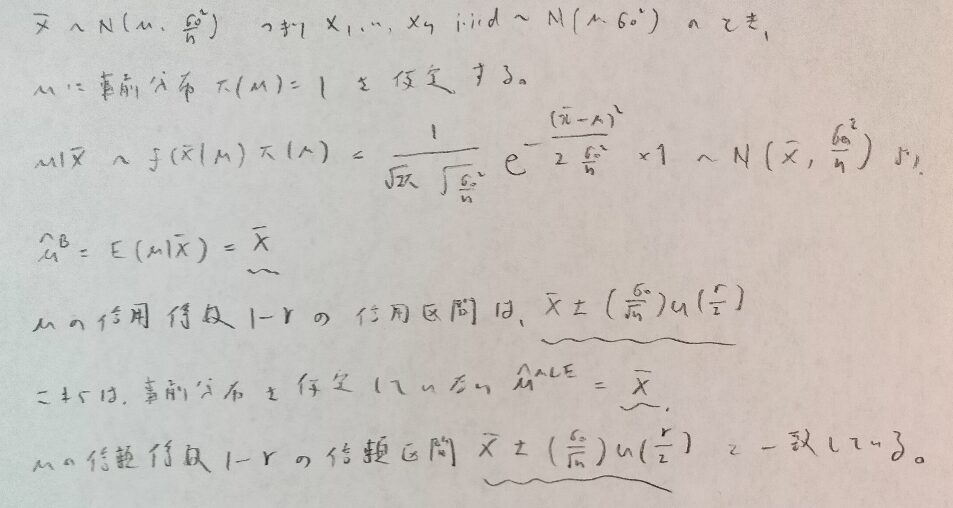
ベルヌーイ分布
最後は正則性を確認する例題を扱います。
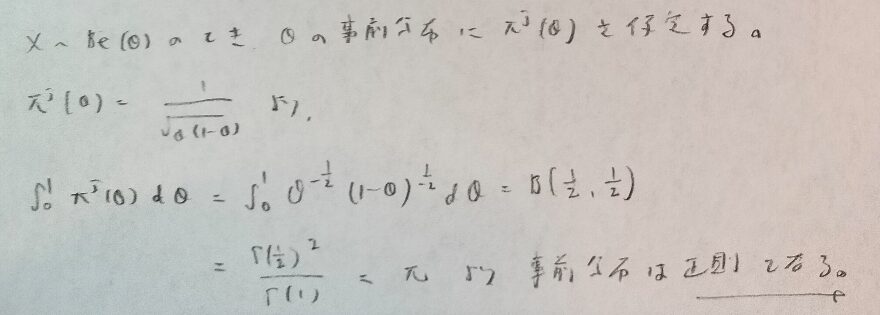
データ解析のための数理統計入門:第14章「演習問題」
記事の後半では『データ解析のための数理統計入門』:第14章「演習問題」を扱います。記事冒頭でもお話ししましたが、今回はMCMC法などの直前までですのでよろしくお願いします。
細かい数値設定などは『データ解析のための数理統計入門』をご覧ください。
データ解析のための数理統計入門:第14章「演習問題」問2
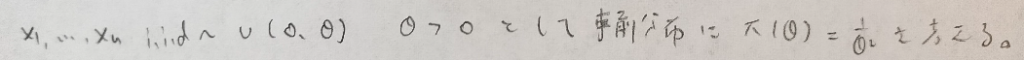
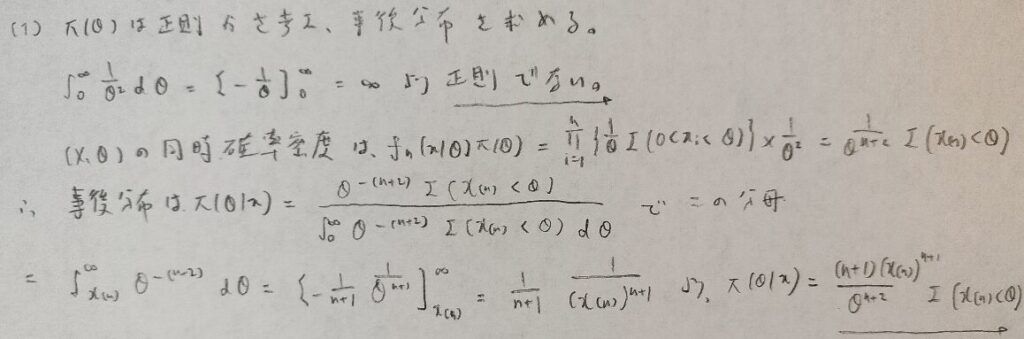
ポイントは定義関数を用いることです。順序統計量との相性が良いですね!
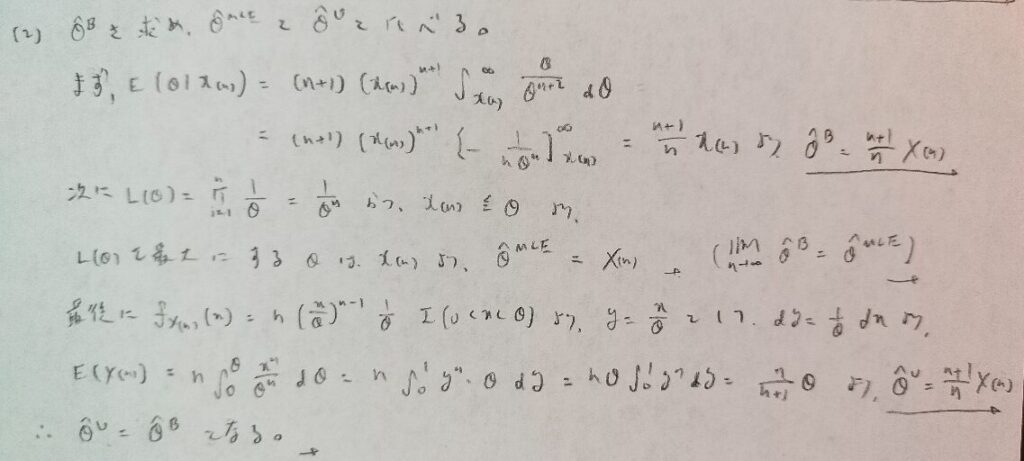
不偏推定量を求めるときは、まず確率密度関数を考えてみるという発想が大切です。
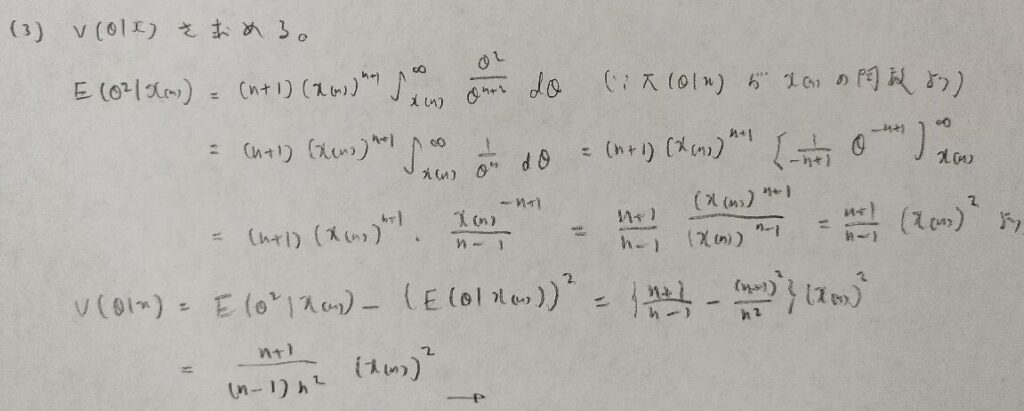
結局は最大統計量のみの関数になることに注目します。
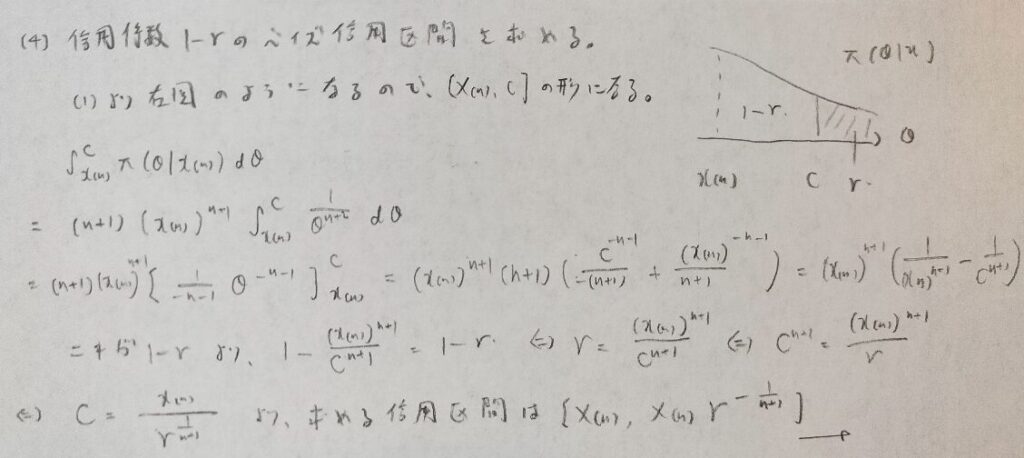
ベイズ信用区間の形の推測では、定義域や単調性がとても大事です。いつも両側とは限りません。
データ解析のための数理統計入門:第14章「演習問題」問3
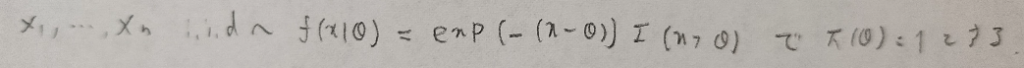
今回は事前分布が1という一様分布なので曖昧なため、そこを突いてくる問題な予感がします。
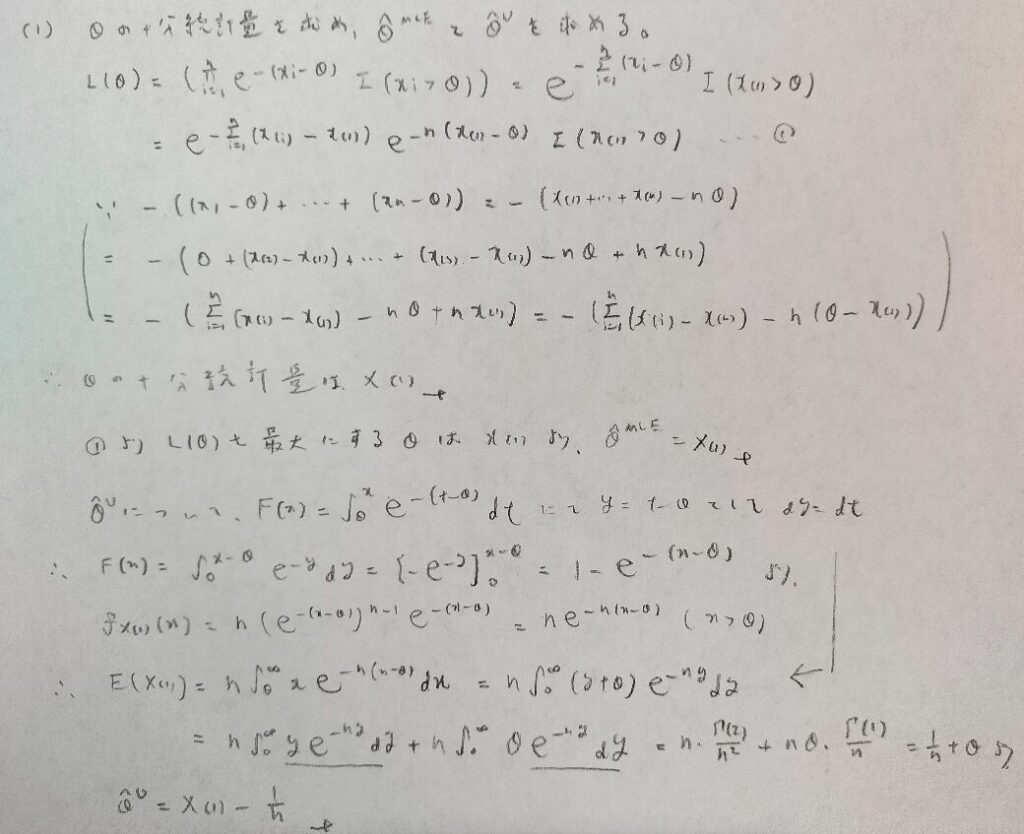
何と言っても大変(というより発想が難しい)のは順序統計量を出すところです。問1の問題に通じるところがあります。
あとは最尤推定量のところですね。対数を取り微分をすることが困難のときは、尤度関数のまま直接考えることになります。
最大統計量と最小統計量の確率密度関数はすぐに出せるようにしておきましょう。
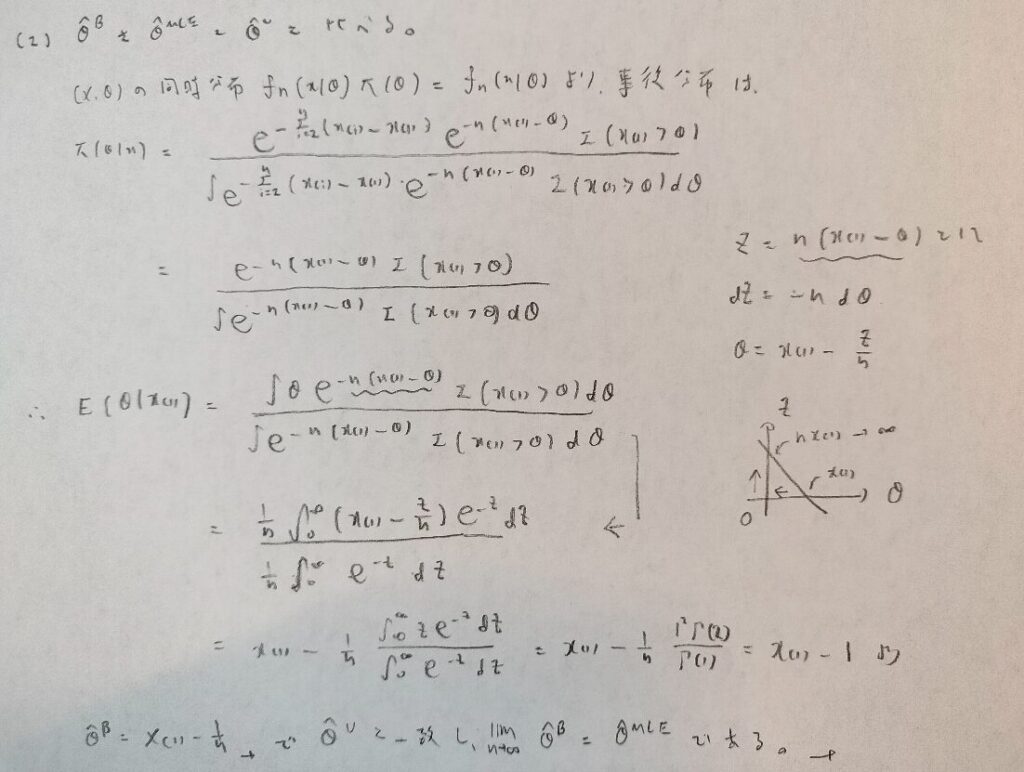
最後の置換積分のところが難しいです。それ以外は素直な問題だと思います。
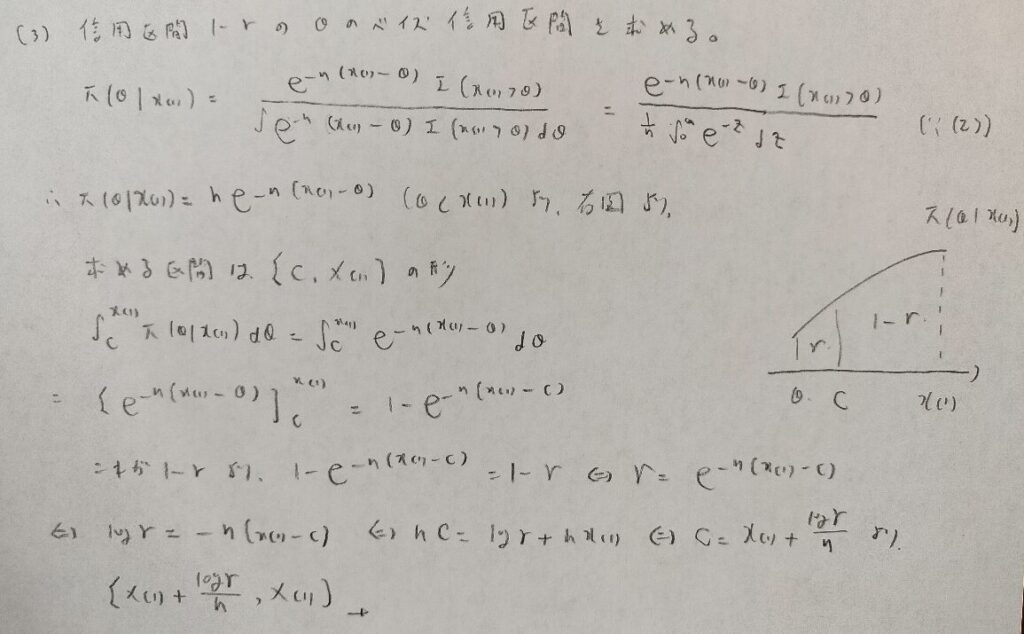
さっきの問題と似てますね!笑
気がつきましたね。もはやテンプレです。
データ解析のための数理統計入門:第14章「演習問題」問4
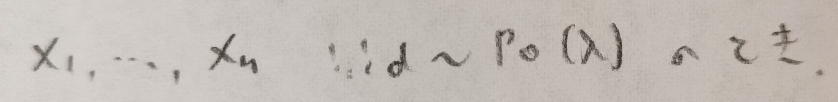
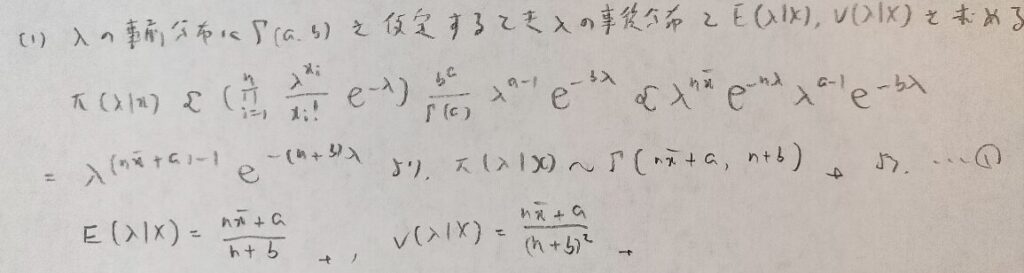
ポアソン分布の尤度関数に注意しましょう。

ガンマ分布が絡む積分をカイ2乗分布に近似させていく難問です。この問題以降の頻出問題となります。
置換積分の根拠は自然対数eの指数部分に注目する方法が最も明快です。

ベイズファクターでは分子に要注意です。分子は原則、同時分布においてパラメータに値を代入するだけでOKです。
例外は記事前半の正規分布を用いたベイズファクターの問題(図30)です。
この問題は(3)ですね笑
僕は間違って(4)と書いてました。すみません。
データ解析のための数理統計入門:第14章「演習問題」問5

この問5は『データ解析のための数理統計入門』に登場した適合度の検定の章にあった問題の続きです。今回は問5を解くために必要な部分だけを抜粋しました。
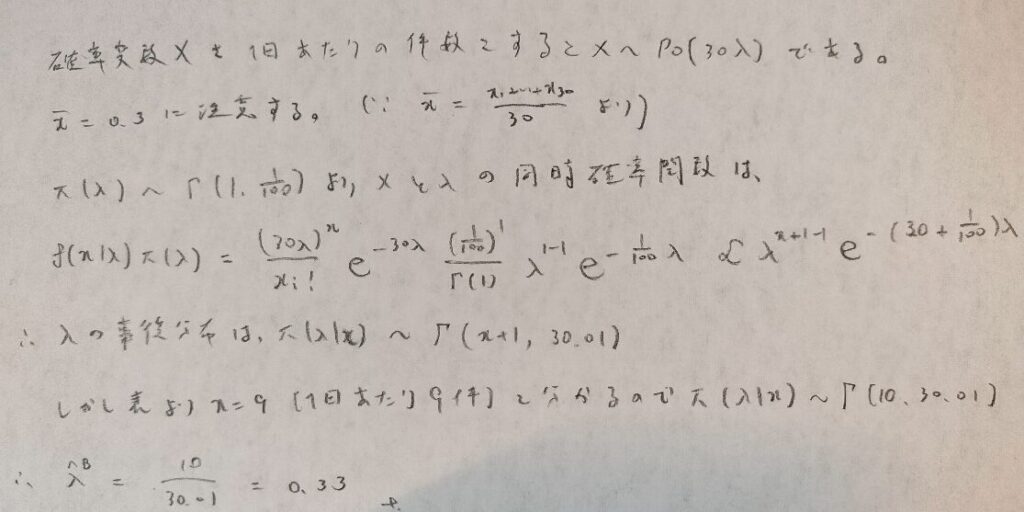
xの値が決まっていることに注意です。
以降は今までの問題の復習問題です。
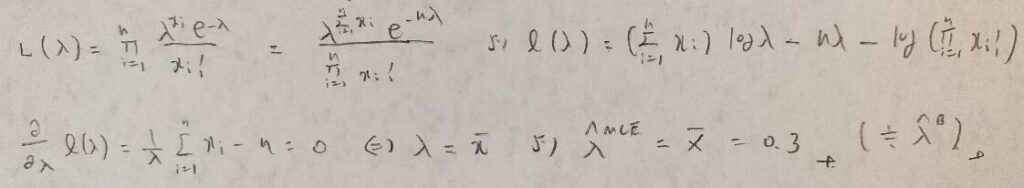
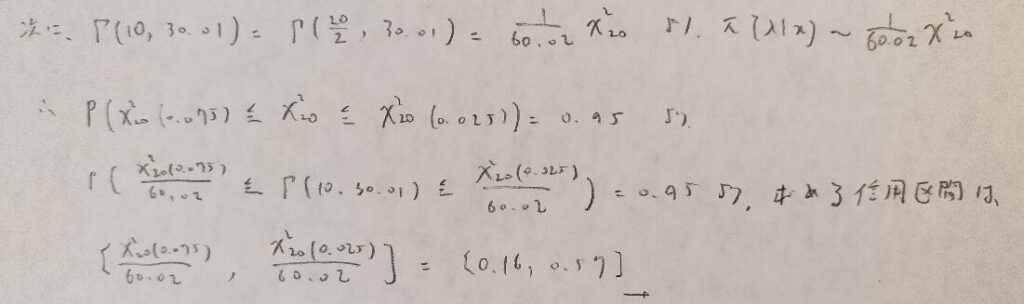
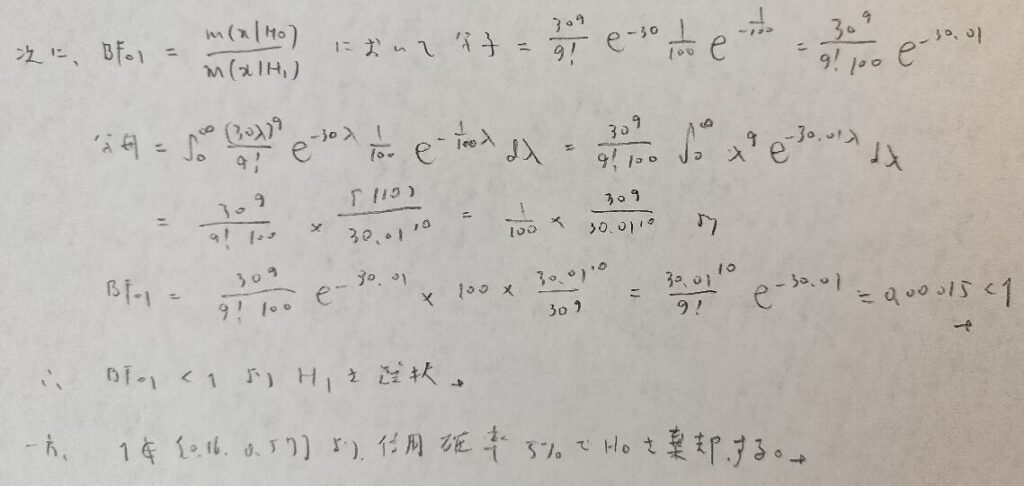
データ解析のための数理統計入門:第14章「演習問題」問6
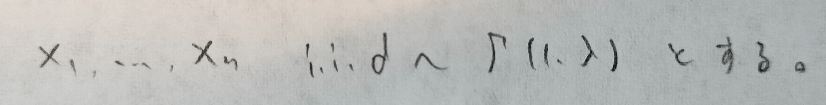
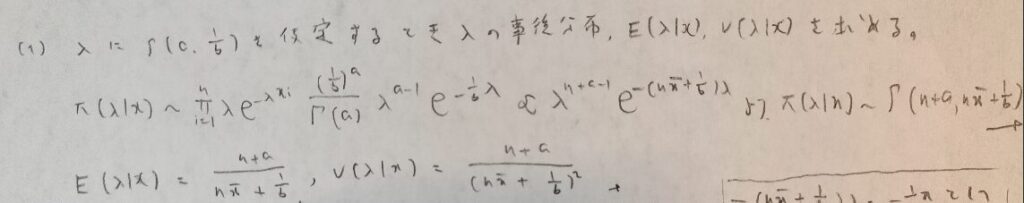
見にくくてすみません。(2)の置換積分の説明が(1)の解答ゾーンに入ってしまいました。

またこのタイプの問題ですね!カイ2乗分布に帰着する流れは慣れてきました!
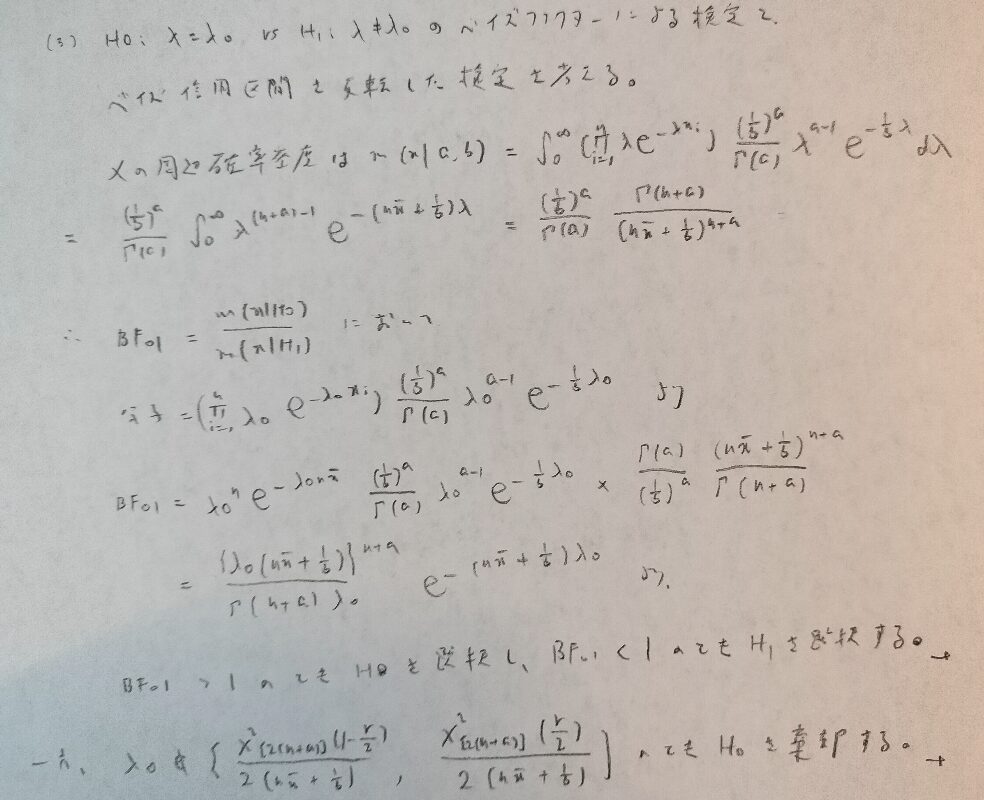
データ解析のための数理統計入門:第14章「演習問題」問7

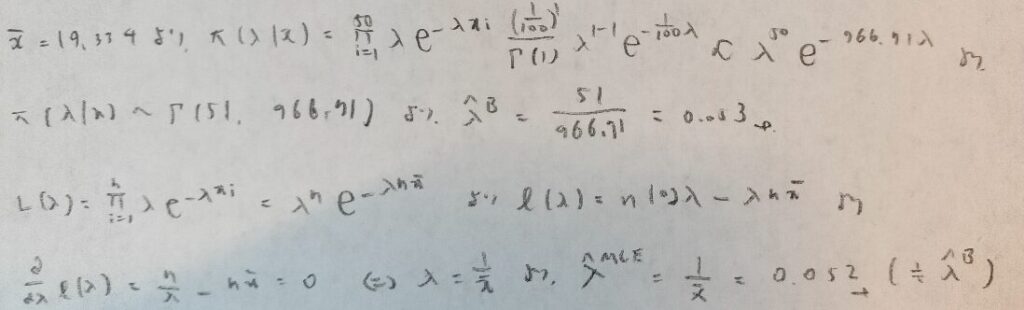
次の後半のベイズファクターの計算は落ち着いて行いましょう。僕は答えが合わず数回やり直しました。

データ解析のための数理統計入門:第14章「演習問題」問8
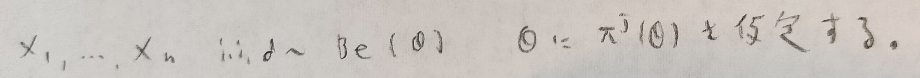
いよいよジェフリーズの事前分布が登場してきました!終盤です。
なぜ解答で1個のデータを用いているのか?を考えてみましょう。ヒントは記事前半にあります。
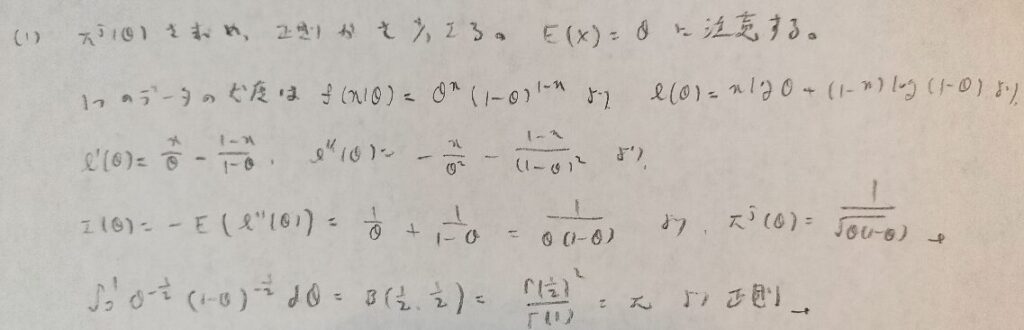
正則かの判定でベータ関数に帰着させることは意外と多い印象です。
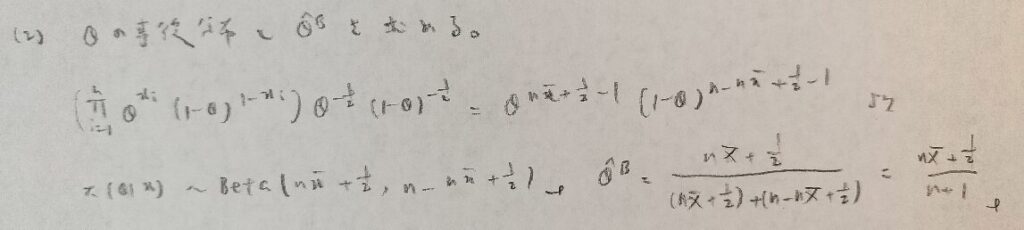
ベイズ推定量なら大文字、ベイズ推定値なら小文字に気をつけましょう。
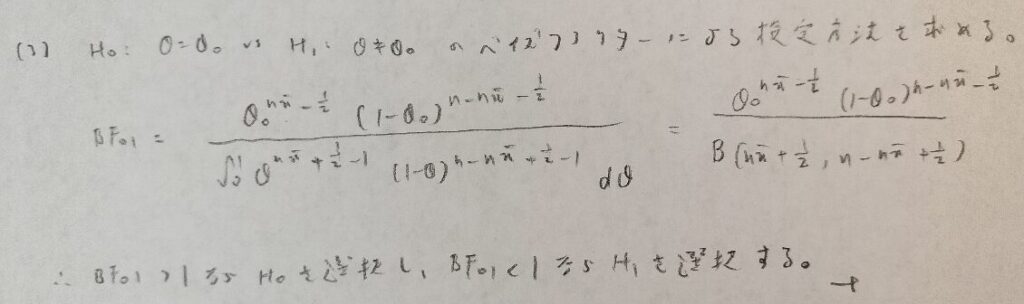
データ解析のための数理統計入門:第14章「演習問題」問9
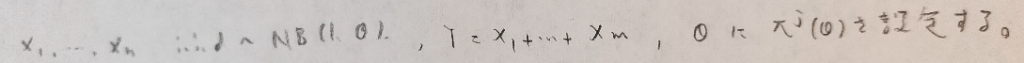
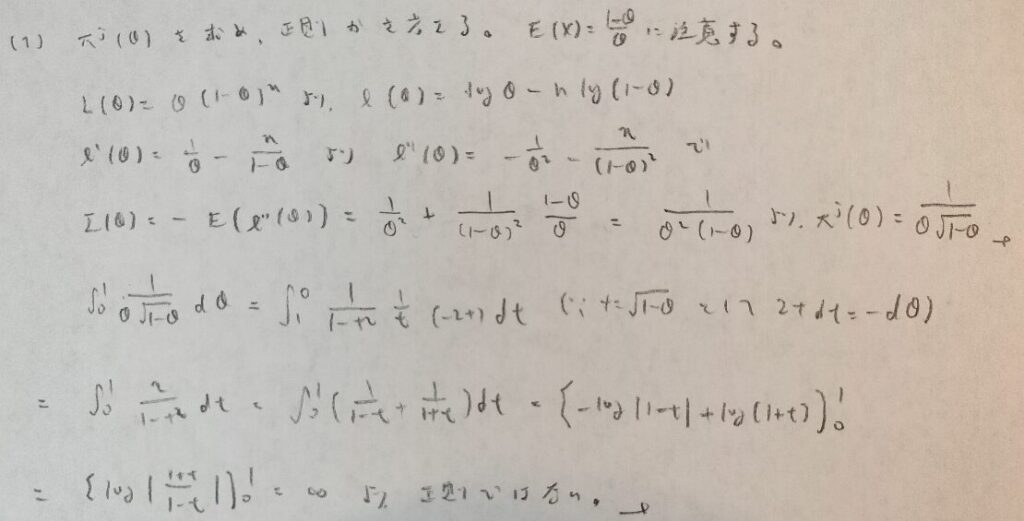
厳密には広義積分で示した方が無難です。
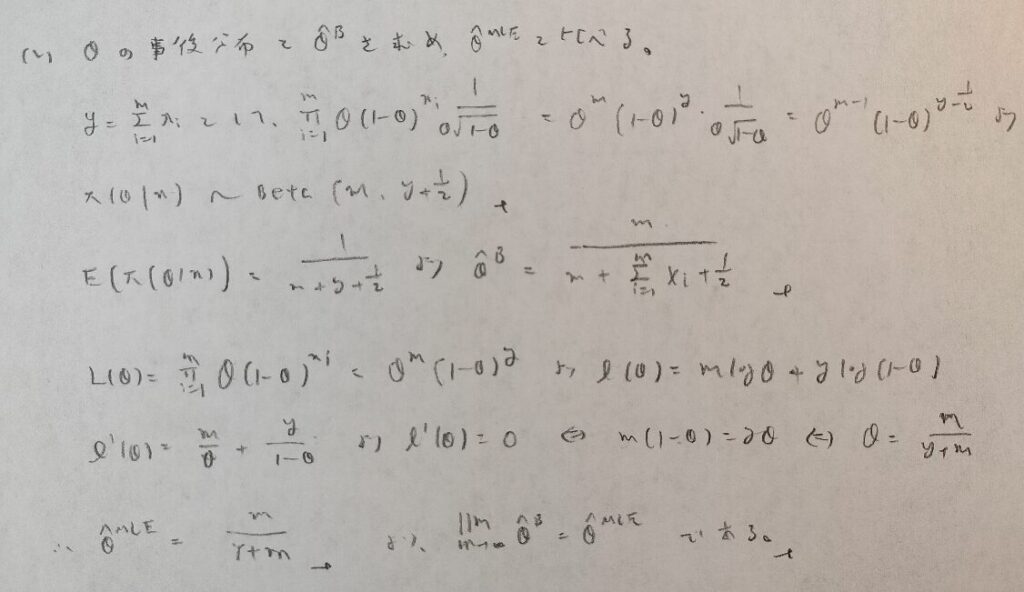
データ解析のための数理統計入門:第14章「演習問題」問10

ベイズ統計では正規分布が出てきてしまったら計算量が多くなることは覚悟した方が良いです。
この記事でも大変な目に遭いましたからね。納得です。
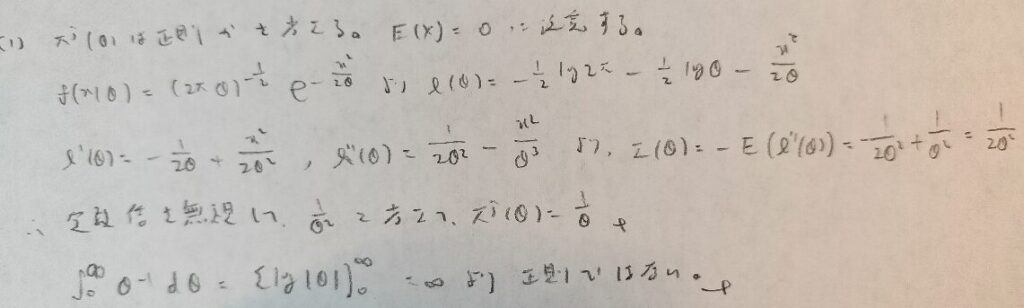
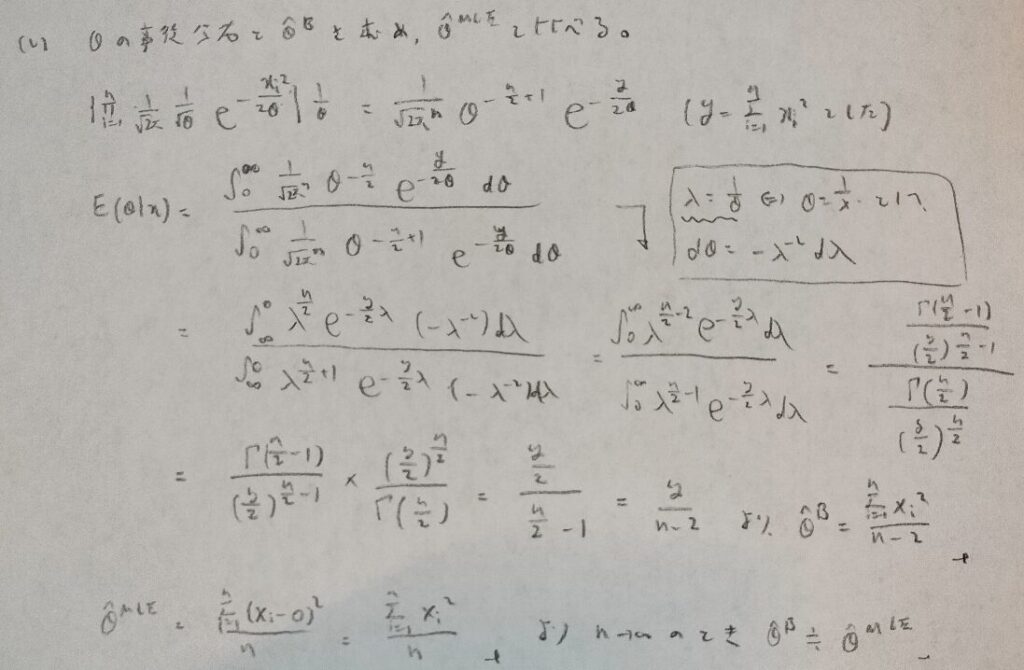
難問です。ベイズファクターを求める流れがいつもと違っています。今回は分母分子を一度に計算していかないと上手く解き崩すことは難しいでしょう。僕はこの問題でも答えが合わずに30分程度足止めしました。
データ解析のための数理統計入門:第14章「演習問題」問16
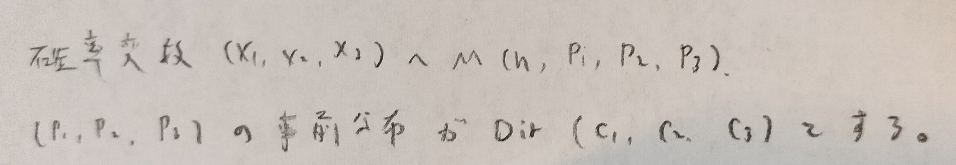
最後はフィッシャー情報量行列が出てくる問題です。一般的に計算量が増します。
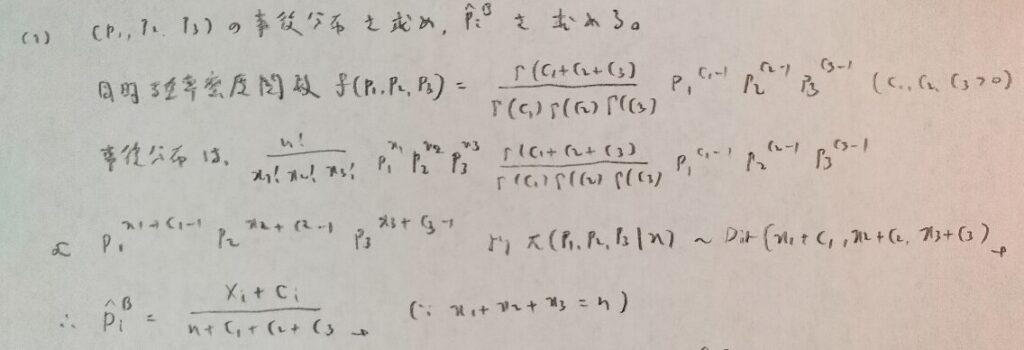
本記事の問題はこの問題で最後です。頑張りましょう!
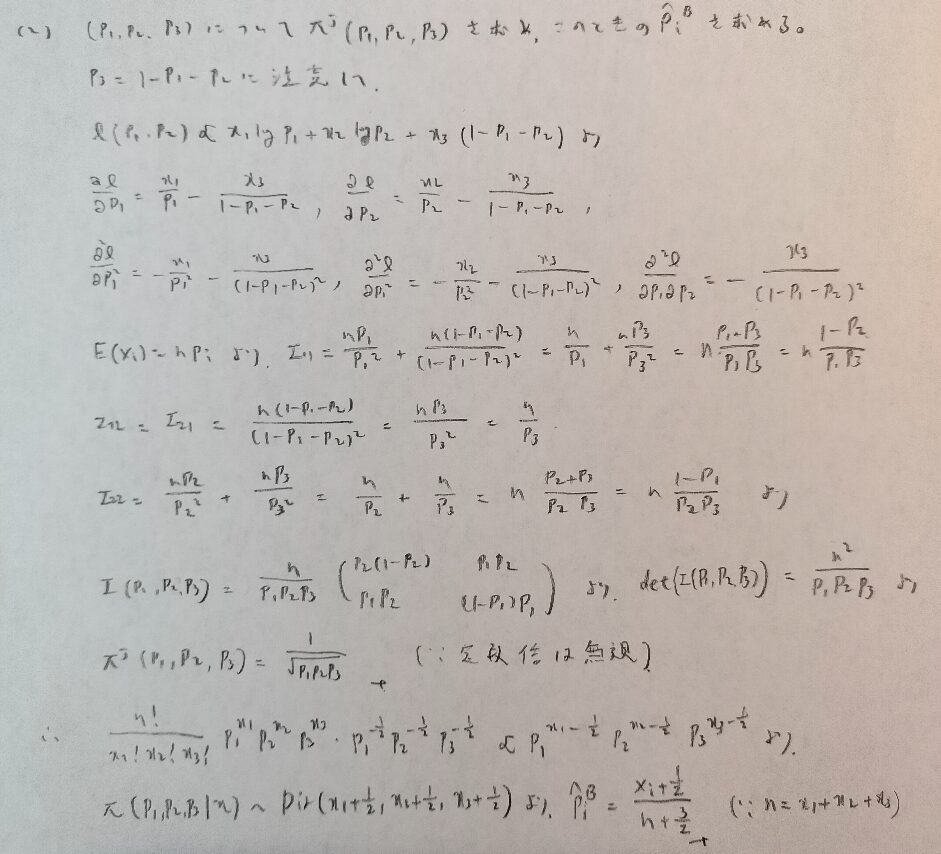
やっと終わりました!長かったです!
実はベイズ統計はまだまだ続きます。具体的にはMCMC法などへと繋がっていきます。また記事で続編を公開しますのでお待ちください。
本記事は『データ解析のための数理統計入門』をベースにして内容を構成しました。
『データ解析のための数理統計入門』は統計検定1級の必携の書になりつつあります。
統計検定準1級と統計検定1級(応用にも)に準拠していますので、是非ともチェックしてみてくださいね!