統計検定1級の定番の書である『現代数理統計学の基礎』の姉妹本である『データ解析のための数理統計入門』を中心に統計検定1級の話題を中心とした統計学の内容をわかりやすくまとめていきたいと思います。
統計学は面白いですよということが伝わってほしいですよね!
そうですね。僕が今まで勉強してきたことをわかりやすくまとめていきたいと思います。
データ解析のための数理統計入門の位置付け
本書は統計検定1級の統計応用に合格する力の土台として大変価値のある本です。
統計数理の対策では『現代数理統計学の基礎』の方が良いと思います。
このことを理解した上で、前半部(統計数理部分)をおさらいしていきたいと思います。
データ解析のための数理統計入門の第1章で面白かった点
第1章では確率モデルについて書かれています。本書はルベーグ積分を用いないタイプの本です。
シンプソンのパラドックスというものが載っていますね。
シンプソンのパラドックスとは、個々には確率が低くても合算すると確率が高くなる現象です。
例えば箱Aと箱Bがあり、それぞれ赤と白の玉が入っています。それぞれの箱から赤や白の玉を取る場合と、
A+Bから同時に赤や白の玉を取る場合で、色の出やすさの度合いが逆転するといった具合です。
ベイズの定理を用いるウィルス検査の問題がありますね。
今回はこの問題を取り上げます。この問題は統計検定1級の2021年の統計応用の共通問題に出ています。
もちろん内容は本番の方が難しいですが、やっている本質部分は変わりません。
ペアワイズ独立という言葉も出てきましたね。
3つの事象A,B,Cがあるときに、互いに異なる2つの事象が独立なことをペアワイズ独立と言います。
ただしペアワイズ独立→独立とは言えません。
本書では演習問題でコイン投げの試行を用いて上の命題について触れています。
久保川先生の著作は、ネット上に詳しい解説もあり、大変便利で素晴らしいと思い活用させていただいております。
あとはモンティホールの問題も載っています。実はこの問題は2023年の統計検定1級の統計応用の共通問題に出た問題です。
やっぱりこの本は統計検定1級と相性がバッチリですね!
ベイズの定理を用いる例題をわかりやすく解説
以下は本書の例題を用いますので、お持ちの方はp.8を開き、例1.6をご覧ください。
ウィルスに感染しているかを検査キットを用いて調べたい。感染している場合には90%の確率で陽性反応が、10%の確率で陰性反応がでる。感染していない場合には99%の確率で陰性反応が、1%の確率で陽性反応が出るという。このウィルスに感染している人は全体の10%であるとする。
データ解析のための数理統計入門
(1)陽性反応が出たときに感染している確率
(2)陰性反応が出たときに感染していない確率を求めよ。
では考え方を大事にして図を用いながら説明します。
この考え方はベイズの定理を用いる広い範囲で使えるので参考にしてくださいね!
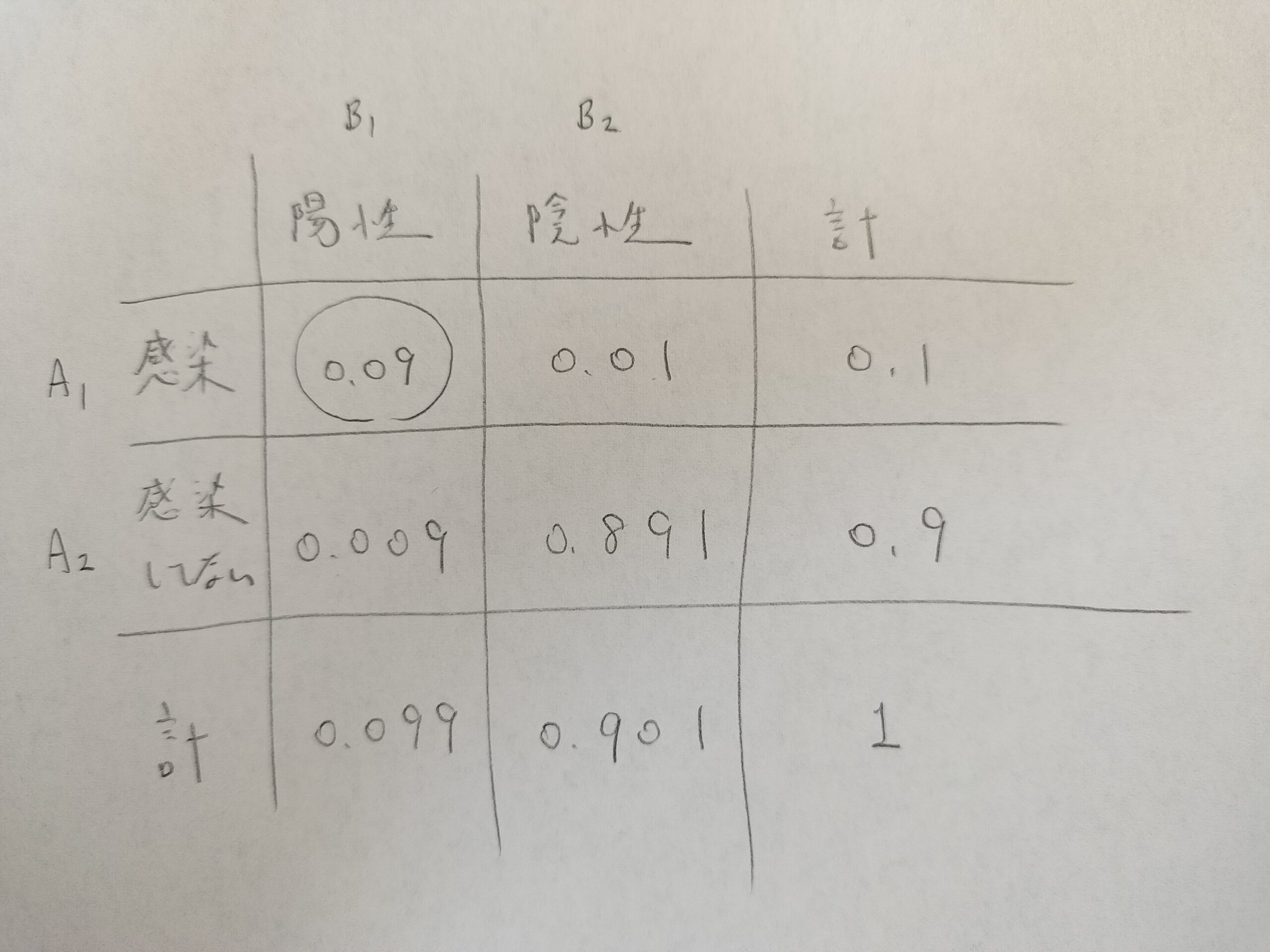
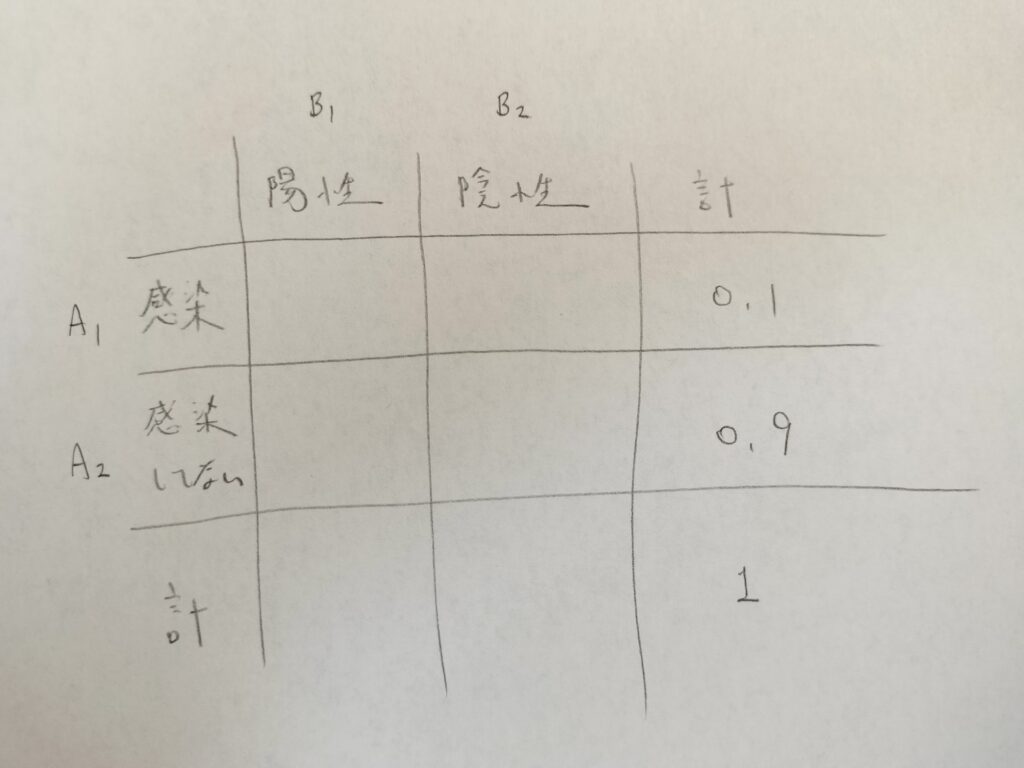
まずは表を用意します。
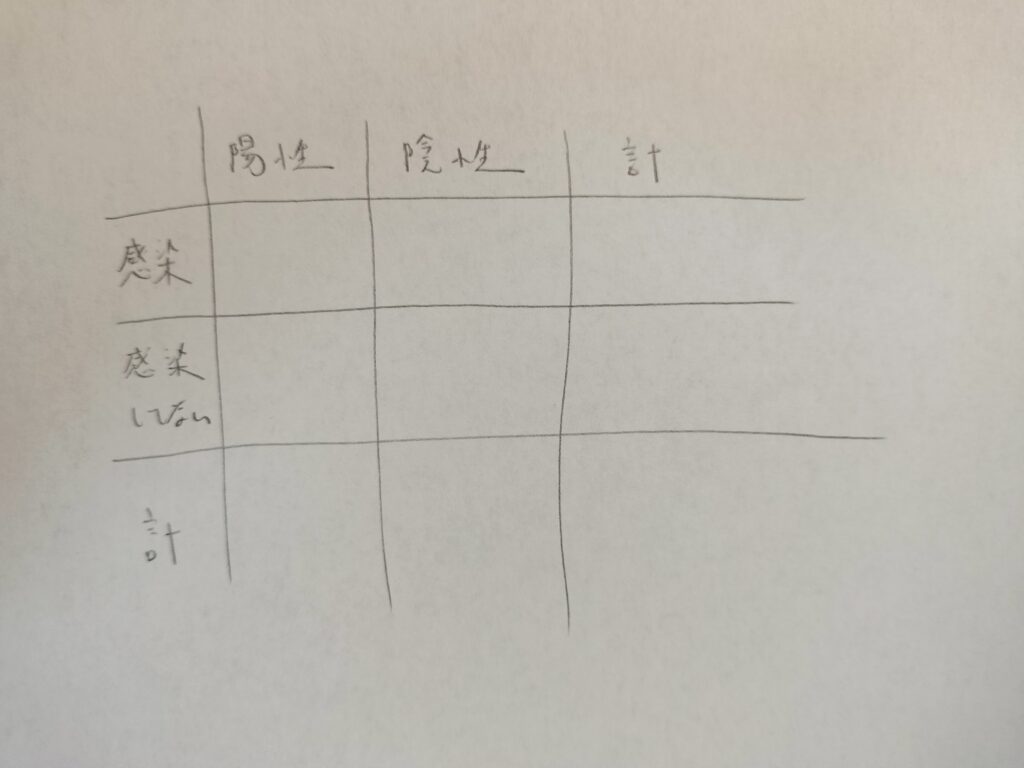
次に感染をAなどとして名前をつけておきます。
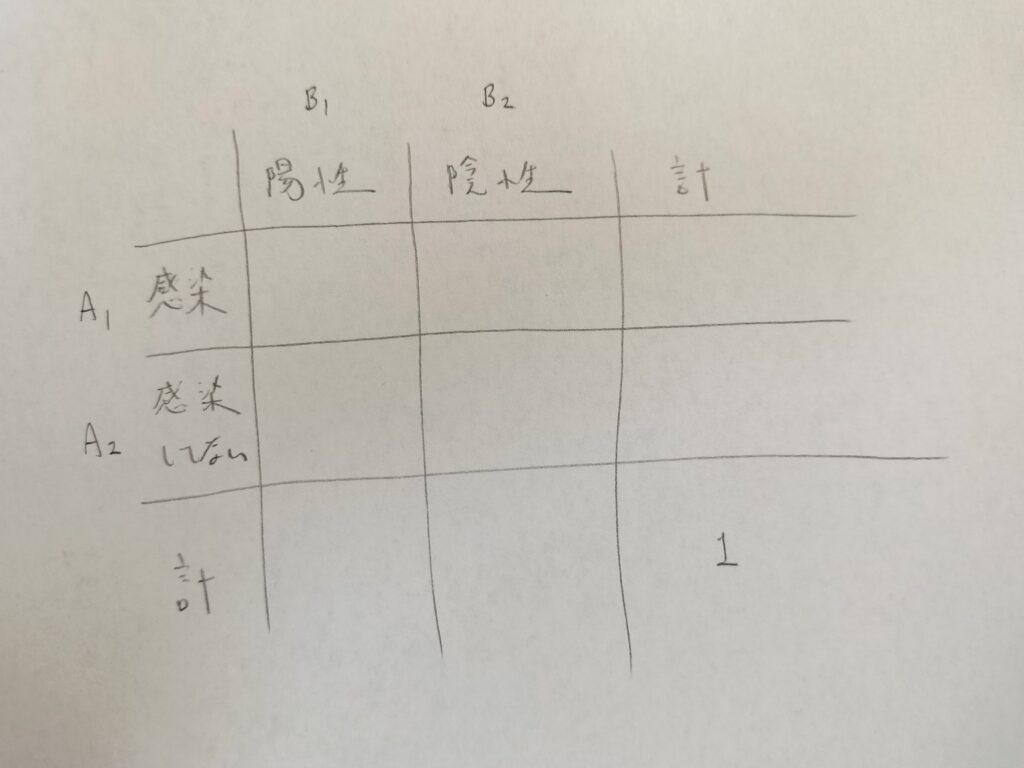
Bのことを表頭、Aのことを表側と言います。
このことはアクチュアリー数学の指定教科書である『統計学入門』ではじめて知りました。本書でしか学べない説明などもあり、おすすめの本です。
次に問題で与えられている条件を数式にして表現してみます。
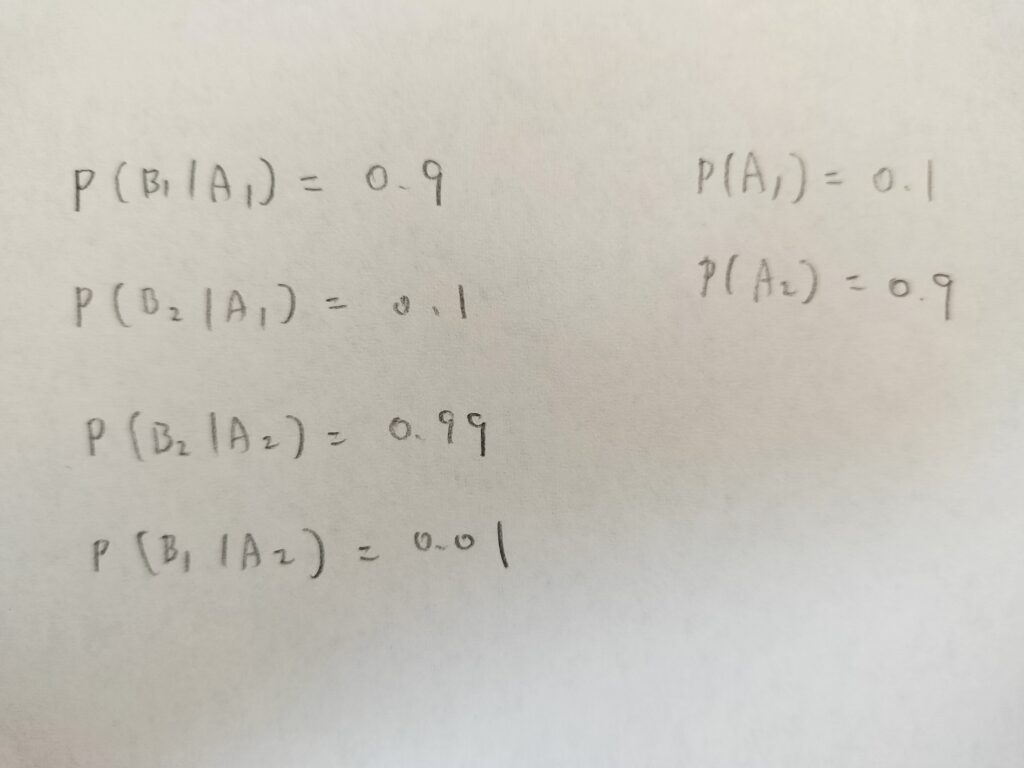
そしたら表に戻って、具体的に表の数値を入れていきます。まずは合計のところが入れやすいです。
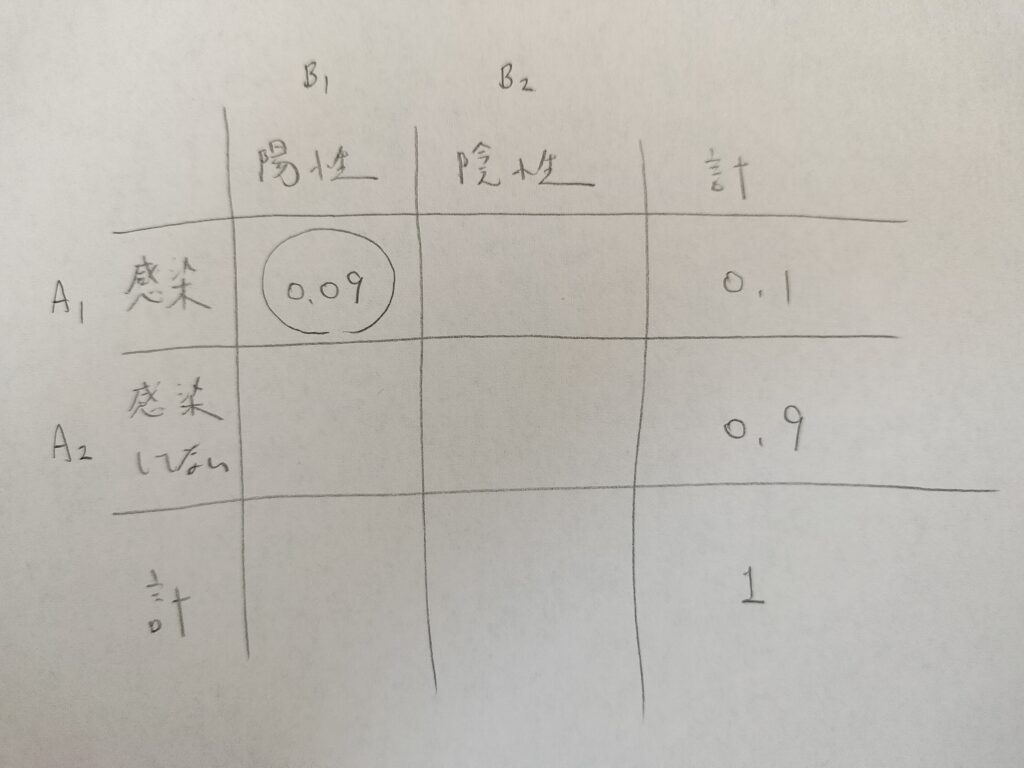
次に図の丸で囲った部分を考えます。
これは条件付き確率の公式を用いて算出します。
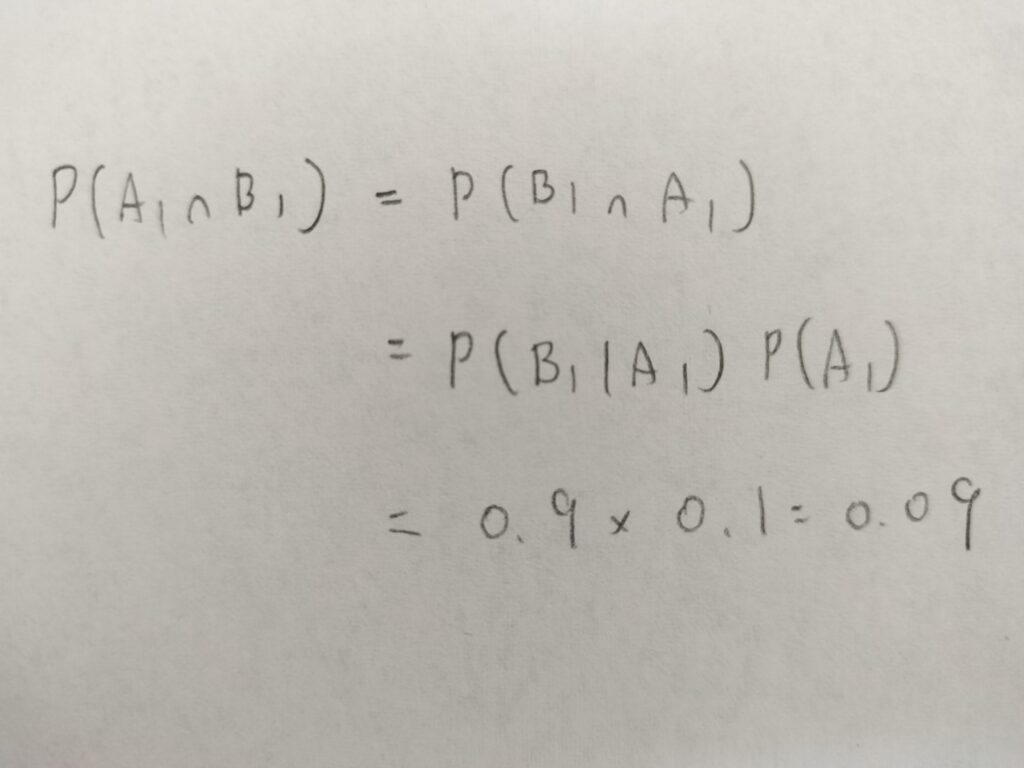
このようにして残りの表の部分を埋めます。
確率和が1となることを用いて引き算してもOKですね!
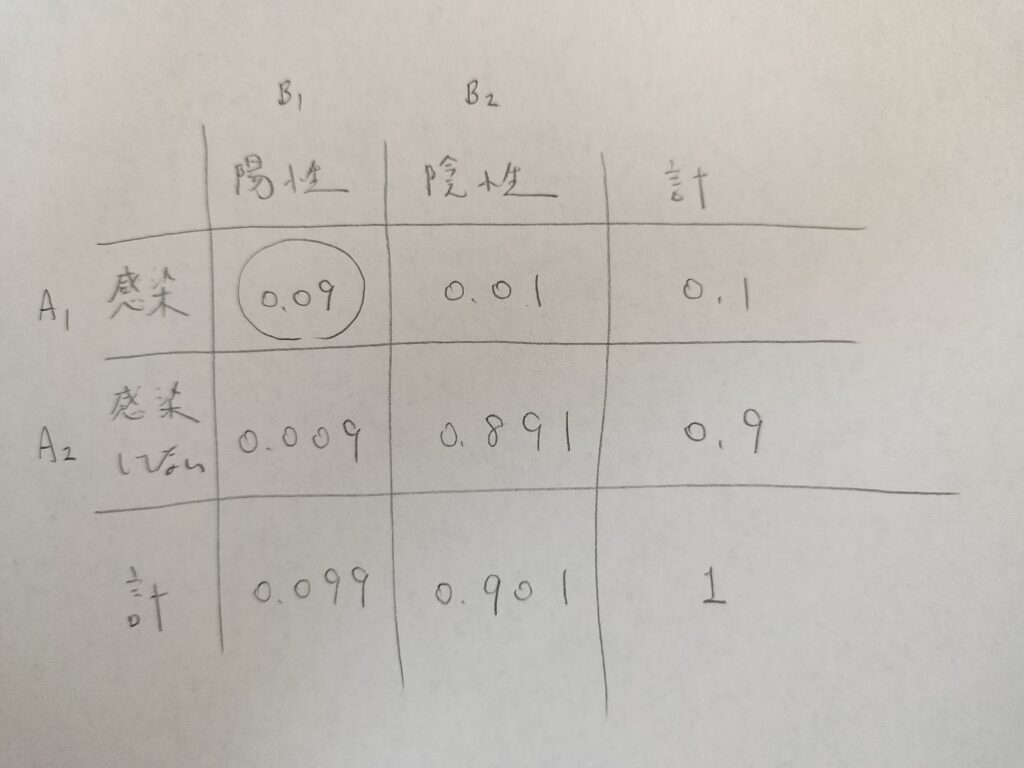
では最後に問題の質問に答えます。
ベイズの定理を用いる問題でのコツは次の2つにつきます。
①問題文にある内容を数式で整理する
②ベイズの定理の公式に当てはめる
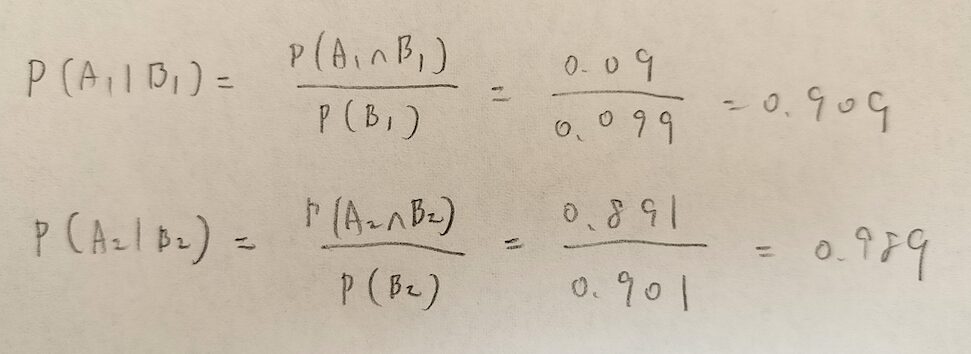
このようになりました。
(1)陽性反応が出たときに感染している確率→0.909で約91%
(2)陰性反応が出たときに感染していない確率→0.989で約99%となりました。
つまりこの検査キットの性能的には(2)の方が良いとわかりました。
今の世の中にとって必要な問題だと思いました。
このように、この本には具体的な問題が多く載っているので本当におすすめです。最後にこの記事で紹介した書籍を一覧として掲載しておきます。
アクチュアリー数学の統計部分の指定教材。到達点は統計検定1級の統計数理には届かない(と感じる)ものの、マセマの『確率統計キャンパスゼミ』からスムーズに接続できます。本記事中の表頭や表側という言葉は本書にのみ登場しており、意外と知られていない統計学の知識も学べます。
統計検定1級の統計数理合格のために最も指示を得ている本です。2023年の統計検定1級の統計応用の理工学では数理寄りの問題も多く、この本の重要性はこれからも高まっていくでしょう。とにかく演習問題の質が素晴らしいです。問題が難しかった2015年頃の問題にも対応しています。
個人的には現在の統計検定1級で最も重宝すると考えている本です。上の本の欠点であった統計応用部分の記述が抽象的に感じるところを具体例を用いた問題を多用することによって、わかりやすさが増しています。回帰分析以降の章はとても素晴らしく、もっと早く出版されていればなあと思うほど素晴らしい本です。